Bakhvalov-Shishkin网格上求解边界层问题的差分进化算法

摘要/Abstract

摘要：

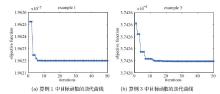
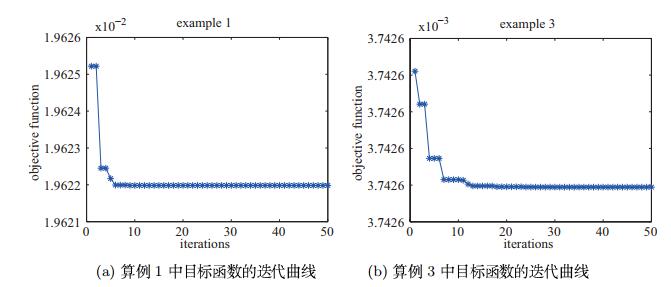
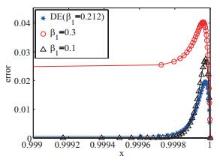
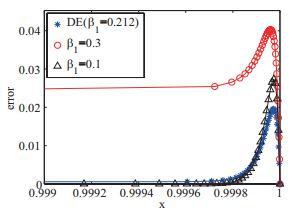
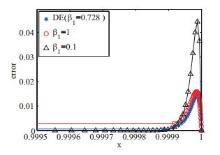
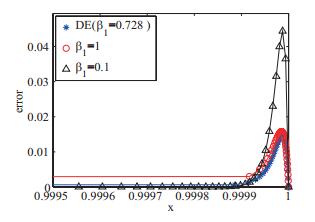
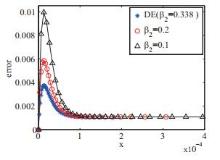
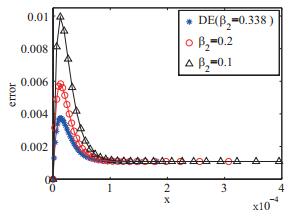
该文在Bakhvalov-Shishkin网格上求解具有左边界层或右边界层的对流扩散方程，并采用差分进化算法对Bakhvalov-Shishkin网格中的参数进行优化，获得了该网格上具有最优精度的数值解.对三个算例进行了数值模拟，数值结果表明：采用差分进化算法求解具有较高的计算精度和收敛性，特别是边界层的数值解精度明显优于选择固定网格参数时的结果.

关键词: 边界层, Bakhvalov-Shishkin网格, 差分进化算法, 网格参数

Abstract:

In this paper, the convection-diffusion equation with left boundary layer or right boundary layer is solved on Bakhvalov-Shishkin mesh. The parameter in Bakhvalov-Shishkin mesh is optimized by differential evolution algorithm, and we obtain numerical solution with optimal accuracy on Bakhvalov-Shishkin mesh. Three numerical examples are simulated, and the numerical results show that the differential evolution algorithm is accurate and convergence. Especially, the numerical solution accuracy of the boundary layer is obviously better than that of fixed mesh parameters.

Key words: Boundary layer, Bakhvalov-Shishkin mesh, Differential evolution algorithm, Mesh parameter

中图分类号:

O241

周琴,程立正. Bakhvalov-Shishkin网格上求解边界层问题的差分进化算法[J]. 数学物理学报, 2021, 41(1): 245-253.

Qin Zhou,Lizheng Cheng. Differential Evolution Algorithms for Boundary Layer Problems on Bakhvalov-Shishkin Mesh[J]. Acta mathematica scientia,Series A, 2021, 41(1): 245-253.

图/表 10

表 1

表 2

表 3

图 1

表 4

表 5

表 6

图 2

图 3

图 4

参考文献 18

1	Linβ T . Layer-adapted meshes for convection-diffusion problems. Comput Methods Appl Mech Engrg, 2003, 192: 1061- 1105 doi: 10.1016/S0045-7825(02)00630-8
2	Zahra W K , Van D M . Discrete spline solution of singularly perturbed problem with two small parameters on a Shishkin-type mesh. Computational Mathematics and Modeling, 2018, 29 (3): 367- 381 doi: 10.1007/s10598-018-9416-3
3	Brdar M , Zarin H . A singularly perturbed problem with two parameters on a Bakhvalov-type mesh. Journal of Computational and Applied Mathematics, 2016, 292: 307- 319 doi: 10.1016/j.cam.2015.07.011
4	Cen Z , Chen J , Xi L . A second-order hybrid finite difference scheme for a system of coupled singularly perturbed initial value problems. Journal of Computational and Applied Mathematics, 2010, 234 (12): 3445- 3457
5	周琴, 杨银. 求解二阶双曲型方程的自适应网格方法. 数学物理学报, 2019, 39A (4): 942- 950 doi: 10.3969/j.issn.1003-3998.2019.04.021
	Zhou Q , Yang Y . Adaptive mesh method for solving a second-order hyperbolic equation. Acta Math Sci, 2019, 39A (4): 942- 950 doi: 10.3969/j.issn.1003-3998.2019.04.021
6	Linβ T , Radojev G , Zarin H . Approximation of singularly perturbed reaction-diffusion problems by quadratic-splines. Numerical Algorithms, 2012, 61 (1): 35- 55 doi: 10.1007/s11075-011-9529-7
7	Shakti D , Mohapatra J . Layer-adapted meshes for parameterized singular perturbation problem. Procedia Engineering, 2015, 127: 539- 544 doi: 10.1016/j.proeng.2015.11.342
8	Yang J M . Improved uniform convergence of a finite difference approximation to a kind of singularly perturbed problems. Journal of Zhejiang University (Science Edition), 2013, 40 (2): 136- 139
9	Chen Y P . Uniform convergence analysis of finite difference approximations for singular perturbation problems on an adapted grid. Advances in Computational Mathematics, 2006, 24 (1): 197- 212
10	Zhou Q , Chen Y P , Yang Y . Two improved algorithms and implementation for a singularly perturbed problem on moving meshes. Journal of Systems Science and Complexity, 2011, 24 (6): 1232- 1240 doi: 10.1007/s11424-011-8138-9
11	Yin Y , Zhu P , Wang B . Analysis of a streamline-diffusion finite element method on Bakhvalov-Shishkin mesh for singularly perturbed problem. Numerical Mathematics:Theory, Methods and Applications, 2017, 10 (1): 44- 64
12	Roos H G , Linβ T . Sufficient conditions for uniform convergence on layer-adapted grids. Computing, 1999, 63 (1): 27- 45 doi: 10.1007/s006070050049
13	周琴. 一类奇异摄动问题差分格式的一致收敛性分析. 湖南工程学院学报(自然科学版), 2009, 19 (3): 34- 36
	Zhou Q . Analysis of uniform convergence for difference scheme of a singularly perturbed problem. Journal of Hunan Institute of Engineering(Natural Science Edition), 2009, 19 (3): 34- 36
14	江山, 孙美玲. 多尺度有限元结合Bakhvalov-Shishkin网格法高效处理边界层问题的研究. 浙江大学学报(理学版), 2015, 42 (2): 142- 146
	Jiang S , Sun M L . Combining the multiscale finite element and Bakhvalov-Shishkin grid to solve the boundary layer problems. Journal of Zhejiang University(Science Edition), 2015, 42 (2): 142- 146
15	Storn R , Price K . Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization, 1997, 11 (4): 341- 359
16	魏文红, 王甲海, 陶铭. 基于泛化反向学习的多目标约束差分进化算法. 计算机研究与发展, 2016, 53 (6): 1410- 1421
	Wei W H , Wang J H , Tao M . Multi-objective constrained differential evolution using generalized opposition-based learning. Journal of Computer Research and Development, 2016, 53 (6): 1410- 1421
17	朱李楠, 王万良, 沈国江. 基于改进差分进化算法的云制造资源优化组合方法. 计算机集成制造系统, 2017, 1: 203- 214
	Zhu L N , Wang W L , Shen G J . Resource optimization combination method based on improved differential evolution algorithm for cloud manufacturing. Computer Integrated Manufacturing Systems, 2017, 1: 203- 214
18	刘利斌, 隆广庆, 上官珍萍. 差分进化与有理谱方法求解奇异摄动问题. 计算机工程与应用, 2018, 54 (17): 225- 230
	Liu L B , Long G Q , Shangguan Z P . Differential evolution and rational spectral methods for singularly perturbed problems. Computer Engineering and Applications, 2018, 54 (17): 225- 230

ε	N = 32		N = 64		N = 128		N = 256
	误差	β₁	误差	β₁	误差	β₁	误差	β₁
10^-2	3.337E-02	0.269	1.766E-02	0.278	9.068E-03	0.296	4.589E-03	0.293
10^-3	3.578E-02	0.213	1.861E-02	0.255	9.468E-03	0.279	4.774E-03	0.282
10^-4	3.664E-02	0.211	1.896E-02	0.245	9.577E-03	0.265	4.808E-03	0.275
10^-5	3.839E-02	0.173	1.962E-02	0.212	9.778E-03	0.238	4.857E-03	0.261
10^-6	4.023E-02	0.156	2.062E-02	0.183	1.017E-02	0.211	4.986E-03	0.234

ε	N = 32		N = 64		N = 128		N = 256
	误差	β₁	误差	β₁	误差	β₁	误差	β₁
10^-2	2.646E-02	0.842	1.403E-02	0.797	7.218E-03	0.837	3.657E-03	0.826
10^-3	2.790E-02	0.711	1.463E-02	0.729	7.447E-03	0.769	3.749E-03	0.806
10^-4	2.808E-02	0.710	1.471E-02	0.728	7.483E-03	0.768	3.765E-03	0.790
10^-5	2.810E-02	0.709	1.472E-02	0.728	7.487E-03	0.768	3.766E-03	0.790
10^-6	2.810E-02	0.709	1.472E-02	0.728	7.487E-03	0.768	3.767E-03	0.790

ε	N = 32		N = 64		N = 128		N = 256
	误差	β₂	误差	β₂	误差	β₂	误差	β₂
10^-2	5.773E-03	0.441	2.879E-03	0.446	1.393E-03	0.430	6.534E-04	0.397
10^-3	6.997E-03	0.345	3.638E-03	0.357	1.851E-03	0.364	9.320E-04	0.368
10^-4	7.154E-03	0.330	3.733E-03	0.340	1.907E-03	0.346	9.636E-04	0.350
10^-5	7.172E-03	0.328	3.743E-03	0.338	1.913E-03	0.344	9.670E-04	0.347
10^-6	7.173E-03	0.328	3.744E-03	0.338	1.914E-03	0.344	9.673E-04	0.347

网格参数选取	ε = 10^-2		ε = 10^-5
	N = 64	N = 128	N = 64	N = 128
差分进化算法	1.766E-02	9.068E-03	1.962E-02	9.778E-03
β₁ = 2/3	2.486E-02	1.372E-02	3.956E+00	1.012E+00
β₁ = 0.3	1.769E-02	9.075E-03	4.028E-02	1.185E-02
β₁ = 0.1	2.676E-02	1.453E-02	2.734E-02	1.481E-02

网格参数选取	ε = 10^-2		ε = 10^-5
	N = 64	N = 128	N = 64	N = 128
差分进化算法	1.403E-02	7.218E-03	1.472E-02	7.487E-03
β₁ = 1	1.441E-02	7.411E-03	1.580E-02	7.983E-03
β₁ = 0.3	2.085E-02	1.116E-02	2.123E-02	1.135E-02
β₁ = 0.1	4.362E-02	2.522E-02	4.441E-02	2.565E-02