含分数阶 $p$-Laplacian 算子基尔霍夫方程解的存在性及其渐近行为

摘要/Abstract

参考文献 31

Metrics

摘要：

该文主要考虑一类含分数阶 $p$ -Laplacian 算子基尔霍夫型方程正规化解的存在性和渐近行为. 利用能量估计技巧, 当 $q\in (p,\ p+\frac{2sp^2}{N})$ 时, 该文得到了含分数阶 $p$ -Laplacian 算子基尔霍夫型方程正规化解的存在性与非线性项指数 $q$ 和预定值 $c$ (其中 $\int_{\mathbb{R}^N}|u|^p{\rm d}x=c^p$ ) 的一个完整的分类. 当 $q\geq p+\frac{2sp^2}{N}$ 时, 该文得到了方程山路型正规化解的存在性. 进一步探讨了正规化解关于 $c$ 的渐近行为.

关键词: 基尔霍夫方程, 正规化解, 存在性, 渐近行为

Abstract:

In this paper, we are interested in the existence of normalized solutions for some fractional Kirchhoff equations with $p$ -Laplacian operator. For the existence and nonexistence of normalized solutions, using the method of energy estimates, we give a complete classification with respect to nonlinear term exponent $q$ and an explicit threshold value of $c$ (with $\int_{\mathbb{R}^N}|u|^p{\rm d}x=c^p$ ) in the range $q\in (p,p+\frac{2sp^2}{N})$ . We also derive some existence of mountain pass type normalized solutions on the $L^2$ manifold in the range $q\geq p+\frac{2sp^2}{N}$ . Furthermore, some asymptotic behaviors with respect to $c$ were also given.

Key words: Kirchhoff equation, normalized solutions, existence, asymptotic behavior

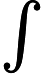
中图分类号:

O175.25

孟笑莹,陆璐. 含分数阶 $p$ -Laplacian 算子基尔霍夫方程解的存在性及其渐近行为[J]. 数学物理学报, 2025, 45(2): 434-449.

Xiaoying Meng,Lu Lu. Existence and Asymptotic Behavior of Solutions for Kirchhoff Equations Involving the Fractional $p$ -Laplacian[J]. Acta mathematica scientia,Series A, 2025, 45(2): 434-449.

[1]	Autuori G, Fiscella A, Pucci P. Stationary Kirchhoff problems involving a fractional elliptic operator and a critical nonlinearity. Nonlinear Anal, 2015, 125: 699-714
[2]	Bellazzini J, Jeanjean L, Luo T J. Existence and instability of standing waves with prescribed norm for a class of Schrödinger-Possion equations. Proc Lond Math Soc, 2013, 107(3): 303-339
[3]	Berestycki H, Lions P L. Nonlinear scalar field equations I. Existence of a ground state. Arch Ration Mech Anal, 1983, 82(4): 313-345
[4]	Caponi M, Pucci P. Existence theorems for entire solutions of stationary Kirchhoff fractional $p$ -Laplacian equations. Ann Mat Pur Appl, 2016, 195(6): 2099-2129
[5]	Fan X L, Zhao Y Z, Zhao D. Compact imbedding theorems with symmetry of Strauss-Lions type for the space $W^{1,p(x)}(\Omega)$ . J Math Analysis Appl, 2001, 255(1): 333-348
[6]	Frank R L, Lenzmann E, Silvestre L. Uniqueness of radial solutions for the fractional Laplacian. Commun Pure Appl Math, 2015, 69(9): 1671-1726
[7]	Frank R L, Seiringer R. Non-linear ground state representations and sharp Hardy inequalities. J Fun Anal, 2008, 255(12): 3407-3430
[8]	古龙江, 孙志禹, 曾小雨. 一类约束变分问题极小元的存在性及其集中行为. 数学物理学报, 2017, 37A(3): 510-518
	Gu L J, Sun Z Y, Zeng X Y. The existence of minimizers for a class of constrained variational problem with its concentration behavior. Acta Math Sci, 2017, 37A(3): 510-518
[9]	郭合林, 王云波. 关于一个约束变分问题的注记. 数学物理学报, 2017, 37A(6): 1125-1128
	Guo H L, Wang Y B. A remark on a constrained variational problem. Acta Math Sci, 2017, 37A(6): 1125-1128
[10]	Guo H L, Zhang Y M, Zhou H S. Blow-up solutions for a Kirchhoff type elliptic equation with trapping potential. Comm Pure Appl Anal, 2018, 17: 1875-1897
[11]	He Q H, Lv Z Y, Zhang Y M, et al. Existence and blow up behavior of positive normalized solution to the Kirchhoff equation with general nonlinearities: Mass super-critical case. J Differ Equ, 2023, 356: 375-406
[12]	He X M, Zou W M. Existence and concentration behavior of positive solutions for a Kirchhoff equation in $\mathbb{R}^3$ . J Differ Equ, 2012, 2: 1813-1834
[13]	He Y, Li G B, Peng S J. Concentrating bound states for Kirchhoff type problems in $\mathbb{R}^3$ involving critical Sobolev exponents. Adv Nonlinear Stud, 2014, 14: 483-510
[14]	Huang X M, Zhang Y M. Existence and uniqueness of minimizers for $L^2$ constrained problems related to fractional Kirchhoff equation. Math Methods Appl Sci, 2020, 43(15): 8763-8775
[15]	Jeanjean L. Existence of solutions with prescribed norm for semilinear elliptic equations. Nonlinear Anal, 1997, 28(10): 1633-1659
[16]	Jeanjean L, Luo T J. Sharp nonexistence results of prescribed $L^2$ -norm solutions for some class of Schrödinger-Possion and qusi-linear equations. Z Angew Math Phys, 2013, 64(4): 937-954
[17]	Kirchhoff G. Mechanik. Leipzig: Teubner, 1883
[18]	Li G B, Niu Y H. The existence and local uniqueness of multi-peak positive solutions to a class of Kirchhoff equation. Acta Math Sci, 2020, 40B(1): 90-112
[19]	Li G B, Yan S S. Eigenvalue problems for quasilinear elliptic equations on $\mathbb{R}^N$ . Commu Partial Differ Equ, 1989, 14(8/9): 1291-1314
[20]	李容星, 王文清, 曾小雨. 带椭球势阱的 Kirchhoff 型方程的变分问题. 数学物理学报, 2019, 39A(6): 1323-1333
	Li R X, Wang W Q, Zeng X Y. A constrained variational problem of Kirchhoff type equation with ellipsoid-shaped potential. Acta Math Sci, 2019, 39A(6): 1323-1333
[21]	Liu Z. Multiple normalized solutions for Choquard equation involving Kirchhoff type perturbation. Top Meth Nonlinear Ana, 2019, 54(1): 297-319
[22]	柳志德, 王征平. 非线性 Kirchhoff 型椭圆方程的最低能量解. 数学物理学报, 2019, 39A(2): 264-276
	Liu Z D, Wang Z P. Least energy solution for nonlinear Kirchhoff type elliptic equation. Acta Math Sci, 2019, 39A(2): 264-276
[23]	Liu Z S, Squassina M, Zhang J J. Ground states for fractional Kirchhoff equaitons with critical nonlinearity in low dimension. Nonlinear Differ Equ Appl, 2017, 24: Article 50
[24]	Mao A M, Chang H J. Kirchhoff type problems in $\mathbb{R}^N$ with radial potentials and locally Lipschitz functional. Applied Math Letters, 2016, 62: 49-54
[25]	Nezza E D, Palatucci G, Valdinoci E. Hitchhiker's guide to the fractional Sobolev spaces. Bulletin des Sciences Mathématiques, 2012, 136(5): 521-573
[26]	Pucci P, Saldi S. Critical stationary Kirchhoff equations in $\mathbb{R}^N$ involving nonlocal operators. Rev Mat Iberoam, 2016, 32(1): 1-22
[27]	Pucci P, Xiang M Q, Zhang B L. Multiple solutions for nonhomogeneous Schrödinger-Kirchhoff equations involving the fractional $p$ -Laplacian in $\mathbb{R}^N$ . Calc Var Partial Differ Equ, 2015, 54: 2785-2806
[28]	Wang Z Z, Zeng X Y, Zhang Y M. Multi-peak solutions of Kirchhoff equations involving subcritical or critical Sobolev exponents. Math Meth Applied Sci, 2020, 43(8): 5151-5161
[29]	许诗敏, 王春花. Kirchhoff 方程单峰解的局部唯一性. 数学物理学报, 2020, 40A(2): 432-440
	Xu S M, Wang C H. Local uniqueness of a single peak solution of a subcritical Kirchhoff problem in $\mathbb{R}^3$ . Acta Math Sci, 2020, 40A(2): 432-440
[30]	Ye H Y. The sharp existence of constrained minimizers for a class of nonlinear Kirchhoff equations. Math Meth Applied Sci, 2015, 38(13): 2663-2679
[31]	Zeng X Y, Zhang Y M. Existence and uniqueness of normalized solutions for the Kirchhoff equation. Applied Math Letters, 2017, 74: 52-59

Just accepted

Online first

Just accepted

Online first

Viewed

Full text

	From	local

	Times	73
	Rate	100%

Abstract

Just accepted	Online first	Issue

0	0	38

From	Others	local

Times	37	1
Rate	97%	3%

Cited

Web of Science	Crossref	ScienceDirect	Search for Citations in Google Scholar >>


This page requires you have already subscribed to WoS.

Shared

Discussed