基于拟共形理论的分数阶多尺度微分同胚图像配准

摘要/Abstract

摘要：

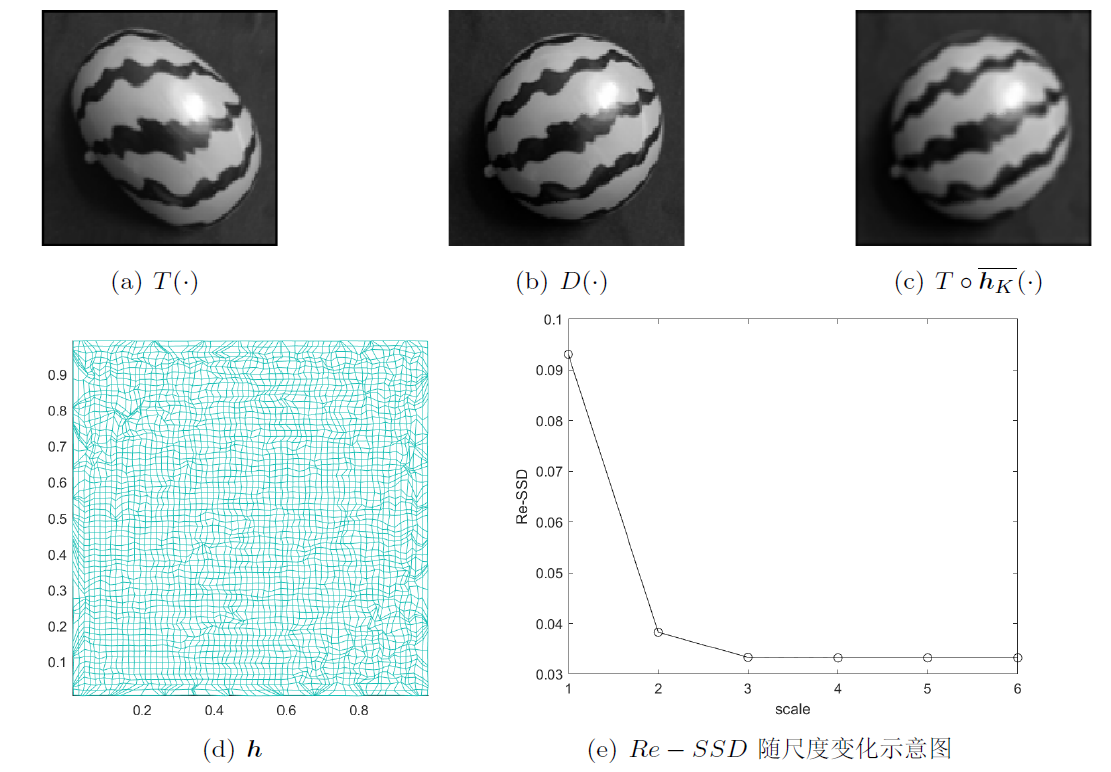
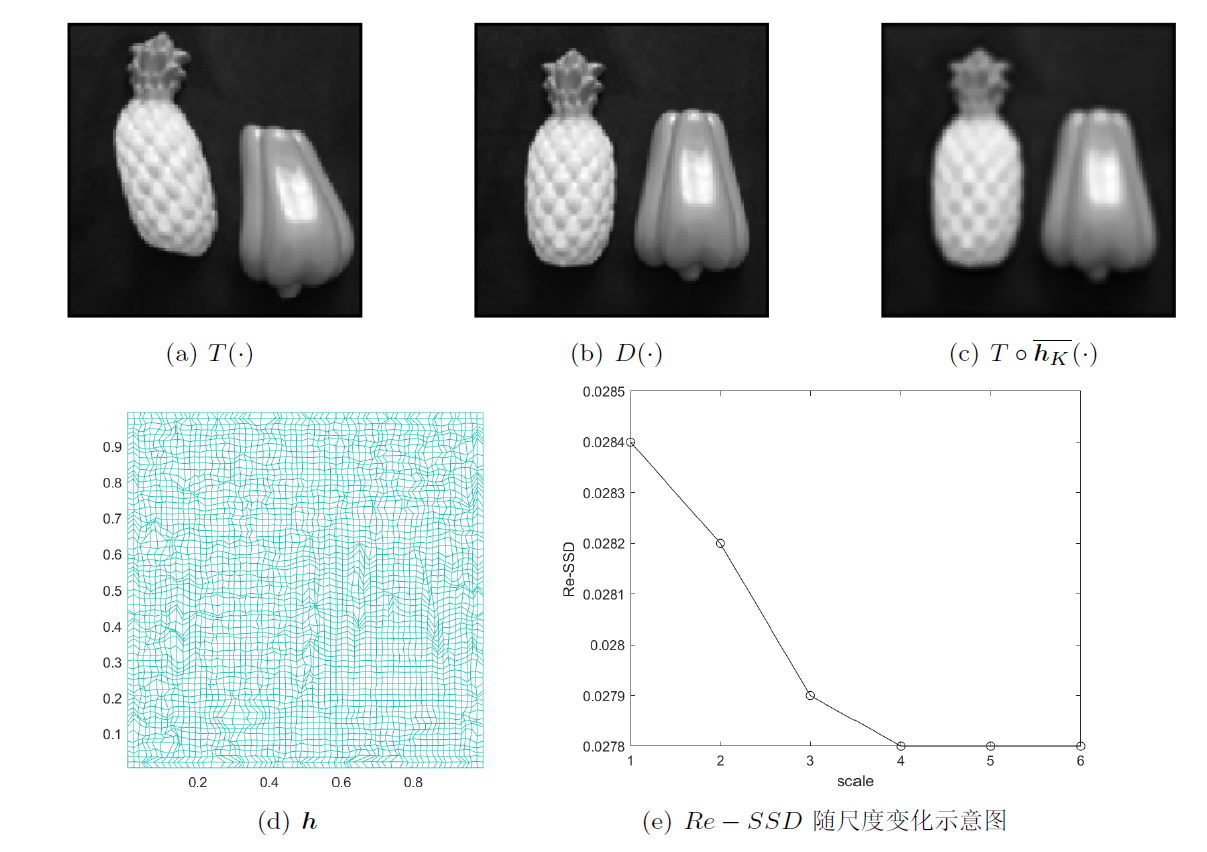
图像配准领域存在着两大挑战: (1) 网格重叠现象; (2) 贪婪配准问题不适定. 针对这两大挑战, 该文提出了一个基于拟共形理论的多尺度分数阶微分同胚图像配准模型, 该模型在无网格重叠及先验正则项的前提下, 得到了相似性度量泛函的一个光滑极小值点. 此外, 该文证明了所提模型解的存在性及多尺度方法的收敛性, 并通过数值实验验证了所提算法能有效避免网格重叠并得到较好的配准结果.

关键词: 微分同胚, 多尺度, 拟共形理论, 分数阶, 图像配准

Abstract:

Two significant challenges relating to image registration include the issue of mesh folding and the unresolved problem of greedy registration. To tackle these challenges, a multi-scale approach for diffeomorphic image registration model with fractional-order regularization based on quasiconformal theory is proposed in this paper. It employs fractional-order differential to achieve a smooth energy functional minima without mesh folding and a priori regular terms. Furthermore, the existence of solution for the proposed model and the convergence of the multi-scale approach are proved. And numerical tests are performed to demonstrate that the proposed algorithm effectively eliminates mesh folding and generates superior registration results.

Key words: Diffeomorphic, Multi-scale, Quasiconformal theory, Fractional-order regularization, Image registration

中图分类号:

TP391

王慧楠, 韩欢. 基于拟共形理论的分数阶多尺度微分同胚图像配准[J]. 数学物理学报, 2024, 44(6): 1665-1688.

Wang Huinan, Han Huan. Multi-Scale Approach for Diffeomorphic Image Registration with Fractional-Order Regularization Based on Quasiconformal Theory[J]. Acta mathematica scientia,Series A, 2024, 44(6): 1665-1688.

图/表 18

图1

图2

图3

图4

图5

表1

图6

图7

图8

图9

表2

图10

图11

图12

图13

图14

图15

表3

参考文献 41

[1]	Brown L G. A survey of image registration techniques. ACM Computing Surveys, 1992, 24(4): 325-376
[2]	Lester H, Arridge S R. A survey of hierarchical non-linear medical image registration. Pattern Recognition, 1998, 32(1): 129-149
[3]	Maintz J B, Viergever M A. A survey of medical image registration. Medical Image Analysis, 1998, 2(1): 1-36 doi: 10.1016/s1361-8415(01)80026-8 pmid: 10638851
[4]	Mohamed A, Zacharaki E I, Shen D, et al. Deformable registration of brain tumor images via a statistical model of tumor-induced deformation. Medical Image Analysis, 2006, 10(5): 752-763 pmid: 16860588
[5]	Sotiras A, Davatzikos C, Paragios N. Deformable medical image registration: a survey. IEEE Transactions on Medical Imaging, 2013, 32(7): 1153-1190 doi: 10.1109/TMI.2013.2265603 pmid: 23739795
[6]	Zitova B, Flusser J. Image registration methods: a survey. Image and Vision Computing, 2003, 21(11): 977-1000
[7]	Budhiraja A, Dupuis P, Maroulas V. Large deviations for stochastic flows of diffeomorphisms. Bernoulli, 2010, 16(1): 234-257
[8]	Chen Y M, Shi J L, Rao M, et al. Deformable multi-modal image registration by maximizing rényi's statistical dependence measure. Inverse Problems and Imaging, 2015, 9(1): Article 79
[9]	Chen Y M, Ye X J. Inverse consistent deformable image registration. The Legacy of Auadi Ramakrishnan in the Mathematical Sciences, 2010: 419-440
[10]	Yang X M, Shen C M, Li F, et al. A combination of the total variation filter and a fourth-order filter for image registration. Mathematical Problems in Engineering, 2015, 1: 235134
[11]	Zhang D P, Chen K. A novel diffeomorphic model for image registration and its algorithm. Journal of Mathematical Imaging and Vision, 2018, 60: 1261-1283
[12]	Zhang J P, Chen K. Variational image registration by a total fractional-order variation model. Journal of Computational Physics, 2015, 293: 442-461
[13]	Zhang J, Chen K, Yu B. An improved discontinuity-preserving image registration model and its fast algorithm. Applied Mathematical Modelling, 2016, 40(23/24): 10740-10759
[14]	Zhang J, Chen K, Yu B. A novel high-order functional based image registration model with inequality constraint. Computers and Mathematics with Applications, 2016, 72(12): 2887-2899
[15]	Machado J T, Kiryakova V, Mainardi F. Recent history of fractional calculus. Communications in Nonlinear Science and Numerical Simulation, 2011, 16(3): 1140-1153
[16]	Abdeljawad T. On conformable fractional calculus. Journal of Computational and Applied Mathematics, 2015, 279: 57-66
[17]	Han H. A variational model with fractional-order regularization term arising in registration of diffusion tensor image. Inverse Problems and Imaging, 2018, 12(6): 1263-1291
[18]	Metzler R, Klafter J. The random walk's guide to anomalous diffusion: a fractional dynamics approach. Physics Reports, 2000, 339(1): 1-77
[19]	Han H, Wang Z Q. An alternating direction implicit scheme of a fractional-order diffusion tensor image registration model. Applied Mathematics and Computation, 2019, 356: 105-118
[20]	Haber E, Modersitzki J. Numerical methods for volume preserving image registration. Inverse Problems, 2004, 20(5): 1621-1638
[21]	Lui L M, Thiruvenkadam S, Wang Y L, et al. Optimized conformal surface registration with shape-based landmark matching. SIAM Journal on Imaging Sciences, 2010, 3(1): 52-78
[22]	Lui L M, Wong T W, Zeng W, et al. Optimization of surface registrations using Beltrami holomorphic flow. Journal of Scientific Computing, 2012, 50(3): 557-585
[23]	Lam K C, Lui L M. Landmark and intensity-based registration with large deformations via quasi-conformal maps. SIAM Journal on Imaging Sciences, 2014, 7(4): 2364-2392
[24]	Han H, Wang Z P, Zhang Y M. Multi-scale approach for two-dimensional diffeomorphic image registration. Multiscale Modeling and Simulation, 2021, 19(4): 1538-1572
[25]	Lehto O, Virtanen K I. Quasiconformal Mappings in the Plane. New York: Springer, 1973
[26]	Gardiner F P, Lakic N. Quasiconformal Teichmuller Theory. Providence RI: American Mathematical Society, 2000
[27]	Ahlfors L V. Lectures on Quasiconformal Mappings. Providence RI: American Mathematical Society, 2006
[28]	Aubert G, Kornprobst P, Aubert G. Mathematical Problems in Image Processing:Partial Differential Equations and the Calculus of Variations. New York: Springer, 2006
[29]	Han H, Wang Z P. A diffeomorphic image registration model with fractional-order regularization and Cauchy-Riemann constraint. SIAM Journal on Imaging Sciences, 2020, 13(3): 1240-1271
[30]	Hou T L, Tang T, Yang J. Numerical analysis of fully discretized Crank-Nicolson scheme for fractional-in-space Allen-Cahn equations. Journal of Scientific Computing, 2017, 72: 1214-1231
[31]	Tian W Y, Zhou H, Deng W H. A class of second order difference approximations for solving space fractional diffusion equations. Mathematics of Computation, 2015, 84(294): 1703-1727
[32]	Barrett R, Berry M, Chan T F, et al. Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods. Philadelphia: Society for Industrial and Applied Mathematics, 1994
[33]	Paige C C, Saunders M A. Solution of sparse indefinite systems of linear equations. SIAM journal on numerical analysis, 1975, 12(4): 617-629
[34]	Burger M, Modersitzki J, Ruthotto L. A hyperelastic regularization energy for image registration. SIAM Journal on Scientific Computing, 2013, 35(1): 132-148
[35]	Kelley C T. Iterative Methods for Optimization. Philadelphia: Society for Industrial and Applied Mathematics, 1999
[36]	Nocedal J, Wright S J. Numerical Optimization. Berlin: Springer, 2006
[37]	Sun W, Yuan Y X. Optimization Theory and Methods:Nonlinear Programming. Berlin: Springer, 2006
[38]	Modersitzki J. FAIR: Flexible Algorithms for Image Registration. Philadelphia: Society for Industrial and Applied Mathematics, 2009
[39]	Pock T, Urschler M, Zach C, et al. A duality based algorithm for TV-L1-optical-flow image registration//International Conference on Medical Image Computing and Computer-Assisted Intervention. Berlin: Springer, 2007: 511-518
[40]	Kroon D J. Multimodality Non-rigid Demon Algorithm Image Registration. MatlabCentral. http://www.mathworks.com/matlabCentral/fileexchange/21451-multimodality-non-rigid-demon-algorithm-image-registration, 2008
[41]	Kroon D J, Slump C H. MRI modalitiy transformation in demon registration//IEEE International Symposium on Biomedical Imaging: From Nano to Macro. Boston: IEEE, 2009: 963-966