引言
高时空分辨率MRI的实现依赖基于欠采样的信号重建技术,特别是在欠采样率较高时,需要使用特殊的数据采集策略和相应的重建算法.随着磁共振技术的发展,越来越多的方法可用以提高成像效率.例如基于SENSE(Sensitivity encoding)[15]和GRAPPA(GeneRalized Autocalibrating Partially Parallel Acquisitions)[16]的并行成像方法已被广泛应用于临床.但是,并行成像技术的性能取决于线圈设计,并且为了保证图像的信噪比,在一定程度上限制了高欠采倍数的使用.而基于k空间和时间相关(k-t)的k-t BLAST/k-t SENSE和k-t GRAPPA[17, 18]等快速MRI方法,则是利用相邻帧之间的冗余信息进行图像重建.并行成像与压缩感知(Compressed Sensing,CS)[19]技术的结合,可以进一步提高稀疏采样下的重建质量.尤其是在动态MRI中,由于图像序列比静态图像[20]具有更强的压缩性,所以在诸如傅里叶变换域、全变分(Total Variation,TV)域和小波域等某些变换域中可以被更稀疏地表示,CS的优势能够进一步发挥,实现更高的欠采样率.笛卡尔采样轨迹和非笛卡尔采样轨迹是两种不同的数据采集方式,其中,非笛卡尔采集可以更大程度地利用磁共振硬件能力,提高采集效率.近年来,研究者已经开发了一系列基于非笛卡尔采样轨迹(如黄金角螺旋轨迹)[21]的数据采集及重建方法,例如时间分辨率加速的约束演化重建(Temporal Resolution Acceleration with Constrained Evolution Reconstruction,TRACER)方法[4]和黄金角径向稀疏并行(Golden-Angle Radial Sparse Parallel,GRASP)方法[6].TRACER对一个时间点的欠采样数据加强了图像保真度,并要求与以前的图像帧保持一致,从而实现高空间分辨率;然而由于其基本假设,这种重建方法容易受到运动的影响.GRASP方法综合了径向采样、并行成像和CS的优点,在数据采集过程中对运动不敏感,并且可以实现相对较高的时空分辨率.
在前面提到的重建算法中,CS重建由于可以实现更高的欠采样率,受到广泛关注.基于CS的重建算法理论上是一个l0最小化问题,但因为其求解困难,实际常将它转化为l1最小化问题,并且针对该问题的求解方法已经得到了较好的应用.之所以通过l1最小化求解,是因为它是一个相对易于处理的凸优化问题,并且当欠采样率适中时,它的解等价于l0最小化的解.对于三维动态MRI,信息更具有冗余空间,高欠采恢复重建可以有效提高重建图像的时空分辨率.而基于l0最小化约束的CS则更有潜力在较高的欠采样率下保持良好的图像质量和时间保真度[22, 23].在具体采集策略上,使用黄金角变密度螺旋轨迹采样具有较高的运动不敏感性和采集效率,相比于径向或者随机笛卡尔采样,使用变密度螺旋轨迹采集形成的混叠伪影具有更强的不相干性[24],可以提高CS重建的性能.
本文将黄金角变密度螺旋轨迹的信号采集、基于l0最小化的CS重建和并行成像技术相结合,对肝脏DCE-MRI在时空分辨率、时间域和空间域的图像保真度,以及运动不敏感性等方面进行了研究,为三维动态MRI的进一步应用做了初步尝试.
1 理论与实验
1.1 基于黄金角变密度螺旋轨迹的MRI数据采集
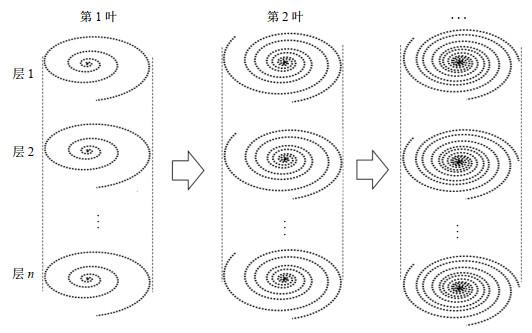
在临床应用中,笛卡尔轨迹由于在重建方面的鲁棒性和简单性被广泛使用,但它们的采集效率较低.而对于高时空分辨率的MRI,由于需要在相对较短的时间内获取大量的数据,所以数据采集效率至关重要,因此常使用非笛卡尔采样轨迹.螺旋轨迹是一种非笛卡尔采集方式,通常从k空间中心开始,以螺旋状的方式不断向外填充,而变密度螺旋(Variable Density Spiral,VDS)轨迹对k空间中心区域采样更密集,对边缘区域采样更稀疏,使得对决定着图像对比度的k空间中心部分的低频信号进行了充分采集,大大提高了图像的对比度.交错螺旋轨迹[25]由几条具有不同起始角度的螺旋轨迹组合而成,因为增加了在k空间中的旋转圈数,所以有助于提高图像的分辨率.
图1
图1
黄金角变密度螺旋叠加的采集策略.首先沿着层方向进行采集;所有层保持固定角度的螺旋交错叶采样,在时间维度,旋转黄金角度继续进行螺旋交错叶采样
Fig.1
The acquisition strategy of stack of golden angle variable density spiral. The acquisition loop is in slice direction first. After spiral interleaves with a fixed angle being sampled in all the slices, in the time dimension, the next spiral interleaves which are rotated by a golden angle will be sampled
1.2 基于并行成像和同伦l0最小化的CS的图像重建
图2
图2
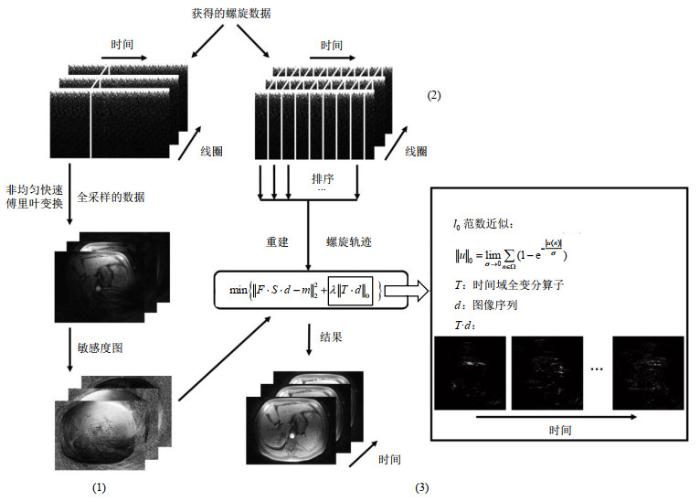
基于l0最小化方法的图像重建过程.(1)中,从随时间推移的全采样螺旋数据中得到敏感度图;(2)中,将获得的k空间数据排序成一些欠采样的组;(3)中,针对中间的最小化问题,将排序后的数据重建为动态图像序列,在右边黑色框中l0范数的近似被表示成一个极限,并且图中展示出了稀疏变换(时间全变分)后的图像序列
Fig.2
The reconstruction process of the proposed method with l0 minimization. In part (1), sensitivity maps are acquired from the full-sampled spiral data through time. In part (2), the acquired k-space data is sorted into several undersampled groups. In part (3), the sorted data is reconstructed to dynamic image series with the minimization problem in the middle. In the right black box, the approximation of l0 norm is expressed with a limitation, and the image series after the sparse transform (temporal total variation) are shown
流程说明如下:
(1)使用标准的平方和技术,利用完全采样的螺旋交错叶计算得到线圈敏感度图.
(2)将所有以螺旋轨迹采集的k空间数据进行分组,每组对应的k空间采集轨迹的数量相同,具体数量根据要求的时间分辨率来确定.时间分辨率越高,每组所放置的k空间的轨迹数目就越少.
(3)按照排序后的分组进行时间序列图像重建,重建的公式如下:
(1) 式中,d为
(2) 式中u表示一个变量或指代,用来演示0范数的作用过程,没有实际含义;σ指代一个趋于0的无穷小量;ρ是构造的先验凸泛函;
于是(1)式可以转化为如下的能量泛函最小化问题:
由拉格朗日方程知,(3)式的解需满足:
其中
令:
于是(6)式可以转换成定点形式,并进行下述迭代:
同时,根据(4)式可以得到:
结合(8)式和(9)式,可以使用如下迭代来计算d:
其中:
最后通过使用共轭梯度法得到(11)式中运算过程的中间量Δ.算法对应的流程描述如表 1所示.
表1 基于同伦l0最小化的算法实现
Table 1
| 目标函数: |
| 输入:F –非均匀快速傅里叶变换算子 S –线圈敏感度图 m – k空间测量数据 |
| 输出:d –目标函数的数值近似解 |
| 初始化: |
| 迭代:while |
| while |
使用共轭梯度法求解 end |
| end |
对于(2)式,理论上σ取值越小越好,但实际上,过小的σ值会使函数变得很不光滑,因此会存在许多局部极小值,为防止算法的解陷入某个局部极小值,可以通过选取一个递减的σ序列,引导每次迭代得到的近似解逐步逼近全局最优解[22].
如在DCE-MRI中,如果信号在一个有限的区域变化,并且运动是平滑而缓慢的,则可以使用时域TV算子来创建一个稀疏域,然后结合基于l0范数的CS进行重建,可以精确恢复高度欠采样的数据.
1.3 仿真和人体实验
仿真实验包含一个大圆环、三个大小不同的圆盘,以及大圆盘上的一个正方形组成的运动图像,如后文图 3所示.图像矩阵大小是256×256,正方形结构的大小是3×3.随着时间的变化,大圆盘在环内从右向左移动,模拟成像物体的运动.在大圆盘移动过程中,大圆盘中心的小圆盘的强度也在同时发生变化(模拟血管等信号变化或者脑功能信号变化等).运动过程中的对比增强曲线的设计与主动脉注射造影剂后的强度曲线类似.利用非均匀快速傅里叶变换(NUFFT)算子,我们从数值动态体模中获得了黄金角变密度螺旋k空间数据,一帧的全采样k空间数据由48个交错叶组成,中心的过采样因子是α=2.重建过程中可以选择不同的欠采样率来评估算法的性能.使用该数据测试了三种不同的重建算法:TRACER,l1最小化和本文提出的l0最小化方法.重建过程中,使用2个或4个交错叶来重建一帧,对应的欠采样率是24或12.在空间域中,通过计算每个重建帧的均方误差来评价图像质量.在时间域中,通过绘制小圆盘的强度曲线,并计算由每个重建算法得到的曲线的均方误差来评估时间保真度.
图3
图3
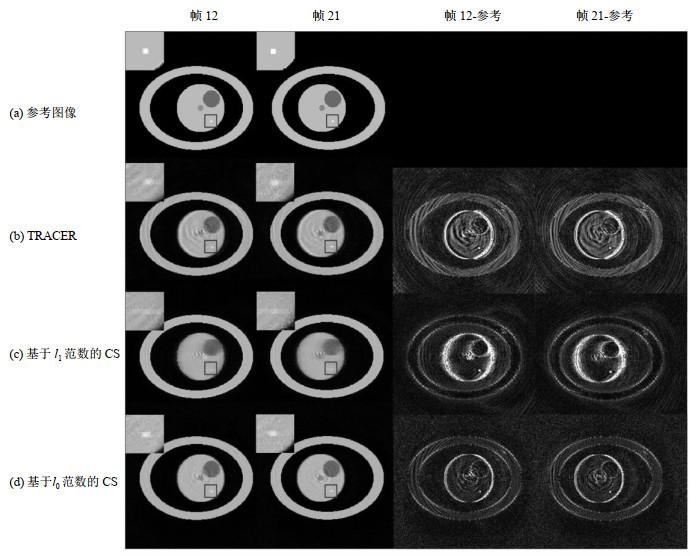
仿真图像的重建效果(1帧有4个交错叶,对应全采集轨迹的48个交错叶,欠采样率为12).四列分别展示帧12、帧21、帧12的差分图和帧21的差分图(7×).(a)图为模拟体模的参考图像,(b)~(d)分别为使用TRACER、基于l1最小化的CS和基于l0最小化的CS方法的重建图像.方框中的区域显示了体模的细节结构,这些被放大并置于每个图像的左上方
Fig.3
Reconstruction results of simulated image (Grouping 4 interleaves for 1 frame, corresponding to 48 interleaves of full sampled track, undersampling rate = 12) and their difference maps (7×) with reference. The four columns show frame 12, frame 21, the difference map of frame 12 and the difference map of frame 21, respectively. Figure (a) shows the reference images of the simulation phantom. Figures (b)~(d) show the reconstruction results using TRACER, CS with l1 minimization and l0 minimization respectively. The boxes indicate the regions of the detailed structure in the phantom, and the regions are zoomed in and placed on the top left side of each image
人体实验中分别对三名志愿者浅呼吸状态下进行了非对比增强的肝脏成像实验,本研究得到了当地机构审查委员会的批准,并在扫描前获得了志愿者的书面同意.采用含8通道射频线圈的GE 3T MR750磁共振扫描仪(GE Healthcare,Waukesha,WI)和具有黄金角变密度螺旋轨迹叠加的三维扰相梯度回波(3D Spoiled Gradient Echo)序列[31].扫描参数是重复时间(Repetition Time,TR)= 5.9 ms,回波时间(Echo Time,TE)= 0.3 ms,视野(Field of View,FOV)= 360×360×160 mm3,平面内分辨率是1.41×1.41 mm2,层内厚度是5 mm.对一帧的全采样k空间数据获得了48个交错叶,并使用高阶匀场来减轻模糊伪影,中心的过采样因子α=2.5,在整个扫描中,每一层的交错叶数目是192个,扫描时间是30 s.使用该数据测试了三种不同的重建算法:TRACER,l1最小化和本文提出的l0最小化方法.重建过程中,使用2个交错叶来重建一帧,对应的欠采样率是24.
2 结果与讨论
2.1 仿真实验结果
图 3显示了欠采样率为12的结果.TRACER重建图像中由运动和欠采样造成的螺旋伪影严重,图像略有模糊.而基于l1和l0最小化的CS重建图像序列中不再存在强度波动,且l0最小化的螺旋伪影相比l1最小化更轻微.在细节结构保存(方框)方面,使用l0最小化得到的结果有着最清晰的边界和最好的定义,计算得出的相对于参考图像的帧的差分图也表明基于l0最小化的CS重建结果是最准确的.
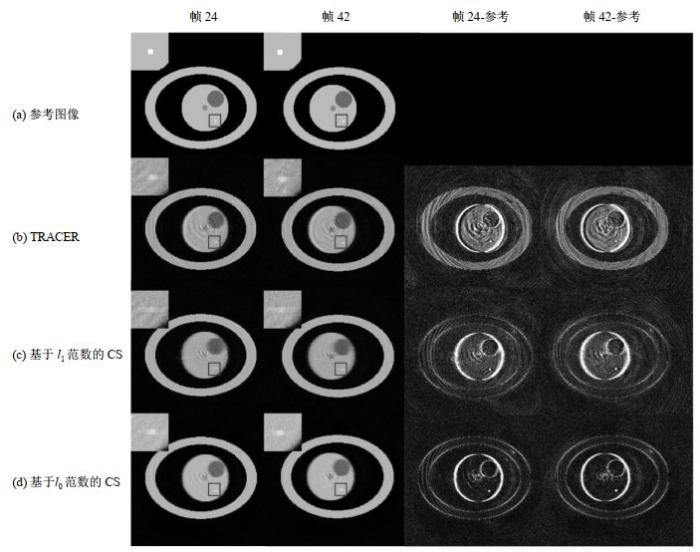
图 4显示了欠采样率为24的重建结果.欠采样率较高时,以牺牲图像质量为代价提高了时间分辨率.在TRACER重建中,螺旋伪影和强度波动比欠采样率为12时更严重.从差分图中可以明显看出基于l1最小化的CS的重建图像的信噪比显著降低.而基于l0最小化的CS的重建结果仍然保持了合理的信噪比和相对较低的伪影水平,并且在细节结构保存方面也仍是三种算法中表现最好的.本实验中,基于l0最小化算法的重建图像在图像质量上显著优于其他两种算法,表明了该算法在欠采样率很高时具有良好的鲁棒性.与TRACER方法相比,l0最小化方法的残差混叠伪影明显更小,并且没有强度波动.与l1最小化方法相比,l0最小化方法的重建图像信噪比高得多.
图4
图4
仿真图像的重建效果(1帧有2个交错叶,对应全采集轨迹的48个交错叶,欠采样率为24).四列分别展示帧24、帧42、帧24的差分图和帧42的差分图(7×).(a)图为模拟体模的参考图像,(b)~(d)分别为使用TRACER,基于l1最小化的CS和基于l0最小化的CS的重建结果.方框中的区域显示了体模的细节结构,这些被放大并置于每个图像的左上方
Fig.4
Reconstruction results of simulated image (Grouping 2 interleaves for 1 frame, corresponding to 48 interleaves of full sampled track, undersampling rate=24) and their difference maps (7×) with reference. The four columns show frame 24, frame 42, the difference map of frame 24 and the difference map (7×) of frame 42 respectively. Figure (a) shows the reference images of the simulation phantom. Figures (b)~(d) show the reconstruction results using TRACER, CS with l1 minimization and l0 minimization respectively. The boxes indicate the regions of the detailed structure in the phantom, and the regions are zoomed in and placed on the top left side of each image
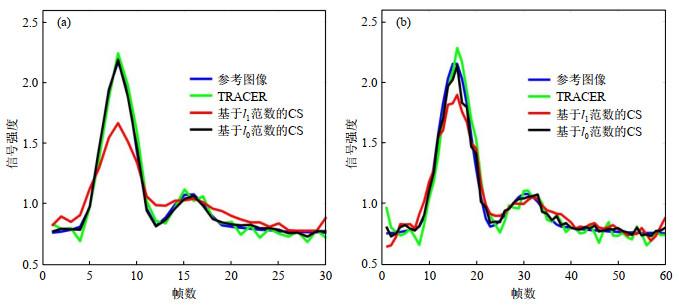
这三种算法中,欠采样率为12时,小圆盘内的时间强度曲线如图 5(a)所示.仿真结果显示,l1最小化的时间强度曲线存在较大的时间模糊.由于强度波动和运动伪影,TRACER的强度曲线有一些噪声,强度波动是TRACER重建的一个不足,虽然在单帧中看不到,但在时间序列成像中表现得很明显,这是由高欠采样率和螺旋混叠伪影的影响而引起的.TRACER曲线和参考曲线之间也存在一个微小的时间延迟(大约0.5帧),而l0最小化的强度曲线与本实验中的参考曲线最一致.欠采样率为24时,小圆盘内对应的时间强度曲线如图 5(b)所示.由于更严重的强度波动和运动伪影,TRACER的强度曲线有更多的噪声,TRACER结果和参考结果之间的时间延迟也更大(大约1帧).l1最小化方法相比于其他两种算法,其对应的曲线中仍然表现出时间模糊,但由于时间分辨率更高,该曲线比欠采样率为12时的曲线更加准确.l0最小化方法在时间域中仍然具有最好的精度.
图5
图5
小圆盘中的模拟信号强度曲线.这些图显示了在固定欠采样率(时间分辨率)下不同算法的性能,(a)和(b)分别显示了12倍欠采样率和24倍欠采样率的结果,蓝色曲线是信号强度曲线的参考,绿色,红色和黑色曲线分别代表TRACER,基于l1最小化的CS和基于l0最小化的CS方法得到的信号强度曲线
Fig.5
The simulated signal intensity curves in the small discs. These figures show the performance of different algorithms in a fixed undersampling rate (temporal resolution). (a) and (b) show the results with 12-fold undersampling rate and 24-fold undersampling rate respectively. The blue curve represents the reference of the signal intensity curve. The green, red, black curves represent the signal intensity curves resulting from TRACER, CS with l1 minimization and l0 minimization respectively
当使用较高的欠采样率时,所有算法重建的图像质量都会下降,但对时间强度曲线有不同的影响.在TRACER重建中,更高的时间分辨率会导致较为严重的时间延迟,强度曲线似乎具有更大的噪声,使得均方误差增加,但强度曲线的整体形状与低时间分辨率时相似.在l1最小化重建中,从高时间分辨率图像中获得的强度曲线比从低时间分辨率图像中得到的强度曲线具有更高的精度,因为更高的时间分辨率减轻了时间模糊,然而,图像质量在很大程度上下降,因为在一个很高的欠采样率下,l1最小化CS不能支持鲁棒重建.在l0最小化重建中,当重建高时间分辨率图像序列时,会导致更严重的采样伪影,使得时间强度曲线精度略有降低,但高时间分辨率情况下的可用点是低分辨率下的两倍,这有利于动态对比增强的模型拟合,图像质量仅略有下降.图 6显示了12倍和24倍欠采样率下三种重建算法的信号强度曲线相对于参考图像的均方误差.
图6
图6
在12倍和24倍欠采样率下小圆盘中重建信号强度曲线相对于参考图像的均方误差(RMSE).分别显示了TRACER,基于l1最小化的CS和基于l0最小化的CS方法的结果
Fig.6
RMSE values of the reconstructed signal intensity curves relative to the reference image in the small discs with 12-fold and 24-fold undersampling rate. The results from TRACER, CS with l1 minimization and l0 minimization are shown respectively
2.2 人体成像实验结果
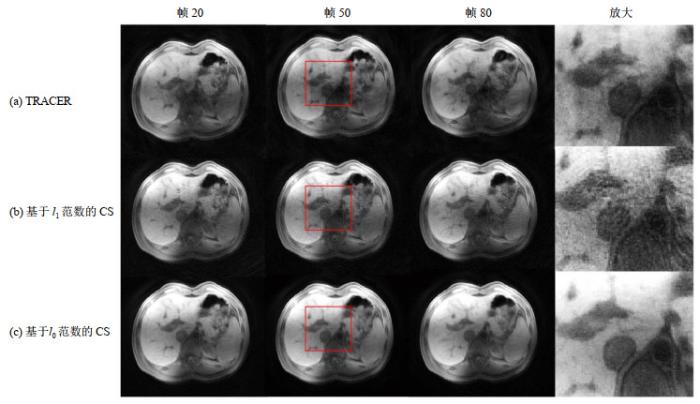
图 7显示了欠采样率为24时的人体肝脏成像结果.在TRACER重建的结果中,伪影较为严重,强度相对不均匀.这些伪影主要是由于TRACER的运动敏感性引起的.由于较大的呼吸信号的运动,TRACER不能在如此高的欠采样率下精确地重建每一帧.在l1最小化重建中,图像的信噪比相对较低,信号损失是由于在极高的欠采样率下使用l1最小化而造成的.l0最小化在这三种算法中显示出了最好的性能,具有足够的信噪比和较少的混叠或运动伪影.放大红色框中的区域,可以看到细节对比.
图7
图7
非对比增强肝脏图像重建结果(欠采样率为24).前三列显示帧20、帧50和帧80,第四列显示帧50中红色框里被放大的区域,图(a)~(c)分别显示了使用TRACER、基于l1最小化的CS和基于l0最小化的CS重建图像
Fig.7
Reconstruction results of the non-contrast-enhanced liver image series (undersampling rate = 24). The first three columns show frame 20, frame 50, frame 80 and the fourth column shows the regions in the red boxes in frame 50 which are zoomed in. Rows (a), (b), (c) show the reconstruction results using TRACER, CS with l1 minimization and l0 minimization respectively
2.3 分析与讨论
针对三维动态MRI,本文提出了一种将黄金角变密度螺旋采样、并行成像与l0最小化CS相结合的成像方法,该方法数据采集效率高,对欠采样恢复具有鲁棒性,对运动不敏感,是一种较好的三维MRI方法.
数据采集效率与高欠采样率相结合,使得l0最小化方法与其他方法相比能够获得更高的时空分辨率,尤其是时间分辨率.结果部分关于时间分辨率的分析表明,在l1最小化的方法中,较高的时间分辨率通常会提高时间精度,而其他两种算法较高的时间分辨率只会略微降低时间精度.另一方面,更高的时间分辨率会带来更多的数据点,可以用来提高模型拟合的性能.TRACER方法的对比强度曲线中出现了时间延迟,已经在结果部分进行了展示,也有关于这个方面更深入的讨论[4].在l1最小化的方法中,较高的时间分辨率提高了时间精度,但由于大量噪声和伪影的出现,使图像质量下降.噪声来自于高欠采样率,因为l1最小化的CS无法从如此高的欠采样数据中恢复图像.但是,l0最小化的CS方法可以使欠采样率接近理论边界,因此在如此高的欠采样率下,图像质量不会受到严重影响.采用l0最小化方法,可以在轻微降低图像质量和时间保真度的情况下获得更高的时间分辨率,这一特性使其可以提供更多、更准确的信息,有助于DCE-MRI中的病灶诊断和药代动力学建模.
CS重建以抑制时间TV域上的小系数为代价,消除了螺旋混叠伪影,但因为一些低于伪噪声的小系数无法恢复,因此也会存在由一些小信号变化而带来的损失.这种副作用在各种CS重建中都很常见,因为所使用的稀疏域是相对稀疏的,而不是真正稀疏.利用l1最小化,不仅小系数不能恢复,大系数也不能完全恢复,这将会抑制一些大的信号变化.l0最小化与l1最小化相比,前者可以保留较小的系数,并以较高的精度恢复大系数,从而获得更好的时间保真度.另一方面,使用时间TV域可能会引入时间模糊,使时间信息的高频分量变平滑.
螺旋轨迹可以用来抑制运动伪影,并且结合CS的并行成像也不如TRACER那样对运动敏感,所以屏住呼吸不是实验必须的.但是由于使用了螺旋堆叠的方法,采样策略在层方向上仍然是笛卡尔的,因此不能抑制平面上的运动伪影.事实上,为所有层(TR×层数)获取一个交错叶的持续时间非常关键,因为在这段时间内运动不能被抑制.在层方向上使用部分傅里叶采集,以减少持续时间,从而减轻这些伪影.但对于正常呼吸运动,持续时间(约100~300 ms)仍然相对较长,因此扫描时需要浅呼吸.
本文提出的算法应用于三维动态MRI时具有较好的效果,后续可将此算法进行进一步的实际应用.如在DCE-MRI应用中,高时空分辨率是一个重要要求:这种空间分辨率对于检测肝脏中小病变具有优势;至于时间分辨率,传统的体积时间分辨率在5 s左右的三维DCE-MRI技术可能会导致诸如动脉相位等一些重要相位的损失,并产生两种相位的混合[13].利用一些先进的技术,可以达到类似的时空分辨率,如TRACER或l1最小化,但很难同时获得高图像质量和高时间保真度.然而,由l0最小化重建的图像序列即使在高时空分辨率下也能很好地平衡时空保真度.精确的对比度增强演化可以提供更多的信息来区分良恶性肿瘤,以及更准确的拟合参数用以药代动力学建模[12].另一方面,运动不敏感使得无法屏住呼吸的患者,包括重症患者或服用镇静剂的患者,得以进行动态腹部成像.因此,l0最小化方法在临床应用中的潜力是巨大的,特别是对于肝脏的动态MRI,可以获得用于诊断的时空分辨率足够高的图像.需要注意的是,本研究只是同伦l0方法在动态MRI上的应用,仿真结果和人体实验初步证实了该重建方法的有效性,不足之处在于没有进行实际的人体DCE成像的重建对比,后续有条件的情况下值得进一步研究.本文利用不同稀疏程度的图像更充分地论证了基于l0最小化的重建算法的优势,也有其他研究[21]讨论了这一点.
本文提出的l0最小化方法也存在一定的局限性.首先,影像开始和结束的几帧都有严重的伪影.这些伪影也出现在用l1最小化方法重建的结果中.当使用时间TV稀疏域时,在第一帧之前或最后一帧之后没有更多的帧,并且在开始和结束时不能保证稀疏性,这是CS重建中的一个常见问题.其次,采用l0最小化方法的计算代价非常大,这主要是因为使用了l0最小化的CS重建,而且时空分辨率也很高.l0范数的近似和非线性迭代求解的计算代价都很高,如果使用较高的欠采样率,重建的帧数就会增加,计算量更大.当使用螺旋堆叠时,首先沿层方向进行快速傅里叶变换,然后对层进行一个接一个地重建,该方法可以减少内存的使用,但重建时间很长.考虑到每个层方向采集的独立性,可以在现代多核计算机上进行重建,如果核数足够大,并对代码进行优化,就可以减少与层数成比例的重建时间.本文提出的l0最小化方法最初是在MATLAB(MathWorks,MA)上实现的,所以通过使用优化的C/C++代码并且/或者使用一个图形处理器(Graphics Processing Unit,GPU)可以进一步减少计算时间[32].其次,所选的权重参数λ没有严格的数学准则来计算,这可能会引入算子之间的变化.在我们的实验中,λ是固定的,可以应用于采用相似序列的同一扫描仪上的不同研究,并且欠采样率不同时,可以根据伪噪声水平对λ进行调整[6].虽然使用上述方法可以在不需要干预的情况下获得质量良好的图像,但需要进行大量的实验来评估其鲁棒性.只有找到一种数学方法来表达由l0最小化重建的图像序列的时空保真度之间的关系时,才能确定具有最佳性能的最优
3 结论
本研究提出了一种将黄金角变密度螺旋采样与l0最小化CS重建相结合的高时空分辨率三维动态MRI方法,在极高的欠采样率下依然可以获得较高的时间分辨率和精确的时间保真度,同时保持了较好的图像质量,并且不受运动的影响.基于这些特性,该方法适用于三维动态MRI,对于可视化微小病灶和获取时间信息有重要意义.但是本文的研究仍有需要改进的地方,本文只是进行了常规的采集和重建,初步验证了同伦l0最小化方法在高欠采倍数的动态MRI上具有潜在优势,其泛化能力有待进一步研究.
参考文献
Respiratory and cardiac self-gated free-breathing cardiac CINE imaging with multiecho 3D hybrid radial SSFP acquisition
[J].DOI:10.1002/mrm.22306 [本文引用: 1]
Combination of compressed sensing and parallel imaging for highly accelerated first-pass cardiac perfusion MRI
[J].
Quantitative high-resolution renal perfusion imaging using 3-dimensional through-time radial generalized autocalibrating partially parallel acquisition
[J].DOI:10.1097/RLI.0000000000000070
Fast 3D contrast enhanced MRI of the liver using temporal resolution acceleration with constrained evolution reconstruction
[J].DOI:10.1002/mrm.24253 [本文引用: 3]
Free-breathing pediatric MRI with nonrigid motion correction and acceleration
[J].
Golden-angle radial sparse parallel MRI: combination of compressed sensing, parallel imaging, and golden-angle radial sampling for fast and flexible dynamic volumetric MRI
[J].DOI:10.1002/mrm.24980 [本文引用: 2]
XD-GRASP: Golden-angle radial MRI with reconstruction of extra motion-state dimensions using compressed sensing
[J].DOI:10.1002/mrm.25665 [本文引用: 1]
Dynamic gadolinium-enhanced 3DFT abdominal MR arteriography
[J].DOI:10.1002/jmri.1880030614 [本文引用: 1]
Abdominal MR imaging with a volumetric interpolated breath-hold examination
[J].DOI:10.1148/radiology.212.3.r99se34876
Advanced liver fibrosis: diagnosis with 3D whole-liver perfusion MR imaging-initial experience
[J].
Hepatic MR imaging with a dynamic contrast-enhanced isotropic volumetric interpolated breath-hold examination: feasibility, reproducibility, and technical quality
[J].DOI:10.1148/radiology.215.2.r00ma16365
Assessment of hepatic perfusion parameters with dynamic MRI
[J].DOI:10.1002/mrm.10045 [本文引用: 1]
Timing bolus dynamic contrast-enhanced (DCE) MRI assessment of hepatic perfusion: Initial experience
[J].
3D high temporal and spatial resolution contrast-enhanced MR angiography of the whole brain
[J].
SENSE: sensitivity encoding for fast MRI
[J].DOI:10.1002/(SICI)1522-2594(199911)42:5<952::AID-MRM16>3.0.CO;2-S [本文引用: 1]
Generalized autocalibrating partially parallel acquisitions (GRAPPA)
[J].DOI:10.1002/mrm.10171 [本文引用: 1]
k-t BLAST and k-t SENSE: Dynamic MRI with high frame rate exploiting spatiotemporal correlations
[J].DOI:10.1002/mrm.10611 [本文引用: 1]
k-t GRAPPA: A k-space implementation for dynamic MRI with high reduction factor
[J].DOI:10.1002/mrm.20641 [本文引用: 1]
Compressed sensing MRI
[J].DOI:10.1109/MSP.2007.914728 [本文引用: 2]
Sparse MRI: The application of compressed sensing for rapid MR imaging
[J].DOI:10.1002/mrm.21391 [本文引用: 1]
Flexible retrospective selection of temporal resolution in real-time speech MRI using a golden-ratio spiral view order
[J].DOI:10.1002/mrm.22714 [本文引用: 3]
Highly undersampled magnetic resonance image reconstruction via homotopic l0-minimization
[J].DOI:10.1109/TMI.2008.927346 [本文引用: 3]
Sparse reconstruction of breast MRI using homotopic l0 minimization in a regional sparsified domain
[J].DOI:10.1109/TBME.2010.2089456 [本文引用: 1]
Fast spiral coronary artery imaging
[J].DOI:10.1002/mrm.1910280204 [本文引用: 1]
An optimal radial profile order based on the golden ratio for time-resolved MRI
[J].DOI:10.1109/TMI.2006.885337 [本文引用: 1]
Highly undersampled magnetic resonance image reconstruction using two-level Bregman method with dictionary updating
[J].DOI:10.1109/TMI.2013.2256464 [本文引用: 1]
Adaptive dictionary learning in sparse gradient domain for image recovery
[J].DOI:10.1109/TIP.2013.2277798 [本文引用: 1]
A sparse reconstruction algorithm for NMR spectroscopy based on approximate l0 norm minimization
[J].DOI:10.3969/j.issn.1000-4556.2013.04.006 [本文引用: 1]
基于近似l0范数最小化的NMR波谱稀疏重建算法
[J].DOI:10.3969/j.issn.1000-4556.2013.04.006 [本文引用: 1]
Imaging lenticulostriate arteries at 3 Tesla using optimized flow-sensitive black-blood technique
[J].
基于优化后流动敏感黑血序列的豆纹动脉3 T磁共振成像
[J].
Accelerating advanced MRI Reconstructions on GPUs
[J].DOI:10.1016/j.jpdc.2008.05.013 [本文引用: 1]
A deep recursive cascaded convolutional network for parallel MRI
[J].
基于深度递归级联卷积神经网络的并行磁共振成像方法
[J].
Reconstruction of simultaneous multi-slice MRI data by combining virtual conjugate coil technology and convolutional neural network
[J].
基于虚拟线圈和卷积神经网络的多层同时激发图像重建
[J].