Table of Content

25 February 2019, Volume 39 Issue 1 Previous Issue    Next Issue

For Selected:

View Abstracts

Download Citations EndNote Reference Manager ProCite BibTeX RefWorks

Toggle Thumbnails

Articles

Select

A LIOUVILLE THEOREM FOR STATIONARY INCOMPRESSIBLE FLUIDS OF VON MISES TYPE Martin FUCHS, Jan MÜLLER Acta mathematica scientia,Series B. 2019, 39 (1):  1-10.  DOI: 10.1007/s10473-019-0101-1 Abstract ( 93 )   RICH HTML PDF   Save We consider entire solutions u of the equations describing the stationary flow of a generalized Newtonian fluid in 2D concentrating on the question, if a Liouville-type result holds in the sense that the boundedness of u implies its constancy. A positive answer is true for p-fluids in the case p>1 (including the classical Navier-Stokes system for the choice p=2), and recently we established this Liouville property for the Prandtl-Eyring fluid model, for which the dissipative potential has nearly linear growth. Here we finally discuss the case of perfectly plastic fluids whose flow is governed by a von Mises-type stress-strain relation formally corresponding to the case p=1. It turns out that, for dissipative potentials of linear growth, the condition of μ-ellipticity with exponent μ<2 is sufficient for proving the Liouville theorem. References | Related Articles | Metrics

Select

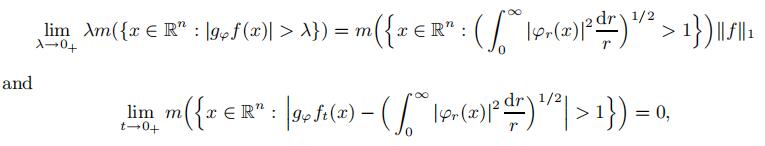
LIMITING WEAK-TYPE BEHAVIORS FOR CERTAIN LITTLEWOOD-PALEY FUNCTIONS Xianming HOU, Huoxiong WU Acta mathematica scientia,Series B. 2019, 39 (1):  11-25.  DOI: 10.1007/s10473-019-0102-0 Abstract ( 90 )   RICH HTML PDF   Save In this paper, we establish the following limiting weak-type behaviors of Littlewood Paley g-function gφ:for nonnegative function f ∈ L1(Rn), where ft(x)=t-nf(t-1x) for t > 0. Meanwhile, the corresponding results for Marcinkiewicz integral and its fractional version with kernels satisfying Lαq-Dini condition are also given. References | Related Articles | Metrics

Select

HARDY’S INEQUALITIES WITH MAXIMIZERS FOR W1,p FUNCTIONS ON BOUNDED STAR DOMAINS Ahmed A. ABDELHAKIM Acta mathematica scientia,Series B. 2019, 39 (1):  26-36.  DOI: 10.1007/s10473-019-0103-z Abstract ( 20 )   RICH HTML PDF   Save With the help of a radially invariant vector field, we derive inequalities of the Hardy kind, with no boundary terms, for W 1,p functions on bounded star domains. Our results are not obtainable from the classical inequalities for W1,p functions. Unlike in W1,p, our inequalities admit maximizers that we describe explicitly. References | Related Articles | Metrics

Select

LONG-TIME ASYMPTOTIC OF STABLE DAWSON-WATANABE PROCESSES IN SUPERCRITICAL REGIMES Khoa LÊ Acta mathematica scientia,Series B. 2019, 39 (1):  37-45.  DOI: 10.1007/s10473-019-0104-y Abstract ( 55 )   RICH HTML PDF   Save Let W=(Wt)t ≥ 0 be a supercritical α-stable Dawson-Watanabe process (with α ∈ (0, 2]) and f be a test function in the domain of -(-△) α/2 satisfying some integrability condition. Assuming the initial measure W0 has a finite positive moment, we determine the long-time asymptotic of arbitrary order of Wt(f). In particular, it is shown that the local behavior of Wt in long-time is completely determined by the asymptotic of the total mass Wt(1), a global characteristic. References | Related Articles | Metrics

Select

CONVERGENCE RATES TO NONLINEAR DIFFUSIVE WAVES FOR SOLUTIONS TO NONLINEAR HYPERBOLIC SYSTEM Shifeng GENG, Yanjuan TANG Acta mathematica scientia,Series B. 2019, 39 (1):  46-56.  DOI: 10.1007/s10473-019-0105-x Abstract ( 58 )   RICH HTML PDF   Save This article is involved with the asymptotic behavior of solutions for nonlinear hyperbolic system with external friction. The global existence of classical solutions is proven, and Lp convergence rates are obtained. Compared with the results obtained by Hsiao and Liu, better convergence rates are obtained in this article. References | Related Articles | Metrics

Select

GLOBAL SOLUTIONS OF THE PERTURBED RIEMANN PROBLEM FOR THE CHROMATOGRAPHY EQUATIONS Ting ZHANG, Wancheng SHENG Acta mathematica scientia,Series B. 2019, 39 (1):  57-82.  DOI: 10.1007/s10473-019-0106-9 Abstract ( 52 )   RICH HTML PDF   Save The Riemann problem for the chromatography equations in a conservative form is considered. The global solution is obtained under the assumptions that the initial data are taken to be three piecewise constant states. The wave interaction problems are discussed in detail during the process of constructing global solutions to the perturbed Riemann problem. In addition, it can be observed that the Riemann solutions are stable under small perturbations of the Riemann initial data. References | Related Articles | Metrics

Select

FINITE TIME EMERGENCE OF A SHOCK WAVE FOR SCALAR CONSERVATION LAWS VIA Zejun WANG, Qi ZHANG Acta mathematica scientia,Series B. 2019, 39 (1):  83-93.  DOI: 10.1007/s10473-019-0107-8 Abstract ( 39 )   RICH HTML PDF   Save In this paper, we use Lax-Oleinik formula to study the asymptotic behavior for the initial problem of scalar conservation law ut + F(u)x=0. First, we prove a simple but useful property of Lax-Oleinik formula (Lemma 2.7). In fact, denote the Legendre transform of F(u) as L(σ), then we can prove that the quantity F(q)-qF'(q) + L(F'(q)) is a constant independent of q. As a simple application, we first give the solution of Riemann problem without using of Rankine-Hugoniot condition and entropy condition. Then we study the asymptotic behavior of the problem with some special initial data and prove that the solution contains only a single shock for t > T*. Meanwhile, we can give the equation of the shock and an explicit value of T*. References | Related Articles | Metrics

Select

PARTIAL REGULARITY OF STATIONARY NAVIER-STOKES SYSTEMS UNDER NATURAL GROWTH CONDITION Lianhua HE, Zhong TAN Acta mathematica scientia,Series B. 2019, 39 (1):  94-110.  DOI: 10.1007/s10473-019-0110-0 Abstract ( 33 )   RICH HTML PDF   Save In this article, we consider the partial regularity of stationary Navier-Stokes system under the natural growth condition. Applying the method of A-harmonic approximation, we obtain some results about the partial regularity and establish the optimal Hölder exponent for the derivative of a weak solution on its regular set. References | Related Articles | Metrics

Select

STABILITY OF SUBHARMONIC SOLUTIONS OF FIRST-ORDER HAMILTONIAN SYSTEMS WITH ANISOTROPIC GROWTH Chungen LIU, Xiaofei ZHANG Acta mathematica scientia,Series B. 2019, 39 (1):  111-118.  DOI: 10.1007/s10473-019-0108-7 Abstract ( 38 )   RICH HTML PDF   Save Using the dual Morse index theory, we study the stability of subharmonic solutions of first-order autonomous Hamiltonian systems with anisotropic growth, that is, we obtain a sequence of elliptic subharmonic solutions (that is, all its Floquet multipliers lying on the unit circle on the complex plane C). References | Related Articles | Metrics

Select

GLOBAL EXPONENTIAL NONLINEAR STABILITY FOR DOUBLE DIFFUSIVE CONVECTION IN POROUS MEDIUM Lanxi XU, Ziyi LI Acta mathematica scientia,Series B. 2019, 39 (1):  119-126.  DOI: 10.1007/s10473-019-0109-6 Abstract ( 25 )   RICH HTML PDF   Save Nonlinear stability of the motionless double-diffusive solution of the problem of an infinite horizontal fluid layer saturated porous medium is studied. The layer is heated and salted from below. By introducing two balance fields and through defining new energy functionals it is proved that for CLe ≥ R, Le ≤ 1 the motionless double-diffusive solution is always stable and for CLe < R, Le < 1 the solution is globally exponentially and nonlinearly stable whenever R < 4π2 + LeC, where Le, C and R are the Lewis number, Rayleigh number for solute and heat, respectively. Moreover, the nonlinear stability proved here is global and exponential, and the stabilizing effect of the concentration is also proved. References | Related Articles | Metrics

Select

STABILITY OF GLOBAL MAXWELLIAN FOR NON-LINEAR VLASOV-POISSON-FOKKER-PLANCK EQUATIONS Jie LIAO, Qianrong WANG, Xiongfeng YANG Acta mathematica scientia,Series B. 2019, 39 (1):  127-138.  DOI: 10.1007/s10473-019-0112-y Abstract ( 44 )   RICH HTML PDF   Save In this article, we establish the exponential time decay of smooth solutions around a global Maxwellian to the non-linear Vlasov—Poisson—Fokker—Planck equations in the whole space by uniform-in-time energy estimates. The non-linear coupling of macroscopic part and Fokker—Planck operator in the model brings new difficulties for the energy estimates, which is resolved by adding tailored weighted-in-v energy estimates suitable for the Fokker—Planck operator. References | Related Articles | Metrics

Select

ON EXISTENCE OF SOLUTIONS OF DIFFERENCE RICCATI EQUATION Zongxuan CHEN, Kwang Ho SHON Acta mathematica scientia,Series B. 2019, 39 (1):  139-147.  DOI: 10.1007/s10473-019-0111-z Abstract ( 38 )   RICH HTML PDF   Save Consider the difference Riccati equation f(z+1)=A(z)f(z)+B(z)/C(z)f(z)+D(z), where A, B, C, D are meromorphic functions, we give its solution family with one-parameter where Q(z) is any constant in C or any periodic meromorphic function with period 1, and f0(z), f1(z), f2(z) are its three distinct meromorphic solutions. References | Related Articles | Metrics

Select

POSITIVE MAPS CONSTRUCTED FROM PERMUTATION PAIRS Jinchuan HOU, Haili ZHAO Acta mathematica scientia,Series B. 2019, 39 (1):  148-164.  DOI: 10.1007/s10473-019-0113-x Abstract ( 44 )   RICH HTML PDF   Save A property (C) for permutation pairs is introduced. It is shown that if a pair {π1, π2} of permutations of (1, 2, …, n) has property (C), then the D-type map Φπ1, π2 on n×n complex matrices constructed from {π1, π2} is positive. A necessary and sufficient condition is obtained for a pair {π1, π2} to have property (C), and an easily checked necessary and sufficient condition for the pairs of the form {πp, πq} to have property (C) is given, where π is the permutation defined by π(i)=i + 1 mod n and 1 ≤ p < q ≤ n. References | Related Articles | Metrics

Select

ANALYTICAL SMOOTHING EFFECT OF SOLUTION FOR THE BOUSSINESQ EQUATIONS Feng CHENG, Chaojiang XU Acta mathematica scientia,Series B. 2019, 39 (1):  165-179.  DOI: 10.1007/s10473-019-0114-9 Abstract ( 45 )   RICH HTML PDF   Save In this article, we study the analytical smoothing effect of Cauchy problem for the incompressible Boussinesq equations. Precisely, we use the Fourier method to prove that the Sobolev H1-solution to the incompressible Boussinesq equations in periodic domain is analytic for any positive time. So the incompressible Boussinesq equations admit exactly same smoothing effect properties of incompressible Navier-Stokes equations. References | Related Articles | Metrics

Select

GLOBAL EXISTENCE AND POINTWISE ESTIMATES OF SOLUTIONS TO GENERALIZED KURAMOTO-SIVASHINSKY SYSTEM IN MULTI-DIMENSIONS Yingshu ZHANG, Lang LI, Shaomei FANG Acta mathematica scientia,Series B. 2019, 39 (1):  180-194.  DOI: 10.1007/s10473-019-0115-8 Abstract ( 36 )   RICH HTML PDF   Save The Cauchy problem of the generalized Kuramoto-Sivashinsky equation in multi-dimensions (n ≥ 3) is considered. Based on Green's function method, some ingenious energy estimates are given. Then the global existence and pointwise convergence rates of the classical solutions are established. Furthermore, the Lp convergence rate of the solution is obtained. References | Related Articles | Metrics

Select

SAMPLED-DATA STATE ESTIMATION FOR NEURAL NETWORKS WITH ADDITIVE TIME–VARYING DELAYS M. SYED ALI, N. GUNASEKARAN, Jinde CAO Acta mathematica scientia,Series B. 2019, 39 (1):  195-213.  DOI: 10.1007/s10473-019-0116-7 Abstract ( 26 )   RICH HTML PDF   Save In this paper, we consider the problem of delay-dependent stability for state estimation of neural networks with two additive time-varying delay components via sampleddata control. By constructing a suitable Lyapunov-Krasovskii functional with triple and four integral terms and by using Jensen's inequality, a new delay-dependent stability criterion is derived in terms of linear matrix inequalities (LMIs) to ensure the asymptotic stability of the equilibrium point of the considered neural networks. Instead of the continuous measurement, the sampled measurement is used to estimate the neuron states, and a sampled-data estimator is constructed. Due to the delay-dependent method, a significant source of conservativeness that could be further reduced lies in the calculation of the time-derivative of the Lyapunov functional. The relationship between the time-varying delay and its upper bound is taken into account when estimating the upper bound of the derivative of Lyapunov functional. As a result, some less conservative stability criteria are established for systems with two successive delay components. Finally, numerical example is given to show the superiority of proposed method. References | Related Articles | Metrics

Select

NEW HYBRID CONJUGATE GRADIENT METHOD AS A CONVEX COMBINATION OF LS AND FR METHODS Snezana S. DJORDJEVIC, Acta mathematica scientia,Series B. 2019, 39 (1):  214-228.  DOI: 10.1007/s10473-019-0117-6 Abstract ( 47 )   RICH HTML PDF   Save In this paper, we present a new hybrid conjugate gradient algorithm for unconstrained optimization. This method is a convex combination of Liu-Storey conjugate gradient method and Fletcher-Reeves conjugate gradient method. We also prove that the search direction of any hybrid conjugate gradient method, which is a convex combination of two conjugate gradient methods, satisfies the famous D-L conjugacy condition and in the same time accords with the Newton direction with the suitable condition. Furthermore, this property doesn’t depend on any line search. Next, we also prove that, moduling the value of the parameter t, the Newton direction condition is equivalent to Dai-Liao conjugacy condition.The strong Wolfe line search conditions are used. The global convergence of this new method is proved. Numerical comparisons show that the present hybrid conjugate gradient algorithm is the efficient one. References | Related Articles | Metrics

Select

EXISTENCE AND CONTROLLABILITY FOR NONLINEAR FRACTIONAL CONTROL SYSTEMS WITH DAMPING IN HILBERT SPACES Xiuwen LI, Zhenhai LIU, Jing LI, Chris TISDELL Acta mathematica scientia,Series B. 2019, 39 (1):  229-242.  DOI: 10.1007/s10473-019-0118-5 Abstract ( 45 )   RICH HTML PDF   Save In this paper, we are concerned with the existence of mild solution and controllability for a class of nonlinear fractional control systems with damping in Hilbert spaces. Our first step is to give the representation of mild solution for this control system by utilizing the general method of Laplace transform and the theory of (α,γ)-regularized families of operators. Next, we study the solvability and controllability of nonlinear fractional control systems with damping under some suitable sufficient conditions. Finally, two examples are given to illustrate the theory. References | Related Articles | Metrics

Select

KAM TORI FOR DEFOCUSING KDV-MKDV EQUATION Wenyan CUI, Lufang MI, Li YIN Acta mathematica scientia,Series B. 2019, 39 (1):  243-258.  DOI: 10.1007/s10473-019-0119-4 Abstract ( 45 )   RICH HTML PDF   Save In this paper, we consider small perturbations of the KdV-mKdV equation ut=-uxxx + 6uux + 6u2ux on the real line with periodic boundary conditions. It is shown that the above equation admits a Cantor family of small amplitude quasi-periodic solutions under such perturbations. The proof is based on an abstract infinite dimensional KAM theorem. References | Related Articles | Metrics

Select

STABILITY OF BOUNDARY LAYER TO AN OUTFLOW PROBLEM FOR A COMPRESSIBLE NON-NEWTONIAN FLUID IN THE HALF SPACE Jie PAN, Li FANG, Zhenhua GUO Acta mathematica scientia,Series B. 2019, 39 (1):  259-283.  DOI: 10.1007/s10473-019-0120-y Abstract ( 46 )   RICH HTML PDF   Save This paper investigates the large-time behavior of solutions to an outflow problem for a compressible non-Newtonian fluid in a half space. The main concern is to analyze the phenomena that happens when the compressible non-Newtonian fluid blows out through the boundary. Based on the existence of the stationary solution, it is proved that there exists a boundary layer (i.e., the stationary solution) to the outflow problem and the boundary layer is nonlinearly stable under small initial perturbation. References | Related Articles | Metrics

Select

A NECESSARY CONDITION FOR CERTAIN INTEGRAL EQUATIONS WITH NEGATIVE EXPONENTS Jiankai XU, Zhong TAN, Weiwei WANG, Zepeng XIONG Acta mathematica scientia,Series B. 2019, 39 (1):  284-296.  DOI: 10.1007/s10473-019-0121-x Abstract ( 53 )   RICH HTML PDF   Save This paper is devoted to studying the existence of positive solutions for the following integral system It is shown that if (u, v) is a pair of positive Lebesgue measurable solutions of this integral system, then 1/p-1+1/q-1=λ/n, which is different from the well-known case of the Lane-Emden system and its natural extension, the Hardy-Littlewood-Sobolev type integral equations. References | Related Articles | Metrics

Select

SUBCLASSES OF BIHOLOMORPHIC MAPPINGS UNDER THE EXTENSION OPERATORS Chaojun WANG, Yanyan CUI, Hao LIU Acta mathematica scientia,Series B. 2019, 39 (1):  297-311.  DOI: 10.1007/s10473-019-0122-9 Abstract ( 33 )   RICH HTML PDF   Save In this article, we mainly study the invariance of some biholomorphic mappings with special geometric characteristics under the extension operators. First we generalize the Roper-Suffridge extension operators on Bergman-Hartogs domains. Then, by the geometric characteristics of subclasses of biholomorphic mappings, we conclude that the modified Roper-Suffridge operators preserve the properties of SΩ*Ω(β, A, B), parabolic and spirallike mappings of type β and order ρ, strong and almost spirallike mappings of type β and order α as well as almost starlike mappings of complex order λ on Ωp1Bn,…,ps,q under different conditions, respectively. The conclusions provide new approaches to construct these biholomorphic mappings in several complex variables. References | Related Articles | Metrics

Select

CLASSFICATION OF HOMOGENEOUS TWO-SPHERES IN G(2, 5; C) Wenjuan ZHANG, Jie FEI, Xiaoxiang JIAO Acta mathematica scientia,Series B. 2019, 39 (1):  312-328.  DOI: 10.1007/s10473-019-0123-8 Abstract ( 51 )   RICH HTML PDF   Save In this article, we determine all homogeneous two-spheres in the complex Grassmann manifold G(2, 5; C) by theory of unitary representations of the 3-dimensional special unitary group SU(2). References | Related Articles | Metrics

Select

BLOW-UP OF SOLUTION FOR A VISCOELASTIC WAVE EQUATION WITH DELAY Shun-Tang WU Acta mathematica scientia,Series B. 2019, 39 (1):  329-338.  DOI: 10.1007/s10473-019-0124-7 Abstract ( 47 )   RICH HTML PDF   Save In this paper, we consider the following viscoelastic wave equation with delay |ut|ρ utt-△u-△utt + ƒ0t g(t - s)△u(s)ds + μ1ut(x, t) + μ2ut(x, t - τ)=b|u|p-2 u in a bounded domain. Under appropriate conditions on μ1, μ2, the kernel function g, the nonlinear source and the initial data, there are solutions that blow up in finite time. References | Related Articles | Metrics