Table of Content

25 April 2019, Volume 39 Issue 2 Previous Issue   

For Selected:

View Abstracts

Download Citations EndNote Reference Manager ProCite BibTeX RefWorks

Toggle Thumbnails

Articles

Select

RIGIDITY THEOREMS OF COMPLETE KÄHLER-EINSTEIN MANIFOLDS AND COMPLEX SPACE FORMS Tian CHONG, Yuxin DONG, Hezi LIN, Yibin REN Acta mathematica scientia,Series B. 2019, 39 (2):  339-356.  DOI: 10.1007/s10473-019-0201-y Abstract ( 71 )   RICH HTML PDF   Save We concentrate on using the traceless Ricci tensor and the Bochner curvature tensor to study the rigidity problems for complete Kähler manifolds. We derive some elliptic differential inequalities from Weitzenbock formulas for the traceless Ricci tensor of Kähler manifolds with constant scalar curvature and the Bochner tensor of Kähler-Einstein manifolds respectively. Using elliptic estimates and maximum principle, several Lp and L∞ pinching results are established to characterize Kähler-Einstein manifolds among Kähler manifolds with constant scalar curvature and complex space forms among Kähler-Einstein manifolds. Our results can be regarded as a complex analogues to the rigidity results for Riemannian manifolds. Moreover, our main results especially establish the rigidity theorems for complete noncompact Kähler manifolds and noncompact Kähler-Einstein manifolds under some pointwise pinching conditions or global integral pinching conditions. To the best of our knowledge, these kinds of results have not been reported. References | Related Articles | Metrics

Select

LIOUVILLE RESULTS FOR STABLE SOLUTIONS OF QUASILINEAR EQUATIONS WITH WEIGHTS Phuong LE, Vu HO Acta mathematica scientia,Series B. 2019, 39 (2):  357-368.  DOI: 10.1007/s10473-019-0202-x Abstract ( 62 )   RICH HTML PDF   Save This paper is devoted to the quasilinear equation where p ≥ 2, Ω is a (bounded or unbounded) domain of RN, w1, w2 are nonnegative continuous functions and f is an increasing function. We establish a Liouville type theorem for nontrivial stable solutions of the equation under some mild assumptions on Ω, w1, w2 and f, which extends and unifies several results on this topic. References | Related Articles | Metrics

Select

APPROXIMATE SOLUTION OF A p-th ROOT FUNCTIONAL EQUATION IN NON-ARCHIMEDEAN (2, β)-BANACH SPACES Iz-iddine EL-FASSI, Hamid KHODAEI, Themistocles M. RASSIAS Acta mathematica scientia,Series B. 2019, 39 (2):  369-381.  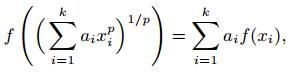DOI: 10.1007/s10473-019-0203-9 Abstract ( 56 )   RICH HTML PDF   Save In this paper, using the Brzd?k’s fixed point theorem [9, Theorem 1] in non-Archimedean (2, β)-Banach spaces, we prove some stability and hyperstability results for an p-th root functional equation where p ∈ {1, …, 5}, a1, …, ak are fixed nonzero reals when p ∈ {1, 3, 5} and are fixed positive reals when p ∈ {2, 4}. References | Related Articles | Metrics

Select

THE CHARACTERIZATION OF EFFICIENCY AND SADDLE POINT CRITERIA FOR MULTIOBJECTIVE OPTIMIZATION PROBLEM WITH VANISHING CONSTRAINTS Anurag JAYSWAL, Vivek SINGH Acta mathematica scientia,Series B. 2019, 39 (2):  382-394.  DOI: 10.1007/s10473-019-0204-8 Abstract ( 41 )   RICH HTML PDF   Save In this article, we focus to study about modified objective function approach for multiobjective optimization problem with vanishing constraints. An equivalent η-approximated multiobjective optimization problem is constructed by a modification of the objective function in the original considered optimization problem. Furthermore, we discuss saddle point criteria for the aforesaid problem. Moreover, we present some examples to verify the established results. References | Related Articles | Metrics

Select

RADIAL CONVEX SOLUTIONS OF A SINGULAR DIRICHLET PROBLEM WITH THE MEAN CURVATURE OPERATOR IN MINKOWSKI SPACE Zaitao LIANG, Yanjuan YANG Acta mathematica scientia,Series B. 2019, 39 (2):  395-402.  DOI: 10.1007/s10473-019-0205-7 Abstract ( 44 )   RICH HTML PDF   Save In this paper, we study the existence of nontrivial radial convex solutions of a singular Dirichlet problem involving the mean curvature operator in Minkowski space. The proof is based on a well-known fixed point theorem in cones. We deal with more general nonlinear term than those in the literature. References | Related Articles | Metrics

Select

TIME-PERIODIC ISENTROPIC SUPERSONIC EULER FLOWS IN ONE-DIMENSIONAL DUCTS DRIVING BY PERIODIC BOUNDARY CONDITIONS Hairong YUAN Acta mathematica scientia,Series B. 2019, 39 (2):  403-412.  DOI: 10.1007/s10473-019-0206-6 Abstract ( 47 )   RICH HTML PDF   Save We show existence of time-periodic supersonic solutions in a finite interval, after certain start-up time depending on the length of the interval, to the one space-dimensional isentropic compressible Euler equations, subjected to periodic boundary conditions. Both classical solutions and weak entropy solutions, as well as high-frequency limiting behavior are considered. The proofs depend on the theory of Cauchy problems of genuinely nonlinear hyperbolic systems of conservation laws. References | Related Articles | Metrics

Select

A FOUR-WEIGHT WEAK TYPE MAXIMAL INEQUALITY FOR MARTINGALES Yanbo REN Acta mathematica scientia,Series B. 2019, 39 (2):  413-419.  DOI: 10.1007/s10473-019-0207-5 Abstract ( 50 )   RICH HTML PDF   Save In this article, some necessary and sufficient conditions are shown in order that weighted inequality of the form holds a.e. for uniformly integrable martingales f = (fn)n≥0 with some constant C > 0, where Φ1, Φ2 are Young functions, wi (i = 1, 2, 3, 4) are weights, and f∞ = fn a.e. As an application, two-weight weak type maximal inequalities of martingales are considered, and particularly a new equivalence condition is presented. References | Related Articles | Metrics

Select

ON INTEGRABILITY UP TO THE BOUNDARY OF THE WEAK SOLUTIONS TO A NON-NEWTONIAN FLUID Shanshan GUO, Zhong TAN Acta mathematica scientia,Series B. 2019, 39 (2):  420-428.  DOI: 10.1007/s10473-019-0208-4 Abstract ( 46 )   RICH HTML PDF   Save This work consider boundary integrability of the weak solutions of a non-Newtonian compressible fluids in a bounded domain in dimension three, which has the constitutive equations as The existence result of weak solutions can be get based on Galerkin approximation. With the linear operator B constructed by BOGOVSKⅡ, we show that the density ρ is square integrable up to the boundary. References | Related Articles | Metrics

Select

ON A MULTI-DELAY LOTKA-VOLTERRA PREDATOR-PREY MODEL WITH FEEDBACK CONTROLS AND PREY DIFFUSION Changyou WANG, Nan LI, Yuqian ZHOU, Xingcheng PU, Rui LI Acta mathematica scientia,Series B. 2019, 39 (2):  429-448.  DOI: 10.1007/s10473-019-0209-3 Abstract ( 58 )   RICH HTML PDF   Save This article is focusing on a class of multi-delay predator-prey model with feedback controls and prey diffusion. By developing some new analysis methods and using the theory of differential inequalities as well as constructing a suitable Lyapunov function, we establish a set of easily verifiable sufficient conditions which guarantee the permanence of the system and the globally attractivity of positive solution for the predator-prey system. Furthermore, some conditions for the existence, uniqueness and stability of positive periodic solution for the corresponding periodic system are obtained by using the fixed point theory and some new analysis techniques. In additional, some numerical solutions of the equations describing the system are given to verify the obtained criteria are new, general, and easily verifiable. Finally, we still solve numerically the corresponding stochastic predator-prey models with multiplicative noise sources, and obtain some new interesting dynamical behaviors of the system. References | Related Articles | Metrics

Select

LOW MACH NUMBER LIMIT OF A COMPRESSIBLE NON-ISOTHERMAL NEMATIC LIQUID CRYSTALS MODEL Jishan FAN, Fucai LI Acta mathematica scientia,Series B. 2019, 39 (2):  449-460.  DOI: 10.1007/s10473-019-0210-x Abstract ( 30 )   RICH HTML PDF   Save In this paper, we study the low Mach number limit of a compressible nonisothermal model for nematic liquid crystals in a bounded domain. We establish the uniform estimates with respect to the Mach number, and thus prove the convergence to the solution of the incompressible model for nematic liquid crystals. References | Related Articles | Metrics

Select

MIXED VARIATIONAL INEQUALITIES DRIVEN BY FRACTIONAL EVOLUTIONARY EQUATIONS Stanisłw MIGÓRSKI, Shengda ZENG Acta mathematica scientia,Series B. 2019, 39 (2):  461-468.  DOI: 10.1007/s10473-019-0211-9 Abstract ( 46 )   RICH HTML PDF   Save The goal of the present paper is to investigate an abstract system, called fractional differential variational inequality, which consists of a mixed variational inequality combined with a fractional evolution equation in the framework of Banach spaces. Using discrete approximation approach, an existence theorem of solutions for the inequality is established under some suitable assumptions. References | Related Articles | Metrics

Select

GLOBAL EXISTENCE AND OPTIMAL CONVERGENCE RATES OF SOLUTIONS FOR THREE-DIMENSIONAL ELECTROMAGNETIC FLUID SYSTEM Yin LI, Ruiying WEI, Zheng-an YAO Acta mathematica scientia,Series B. 2019, 39 (2):  469-490.  DOI: 10.1007/s10473-019-0212-8 Abstract ( 50 )   RICH HTML PDF   Save In this article, we study the electromagnetic fluid system in three-dimensional whole space R3. Under assumption of small initial data, we establish the unique global solution by energy method. Moreover, we obtain the time decay rates of the higher-order spatial derivatives of the solution by combining the Lp - Lq estimates for the linearized equations and an elaborate energy method when the L1-norm of the perturbation is bounded. References | Related Articles | Metrics

Select

LIOUVILLE TYPE THEOREM FOR THE STATIONARY EQUATIONS OF MAGNETO-HYDRODYNAMICS Simon SCHULZ Acta mathematica scientia,Series B. 2019, 39 (2):  491-497.  DOI: 10.1007/s10473-019-0213-7 Abstract ( 36 )   RICH HTML PDF   Save We show that any smooth solution (u, H) to the stationary equations of magnetohydrodynamics belonging to both spaces L6(R3) and BMO-1(R3) must be identically zero. This is an extension of previous results, all of which systematically required stronger integrability and the additional assumption ▽u, ▽H ∈ L2(R3), i.e., finite Dirichlet integral. References | Related Articles | Metrics

Select

LUMP AND INTERACTION SOLUTIONS TO LINEAR(4+1)-DIMENSIONAL PDES Wen-Xiu MA Acta mathematica scientia,Series B. 2019, 39 (2):  498-508.  DOI: 10.1007/s10473-019-0214-6 Abstract ( 51 )   RICH HTML PDF   Save Taking a class of linear (4+1)-dimensional partial differential equations as examples, we would like to show that there exist lump solutions and interaction solutions in (4+1)-dimensions. We will compute abundant lump solutions and interaction solutions to the considered linear (4+1)-dimensional partial differential equations via symbolic computations, and plot three specific solutions with Maple plot tools, which supplements the existing literature on lump, rogue wave and breather solutions and their interaction solutions in soliton theory. References | Related Articles | Metrics

Select

RIEMANN-HILBERT PROBLEMS OF A SIX-COMPONENT MKDV SYSTEM AND ITS SOLITON SOLUTIONS Wen-Xiu MA Acta mathematica scientia,Series B. 2019, 39 (2):  509-523.  DOI: 10.1007/s10473-019-0215-5 Abstract ( 43 )   RICH HTML PDF   Save Based on a 4×4 matrix spectral problem, an AKNS soliton hierarchy with six potentials is generated. Associated with this spectral problem, a kind of Riemann-Hilbert problems is formulated for a six-component system of mKdV equations in the resulting AKNS hierarchy. Soliton solutions to the considered system of coupled mKdV equations are computed, through a reduced Riemann-Hilbert problem where an identity jump matrix is taken. References | Related Articles | Metrics

Select

VECTORIAL EKELAND VARIATIONAL PRINCIPLE AND CYCLICALLY ANTIMONOTONE EQUILIBRIUM PROBLEMS Jinghui QIU Acta mathematica scientia,Series B. 2019, 39 (2):  524-544.  DOI: 10.1007/s10473-019-0216-4 Abstract ( 41 )   RICH HTML PDF   Save In this article, we extend the cyclic antimonotonicity from scalar bifunctions to vector bifunctions. We find out a cyclically antimonotone vector bifunction can be regarded as a family of cyclically antimonotone scalar bifunctions. Using a pre-order principle (see Qiu, 2014), we prove a new version of Ekeland variational principle (briefly, denoted by EVP), which is quite different from the previous ones, for the objective function consists of a family of scalar functions. From the new version, we deduce several vectorial EVPs for cyclically antimonotone equilibrium problems, which extend and improve the previous results. By developing the original method proposed by Castellani and Giuli, we deduce a number of existence results (no matter scalar-valued case, or vector-valued case), when the feasible set is a sequentially compact topological space or a countably compact topological space. Finally, we propose a general coercivity condition. Combining the general coercivity condition and the obtained existence results with compactness conditions, we obtain several existence results for equilibrium problems in noncompact settings. References | Related Articles | Metrics

Select

NEW BOUNDS ON EIGENVUALUES OF LAPLACIAN Zhengchao JI Acta mathematica scientia,Series B. 2019, 39 (2):  545-550.  DOI: 10.1007/s10473-019-0217-3 Abstract ( 43 )   RICH HTML PDF   Save In this paper, we investigate non-zero positive eigenvalues of the Laplacian with Dirichlet boundary condition in an n-dimentional Euclidean space Rn, then we obtain an new upper bound of the (k + 1)-th eigenvalue λk+1, which improve the previous estimate which was obtained by Cheng and Yang, see (1.8). References | Related Articles | Metrics

Select

APPROXIMATE SOLUTION OF P-RADICAL FUNCTIONAL EQUATION IN 2-BANACH SPACES Muaadh ALMAHALEBI, Abdellatif CHAHBI Acta mathematica scientia,Series B. 2019, 39 (2):  551-566.  DOI: 10.1007/s10473-019-0218-2 Abstract ( 45 )   RICH HTML PDF   Save The aim of this paper is to introduce and solve the p-radical functional equation We also state an analogue of the fixed point theorem [12, Theorem 1] in 2-Banach spaces and investigate stability for this equation in 2-Banach spaces. References | Related Articles | Metrics

Select

BLOW-UP PHENOMENA FOR A CLASS OF GENERALIZED DOUBLE DISPERSION EQUATIONS Huafei DI, Yadong SHANG Acta mathematica scientia,Series B. 2019, 39 (2):  567-579.  DOI: 10.1007/s10473-019-0219-1 Abstract ( 53 )   RICH HTML PDF   Save In this article, we study the blow-up phenomena of generalized double dispersion equations utt - uxx - uxxt + uxxxx - uxxtt = f(ux)x. Under suitable conditions on the initial data, we first establish a blow-up result for the solutions with arbitrary high initial energy, and give some upper bounds for blow-up time T* depending on sign and size of initial energy E(0). Furthermore, a lower bound for blow-up time T* is determined by means of a differential inequality argument when blow-up occurs. References | Related Articles | Metrics

Select

A NONTRIVIAL SOLUTION OF A QUASILINEAR ELLIPTIC EQUATION VIA DUAL APPROACH Xianyong YANG, Wei ZHANG, Fukun ZHAO Acta mathematica scientia,Series B. 2019, 39 (2):  580-596.  DOI: 10.1007/s10473-019-0220-8 Abstract ( 41 )   RICH HTML PDF   Save In this article, we are concerned with the existence of solutions of a quasilinear elliptic equation in RN which includes the so-called modified nonlinear Schrödinger equation as a special case. Combining the dual approach and the nonsmooth critical point theory, we obtain the existence of a nontrivial solution. References | Related Articles | Metrics

Select

LARGE TIME BEHAVIOR OF SOLUTION TO NONLINEAR DIRAC EQUATION IN 1+1 DIMENSIONS Yongqian ZHANG, Qin ZHAO Acta mathematica scientia,Series B. 2019, 39 (2):  597-606.  DOI: 10.1007/s10473-019-0221-7 Abstract ( 36 )   RICH HTML PDF   Save This paper studies the large time behavior of solution for a class of nonlinear massless Dirac equations in R1+1. It is shown that the solution will tend to travelling wave solution when time tends to infinity. References | Related Articles | Metrics

Select

NUMERICAL ANALYSIS FOR VOLTERRA INTEGRAL EQUATION WITH TWO KINDS OF DELAY Weishan ZHENG, Yanping CHEN Acta mathematica scientia,Series B. 2019, 39 (2):  607-617.  DOI: 10.1007/s10473-019-0222-6 Abstract ( 58 )   RICH HTML PDF   Save In this article, we study the Volterra integral equations with two kinds of delay that are proportional delay and nonproportional delay. We mainly use Chebyshev spectral collocation method to analyze them. First, we use variable transformation to transform the equation into an new equation which is defined in [-1, 1]. Then, with the help of Gronwall inequality and some other lemmas, we provide a rigorous error analysis for the proposed method, which shows that the numerical error decay exponentially in L∞ and Lωc2-norm. In the end, we give numerical test to confirm the conclusion. References | Related Articles | Metrics

Select

A GENERAL DECAY AND OPTIMAL DECAY RESULT IN A HEAT SYSTEM WITH A VISCOELASTIC TERM Abderrahmane YOUKANA, Salim A. MESSAOUDI, Aissa GUESMIA Acta mathematica scientia,Series B. 2019, 39 (2):  618-626.  DOI: 10.1007/s10473-019-0223-5 Abstract ( 44 )   RICH HTML PDF   Save We consider a quasilinear heat system in the presence of an integral term and establish a general and optimal decay result from which improves and generalizes several stability results in the literature. References | Related Articles | Metrics