[1] Auslander J.Minimal Flows and their Extensions. North-Holland Math Studies, Vol 153. Amsterdam: North-Holland, 1988
[2] Blanchard F. A disjointness theorem involving topological entropy. Bull Soc Math France, 1993, 121: 465-478
[3] Buzzi J. Piecewise isometries have zero topological entropy. Ergod Theor Dyn Syst, 2001, 21: 1371-1377
[4] Carvalho M D. Entropy dimension of dynamical systems. Portugaliae Math, 1997, 54: 19-40
[5] Cecherini-Silberstein T, Coornaert M.Cellular Automata and Groups. Berlin: Springer-Verlag, 2010
[6] Cao K, Dai X.Lifting the regionally proximal relation and characterizations of distal extensions. Discrete Contin Dyn Syst, 2022, 42: 2103-2174
[7] Dou D, Huang W, Park K K. Entropy dimension of topological dynamical systems. Trans Amer Math Soc, 2011, 363: 659-680
[8] Dou D, Huang W, Park K K. Entropy dimension of measure preserving systems. Trans Amer Math Soc, 2019, 371: 7029-7065
[9] Dai X, Liang H, Xiao Z. Characterizations of relativized distal points of topological dynamical systems. Topology and its Applications, 2021, 302: 107832
[10] Ellis R.Lectures on Topological Dynamics. New York: Benjamin, 1969
[11] Ferenczi S, Park K K. Enropy dimensions and a class of constructive examples. Discret Contin Dyn Sys, 2007, 17: 133-141
[12] Furstenberg H. Disjointness in ergodic theory, minimal sets,a problem in Diophantine approximation. Math Systems Theory, 1967, 1: 1-49
[13] Furstenberg H.Recurrence in Ergodic Theory and Combinatorial Number Theory. Princeton, New Jersey: Princeton University Press, 1981
[14] Gao J, Huang X, Zhu C. Sequence entropies and mean sequence dimension for amenable group actions. J Diff Equa, 2020, 269: 9404-9431
[15] Huang W, Park K K, Ye X. Topological disjointness from entropy zero systems. Bull Soc Math France, 2007, 135: 259-282
[16] Huang W, Ye X. Dynamical systems disjoint from any minmal system. Trans Amer Math Soc, 2004, 357: 669-694
[17] Huang W, Ye X, Zhang G. Local entropy theory for a countable discrete amenable group action. J Funct Anal, 2011, 261: 1028-1082
[18] Huang W, Ye X, Zhang G. Relative entropy tuples, relative U.P.E. and C.P.E. extensions. Israel J Math, 2007, 158: 249-283
[19] Lindenstrauss E. Pointwise theorems for amenable groups. Invent Math, 2001 146(2): 259-295
[20] Kuang R, Cheng W, Ma D, Li B. Different forms of entropy dimension for zero entropy systems. Dynamical Systems, 2014, 29(2): 239-254
[21] Kerr D, Li H. Ergodic Theory, Independence and Dicaotomies. Switzerland: Springer, 2016
[22] Kerr D, Li H. Independence in topological  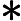 -dynamics. Math Ann, 2007, 338: 869-926 -dynamics. Math Ann, 2007, 338: 869-926
[23] McMahon D C. Relativized weak disjointness and relatively invariant measures. Trans Amer Math Soc, 1978, 236: 225-237
[24] Pan J, Zhou Y. Some results on bundle systems for a countable discrete amenable group action. Acta Math Sci, 2023, 43B(3): 1382-1402
[25] Sun P. Unique ergodicity for zero-entropy dynamical systems with the approximate product property. Acta Math Sin, 2021, 37: 362-376
[26] Zhou X. Relative entropy dimension of topological dynamical systems. Discrete Cont Dyn Syst, 2019, 39: 6631-6642 |