1 引言
21 世纪, 人类已经进入了信息化的时代, P2P 网络的应用已经遍布在社会活动和生产生活的各个领域当中. 王学龙和张璟[1]对 P2P 网络中各类关键技术进行分析研究, 如网络中的安全问题、资源搜索等技术, 分析了各类技术的研究现状等. 贺文华等[2]分析了 P2P 网络的特点及主要应用, 与传统网络节点在资源分散、拓扑结构等方面进行了比较, 最后分析了 P2P 网络的安全问题及面临的挑战. 穆筝等[3]对高速网络下 P2P 网络的流量进行了识别和研究, 主要研究了 P2P 流量的二元分类法, 其可以准确高效的对网络中的流量进行识别. 由于离散时间排队有着非常广泛的应用背景, 许多学者对其进行研究并取得了大量的成果. Tian 等[4]研究了多重工作休假的离散时间 Geom/Geom/1 排队, 利用拟生灭链和矩阵几何解的方法, 给出了系统队长、顾客等待时间的分布及其随机分解结构, 得到附加队长和附加延迟的分布. Wang 和 Zhang[5] 考虑了一个离散时间单服务台重试排队, 服务台可能出现故障和进行维修, 分析该排队系统的嵌入 Markov 链, 得到其遍历条件, 推导出重试轨道和系统内顾客数的概率母函数, 以及服务台空闲、繁忙或故障时轨道队长的边际分布. 陈佩树等[6]研究了有 Bernoulli 休假和可选服务的 Geo/G/1 重试排队.
在一些排队系统中, 如果到达的顾客不能立即得到服务, 顾客就会离开服务区, 进入重试轨道等待接受服务, 这就是排队中的重试现象. 重试排队已经被广泛应用于模拟计算机系统和电信网络中的许多实际问题. 在排队系统中经常会遇到服务台休假的问题, 在排队系统中引入各种休假策略可以更好的模拟现实生活中遇到的问题. Li 等[7]考虑了一个有工作休假和休假中断的 Geo/Geo/1 重试排队, 推导出了模型的稳定条件, 使用矩阵分析方法得到了稳态概率分布和系统的一些性能指标. Yang 等[8]考虑了一个有固定重试率和 J 可选休假的单服务台重试排队, 使用补充变量法得到系统队长分布的概率母函数, 得到一系列系统性能指标和两个可靠性指标. Arivudainambi 等[9]研究了一个有工作休假的单服务台重试排队系统, 得到了服务台状态的稳态分布和一些性能指标. 薛红和唐应辉[10]利用补充变量法和母函数法分析了有 Bernoulli 休假和负顾客到达的 Geo/G/1 重试排队并通过数值实例讨论不同参数对系统性能的影响. Manoharan 和 Sankarasasi[11] 考虑了一个带二次可选服务和二次可选休假的 M/G/1 违约排队模型并给出了该模型的几种特殊情况. 蔡梨等[12]考虑了一个有二次可选休假和一般重试时间的 Geo/G/1 离散时间重试排队模型.
在我们的实际生活当中, 具有优先权、不耐烦顾客的排队现象普遍存在. Wu 等[13]考虑了一个 Geo/G/1 重试排队, 给出了它的遍历条件, 得到系统的稳态分布和系统队长. Drekic 和 Woolford [14] 研究了一个有两类顾客的单服务台抢占优先权排队模型, 考虑了两种特定形式下的不耐烦行为, 通过广义特征值的方法推导系统中两种优先级顾客数的稳态联合分布. Rajadurai [15] 对有 Bernoulli 工作休假的单服务台优先权重试排队进行了稳态分析. Manoharan 和 Jeeva [16] 研究了有等待服务台和启动时间的 M/M/1 工作休假排队中的不耐烦顾客, 运用母函数法, 得到了稳态下系统的一系列关键性能指标. Lan 和 Tang [17] 研究了有优先权和不耐烦顾客的不可靠 Geo/G/1 重试排队系统, 利用补充变量法和母函数法, 推导出重试轨道和系统中顾客数的母函数以及稳态下系统的一些关键性能指标.
关于二次可选休假排队的研究较少, 本文将 P2P 网络中节点的动态变化抽象为排队模型, 将 P2P 网络中的请求节点和服务节点分别比作排队模型中的顾客和服务器, 把二次可选休假策略、优先权和不耐烦请求节点引入到离散时间 Geo/G/1 重试排队系统中, 建立排队模型. 利用嵌入 Markov 链的方法, 构造相应维数的 Markov 链, 利用补充变量法推导系统演化的平衡方程组, 求解得到该系统的一系列性能指标, 最后通过具体的数值例子讨论参数的变化对系统性能指标的影响.
2 模型描述
本文将 P2P 网络与排队论进行结合分析, 将 P2P 网络中请求节点比作排队论中的顾客, 将服务节点比作服务台, 将 P2P 网络的动态变化比作排队模型中的服务过程. 此外, 本文考虑一个单服务节点的早到系统, 假设时间轴被分割为等长的时隙, 被标记为
(1) 请求节点的到达间隔服从参数为
(2) 服务节点的服务时间独立同分布, 服从一般分布, 分布列为
(3) 假设到达过程、服务过程、重试过程和两次休假过程都是相互独立的, 且按先到先服务顺序.
3 模型分析
3.1 嵌入 Markov 链
在时刻
3.2 系统稳态分析
假设 Markov 链
令
如: 当
以此类推
根据平稳分布条件
其中
为求解方程 (3.1)-(3.5) 式, 引入部分母函数
通过求解以上方程组, 系统稳态分布的概率母函数被推导出来, 具体的解析表达式由以下的定理给出.
定理3.1 若
其中
证 将 (3.4)-(3.5) 式两边同乘
对
将 (3.2) 式两边同乘
在 (3.9) 式中令
在 (3.9) 式中令
将 (3.11)-(3.12) 式代入 (3.9)-(3.10) 式中, 将 (3.8) 式代入 (3.6)-(3.7) 式中, 再利用归一化条件确定常数
基于以上定理, 可以得到下面的结论
(1) 当服务节点空闲时, 重试轨道中请求节点数的概率母函数为
(2) 当服务节点工作时, 重试轨道中请求节点数的概率母函数为
(3) 当服务节点休假时, 重试轨道中请求节点数的概率母函数为
(4) 重试轨道中请求节点数 (用随机变量
(5) 系统中请求节点数 (用随机变量
其中,
3.3 系统的性能指标
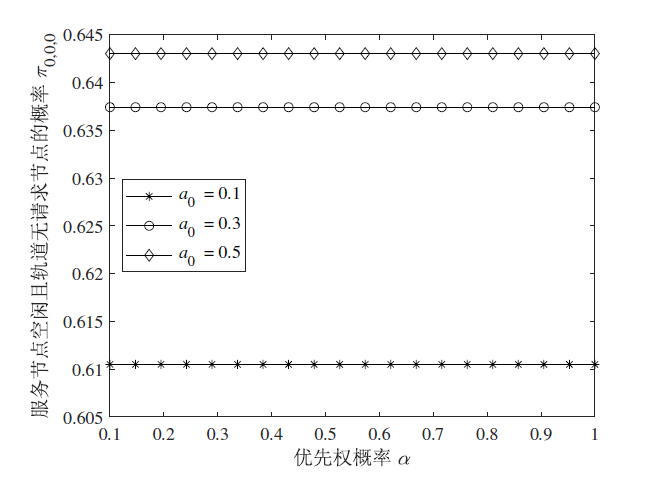
(1) 服务节点空闲且重试轨道无请求节点的概率为
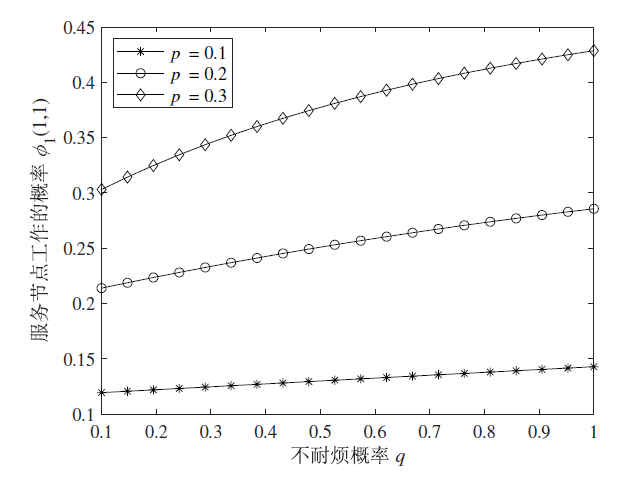
(2) 服务节点工作的概率为
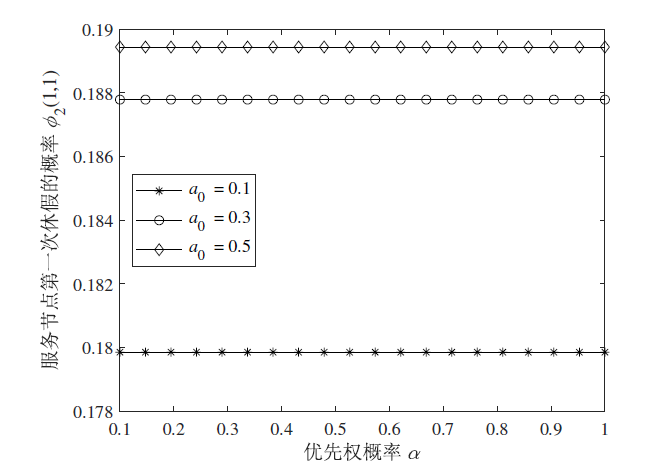
(3) 服务节点第一次休假的概率为
(4) 服务节点第二次休假的概率为
(5) 顾客在系统中的平均逗留时间为
其中
4 数值分析
图1
图2
图3
图4
图 1 描述的是当
图 2 描述的是当
图 3 描述的是当
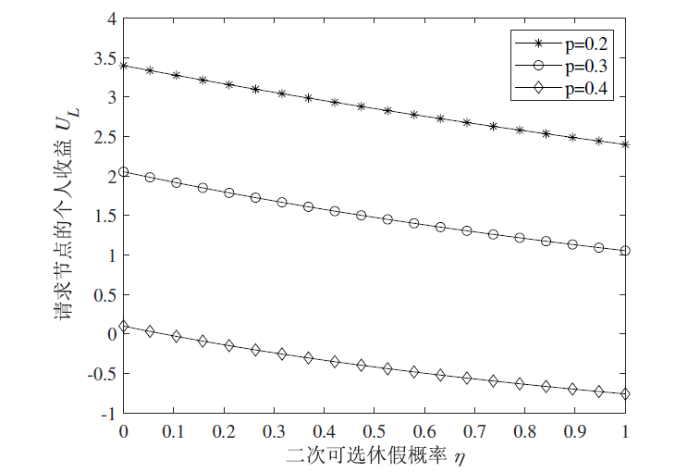
图 4 描述的是当
5 个人收益
假设请求节点完成服务获取收益为
假设服务时间服从参数为 0.7 的几何分布, 第一次休假时间和第二次休假时间分别服从参数为 0.4 和 0.6 的几何分布, 重试时间服从几何分布, 其母函数为
图5
6 结论
为分析 P2P 网络中请求节点的不同到达过程及服务节点的服务情况, 本文将 P2P 网络和排队论进行结合分析, 建立了基于 Geo/G/1 排队模型, 研究带二次可选休假、优先权和不耐烦请求节点的 Geo/G/1 重试排队模型. 利用嵌入 Markov 链的方法, 构造相应维数的 Markov 链, 再利用补充变量法求解得到该模型重试轨道和系统中请求节点数的概率母函数, 进而得到该系统的一系列性能指标如服务台处于各个状态的概率等, 通过分析一些具体的数值例子, 进一步研究不同的参数变化对系统性能指标的影响.
参考文献
P2P 关键技术研究综述
Survey on peer-to-peer key technologies
P2P 网络现状与发展研究
Research on the current situation and development of P2P network
高速网络下 P2P 流量识别研究
Research on P2P traffic identification under the high speed network
The discrete time Geom/Geom/1 queue with multiple working vacations
A discrete-time retrial queue with negative customers and unreliable server
有Bernoulli休假和可选服务的Geo/G/1重试排队
A discrete-time Geo/G/1 retrial queue with Bernoulli vacation and second optional service
Geo/Geo/1 retrial queue with working vacations and vacation interruption
On an unreliable retrial queue with general repeated attempts and J optional vacations
Performance analysis of a single server retrial queue with working vacation
具有 Bernoulli休假和负顾客到达的Geo/G/1早到达重试排队系统
Geo/G/1 early arrival retrial queueing system with negative customers and Bernoulli vacation
An M/G/1 reneging queueing system with second optional service and second optional vacation
带有二次可选休假和一般重试时间的Geo/G/1重试排队
A discrete-time Geo/G/1 retrial queue with second optional vacation and general retrial times
A discrete-time Geo/G/1 retrial queue with preferred and impatient customers
A preemptive priority queue with balking
A study on M/G/1 preemptive priority retrial queue with Bernoulli working vacations and vacation interruption
Impatient customers in an M/M/1 working vacation queue with a waiting server and setup time
An unreliable discrete-time retrial queue with probabilistic preemptive priority, balking customers and replacements of repair times
基于 N 抢占策略且播放器数可变的 P2P 网络性能分析
Performance analysis of P2P networks based on N-preemptive strategy and variable number of players
Performance analysis of a queueing system based on working vacation with repairable fault in the P2P network
Performance analysis of P2P network with dynamic changes of servers based on M/M/