具有复发和年龄结构的肺结核病传播模型的参数辨识性研究

图 1 状态变量转化流程图

由于肺结核病潜伏期到感染期进程缓慢, 因此将潜伏类到感染类的转化速率定义为一类依赖于年龄的函数 $\alpha(a)$

$\begin{equation}\label{eqn:2} \alpha(a)=\left\{\begin{aligned} &\bar {\alpha},&a\ge\tau, \\ &0,&a\le \tau, \end{aligned}\right. \end{equation}$

(1.2)

其中, $\tau$ 表示感染肺结核到表现出临床症状的时间. $\frac{1}{\bar {\alpha}}$ 表示潜伏期, 其他参数参见表 1.

表 1 参数的生物学意义及取值

模型 (1.1) 的初始条件为

$\begin{equation}\label{eqn:3} S(t) = S_0 \ge0, E(0,a)=E_0(a) \in L_+^1(0,+\infty), I(0)=I_0\ge0, T(0)=T_0\ge0. \end{equation}$

(1.3)

定义1.1 模型 (1.1) 的基本再生数为

$\begin{equation}\label{eqn:4} R_0 = \frac {\beta\Lambda\left( \int_0^\infty \alpha(a) {\rm e}^{-\int_0^a \delta(\theta){\rm d} \theta}{\rm d}a+ \frac{k }{k+d} \int_0^\infty \gamma_1 {\rm e}^{-\int_0^a \delta(\theta){\rm d} \theta}{\rm d}a \right)} {\mu(d+\mu+\gamma_2 -\frac{k}{k+d}\gamma_2)}, \end{equation}$

(1.4)

其中, ${\rm e}^{-\int_0^a \delta(\theta){\rm d} \theta}$ 表示潜伏个体待在潜伏态的时间为 $a$ 的概率, $\int_0^\infty \alpha(a) {\rm e}^{-\int_0^a \delta(\theta){\rm d} \theta}{\rm d}a$ 表示一个潜伏个体在整个生命周期内发展成染病个体的概率, $\frac{k }{k+d} \int_0^\infty \gamma_1 {\rm e}^{-\int_0^a \delta(\theta){\rm d} \theta}{\rm d}a$ 表示治愈个体在其生命周期内二次复发产生感染的概率, $\frac{1}{d+\mu+\gamma_2-\frac{k}{k+d}\gamma_2}$ 表示平均感染时间.

根据文献 [5,定理 1-3] 有如下引理

引理1.1 当 $R_0<1$ 时, 无病平衡点 $E^0=(\frac{\Lambda}{\mu},0,0,0)$ 是全局渐近稳定的. 当 $R_0>1$ 时, 地方病平衡点 $E^*=(S_*,E_*(a),I_*,T_*)$ 是全局渐近稳定的, 其中 $S_*= \frac{\Lambda}{{\rm d}R_0}$ , $E_*(a)=\Lambda {\rm e}^{-\int_0^a \delta(\theta){\rm d} \theta} (1-\frac{1}{R_0})$ , $I_*=\frac{d}{\beta}(R_0-1)$ , $T_*=\frac{\gamma_2 {\rm d} R_0+\gamma_1 \beta \Lambda}{R_0 \beta (k+d)}(R_0-1)$ .

若模型的参数是可辨识的, 则意味着由模型输出可以唯一确定一组参数值. 模型 (1.1) 是由常微分和偏微分方程组成的混合系统, 且模型中部分参数依赖病程 $a$ , 结构复杂. 目前鲜有针对具有结构性的偏微分系统模型参数辨识方面的研究结果^[8]. 经典的传染病模型参数辨识方法不再适用. 本文定量研究模型 (1.1) 参数辨识问题及模型参数不确定性对肺结核病传播和控制的影响.

2 模型参数的结构辨识性分析

模型参数的结构辨识性是指通过输入输出数据 (不考虑数据噪声) 确定模型的参数是否唯一的方法, 因此称为先验可辨识性分析. 假设模型满足如下系统

$\begin{matrix} \frac{{\rm d}x}{{\rm d}t}=f(x,p),\notag\\ y(x,p)=g(x,p),\label{eqn:abs} \end{matrix}$

(2.1)

其中 $x=(S,\int_0^\infty E(a,\cdot){\rm d}a,I,T)$ 表示模型 (1.1) 的状态变量, $y$ 表示输出变量, $p$ 表示模型 (1.1) 的参数.

定义2.1^[6] 对于系统 (2.1) 的任意两个参数集 $p_1,p_2$ , 如果有 $y(x,p_1)=y(x,p_2)\Longleftrightarrow p_1=p_2,$ 则称该系统是全局结构可辨识的.

定义 (2.1)表明, 参数值的微小变化导致模型不同的输出或预测. 换言之, 当 $p_1\neq p_2$ 时, $y(x,p_1)\neq y(x,p_2)$ . 本节延拓传统的特征值方法研究模型 (1.1) 的结构可辨识性^[6]. 由文献 [9] 知, 我们定义如下敏感性矩阵

$\begin{equation}\label{eqn:juzhen} S= \begin{bmatrix} s_{1,1} &\cdots & s_{1,i}\\ \vdots & \ddots & \vdots \\ s_{j,1} &\cdots& s_{j,i}\\ \end{bmatrix},s_{j,i} = \frac{\partial y(t_j,p)}{\partial p^i}, \end{equation}$

(2.2)

其中, $p^i$ 表示参数 $p$ 的第 $i$ 个参数, $y(t_j,p)$ 表示在 $t_j$ 时刻系统 (2.1) 的输出变量. 输出变量 $y$ 沿着某个参数的特征向量 $\gamma$ 线性近似可表示为

$y(t_j,p+\epsilon\gamma) \approx y (t_j,p)+\epsilon\sum\limits_{i}\frac{\partial y (t_j,p)}{\partial p^i}\gamma_i,$

这里 $\epsilon$ 为任意小常数. 若残差成本函数为 $SSE=\sum\limits_{j=1}^m | y(t_j,p)-Y^j|^2$ , 则我们有

$\frac{\partial (SSE)}{\partial p^i} (p)=2\sum\limits_{j=1}^m \left( y(t_j,p)-Y^j\right)s_{j,i}(p)=0, \forall i=1,\cdots,4,$

其中 $Y^j$ 表示真实数据集的第 $j$ 个分量. 进而, 残差成本函数沿某个参数的特征向量 $\gamma$ 的扰动可以近似为

$\begin{equation}\label{eqn:perturbation} SSE\left( p+\epsilon\gamma \right)-SSE(p)\approx \epsilon^2\gamma^TS^TS\gamma, \end{equation}$

(2.3)

其中, $S$ 为敏感性矩阵 (2.2). 假设 $S^TS$ 的特征值 $\lambda$ 及其对应的正规化特征向量为 $\gamma$ , 即 $S^TS\gamma=\lambda \gamma,$ 那么方程 (2.3) 可化简为

$SSE\left( p+\epsilon\gamma \right)-SSE(p)\approx \epsilon^2\lambda\in \mathcal{O}(\lambda).$

如果 $\lambda$ 充分小, 则意味着沿 $\gamma$ 方向成本函数相当平坦, 进而在 $\gamma$ 中可以寻找不可辨识的参数. 重复上述过程, 我们将 $S$ 中所有的特征值和特征向量进行排序和比较, 获得参数不可辨识的排序. 详细步骤如下

(i) 计算敏感性矩阵乘积 $S^TS:=S_A$ ;

(ii) 计算矩阵 $S_A$ 的特征值及其对应特征向量;

(iii) 将特征值按照从小到大排序;

(iv) 寻找步骤 (iii) 中绝对值最小的特征值及其特征向量中绝对值最大分量, 定义该分量对应的参数为最不可辨识的参数;

(v) 重复步骤 (iv) 将其他参数进行排序, 即可得到参数辨识可能性的排序.

由于报道病例和实际感染病例间存在误差, 我们引入参数 $\varsigma$ 表示报道率. 故本文选择残差成本函数为 $SSE=\sum\limits_{j=1}^m |\varsigma y(t_j,p)-Y^j|^2$ . 由 (2.2) 式得

$\begin{equation}\label{eqn:juzhenM} S_A= \begin{pmatrix} -1.08\times10^{48}& -9.59\times10^{56}& -4.60\times10^{47}& 4.94\times10^{47}& -1.28\times10^{49}\\ -9.59\times 10^{56}& 8.52\times 10^{65}& 4.09\times 10^{56}& -4.39\times 10^{56}& 1.14\times10^{58} \\ -4.60\times 10^{47}& 4.09\times 10^{56}& 1.96\times 10^{47}& -2.10\times 10^{47}& 5.46\times10^{48}\\ 4.94\times 10^{47}& -4.39\times 10^{56}& -2.10\times 10^{47}& 2.26\times 10^{47}& -5.86\times10^{48}\\ -1.28\times 10^{49}& 1.14\times 10^{58}& 5.46\times 10^{48}& -5.68\times 10^{48}& 1.52\times10^{50}\\ \end{pmatrix}. \end{equation}$

(2.4)

事实上, 矩阵 (2.4) 的对角线元素表征参数 $\alpha$ , $\beta$ , $k$ , $\gamma_2$ , $\varsigma$ 对输出变量的敏感性大小. 进一步计算其对应的特征值为 $-3.06\times10^{33},2.14\times10^{31},1.76\times10^{49},1.87\times10^{50},8.52\times10^{65}$ 及对应特征向量为

$\begin{array}{l} \gamma_{\alpha}=\left(\begin{array}{lllll} 9.97 \times 10^{-1} & 1.08 \times 10^{-9} & 8.35 \times 10^{-2} & 1.54 \times 10^{-8} & -2.13 \times 10^{-16} \end{array}\right)^{T}, \\ \gamma_{\beta}=\left(\begin{array}{lllll} -8.35 \times 10^{-2} & -5.72 \times 10^{-10} & 9.97 \times 10^{-1} & -7.33 \times 10^{-10} & 1.67 \times 10^{-17} \end{array}\right)^{T} \\ \gamma_{k}=\left(\begin{array}{lllll} -1.54 \times 10^{-8} & 5.15 \times 10^{-10} & -5.55 \times 10^{-10} & 1.00 & -1.47 \times 10^{-8} \end{array}\right)^{T} \\ \gamma_{\gamma_{2}}=\left(\begin{array}{lllll} 1.48 \times 10^{-17} & 1.34 \times 10^{-8} & 1.35 \times 10^{-17} & -1.47 \times 10^{-8} & -1.00 \end{array}\right)^{T} \\ \gamma_{\varsigma}=\left(\begin{array}{lllll} -1.13 \times 10^{-9} & 1.00 & 4.79 \times 10^{-10} & -5.15 \times 10^{-10} & 1.34 \times 10^{-8} \end{array}\right)^{T} \end{array}$

观察发现, 参数辨识可能性的排序依次为 $p=\{k,\alpha,\gamma_2,\varsigma,\beta\}$ . 其中, $k$ 最不可辨识, $\beta$ 最可辨识.

3 数据拟合和参数选择

我们选取公共卫生数据中心提供的中国 2010--2018 年肺结核病例数为研究对象. 依据 2011 年中国统计年鉴^[10]计算得总人口为 $N(2010)=1.33474\times10^9$ . 2010 年全国结核病抽样调查结果^[7]表明 $S(0)= 0.8 \times N(0)= 1.0678 \times 10^9$ . 另外, 由文献[11] 知 $I(0)= 4.99 \times 10^6$ . 利用 2010 年肺结核病年龄分布的数据^[10]拟合潜伏类肺结核初值为 $E(0,a) = - 0.4434a^2+380.9524a+4353$ (如图 2(a)). 通过查阅文献 [10,12] 知出生率 $\Lambda=1.6346\times10^7/$ 年, 自然死亡率 $d= 0.007/$ 年, 因病死亡率 $\mu= 0.0025/$ 年. 选取与第2节一致的成本函数, 利用如下最小二乘法

$\begin{equation}\label{eqn:5} SSE=\sum\limits_{j=1}^m |\varsigma y(t_j)-Y^j|^2,~ y(t_j) = \int_0^\infty E(t_j,a){\rm d}a+I(t_j), \end{equation}$

(3.1)

结合 Matlab 程序拟合数据, 其中 $y(t_j)$ 表示输出变量, $\varsigma$ 表示报道率, $Y^j(j=1,2\cdots9)$ 表示真实数据集, SSE 表示残差成本函数.

图 2

图 2 (a) 2010 年各年龄段潜伏类病例拟合图 (b) 肺结核病报道病例和模型解的拟合图

图 2(b) 给出模型 (1.1) 解和报道肺结核病例的拟合图. 表 2 给出拟合得到的模型 (1.1) 参数值. 不难发现, 图 2(b) 表明模型 (1.1) 的解能有效拟合 2010--2018 年中国肺结核病例数, 拟合效果较好. 接下来, 我们致力于探究模型参数的实用辨识性及各参数对肺结核传播的影响.

表 2 拟合的参数值

4 实用辨识性分析

在实际中, 由于测量误差和技术等限制, 观测数据往往耦含大量观测误差. 因此, 模型 (1.1) 的参数即使是结构可辨识的, 但由于数据噪声的影响, 其也有可能是实用不可辨识的. 本节利用蒙特卡洛模拟验证模型参数的实用辨识性. 首先, 利用表 2 中估计出的参数集生成具有某种误差分布的数据集 $Y$ . 我们假设测量误差与数据成正比且满足正态分布, 即观测数据有如下形式^[13]误差结构

$\begin{equation}\label{eqn:6} \omega_j = y(t_j,\hat{p})\varepsilon_j,Y_j=N(y (t_j,\hat{p}),y (t_j,\hat{p}) \sigma_0),j=1,2 \cdots n, \end{equation}$

(4.1)

其中, 随机变量 $\varepsilon_j$ 是独立分布的, 其平均值为 $0$ 、标准差为 $\sigma_0$ , $\hat{p}$ 表示估计的参数值. 因此, 随机变量 $Y_j$ 的均值为 $y(t_j,\hat{p})$ , 标准差为 $y (t_j,\hat{p})\sigma_0$ .

接着, 我们将误差水平从 $\sigma_0=0.01$ 逐渐增加到 $0.05$ , $0.1$ 和 $0.2$ , 使用 Matlab 软件进行蒙特卡洛模拟. 从图 3 可以看出, 随着误差水平的增大, 拟合效果越差. 比较图 3(b) 和图 2(b), 实验生成的具有误差水平 $5\%$ 的数据集与真实数据集相似. 因此, 在数据拟合时, 考虑数据的噪声强度, 避免拟合结论错误.

图 3

图 3 不同误差水平的蒙特卡洛模拟: 红点表示从 2010 到 2018 年数据集, 蓝线表示模型的解

为了定量评价不同误差水平对参数估计的影响, 我们通过求解最优化问题(3.1) 生成参数集 $p$ , 并计算每个噪声水平下的平均相对误差 (ARE)

$\begin{equation}\label{eqn:7} ARE(p^i)=\frac{1}{M}\sum\limits_{j=1}^M \frac{\hat{p}^i-p_j^i }{\hat{p}^i}, \end{equation}$

(4.2)

这里取 $M=1000$ , 表示进行了 1000 次蒙特卡洛模拟, $\hat{p}^i$ 表示拟合得到的参数集 $\hat{p}$ 中的第 $i$ 个参数, $p_j^i$ 表示第 $j$ 次生成随机变量参数集中的第 $i$ 个参数. 各参数在每个误差水平下的 ARE 值参见表 3.

表 3 各噪声水平下参数的 ARE 值

通常, 参数的 ARE 水平用于评估模型参数的实用辨识性. 表 3 表明参数 $\gamma_2$ 、 $k$ 和 $\alpha$ 的 ARE 水平随着误差水平的增加而增加且增幅不大. 参数 $\beta$ 和 $\varsigma$ 的 ARE 值始终小于误差水平, 且处于合理的波动范围. 因此, 模型 (1.1) 的参数 $\gamma_2$ 、 $k$ 、 $\alpha$ 、 $\beta$ 、 $\varsigma$ 是可辨识的. 这也验证了第 3 节中模型拟合的合理性和正确性.

在信息论中, 熵是度量信息不确定性的重要概念. 在数理统计中, 通常用 Fisher 信息来度量随机变量关于随机分布函数中未知参数 $p$ 的信息量. 简单来说, Fisher 信息可以认为是熵的曲率. 本文我们利用 Fisher 信息矩阵表征模型中参数的不确定性程度^[14], 即对应的 Fisher 信息矩阵中对角线元素数值越大, 参数不确定性越高. 定义如下 Fisher 信息矩阵^[6]

$\begin{equation}\label{eqn:8} FIM=\sum\limits_{i=1}^N \left(\frac{\partial \hat{y}_i}{\partial \hat{p}}\right)^TV^{-1} \left(\frac{\partial \hat{y}_i}{\partial \hat{p}}\right), \end{equation}$

(4.3)

其中, $N$ 表示总观测值的数量, $\hat{y}_i$ 表示模型的解, $\hat{p}$ 表示估计出的模型参数近似值, $V$ 表示协方差矩阵. 利用 (4.3) 式计算得

$\begin{equation}\label{eqn:9} FIM= \begin{pmatrix} 1.3878 & -1.0960\times10^{10} &0.6614 & 8.9105\\ -1.0960\times10^{10} & 9.29\times10^{19} & -5.9546\times10^9 & -7.5580\times10^{10}\\ 0.6614 & -5.9546\times10^9 & 0.5139 & 4.7661\\ 8.9105\times10^{10} & -7.5580\times10^{10} & -5.9546\times10^9 & 61.5560\\ \end{pmatrix}. \end{equation}$

(4.4)

矩阵 (4.4) 中对角线元素依次表征参数 $\alpha$ , $\beta$ , $k$ , $\gamma_2$ 不确定性的大小. 从矩阵 (4.4) 的对角线元素可以看出, $\beta$ 的不确定性最大. 因此, 我们认为 $\beta$ 最敏感, 这与矩阵 (2.4) 得到的结果一致.

5 敏感性分析

敏感性分析研究数学模型或系统输入的不确定性对输出结果的影响, 是衡量模型参数变化对传染病动力学行为影响的有用工具, 尤其是对于量化疾病控制策略的预期疗效至关重要^[15]. 该方法已被广泛用于常微分组成的传染病动力学模型, 本节对具有初边值条件的年龄结构传染病模型进行敏感性分析.

5.1 局部敏感性分析

引理 1.1表明系统 (1.1) 展现出阈值动力学, 其动力学性态完全由 $R_0$ 决定, 即, 当 $R_0<1$ , 疾病灭绝; 当 $R_0>1$ , 疾病流行. 因此, 我们应优先考虑参数对 $R_0$ 的敏感性.

本小节主要考虑 $p = \{\alpha,\beta, k, \gamma_2 \}$ 对基本再生数的敏感性. 为此, 定义敏感性分析指标^[15] 为

$\varphi_p^{R_0} :=\frac{\partial R_0}{\partial p}\frac{p}{ R_0}.$

若 $\varphi_p>0$ , 即当 $p$ 增加 1% 时, 基本再生数 $R_0$ 增加 $\varphi_p \%$ . 计算结果如表 4

表 4 参数对 $R_0$ 的影响

从表 4 可以看出, 基本再生数和传染率 $\beta$ 是正相关的. 也就是说, 对于控制肺结核病, 增加社交距离及增强自身免疫力 (降低有效接触率 $\beta$ ) 对降低肺结核传播风险最为显著. 其次, 延长潜伏期 $1/\alpha$ 能有效缓减肺结核暴发风险. 因此对于通过凃阳及 X 光检测发现的潜伏肺结核患者, 应积极服用异烟肼药物延迟进入感染类风险. 再次, 提高治愈率 $\gamma_2$ 或缩短病程可有效降低基本再生数 $R_0$ . 最后, 降低复发率 $k$ 能减小 $R_0$ , 因此对于初次患病的结核病患者, 应及时服用异烟肼、利福平、吡嗪酰胺、乙胺丁醇等一线药物并严格按疗程服用, 避免二次感染肺结核杆菌.

5.2 全局敏感性分析

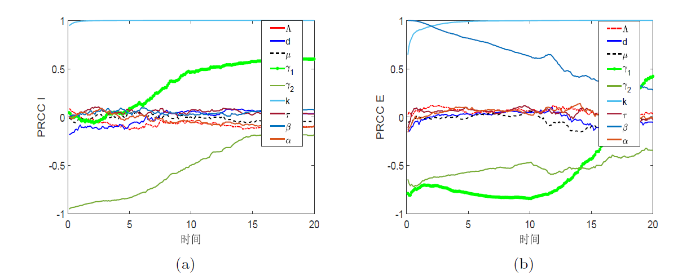
上述弹性分析是基于某个参数变化其余参数固定的局部静态结论. 对于疾病的控制, 我们需要考虑社会资源, 即最好在适当的时机采取恰当的措施, 利用现有的人力物力达到最好的控制效果. 因此我们对模型中参数利用偏秩相关系数 (PRCC) 进行全局敏感性分析^[16]. PRCC 衡量各个参数关于感兴趣的状态变量随时间变化的影响, 特别地, PRCC 清晰的呈现参数对变量的依赖程度, 大于 0 表示正相关, 小于 0 表示负相关, 并且绝对值越大意味着相关性越强 (如图 4).

从图 4 可以发现, 不论对于染病群体 $I$ 还是潜伏群体 $E$ , 疾病的复发率 $k$ 在整个疾病周期内始终接近 1, 和肺结核的传播呈现正相关性. 在整个肺结核传播周期内, 控制疾病的复发率可显著降低染病者的数量, 从而抑制肺结核病例的增长. 因此, 对于初次痊愈的结核病患者及时服用异烟肼、利福平、吡嗪酰胺、乙胺丁醇等药物, 严格遵照医嘱服用避免肺结核病的二次复发.

图 4

图 4 (a) 参数对变量 I 的 PRCC 动态龙卷分析图 (b) 参数对变量 E 的 PRCC 动态龙卷分析图

此外, 在肺结核病感染初期提高潜伏个体的恢复率 $\gamma_1$ 或缩短治疗病程能有效缓减肺结核病传播风险. 对于复发的潜伏患者, 往往是耐药或耐多药性患者, 此时应结合氟喹诺酮类、阿米卡星、卷曲霉素、乙硫异烟胺等二线药物进行治疗, 注意佩戴口罩和个人防护, 从而有效减少凃阳患者数量^[17].

图 4(a) 表明恢复率 $\gamma_2$ 在整个染病周期内对肺结核患者有较强的负相关性. 需要注意的是, 与初次感染的结核病患者相比, 对重复染病者采取以中西医结合为代表的综合疗法, 从补虚, 杀菌和活血化瘀三个方面进行, 内服与外贴相配合, 破环结核菌生存的内环境, 有效缩短疗程[18]. 对于药物治疗失败或威胁生命的单侧肺结核病变应积极进行手术治疗.

此外, 从图 4(b) 注意到, 随着肺结核病的发展, 传染率 $\beta$ 与潜伏类个体的正相关性随病程逐渐减弱. 因此, 对于初次感染痊愈的肺结核患者, 应做好定期检测, 发现异常及时进行自我隔离, 避免去人群密集的地方造成大范围传播. 在日常生活中要积极提高免疫力、按时作息、保持良好的生活习惯, 有效避免外界肺结核菌造成自身二次感染.

6 总结

模型的参数辨识是通过观测模型结构并依据数据分析, 估计模型中的未知参数的数值. 在实际中, 由于模型的复杂性及数据数量和噪声等因素, 通常参数是不可辨识的, 那么预测结果可能不准确. 尽管目前已有许多针对常微分系统参数辨识的方法, 但鲜有针对年龄结构偏微分系统参数辨识的结论^[8].

本文首先利用特征值方法对模型中参数进行结构辨识性分析, 依据辨识结果对不可辨识参数的可能性排序. 其次利用中国肺结核病数据拟合一类具有复发和年龄结构的肺结核病模型. 接着, 通过蒙特卡洛模拟及计算参数的相对误差值 (ARE), 得出在控制其他参数后, 我们研究的参数都是实用可辨识的. 这也验证了拟合结果的正确性. 最后, 通过局部敏感性分析和全局敏感性分析 (PRCC) 得知, 传染率 $\beta$ 和康复率 $\gamma_2$ 是相对敏感的. 参数的敏感性表明在控制和预防肺结核病传播时, 尽可能地减少个体间接触, 提高对潜伏期和感染期个体的治疗水平, 降低复发, 从而有效降低肺结核病传播的风险.

本文虽然利用特征值方法, Fisher 熵理论及蒙特卡洛模拟评估了模型的可辨识性, 但没有考虑有限元差分结构对模型误差收敛阶数及收敛速度. 另外, 尽管模型结构的复杂性为参数的结构辨识性带来挑战, 但主成分分析法可以规避一些结构辨识性计算问题^[9]. 因此, 我们接下来继续讨论模型的差分格式的精度和参数结构可辨识性等方面的问题.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

世界卫生组织.[2022-10-27]. https://www.who.int/zh/news-room/fact-sheets/detail/tuberculosis.

URL [本文引用: 2]

WHO World Health Organization. [2022-10-27]. https://www.who.int/zh/news-room/fact-sheets/detail/tuberculosis.

URL [本文引用: 2]

[2]

中国疾病预防控制中心. [2022-05-26]. https://www.chinacdc.cn/jkzt/crb/zl/jhb/jszl-2221.

Chinese Center for Disease Control and Prevention. [2022-05-26]. https://www.chinacdc.cn/jkzt/crb/zl/jhb/jszl-2221.

[3]

Van den Driessche

, Zou

Modeling relapse in infectious diseases

Mathematical Biosciences, 2007, 207(1): 89-103

PMID:17112547 [本文引用: 1]

An integro-differential equation is proposed to model a general relapse phenomenon in infectious diseases including herpes. The basic reproduction number R(0) for the model is identified and the threshold property of R(0) established. For the case of a constant relapse period (giving a delay differential equation), this is achieved by conducting a linear stability analysis of the model, and employing the Lyapunov-Razumikhin technique and monotone dynamical systems theory for global results. Numerical simulations, with parameters relevant for herpes, are presented to complement the theoretical results, and no evidence of sustained oscillatory solutions is found.

[4]

Wallis

R S

Mathematical models of tuberculosis reactivation and relapse

Frontiers in Microbiology, 2016, 7: Article 669

DOI:10.3389/fmicb.2016.00669 PMID:27242697 [本文引用: 1]

The natural history of human infection with Mycobacterium tuberculosis (Mtb) is highly variable, as is the response to treatment of active tuberculosis. There is presently no direct means to identify individuals in whom Mtb infection has been eradicated, whether by a bactericidal immune response or sterilizing antimicrobial chemotherapy. Mathematical models can assist in such circumstances by measuring or predicting events that cannot be directly observed. The 3 models discussed in this review illustrate instances in which mathematical models were used to identify individuals with innate resistance to Mtb infection, determine the etiologic mechanism of tuberculosis in patients treated with tumor necrosis factor blockers, and predict the risk of relapse in persons undergoing tuberculosis treatment. These examples illustrate the power of various types of mathematic models to increase knowledge and thereby inform interventions in the present global tuberculosis epidemic.

[5]

Liu

, Zhang

, Li

, Liu

On the global stability of an age-structured tuberculosis transmission model with relapse

Mathematical Methods in the Applied Sciences, 2022, 45(9): 5622-5630

[本文引用: 2]

[6]

Miao

, Xia

, Perelson

A S

, Wu

On identifiability of nonlinear ODE models and applications in viral dynamics

SIAM Review, 2011, 53(1): 3-39

PMID:21785515 [本文引用: 4]

Ordinary differential equations (ODE) are a powerful tool for modeling dynamic processes with wide applications in a variety of scientific fields. Over the last 2 decades, ODEs have also emerged as a prevailing tool in various biomedical research fields, especially in infectious disease modeling. In practice, it is important and necessary to determine unknown parameters in ODE models based on experimental data. Identifiability analysis is the first step in determing unknown parameters in ODE models and such analysis techniques for nonlinear ODE models are still under development. In this article, we review identifiability analysis methodologies for nonlinear ODE models developed in the past one to two decades, including structural identifiability analysis, practical identifiability analysis and sensitivity-based identifiability analysis. Some advanced topics and ongoing research are also briefly reviewed. Finally, some examples from modeling viral dynamics of HIV, influenza and hepatitis viruses are given to illustrate how to apply these identifiability analysis methods in practice.

[7]

Cao

, Gao

, Yan

, Zhang

The dynamics of an age-structured TB transmission model with relapse

Mathematical Methods in the Applied Sciences, 2020, 43(6): 3807-3826

[本文引用: 2]

[8]

Tuncer

, Gulbudak

, Cannataro

V L

, Martcheva

Structural and practical identifiability issues of immuno-epidemiological vector-host models with application to rift valley fever

Bulletin of Mathematical Biology, 2016, 78: 1796-1827

PMID:27651156 [本文引用: 2]

In this article, we discuss the structural and practical identifiability of a nested immuno-epidemiological model of arbovirus diseases, where host-vector transmission rate, host recovery, and disease-induced death rates are governed by the within-host immune system. We incorporate the newest ideas and the most up-to-date features of numerical methods to fit multi-scale models to multi-scale data. For an immunological model, we use Rift Valley Fever Virus (RVFV) time-series data obtained from livestock under laboratory experiments, and for an epidemiological model we incorporate a human compartment to the nested model and use the number of human RVFV cases reported by the CDC during the 2006-2007 Kenya outbreak. We show that the immunological model is not structurally identifiable for the measurements of time-series viremia concentrations in the host. Thus, we study the non-dimensionalized and scaled versions of the immunological model and prove that both are structurally globally identifiable. After fixing estimated parameter values for the immunological model derived from the scaled model, we develop a numerical method to fit observable RVFV epidemiological data to the nested model for the remaining parameter values of the multi-scale system. For the given (CDC) data set, Monte Carlo simulations indicate that only three parameters of the epidemiological model are practically identifiable when the immune model parameters are fixed. Alternatively, we fit the multi-scale data to the multi-scale model simultaneously. Monte Carlo simulations for the simultaneous fitting suggest that the parameters of the immunological model and the parameters of the immuno-epidemiological model are practically identifiable. We suggest that analytic approaches for studying the structural identifiability of nested models are a necessity, so that identifiable parameter combinations can be derived to reparameterize the nested model to obtain an identifiable one. This is a crucial step in developing multi-scale models which explain multi-scale data.

[9]

Guillén-González

, Sevillano-Castellano

, Suárez

Fitting parameters and therapies of ODE tumor models with senescence and immune system

Journal of Mathematical Biology, 2023, 87(5): Article 67

DOI:10.1007/s00285-023-02000-9 PMID:37805974 [本文引用: 2]

This work is devoted to introduce and study two quasispecies nonlinear ODE systems that model the behavior of tumor cell populations organized in different states. In the first model, replicative, senescent, extended lifespan, immortal and tumor cells are considered, while the second also includes immune cells. We fit the parameters regulating the transmission between states in order to approximate the outcomes of the models to a real progressive tumor invasion. After that, we study the identifiability of the fitted parameters, by using two sensitivity analysis methods. Then, we show that an adequate reduced fitting process (only accounting to the most identifiable parameters) gives similar results but saving computational cost. Three different therapies are introduced in the models to shrink (progressively in time) the tumor, while the replicative and senescent cells invade. Each therapy is identified to a dimensionless parameter. Then, we make a fitting process of the therapies' parameters, in various scenarios depending on the initial tumor according to the time when the therapies started. We conclude that, although the optimal combination of therapies depends on the size of initial tumor, the most efficient therapy is the reinforcement of the immune system. Finally, an identifiability analysis allows us to detect a limitation in the therapy outcomes. In fact, perturbing the optimal combination of therapies under an appropriate therapeutic vector produces virtually the same results.© 2023. The Author(s).

[10]

国家统计局. [2017]. http://www.stats.gov.cn/tjst/ndsj/.

URL [本文引用: 3]

National Bureau of Statistics. [2017]. http://www.stats.gov.cn/tjst/ndsj/.

URL [本文引用: 3]

[11]

全国结核病学抽样调查技术指导组.

2000年全国结核病流行病学抽样调查报告

中国防痨杂志, 2022, 4: 65-66

National Technical Steering Group of the Epidemiological Sampling Survey for Tuberculosis.

Report on nationwide random survey for the epidemiology of tuberculosis in 2000

Chinese Journal of Tuberculosis Prevention, 2002, 4: 65-66

[12]

全球结核病报告. [2018]. http://www.who.int/tb/publications/global{-}report/en/.

Global Tuberculosis Report. [2018]. http://www.who.int/tb/publications/global{-}report/en/.

[13]

Tuncer

, Timsina

, Nuno

, et al.

Parameter identifiability and optimal control of an SARS-CoV-2 model early in the pandemic

Journal of Biological Dynamics, 2022, 16(1): 412-438

DOI:10.1080/17513758.2022.2078899 PMID:35635313 [本文引用: 1]

We fit an SARS-CoV-2 model to US data of COVID-19 cases and deaths. We conclude that the model is not structurally identifiable. We make the model identifiable by prefixing some of the parameters from external information. Practical identifiability of the model through Monte Carlo simulations reveals that two of the parameters may not be practically identifiable. With thus identified parameters, we set up an optimal control problem with social distancing and isolation as control variables. We investigate two scenarios: the controls are applied for the entire duration and the controls are applied only for the period of time. Our results show that if the controls are applied early in the epidemic, the reduction in the infected classes is at least an order of magnitude higher compared to when controls are applied with 2-week delay. Further, removing the controls before the pandemic ends leads to rebound of the infected classes.

[14]

Renardy

, Kirschner

, Eisenberg

Structural identifiability analysis of age-structured PDE epidemic models

Journal of Mathematical Biology, 2022, 84(1): Article 9

[15]

Gulbudak

, Qu

, Milner

, Tuncer

Sensitivity analysis in an immuno-epidemiological vector-host model

Bulletin of Mathematical Biology, 2022, 84(2): Article 27

DOI:10.1007/s11538-021-00979-0 PMID:34982249 [本文引用: 2]

Sensitivity Analysis (SA) is a useful tool to measure the impact of changes in model parameters on the infection dynamics, particularly to quantify the expected efficacy of disease control strategies. SA has only been applied to epidemic models at the population level, ignoring the effect of within-host virus-with-immune-system interactions on the disease spread. Connecting the scales from individual to population can help inform drug and vaccine development. Thus the value of understanding the impact of immunological parameters on epidemiological quantities. Here we consider an age-since-infection structured vector-host model, in which epidemiological parameters are formulated as functions of within-host virus and antibody densities, governed by an ODE system. We then use SA for these immuno-epidemiological models to investigate the impact of immunological parameters on population-level disease dynamics such as basic reproduction number, final size of the epidemic or the infectiousness at different phases of an outbreak. As a case study, we consider Rift Valley Fever Disease utilizing parameter estimations from prior studies. SA indicates that [Formula: see text] increase in within-host pathogen growth rate can lead up to [Formula: see text] increase in [Formula: see text] up to [Formula: see text] increase in steady-state infected host abundance, and up to [Formula: see text] increase in infectiousness of hosts when the reproduction number [Formula: see text] is larger than one. These significant increases in population-scale disease quantities suggest that control strategies that reduce the within-host pathogen growth can be important in reducing disease prevalence.© 2021. The Author(s), under exclusive licence to Society for Mathematical Biology.

[16]

邓萌, 徐瑞.

一类具有 CTL 免疫反应和免疫损害的 HIV 感染动力学模型的稳定性分析

数学物理学报, 2022, 42A(5): 1592-1600

Deng

, Xu

Stability analysis of an HIV infection dynamic model with CTL immune response and immune impairment

Acta Math Sci, 2022, 42A(5): 1592-1600

[17]

张洪铎

个体化治疗耐多药肺结核失败的影响因素分析

临床合理用药杂志, 2017, 15: 108-109

Zhang

H Z

Analysis of the influencing factors of individualized treatment failure for multidrug-resistant pulmonary tuberculosis

Journal of Clinical Rational Drug Use, 2017, 15: 108-109

[18]

张雪元

利福喷丁与利福平在肺结核治疗中的药效比较及安全性分析

中国医药指南, 2021, 1: 36-37

Zhang

X Y

Comparison of efficacy and safety analysis of rifampicin and rifampicin in the treatment of pulmonary tuberculosis

Guide of China Medicine, 2021, 1: 36-37