一类具有变系数的非线性延迟微分方程数值解的振动性分析

一类具有变系数的非线性延迟微分方程数值解的振动性分析

胡冰冰^,¹, 高建芳^,¹^,²^,^*

¹哈尔滨师范大学数学科学学院哈尔滨 150025

²哈尔滨师范大学黑龙江省机器学习与动态系统分析重点实验室哈尔滨 150025

Oscillation Analysis of Numerical Solutions for a Class of Nonlinear Delay Differential Equations with Variable Coefficients

Hu Bingbing^,¹, Gao Jianfang^,¹^,²^,^*

¹School of Mathematical Sciences, Harbin Normal University, Harbin 150025

²Heilongjiang Key Laboratory of Analysis on Machine Learing and Dynamic System, Harbin Normal University, Harbin 150025

通讯作者: * 高建芳,E-mail:09151108@163.com

收稿日期: 2023-05-22 修回日期: 2024-06-6

基金资助:

黑龙江省机器学习与动态系统分析重点实验室开放研究基金(HLJKL2505)

Received: 2023-05-22 Revised: 2024-06-6

Fund supported:

Open Research Fund of Heilongjiang Key Laboratory of Analysis on Machine Learning and Dynamic System(HLJKL2505)

作者简介 About authors

胡冰冰,E-mail:2836522449@qq.com

摘要

该文主要考虑了一类具有变系数的非线性延迟微分方程数值解的振动性, 运用线性 $\theta$ -方法和线性化理论, 将非线性差分方程的振动性转化为其对应的线性化方程的振动性, 运用不等式比较和放缩技巧, 得到了数值解振动的条件.

关键词： 延迟微分方程; 数值解; 振动性; 最终正解

Abstract

This article considers the oscillation of numerical solutions for a class of nonlinear delay differential equations with variable coefficients. By using the linear $\theta$ -methods and linearization theory, the oscillation of the nonlinear difference equation is transformed into that of its corresponding linearized equation. By using inequality comparisons and scaling techniques, the conditions of the oscillation for the numerical solutions are obtained.

Keywords： delay differential equation; numerical solutions; oscillation; eventually positive solution

PDF (530KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

胡冰冰, 高建芳. 一类具有变系数的非线性延迟微分方程数值解的振动性分析[J]. 数学物理学报, 2025, 45(1): 203-213

Hu Bingbing, Gao Jianfang. Oscillation Analysis of Numerical Solutions for a Class of Nonlinear Delay Differential Equations with Variable Coefficients[J]. Acta Mathematica Scientia, 2025, 45(1): 203-213

1 引言

振动性理论是微分方程定性理论中的一个重要的分支, 它起源于研究热传导方程时提出的二阶齐次线性常微分方程的振动问题. 振动性理论在物理学, 疾病动力学, 生物学等众多领域都有广泛的应用. 1977 年, 文献 [1] 研究了一类描述生理控制系统的一阶非线性延迟微分方程的动力学行为, 涵盖了振动性问题, 由此推动了延迟微分方程振动性的研究.

近年来, 有关延迟微分方程振动性的研究成果非常丰富^{[2⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-16]}, 其中文献 [14 ⇓-16]是有关非线性模型的振动性研究. 在这些研究成果中, 大多都是关于方程解析解的振动性, 而对数值解的振动性研究相对较少. 2011 年, 文献[17]讨论了一类动力系统疾病模型

$x'(t)+\dfrac{\alpha V_m x(t)x^p(t-\tau)}{\beta^p+x^p(t-\tau)}=\gamma$

数值解的振动性, 得到了数值解振动的条件.

文献 [18]应用隐式 Euler 法研究了单物种人口模型的延迟 Logistic 方程

$\begin{equation*}\ \dot{N}(t)=rN(t)\Big[1-\frac{N(t-\tau)}{K}\Big] \end{equation*}$

数值解的振动性, 证明了隐式 Euler 法可以保持解析解的振动性, 并研究了非振动数值解的渐近行为.

2015 年, 文献 [19] 研究了具有单峰造血率的非线性延迟微分方程

$y'(t)=\dfrac{\beta \eta^\alpha y(t-\tau)}{\eta^\alpha+y^\alpha (t-\tau)}-\gamma y(t)$

数值解的振动性.

2018 年, 文献 [20]研究了一类具有正负系数的延迟微分方程数值解的振动性.

以上关于数值解振动性的研究结果以及文献[21 ⇓-23] 的研究, 都是关于常系数延迟微分方程的讨论, 这里我们利用已有的振动性研究成果, 将常系数延迟微分方程推广到变系数延迟微分方程, 研究模型数值解的振动性. 考虑以下延迟微分方程

$\begin{equation}\label{eq:a1} \dot{x}(t)=-\alpha(t) x(t)+\frac{\beta(t)}{1+x^{p}(t-\tau)}, \end{equation}$

(1.1)

其中 $\alpha$ , $\beta$ 是 Lebesgue 可测局部有界函数, 满足 $\alpha(t)\geq0$ , $\beta(t)\geq0$ , 模型的详细介绍可参阅文献 [24].

1.1 预备知识

定义1.1^[3] 若函数 $x(t)-K$ 有任意大的零点, 则称函数 $x(t)$ 是关于 $K$ 振动的, 当 $K =0$ 时, 称函数 $x(t)$ 是振动的.

定义1.2^[3] 若差分方程所有解是振动的, 则称此差分方程是振动的.

定义1.3^[3] 考虑非线性差分方程

$\begin{equation}\label{eq:a2} a_{n+1}-a_{n}+\sum\limits_{i=1}^{n}p_{i}f_{i}(x(t-\tau))=0, n=0,1,2,\cdots, \end{equation}$

(1.2)

其中当 $i=1, 2, 3, \cdots$ , $n$ 时,

$\begin{equation}\label{eq:a3} p_{i}\in (0, \infty), \tau_{i}\in[\mathbb{R}], \end{equation}$

(1.3)

$\begin{equation}\label{eq:a4} uf_{i}(u)>0, u\neq0, \end{equation}$

(1.4)

当

$\begin{equation}\label{eq:a5} \lim\limits_{n \to \infty}\frac{f_{i}(u)}{u}=1 \end{equation}$

(1.5)

时, 线性方程

$\begin{equation}\label{eq:a6} b_{n+1}-b_{n}+\sum\limits_{i=1}^{n}p_{i}b_{n-k_{i}}=0, n=0, 1, 2, \cdots \end{equation}$

(1.6)

叫做 (1.1) 式对应的线性化方程.

定理1.1^[3] 假设 (1.3), (1.4), (1.5)式成立且存在 $\delta >0$ , 使得对 $i=1, 2, \cdots n$ 或者 $f_{i}(u)\leq u,$ $0\leq u\leq\delta$ 或者 $f_{i}(u)\geq u, -\delta\leq u\leq0$ 成立, 则(1.2)式的所有解振动等价于线性化方程 (1.6) 的所有解振动.

下面引理是显然的

引理1.1 $(1-\frac{x}{k})^{-k}$ $\geq$ $x$ ${(\frac{k+1}{k})}^{k+1}$ , $0 \leq x< k$ .

引理1.2 $(1-x-y)^{k}$ $\leq$ $(1-x)^{k}$ $(1-y)^{k}$ , $k>0$ .

引理1.3 $\frac{a_{1}+a_{2}+\cdots+a_{n}}{n}$ $\geq$ $\sqrt[n]{a_{1}\cdot a_{2}\cdot\cdots\cdot a_{n}}$ , $(a_{1}, a_{2}, \cdots, a_{n}>0)$ .

引理1.4 当 $x\geq 1$ 和 $0\leq a \leq1$ 时, 有

$(1+x)^{a}\leq 1+ax;$

当

$-1<x<\frac{1}{(a-1)}$

和 $a>1$ 时, 有

$(1+x)^{a}\leq \frac{1+ax}{1+(1-a)x}.$

考虑带有初始条件

$\begin{equation} x(t)=\varphi(t), t\leq 0 \label{eq:a77} \end{equation}$

(1.7)

的方程 (1.1) 的解. 令 $x(t)=k_{1}+y(t)$ , 这里 $k_{1}$ 为方程 (1.1) 的平衡解. 由 (1.1) 式得到

$\begin{equation}\label{eq:a159} \dot{y}(t)+\alpha(t)y(t)+\frac{k_{1}\alpha(t)[(y(t-\tau)+k_{1})^{p}-k_{1}^{p}]}{1+[y(t-\tau)+k_{1}]^{p}}=0,\\ \end{equation}$

(1.8)

为了保证 $x(t)\geq 0$ . 要求 $y(t)\geq-k_{1}$ , 方程 (1.8) 等价于下面方程

$\begin{equation}\label{eq:a7} \dot{y}(t)+\alpha(t)f_{1}(y(t))+\alpha(t)Mf_{2}y((t-\tau))=0, \end{equation}$

(1.9)

其中

$f_{1}(u)=u, f_{2}(u)=\frac{1+k_{1}^{p}}{pk_{1}^{p-1}}\times\frac{(u+k_{1}^{p})-k_{1}^{p}}{1+(k_{1}+u)^{p}}, M=\frac{pk_{1}^{p}}{1+k_{1}^{p}}.$

引理1.5 方程 (1.9) 中的 $f_1(u)$ 和 $f_2(u)$ 满足定理 1.1 的条件, 即方程 (1.9) 的振动性可以转化为其线性方程的振动性.

证显然当 $u\neq0, u\geq-k$ , 有

$uf_{1}(u)>0,~~ uf_{2}(u)>0,$

$\lim\limits_{n \to \infty}\frac{f_{1}(u)}{u}=1,~~ \lim\limits_{n \to \infty}\frac{f_{2}(u)}{u}=1,$

$f_{1}(u)\leq u,~~ 0 \leq u\leq\delta.$

我们只需证明存在一个 $\delta>0$ 使得

$f_{2}(u)\leq u,~~ 0\leq u\leq\delta,$

即

$\begin{equation*} \frac{(u+k_{1}^{p})-k_{1}^{p}}{1+(k_{1}+u)^{p}}\leq\frac{pk_{1}^{p-1}}{1+k_{1}^{p}}. \end{equation*}$

我们先考虑 $0<p\leq1$ , 由引理 1.4 可知

$\begin{equation*} \frac{(u+k_{1}^{p})-k_{1}^{p}}{1+(k_{1}+u)^{p}}\leq\frac{pk_{1}^{p-1}}{1+(u+k_{1}^{p})}, \end{equation*}$

又

$\begin{equation*} \frac{pk_{1}^{p-1}}{1+(u+k_{1}^{p})}\leq\frac{pk_{1}^{p-1}}{1+k_{1}^{p}}, \end{equation*}$

$0<p\leq1$ 情形得证.

下面证明 $p>1$ 的情况, 可以看出 $f_{2}(u)\leq u$ 等价于

$\begin{equation}\label{eq:a8} \frac{(u+k_{1}^{p})-k_{1}^{p}}{1+(k_{1}+u)^{p}}\leq\frac{pk_{1}^{p-1}}{1+k_{1}^{p}}. \end{equation}$

(1.10)

记

$g_{1}(u)=\frac{(u+k_{1}^{p})-k_{1}^{p}}{1+(k_{1}+u)^{p}},$

$g_{2}(u)=\frac{pk_{1}^{p-1}}{1+k_{1}^{p}}.$

令

$F(u)=g_{1}(u)-g_{2}(u),$

当 $u=0$ 时, $F(u)=0$ , 所以我们只需要证明 $F(u)$ 在 $u>0$ 时是减函数即可, 即

$g_{1}'(u)\leq g_{2}'(u),$

往证

$\begin{equation*} \frac{p(k_{1}+u)^{p-1}(1+k_{1}^{p})}{[1+(k_{1}+u)^{p}]^{2}}\leq\frac{pk_{1}^{p-1}}{1+k_{1}^{p}}. \end{equation*}$

记

$\begin{equation*} h(x)=\frac{x^{p-1}}{(1+x^{p})^{2}}. \end{equation*}$

接下来, 若能证明 $k\leq x\leq k+\delta$ 时, $h(x)$ 为减函数即可. 令

$x=k+a\delta,$

这里 $\delta>0$ , $0\leq a\leq1$ ,

$\begin{equation*} h'(x)=\frac{x^{p-2}(1+x^{p})[p-1-(1+p)x^{p}]}{(1+x^{p})^{4}}, \end{equation*}$

得到当 $a\delta\geq(\frac{p-1}{p+1})^{\frac{1}{p}}-k_{1}$ 时

$h'(x)<0.$

令

$a\delta\geq(\frac{p-1}{p+1})^{\frac{1}{p}}-k_{1}=Q,$

当 $Q<0$ 时, 对于任意的 $\delta>0$ , 都有不等式 (1.10) 成立, 若 $Q>0$ , 只要取 $\delta=\frac{Q}{a}$ , 此时就验证了 $p>1$ 的情形.

2 数值解的振动性

对方程 (1.9) 应用线性 $\theta$ -方法可以得到

$\begin{equation}\label{eq:a9} \begin{split} y_{n+1}=\,&y_{n}-h\theta\alpha(t_{n+1})f_{1}(y_{n+1})-h\theta M \alpha(t_{n+1})f_{2}(y_{n+1-m})\\ &-h(1-\theta)\alpha(t_{n})f_{1}(y_{n})-h(1-\theta)M\alpha(t_{n})f_{1}(y_{n-m}), \end{split} \end{equation}$

(2.1)

其中 $0\leq\theta\leq1$ , $h=\frac{\tau}{m}$ , $m$ 是正整数, $y_{n+1}$ 和 $y_{n+1-m}$ 是方程 (1.9) 的解析解 $y(t)$ 在 $t_{n+1}$ 和 $t_{n+1-\tau}$ 处的近似值. 令

$y_{n}=x_{n}-k_{1}$

有

$\begin{equation}\label{eq:a10} \begin{split} (1+h\theta\alpha(t_{n+1}))x_{n+1}=\,&(1-h(1-\theta)\alpha(t_{n}))x_{n}+k_{1}h\theta\alpha(t_{n+1})+k_{1}h(1-\theta)\alpha(t_{n})\\ &-h\theta\alpha(t_{n+1})k_{1}\frac{(x_{n+1-m}+k_{1})^{p}-k_{1}^{p}}{1+(x_{n+1-m}+k_{1})^{p}}\\ &-h(1-\theta)k_{1}\alpha(t_{n})\frac{(x_{n-m}+k_{1})^{p}-k_{1}^{p}}{1+(x_{n-m}+k_{1})^{p}}, \end{split} \end{equation}$

(2.2)

所以方程 (2.1) 的解振动等价于方程 (2.2) 的解关于 $k_{1}$ 振动.

定理2.1 数值方法 (2.2) 是收敛的, 并且当 $\theta\neq\frac{1}{2}$ 时收敛阶为一阶, 当 $\theta=\frac{1}{2}$ 时收敛阶为二阶.

证当 $t\in[\tau]$ 时, 方程 (1.9) 变成

$\begin{equation}\label{eq:a88} \dot{y}(t)+\alpha(t)f_{1}(y(t))+\alpha(t)Mf_{2}\phi((t-\tau)-k_{1})=0, \end{equation}$

(2.3)

记 (2.3) 式的解为 $z_{1}(t)$ . 当 $t\in[\tau, 2\tau]$ 时, 方程 (1.9) 变成

$\begin{equation}\label{eq:a89} \dot{y}(t)+\alpha(t)f_{1}(y(t))+\alpha(t)Mf_{2}(z_{1}(t-\tau))=0, \end{equation}$

(2.4)

记 (2.4) 式的解为 $z_{2}(t)$ . 当 $t\in[3\tau]$ 时, 方程 (1.9) 变成

$\begin{equation}\label{eq:a189} \dot{y}(t)+\alpha(t)f_{1}(y(t))+\alpha(t)Mf_{2}(z_{2}(t-\tau))=0, \end{equation}$

(2.5)

记 $z_{3}(t)$ 为方程 (2.5) 的解, $t\in[3\tau]$ . 重复此过程, 在每个区间长度为 $\tau$ 的小区间上都可以得到一个常微分方程. 将线性 $\theta$ -方法应用到常微分方程, 当 $\theta\neq \frac{1}{2}$ 时, 收敛阶为一阶; 当 $\theta= \frac{1}{2}$ 时, 收敛阶为二阶. 因此, 有

$\begin{equation} z_{n}-z(t_{n})=O(h^{p}), \end{equation}$

(2.6)

$\begin{equation} x_{n}-x(t_{n})=k_{1}+z_{n}-(k_{1}+z(t_{n}))=z_{n}-z(t_{n})=O(h^{p}), \end{equation}$

(2.7)

这里 $p$ 为 $\theta$ -方法的收敛阶, $\theta=\frac{1}{2}$ 时, $p=2$ , $\theta\neq\frac{1}{2}$ 时, $p=1$ .

方程 (2.1) 对应的线性化方程为

$\begin{matrix}\label{eq:a11} & y_{n+1}-y_{n}+\alpha(t_{n+1})h\theta y_{n+1}+h\theta M\alpha(t_{n+1})y_{n+1-m}\\ & +h(1-\theta)\alpha(t_{n})y_{n}+h(1-\theta)M\alpha(t_{n})y_{n-m}=0, \end{matrix}$

(2.8)

由 (2.8) 式可得

$\begin{matrix}\label{eq:a12} & [1+\alpha(t_{n+1})h\theta]y_{n+1}+[h(1-\theta)\alpha(t_{n})-1]y_{n}\\ & +h\theta M\alpha(t_{n+1})y_{n+1-m}+h(1-\theta)M\alpha(t_{n})y_{n-m}=0, \end{matrix}$

(2.9)

将 (2.9) 式两端同时除以 $y_{n}$ 得

$\begin{matrix}\label{eq:a13} & [1+\alpha(t_{n+1})h\theta]\frac{y_{n+1}}{y_{n}}+(h(1-\theta)\alpha(t_{n})-1)\\ & +h\theta M\alpha(t_{n+1})\frac{y_{n+1-m}}{y_{n}}+h(1-\theta)M\alpha(t_{n})\frac{y_{n-m}}{y_{n}}=0. \end{matrix}$

(2.10)

对 (2.10) 式放缩

$\begin{equation*} [1+\alpha(t_{n+1})h\theta]\frac{y_{n+1}}{y_{n}}-1+h\theta M\alpha(t_{n+1})\frac{y_{n+1-m}}{y_{n}}+h(1-\theta)M\alpha(t_{n})\frac{y_{n-m}}{y_{n}}\leq0, \end{equation*}$

即

$\frac{y_{n+1}}{y_{n}}\leq\frac{1}{1+\alpha(t_{n+1})h\theta}-\frac{h\theta M\alpha(t_{n+1})}{1+\alpha(t_{n+1})h\theta}\cdot\frac{y_{n+1-m}}{y_{n}}-\frac{h(1-\theta)M\alpha(t_{n})}{1+\alpha(t_{n+1})h\theta}\cdot\frac{y_{n-m}}{y_{n}},$

(2.11)

$\frac{y_{n+1}}{y_{n}}\leq1-\frac{h\theta M\alpha(t_{n+1})}{1+\alpha(t_{n+1})h\theta}\cdot\frac{y_{n+1-m}}{y_{n}}-\frac{h(1-\theta)M\alpha(t_{n})}{1+\alpha(t_{n+1})h\theta}\cdot\frac{y_{n-m}}{y_{n}}.$

(2.12)

令

$p_{1}(n)=\frac{h\theta M\alpha(t_{n+1})}{1+\alpha(t_{n+1})h\theta},$

$p_{2}(n)=\frac{h(1-\theta)M\alpha(t_{n})}{1+\alpha(t_{n+1})h\theta}.$

所以 (2.12) 式等价于

$\begin{equation}\label{eq:a16} \frac{y_{n+1}}{y_{n}}\leq1-p_{1}(n)\frac{y_{n+1-m}}{y_{n}}-p_{2}(n)\frac{y_{n-m}}{y_{n}}. \end{equation}$

(2.13)

定理2.2 令 $k=m-1$ , 如果存在正整数 $N_{0}>k$ , 使得 $n>N_{0}$ 时，

$\begin{equation}\label{eq:a17} \displaystyle\liminf_{n\longrightarrow \infty}\sum_{j=n-k}^{n-1} p_{2}(j)\geq(\frac{k}{k+1})^{k+1}, \end{equation}$

(2.14)

$\begin{equation}\label{eq:a18} \displaystyle\liminf_{n\longrightarrow \infty}\sum_{j=n-k}^{n-1}[p_{1}(j)+p_{2}(j)-(\frac{k}{k+1})^{k+1}]<k, \end{equation}$

(2.15)

$\begin{equation}\label{eq:a119} \sum_{n=N_0 +1}^{+\infty}p_{2}(n)\Big\{\Big[1-\frac{1}{k}\Big(\sum_{j=n-k}^{n-1}(p_{1}(j)+p_{2}(j))-(\frac{k}{k+1})^{k+1}\Big)\Big]^{-k}-1\Big\}=+\infty \end{equation}$

(2.16)

成立, 则方程 (2.8) 振动.

证不妨假设方程 (2.8) 存在最终正解 $\{y_{n}\}$ , 存在正整数 $n_{1}\geq N_{0}$ , 使得

$\begin{equation*} y_{n-k}\geq y_{n}\geq0,~~ y_{n+1}-y_{n}\leq0,~~ y_{n+1-m}-y_{n-m}\leq0,~~ n\geq n_{1}. \end{equation*}$

由 (2.13) 式可知

$\begin{equation*} \frac{y_{n+1}}{y_{n}}\leq1-p_{1}(n)\frac{y_{n+1-m}}{y_{n}}-p_{2}(n)\frac{y_{n-m}}{y_{n}},~~ n\geq n_{1}. \end{equation*}$

为了方便, 将上式中的 $n$ 改为 $i$ , 并令

$\frac{y_{i-m}}{y_{i}}=T_{i},~~ \frac{y_{i-m+1}}{y_{i}}=Q_{i+1},$

则上式为

$\begin{equation}\label{eq:a19} \frac{y_{i+1}}{y_{i}}\leq1-p_{1}(i){Q_{i+1}}-p_{2}(i){T_{i}}, \end{equation}$

(2.17)

这里

$\begin{equation}\label{eq:a20} p_{1}(i){Q_{i+1}}-p_{2}(i){T_{i}}<1. \end{equation}$

(2.18)

对 (2.17) 式从 $i=n-k$ 到 $i=n-1$ 求积得到

$\begin{equation}\label{eq:a21} \frac{1}{{T_{n}}}\leq\prod_{i=n-k}^{n-1}[1-(p_{1}(i){Q_{i+1}}+p_{2}(i){T_{i}})],~~ n\geq n_{1}+2k. \end{equation}$

(2.19)

根据引理 1.3 得

${T_{n}}\geq\bigg[1-\frac{1}{k}\sum_{j=n-k}^{n-1}(p_{1}(i){Q_{i+1}}+p_{2}(i){T_{i}})\bigg]^{-k},$

(2.20)

且由 (2.18) 式得

$\begin{equation}\label{eq:a22} \sum_{j=n-k}^{n-1}(p_{1}(i){Q_{i+1}}+p_{2}(i){T_{i}})<k,~~ n\geq n_{1}+2k. \end{equation}$

(2.21)

记

$\mathbb{K}=(\frac{k}{k+1})^{k+1}.$

根据引理 1.2 有

$\begin{equation}\label{eq:a23} \begin{split} {T_{n}}&\geq\bigg[1-\frac{1}{k}\sum_{j=n-k}^{n-1}(p_{1}(i){Q_{i+1}}+p_{2}(i){T_{i}})\bigg]^{-k}\\ &=\Big\{1-\frac{1}{k}\Big[\sum_{j=n-k}^{n-1}(p_{1}(i)({Q_{i+1}}-1)+p_{2}(i)({T_{i}}-1))+\mathbb{K}\Big]\\ &~~~-\frac{1}{k}\bigg[\sum_{j=n-k}^{n-1}(p_{1}(i)+p_{2}(i))-\mathbb{K}\bigg]\bigg\} ^{-k}\\ &\geq\bigg\{1-\frac{1}{k}\bigg[\sum_{j=n-k}^{n-1}(p_{1}(i)({Q_{i+1}}-1)+p_{2}(i)({T_{i}}-1))+\mathbb{K}\bigg]\bigg\}^{-k}\\ &~~~\times\bigg\{1-\frac{1}{k}\bigg[\sum_{j=n-k}^{n-1}(p_{1}(i)+p_{2}(i))-\mathbb{K}\bigg]\bigg\}^{-k}. \end{split} \end{equation}$

(2.22)

由引理 1.1 及 (2.22) 式可得

$\begin{matrix}\label{eq:a24} {T_{n}}& \geq\bigg\{\frac{1}{k}\bigg[\sum_{j=n-k}^{n-1}(p_{1}(i)({Q_{i+1}}-1)+p_{2}(i)({T_{i}}-1))+1\bigg]\bigg\}\\ &~~~\times\bigg\{1-\frac{1}{k}\bigg[\sum_{j=n-k}^{n-1}(p_{1}(i)+p_{2}(i))-\mathbb{K}\bigg]\bigg\}^{-k}. \end{matrix}$

(2.23)

令

$Q_{n+1}-1=W_{n+1}, T_{n}-1=Z_{n}, n\geq n_{1}+k,$ 则 $Z_{n}\geq0, n\geq n_{1}+k.$

由 (2.14), (2.15) 及 (2.23) 式得

$\begin{matrix}\label{eq:a25} &~~~~p_{2}(n)\bigg[Z_{n}-\frac{1}{k}\sum_{j=n-k}^{n-1}(p_{1}(i)W_{i+1}+p_{2}(i)Z_{i})\bigg]\\ &\geq p_{2}(n)\bigg\{\bigg[1-\frac{1}{k}\bigg(\sum_{j=n-k}^{n-1}(p_{1}(i)+p_{2}(i))-\mathbb{K}\bigg)^{-k}\bigg]-1\bigg\}. \end{matrix}$

(2.24)

将 (2.24) 式从 $n_{2}=n_{1}+2k$ 到 $N>n_{2}+2k$ 求和得

$\begin{matrix}\label{eq:a26} &~~~~\sum_{j=n_{2}}^{N}p_{2}(n)\bigg[Z_{n}-\frac{1}{k}\sum_{j=n-k}^{n-1}(p_{1}(i)W_{i+1}+p_{2}(i)Z_{i})\bigg]\\ &\geq \sum_{j=n_{2}}^{N} p_{2}(n)\bigg\{\bigg[1-\frac{1}{k}\bigg(\sum_{j=n-k}^{n-1}(p_{1}(i)+p_{2}(i))-\mathbb{K}\bigg)\bigg]^{-k}-1\bigg\}, \end{matrix}$

(2.25)

我们可以看出

$\begin{matrix}\label{eq:a27} \sum_{n=n_{2}}^{N} p_{2}(n)\sum_{i=n-k}^{n-1}(p_{1}(i)W_{i+1}+p_{2}(i)Z_{i})&\geq \sum_{n=n_{2}}^{N-k}(p_{1}(n)W_{n+1}+p_{2}(n)Z_{n})\sum_{i=n-k}^{n-1}p_{2}(i)\\ &\geq\mathbb{K}\sum_{n=n_{2}}^{N-k}(p_{1}(n)W_{n+1}+p_{2}(n)Z_{n}) \end{matrix}$

(2.26)

和

$\begin{matrix}\label{eq:a28} &~~~~\sum_{j=n_{2}}^{N}p_{2}(n)[Z_{n}-\frac{1}{\mathbb{K}}\sum_{j=n-k}^{n-1}(p_{1}(i)W_{i+1}+p_{2}(i)Z_{i})]\\ &\leq\sum_{n=n_{2}}^{N}p_{2}(n)Z_{n}-\sum_{n=n_{2}}^{N-k}(p_{1}(n)W_{n+1}+p_{2}(n)Z_{n})\\ &\leq\sum_{n=n_{2}}^{N}(p_{1}(n)W_{n+1}+p_{2}(n)Z_{n})-\sum_{n=n_{2}}^{N-k}(p_{1}(n)W_{n+1}+p_{2}(n)Z_{n})\\ &=\sum_{n=N-k+1}^{N}(p_{1}(n)W_{n+1}+p_{2}(n)Z_{n}). \end{matrix}$

(2.27)

由 (2.25) 式可得

$\begin{matrix}\label{eq:a29} &~~~~\sum_{n=N-k+1}^{N}(p_{1}(n)W_{n+1}+p_{2}(n)Z_{n})\\ &\geq\sum_{n=n_{2}}^{N}p_{2}(n)\bigg\{\bigg[1-\frac{1}{k}\bigg(\sum_{j=n-k}^{n-1}(p_{1}(i)+p_{2}(i))-\mathbb{K}\bigg)\bigg]^{-k}-1\bigg\}, \end{matrix}$

(2.28)

考虑 (2.16)式可知

$\begin{equation*} \lim\limits_{ N \to \infty}\sum_{n=N-k+1}^{N}(p_{1}(n)W_{n+1}+p_{2}(n)Z_{n})=+\infty, \end{equation*}$

进一步推导出

$\begin{equation*} \lim\limits_{ N \to \infty}\sum_{n=N-k+1}^{N}(p_{1}(n)Q_{n+1}+p_{2}(n)T_{n})=+\infty, \end{equation*}$

与 (2.21) 式矛盾. 所以方程 (2.8) 无最终正解, 从而也无最终负解. 这说明方程 (2.8) 振动.

3 数值算例

为了验证我们的结论, 本节给出如下算例.

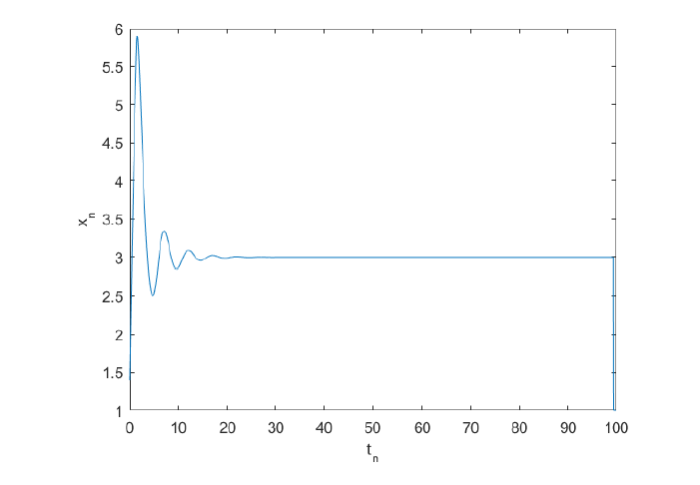
例3.1 考虑方程

$\begin{equation}\label{eq:3.1} x'(t)=-t^2x(t)+\frac{2t^2}{1+x^{2}(t-1.75)}, x(t)=1, -1.75\leq t\leq 0, \end{equation}$

(3.1)

其中

$\alpha(t)=t^2, \beta(t)=2t^2, p=2, \tau=1.75.$

通过计算可得, 方程的平衡解为

$k_1=1, M=\frac{pk_{1}^{p}}{1+k_{1}^{p}}=1.$

取 $\theta=0.4, h=0.05$ , 则

$m=35, k=34,$

$p_{1}(n)=\frac{h\theta t_{n+1}^2}{1+h\theta t_{n+1}^2 }=\frac{ t_{n+1}^2}{50+ t_{n+1}^2 },$

$p_{2}(n)=\frac{h(1-\theta)t_{n}^2}{1+h\theta t_{n+1}^2 }=\frac{ 3t_{n}^2}{100+2 t_{n+1}^2 }.$

取 $N_0=162$ , 通过 Matlab 计算可得 (2.14) 和 (2.15) 式的左端值分别为 0.4510, 22.5519, 右端值分别为 0.3626 和 34, 显然 (2.14) 和 (2.15) 式满足; 同时可计算 (2.16)式的左端值为 0.3842e+107, 显然 (2.16)式也满足. 所以定理2.2 的条件成立, 故方程 (3.1) 的数值解振动. 图 1 给出了方程 (3.1) 的数值解. 由图 1 可以看出数值解是振动的, 与定理2.2 是吻合的.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 方程 (3.1) 的数值解, $\theta=0.8, h=0.05$

例3.2 考虑方程

$\begin{equation}\label{eq:3.2} x'(t)=-tx(t)+\frac{18t}{1+x^{3}(t-0.8)}, x(t)=t, -0.8\leq t\leq 0, \end{equation}$

(3.2)

其中 $\alpha(t)=t, \beta(t)=18t$ , $p=3, \tau=0.8$ . 通过计算可得方程平衡解 $k_1=2$ , $M=\frac{pk_{1}^{p}}{1+k_{1}^{p}}=\frac{8}{3}$ . 取 $\theta=0.2, h=0.025$ , 则

$m=32, k=31,$

$p_{1}(n)=\frac{\frac{8}{3}h \theta t_{n+1}}{1+h\theta t_{n+1} }=\frac{ \frac{40}{3}t_{n+1}}{1000+ 5t_{n+1} },$

$p_{2}(n)=\frac{\frac{8}{3}h(1-\theta)t_{n}}{1+h\theta t_{n+1} }=\frac{ \frac{160}{3}t_{n}}{1000+5 t_{n+1} }.$

取 $N_0=115$ , 通过 Matlab 计算可得 (2.14) 和 (2.15) 式的左端值分别为 0.4346, 8.4817, 右端值分别为 0.3621 和 31, 显然 (2.14) 和 (2.15) 式满足; 同时可计算 (2.16)式的左端值为 0.3943e+72, 显然 (2.16)式也满足. 所以定理2.2 的条件成立, 方程(3.2)的数值解振动. 图 2 给出了方程 (3.2)的数值解. 由图可以看出数值解是振动的, 与定理2.2 是吻合的.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 方程 (3.2) 的数值解, $\theta=0.2, h=0.025$

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Mackey

M C

, Glass

Oscillation and chaos in physiological control systems

Science, 1977, 197(4300): 287-289

DOI:10.1126/science.267326 PMID:267326 [本文引用: 1]

First-order nonlinear differential-delay equations describing physiological control systems are studied. The equations display a broad diversity of dynamical behavior including limit cycle oscillations, with a variety of wave forms, and apparently aperiodic or "chaotic" solutions. These results are discussed in relation to dynamical respiratory and hematopoietic diseases.

[2]

Gopalsamy

, Zhang

B G

On delay differential equations with impulses

J Math Anal Appl, 1989, 139(1): 110-121