加权线性互补问题 (weighted Linear Complementarity Problems, 简记为 wLCP ) 由著名优化专家 Potra 在 2012 年提出 ^[1],其数学模型为: 求 $({\mathbf{x}},{\mathbf{s}},\mathbf{y})\in\mathbb{R}^n\times\mathbb{R}^n\times\mathbb{R}^m$, 使得

这里 $P\in \mathbb{R}^{(n+m)\times n}, Q\in \mathbb{R}^{(n+m)\times n}, R\in \mathbb{R}^{(n+m)\times m}$ 为给定的矩阵, $d\in \mathbb{R}^{n+m}$ 为给定的向量, $w\geq0$ 为给定的权向量, $\mathbf{xs}$ 表示向量 $\mathbf{x}$ 和 $\mathbf{s}$ 对应分量相乘组成的向量, 即 ${\mathbf{xs}}:=(\mathbf{x}_1\mathbf{s}_1,\cdots,\mathbf{x}_n\mathbf{s}_n)^T$. 加权线性互补问题并不是现有线性互补问题简单的推广, 其自身有着非常广泛的应用背景和非常深的研究价值. 一方面, 经济、管理等领域中的许多均衡问题都可以转化成加权线性互补问题模型进行求解 ^[1]. 此外, 二次规划和加权中心问题也可以转化为单调加权线性互补问题进行求解 ^[1]. 另一方面, 有些均衡问题既可以转化成标准的互补问题, 也可以转化成加权线性互补问题, 但后者往往可以更有效地进行求解. 比如 Fisher 竞争市场均衡问题既可以转化为非线性互补问题, 也可以转化为单调加权线性互补问题, 而后者可以被内点法有效地求解 ^[1]. 自从 Potra 教授提出 wLCP 的数学模型以后, 许多学者对该问题展开了深入研究, 提出了许多有效的求解方法, 比如内点法^[1,2], 阻尼高斯-牛顿法[3], Broyden-like 拟牛顿法 ^[4], Levenberg-Marquardt 法 ^[5]和光滑牛顿法 ^[6⇓-8].

本文考虑加权水平线性互补问题 (weighted Horizontal Linear Complementarity Problems, 简记为 wHLCP), 其数学模型定义如下: 求 $(\mathbf{x},\mathbf{s})\in\mathbb{R}^n\times\mathbb{R}^n$, 使得

这里 $M,N\in \mathbb{R}^{n\times n}$ 为给定矩阵, $q\in \mathbb{R}^{n}$ 为给定向量, $w\geq0$ 为给定的权向量. wHLCP 由 Potra 教授在 2016 年提出 ^[9], 其与 wLCP 有如下关系: 对任意矩阵 $K$, 其列构成 $\mathrm{Ker} R^T$ 的一组基, wLCP 等价于求 $({\mathbf{x}},{\mathbf{s}})\in\mathbb{R}^n\times\mathbb{R}^n$, 使得

即取 $M=K^TP$, $N=-K^TQ$, $q=K^Td$ 的 wHLCP. 此外, 如果 $w$ 为零向量, 则 wHLCP 即为如下水平线性互补问题 (Horizontal Linear Complementarity Problems, 简记为 HLCP)

HLCP 是一类非常广泛的互补问题, 其包含线性互补问题、线性规划问题和二次规划问题. 许多求解 HLCP 的数值算法已经被提出 ^[10⇓-12]. 但目前求解 wHLCP 的数值算法很少.

近年来, 人们对求解各种数学规划问题的光滑牛顿法产生了浓厚的兴趣. 这类方法的基本思想是利用光滑函数将所求解的问题等价转化成一个光滑方程组, 然后用牛顿法求解此光滑方程组. 许多光滑牛顿法已被提出用来求解 wLCP ^[6⇓-8]. 注意到, 为获得局部二次收敛速率, 光滑牛顿法通常要求满足非奇异条件, 而这个条件比较强. 2021 年, Tang 和 Zhang^[13] 提出了一个求解对称锥加权互补问题的非单调光滑牛顿法, 分析了算法在局部误差界条件下的收敛速率, 而局部误差界条件比非奇异条件弱. 但文献 [13] 中的非单调光滑牛顿法在每次迭代时都要求解非线性方程组的精确解, 而当问题的规模非常大时, 求解此精确解的计算代价会很昂贵.

本文在文献 [13] 的基础上, 研究一个求解 wHLCP 的非单调光滑非精确牛顿法. 相比于现有的光滑牛顿法, 我们的算法有如下优点

(a) 算法在每次迭代时只需求解非线性方程组的近似解, 相比于文献 [13] 中的非单调光滑牛顿法可节省大量的计算时间. 数值实验结果验证了这一优点.

(b) 在列 $W_0$ 性质下, 算法具有好的定义和全局收敛性, 而列 $W_0$ 性质弱于文献 [10⇓–12] 中的列单调性质.

(c) 如果 $[M,-N]$ 为 ${P}$ 对, 则算法生成的迭代序列有界.

(d) 算法在 Hölderian 局部误差界条件下具有局部快速收敛速率, 该条件比文献 [13] 中的局部误差界条件更广泛, 比文献 [6⇓-8] 中的非奇异条件弱很多.

在本文中, $\mathbb{R}^n$ 表示所有的 $n$ 维实列向量. $\mathbb{R}^n_+$ 和 $\mathbb{R}^n_{++}$ 分别表示 $\mathbb{R}^n$ 中的非负和正象限. 为简单起见, 记列向量 $(u_1^T, \cdots, u_n^T)^T$ 为 $(u_1, \cdots, u_n)$, 这里 $u_i\in\mathbb{R}^{n_i}$. $\|\cdot\|$ 表示 2-范数. 对任意向量 $x\in{\mathbb{R}}^n$, ${\rm diag}(x_i)$ 表示第 $i$ 个对角元素是 $x_i$ 的对角矩阵. 对给定的集合 $S\subset\mathbb{R}^n$ 和向量 $u\in\mathbb{R}^n$, 定义$\mbox{dist}(u,S)=\inf\limits_{v\in S}\{\|u-v\|\}$. $\alpha={O}(\beta)$ ($\alpha=o(\beta))$ 表示 % $\mathop{\lim\sup}\limits_{\beta\rightarrow0}\frac{\alpha}{\beta}<\infty$$\limsup\limits_{\beta\rightarrow0}\frac{\alpha}{\beta}<\infty$ ($\limsup\limits_{\beta\rightarrow0}\frac{\alpha}{\beta}=0$).

本节首先给出函数强半光滑的定义. 设 $\Phi(\mathbf{x}):\mathbb{R}^{n_1}\rightarrow \mathbb{R}^{n_2}$ 是局部 Lipschitz 连续函数, 则由著名的 Rademacher 定理可知 $\Phi$ 几乎处处可微. 设 $D_{\Phi}\subseteq \mathbb{R}^{n_1}$ 是 $\Phi$ 的所有可微点组成的集合, 则 $\Phi$ 在 $\mathbf{x}$ 点的 $B$-次微分 $\partial_{B}\Phi(\mathbf{x})$ 定义为 $\partial_{B}\Phi(\mathbf{x}):=\{V\in\mathbb{R}^{n_2\times n_1}\mid V=\lim\limits_{\mathbf{x}^{k}\rightarrow \mathbf{x}}\Phi^{'}(\mathbf{x}^{k}), \mathbf{x}^{k}\subseteq D_{\Phi}\}.$$\Phi$ 在 $\mathbf{x}$ 点的 Clarke 广义雅可比为集合 $\partial_{B}\Phi(\mathbf{x})$ 的凸包, 即 $\partial\Phi(\mathbf{x}):={{conv}}(\partial_{B}\Phi(\mathbf{x})).$ 如果 $\Phi$ 在点 $\mathbf{x}$ 处方向可导并且对任意的 $V\in\partial \Phi(\mathbf{x}+\Delta \mathbf{x})$, 有

则称 $\Phi$ 在点 $\mathbf{x}$ 处是半光滑的. 如果 $\Phi$ 在点 $\mathbf{x}$ 处半光滑且

则称 $\Phi$ 在点 $\mathbf{x}$ 处是强半光滑的.

接下来, 我们回顾 Sznajder 和 Gowda[14] 定义的列单调和列 $W_0$ 性质. 给定一个分块矩阵 $[M,N]$, 其中 $M,N\in \mathbb{R}^{n\times n}$, 如果对任意的 ${\mathbf{u}},{\mathbf{v}}\in \mathbb{R}^{n}$ 有

则称 $[M,N]$ 是列单调的. 该列单调性质已被广泛应用于 HLCP [10⇓–12]. 如果 $C_j\in\{M_j, N_j\}$ ($j = 1, \cdots, n$), 其中 $C_j$, $M_j$, $N_j$ 分别表示矩阵 $C$、 $M$ 和 $N$ 的第 $j$ 列, 则称矩阵 $C$ 为 $[M, N]$ 的一个列代表. 如果 $[M, N]$ 的所有列代表矩阵的行列式都是非负的, 并且至少有一个行列式是正的, 则称 $[M, N]$ 具有列 $W_0$ 性质. 下面的引理表明列 $W_0$ 性质比列单调性质弱, 其证明见文献 [定理 8].

$\textbf{引理 2.1}$ 如果 $[M, N]$ 是列单调的, 那么 $[M, N]$ 具有列 $W_0$ 性质.

本文考虑如下光滑函数

其中 $c\geq0$ 是一个固定常数. 下面引理给出了 $\psi_c$ 的一些性质, 其证明见文献 [13].

$\textbf{引理 2.2}$ (i) $\psi_c(0,a,b)=0\Longleftrightarrow a\geq0, b\geq0, ab=c.$

(ii) $\psi_c$ 在 $\mathbb{R}^3$ 上全局 Lipschitz 连续并且 Lipschitz 常数为 $\sqrt{2}+2.$

(iii) $\psi_c$ 在 $\mathbb{R}^3$ 上是强半光滑的.

(iv) $\psi_c$ 在任意点 $(\mu,a,b)\in\mathbb{R}_{++}\times\mathbb{R}^2$ 处连续可微, 其梯度为

令 ${\mathbf{z}}:=(\mu,{\mathbf{x}},{\mathbf{s}})\in\mathbb{R}\times\mathbb{R}^{n}\times\mathbb{R}^{n}$. 利用光滑函数 $\psi_c$, 定义

这里 $w=(w_1,\cdots,w_n)^T$ 为 wHLCP 中的权重向量.

$\textbf{引理 2.3}$ (i) $\mathrm{F}(\mathbf{z})=0\Longleftrightarrow \mu=0$ 且 $({\mathbf{x}},{\mathbf{s}})$ 是 wHLCP 的一个解.

(ii) $\mathrm{F}(\mathbf{z})$ 在 $\mathbb{R}^{1+2n}$ 上全局 Lipschitz 连续, 即存在一个常数 $L>0$ 使得

(iii) $\mathrm{F}(\mathbf{z})$ 在 $\mathbb{R}^{1+2n}$ 上是强半光滑的.

(iv) $\mathrm{F}(\mathbf{z})$ 在任意点 $\mathbf{{z}}\in\mathbb{R}_{++}\times\mathbb{R}^{2n}$ 处连续可微, 其雅可比矩阵为

其中

而 $g_{w_i}(\mu,\mathbf{x}_i,\mathbf{s}_i):=\sqrt{\mathbf{x}_i^2+\mathbf{s}_i^2+2w_i+4\mu^2}, i=1,\cdots,n.$

(v) 如果 $[M, N]$ 具有列 $W_0$ 性质, 则 $\mathrm{F}'(\mathbf{z})$ 在任意点 ${\mathbf{z}}=(\mu,{\mathbf{x}},{\mathbf{s}})\in\mathbb{R}_{++}\times\mathbb{R}^{2n}$ 处非奇异.

证 由引理 2.2 可知结论 (i)-(iv) 成立. 由文献 [14] 可知 $[M, N]$ 具有列 $W_0$ 性质当且仅当对任意正对角矩阵 $X$ 和 $Y$, 矩阵 $\left[ \begin{array}{cccc} M&-N\\ X&Y \end{array} \right]$ 是非奇异的. 对任意 ${\mathbf{z}}=(\mu,{\mathbf{x}},{\mathbf{s}})\in\mathbb{R}_{++}\times\mathbb{R}^{2n}$, 由 $\mu>0$ 可得

这表明 $D_{\mathbf{x}}$ 和 $D_{\mathbf{s}}$ 是正对角矩阵. 因此, 矩阵 $\left[ \begin{array}{cccc} M&-N\\ D_{\mathbf{x}}&D_{\mathbf{s}} \end{array} \right]$ 非奇异, 进而可知 $\mathrm{F}'(\mathbf{z})$ 非奇异.

定义价值函数 $f:\mathbb{R}^{1+2n}\rightarrow\mathbb{R}_+$ 如下

下面给出我们的算法.

${\bf 算法 3.1}$ 选取 $\theta, \delta\in(0,1)$ 和 $\mu_0>0$. 选取初始点 $(\mathbf{x}^0,\mathbf{s}^0)\in\mathbb{R}^n \times \mathbb{R}^n$ 并且令 $\mathbf{z}^0:=(\mu_0,\mathbf{x}^0,\mathbf{s}^0)$. 选取 $\eta\in (0,1)$ 和一个序列 $\{\eta_k\}$ 使得 $0\leq\eta_k\leq\eta$. 选取一个正序列 $\{\zeta_k\}$ 满足 $\sum\limits_{k=0}^\infty\zeta_k\le\zeta$, 其中 $\zeta>0$ 是一个常数. 选取 $\gamma\in(0,1)$ 使得 $\gamma\le\min\{\mu_0,1-\eta\}$. 令 $\tau_0:= \gamma\min\{1,f(\mathbf{z}^0)\}$, $\mathcal{C}_0:=f(\mathbf{z}^0).$ 令 $k:=0.$

${\bf 步骤 1}$ 如果 $\|\mathrm{F}(\mathbf{z}^k)\|=0$, 算法停止迭代.

${\bf 步骤 2}$ 求解搜索方向 $\Delta \mathbf{z}^k:=(\Delta \mu_k, \Delta \mathbf{x}^k, \Delta \mathbf{s}^k)\in\mathbb{R}\times \mathbb{R}^n\times\mathbb{R}^n$ 使其满足

这里 $r_k:={\mathrm{\Phi}}'(\mathbf{z}^k)\Delta \mathbf{z}^k+{\mathrm{\Phi}}(\mathbf{z}^k).$

${\bf 步骤 3}$ 令 $l_k$ 是满足下列不等式最小的非负整数 $l$

令 $\alpha_k:=\delta^{l_k}$.

${\bf 步骤 4}$ 令 $\mathbf{z}^{k+1}:=\mathbf{z}^k+\alpha_k\Delta \mathbf{z}^k$. 令

令 $k:=k+1$ 并转步骤 1.

$\textbf{注:}$ 文献 [13] 中的非单调光滑牛顿法在每次迭代时都要求解方程组

从而得到搜索方向 $\Delta \mathbf{z}^k=(\Delta \mu_k, \Delta \mathbf{x}^k, \Delta \mathbf{s}^k)$, 而求解方程组 (3.6) 等价于令 $\Delta\mu_k=-\mu_k+\tau_k$, 然后求解方程组

的精确解 $(\Delta \mathbf{x}^k, \Delta \mathbf{s}^k)$, 进而获得搜索方向 $\Delta \mathbf{z}^k=(\Delta \mu_k, \Delta \mathbf{x}^k, \Delta \mathbf{s}^k)$. 而当问题的规模非常大时, 求解方程组 (3.7) 精确解的计算代价会很昂贵. 而在算法 3.1 中, 我们令 $\Delta\mu_k=-\mu_k+\tau_k$, 然后求解 $(\Delta \mathbf{x}^k, \Delta \mathbf{s}^k)$ 使其满足

即我们只求解方程组 (3.7) 的一个近似解, 从而节省大量的计算工作. 此外, 由于非精确方向一般不是下降方向, 文献 [13] 中的非单调线搜索技术无法保证算法 3.1 的全局收敛性. 为了克服这个困难, 我们在算法 3.1 中引入一种新的非单调线搜索技术.

$\textbf{定理 3.1}$ 如果 $[M, N]$ 具有列 $W_0$ 性质, 那么算法 3.1 是定义良好的, 其生成的序列 $\{\mathbf{z}^k=(\mu_k,\mathbf{x}^k,\mathbf{s}^k)\}$ 满足 $\mathbf{z}^k\in\mathbb{R}_{++}\times\mathbb{R}^n\times \mathbb{R}^n$ 和 $\mathcal{C}_k\ge f(\mathbf{z}^k)$.

证 假设 $\mathbf{z}^k\in\mathbb{R}_{++}\times\mathbb{R}^n\times \mathbb{R}^n$ 和 $\mathcal{C}_k\ge f(\mathbf{z}^k)$ 对某个 $k$ 成立. 根据引理 2.3(v), $\mathrm{F}'(\mathbf{z}^k)$ 是非奇异的, 故步骤 2 是定义良好的. 因为

不等式 (3.3) 对所有充分大的 $l>0$ 都成立. 因此, 我们可以在步骤 3 找到一个步长 $\alpha_k\in(0,1]$ 从而得到第 $k+1$ 个迭代点 $\mathbf{z}^{k+1}=\mathbf{z}^k+\alpha_k\Delta \mathbf{z}^k$. 接下来, 我们证明 $\mathbf{z}^{k+1}\in \mathbb{R}_{++}\times\mathbb{R}^n\times \mathbb{R}^n$ 和 $\mathcal{C}_{k+1}\ge f(\mathbf{z}^{k+1})$. 由 (3.2) 式中的第一个方程可知 $\Delta\mu_k=-\mu_k+\tau_k$, 进而可得

即 $\mathbf{z}^{k+1}\in \mathbb{R}_{++}\times\mathbb{R}^n\times \mathbb{R}^n$. 另外, 由 (3.3) 式可知

再由 (3.4) 式可得

因此, 我们可以得出如下结论: 如果 $\mathbf{z}^k\in\mathbb{R}_{++}\times\mathbb{R}^n\times \mathbb{R}^n$ 并且 $\mathcal{C}_k\ge f(\mathbf{z}^k)$ 对某个 $k$ 成立, 则序列 $\{\mathbf{z}^{k+1}\}$ 可以通过算法 3.1 产生并且满足 $\mathbf{z}^{k+1}\in \mathbb{R}_{++}\times\mathbb{R}^n\times \mathbb{R}^n$ 和 $\mathcal{C}_{k+1}\ge f(\mathbf{z}^{k+1})$. 因为 $\mathbf{z}^{0}\in \mathbb{R}_{++}\times\mathbb{R}^n\times \mathbb{R}^n$ 并且 $\mathcal{C}_{0}= f(\mathbf{z}^{0})$, 由数学归纳法可知定理成立.

$\textbf{引理 3.1}$ 设 $\{\mathbf{z}^k=(\mu_k, \mathbf{x}^k,\mathbf{s}^k)\}$ 是由算法 3.1 生成的迭代序列, 则对所有的 $k\geq0$ 满足 $f(\mathbf{z}^k)\le f(\mathbf{z}^0)+\zeta$ 和 $\mu_k\geq\tau_k$.

证 由 (3.3) 式可知

进而由 (3.4) 式可得

由 (3.9) 式和 (3.10) 式可知

这证明了第一个结论. 假设 $\mu_k\geq\tau_k$ 对某个 $k$ 成立, 则由 (3.8) 式可得

因为 $\mu_0\geq\gamma\geq\tau_0$, 由数学归纳法可知 $\mu_k\geq\tau_k$ 对所有的 $k\geq0$ 都成立.

$\textbf{引理 3.2}$ 设 $\{\mathbf{z}^k\}$ 是由算法 3.1 生成的迭代序列, 则有

证 由 (3.3) 式可知

结合 (3.4) 式可得

进而由引理 3.1 中的第一个结论可推出

因为 $\sum\limits_{k=0}^\infty\zeta_k\le\zeta,$ 将 (3.12) 式两边同时求和可得到 (3.11) 式.

为了分析算法 3.1 的全局收敛性, 我们做如下假设.

$\textbf{假设 4.1}$ 算法 3.1 生成的序列 $\{\mathbf{z}^k=(\mu_k,\mathbf{x}^k,\mathbf{s}^k)\}$ 有界.

假设 4.1 确保 $\{\mathbf{z}^k=(\mu_k,\mathbf{x}^k,\mathbf{s}^k)\}$ 至少存在一个聚点. 注意到, 如果水平集

是有界的, 则由引理 3.1 可知假设 4.1 成立. 最近, Chi 等人[15]引入了 ${P}$ 对的定义. 对任意矩阵 $A,B\in \mathbb{R}^{n\times n}$, 称 $[A, B]$ 是 $\mathbb{R}^n$ 上的一个 ${P}$ 对, 如果其满足

Chi 等人[15]证明了对每个 $(w, q) \in \mathbb{R}_+^n\times \mathbb{R}^n$, wHLCP 有唯一解当且仅当 $[M, -N]$ 是一个 ${P}$ 对. 下面定理表明如果 $[M, -N]$ 是一个 ${P}$ 对, 那么假设 4.1 成立.

$\textbf{定理 4.1}$ 如果 $[M, -N]$ 是一个 ${P}$ 对, 那么算法 3.1 生成的序列 $\{\mathbf{z}^k=(\mu_k,\mathbf{x}^k,\mathbf{s}^k)\}$ 有界.

证 由引理 3.1 和 (3.1) 式可知

现在我们假设 $\lim\limits_{k\rightarrow\infty}\|(\mu_k,\mathbf{x}^k,\mathbf{s}^k)\|=+\infty$, 从而推出一个矛盾. 因为 $0<\mu_k\le\sqrt{f(\mathbf{z}^{k}})\le \sqrt{f(\mathbf{z}^0)+\zeta}$ 对所有的 $k\ge0$ 都成立, 故知 $\lim\limits_{k\rightarrow\infty}\|(\mathbf{x}^k,\mathbf{s}^k)\|=+\infty.$ 因为序列 $\Big\{\frac{\mathbf{x}^k}{\|(\mathbf{x}^k,\mathbf{s}^k)\|}\Big\}$ 和 $\Big\{\frac{\mathbf{s}^k}{\|(\mathbf{x}^k,\mathbf{s}^k)\|}\Big\}$ 都有界, 它们一定存在收敛的子序列. 不失一般性, 我们假设

显然, $\|(\mathbf{x}^*,\mathbf{s}^*)\|=1$. 由引理 3.1 和 (4.1) 式可知

在 (4.2) 式中令 $k\rightarrow\infty$ 可得

同样地, 由 (2.1) 式可知对所有的 $i=1,\cdots,n$,

这表明

另一方面, 由 (4.1) 式可知对所有的 $i=1,\cdots,n$,

因此, 对所有的 $i=1,\cdots,n$, 我们有 $\psi_{0}(0,\mathbf{x}_i^*,\mathbf{s}_i^*)=0$, 其等价于 $\mathbf{x}_i^*\ge0, \mathbf{s}_i^*\ge0, \mathbf{x}_i^* \mathbf{s}_i^*=0$, 即

由 (4.3) 式和 (4.4) 式可知 $(\mathbf{x}^*,\mathbf{s}^*)$ 是 wHLCP 当 $(w, q)=(0,0)$ 时的一个解. 显然, $(0,0)$ 也是 wHLCP 当 $(w, q)=(0,0)$ 时的解. 因为 $[M, -N]$ 是一个 ${P}$ 对, 由文献 [定理 3]CGT-2019 可知 wHLCP 当 $(w, q)=(0,0)$ 时有唯一解. 因此, $(\mathbf{x}^*,\mathbf{s}^*)=(0,0)$, 这与 $\|(\mathbf{x}^*,\mathbf{s}^*)\|=1$ 矛盾.

$\textbf{定理 4.2}$ 设 $[M, N]$ 具有列 $W_0$ 性质并且 $\{\mathbf{z}^k=(\mu_k,\mathbf{x}^k,\mathbf{s}^k)\}$ 是由算法 3.1 生成的序列. 如果假设 4.1 成立, 则要么 $\liminf\limits_{k\rightarrow\infty}f(\mathbf{z}^{k})=0,$ 要么序列 $\{\mathbf{z}^k\}$ 的任意聚点 $\mathbf{z}^*:=(\mu^*,\mathbf{x}^*,\mathbf{s}^*)$ 满足 $f(\mathbf{z}^{*})=0$.

证 因为 $\{\tau_k\}$ 单调递减并且有下界 0, 故存在 $\tau^*\geq0$ 使得 $\lim\limits_{k\rightarrow\infty}\tau_k=\tau^*$. 如果 $\tau^*=0$, 那么由 $\tau_k$ 的定义可知一定存在一个子列 $\{f(\mathbf{z}^{k})\}_{k\in N}$ ($N\subset\{0,1,\cdots\}$) 使得 $\lim\limits_{k(\in N)\rightarrow\infty}f(\mathbf{z}^{k})=0$, 进而由 $f(\mathbf{z}^k)\ge0$ 可得 $\liminf\limits_{k\rightarrow\infty}f(\mathbf{z}^{k})=0$.

接下来, 我们考虑 $\tau^*>0$. 因为 $\mathbf{z}^*=(\mu^*,\mathbf{x}^*,\mathbf{s}^*)$ 是序列 $\{\mathbf{z}^k\}$ 的一个聚点, 故存在一个子列 $\{\mathbf{z}^k\}_{k\in K}$ 使得 $\lim\limits_{k(\in K)\rightarrow\infty}\mathbf{z}^k=\mathbf{z}^*$, 其中 $K\subset\{0,1,\cdots\}$. 由 $f$ 的连续性可知

现在我们假设 $f(\mathbf{z}^*)>0$, 从而推出一个矛盾. 由引理 3.1 可知 $\mu_k\ge\tau_k$ 对所有的 $k\ge0$ 都成立, 故 $\mu^*\ge \tau^*>0$, 即 $\mathbf{z}^*\in\mathbb{R}_{++}\times\mathbb{R}^n\times \mathbb{R}^n$. 根据引理 2.3(v), $\mathrm{F}'(\mathbf{z}^*)$ 是非奇异的. 因此, 存在一个常数 $\vartheta>0$ 使得对任意充分大的 $k\in K$, $\mathrm{F}'(\mathbf{z}^k)$ 非奇异且 $\|\mathrm{F}'(\mathbf{z}^k)^{-1}\|\leq \vartheta$. 此外, 由 (3.5) 式可知

这里第二个不等式成立是因为 $\min\{1,\alpha\}\le\sqrt{\alpha}$ 对任意的 $\alpha\ge0$ 都成立. 因此, 由 (3.2) 式可得

这表明 $\{\Delta \mathbf{z}^k\}_{k\in K}$ 有界, 因此它必有一个收敛的子序列. 不失一般性, 假设 $\lim\limits_{k(\in K)\rightarrow\infty}\Delta \mathbf{z}^k=\Delta \mathbf{z}^*.$ 由引理 3.2 可知 $\lim\limits_{k\rightarrow\infty}\alpha_k f(\mathbf{z}^k)=0$, 再结合 $\lim\limits_{{k(\in K)}\rightarrow\infty} f(\mathbf{z}^k)=f(\mathbf{z}^*)>0$ 可得 $\lim\limits_{{k(\in K)}\rightarrow\infty} \alpha_{k}=0$. 此外, 根据线搜索准则 (3.3), 对任意充分大的 $k\in K$,

再结合 $\mathcal{C}_k\ge f(\mathbf{z}^k)$ 可推出

由于 $f$ 在点 $\mathbf{z}^*\in\mathbb{R}_{++}\times\mathbb{R}^n\times \mathbb{R}^n$ 处连续可微, 在 (4.6) 式中令 $k(\in K)\rightarrow\infty$ 可得

另一方面, 因为 $\mu_k\le \sqrt{f(\mathbf{z}^{k})}$, $\tau_k\le \gamma \sqrt{f(\mathbf{z}^{k})}$, $\|\mathrm{\Phi}(\mathbf{z}^k)\|\le \sqrt{f(\mathbf{z}^{k})}$ 和 $\|r_k\|\le \eta\sqrt{f(\mathbf{z}^{k})}$, 故由 (3.2) 式可得

这表明

由 (4.7) 式和 (4.8) 式可知 $(1-\gamma-\eta)f(\mathbf{z}^{*})\le0$, 进而再由 $0<\gamma+\eta<1$ 可得 $f(\mathbf{z}^{*})=0$. 这与假设 $f(\mathbf{z}^{*})>0$ 矛盾. 因此, 当 $\tau^*>0$ 时, 必有 $f(\mathbf{z}^{*})=0$.

本节讨论算法 3.1 的局部收敛速率. 令 ${\mathcal{Z}}^*$ 为 $\mathrm{F}(\mathbf{z})=0$ 的解集, 即

对任意的 ${\mathbf{z}}\in \mathbb{R}^{1+2n}$, 我们令 $\bar{{\mathbf{z}}}$ 为 ${\mathcal{Z}}^*$ 中满足 $\|{\mathbf{z}}-\bar{{\mathbf{z}}}\|=\mathrm{dist}({\mathbf{z}}, {\mathcal{Z}}^*)$ 的向量. 假设算法 3.1 生成的迭代序列 $\{\mathbf{z}^k\}$ 收敛到 $\mathbf{z}^*$ 并且 $\mathbf{z}^*\in {\mathcal{Z}}^*$. 为分析算法 3.1 的局部收敛速率, 我们考虑如下假设.

$\textbf{假设 5.1}$ (I) $\mathrm{F}(\mathbf{z})$ 在 $\mathbf{z}^*$ 的某个邻域内具有 $\alpha\in (0,1]$ 阶 Hölderian 局部误差界, 即存在常数 $\xi>0$ 和 $\epsilon>0$, 使得

这里 $N(\mathbf{z}^*,\epsilon):=\{{\mathbf{z}}=(\mu,{\mathbf{x}},{\mathbf{s}})\in {\mathbb{R}}^{1+2n}| \|{\mathbf{z}}-\mathbf{z}^*\|\leq \epsilon\}$.

(II) 存在常数 $\varrho>0$ 和 $\beta\in(1,2]$, 使得当 $\|{\mathbf{z}}-\bar{{\mathbf{z}}}\|= \mbox{dist}({\mathbf{z}}, {\mathcal{Z}}^*)$ 充分小时有

(III) 存在常数 $C>0$ 和 $\varepsilon>0$, 使得

这里 $U(\mathbf{z}^*,\varepsilon):=\{{\mathbf{z}}=(\mu,{\mathbf{x}},{\mathbf{s}})\in {\mathbb{R}}_{++}\times{\mathbb{R}}^{2n}| \|{\mathbf{z}}-\mathbf{z}^*\|\leq \varepsilon\}$.

对假设 5.1, 我们有如下说明.

(i) 假设 5.1(I) 称为 Hölderian 局部误差界条件, 当 $\alpha=1$ 时, 其即为文献 [13] 中的局部误差界条件. 最近,Wang 和 Fan^[16,17] 分析了 Levenberg-Marquardt 法在 Hölderian 局部误差界条件下的收敛速率.

(ii) 当 $\beta=2$ 时, 假设 5.1(II) 即退化为文献 [13,假设 5.3]. 文献 [13,定理 10] 已给出了保证假设 5.1(II) 当 $\beta=2$ 时成立的三个条件.

(iii) 假设 5.1(III) 已被许多文献用来证明算法的超线性或二次收敛速度^[18,19]. 注意到, 如果非奇异条件成立, 则假设 5.1(III) 成立.此外, 对于本文研究的 wHLCP, 当 $M$ 为正定矩阵并且 $N$ 为单位矩阵时, 假设 5.1(III) 成立, 其具体证明可参见文献 [13].

$\textbf{定理 5.1}$ 令 $[M, N]$ 具有列 $W_0$ 性质并且算法 3.1 生成的序列 $\{\mathbf{z}^k\}$ 收敛到 $\mathbf{z}^*\in \mathcal{Z}^*$. 令假设 5.1 在 $\mathbf{z}^*$ 处成立. 如果 $\alpha\beta>1$ 并且 $\eta_k=O(\|\mathrm{F}(\mathbf{z}^{k})\|^{\beta-1})$, 则有

证 因为 $\lim\limits_{k \to \infty} \| \mathrm{F}(\mathbf{z}^k)\|=\|\mathrm{F}(\mathbf{z}^*)\|=0$, 由假设 5.1(I) 可得

根据引理 2.3(ii), 对所有充分大的 $k$, $\|\mathrm{F}(\mathbf{z}^k)\| \leq L\|\mathbf{z}^k-\bar{{\mathbf{z}}}^k\|.$ 因此

并且由 $\eta_k=O(\|\mathrm{F}(\mathbf{z}^{k})\|^{\beta-1})$ 可知

由 (3.2) 式, (5.4) 式, (5.5)式, 假设 5.1(II) 和假设 5.1(III) 可知对所有充分大的 $k$,

其中 $c>0$ 是一个常数. 因此, 由引理 2.3(ii), (5.6) 式和假设 5.1(I) 可知对所有充分大的 $k$,

再结合 $\lim\limits_{k\rightarrow\infty}f(\mathbf{z}^k)=0$ 和 $\alpha\beta>1$ 可知对所有充分大的 $k$,

因此, 由线搜索 (3.3) 式可知对所有充分大的 $k$, $\alpha_k=1$ 并且

再结合 (5.7) 式可知 $f(\mathbf{z}^{k+1})=O(f(\mathbf{z}^k)^{\alpha\beta})$, 进而由 $f(\mathbf{z}^k)=\|\mathrm{F}(\mathbf{z}^k)\|^2$ 可得 (5.1) 式. 此外, 由 (5.6) 式和 (5.8)式可知对所有充分大的 $k$,

进而由 (5.3)式和 $\beta\in(1,2]$ 可得

根据 (3.2) 式, (5.4) 式, (5.5)式, (5.9)式, 引理 2.3(ii) 以及假设 5.1(III) 可知对所有充分大的 $k$,

另外, 由 (5.8) 式可知对所有充分大的 $k$,

再结合 (5.10)式可推出

由 (5.11) 式和 (5.12) 式可知对所有充分大的 $k$,

这里第二个不等式成立是因为 $\beta\in(1,2]$ 并且 $\lim\limits_{k\rightarrow\infty}\|\Delta \mathbf{z}^{k}\|=0$. 由 (5.13) 式可知, 对所有充分大的 $k$ 有

对上面所有不等式左右相加求和可得

即

从而可知

因此, 当 $k$ 充分大时可得

根据 (5.11) 式和 (5.14) 式可知

因此, 定理成立.

本节报告一些数值结果. 在实验中, 我们比较以下两个算法

$\bullet$ 本文研究的非单调光滑非精确牛顿法, 即算法 3.1, 记为 FTZ-A. 在 FTZ-A 中, 参数选取为 $\mu_0=10^{-3}, \delta=0.8, \theta=10^{-5}, \gamma=10^{-7}, \eta_k=1/2^{k+1}, \zeta_k=1/(k+1)^2$. 在步骤 2 中, 我们采用 GMRES 算法求解方程组的解.

$\bullet$ Tang 和 Zhang[13] 研究的非单调光滑牛顿法, 记为 TZ-A. 对 TZ-A, 我们采用与文献 [13] 中相同的参数.

$\textbf{例 6.1}$ 考虑 wHLCP, 其中

这里 $M_i=\mathrm{rand}(n_i,n_i)$. 此外, 令 $N=\mathrm{eye}(n)$, $q=-\mathrm{rand}(n,1)$ 以及 $w=\mathrm{rand}(n,1)$.

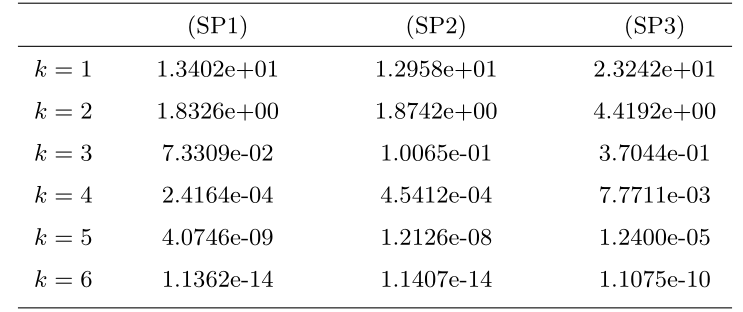
为观察 FTZ-A 的局部收敛速率, 我们随机产生一个规模为 $n=1000$ 的测试问题, 并分别应用下面三个初始点求解

(SP1) $\mathbf{x}^0=\mathbf{s}^0=(1,0,\cdots,0)^T;$

(SP2) $\mathbf{x}^0=\mathbf{s}^0=(1,1,\cdots,1)^T$ ;

(SP3) $\mathbf{x}^0=\mathrm{rand}(n,1), \mathbf{s}^0=\mathrm{rand}(n,1).$

表 1 给出了迭代过程中 $\|\mathrm{F}(\mathbf{z}^k)\|$ 的值, 其清楚地表明 FTZ-A 具有局部二次收敛速率.

接下来, 对每个不同规模的测试问题, 我们随机生成 10 个算例, 并利用前面三个初始点进行求解. 我们使用 $\| {\mathrm{F}}(\mathbf{z}^k)\|\le 10^{-6}$ 作为停止准则. 数值结果列于表 2, 其中 SP 表示初始点, AIT 和 ACPU 分别表示平均迭代次数和平均 CPU 时间 (单位为秒), AFK 表示算法终止时 $\| {\mathrm{F}}(\mathbf{z}^k)\|$ 的平均值. 从表 2 中可以看出, FTZ-A 和 TZ-A 需要的迭代次数几乎相同, 但是相比 TZ-A, FTZ-A 可以节省大量的计算时间, 特别是对大规模问题.

$\textbf{例 6.2}$ 考虑 wHLCP, 其中 $M=\frac{{U}{U}^{T}}{\|{U}{U}^{T}\|}, {U}=\mathrm{rand}(n,n)$, $N=\mathrm{eye}(n)+\frac{{V}{V}^{T}}{\|{V}{V}^{T}\|}$, ${V}=\mathrm{rand}(n,n)$. 此外, 令 $w=\mathrm{rand}(n,1)$, 并且选择 $\hat{x}=\mathrm{rand}(n,1)$ 和 $\hat{s}=\mathrm{rand}(n,1)$, 令 $q=M\hat{x}-N\hat{s}$.

同样的, 我们随机生成一个 $n=1000$ 的测试问题, 再用 FTZ-A 求解此算例. 初始点的选取与例 6.1 相同. 表 3 给出了迭代过程中 $\|\mathrm{F}(\mathbf{z}^k)\|$ 的值, 其再次表明 FTZ-A 具有局部快速收敛速率.

接下来, 对不同规模的测试问题, 我们随机生成 10 个算例, 并使用与例 6.1 相同的初始点来求解它们. 数值结果列于表 4, 其再次表明 FTZ-A 比 TZ-A 可节省大量的计算工作. 这些数值结果证实了我们的算法具有更好的实际计算性能.