数学物理学报, 2024, 44(6): 1652-1664

求解Stein张量方程的张量格式BCGSTAB算法

马昌凤,1, 谢亚君,1,*, 卜凡,2

1福州外语外贸学院大数据学院, 数据科学与智能计算重点实验室 福州 350202

2福建师范大学数学与信息学院 福州 350117

The Tensor Scheme BCGSTAB Algorithm for Solving Stein Tensor Equations

Ma Changfeng,1, Xie Yajun,1,*, Bu Fan,2

1School of Big Data & Key Laboratory of Data science and intelligent computing, Fuzhou University of International Studies and Trade, Fuzhou 350202

2School of Mathematics and Information, Fujian Normal University, Fuzhou 350117

通讯作者: *谢亚君,Email：xyj@fzfu.edu.cn

收稿日期: 2023-12-29   修回日期: 2024-05-6  

基金资助: 国家自然科学基金(12371378)
福建省自然科学基金(2024J01980)

Received: 2023-12-29   Revised: 2024-05-6  

Fund supported: NSFC(12371378)
Natural Science Foundation of Fujian Province(2024J01980)

作者简介 About authors

马昌凤,Email：mcf@fzfu.edu.cn;

卜凡,Email：2669299068@qq.com

摘要

双共轭梯度稳定化方法(BCGSTAB) 是双共轭梯度方法的快速和光滑收敛的变形. 该文将 BCGSTAB 算法推广到求解 Stein 张量方程, 给出了张量格式的算法以及解的存在性的具体证明过程, 并得到了该算法的收敛性结果. 数值实验证实了该算法用于求解 Stein 张量方程是有效且可行的.

关键词： Stein 张量方程; BCGSTAB 算法; 收敛性分析; 数值实验

Abstract

The biconjugate gradient stabilized (BCGSTAB) method is a fast and smoothly converging variant of biconjugate gradient (BiCG) method. In this paper, we generalize BCGSTAB method to solve the Stein tensor equation. We raise the algorithm of tensor format and specific proof process of existence of a solution. And we present the convergence theorem of this algorithm. Numerical experiments demonstrate this algorithm is effective and feasible for solving the Stein tensor equation.

Keywords： tein tensor equation; BCGSTAB method; Convergence analysis; Numerical experiment

PDF (638KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

马昌凤, 谢亚君, 卜凡. 求解Stein张量方程的张量格式BCGSTAB算法[J]. 数学物理学报, 2024, 44(6): 1652-1664

Ma Changfeng, Xie Yajun, Bu Fan. The Tensor Scheme BCGSTAB Algorithm for Solving Stein Tensor Equations[J]. Acta Mathematica Scientia, 2024, 44(6): 1652-1664

1 引言

考虑如下形式的 Stein 张量方程

$\begin{equation} \mathcal{X}-\mathcal{X}\times_1A_1\times_2A_2\times\cdots\times_nA_n=\mathcal{F}, \end{equation}$

其中矩阵 $A_i\in \mathbf{R}^{I_i\times I_i}$($i=1,2,\cdots,n$) 和张量 $\mathcal{F}$ 是给定的, 张量 $\mathcal{X}\in \mathbf{R}^{I_1\times I_2\times\cdots\times I_n}$ 是待求张量. 当 $\mathcal{X}\in \mathbf{R}^{I_1 \times I_2}$ 时, 方程(1.1)退化为

$\begin{equation*} X-A_1XA_2^{\rm T}=F, \end{equation*}$

上式显然是 Stein 矩阵方程, 因此方程(1.1)称为 Stein 张量方程.

为了建立求解 Stein 张量方程(1.1)的有效算法, 先回顾一些求解线性方程组的子空间方法. 对于求解下列大型稀疏线性方程组$ A{x}={b},$式中矩阵 $A\in \mathbf{R}^{n \times n}$ 和向量 ${b} \in \mathbf{R}^n$ 是已知的, ${x} \in \mathbf{R}^n$ 是未知的.许多学者已经提出一些有效的算法用于求解该方程组[1⇓⇓⇓⇓⇓⇓⇓-9]. 众所周知,使用最广泛的方法是 Krylov 子空间方法. Krylov 子空间方法最显著的特点是只涉及矩阵与向量的乘积, 并且在所提出的算法中可以充分利用 $A$ 的特殊结构. 当 $A$ 是对称正定矩阵时, 共轭梯度法 (CG) 是最行之有效的 Krylov 子空间方法之一. 当 $A$ 是对称半正定矩阵时, 极小残差法 (MINRES) 和共轭残差法 (CR) 也有非常好的效果. 对于 $A$ 不是对称矩阵的情形, 可由 CG 法、MINRES 法和 CR 法推广得到 BiCG 法、GMRES 法和 GCR 法. 由 BiCG 算法短循环的特点, 其有效的变形, 即双共轭梯度稳定化方法 (BCGSTAB) 被提出. 此外, BiCG 算法的一些推广也逐渐被提出[10⇓-12].

为求解Stein 矩阵方程, 许多理论分析及算法已经被提出[13⇓⇓⇓⇓-18]. Zhou 等人在文献 [13] 讨论了Smith 迭代算法的计算复杂性并给出其变形, 并且由他们提出的新的 Smith 加速迭代算法在求解 Stein 矩阵方程时有更好的效果. Fuhrmann[15]运用张量积理论的函数模型来分析Stein 矩阵方程. Goureia[16]运用广义逆和非交换环的理论讨论矩阵方程 $AXB-X=C$ 的连续性. Chiang[18]提出一类特殊的 Stein 矩阵方程, 并通过收缩子空间来求解. 此外, 他们还给出了解的存在性的充分必要条件.

Xu 和 Wang 等[19⇓-21]推广 RGI、BiCG 和 BiCR 算法用于求解 Stein 张量方程, 并研究了所提出的迭代算法的收敛性. 此外, 他们给出与式(1.1)等价的线性方程组并讨论在一定条件下方程(1.1)的解. 在他们的数值实验中, 将所提出的算法与张量格式的 CGNR 算法和 CGNE 算法进行了对比, 显然张量格式的 BiCG 和 BiCR 算法更具优势. 受其启发, 本文尝试构造 BCGSTAB 算法的张量格式, 并通过数值实验验证了算法的可行性和有效性.

2 BCGSTAB 算法及其收敛性

在本节, 将提出求解 Stein 张量方程的张量格式的 BCGSTAB 算法. 为分析 Stein 张量方程解的存在性, 先给出一些基本引理.

引理 2.1 设 $A\in \mathbf{R}^{n\times n}$, $B\in \mathbf{R}^{m\times m}$, “$\otimes$” 为 Kronecker 积, 则

(1) $\|A\otimes B\|_2=\|A\|_2\cdot\|B\|_2$;

(2) $\rho(A\otimes B)=\rho(A)\cdot\rho(B)$.

证 (1) 首先证明第一个等式. 事实上,

$\begin{eqnarray*} \|A\otimes B\|_2& =& \sqrt{\lambda_{\max}((A\otimes B)^H(A\otimes B)) } = \sqrt{\lambda_{\max}(A^HA\otimes B^HB)}\\[8pt] &=& \sqrt{\lambda_{\max}(A^HA)\cdot \lambda_{\max}(B^HB)}=\|A\|_2\cdot \|B\|_2; \end{eqnarray*}$

(3) 设 $\lambda_1, \lambda_2, \cdots, \lambda_n$ 是矩阵 $A$ 的特征值, $\mu_1, \mu_2, \cdots, \mu_m$ 是 $B$ 的特征值. 不失一般性, 设 $|\lambda_1|\geq|\lambda_2|\geq\cdots\geq|\lambda_n|$, $|\mu_1|\geq|\mu_2|\geq\cdots\geq|\mu_m|$. 则 $A\otimes B$ 的特征值是 $\lambda_l\mu_r$, 其中 $l=1,2,\cdots,n, r=1,2,\cdots,m$.由于

$\begin{equation*} \left\{\begin{array}{ll} \rho(A)=\max\{|\lambda_1|,|\lambda_2|,\cdots,|\lambda_n|\}=|\lambda_1|,\\ \rho(B)=\max\{|\mu_1|,|\mu_2|,\cdots,|\mu_m|\}=|\mu_1|, \end{array}\right. \end{equation*}$

故

$\begin{eqnarray*} \rho(A\otimes B) &=& \max\{|\lambda_1\mu_1|,|\lambda_2\mu_2|,\cdots,|\lambda_n\mu_m|\} \\ &=& |\lambda_1\mu_1|=|\lambda_1|\cdot|\mu_1| = \rho(A)\cdot\rho(B). \end{eqnarray*}$

证毕.

引理 2.2[19] 设 $A\in \mathbf{R}^{n\times n}$, 则

(1) 矩阵序列 $\sum\limits_{k=0}^\infty A^k$ 收敛当且仅当 $\rho(A)<1$;

(2) 若矩阵序列 $\sum\limits_{k=0}^\infty A^k$ 收敛, 则 $\sum\limits_{k=0}^\infty A^k=(I-A)^{-1}$.

张量 $\mathcal{X}\in \mathbf{R}^{I_1\times I_2\times\cdots\times I_n}$ 的 $k$-模式矩阵化可记为 $\mathcal{X}(k)$, 并且 $k$-模式纤维用来表示所得到的矩阵的列. 算子 "$vec$" 表示将矩阵或张量的列拉直, 从而将其转换成一个向量. 对于矩阵 $A\in \mathbf{R}^{m\times n}$ 和张量 $\mathcal{X}\in \mathbf{R}^{I_1\times I_2\times\cdots\times I_n}$, 经过列拉直后得到的向量 ${vec}(A)$ 和 ${vec}(\mathcal{X})$ 分别定义为

$\begin{equation*} {vec}(A)=(a_1^{\rm T},a_2^{\rm T},\cdots,a_n^{\rm T})^{\rm T}, {vec}(\mathcal{X})= {vec}(\mathcal{X}(1)), \end{equation*}$

式中 $a_k$ 是矩阵 $A$ 的第 $k\,(k=1,2,\cdots,n)$ 列且 $\mathcal{X}(1)$ 表示张量 $\mathcal{X}$ 的 1-模式矩阵化. 由于

$\begin{equation*} {vec}(\mathcal{X}\times_1A_1\times_2A_2\times\cdots\times_nA_n)=(A_n\otimes\cdots\otimes A_2\otimes A_1) {vev}(\mathcal{X}), \end{equation*}$

若将算"$ {vec}$"作用于等式(1.1)的两边,即

$\begin{equation} (I-A_n\otimes\cdots\otimes A_2\otimes A_1) {vec}(\mathcal{X})= {vec}(\mathcal{F}), \end{equation}$

(2.1) 式中 $I$ 是阶数为 $I_1I_2\cdots I_n$ 的单位矩阵. 令

$\begin{equation*} E=A_n\otimes\cdots\otimes A_2\otimes A_1. \end{equation*}$

易知 $I-E$ 的谱集为

$\begin{equation*} \lambda(I-E)=\{1-\lambda_{i_1}\lambda_{i_2}\cdots\lambda_{i_n}|\lambda_{i_k}\in\lambda(A_k),k=1,2,\cdots,n\}. \end{equation*}$

如果方程组(2.1)有唯一解, 则它的系数矩阵 $I-E$ 满秩, 这表明系数矩阵的特征值非零, 可以立即得到下面的引理.

引理 2.3 Stein张量方程(1.1)有唯一解当且仅当对任意 $\lambda_{i_k}\in\lambda(A_k)$, $i_k\in{1,2,\cdots,n_k}$, $k=1,2,\cdots,n$, 有

$\lambda_{i_1}\lambda_{i_2}\cdots\lambda_{i_n}\neq1.$

基于矩阵谱条件数的定义, 即对于矩阵 $A$, 其谱条件数定义为

$\begin{equation*} {\rm cond}_2(A)=\|A\|_2\|A^{-1}\|_2. \end{equation*}$

根据此定义，可以得到系数矩阵 $I-E$ 的谱条件数的上界和下界.一方面,

$\begin{eqnarray*} {\rm cond}_2(I-E)\geqslant \rho(I-E)\rho((I-E)^{-1}) =\frac{\max\limits_{\lambda_{i_k}\in\lambda(A_k),1\leqslant k\leqslant n}\big|1-\lambda_{i_1}\lambda_{i_2}\cdots\lambda_{i_n}\big|} {\min\limits_{\lambda_{i_k}\in\lambda(A_k),1\leqslant k\leqslant n}\big|1-\lambda_{i_1}\lambda_{i_2}\cdots\lambda_{i_n}\big|}. \end{eqnarray*}$

由于谱半径小于或等于任何范数, 因此可知当 $\|E\|_2<1$ 时, $\rho(E)<1$. 此外, 由 $\|E\|_2<1$ 可知 $I-E$ 是非奇异的且有 $\|(I-E)^{-1}\|_2\leqslant\frac{1}{1-\|E\|_2}$. 另一方面,

$\begin{eqnarray*} \|I-E\|_2&\leqslant &\|I\|_2+\|E\|_2 = 1+\|A_n\otimes\cdots\otimes A_2\otimes A_1\|_2 \\ &=&1+\|A_1\|_2 \|A_2\|_2 \cdots \|A_n\|_2 = 1+\prod_{i=1}^n\|A_i\|_2. \end{eqnarray*}$

显然, $\mathrm{cond}_2(I-E)$ 的上界为

$\begin{equation*} {\rm cond}_2(I-E)\leqslant\frac{1+\prod\limits_{i=1}^n\|A_i\|_2}{1-\prod\limits_{i=1}^n\|A_i\|_2}. \end{equation*}$

由 (2.1) 式以及引理2.2, 可知

$\begin{equation*} {\rm{vec}}(\mathcal{X})=(I-E)^{-1}{\rm{vec}}(\mathcal{F})=(I+E+E^2+\cdots){\rm{vec}}(E). \end{equation*}$

由此, 得到下面引理.

引理 2.4[19] Stein 张量方程 (1.1) 有唯一解 $\mathcal{X}$, 且 $\mathcal{X}$ 有序列表示

$\begin{equation*} \mathcal{X}=\sum_{k=0}^\infty\mathcal{F}\times_1A_1^k\times_2A_2^k\times\cdots\times_nA_n^k \end{equation*}$

当且仅当 $\rho(A_1)\rho(A_2)\cdots\rho(A_n)<1$.

根据上述引理, 也可用部分和序列来估计Stein张量方程(1.1)的解, 即

$\begin{equation} \mathcal{X}_m=\sum_{k=0}^m\mathcal{F}\times_1A_1^k\times_2A_2^k\times\cdots\times_nA_n^k \end{equation}$

或者表示为下面的迭代格式

$\begin{equation} \mathcal{X}_k=\mathcal{X}_{k-1}\times_1A_1\times_2A_2\times\cdots\times_nA_n+\mathcal{F}. \end{equation}$

若使用 (2.2) 式的部分和的形式来表示(1.1)的解, 则有如下误差估计.

引理 2.5 令 $\tau=\|E\|_2=\prod\limits_{i=1}^n\|A_i\|_2$. 若 $\tau<1$ 且 $\mathcal{X}^*$ 是 Stein 张量方程 (1.1) 的唯一解, 则不等式

$\begin{equation*} \|\mathcal{X}^*-\mathcal{X}_m\|_{\rm F}\leqslant\frac{\tau^{m+1}}{1-\tau}\|\mathcal{F}\|_{\rm F} \end{equation*}$

成立, 式中 $\mathcal{X}_m=\sum\limits_{k=0}^m\mathcal{F}\times_1A_1^k\times_2A_2^k\times\cdots\times_nA_n^k$.

证 由 $\mathcal{X}^*$ 和 $\mathcal{X}_l$ 的序列表示, 可得

$\begin{eqnarray*} \|\mathcal{X}^*-\mathcal{X}_m\|_{\rm F}&=&\Big\|\sum_{k=0}^\infty\mathcal{F}\times_1A_1^k\times_2 A_2^k\times\cdots\times_nA_n^k-\sum_{k=0}^m\mathcal{F}\times_1A_1^k\times_2A_2^k\times\cdots\times_nA_n^k\Big\|_{\rm F}\\ &=&\Big\|\sum_{k=m+1}^\infty\mathcal{F}\times_1A_1^k\times_2A_2^k\times\cdots\times_nA_n^k\Big\|_{\rm F} \\ &=&\Big\|\sum_{k=m+1}^\infty E^k {vec}(\mathcal{F})\Big\|_{\rm F}= \|E^{m+1}+E^{m+2}+\cdots\|_{\rm F}\cdot\|\mathcal{F}\|_{\rm F}\\ &\leqslant&\|E^{m+1}\|_{\rm F}\cdot\|(I-E)^{-1}\|_{\rm F}\cdot\|\mathcal{F}\|_{\rm F}\leqslant\frac{\tau^{m+1}}{1-\tau}\|\mathcal{F}\|_{\rm F}. \end{eqnarray*}$

证毕.

引理 2.6 令 $\tau=\prod_{i=1}^n\|A_i\|_2$. 若 $\tau<1$ 且 $\mathcal{X}^*$ 是Stein张量方程的唯一解, 则

(1) $\|\mathcal{X}^*-\mathcal{X}_k\|_{\rm F}\leqslant\tau^k\|\mathcal{X}^*-\mathcal{X}_0\|_{\rm F}$;

(2) $\|\mathcal{X}^*-\mathcal{X}_k\|_{\rm F}\leqslant\frac{\tau}{1-\tau}\|\mathcal{X}^*-\mathcal{X}_{k-1}\|_{\rm F}$;

(3) $\|\mathcal{X}^*-\mathcal{X}_k\|_{\rm F}\leqslant\frac{\tau^k}{1-\tau}\|\mathcal{X}_1-\mathcal{X}_0\|_{\rm F}$.

证 (1) 注意到

$\begin{eqnarray*} \|\mathcal{X}^*-\mathcal{X}_k\|_{\rm F}&=&\|\mathcal{X}^*\times_1A_1\times_2A_2\times\cdots\times_nA_n-\mathcal{X}_{k-1}\times_1A_1\times_2A_2\times\cdots\times_nA_n\|_{\rm F} \\ &=&\|(\mathcal{X}^*-\mathcal{X}_{k-1})\times_1A_1\times_2A_2\times\cdots\times_nA_n\|_{\rm F} \\ &=&\|(A_n\otimes\cdots\otimes A_2\otimes A_1)\cdot {vec}(\mathcal{X}^*-\mathcal{X}_{k-1})\|_{\rm F} \\ &\leqslant&\|A_n\otimes\cdots\otimes A_2\otimes A_1\|_{\rm F}\cdot\|\mathcal{X}^*-\mathcal{X}_{k-1}\|_{\rm F} \\ &=&\tau\|\mathcal{X}^*-\mathcal{X}_{k-1}\|_{\rm F}=\cdots =\tau^k\|\mathcal{X}^*-\mathcal{X}_0\|_{\rm F}; \end{eqnarray*}$

(2) 由 $ {vec}(\mathcal{X}_k)=E {vec}(\mathcal{X}_{k-1})+ {vec}(\mathcal{F})$ 及 $ {vec}(\mathcal{X}^*)=E {vec}(\mathcal{X}^*)+ {vec}(\mathcal{F})$, 可得

$\begin{eqnarray*} \|\mathcal{X}^*-\mathcal{X}_k\|_{\rm F} &=& \|E {vec}(\mathcal{X}^*)-E {vec}(\mathcal{X}_{k-1})\|_{\rm F} \\ & =& \|E(I-E)^{-1} {vec}(\mathcal{F})-E {vec}(\mathcal{X}_{k-1})\|_{\rm F} \\ &=& \|E(I-E)^{-1}[ {vec}(\mathcal{F})-(I-E) {vec}(\mathcal{X}_{k-1})]\|_{\rm F} \\ &=& \|E(I-E)^{-1}[ {vec}(\mathcal{F})+E {vec}(\mathcal{X}_{k-1})- {vec}(\mathcal{X}_{k-1})]\|_{\rm F} \\ & =& \|(I-E)^{-1}[ {vec}( {vec}(\mathcal{X}_k)- {vec}(\mathcal{X}_{k-1})]\|_{\rm F} \\ &\leqslant& \frac{\tau}{1-\tau}\|\mathcal{X}^*-\mathcal{X}_{k-1}\|_{\rm F}; \end{eqnarray*}$

(3) 因为

$\begin{eqnarray*} \|\mathcal{X}^*-\mathcal{X}_0\|_{\rm F}&=& \|(I-E)^{-1} {vec}(\mathcal{F})- {vec}(\mathcal{X}_0)\|_{\rm F} \\ &=& \|(I-E)^{-1}[ {vec}(\mathcal{F})-(I-E) {vec}(\mathcal{X}_0)\|_{\rm F} \\ &=& \|(I-E)^{-1}[ {vec}(\mathcal{X}_1)- {vec}(\mathcal{X}_0)\|_{\rm F} \\ &\leqslant&\frac{1}{1-\tau}\|\mathcal{X}_1-\mathcal{X}_0\|_{\rm F}, \end{eqnarray*}$

所以,

$\|\mathcal{X}^*-\mathcal{X}_k\|_{\rm F}\leqslant\tau^k\|\mathcal{X}^*-\mathcal{X}_0\|_{\rm F}\leqslant\frac{\tau^k}{1-\tau}\|\mathcal{X}_1-\mathcal{X}_0\|_{\rm F}.$

证毕.

在Krylov子空间方法中, BiCG 算法具有双正交性, 这种性质同样可以推广至张量情形中.因此文献 [19] 中提出了张量格式的 BiCG 算法, 具体如下

算法 1 (张量格式的 BiCG 算法)

步骤 1 输入初始张量 $\mathcal{X}_0$, $\varepsilon>0$, 计算 $\mathcal{R}_0=\mathcal{F}-\mathcal{X}_0+\mathcal{X}_0\times_1A_1\times_2A_2\times\cdots \times_nA_n$;

步骤 2 选取 $\widetilde{\mathcal{R}}_0$ (可选取 $\widetilde{\mathcal{R}}_0=\mathcal{R}_0$). 令 $\mathcal{P}_0=\mathcal{R}_0,\widetilde{\mathcal{P}}_0=\widetilde{\mathcal{R}}_0$.置 $k=:0$;

步骤 3 计算

$\begin{eqnarray*} && \mathcal{Q}_k=\mathcal{P}_k-\mathcal{P}_k\times_1A_1\times_2A_2\times\cdots \times_nA_n; \\ && \widetilde{\mathcal{Q}}_k=\widetilde{\mathcal{P}}_k-\widetilde{\mathcal{P}}_k\times_1A_1\times_2A_2\times\cdots \times_nA_n;\\ && \alpha_k=\frac{\langle\mathcal{R}_k,\widetilde{\mathcal{R}}_k\rangle}{\langle\mathcal{Q}_k,\widetilde{\mathcal{P}}_k\rangle}; \mathcal{X}_{k+1}=\mathcal{X}_k+\alpha_k\mathcal{P}_{k};\\ && \mathcal{R}_{k+1}=\mathcal{R}_k+\alpha_k\mathcal{Q}_{k}; \widetilde{\mathcal{R}}_{k+1}=\widetilde{\mathcal{R}}_k+\alpha_k\widetilde{\mathcal{Q}}_{k};\\ && \beta_k=\frac{\langle\mathcal{R}_{k+1},\widetilde{\mathcal{R}}_{k+1}\rangle}{\langle\mathcal{R}_k,\widetilde{\mathcal{R}_{k}}\rangle}; \mathcal{P}_{k+1}=\mathcal{R}_{k+1}+\beta_k\mathcal{P}_k;\\ && \widetilde{\mathcal{P}}_{k+1}=\widetilde{\mathcal{R}}_{k+1}+\beta_k\widetilde{\mathcal{P}}_k; {\rm Err}=\frac{\parallel\mathcal{R}_k\parallel_{\rm F}}{\parallel\mathcal{R}_0\parallel_{\rm F}}. \end{eqnarray*}$

步骤 4 置$k=:k+1$. 若 Err $\leqslant\varepsilon$ 停算, 输出迭代次数 $k$ 和误差Err. 否则转步骤 3.

定义两个算子

$\begin{equation} \begin{array}{l} \mathcal{L}(\mathcal{X})=\mathcal{X}-\mathcal{X}\times_1A_1\times_2A_2\times\cdots\times_nA_n,\\[3pt] \mathcal{L}^{\rm T}(\mathcal{X})=\mathcal{X}-\mathcal{X}\times_1A_1^{\rm T}\times_2A_2^{\rm T}\times\cdots\times_nA_n^{\rm T}. \end{array} \end{equation}$

根据张量和矩阵模式积的定义, 有下面的等量关系

$\begin{eqnarray*} \langle\mathcal{L}(\mathcal{X}),\mathcal{Y}\rangle &=& \langle\mathcal{X}-\mathcal{X}\times_1A_1\times_2A_2\times\cdots\times_nA_n,\mathcal{Y}\rangle \\ &=& \langle\mathcal{X},\mathcal{Y}\rangle-\langle\mathcal{X}\times_1A_1\times_2A_2\times\cdots\times_nA_n,\mathcal{Y}\times_nA_n^{\rm T}\rangle \\ &=& \cdots \\ &=& \langle\mathcal{X},\mathcal{Y}\rangle-\langle\mathcal{X},\mathcal{Y}\times_nA_n^{\rm T}\times\cdots\times_2A_2^{\rm T}\times_1A_1^{\rm T}\rangle \\ &=& \langle\mathcal{X},\mathcal{Y}\rangle-\langle\mathcal{X},\mathcal{Y}\times_1A_1^{\rm T}\times_2A_2^{\rm T}\times\cdots\times_nA_n^{\rm T}\rangle \\ & =& \langle\mathcal{X},\mathcal{L}^{\rm T}\mathcal{Y}\rangle. \end{eqnarray*}$

下面的定理是文献 [19] 中张量格式的 BiCG 算法的双正交性质, 其具体证明过程如下

定理 2.1 设张量序列 ${\mathcal{R}_i}$, ${\widetilde{\mathcal{R}}_i}$, ${\mathcal{P}_i}$ 和 ${\widetilde{\mathcal{P}}_i}(i=0,1,\cdots,k)$ 由算法 1 生成, 则成立

$\begin{equation} \langle\mathcal{R}_i,\widetilde{\mathcal{R}}_j\rangle=0, \langle\mathcal{L}(\mathcal{P}_i),\widetilde{\mathcal{P}}_j\rangle=0, (i,j=0,1,\cdots,k,i\neq j), \end{equation}$

(2.5) 式中 $\mathcal{L}$ 由 (2.4) 式所定义.

证 使用归纳法证明当 $i\neq j$ 时 $\langle\mathcal{R}_i,\widetilde{\mathcal{R}}_j\rangle=0$. 首先, 证明 $j<i$ 的情形. 当 $i=1$ 时, 若 $j=0$, 那么显然成立

$\begin{eqnarray*} \langle\mathcal{R}_1,\widetilde{\mathcal{R}}_0\rangle&=&\langle\mathcal{R}_0-\alpha_0\mathcal{Q}_0,\widetilde{\mathcal{R}}_0\rangle \\ & =&\langle\mathcal{R}_0,\widetilde{\mathcal{R}}_0\rangle-\alpha_0 \langle\mathcal{Q}_0,\widetilde{\mathcal{R}}_0\rangle \\ &=&\langle\mathcal{R}_0,\widetilde{\mathcal{R}}_0\rangle-\frac{\langle\mathcal{R}_0,\widetilde{\mathcal{R}}_0\rangle}{\langle\mathcal{Q}_0, \widetilde{\mathcal{P}}_0\rangle}\langle\mathcal{Q}_0,\widetilde{\mathcal{R}}_0\rangle =0. \end{eqnarray*}$

假设当 $j<i\leqslant k$ 时, $\langle\mathcal{R}_i,\widetilde{\mathcal{R}}_j\rangle=0$. 则当 $i=k+1$ 时, 若 $j<k$, 那么

$\begin{eqnarray*} \langle\mathcal{R}_{k+1},\widetilde{\mathcal{R}}_j\rangle&=&\langle\mathcal{R}_k-\alpha_k\mathcal{Q}_k,\widetilde{\mathcal{R}}_j\rangle\\ &=&\langle\mathcal{R}_k,\widetilde{\mathcal{R}}_j\rangle-\alpha_k\langle\mathcal{Q}_k,\widetilde{\mathcal{R}}_j\rangle =-\alpha_k\langle\mathcal{Q}_k,\widetilde{\mathcal{R}}_j\rangle \\ &=&-\alpha_k\langle\mathcal{L}(\mathcal{P}_k),\widetilde{\mathcal{P}}_j-\beta_{j-1}\widetilde{\mathcal{P}}_{j-1}\rangle \\ &=&-\alpha_k\langle\mathcal{L}(\mathcal{P}_k),\widetilde{\mathcal{P}}_j\rangle+\alpha_k\beta_{j-1}\langle\mathcal{L}(\mathcal{P}_k), \widetilde{\mathcal{P}}_{j-1}\rangle =0. \end{eqnarray*}$

若 $j=k$, 则

$\begin{eqnarray*} \langle\mathcal{R}_{k+1},\widetilde{\mathcal{R}}_k\rangle&=& \langle\mathcal{R}_k,\widetilde{\mathcal{R}}_k\rangle-\alpha_k\langle\mathcal{Q}_k,\widetilde{\mathcal{P}}_k-\beta_{k-1}\widetilde{\mathcal{P}}_{k-1}\rangle \\ &=&\langle\mathcal{R}_k,\widetilde{\mathcal{R}}_k\rangle-\alpha_k\langle\mathcal{Q}_k,\widetilde{\mathcal{P}}k\rangle+\alpha_k\beta_{k-1}\langle\mathcal{Q}_k,\widetilde{\mathcal{P}}_{k-1}\rangle \\ &=&\langle\mathcal{R}_k,\widetilde{\mathcal{R}}_k\rangle-\frac{\langle\mathcal{R}_k,\widetilde{\mathcal{R}}_k\rangle}{\langle\mathcal{Q}_k,\widetilde{\mathcal{P}}_k\rangle}\langle\mathcal{Q}_k, \widetilde{\mathcal{P}}k\rangle =0. \end{eqnarray*}$

因此, 当 $i=k+1$ 时结论成立. 用同样的方法, 也可证明当 $j>i$ 时的情形.

下面, 需证明 $\langle\mathcal{L}(\mathcal{P}_i),\widetilde{\mathcal{P}}_j\rangle=0 (i\neq j)$. 首先, 证明 $j<i$ 的情形.

$\begin{eqnarray*} \langle\mathcal{L}(\mathcal{P}_i),\widetilde{\mathcal{P}}_j\rangle &=&\langle\mathcal{L}(\mathcal{R}_i+\beta_{i-1}\mathcal{P}_{i-1}),\widetilde{\mathcal{P}}_j\rangle \\ &=&\langle\mathcal{L}(\mathcal{R}_i,\widetilde{\mathcal{P}}_j\rangle+\beta_{i-1}\langle\mathcal{L}(\mathcal{P}_{i-1}),\widetilde{\mathcal{P}}_j\rangle \\ &=&\langle\mathcal{R}_i,\mathcal{L}^{\rm T}(\widetilde{\mathcal{P}}_j)\rangle+\beta_{i-1}\langle\mathcal{L}(\mathcal{P}_{i-1}),\widetilde{\mathcal{P}}_j\rangle \\ &=&\langle\mathcal{R}_i,\frac{\widetilde{\mathcal{R}}_j-\widetilde{\mathcal{R}}_{j+1}} {\alpha_j}\rangle+\beta_{i-1}\langle\mathcal{L}(\mathcal{P}_{i-1}),\widetilde{\mathcal{P}}_j\rangle. \end{eqnarray*}$

当 $i=1$, $j=0$ 时,

$\begin{eqnarray*} \langle\mathcal{L}(\mathcal{P}_1),\widetilde{\mathcal{P}}_0\rangle &=&\frac{1}{\alpha_0}\langle\mathcal{R}_1,\widetilde{\mathcal{R}}_0\rangle-\frac{1}{\alpha_0}\langle\mathcal{R}_1,\widetilde{\mathcal{R}}_1\rangle+\beta_0\langle\mathcal{L}(\mathcal{P}_0),\widetilde{\mathcal{P}}_0\rangle\\ &=&-\frac{\langle\mathcal{Q}_0,\widetilde{\mathcal{P}}_0\rangle}{\langle\mathcal{R}_0,\widetilde{\mathcal{R}}_0\rangle}\langle\mathcal{R}_1,\widetilde{\mathcal{R}}_1\rangle+\frac{\langle\mathcal{R}_1,\widetilde{\mathcal{R}}_1\rangle} {\langle\mathcal{R}_0,\widetilde{\mathcal{R}}_0\rangle}\langle\mathcal{Q}_0,\widetilde{\mathcal{P}}_0\rangle =0. \end{eqnarray*}$

假设当 $j<i\leqslant k$ 时, $\langle\mathcal{L}(\mathcal{P}_i),\widetilde{\mathcal{P}}_j\rangle=0$. 则当 $i=k+1$ 时, 若 $j<k$, 那么

$\begin{eqnarray*} \langle\mathcal{L}(\mathcal{P}_{k+1}),\widetilde{\mathcal{P}}_j\rangle &=&\frac{1}{\alpha_j}\langle\mathcal{R}_{k+1},\widetilde{\mathcal{R}}_j\rangle-\frac{1}{\alpha_j} \langle\mathcal{R}_{k+1},\widetilde{\mathcal{R}}_{j+1}\rangle+\beta_k\langle\mathcal{L}(\mathcal{P}_k),\widetilde{\mathcal{P}}_j\rangle\\[5pt] &=&0. \end{eqnarray*}$

若 $j=k$, 则

$\begin{eqnarray*} \langle\mathcal{L}(\mathcal{P}_{k+1}),\widetilde{\mathcal{P}}_k\rangle &=&\frac{1}{\alpha_k}\langle\mathcal{R}_{k+1},\widetilde{\mathcal{R}}_{k+1}\rangle+\beta_k\langle\mathcal{L} (\mathcal{P}_k),\widetilde{\mathcal{P}}_k\rangle\\[3pt] &=&-\frac{\langle\mathcal{Q}_k,\widetilde{\mathcal{P}}_k\rangle}{\langle\mathcal{R}_k,\widetilde{\mathcal{R}}_k\rangle} \langle\mathcal{R}_{k+1},\widetilde{\mathcal{R}}_{k+1}\rangle+ \frac{\langle\widetilde{\mathcal{R}}_{k+1},\mathcal{R}_{k+1}\rangle}{\langle\widetilde{\mathcal{R}}_k,\mathcal{R}_k \rangle}\langle\mathcal{L}(\mathcal{P}_k),\widetilde{\mathcal{P}}_k\rangle\\[5pt] & =&0. \end{eqnarray*}$

因此, 当 $i=k+1$ 时, 结论成立.用同样的方法, 可证明 $j>i$ 的情形.

推论 2.1 设张量序列 ${\mathcal{R}_i}$, ${\widetilde{\mathcal{R}}_i}$, ${\mathcal{P}_i}$ 和 ${\widetilde{\mathcal{P}}_i}(i=0,1,\cdots,k)$ 由算法1 生成, 则成立

$\begin{eqnarray*} \langle\mathcal{R}_i,\widetilde{\mathcal{R}}_i\rangle=\langle\mathcal{R}_i,\widetilde{\mathcal{P}}_i\rangle, \langle\mathcal{R}_i,\widetilde{\mathcal{P}}_j\rangle=0, \text{当} i>j, \langle\mathcal{L}(\mathcal{P}_i),\widetilde{\mathcal{R}}_i\rangle=\langle\mathcal{L}(\mathcal{P}_i),\widetilde{\mathcal{P}}_j\rangle, \end{eqnarray*}$

式中 $\mathcal{L}$ 由(2.4) 式所定义.

定理 2.2[19] 假设Stein张量方程 (1.1) 是相容的, 在不考虑舍入误差的情况下, 对任意的初始张量 $\mathcal{X}_0\in \mathbf{R}^{I_1\times I_2\times\cdots\times I_n}$, 由算法1 生成的序列 $\{\mathcal{X}_k\}$ 至多 N 步迭代收敛到 (1.1)式的精确解.

受张量格式 BiCG 算法的启发, 给出求解 Stein 张量方程的张量格式的 BCGSTAB 迭代算法如下.

算法 2 (张量格式的 BCGSTAB 算法)

步骤 1 输入初始张量 $\mathcal{X}_0$, $0\leqslant\varepsilon\ll1$, 计算 $\mathcal{R}_0=\mathcal{F}-\mathcal{X}_0+\mathcal{X}_0\times_1A_1\times_2A_2\times\cdots \times_n A_n$;

步骤 2 选取 $\widetilde{\mathcal{R}}_0$ (可选取 $\widetilde{\mathcal{R}}_0=\mathcal{R}_0$);令 $\mathcal{P}_0=\mathcal{R}_0$, 计算 $\rho_0=\langle\widetilde{\mathcal{R}}_0,\mathcal{R}_0\rangle$; 置 $k:=0$;

步骤 3 依次计算

$\begin{eqnarray*} &&\mathcal{U}_k=\mathcal{P}_k-\mathcal{P}_k\times_1A_1\times_2A_2\times\cdots \times_nA_n, \\ &&\alpha_k=\frac{\rho_k}{\langle\mathcal{\widetilde{R}}_0,\mathcal{U}_k\rangle},\\[6pt] &&\mathcal{S}_k=\mathcal{R}_k-\alpha_k\mathcal{U}_k,\\[3pt] &&\mathcal{Q}_k=\mathcal{S}_k-\mathcal{S}_k\times_1A_1\times_2A_2\times\cdots \times_nA_n,\\[6pt] &&\omega_{k+1}=\frac{\langle\mathcal{S}_k,\mathcal{Q}_k\rangle}{\langle\mathcal{Q}_k,\mathcal{Q}_k\rangle},\\[6pt] &&\mathcal{X}_{k+1}=\mathcal{X}_k+\alpha_k\mathcal{P}_k+\omega_{k+1}\mathcal{S}_k,\\ &&\mathcal{R}_{k+1}=\mathcal{S}_{k}-\omega_{k+1}\mathcal{Q}_k,\\[3pt] &&\rho_{k+1}=\langle\widetilde{\mathcal{R}}_0,\mathcal{R}_{k+1}\rangle,\\[6pt] &&\beta_{k+1}=\frac{\alpha_k\rho_{k+1}}{\omega_{k+1}\rho_k},\\[3pt] &&\mathcal{P}_{k+1}=\mathcal{R}_{k+1}+\beta_{k+1}(\mathcal{P}_k-\omega_{k+1}\mathcal{U}_k),\\[6pt] && \mathrm{Err}=\frac{\parallel\mathcal{R}_k\parallel}{\parallel\mathcal{R}_0\parallel}. \end{eqnarray*}$

步骤 4 置 $k:=k+1$. 若 ${\rm Err}\leqslant\varepsilon$, 则停止迭代, 输出近似解 $\mathcal{X}_k$ 和迭代次数 $k$ 及残差 Err. 否则, 转步骤 3.

同样, 类似于文献 [19] 的证明, 容易得到算法2 的收敛性定理.

定理 2.3 假设 Stein 张量方程 (1.1) 是相容的, 在不考虑舍入误差的情况下, 对任意的初始张量 $\mathcal{X}_0\in \mathbf{R}^{I_1\times I_2\times\cdots\times I_n}$, 由算法2 生成的序列 $\{\mathcal{X}_k\}$ 至多 N 步迭代收敛到 (1.1) 式的精确解.

3 数值实验

本节, 将给出几个数值例子来说明我们提出算法的有效性, 并且将提出的算法与张量格式的 CGNR (关于法方程残差的共轭梯度) 算法和 CGNE (关于法方程误差的共轭梯度) 算法进行比较. 所有实验都是在如下环境中实现的: Windows 10 系统, 处理器Intel(R) Core(TM) i5-6500 CPU 3.20GHz, 8GB RAM. 利用 Matlab R2014b 软件环境以及 Bader 和 Kolda 开发的 MATLAB 张量工具箱执行实验. 在实验过程中, 记录了所需的迭代次数("IT")、 所消耗的 CPU 时间(以秒为单位, 记为 "CPU"),在数值实验中, 初始张量取为 $\mathcal{X}_0=\mathcal{O}$, 且终止准则为

$\begin{equation*} {\rm Err}=\frac{\parallel\mathcal{R}_k\parallel_{\rm F}}{\parallel\mathcal{R}_0\parallel_{\rm F}}<10^{-16}. \end{equation*}$

下面两个算法分别是张量格式的CGNR算法和CGNE算法.

算法 3 (张量格式的 CGNR 算法)

步骤 1 输入初始张量 $\mathcal{X}_0$, $0\leqslant \varepsilon\ll 1$, 计算 $\mathcal{R}_0=\mathcal{F}-\mathcal{X}_0+\mathcal{X}_0\times_1A_1\times_2A_2\times\cdots \times_nA_n$;

步骤 2 计算 $\mathcal{Z}_0=\mathcal{R}_0-\mathcal{R}_0\times_1A_1^{\rm T}\times_2A_2^{\rm T}\times\cdots \times_nA_n^{\rm T}$; 令 $\mathcal{P}_0=\mathcal{Z}_0$; 置 $k:=0$;

步骤 3 依次计算

$\begin{eqnarray*} &&\mathcal{Q}_k=\mathcal{P}_k-\mathcal{P}_k\times_1A_1\times_2A_2\times\cdots \times_nA_n, \\[5pt] &&\alpha_k=\frac{\|\mathcal{Z}_k\|_{\rm F}^2}{\|\mathcal{Q}_k\|_{\rm F}^2},\\[5pt] &&\mathcal{X}_{k+1}=\mathcal{X}_k+\alpha_k\mathcal{P}_k,\\ &&\mathcal{R}_{k+1}=\mathcal{R}_k-\alpha_k\mathcal{Q}_k,\\ &&\mathcal{Z}_{k+1}=\mathcal{R}_{k+1}-\mathcal{R}_{k+1}\times_1A_1^{\rm T}\times_2A_2^{\rm T}\times\cdots \times_nA_n^{\rm T},\\[5pt] &&\beta_k=\frac{\|\mathcal{Z}_{k+1}\|_{\rm F}^2}{\|\mathcal{Z}_k\|_{\rm F}^2},\\[5pt] &&\mathcal{P}_{k+1}=\mathcal{Z}_{k+1}+\beta_k\mathcal{P}_k,\\[5pt] &&{\rm Err}=\frac{\parallel\mathcal{R}_k\parallel_{\rm F}}{\parallel\mathcal{R}_0\parallel_{\rm F}}. \end{eqnarray*}$

步骤 4 置 $k:=k+1$. 若 ${\rm Err}\leqslant\varepsilon$, 则停止迭代, 输出近似解 $\mathcal{X}_k$ 和迭代次数 $k$ 及残差 Err. 否则, 转第 3 步.

算法 4 (张量格式的 CGNE 算法)

步骤 1 输入初始张量 $\mathcal{X}_0$, $0\leqslant \varepsilon\ll 1$, 计算 $\mathcal{R}_0=\mathcal{F}-\mathcal{X}_0+\mathcal{X}_0\times_1A_1\times_2A_2\times\cdots \times_nA_n$;

步骤 2 计算 $\mathcal{Z}_0=\mathcal{R}_0-\mathcal{R}_0\times_1A_1^{\rm T}\times_2A_2^{\rm T}\times\cdots \times_nA_n^{\rm T}$; 令 $\mathcal{P}_0=\mathcal{Z}_0$; 置 $k:=0$;

步骤 3 依次计算

$\begin{eqnarray*} && \mathcal{Q}_k=\mathcal{P}_k-\mathcal{P}_k\times_1A_1\times_2A_2\times\cdots \times_nA_n, \\[5pt] && \alpha_k=\frac{\|\mathcal{R}_k\|_{\rm F}^2}{\|\mathcal{P}_k\|_{\rm F}^2},\\[5pt] && \mathcal{X}_{k+1}=\mathcal{X}_k+\alpha_k\mathcal{P}_k,\\ && \mathcal{R}_{k+1}=\mathcal{R}_k-\alpha_k\mathcal{Q}_k,\\[5pt] && \beta_k=\frac{\|\mathcal{R}_{k+1}\|_{\rm F}^2}{\|\mathcal{P}_k\|_{\rm F}^2},\\[2pt] && \mathcal{Z}_{k+1}=\mathcal{R}_{k+1}-\mathcal{R}_{k+1}\times_1A_1^{\rm T}\times_2A_2^{\rm T}\times\cdots \times_nA_n^{\rm T},\\ && \mathcal{P}_{k+1}=\mathcal{Z}_{k+1}+\beta_k\mathcal{P}_k,\\[5pt] && {\rm Err}=\frac{\parallel\mathcal{R}_k\parallel_{\rm F}}{\parallel\mathcal{R}_0\parallel_{\rm F}}. \end{eqnarray*}$

步骤 4 置 $k:=k+1$. 若 ${\rm Err}\leqslant\varepsilon$, 则停止迭代, 输出近似解 $\mathcal{X}_k$ 和迭代次数 $k$ 及残差 Err. 否则, 转步骤 3.

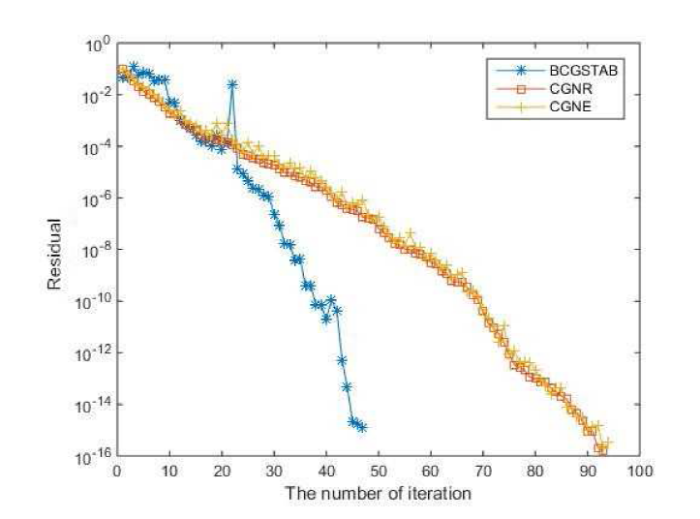
例 3.1 求解下面Stein张量方程的解:$ \mathcal{X}-\mathcal{X}\times_1A_1\times_2A_2\times_3A_3=\mathcal{F},$ 其中 $A_i (i=1,2,3)$ 由 MATLAB 随机生成.

下面列出随机生成的 $A_1\in \mathbf{R}^{6\times 6}, A_2\in \mathbf{R}^{5\times 5}, A_3\in \mathbf{R}^{4\times 4}$, 并且构造张量 $\mathcal{F}$, 使得元素都为1 的张量 $\mathcal{X}^*$ 为精确解.实验结果可见图1, 显然从图上可知张量格式的 BCGSTAB 算法有更佳的收敛效果, 它的迭代次数远远少于张量格式的CGNR 和CGNE 算法.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   例3.1的实验结果


$\begin{equation*} A_1=\left(\begin{array}{llllll} 0.7970 & 0.4983 & 0.5829 & 0.2975 & 0.1604 & 0.8439 \\ 0.9969 & 0.9491 & 0.5647 & 0.0747 & 0.1579 & 0.7823 \\ 0.2813 & 0.9532 & 0.3552 & 0.2937 & 0.5087 & 0.2646 \\ 0.7104 & 0.7329 & 0.8802 & 0.2347 & 0.6033 & 0.3147 \\ 0.6646 & 0.3847 & 0.6245 & 0.3459 & 0.1614 & 0.1832 \\ 0.4148 & 0.0401 & 0.6240 & 0.8485 & 0.6355 & 0.4475 \end{array}\right), \end{equation*}$

$\begin{equation*} A_2=\left(\begin{array}{lllll} 0.3267 & 0.5928 & 0.2002 & 0.1851 & 0.5579 \\ 0.2798 & 0.0685 & 0.8435 & 0.0817 & 0.6388 \\ 0.9318 & 0.2052 & 0.4237 & 0.4641 & 0.0342 \\ 0.3997 & 0.7236 & 0.5448 & 0.0306 & 0.7099 \\ 0.3794 & 0.5751 & 0.5280 & 0.4350 & 0.1693 \end{array}\right), \end{equation*}$$\begin{equation*} A_3=\left(\begin{array}{llll} 0.5934 & 0.8547 & 0.5554 & 0.6302 \\ 0.6081 & 0.3832 & 0.2954 & 0.6644 \\ 0.7724 & 0.3996 & 0.3661 & 0.9921 \\ 0.0563 & 0.3254 & 0.3490 & 0.9444 \end{array}\right), \end{equation*}$

$\begin{equation*} C(:,:,1)=\left(\begin{array}{lllll} -14.5920 & -15.0067 & -16.2352 & -19.1605 & -16.4680 \\ -16.2959 & -16.7560 & -18.1188 & -21.3637 & -18.3769 \\ -12.0331 & -12.3797 & -13.4066 & -15.8518 & -13.6012 \\ -16.0542 & -16.5078 & -17.8515 & -21.0511 & -18.1060 \\ -10.5993 & -10.9078 & -11.8217 & -13.9979 & -11.9948 \\ -13.7685 & -14.1613 & -15.3250 & -18.0958 & -15.5454 \end{array}\right), \end{equation*}$
$\begin{equation*} C(:,:,2)=\left(\begin{array}{lllll} -10.5574 & -10.8648 & -11.7754 & -13.9437 & -11.9479 \\ -11.8204 & -12.1614 & -13.1715 & -15.5768 & -13.3629 \\ -8.6606 & -8.9176 & -9.6787 & -11.4912 & -9.8229 \\ -11.6412 & -11.9774 & -12.9734 & -15.3451 & -13.1621 \\ -7.5978 & -7.8265 & -8.5039 & -10.1170 & -8.6322 \\ -9.9470 & -10.2381 & -11.1007 & -13.1545 & -11.2641 \end{array}\right), \end{equation*}$
$\begin{equation*} C(:,:,3)=\left(\begin{array}{lllll} -13.9791 & -14.3775 & -15.5578 & -18.3681 & -15.7813 \\ -15.6161 & -16.0580 & -17.3672 & -20.4846 & -17.6152 \\ -11.5208 & -11.8538 & -12.8403 & -15.1894 & -13.0272 \\ -15.3838 & -15.8196 & -17.1105 & -20.1843 & -17.3550 \\ -10.1433 & -10.4397 & -11.3177 & -13.4083 & -11.4840 \\ -13.1880 & -13.5654 & -14.6833 & -17.3451 & -14.8950 \end{array}\right), \end{equation*}$
$\begin{equation*} C(:,:,4)=\left(\begin{array}{lllll} -8.9168 & -9.1806 & -9.9620 & -11.8225 & -10.1100 \\ -10.0006 & -10.2932 & -11.1599 & -13.2238 & -11.3241 \\ -7.2893 & -7.5098 & -8.1629 & -9.7181 & -8.2866 \\ -9.8468 & -10.1353 & -10.9899 & -13.0249 & -11.1518 \\ -6.3774 & -6.5736 & -7.1549 & -8.5390 & -7.2650 \\-8.3931 & -8.6429 & -9.3830 & -11.1453 & -9.5232 \end{array}\right). \end{equation*}$

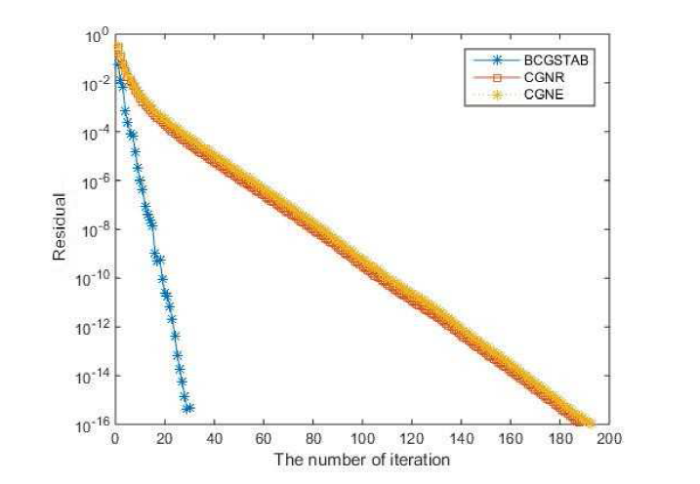
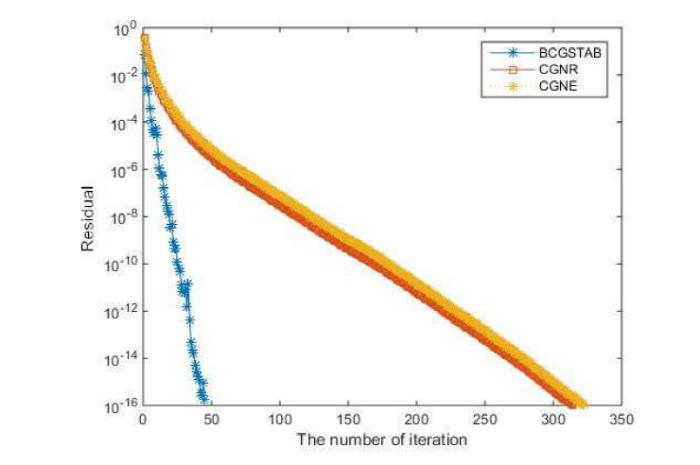
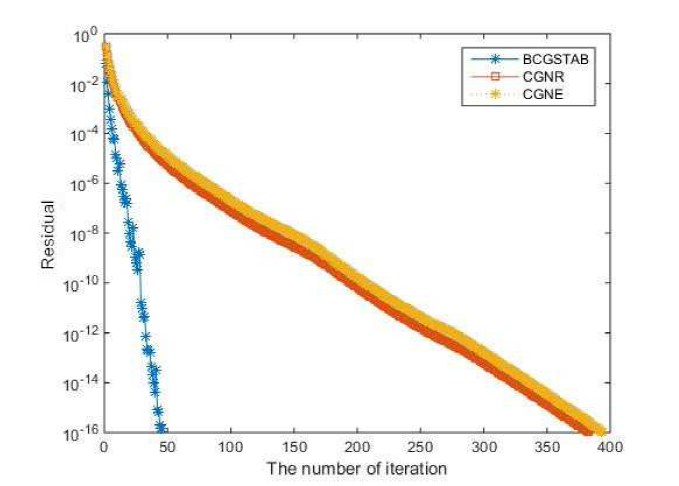
例 3.2 求解下面Stein张量方程的解

$\begin{equation} \mathcal{X}-\mathcal{X}\times_1A_1\times_2A_2\times_3A_3=\mathcal{F}, \end{equation}$

其中系数矩阵 $A_i (i=1,2,3)$ 为稀疏矩阵, 令

$\begin{equation*} \begin{array}{l} A_1=\mathrm{diag}(\mathrm{rand}(n-1,1),-1)+\mathrm{diag}(2.5+\mathrm{diag}(\mathrm{rand}(n,n)))+\mathrm{diag}(\mathrm{rand}(n-1,1),1),\\ A_2=\mathrm{diag}(\mathrm{rand}(n-1,1),1)+\mathrm{diag}(1.5+\mathrm{diag}(\mathrm{rand}(n,n))),\\ A_3=\mathrm{diag}(\mathrm{rand}(n-1,1),-1)+\mathrm{diag}(2+\mathrm{diag}(\mathrm{rand}(n,n))). \end{array} \end{equation*}$

初始张量 $\mathcal{X}_0=\mathcal{O}$, 构造的右端项 $\mathcal{F}$ 使得 $\mathcal{X}^*=\mathrm{ones}(n,n,n)$ 是(3.1)式的精确解.

分别令 $n=20,50,100$, 计算结果见图2、图3、图4 及表1. 尽管当维数增加到 100 时, 张量格式的 CGNR 和 CGNE 算法迭代步数大大增加, 但张量格式的 BCGSTAB 算法仍保持着较好的收敛效果.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   $n=20$ 时的残差曲线图


图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   $n=50$ 时的残差曲线图


图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   $n=100$ 时的残差曲线图


表1   例3.2的CPU 时间(秒)

新窗口打开| 下载CSV


4 小结

本文针对下列 Stein 张量方程方程$ \mathcal{X}-\mathcal{X}\times_1A_1\times_2A_2\times\cdots\times_nA_n=\mathcal{F},$设计了基于张量形式求解该方程的双共轭梯度稳定化 (BCGSTAB) 方法. 从两个数值算例的实验结果来看, BCGSTAB 方法较 CGNR 和 CGNE 有较快的收敛速度, 不仅表现在迭代次数大大较少, CPU 时间也缩短了许多.

参考文献

Hestenes M R, Stiefel E.

Methods of conjugate gradients for solving linear systems

Journal of Research of the National Bureau of Standards (United States), 1952, 49(6): 409-436

[本文引用: 1]

Paige C C, Saunders M A.

Solution of sparse indefinite systems of linear equations

SIAM Journal on Numerical Analysis, 1975, 12(4): 617-629

[本文引用: 1]

Saad Y.

Iterative Methods for Sparse Linear Systems

SIAM: Philadelphia PA USA, 2003

[本文引用: 1]

Lanczos C.

Solution of systems of linear equations by minimized iterations

Journal of Research of the National Bureau of Standards, 1952, 49: 33-53

[本文引用: 1]

Fletcher R.

Conjugate gradient methods for indefinite systems

Springer, 1976, 506: 73-89

[本文引用: 1]

Saad Y, Shultz M H.

GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems

SIAM Journal on Scientific and Statistical Computing, 1986, 7(3): 856-869

[本文引用: 1]

Eisenstat S C, Elman M H, Schultz M H.

Variational iterative methods for nonsymmetric systems of linear equations

SIAM Journal on Numerical Analysis, 1983, 20(2): 345-357

[本文引用: 1]

Sogabe T, Sugihara M, Zhang S L.

An extension of the conjugate residual method to nonsymmetric linear systems

Journal of Computational and Applied Mathematics, 2009, 226(1): 103-113

[本文引用: 1]

Kressner D, Tobler C.

Krylov subspace methods for linear systems with tensor product structure

SIAM Journal on Matrix Analysis and Applications, 2010, 31(4): 1688-1714

[本文引用: 1]

Van der Vorst H A.

Bi-CGSTAB: A fast and smoothly converging variant of Bi-CG for the solution of nonsymmetric linear systems

SIAM Journal on Scientific and Statistical Computing, 1992, 13(2): 631-644

[本文引用: 1]

Gutknecht M H.

Variants of BICGSTAB for matrices with complex spectrum

SIAM Journal on Scientific Computing, 1993, 14(5): 1020-1033

[本文引用: 1]

Zhang S L.

GPBi-CG: Generalized product-type methods based on Bi-CG for solving nonsymmetric linear systems

SIAM Journal Scientific Computing, 1997, 18(3): 537-551

[本文引用: 1]

Zhou B, Lam J, Duan G R.

On smith-type iterative algorithms for the stein matrix equation

Applied Mathematics Letters, 2009, 22(7): 1038-1044

[本文引用: 2]

DeAlba L M, Johnson C R.

Possible inertia combinations in the stein and lyapunov euations

Linear Algebra and its Applications, 1995, 222: 227-240

[本文引用: 1]

Fuhrmann P A.

A functional approach to the stein equation

Linear Algebra and its Applications, 2010, 432(12): 3031-3071

[本文引用: 2]

Gouveia M C.

On the solution of sylvester, lyapunov and stein equations over arbitrary rings

International Journal of Pure and Applied Mathematics, 2005, 24(1): 135-141

[本文引用: 2]

Betser A, Cohen N, Zeheb E.

On solving the lyapunov and stein equations for a companion matrix

Systems and Control Letters, 1995, 25(3): 211-218

[本文引用: 1]

Chiang C Y.

A note on the $\top$-Stein matrix equation. Abstract and Applied Analysis

Hindawi Publishing Corporation, 2013, 2013(1): 824641

[本文引用: 2]

Xu X J, Wang Q W.

Extending BiCG and BiCR methods to solve the Stein tensor equation

Computers & Mathematics with Applications, 2019, 77(12): 3117-3127

[本文引用: 7]

Zhang X F, Wang Q W.

On RGI algorithms for solving sylvester tensor equations

Taiwanese Journal of Mathematics, 2022, 26(3): 501-519

[本文引用: 1]

Chen Y, Li C.

Preconditioned tensor format conjugate gradient squared and biconjugate gradient stabilized methods for solving stein tensor equations

Numerical Linear Algebra with Applications, 2023, 30(5): e2502

[本文引用: 1]

/

〈 〉

版权所有 © 《数学物理学报》杂志社
地址： 武汉市71010号信箱(430071)　电话: 027-87199206(中文版)　027-87199087(英文版)
E-mail: actams@apm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发