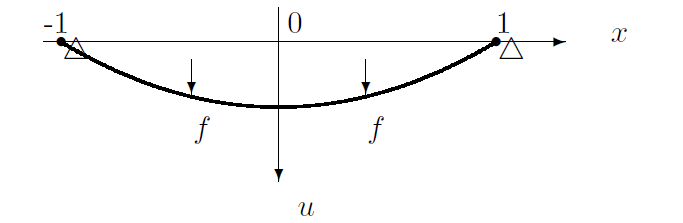
两端简单支撑的弹性梁的静态形变可用区间 $ [-1,\,1] $ 上的四阶常微分方程边值问题 (BVP)

来描述^[1,2], 其中 $ u(x) $ 为梁形变的位移, $ u''(x) $ 为弯矩. 当梁左右对称时, 其解 $ u $ 具有对称性: $ u(-x)=u(x),x\in [0,1] $, 从而 $ u'(0)=0, u'''(0)=0 $. 因此 $ u $ 在区间 $ [0,1] $ 上满足方程

因此, BVP (1.1) 及 BVP (1.2) 具有重要的应用背景. 在一些实际问题, 按梁的受力分析, 只有正解才有实际意义, 如图1

设 $ f:[0,1]\times\mathbb{R}^{+}\times\mathbb{R}^{-}\to\mathbb{R}^{+} $ 连续, 本文讨论 BVP (1.2) 正解的存在性.

近 30 年来, $ [0,1] $ 区间上有关弹性梁的四阶常微分方程边值问题正解的存在性已被许多学者关注和研究^{[3⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-15]}. 已有的工作主要涉及到三种边界支撑条件, 其一是两端简单支撑的边界条件

见文献 [3⇓⇓⇓⇓-8]. 其中文献 [3] 研究了非线性项 $ f $ 不含弯矩项 $ u'' $ 的特殊情形, 作者应用锥压缩与锥拉伸不动点定理, 在非线性项 $ f $ 关于 $ u $ 超线性或次线性增长的条件下, 获得到了正解的存在性结果;文献 [4] 扩充了文献 [3] 的工作, 获得了两个正解的存在性结果; 文献 [5] 把文献 [3] 的结果推广到了在 $ f $ 含弯矩项 $ u'' $ 的一般情形, 在 $ f(x,\,u,\,v) $ 关于 $ u,\,v $ 超线性或次线性增长的条件下,获得正解的存在性结果; 文献 [6] 改进了文献 [5] 的结果, 在 $ f $ 满足一些最优的不等式条件下, 应用锥上的不动点指数理论获得了正解的存在性结果. 文献 [7] 在 $ f(x,\,u,\,v) $ 当 $ |(u,\,v)|\rightarrow 0 $及 $ |(u,\,v)|\rightarrow\infty $ 时关于 $ u,\,v $ 渐进线性的条件下, 应用全局分歧理论, 获得了正解的存在性结果; 最近, 文献 [8] 在不假设 $ f $ 非负的情形, 用上下解的方法与截断函数技巧获得了正解的存在性结果.

弹性梁方程的第二种边界支撑条件是两端固定支撑的边界条件

研究这种情形的见文献 [9⇓-11]. 其中文献 [9,10] 研究了非线性项为 $ f(x,\,u) $ 的特殊情形, 文献 [9] 通过研究对应的线性积分方程的 Green 函数的正性, 应用锥压缩与锥拉伸不动点定理获得了正解的存在性结果;文献 [10] 通过估计对应的线性特征值问题的主特征值, 应用不动点指数理论建立了正解存在的特征值判据; 文献 [11] 研究了非线性项为 $ f(x,\,u,\,u') $ 的情形,在 $ f(x,\,u,\,v) $ 关于$ u,\,v $ 可一边超线性增长的不等式条件下, 应用 Leray-Schauder 不动点定理获得了解的存在性与唯一性结果.

弹性梁方程的另一种边界支撑条件是一端固定支撑另一端自由(悬臂梁)的边界条件

研究这种情形的见文献 [12⇓⇓-15]. 其中文献 [12⇓-14] 讨论了非线性项为 $ f(x,\,u,\,u') $ 的情形, 文献 [12] 构造了一个从 $ 0 $ 开始的单调迭代程序, 求得了方程的正解;文献 [13] 应用压缩与锥拉伸不动点定理, 获得了正解的存在性结果; 文献 [14] 应用锥上的不动点定理与控制函数技巧, 获得了正解的存在性与多解性结果;文献 [15] 研究了非线性项为 $ f(x,\,u,\,u',\,u'',\,u''') $ 的一般情形, 在 $ f(x,\,u,\,v,\,w,\,p) $ 关于 $ u,\,v,\,w,\,p $ 超线性或次线性增长的条件下, 用锥上的不动点指数理论获得了正解的存在性结果.还有一些作者研究了带有非线性边界条件的悬臂梁梁方程解的存在性, 见文献 [16⇓⇓-19].

BVP (1.2) 的边界条件

与上述边界条件均不相同. 我们知道, 边界条件对解的存在性及解的性质有很大的影响, 目前尚未见到有对 BVP (1.2) 解的存在性的研究文献. 本文的目的是研究 BVP (1.2) 正解的存在性.我们通过建立对应的线性方程的解 $ \,u\, $ 正性与弯矩项 $ \,u'' $ 负性的估计, 应用锥上的不动点指数理论, 在 $ f $ 满足一些不等式条件下, 获得了BVP (1.2) 正解的存在性结论.我们的主要结果如下

定理 1.1 设 $ f:[\,1]\times\mathbb{R}^+\times\mathbb{R}^-\to\mathbb{R}^+ $ 连续, 满足下列条件

(F1) 存在常数 $ \,a_0,\, b_0\ge 0\, $ 满足 $ \, \frac{16a_0}{\pi ^4}+\frac{4b_0}{\pi ^2}<1\, $ 及常数 $ \,\delta>0\, $, 使得

(F2) 存在常数 $ \,a_{1},\, b_{1}\ge 0\, $, 满足 $ \, \frac{16a_{1}}{\pi ^{4}}+\frac{4b_{1}}{\pi ^{2}}>1\, $ 及 $ \,H>0\, $, 使得

则 BVP (1.2) 至少有一个正解.

定理 1.2 设 $ f:[\,1]\times\mathbb{R}^+\times\mathbb{R}^-\to\mathbb{R}^{+} $ 连续, 满足下列条件

(F3) 存在常数 $ \,a_1,\, b_1\ge 0\, $, 满足 $ \, \frac{16a_1}{\pi ^4}+\frac{4b_1}{\pi ^2}>1\, $ 及 $ \,\delta>0\, $, 使得

(F4) 存在常数 $ \,a_0,\, b_0\ge 0\, $, 满足 $ \,\frac{16a_0}{\pi ^{4}}+\frac{4b_0}{\pi ^{2}}<1\, $ 及 $ \,H>0\, $, 使得

则 BVP (1.2) 至少有一个正解.

上述定理中的条件 (F1)-(F4) 是关于 $ (u,\,v) $ 在 $ \mathbf{0} $ 点与 $ \infty $ 点的局部不等式条件, 这些条件是容易验证的. 其中, 定理 1.1 中的条件 (F1) 与 (F2) 分别允许 $ f(x,\,u,\,v) $ 当 $ |(u,\,v)|\to 0 $ 及 $ |(u,\,v)|\to +\infty $ 时,关于 $ u $ 与 $ v $ 超线性增长, 例如

易验证, 当 $ a,\,b\ge 0 $ 及 $ \frac{16a}{\pi ^4}+\frac{4b}{\pi ^2}<1\, $ 时, $ f $ 满足条件 (F1) 和 (F2). 因此, 按定理 1.1, 该 $ f $ 对应的 BVP (1.2) 有非平凡的正解. 定理 1.2 中的条件 (F3) 与 (F4) 分别允许 $ f(x,\,u,\,v) $ 当 $ |(u,\,v)|\to 0 $ 及 $ |(u,\,v)|\to+\infty $ 时, 关于 $ u $ 与 $ v $ 次线性增长, 例如

应用 Young 不等式可验证, 当 $ a,\,b\ge 0\, $ 及 $ \,ab>0 $ 时, 这个 $ f $ 满足条件 (F3) 和 (F4). 因此, 按定理 1.2, 其对应的 BVP (1.2) 有非平凡的正解.这两个例子说明了定理 1.1 与定理 1.2 的适用性.

记 $ I=[0,1] $, $C(I)$ 为 $I$ 上连续函数之集按范数 $\|u\|_C=\max\limits_{x\in I}|u(x)|$ 构成的 Banach 空间. 对 $ n\in\mathbb{N} $, $C^{n}(I)$ 表示 $I$ 上的 $ n $ 阶连续可微函数之集按范数 $\|u\|_{C^n}=\max\{\|u\|_C,\|u'\|_C,\cdots,$$\|u^{(n)}\|_C\} $ 构成的 Banach 空间. $ C^+(I)=\{u\in C(I)\;|\,u(x)\ge0,\,x\in I\} $ 为 $ C(I) $ 中的非负函数锥.

设 $ \,h\in C(I) $. 考虑 BVP (1.2) 对应的线性四阶边值问题 (LBVP)

引理 2.1 对 $ \;\forall\;h\in C(I) $, LBVP (2.1) 有唯一解 $ \,u:=Sh\in C^4(I) $, 且解算子 $ S: C(I)\to C^2(I) $ 是线性全连续算子.

证 在 LBVP (2.1) 中, 令 $ v=-u'' $, 则其化为线性二阶边值问题

对$\forall\;h\in C(I) $, 易验证 LBVP (2.2) 有唯一解 $ v\in C^2(I) $, 可表示为

其中

是相应的 Green 函数. 因此, LBVP (2.1) 有唯一解 $ u\in C^4(I) $

由 (2.3) 式,

由 (2.5) 与 (2.6) 式易知, 解算子 $ \,S: C(I)\to C^2(I) $ 是线性全连续算子.

引理 2.2 设 $ \,h\in C^{+}(I) $, 则 LBVP (2.1) 的解 $ u=Sh $ 具有下列性质

(a) $ u(x)\geq (1-x)\|u\|_C,\;\; x\in I $; $ \|u\|_C\le \frac{\pi ^2}{4}\int_0^1 u(x)\cos\frac{\pi }{2}x\,{\rm d}x $;

(b) $ u''(x)\leq -(1-x)\|u''\|_C,\;\; x\in I $; $ \|u''\|_C\le\frac{\pi ^{4}}{16}\int_0^1u(x)\cos\frac{\pi }{2}x\,{\rm d}x $;

(c) $ \|u\|_{C^2}=\|u''\|_C $.

证 由 (2.4) 式易验证, LBVP (2.2) 的 Green 函数 $ \,G(x,\,y)\, $ 有下列性质

(1) $ G(x,\,y)>0 $, $ x,\,y\in(0,\,1) $;

(2) $ G(x,\,y)\le G(y,\,y) $, $ x,\,y\in I $;

(3) $ G(x,\,y)\ge G(x,\,x)G(y,\,y) $, $ x,\,y\in I $.

对 $ \;\forall\;h\in C^{+}(I) $, 由引理 2.1, LBVP (2.1) 的有唯一解 $ \,u=Sh\, $. 令 $ \,v=-u'' $, 则由 (2.3) 式及 $ \,G(x,\,y)\, $ 的非负性知, $ \,v\ge 0 $. 因此, $ \,u''\le 0 $. 对 $ \;\forall\;x\in I $, 由 (2.5) 式及 $ G(x,\,y) $ 的性质 (2), 有

因此,

由上式及 $ G(x,\,y) $ 的性质 (3), 有

上式两边同乘以 $ \,\cos\frac{\pi }{2}x $, 并在 $ \,I\, $ 上积分, 得

因此, (a) 成立.

由 $ v $ 的表示 (2.3) 式, 通过与上述 $ u $ 相同的论证, 可得

因此 $ v=-u'' $ 满足

即 (b) 成立.

对 $ \forall\;x\in I $, 按 LBVP (2.1) 的边界条件, 有

因此, 有

于是, $ \,\|u\|_{C^2}=\max\{\|u\|_C,\,\|u'\|_C,\,\|u''\|_C\}=\|u''\|_C $. 即 (c) 成立.

考虑 BVP (1.2). 在 $ \,C^2(I)\, $ 中定义闭凸锥 $ \,K $

由引理 2.2 的 (a) 与 (b) 知, $ \,S(C^+(I))\subset K $. 因此, 由引理 2.1, $ S: C^+(I)\to K $ 全连续. 设 $ \,f: I\times\mathbb{R}^+\times\mathbb{R}^-\to\mathbb{R}^+ $ 连续, 定义非线性映射 $ F: K\to C^+(I)$

按 $ \,f: I\times\mathbb{R}^+\times\mathbb{R}^-\to\mathbb{R}^+ $ 的连续性, $ F: K\rightarrow C^{+}(I) $ 连续. 按 $ \,S: C^{+}(I)\to K $ 的全连续性, 复合映射

为全连续锥映射. 按 $ \,S\, $ 与 $ \,K\, $ 的定义及引理 2.2,BVP(1.2) 的正解等价于 $ \,A\, $ 的非零不动点. 我们用锥上的不动点指数理论寻找 $ \,A\, $ 的非零不动点. 我们的论证需要文献 [20] 中的下面两个引理

引理 2.3 设 $ \,E\, $ 为 Banach 空间, $ K\subset E $ 为闭凸锥, $ \Omega\subset E $ 为有界开集, $ \mathbf{0}\in\Omega $, $ A: K\cap\overline{\Omega}\to K $ 为全连续映射.若对 $ \,\forall\;u\in K\cap\partial\Omega\, $ 及 $ \,0<\mu\le 1 $, 有 $ \mu\, Au\ne u $, 则不动点指数 $ i\,(A,\, K\cap\Omega,\, K)=1 $.

引理 2.4 设 $ \,E\, $ 为 Banach 空间, $ K\subset E $ 为闭凸锥, $ \Omega\subset E $ 为有界开集, $ A: K\cap\overline\Omega\to K $ 为全连续映射. 若存在 $ v_0\in K\setminus\{\mathbf{0}\} $ 使得对 $ \,\forall\;u\in K\cap\partial\Omega $ 及 $ \tau\ge 0 $, 有 $ u-Au\ne \tau\,v_0 $,则不动点指数 $ i\,(A,\, K\cap\Omega,\, K)=0 $.

定理 1.1 的证明 取 Banach 空间 $ E=C^{2}(I) $. 设 $ K\subset E $ 为 (2.7) 式定义的闭凸锥, $ \,A: K\rightarrow K $ 为(2.9) 定义的全连续算子,则方程 BVP(1.2) 的正解等价于 $ A $ 的非零不动点. 设 $ \,0<r<R<+\infty $, 在 $ E $ 中取球形区域

用锥上的不动点指数理论证明当 $ \,r\, $ 适当小, $ \,R\, $ 适当大时, $ \,A\, $ 在$ \,K\cap(\Omega_2\setminus\overline{\Omega}_1) $ 中有不动点.

取 $ \,r\in(0,\,\delta/\sqrt{2}) $, 其中 $ \delta $ 是条件 (F1) 中的常数. 下证 $ \,A\, $ 在 $ \,K\cap\partial\Omega_1 $ 上满足引理 2.3 的条件

反设 (3.2) 式不成立, 则存在 $ \,u_0\in K\cap\partial\Omega_1 $ 及 $ \,0<\mu_0\le 1 $, 使得 $ \,\mu_0Au_0=u_0 $. 按 $ \,A\, $ 的定义, $ u_0=\mu_0\,S(F(u_0))=S(\mu_0\,F(u_0)) $.按 $ \,S\, $ 的定义, $ u_0\, $ 为 $ \,h=\mu_0\,F(u_0)\in C^+(I)\, $ 对应的 LBVP (2.1) 的解, 因此 $ \,u_0\in C^4(I)\, $ 满足方程

因为 $ \,u_0\in K\cap\partial\Omega_1 $, 按 $ \,K\, $ 及 $ \,\Omega_1\, $ 的定义, 对 $ \;\forall\;x\in I $, 有

因此, 按条件 (F1), 有

方程 (3.3) 两边同乘以 $ \,\cos\frac{\pi }{2}x $, 然后在 $ \,I\, $ 上积分, 并应用不等式 (3.4) 及分部积分公式, 有

对上式左端应用分部积分公式, 得

因此有

按引理 2.2(a), 有: $ u_0(x)\ge (1-x)\|u_0\|_C>0 $, $ \,x\in I $. 因此, $ \int_0^1u_0(x)\,\cos\frac{\pi }{2}x\,{\rm d}x>0 $.故由 (3.5) 式得 $ \frac{16a_0}{\pi ^{4}}+\frac{4b_0}{\pi ^{2}}\ge 1 $, 这与 (F1) 的假设 $ \frac{16a_0}{\pi ^{4}}+\frac{4b_0}{\pi ^{2}}<1 $ 矛盾!因此, (3.2) 式成立, 即 $ \,A\, $ 在 $ \,K\cap\partial\Omega_1 $ 上满足引理 2.3 的条件. 由引理 2.3

取正常数 $ \,C_0=\max\{\;|f(x,\,u,\,v)-a_1u+b_1v|\;\;|\;\; x\in I,\; u\ge 0,\;\ v\le 0,\;|(u,\,v)|\leq H\,\}+1 $, 则由条件 (F2), 有

在 $ \,E\, $ 中取 $ \,v_0=\cos\frac{\pi }{2}x $. 易见 $ \,v_0\in K\setminus\{\mathbf{0}\} $. 因为 $ v_0^{(4)}=\frac{\pi ^4}{16}v_0 $, 由 $ \,S\, $ 的定义, $ v_0=S\big(\frac{\pi ^4}{16}v_0\big) $.取

则 $ R>r $. 下证 $ \,A\, $ 在 $ K\cap\partial\Omega_{2} $ 上对 $ v_0 $ 满足引理 2.4 的条件

反设 (3.9) 式不成立, 则存在 $ \,u_1\in K\cap\partial\Omega_2 $ 及 $ \,\tau_1\ge0 $, 使得 $ \,u_1-A\,u_1=\tau_1v_0 $. 因为

按 $ \,S\, $ 的定义, $ \,u_1 $ 是 $ h=F(u_1)+\frac{\tau_1\pi ^4}{16}v_0\in C^+(I)\, $ 对应的 LBVP (2.1) 的解. 因此, $ \,u_1\in C^4(I)\, $ 满足方程

上式两边同乘以 $ \,\cos\frac{\pi }{2}x $, 然后在 $ \,I\, $ 上积分, 并应用不等式 (3.7), 得

\begin{align*} \int_0^1u_1^{(4)}(x)\,\cos\frac{\pi }{2}x\,{\rm d}x &=\int_0^1\Big(f(x,\,u_1(x),\,u_1''(x))+\frac{\tau_1\pi ^4}{16}v_0(x)\Big)\,\cos\frac{\pi }{2}x\,{\rm d}x\\ &\ge\int_0^1 (a_1u_1(x)-b_1u_1''(x)-C_0)\,\cos\frac{\pi }{2}x\,{\rm d}x\\ &=\Big(a_1+\frac{\pi ^2b_1}{4}\Big)\int_0^1 u_1(x)\,\cos\frac{\pi }{2}x\,{\rm d}x-\frac{2C_0}{\pi }. \end{align*}

而上式左端

故由上述两式得,

因此, 由引理 2.2(c) 和 (b) 及 (3.8) 式, 有

这与因为 $ \,u_1\in \partial\Omega_2 $ 矛盾!因此, (3.9) 式成立, 即 $ A $ 在 $ K\cap\partial\Omega_{2} $ 上对 $ v_0 $ 满足引理 2.4 的条件. 按引理 2.4,

于是, 由 (3.8) 式、(3.12) 式及不动点指数的区域可加性, 有

故由不动点指数的可解性, $ \,A\, $ 在 $ \,K\cap(\Omega_2\setminus\overline{\Omega}_1) $ 中有一个不动点, 该不动点为 BVP (1.2) 的正解.

定理 1.2 的证明 类似于定理 2.1 的证明, 当 $ r $ 适当小时, 应用条件 (F3) 与引理 2.4, 可证得

当 $ R $ 适当大时, 应用条件 (F4) 与引理 2.3, 可证得

于是由 (3.14) 及 (3.15) 式, 有

故 $ \,A\, $ 在 $ \,K\cap(\Omega_2\setminus\overline{\Omega}_1)\, $ 中有不动点, 该不动点为方程 (1.2) 的正解.