数学物理学报, 2024, 44(6): 1433-1444

多项 Caputo 分数阶微分方程 Dirichlet 问题 Lyapunov 型不等式

张伟,*, 陈柯元, 毋祎, 倪晋波

安徽理工大学数学与大数据学院 安徽淮南 232001

Lyapunov-Type Inequalities for Dirichlet Problems of Multi-Term Caputo Fractional Differential Equations

Zhang Wei,*, Chen Keyuan, Wu Yi, Ni Jinbo

School of Mathematics and Big Data, Anhui University of Science and Technology, Anhui Huainan 232001

通讯作者: *张伟, E-mail: zhangwei_azyw@163.com

收稿日期: 2024-04-30   修回日期: 2024-08-19  

基金资助: 国家自然科学基金(11601007)
安徽省自然科学基金资助(2208085-QA05)
安徽理工大学大学生创新创业训练计划(202210361102)

Received: 2024-04-30   Revised: 2024-08-19  

Fund supported: NSFC(11601007)
Anhui Provincial Natural Science Foundation(2208085-QA05)
University Students' Innovation and Pioneering Training Plan Project of Anhui University of Science and Technology(202210361102)

摘要

该文探讨了一类含参数的多项分数阶微分方程在 Dirichlet 边值条件下的 Lyapunov 型不等式. 首先将分数阶微分方程边值问题等价转化为带 Green 函数的积分方程, 再证明出 Green 函数的相关性质, 最后结合先验估计方法得出相应的 Lyapunov 型不等式. 多项分数阶微分方程属于非局部方程类别, 其复杂性超越了单项分数阶微分方程. 研究多项分数阶微分方程边值问题的 Lyapunov 型不等式, 对定性分析多项分数阶非线性微分方程边值问题具有重要意义.

关键词： 多项分数阶微分方程; Dirichlet 问题; Green 函数; Lyapunov 型不等式

Abstract

This paper investigates the Lyapunov-type inequalities for a class of multi-term fractional differential equations with with a parameter, subject to Dirichlet boundary conditions. We first transform the fractional boundary value problem into an integral equation with Green's functions, then prove the relevant properties of the Green's functions, and finally obtain the corresponding Lyapunov-type inequalities using a priori estimation method. Multi-term fractional differential equations belong to the category of non-local equations, and their complexity exceeds that of single-term fractional differential equations. Studying the Lyapunov-type inequalities for multi-term fractional boundary value problems is of significant importance for the qualitative analysis of boundary value problems of multi-term fractional nonlinear differential equations.

Keywords： Multi-term fractional differential equation; Dirichlet problem; Green's function; Lyapunov-type inequality

PDF (542KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

张伟, 陈柯元, 毋祎, 倪晋波. 多项 Caputo 分数阶微分方程 Dirichlet 问题 Lyapunov 型不等式[J]. 数学物理学报, 2024, 44(6): 1433-1444

Zhang Wei, Chen Keyuan, Wu Yi, Ni Jinbo. Lyapunov-Type Inequalities for Dirichlet Problems of Multi-Term Caputo Fractional Differential Equations[J]. Acta Mathematica Scientia, 2024, 44(6): 1433-1444

1 引言

对于 Lyapunov 不等式的研究可追溯到 1892 年[1], Lyapunov 证明了如下结果

定理 1.1 设 $q(t) \in C([a,b],\mathbb{R})$. 如果 Hill 方程

$x''(t) + q(t)x(t) = 0,\quad t \in (a,b),$

在 Dirichlet 边值条件

$x(a) = x(b) = 0,$

下, 存在非平凡连续解, 那么 $q(t)$ 满足如下不等式

$\int_{a}^{b}|q(s)| \mathrm{d} s>\frac{4}{b-a}.$

不等式 (1.1) 被称为 Lyapunov 不等式. 该不等式及其推广结果已被广泛应用于各类数学问题, 如稳定性问题, 振荡理论和常微分方程的特征值问题[2,3]. 对于不等式 (1.1) 的推广形式, 包括高阶微分方程、$p$-Laplacian 微分方程、偏微分方程、差分方程、脉冲微分方程、时间尺度上的动态方程以及分数阶微分方程等各类方程的 Lyapunov 型不等式[4⇓⇓⇓⇓⇓⇓⇓-12]. 2013 年[11], Ferreira 率先将不等式 (1.1) 推广到分数阶微分方程边值问题情形, 基于 Riemann-Liouville 分数阶微积分框架下, 讨论了一类分数阶微分方程 Dirichlet 边值问题的 Lyapunov 型不等式, 得到了如下结果

定理 1.2 设 $q(t) \in C([a,b],\mathbb{R})$. 若分数阶微分方程边值问题

$\begin{align*} \textstyle\begin{cases} (D_{a + }^\alpha x)(t) + q(t)x(t) = 0,\quad t \in (a,b),\\ x(a) = x(b) = 0, \end{cases} \end{align*}$

有非平凡连续解, 其中 $D_{a + }^\alpha$ 是 $\alpha$ 阶 Riemann-Liouville 分数阶微分算子, $1 < \alpha \le 2$, 则 $q(t)$ 满足如下不等式

$\int_{a}^{b}|q(s)| \mathrm{d} s>\Gamma(\alpha)\left(\frac{4}{b-a}\right)^{\alpha-1}.$

2014 年[12], 基于 Caputo 分数阶微积分框架下, Ferreira 讨论了一类分数阶微分方程 Dirichlet 边值问题的 Lyapunov 型不等式, 得到了如下结果

定理 1.3 设 $q(t) \in C([a,b],\mathbb{R})$. 若分数阶微分方程边值问题

$\begin{align*} \textstyle\begin{cases} ({}^CD_{a + }^\alpha x)(t) + q(t)x(t) = 0,\quad t \in (a,b),\\ x(a) = x(b) = 0, \end{cases} \end{align*}$

有非平凡连续解, 其中 $1 < \alpha \le 2$, ${}^CD_{a + }^\alpha$ 是 $\alpha$ 阶 Caputo 分数阶微分算子, 则 $q(t)$ 满足如下不等式

$\int_{a}^{b}|q(s)| \mathrm{d} s>\frac{\alpha^{\alpha} \Gamma(\alpha)}{[(\alpha-1)(b-a)]^{\alpha-1}}.$

不等式 (1.2) 与 (1.3) 是对 (1.1) 式的推广, 当 $\alpha\rightarrow2$ 时, 可退化为 (1.1). 鉴于 Ferreira 的开创性工作, 对分数阶微分方程边值问题的 Lyapunov 型不等式的研究受到了学者们的广泛关注, 得到了一系列有趣的结果. 关于该主题最新的一些研究成果, 可参阅文献 [13⇓⇓⇓⇓⇓⇓⇓-21]. 例如, 2024 年[13], 基于 Katugampola 分数阶微积分框架下, Ƚupińska 研究了如下分数阶微分方程混合边值问题的 Lyapunov 型不等式

$\left\{\begin{array}{l} D_{a+}^{\alpha, \rho} u(t)+g(t) u(t)=0, \quad t \in(a, b), \quad 1＜\alpha \leq 2, \\ u(a)=u^{\prime}(b)=0, \end{array}\right.$

其中 $D_{a + }^{\alpha,\rho }$ 是 $\alpha$ 阶 Katugampola 分数阶微分算子. 作者得到如下结果

定理 1.4 设 $g(t) {\in} C([a,b],\mathbb{R})$. 若边值问题 (1.4) 存在非平凡连续解, 则有如下不等式成立

$\begin{align*} \int_a^b {{s^{\rho - 1}}} {({b^\rho } - {s^\rho })^{\alpha - 2}}|g(s)|{\rm d}s \ge \frac{{\Gamma (\alpha )}}{{{\rho ^{1 - \alpha }}({b^\rho } - {a^\rho })}}. \end{align*}$

注意到, $(D_{a + }^\alpha y)(t) + q(t)y(t) = 0$ 称为单项分数阶微分方程. 在某些情况中, 微分方程含有函数的多个导数. 这种含有多个导数的微分方程称为多项微分方程. 例如, Bagley-Torvik 方程

$m x^{\prime \prime}(t)+2 A \sqrt{\mu \rho}{ }^{C} D_{0+}^{3 / 2} x(t)+K x(t)=0$

是典型的多项微分方程. 方程 (1.5) 用来描述牛顿流体中刚性板的运动, 最早由文献 [22] 提出.

尽管许多学者已经研究了分数阶微分方程边值问题的 Lyapunov 型不等式, 但迄今为止对多项微分方程边值问题的 Lyapunov 型不等式研究结果还很少. 2021 年[19], Pourhadi 和 Mursaleen 讨论了带有 Caputo 分数阶微分算子的多项微分方程混合边值问题的 Lyapunov 型不等式, 即, 作者考虑了如下多项微分方程边值问题

$ \textstyle\begin{cases} {}^CD_{a + }^\alpha y(t) + p(t)y'(t) + q(t)y(t) = 0,\quad a < t < b,\\ y(a) = y'(a) = y(b) = 0, \end{cases} $

其中 ${}^CD_{a + }^\alpha$ 是 $\alpha$ 阶 Caputo 分数阶微分算子, $2 < \alpha \le3$. 作者得出了如下结果

定理 1.5 设 $p(t) \in {C^1}([a,b])$ 和 $q(t) \in C([a,b])$. 若边值问题 (1.6) 存在非平凡连续解, 则有如下不等式成立

(i) 当 $\alpha \le b-a+1$ 时, 有

$\int_a^b {(|p(s)| + |q(s)| + |p'(s)|){\rm d}s} \ge \frac{{\Gamma (\alpha ){{(b - a)}^{1 - \alpha }}}}{{\max \{ g(\alpha ),h(\alpha ),A(\alpha + 1)\} }};$

(ii) 当 $\alpha \ge b-a+1$ 时, 有

$\int_a^b {(|p(s)| + |q(s)| + |p'(s)|){\rm d}s} \ge \frac{{\Gamma (\alpha ){{(b - a)}^{2 - \alpha }}}}{{(\alpha - 1)\max \{ g(\alpha ),h(\alpha ),A(\alpha + 1)\} }},$

其中

$\begin{align*} &g(\alpha)=\frac{1}{4}{(4-\alpha)^2}, A(\alpha )=4{\alpha^{ - \alpha}}{(\alpha- 2)^{\alpha - 2}},\\ &h(\alpha) = {\bigg( {\frac{{\alpha - 2}}{2}} \bigg)^{\frac{{(\alpha - 2)(3-\alpha)}}{{4-\alpha }}}}-{\bigg( {\frac{{\alpha - 2}}{2}} \bigg)^{\frac{{2 - {{(\alpha - 2)}^2}}}{{4 - \alpha}}}}. \end{align*}$

基于以上文献的启发, 本文研究如下含参数的多项分数阶微分方程

$ \mu {}^CD_{a + }^\alpha u(t) + (1 - \mu ){}^CD_{a + }^\beta u(t) + q(t)u(t) = 0,\quad a < t < b, $

在 Dirichlet 边值条件

$ u(a) = u(b) = 0, $

下的 Lyapunov 型不等式, 其中 $0 < \beta < 1 < \alpha < 2$, ${}^CD_{a + }^\rho$ 是 $\rho = \alpha,\beta$ 阶 Caputo 分数阶微分算子, $q(t)$ 是实值连续函数, $\mu \in (0,1]$. 该文分别在 $\alpha - \beta \ge 1$ 和 $\alpha-\beta<1$ 两种情形下给出边值问题 (1.7)-(1.8) 的 Lyapunov 型不等式. 注意到, 方程 (1.7) 含有多个分数阶导数, 因此, 边值问题 (1.7)-(1.8) 比 (1.6) 式更具一般性; 其次, 当参数 $\mu \to 1$ 时, 边值问题 (1.7)-(1.8) 将退化为文献 [12] 讨论的问题.

论文内容安排如下: 在第 2 节中, 回顾了 Riemann-Liouville 分数阶积分、Caputo 分数阶微分定义以及相关基本性质. 在第 3 节中, 利用第 2 节的相关结论将边值问题 (1.7)-(1.8) 转化为带有 Green 函数的等价积分方程, 并给出 Green 函数的性质. 同时, 利用先验估计方法, 建立问题 (1.7)-(1.8) 的 Lyapunov 型不等式. 在第 4 节中, 举例验证所得结果的合理性. 最后, 在第 5 节中, 总结全文, 并为未来的工作指明了新的方向.

2 预备知识

本节主要回顾分数阶微积分定义及其相关性质.

定义 2.1[23] 令 $[a,b](-\infty < a < b < + \infty )$ 是实轴 $\mathbb{R}$ 上的有限区间, 则定义在 $[a,b]$ 上的可积实值函数 $x$ 的 $\alpha$$(\alpha > 0)$ 阶 Riemann-Liouville 分数阶积分 $I_{a + }^\alpha x(t)$ 定义为

$I_{a + }^\alpha x(t) = \frac{1}{{\Gamma (\alpha)}}\int_a^t {{{(t - s)}^{\alpha - 1}}x(s){\rm d}s},$

其中$\Gamma (\cdot)$ 是 Gamma 函数.

定义 2.2[23] 令 $[a,b]( - \infty < a < b < + \infty )$ 是实轴 $\mathbb{R}$ 上的有限区间, 则函数 $x \in A{C^n}$$([a,b],\mathbb{R})$ 的 $\alpha (\alpha > 0)$ 阶 Caputo 分数阶导数${}^CD_{a + }^\alpha x(t)$ 定义为

$\begin{align*} {}^CD_{a + }^\alpha x(t) &= (I_{a + }^{n - \alpha }{D^n}x)(t)\\ &= \frac{1}{{\Gamma (n - \alpha )}}\int_a^t {{{(t - s)}^{n - \alpha - 1}}{x^{(n)}}(s){\rm d}s}, \end{align*}$

其中

$n = [\alpha ] + 1, D = {\rm d}/{\rm d}t,$
$ A{C^n}[a,b] = \left\{ {x:[a,b] \to \mathbb{R}|{D^{n - 1}}x(t) \in AC[a,b]} \right\},$

$AC[a,b]$ 表示 $[a,b]$ 上绝对连续函数全体.

引理 2.1[23] 令 $\alpha > 0$. 假设 $x \in A{C^n}[a,b],$ 则

$\begin{align*} & I_{a + }^\alpha {}^CD_{a + }^\alpha x(t)\\ &= x(t) + {c_0} + {c_1}(t - a) + {c_2}{(t - a)^2} + \cdots + {c_{n - 1}}{(t - a)^{n - 1}}, \end{align*}$

其中 $n = [\alpha ] + 1,\; {c_i} = - \displaystyle\frac{{{x^{(i)}}(a)}}{{i!}}\;(i = 0,1,2, \cdots,n - 1).$

引理 2.2 令 $\alpha > \beta > 0$. 假设 $x \in {L^\infty }(a,b),$ 则

$I_{a + }^\alpha I_{a + }^\beta x(t) = I_{a + }^{\alpha + \beta }x(t),{}^CD_{a + }^\alpha I_{a + }^\alpha x(t) = x(t).$

引理 2.3 令 $\alpha > 0,\; \lambda > - 1,\; t > 0,$ 则

$I_{a + }^\alpha {(t - a)^\lambda } = \frac{{\Gamma (\lambda + 1)}}{{\Gamma (\lambda + 1 + \alpha )}}{(t - a)^{\alpha + \lambda }},$
$ {}^CD_{0 + }^\alpha {(t - a)^\lambda } = \frac{{\Gamma (\lambda + 1)}}{{\Gamma (\lambda + 1 - \alpha )}}{(t - a)^{\lambda - \alpha }},$

特别地

${}^CD_{0 + }^\alpha {t^k} = 0,\;k{\rm{ = 0,1,2,}} \cdots,n - 1,$

其中 $n = [\alpha ] + 1.$

3 主要结果

3.1 问题 (1.7)-(1.8) 的 Green 函数及其性质

在这一节, 先证明一个辅助引理并结合第二节中的引理将边值问题 (1.7)-(1.8) 等价转化为带有 Green 函数的积分方程, 并给出 Green 函数相关性质.

引理 3.1 则有

$I_{a + }^\alpha {}^CD_{a + }^\beta x(t) = I_{a + }^{\alpha - \beta }x(t) - \frac{{x(a){{(t - a)}^{\alpha - \beta }}}}{{\Gamma (\alpha - \beta + 1)}}.$

证 事实上, 由定义 2.1, 引理 2.1, 2.2, 得到

$\begin{align*} I_{a + }^\alpha {}^CD_{a + }^\beta x(t) &= I_{a + }^{\alpha - \beta }I_{a + }^\beta {}^CD_{a + }^\beta x(t) = I_{a + }^{\alpha - \beta }(x(t) - x(a))\\ &= I_{a + }^{\alpha - \beta }x(t) - \frac{{x(a)}}{{\Gamma (\alpha - \beta )}}\int_a^t {{{(t - s)}^{\alpha - \beta - 1}}{\rm d}s}\\ &= I_{a + }^{\alpha - \beta }x(t) - \frac{{x(a){{(t - a)}^{\alpha - \beta }}}}{{\Gamma (\alpha - \beta + 1)}}. \end{align*}$

因此, 结论成立.

引理 3.2 对 $u \in C[a,b]$ 是边值问题 (1.7)-(1.8) 的解当且仅当 $u$ 满足如下积分方程

$\begin{align*} u(t) &= \frac{{1 - \mu }}{\mu }\frac{1}{{\Gamma (\alpha - \beta )}}\int_a^b {{G_1}(t,s)u(s){\rm d}s}\\ & + \frac{1}{\mu }\frac{1}{{\Gamma (\alpha )}}\int_a^b {{G_2}(t,s)q(s)u(s){\rm d}s}, \end{align*}$

其中

$\begin{align*} &{G_1}(t,s) = \textstyle\begin{cases} \displaystyle\frac{{t - a}}{{b - a}}{(b - s)^{\alpha - \beta - 1}} - {(t - s)^{\alpha - \beta - 1}},\quad a \le s \le t \le b,\\[3mm] \displaystyle\frac{{t - a}}{{b - a}}{(b - s)^{\alpha - \beta - 1}}, \qquad\qquad\qquad\quad \, a \le t \le s \le b, \end{cases}\\ &{G_2}(t,s) =\textstyle\begin{cases} \displaystyle\frac{{t - a}}{{b - a}}{(b - s)^{\alpha - 1}} - {(t - s)^{\alpha - 1}},\quad\qquad\ a \le s \le t \le b,\\[3mm] \displaystyle\frac{{t - a}}{{b - a}}{(b - s)^{\alpha - 1}}, \quad\qquad\qquad\qquad\qquad a \le t \le s \le b. \end{cases} \end{align*}$

证 利用算子 $I_{a + }^\alpha$ 作用到方程 (1.7) 的两端, 并结合引理 2.1, 3.1 以及边值条件 $u(a) {=} 0$, 可得

$\mu [u(t) - u'(a)(t - a)] + (1 - \mu )I_{a + }^{\alpha - \beta }u(t) + I_{a + }^\alpha q(t)u(t) = 0,$

即

$ u(t) = u'(a)(t - a) - \frac{{1 - \mu }}{\mu }I_{a + }^{\alpha - \beta }u(t) - \frac{1}{\mu }I_{a + }^\alpha q(t)u(t). $

考虑到边值条件 $u(b) {=} 0$, 则有

$u(b) = u'(a)(b - a) - \frac{{1 - \mu }}{\mu }I_{a + }^{\alpha - \beta }u(t){{\rm{|}}_{t = b}} - \frac{1}{\mu }I_{a + }^\alpha q(t)u(t){{\rm{|}}_{t = b}} = 0,$

即

$ u'(a) = \frac{1}{{b - a}}\left[ {\frac{{1 - \mu }}{\mu }I_{a + }^{\alpha - \beta }u(t){{\rm{|}}_{t = b}} + \frac{1}{\mu }I_{a + }^\alpha q(t)u(t){{\rm{|}}_{t = b}}} \right]. $

将 (3.2) 式代入到 (3.1) 式, 得到

$\begin{aligned} u(t)= & \frac{t-a}{b-a}\left[\left.\frac{1-\mu}{\mu} I_{a+}^{\alpha-\beta} u(t)\right|_{t=b}+\left.\frac{1}{\mu} I_{a+}^{\alpha} q(t) u(t)\right|_{t=b}\right] \\ & -\frac{1-\mu}{\mu} I_{a+}^{\alpha-\beta} u(t)-\frac{1}{\mu} I_{a+}^{\alpha} q(t) u(t) \\ = & \frac{1-\mu}{\mu}\left[\left.\frac{t-a}{b-a} I_{a+}^{\alpha-\beta} u(t)\right|_{t=b}-I_{a+}^{\alpha-\beta} u(t)\right] \\ & +\frac{1}{\mu}\left[\left.\frac{t-a}{b-a} I_{a+}^{\alpha} q(t) u(t)\right|_{t=b}-I_{a+}^{\alpha} q(t) u(t)\right] \\ = & \frac{1-\mu}{\mu}\left[\frac{t-a}{b-a} \frac{1}{\Gamma(\alpha-\beta)} \int_{a}^{b}(b-s)^{\alpha-\beta-1} u(s) \mathrm{d} s\right. \\ & \left.-\frac{1}{\Gamma(\alpha-\beta)} \int_{a}^{t}(t-s)^{\alpha-\beta-1} u(s) \mathrm{d} s\right] \\ & +\frac{1}{\mu}\left[\frac{t-a}{b-a} \frac{1}{\Gamma(\alpha)} \int_{a}^{b}(b-s)^{\alpha-1} q(s) u(s) \mathrm{d} s\right. \\ & \left.-\frac{1}{\Gamma(\alpha)} \int_{a}^{t}(t-s)^{\alpha-1} q(s) u(s) \mathrm{d} s\right] \\ = & \frac{1-\mu}{\mu} \frac{1}{\Gamma(\alpha-\beta)} \int_{a}^{b} G_{1}(t, s) u(s) \mathrm{d} s \\ & +\frac{1}{\mu} \frac{1}{\Gamma(\alpha)} \int_{a}^{b} G_{2}(t, s) q(s) u(s) \mathrm{d} s. \end{aligned} $

反之, 利用引理 2.2, 2.3, 易验证 (3.3) 式满足方程 (1.7) 和边值条件 (1.8). 故, 引理 3.2 证毕.

下面介绍引理 3.2 中积分核函数相关性质.

引理 3.3 定义 ${G_\gamma}(t,s)$ 如下

$\begin{align*} {G_\gamma }(t,s) = \textstyle\begin{cases} \displaystyle\frac{{t - a}}{{b - a}}{(b - s)^{\gamma - 1}} - {(t - s)^{\gamma - 1}},\quad a \le s \le t \le b,\\[3mm] \displaystyle\frac{{t - a}}{{b - a}}{(b - s)^{\gamma - 1}}, \qquad\qquad\qquad\ \ a \le t \le s \le b, \end{cases} \end{align*}$

则有(i) 当 $\gamma > 1$ 时

$|G(t,s)| \le \frac{{{{(\gamma - 1)}^{\gamma - 1}}}}{{{\gamma ^\gamma }}}{(b - a)^{\gamma - 1}} = {M_\gamma },\quad(t,s) \in [a,b] \times [a,b],$

当且仅当 $t = s = \frac{{b + (\gamma - 1)a}}{\gamma }$ 时等号成立.

(ii) 当 $0 < \gamma < 1$ 时

$\int_a^b {|{G_\gamma}(t,s)|{\rm d}s}=k(t),$

其中

$k(t) = \frac{1}{\gamma }\frac{{t - a}}{{b - a}}[2{(b - t)^\gamma } - {(b - a)^\gamma }] + \frac{1}{\gamma }{(t - a)^\gamma },\quad t \in [a,b].$

证 (i) 的证明参见文献 [引理 2]. 接下来, 我们证明引理 3.3(ii) 成立. 事实上, 由 $0<\gamma$$<1$, 当 $a\leq s\leq t\leq b$ 时, 有

$\begin{align*} \frac{{t - a}}{{b - a}}{(b - s)^{\gamma - 1}} - {(t - s)^{\gamma - 1}} = {(t - s)^{\gamma - 1}}\bigg[ {\frac{{t - a}}{{b - a}}{{\bigg( {\frac{{t - s}}{{b - s}}} \bigg)}^{1 - \gamma }} - 1} \bigg] \le 0.\end{align*}$

从而

$\begin{align*} & \int_a^b {\left| {{G_\gamma }(t,s)} \right|{\rm d}s}\\ &= \int_a^t {\bigg[{{(t - s)}^{\gamma - 1}} - \frac{{t - a}}{{b - a}}{{(b - s)}^{\gamma - 1}}\bigg]{\rm d}s + } \int_t^b {\frac{{t - a}}{{b - a}}{{(b - s)}^{\gamma - 1}}{\rm d}s}\\ &= - \frac{1}{\gamma }{(t - s)^{\gamma}}\Big|_a^t + \frac{1}{\gamma }\frac{{t - a}}{{b - a}}{(b - s)^\gamma }\Big|_a^t - \frac{1}{\gamma }\frac{{t - a}}{{b - a}}{(b - s)^\gamma }\Big|_t^b\\ &= \frac{1}{\gamma }{(t - a)^{\gamma}} + \frac{1}{\gamma }\frac{{t - a}}{{b - a}}{(b - t)^\gamma } - \frac{1}{\gamma }\frac{{t - a}}{{b - a}}{(b - a)^\gamma } + \frac{1}{\gamma }\frac{{t - a}}{{b - a}}{(b - t)^\gamma }\\ &= \frac{1}{\gamma }\frac{{t - a}}{{b - a}}[2{(b - t)^\gamma } - {(b - a)^\gamma }] + \frac{1}{\gamma }{(t - a)^\gamma}\\ &= k(t). \end{align*}$

综上, 引理 3.3 证毕.

3.2 问题 (1.7)-(1.8) 的 Lyapunov 型不等式

本节给出边值问题 (1.7)-(1.8) 的 Lyapunov 型不等式, 为此我们定义 Banach 空间 $C[a,b]$, 并赋予范数

$||x|{|_\infty } = \mathop {\max }\limits_{t \in [a,b]} |x(t)|,\;x(t) \in C[a,b].$

定理 3.1 设 $0 < \beta < 1 < \alpha < 2, \; \alpha - \beta > 1,\; q(t) \in C([a,b],\mathbb{R}).$ 若边值问题 (1.7)-(1.8) 存在非平凡连续解, 则

$ \int_a^b {|q(s)} |{\rm d}s \ge \frac{{\mu \Gamma (\alpha )}}{{{M_\alpha }}}\bigg[ {1 - \frac{{1 - \mu }}{\mu }\frac{{{M_{\alpha - \beta }}}}{{\Gamma (\alpha - \beta )}}(b - a)} \bigg]. $

证 事实上, 由引理 3.2 知边值问题 (1.7)-(1.8) 的解 $u$ 满足积分方程

$\begin{align*} u(t) &= \frac{{1 - \mu }}{\mu }\frac{1}{{\Gamma (\alpha - \beta )}}\int_a^b {{G_1}(t,s)u(s){\rm d}s}\\ & + \frac{1}{\mu }\frac{1}{{\Gamma (\alpha )}}\int_a^b {{G_2}(t,s)q(s)u(s){\rm d}s},\quad t \in [a,b]. \end{align*}$

则有

$\begin{align*} |u(t)| &\le \frac{{1 - \mu }}{\mu }\frac{1}{{\Gamma (\alpha - \beta )}}\int_a^b {|{G_1}(t,s)|{\rm{|}}u(s){\rm{|}}{\rm d}s}\\ & + \frac{1}{\mu }\frac{1}{{\Gamma (\alpha )}}\int_a^b {{\rm{|}}{G_2}(t,s){\rm{||}}q(s){\rm{||}}u(s){\rm{|}}{\rm d}s}. \end{align*}$

利用引理 3.3(i), 得出

$\begin{align*} |u(t)| &\le \frac{{1 - \mu }}{\mu }\frac{1}{{\Gamma (\alpha - \beta )}}{M_{\alpha - \beta }}\int_a^b {|u(s){\rm{|}}{\rm d}s}\\ & + \frac{1}{\mu }\frac{1}{{\Gamma (\alpha )}}{M_\alpha }\int_a^b {|q(s)||u(s)|{\rm d}s} \\ &\le ||u|{|_\infty }\bigg[ {\frac{{1 - \mu }}{\mu }\frac{{{M_{\alpha - \beta }}}}{{\Gamma (\alpha - \beta )}}(b - a) + \frac{1}{\mu }\frac{{{M_\alpha }}}{{\Gamma (\alpha )}}\int_a^b {|q(s)|{\rm d}s} } \bigg]. \end{align*}$

从而

$ ||u|{|_\infty } \le ||u|{|_\infty }\bigg[ {\frac{{1 - \mu }}{\mu }\frac{{{M_{\alpha - \beta }}}}{{\Gamma (\alpha - \beta )}}(b - a) + \frac{1}{\mu }\frac{{{M_\alpha }}}{{\Gamma (\alpha )}}\int_a^b {|q(s)|{\rm d}s} } \bigg]. $

解不等式 (3.5), 得

$\begin{align*} \int_a^b {|q(s)} |{\rm d}s \ge \frac{{\mu \Gamma (\alpha )}}{{{M_\alpha }}}\bigg[ {1 - \frac{{1 - \mu }}{\mu }\frac{{{M_{\alpha - \beta }}}}{{\Gamma (\alpha - \beta )}}(b - a)} \bigg]. \end{align*}$

综上, 定理 3.1 证明完成.

定理 3.2 设 $0 < \beta < 1 < \alpha < 2$, $0 < \alpha - \beta < 1$, $q(t) \in C([a,b],\mathbb{R})$. 若边值问题 (1.7)-(1.8) 存在非平凡连续解, 则

$ \int_a^b {{\rm{|}}q(s){\rm{|}}{\rm d}s} \ge \frac{{\mu \Gamma (\alpha )}}{{{M_\alpha }}}\bigg[ {1 - \frac{{1 - \mu }}{\mu }\frac{1}{{\Gamma (\alpha - \beta )}}||k|{|_\infty }} \bigg], $

其中

$k(t) = \frac{1}{\gamma }\frac{{t - a}}{{b - a}}[2{(b - t)^\gamma } - {(b - a)^\gamma }] + \frac{1}{\gamma }{(t - a)^\gamma }, \gamma = \alpha - \beta, t \in [a,b].$

证 事实上, 由引理 3.2 知边值问题 (1.7)-(1.8) 的解 $u$ 满足积分方程

$\begin{align*} u(t) &= \frac{{1 - \mu }}{\mu }\frac{1}{{\Gamma (\alpha - \beta )}}\int_a^b {{G_1}(t,s)u(s){\rm d}s}\\ & + \frac{1}{\mu }\frac{1}{{\Gamma (\alpha )}}\int_a^b {{G_2}(t,s)q(s)u(s){\rm d}s},\quad t \in [a,b], \end{align*}$

则有

$\begin{align*} |u(t)| &\le \frac{{1 - \mu }}{\mu }\frac{1}{{\Gamma (\alpha - \beta )}}\int_a^b {|{G_1}(t,s)|{\rm{|}}u(s){\rm{|}}{\rm d}s}\\ & + \frac{1}{\mu }\frac{1}{{\Gamma (\alpha )}}\int_a^b {{\rm{|}}{G_2}(t,s){\rm{||}}q(s){\rm{||}}u(s){\rm{|}}{\rm d}s}, \end{align*}$

利用引理 3.3, 有

$\begin{align*} |u(t)| &\le \frac{{1 - \mu }}{\mu }\frac{1}{{\Gamma (\alpha - \beta )}}\int_a^b {|{G_1}(t,s)|{\rm{|}}u(s){\rm{|}}{\rm d}s}\\ &\quad{}+ \frac{1}{\mu }\frac{1}{{\Gamma (\alpha )}}\int_a^b {{\rm{|}}{G_2}(t,s){\rm{||}}q(s){\rm{||}}u(s){\rm{|}}{\rm d}s} \\ &\le \frac{{1 - \mu }}{\mu }\frac{1}{{\Gamma (\alpha - \beta )}}\int_a^b {|{G_1}(t,s)|{\rm{|}}u(s){\rm{|}}{\rm d}s}\\ &\quad{}+ \frac{1}{\mu }\frac{1}{{\Gamma (\alpha )}}{M_\alpha }\int_a^b {{\rm{|}}q(s){\rm{||}}u(s){\rm{|}}{\rm d}s} \\ &\le ||u{\rm{|}}{{\rm{|}}_\infty }\bigg[ {\frac{{1 - \mu }}{\mu }\frac{{k(t)}}{{\Gamma (\alpha - \beta )}} + \frac{{{M_\alpha }}}{{\mu \Gamma (\alpha )}}\int_a^b {{\rm{|}}q(s){\rm{|}}{\rm d}s} } \bigg]\\ &\le ||u{\rm{|}}{{\rm{|}}_\infty }\bigg[ {\frac{{1 - \mu }}{\mu }\frac{{||k|{|_\infty }}}{{\Gamma (\alpha - \beta )}} + \frac{{{M_\alpha }}}{{\mu \Gamma (\alpha )}}\int_a^b {{\rm{|}}q(s){\rm{|}}{\rm d}s} } \bigg]. \end{align*}$

从而有

$ ||u{\rm{|}}{{\rm{|}}_\infty } \le ||u{\rm{|}}{{\rm{|}}_\infty }\bigg[ {\frac{{1 - \mu }}{\mu }\frac{{||k|{|_\infty }}}{{\Gamma (\alpha - \beta )}} + \frac{{{M_\alpha }}}{{\mu \Gamma (\alpha )}}\int_a^b {{\rm{|}}q(s){\rm{|}}{\rm d}s} } \bigg]. $

解不等式 (3.7), 得

$\int_a^b {{\rm{|}}q(s){\rm{|}}{\rm d}s} \ge \frac{{\mu \Gamma (\alpha )}}{{{M_\alpha }}}\bigg[ {1 - \frac{{1 - \mu }}{\mu }\frac{1}{{\Gamma (\alpha - \beta )}}||k|{|_\infty }} \bigg].$

综上, 定理 3.2 证明完成.

推论 3.1 设 $1 < \alpha < 2$, $q(t) \in C([a,b],\mathbb{R})$. 若分数阶微分方程边值问题

$\begin{align*} \textstyle\begin{cases} {}^CD_{a+}^\alpha u(t) + q(t)u(t) = 0,\quad a < t < b,\\ u(a) = u(b) = 0, \end{cases} \end{align*}$

存在非平凡连续解, 则

$\int_{a}^{b}|q(s)| \mathrm{d} s \geq \frac{\Gamma(\alpha)}{M_{\alpha}}$

证 事实上，由

$\begin{aligned} & \lim _{\mu \rightarrow 1} \frac{\mu \Gamma(\alpha)}{M_{\alpha}}\left[1-\frac{1-\mu}{\mu} \frac{M_{\alpha-\beta}}{\Gamma(\alpha-\beta)}(b-a)\right] \\ = & \frac{\Gamma(\alpha)}{M_{\alpha}}=\lim _{\mu \rightarrow 1} \frac{\mu \Gamma(\alpha)}{M_{\alpha}}\left[1-\frac{1-\mu}{\mu} \frac{\|k\|_{\infty}}{\Gamma(\alpha-\beta)}\right]. \end{aligned}$

利用定理 3.1 或 3.2 知, (3.8) 式成立. 显然, 这与文献 [12] 所得结果重合.

4 例子

例 4.1 考虑如下分数阶微分方程边值问题

$\left\{\begin{array}{l} \frac{2}{3} C D_{a+}^{3 / 2} u(t)+\frac{1}{3} C D_{a+}^{1 / 4} u(t)+t u(t)=0, \quad 1＜t＜2, \\ u(1)=u(2)=0 \end{array}\right.$

对应边值问题 (1.7)-(1.8), 这里 $\mu=\frac{2}{3},\;\alpha = \frac{3}{2},\;\beta = \frac{1}{4},\;q(t)=t,\;a = 1,\;b = 2$. 通过计算得到

$\alpha - \beta = \frac{5}{4} > 1,$
$ \Gamma(3 / 2)=\frac{\sqrt{\pi}}{2} \approx 0.8862, \quad \Gamma(5 / 4) \approx 0.9064,$
$M_{5 / 4}=\frac{(1 / 4)^{1 / 4}}{(5 / 4)^{5 / 4}}=\frac{4}{5^{5 / 4}} \approx 0.5350$
$M_{3 / 2}=\frac{(1 / 2)^{1 / 2}}{(3 / 2)^{3 / 2}}=\frac{2}{3^{3 / 2}} \approx 0.3849$
$\begin{aligned} 1.5 & =\int_{1}^{2}|t| \mathrm{d} t \\ & \geq \frac{\mu \Gamma(\alpha)}{M_{\alpha}}\left[1-\frac{1-\mu}{\mu} \frac{M_{\alpha-\beta}}{\Gamma(\alpha-\beta)}(b-a)\right] \\ & \approx \frac{0.6666 \times 0.8862}{0.3849}\left(1-\frac{0.535}{2 \times 0.9064}\right) \\ & \approx 1.0818. \end{aligned}$

故, 定理 3.1 中的条件成立.

例 4.2 考虑如下分数阶微分方程边值问题

$\left\{\begin{array}{l} \frac{3}{4} C D_{a+}^{3 / 2} u(t)+\frac{1}{4} C D_{a+}^{3 / 4} u(t)+t^{3 / 2} u(t)=0, \quad 1＜t＜2, \\ u(1)=u(2)=0, \end{array}\right.$

对应边值问题 (1.7)-(1.8), 这里 $\mu=\frac{3}{4}, \alpha=\frac{3}{2}, \beta=\frac{3}{4}, q(t)=t^{3 / 2}, a=1, b=2.$. 通过计算可得

$0 < \gamma = \alpha - \beta = \frac{3}{4} < 1.$

此外,

$k(t) = \frac{4}{3}(t - 1)[2{(2 - t)^{3/4}} - 1] + \frac{4}{3}{(t - 1)^{3/4}},\quad t \in [1,2].$
$\begin{aligned} 1.8627 & \approx \int_{1}^{2}\left|t^{3 / 2}\right| \mathrm{d} t \\ & \geq \frac{\mu \Gamma(\alpha)}{M_{\alpha}}\left[1-\frac{1-\mu}{\mu} \cdot \frac{\|k\|_{\infty}}{\Gamma(\alpha-\beta)}\right] \\ & \approx \frac{3}{4} \cdot \frac{0.8862}{0.3849}\left(1-\frac{1}{3} \cdot \frac{0.9242}{1.2254}\right) \\ & \approx 1.2927. \end{aligned}$

故, 定理 3.2 中的条件成立.

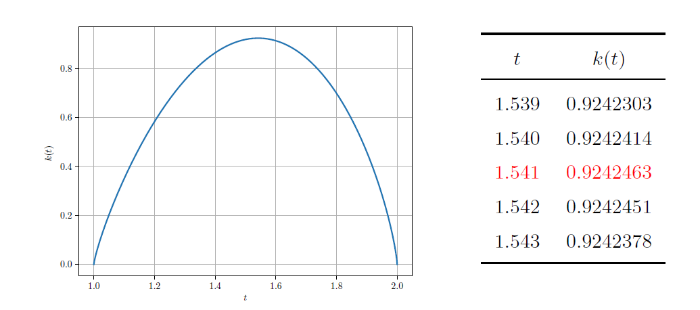
图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   图表分别表示函数 $k(t)$ 在区间 $[1,2]$ 上的函数图像以及 $k(t)$ 在区间 $[1,2]$ 上取最大值为 $||k|{|_\infty } \approx 0.9242$


5 总结

本文对多项 Caputo 分数阶微分方程 Dirichlet 问题的 Lyapunov 型不等式进行了深入探讨. 通过将边值问题转化为带有 Green 函数的积分方程, 并结合先验估计方法, 有效地建立了相应的 Lyapunov 型不等式. 本文的结果不仅为研究分数阶微分方程边值问题的 Lyapunov 型不等式提供了新的理论视角, 而且丰富了现有文献的工作, 对定性分析多项分数阶微分方程边值问题的研究具有重要的理论意义. 我们期待未来的研究能够在此基础上进一步探索, 特别地, 我们将讨论多项分数阶微分方程非局部边值问题的 Lyapunov 型不等式及其推广与应用.

参考文献

Liapounoff A.

Problème général de la stabilité du mouvement

Ann Fac Sci Toulouse Sci Math Sci Phys, 1907, 9(2): 203-474

[本文引用: 1]

De Nápoli P L, Pinasco J P.

Lyapunov-type inequalities for partial differential equations

J Funct Anal, 2016, 270(6): 1995-2018

[本文引用: 1]

Agarwal R P, Bohner M, Özbekler A. Lyapunov Inequalities and Applications. Cham: Springer, 2021

[本文引用: 1]

Aktaş M F, Erçikti B B.

On Lyapunov-type inequalities for five different types of higher order boundary value problems

Turkish J Math, 2024, 48(1): 90-105

[本文引用: 1]

Aktaş M F.

On Lyapunov-type inequalities for ($n+1$)st order nonlinear differential equations with the antiperiodic boundary conditions

Turkish J Math, 2021, 45(6): 2614-2622

[本文引用: 1]

Takeuchi S, Watanabe K.

Lyapunov-type inequalities for a Sturm-Liouville problem of the one-dimensional $p$-Laplacian

Differential Integral Equations, 2021, 34(7/8): 383-399

[本文引用: 1]

Kassymov A, Kirane M, Torebek B T.

Lyapunov,Hartman-Wintner and de La Vallée Poussin-type inequalities for fractional elliptic boundary value problems

Complex Var Elliptic Equ, 2022, 67(1): 246-258

[本文引用: 1]

Stegliński R.

Sharp Lyapunov-type inequalities for second-order half-linear difference equations with different kinds of boundary conditions

Rev R Acad Cienc Exactas Fís Nat Ser A Mat RACSAM, 2021, 115(3): Article 140

[本文引用: 1]

Kayar Z, Zafer A.

Lyapunov-type inequalities for nonlinear impulsive systems with applications

Electron J Qual Theory Differ Equ, 2016, 2016: Article 27

[本文引用: 1]

Agarwal R P, Denk Oğuz A, Özbekler A.

Lyapunov-type inequalities for Lidstone boundary value problems on time scales

Rev R Acad Cienc Exactas Fís Nat Ser A Mat RACSAM, 2020, 114(2): Article 98

[本文引用: 1]

Ferreira R A C.

A Lyapunov-type inequality for a fractional boundary value problem

Fract Calc Appl Anal, 2013, 16(4): 978-984

[本文引用: 2]

Ferreira R A C.

On a Lyapunov-type inequality and the zeros of a certain Mittag-Leffler function

J Math Anal Appl, 2014, 412(2): 1058-1063

[本文引用: 4]

Ƚupińska B.

Existence and nonexistence results for fractional mixed boundary value problems via a Lyapunov-type inequality

Period Math Hungar, 2024, 88(1): 118-126

[本文引用: 2]

Ntouyas S K, Ahmad B.

Lyapunov-type inequalities for fractional differential equations: a survey

Surv Math Appl, 2021, 16: 43-93

[本文引用: 1]

Zohra B F, Benaouda H, Mokhtar K.

Lyapunov- and Hartman-Wintner-type inequalities for a nonlinear fractional BVP with generalized $\Psi$-Hilfer derivative

Math Methods Appl Sci, 2021, 44(3): 2637-2649

[本文引用: 1]

Ntouyas S K, Ahmad B, Tariboon J.

A Survey on recent results on Lyapunov-type inequalities for fractional differential equations

Fractal Fract, 2022, 6(5): 273

[本文引用: 1]

Zhang W, Zhang J, Ni J.

Lyapunov-type inequalities for fractional Langevin-type equations involving Caputo-Hadamard fractional derivative

J Inequal Appl, 2022, 2022: Article 48

[本文引用: 1]

Laadjal Z, Ma Q.

Lyapunov-type inequalities for fractional Langevin differential equations

J Math Inequal, 2023, 17(1): 67-82

[本文引用: 1]

Pourhadi E, Mursaleen M.

A new fractional boundary value problem and Lyapunov-type inequality

J Math Inequal, 2021, 15(1): 81-93

DOI:10.7153/jmi-2021-15-08      [本文引用: 2]

Throughout this paper, we study a new modified version of fractional boundary value problem (BVP) of the form

Wang Y, Wang Q.

Lyapunov-type inequalities for nonlinear fractional differential equation with Hilfer fractional derivative under multi-point boundary conditions

Fract Calc Appl Anal, 2018, 21(3): 833-843

[本文引用: 1]

马德香, Özbekler A.

一类带强迫项的高阶半线性分数阶微分方程的广义 Lyapunov 不等式

数学物理学报, 2020, 40A(6): 1537-1551

[本文引用: 1]

Ma D X, Özbekler A.

Generalized Lyapunov inequalities for a higher-order sequential fractional differential equation with half-linear terms

Acta Math Sci, 2020, 40A(6): 1537-1551

[本文引用: 1]

Torvik P J, Bagley R L.

On the appearance of the fractional derivative in the behavior of real materials

J Appl Mech, 1984, 51(2): 294-298

[本文引用: 1]

Kilbas A A, Srivastava H M, Trujillo J J. Theory and Applications of Fractional Differential Equations. Amsterdam: Elsevier, 2006

[本文引用: 3]

/

〈 〉

版权所有 © 《数学物理学报》杂志社
地址： 武汉市71010号信箱(430071)　电话: 027-87199206(中文版)　027-87199087(英文版)
E-mail: actams@apm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发