数学物理学报, 2024, 44(5): 1334-1350

不等式的推广以及在加性时变时滞系统中的应用

樊天娇,, 冯立超,*, 杨艳梅,

华北理工大学理学院 河北唐山 063210

Generalization of Inequality and Its Application in Additive Time-Varying Delay Systems

Fan Tianjiao,, Feng Lichao,*, Yang Yanmei,

College of Sciences, North China University of Science and Technology, Hebei Tangshan 063210

通讯作者: *冯立超, E-mail: fenglichao19820520@163.com

收稿日期: 2023-07-11   修回日期: 2023-11-28  

基金资助: 教育部人文社会科学研究规划基金(23YJAZH031)
河北省自然科学基金(A2023209002)
河北省自然科学基金(A2019209005)
唐山市科学技术研究与发展计划项目(19130222g)

Received: 2023-07-11   Revised: 2023-11-28  

Fund supported: Humanities and Social Science Fund of Ministry of Education(23YJAZH031)
Natural Science Foundation of Hebei Province(A2023209002)
Natural Science Foundation of Hebei Province(A2019209005)
Tangshan Science and Technology Bureau Program of Hebei Province(19130222g)

作者简介 About authors

樊天娇,E-mail:Fantianjiao@stu.ncst.edu.cn;

杨艳梅,E-mail:yanmyang@163.com

摘要

该文主要研究积分不等式的改进问题, 并将其应用于加性时变时滞系统的稳定性研究: 首先, 采用含参函数构造方法, 从单调性和增加正项两个角度, 对现有的 Wirtinger 不等式进行了证明; 其次, 提出了扩展不等式, 其中包括扩展 Wirtinger 不等式和基于三阶矩阵的扩展互凸不等式; 再次, 分别利用这两个扩展不等式, 以线性矩阵不等式的形式给出了加性时变时滞系统渐近稳定的判定准则; 最后, 通过数值算例说明所提方法的优越性.

关键词： 加性时变时滞系统; Wirtinger 不等式; 稳定性分析

Abstract

This article mainly studies the improvement problem of integral inequality and applies it to the stability study of additive time-varying delay systems: Firstly, the existing Wirtinger inequality is proven from the perspectives of monotonicity and adding positive terms using the method of constructing parameter functions. Secondly, we propose extended inequalities, including the extended Wirtinger inequality and the extended cross-convex inequality which is based on third-order matrices. Thirdly, utilizing these two extended inequalities, we provide criteria for determining the asymptotic stability of additive time-varying delay systems in the form of Linear Matrix Inequalities (LMIs). Finally, numerical examples are presented to demonstrate the effectiveness and superiority of the proposed method.

Keywords： Additive time-varying delay system; Wirtinger inequality; Stability analysis

PDF (810KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

樊天娇, 冯立超, 杨艳梅. 不等式的推广以及在加性时变时滞系统中的应用[J]. 数学物理学报, 2024, 44(5): 1334-1350

Fan Tianjiao, Feng Lichao, Yang Yanmei. Generalization of Inequality and Its Application in Additive Time-Varying Delay Systems[J]. Acta Mathematica Scientia, 2024, 44(5): 1334-1350

1 引言

近年来, 各种时变时滞系统的稳定性分析引起了许多研究人员的广泛关注, 并取得了许多研究成果[1,3⇓⇓-6,8,12,14,21,27]. 在时变时滞系统稳定性分析中, 主流方法是 Lyapunov-Krasovskii 泛函 (LKF) 方法. 在使用 LKF 方法导出保守性较低的稳定性准则中, 主要从以下两个方面考虑: (1) 构造合适的 LKF; (2) 精确地估计 LKF 的时间导数. 因此, 对于 LKF 时间导数的精确估计是十分必要的. 本文的研究动机在于获得 LKF 时间导数的精确估计, 并利用此估计推导出保守性较低的稳定性准则.

LKF 时间导数中积分项的存在使得获取 LKF 时间导数的准确上界很难. 近些年来, 学者们提出了多种方法和技术估计LKF 的导数, 如广义模型变换[3], 自由加权矩阵[20], 积分不等式方法[2,4,10,13,17⇓-19,22,24,25], 其中积分不等式方法是重要的方法之一. 文献 [17] 基于 Jensen 不等式提出了 Wirtinger 不等式, 用于获得时滞系统的稳定性; 文献 [13] 提出了贝塞尔-勒让德不等式, 研究了时变时滞系统的时滞相关稳定性. 然而, 一般情况下, 各种方法都很难做到 '估计精度' 与 '运算简便性' 同时兼顾. 例如, 利用自由矩阵可减少估计的保守性, 但自由矩阵的出现使得在后续计算中比较麻烦; Wirtinger 不等式较 Jensen 不等式虽提高了估计精度, 却增加了运算量. 这为处理 LKF 时间导数中积分项的估计方法的改进留下了很大的空间. 在这一思想的启发下, 本文将提出一个基于含参函数构造方法的扩展 Wirtinger 不等式, 其在不增加计算负担的情况下, 能够获得 LKF 时间导数的精确估计.

积分不等式用于估计积分项虽有效但也会出现新问题, 即估计得到的项具有非凸性. 为了应对这个问题, 学者们提出了诸多互凸方法[16]. 例如, Park 等人提出了逆凸引理[16]; Zhang 等人提出了参数相关的互凸矩阵不等式[26,28]; Zeng 等人提出了互凸二次矩阵不等式[23]. 然而, 在研究具有加性时变时滞系统的稳定性时, 通常需要将时滞区间划分为多个子区间, 现有的互凸矩阵不等式不能直接应用. 因此, 本文将提出一个基于三阶矩阵的扩展互凸不等式, 并应用于加性时变时滞系统的稳定性推导中, 获得保守性较低的稳定性准则.

符号: 在本文中, $\mathbb{R}^{n}$ 表示 $n$ 维列向量, $\mathbb{R}^{m \times n}$ 表示 $m$ 行和 $n$ 列的所有实矩阵的集合, 上标 $T$ 和 $-1$ 分别表示矩阵的转置和逆, $P>0(P<0)$ 表示 $P$ 是实对称正定(负定)矩阵,$\mathbb{R}$ 表示实数集, $I_{n}$ 是 $n$ 维单位矩阵, $\ast$ 表示对称矩阵中的对称项, $Sym\{X\}=X+X^{T}$.

2 问题表述

考虑以下具有加性时变时滞的连续系统

$\begin{equation}\label{eq:a1} \left\{ \begin{array}{*{35}{l}} \dot{x}(t)=Ax(t)+Bx(t-{{d}_{1}}(t)-{{d}_{2}}(t)),\begin{matrix} {} & t\ge 0 \\ \end{matrix} \\ x(t)=\phi (t),\begin{matrix} {} & t\in \left[ -({{{\bar{d}}}_{1}}+{{{\bar{d}}}_{2}}),0 \right], \\ \end{matrix} \\ \end{array} \right. \end{equation}$

其中, $x(t) \in {\mathbb{R}^n}$ 是状态向量, $\phi (t) \in {\mathbb{R}^n}$ 是初始值, $A,B \in {\mathbb{R}^{n \times n}}$ 是常数矩阵, 时变可微函数 ${d_1}(t)$ 和 ${d_2}(t)$ 满足以下条件

$\begin{equation} 0\le {{d}_{j}}(t)\le {{\bar{d}}_{j}},{{\dot{d}}_{j}}(t)\le {{\mu }_{j}}\begin{matrix} {} & (j=1,2) \\ \end{matrix}, \end{equation}$

其中, ${\bar d_j}$ 和 ${\mu _j}(j = 1,2)$ 是已知的正常数.

利用以下引理来发展时变时滞系统的稳定性准则.

引理 2.1[17] (Jensen 不等式) 给定 $\forall W\in {\mathbb{R}^{n \times n}}$且$W > 0$, 对于任一可微向量函数 $x:[a,b] \to {\mathbb{R}^n}$, 有

$\begin{equation} \int_{a}^{b}{{{{\dot{x}}}^{T}}(u)W\dot{x}(u){\rm d}u\ge \frac{1}{b-a}}\int_{a}^{b}{{{{\dot{x}}}^{T}}(u){\rm d}u}W\int_{a}^{b}{\dot{x}(u){\rm d}u}. \end{equation}$

引理 2.2[17] (Wirtinger 不等式) 给定 $\forall W\in {\mathbb{R}^{n \times n}}$且$W > 0$, 对于任一可微向量函数 $x:[a,b] \to {\mathbb{R}^n}$, 有

$\begin{align*} \int_{a}^{b}{{{{\dot{x}}}^{T}}(u)}W\dot{x}(u){\rm d}u\ge\ & \frac{1}{b-a}\int_{a}^{b}{{{{\dot{x}}}^{T}}(u)}{\rm d}uW\int_{a}^{b}{\dot{x}(u)}{\rm d}u+\frac{3}{b-a}{{x}^{T}}(a)Wx(a) \nonumber\\ &+\frac{6}{b-a}{{x}^{T}}(a)Wx(b)+\frac{3}{b-a}{{x}^{T}}(b)Wx(b)\nonumber\\ &-\frac{12}{{{(b-a)}^{2}}}{{x}^{T}}(a)W\int_{a}^{b}{x(u){\rm d}u} -\frac{12}{{{(b-a)}^{2}}}{{x}^{T}}(b)W\int_{a}^{b}{x(u){\rm d}u} \\ &+\frac{12}{{{(b-a)}^{3}}}\int_{a}^{b}{x{}^{T}(u){\rm d}u}W\int_{a}^{b}{x(u){\rm d}u}. \end{align*}$

引理 2.3[17] 给定 $\forall W\in {\mathbb{R}^{n \times n}}$且$W>0$, 对于任一满足 $Z(a) = Z(b) = 0$ 的可微函数 $Z$, 有

$\begin{equation} \int_a^b {{{\dot Z}^T}(u)} W\dot Z(u){\rm d}u \ge \frac{{{\pi ^2}}}{{{{(b - a)}^2}}}\int_a^b {{Z^T}(u)WZ(u){\rm d}u}. \end{equation}$

引理 2.4[11] (扩展互凸矩阵不等式) 对于标量 ${\alpha _j} > 0,(j = 1,2, \cdots m)$, 对称正定矩阵 ${W_j} \in {\mathbb{R}^{n \times n}},(j = 1,2, \cdots m)$ 以及矩阵 $M \in {\mathbb{R}^{mn \times mn}}$, 有

$\begin{equation} \left[ \begin{matrix} \begin{matrix} \frac{1}{{{\alpha }_{1}}}{{W}_{1}} \\ 0 \\ \vdots \\ 0 \\ \end{matrix} & \begin{matrix} 0 \\ \frac{1}{{{\alpha }_{2}}}{{W}_{2}} \\ \vdots \\ 0 \\ \end{matrix} & \begin{matrix} \cdots \\ \cdots \\ \ddots \\ \cdots \\ \end{matrix} & \begin{matrix} 0 \\ 0 \\ \vdots \\ \frac{1}{{{\alpha }_{m}}}{{W}_{m}} \\ \end{matrix} \\ \end{matrix} \right]\ge -M-{{M}^{T}}-{{M}^{T}}\left[ \begin{matrix} \begin{matrix} {{\alpha }_{1}}W_{1}^{-1} \\ 0 \\ \vdots \\ 0 \\ \end{matrix} & \begin{matrix} 0 \\ {{\alpha }_{2}}W_{2}^{-1} \\ \vdots \\ 0 \\ \end{matrix} & \begin{matrix} \cdots \\ \cdots \\ \ddots \\ \cdots \\ \end{matrix} & \begin{matrix} 0 \\ 0 \\ \vdots \\ {{\alpha }_{m}}W_{m}^{-1} \\ \end{matrix} \\ \end{matrix} \right]M. \end{equation}$

引理 2.5(三阶矩阵负定等价条件) 对给定的矩阵 $S=\left[ \begin{matrix} {{s}_{11}} & {{s}_{12}} & {{s}_{13}} \\ * & {{s}_{22}} & 0 \\ * & * & {{s}_{33}} \\ \end{matrix} \right]$, 其中 ${s_{11}},{s_{22}},{s_{33}} \in {\mathbb{R}^{n \times n}}$, $S < 0$ 的充分必要条件 ${{s}_{22}}<0,\begin{matrix} {} & {{s}_{33}} \\ \end{matrix}<0,\begin{matrix} {} & {{s}_{11}} \\ \end{matrix}-{{s}_{12}}s_{22}^{-1}s_{12}^{T}-{{s}_{13}}s_{33}^{-1}s_{13}^{T}<0$.

证 矩阵 $S$ 作如下初等变换

$\begin{align*} & \left[ \begin{matrix} I & -{{s}_{12}}s_{22}^{-1} & -{{s}_{13}}s_{33}^{-1} \\ 0 & I & 0 \\ 0 & 0 & I \\ \end{matrix} \right]\left[ \begin{matrix} {{s}_{11}} & {{s}_{12}} & {{s}_{13}} \\ * & {{s}_{22}} & 0 \\ * & * & {{s}_{33}} \\ \end{matrix} \right]{{\left[ \begin{matrix} I & -{{s}_{12}}s_{22}^{-1} & -{{s}_{13}}s_{33}^{-1} \\ 0 & I & 0 \\ 0 & 0 & I \\ \end{matrix} \right]}^{T}} \\ = & \left[ \begin{matrix} {{s}_{11}}-{{s}_{12}}s_{22}^{-1}s_{12}^{T}-{{s}_{13}}s_{33}^{-1}s_{13}^{T} & 0 & 0 \\ * & {{s}_{22}} & 0 \\ * & * & {{s}_{33}} \\ \end{matrix} \right]. \end{align*}$

证毕.

引理 2.6 (基于三阶矩阵的扩展互凸不等式) 对于标量 ${\alpha _j} > 0,(j = 1,2, \cdots m)$, 对称正定矩阵 ${W_j} \in {\mathbb{R}^{n \times n}},(j = 1,2, \cdots m)$ 以及矩阵 $M,N \in {\mathbb{R}^{mn \times mn}}$, 有

$\begin{align*} & \left[ \begin{matrix} \begin{matrix} \frac{1}{{{\alpha }_{1}}}{{W}_{1}} \\ 0 \\ \vdots \\ 0 \\ \end{matrix} & \begin{matrix} 0 \\ \frac{1}{{{\alpha }_{2}}}{{W}_{2}} \\ \vdots \\ 0 \\ \end{matrix} & \begin{matrix} \cdots \\ \cdots \\ \ddots \\ \cdots \\ \end{matrix} & \begin{matrix} 0 \\ 0 \\ \vdots \\ \frac{1}{{{\alpha }_{m}}}{{W}_{m}} \\ \end{matrix} \\ \end{matrix} \right]\\ \ge& -\frac{(M+N+{{M}^{T}}+{{N}^{T}})}{2}-\frac{1}{2}{{M}^{T}}\left[ \begin{matrix} \begin{matrix} {{\alpha }_{1}}W_{1}^{-1} \\ 0 \\ \vdots \\ 0 \\ \end{matrix} & \begin{matrix} 0 \\ {{\alpha }_{2}}W_{2}^{-1} \\ \vdots \\ 0 \\ \end{matrix} & \begin{matrix} \cdots \\ \cdots \\ \ddots \\ \cdots \\ \end{matrix} & \begin{matrix} 0 \\ 0 \\ \vdots \\ {{\alpha }_{m}}W_{m}^{-1} \\ \end{matrix} \\ \end{matrix} \right]M \\ & -\frac{1}{2}{{N}^{T}}\left[ \begin{matrix} \begin{matrix} {{\alpha }_{1}}W_{1}^{-1} \\ 0 \\ \vdots \\ 0 \\ \end{matrix} & \begin{matrix} 0 \\ {{\alpha }_{2}}W_{2}^{-1} \\ \vdots \\ 0 \\ \end{matrix} & \begin{matrix} \cdots \\ \cdots \\ \ddots \\ \cdots \\ \end{matrix} & \begin{matrix} 0 \\ 0 \\ \vdots \\ {{\alpha }_{m}}W_{m}^{-1} \\ \end{matrix} \\ \end{matrix} \right]N. \end{align*}$

证 定义

$W:=\left[ \begin{matrix} \begin{matrix} \frac{1}{{{\alpha }_{1}}}{{W}_{1}} \\[3mm] 0 \\ \vdots \\ 0 \\ \end{matrix} & \begin{matrix} 0 \\[3mm] \frac{1}{{{\alpha }_{2}}}{{W}_{2}} \\ \vdots \\ 0 \\ \end{matrix} & \begin{matrix} \cdots \\[3mm] \cdots \\ \ddots \\ \cdots \\ \end{matrix} & \begin{matrix} 0 \\[3mm] 0 \\ \vdots \\ \frac{1}{{{\alpha }_{m}}}{{W}_{m}} \\ \end{matrix} \\ \end{matrix} \right],$

依据引理 2.5, 有

$ \left[ \begin{matrix} M{{W}^{-1}}{{M}^{T}}+N{{W}^{-1}}{{N}^{T}} & M & N \\ {{M}^{T}} & W & 0 \\ {{N}^{T}} & 0 & W \\ \end{matrix} \right]\ge 0,$

在上式的基础上, 左乘 $\left[ {{I_{mn}},{I_{mn}},{I_{mn}}} \right]$, 右乘其转置可得

$W+\frac{1}{2}({{M}^{T}}+{{N}^{T}}+M+N)+\frac{1}{2}({{M}^{T}}{{W}^{-1}}M+{{N}^{T}}{{W}^{-1}}N)\ge 0,$

移项, 代入 $W$ 知引理 2.6 成立.

3 不同角度论证 Wirtinger 不等式

1) 单调性角度

证 对于有连续导数的函数 $x$, 变量 ${t_1}({t_1} \ne 0)$, 构造定义在 $[a,b] \times \mathbb{R}$ 上的函数${Z_1}$,

$\begin{equation} {Z_1}(u;{t_1}) = \frac{{(u - a)(b - u)}}{{{{(b - a)}^2}}}\int_a^b {(u - \frac{{a + b}}{2})} \dot x(u){\rm d}u + \frac{{b - a}}{{{t_1}}}\int_a^u {\dot x(u){\rm d}u - \frac{{u - a}}{{{t_1}}}\int_a^b {\dot x(u){\rm d}u} }, \end{equation}$

容易验证函数 ${Z_1}$ 满足 ${Z_1}(a) = {Z_1}(b) = 0$. 给定任意一个对称正定矩阵 $W \in {\mathbb{R}^{n \times n}}$, 可得

$\begin{align*} &\int_{a}^{b}{{{{\dot{Z}}}_{1}}^{T}(u)}W{{{\dot{Z}}}_{1}}(u){\rm d}u\\ =\ & \frac{{{(b-a)}^{2}}}{t_{1}^{2}}\int_{a}^{b}{{{{\dot{x}}}^{T}}(u)W\dot{x}(u){\rm d}u}-\frac{b-a}{t_{1}^{2}}\int_{a}^{b}{{{{\dot{x}}}^{T}}(u){\rm d}uW\int_{a}^{b}{\dot{x}(u){\rm d}u}} \nonumber \\ & +\frac{(b-a)({{t}_{1}}-12)}{12{{t}_{1}}}{{x}^{T}}(a)Wx(a)+\frac{(b-a)({{t}_{1}}-12)}{6{{t}_{1}}}{{x}^{T}}(a)Wx(b) \nonumber \\ & +\frac{(b-a)({{t}_{1}}-12)}{12{{t}_{1}}}{{x}^{T}}(b)Wx(b)-\frac{{{t}_{1}}-12}{3{{t}_{1}}}{{x}^{T}}(a)W\int_{a}^{b}{x(u){\rm d}u} \nonumber \\ & -\frac{{{t}_{1}}-12}{3{{t}_{1}}}{{x}^{T}}(b)W\int_{a}^{b}{x(u){\rm d}u}+\frac{{{t}_{1}}-12}{3{{t}_{1}}(b-a)}\int_{a}^{b}{{{x}^{T}}(u){\rm d}u}W\int_{a}^{b}{x(u){\rm d}u}, \end{align*}$

由引理 2.3 并结合引理 2.1, 有

$\begin{align*} &~~~\int_{a}^{b}{{{{\dot{Z}}}_{1}}^{T}(u)}W{{{\dot{Z}}}_{1}}(u){\rm d}u \\ &\ge \frac{{{\pi }^{2}}}{{{(b-a)}^{2}}}\int_{a}^{b}{{{Z}_{1}}^{T}(u)}W{{Z}_{1}}(u){\rm d}u \\ & \ge \frac{{{\pi }^{2}}}{{{(b-a)}^{3}}}\int_{a}^{b}{{{Z}_{1}}^{T}(u)}{\rm d}uW\int_{a}^{b}{{{Z}_{1}}(u)}{\rm d}u \nonumber\\ & =\frac{{{\pi }^{2}}(b-a){{({{t}_{1}}-6)}^{2}}}{144t_{1}^{2}}{{x}^{T}}(a)Wx(a)+\frac{{{\pi }^{2}}(b-a){{({{t}_{1}}-6)}^{2}}}{72t_{1}^{2}}{{x}^{T}}(a)Wx(b) \nonumber \\ &~~~ +\frac{{{\pi }^{2}}(b-a){{({{t}_{1}}-6)}^{2}}}{144t_{1}^{2}}{{x}^{T}}(b)Wx(b)-\frac{{{\pi }^{2}}{{({{t}_{1}}-6)}^{2}}}{36t_{1}^{2}}{{x}^{T}}(a)W\int_{a}^{b}{x(u){\rm d}u} \nonumber \\ &~~~ -\frac{{{\pi }^{2}}{{({{t}_{1}}-6)}^{2}}}{36t_{1}^{2}}{{x}^{T}}(b)W\int_{a}^{b}{x(u){\rm d}u}+\frac{{{\pi }^{2}}{{({{t}_{1}}-6)}^{2}}}{36t_{1}^{2}(b-a)}\int_{a}^{b}{{{x}^{T}}(u){\rm d}u}W\int_{a}^{b}{x(u){\rm d}u}, \end{align*}$

进一步将上述式 (3.2) 和式 (3.3) 结合, 下式成立

$\begin{equation} \int_a^b {{{\dot x}^T}(u)W\dot x(u){\rm d}u} \ge \frac{1}{{b - a}}\int_a^b {{{\dot x}^T}(u){\rm d}uW\int_a^b {\dot x(u){\rm d}u} } + {F_1}({t_1})Y, \end{equation}$

其中, ${F_1}({t_1}) = \frac{{{\pi ^2}{{({t_1} - 6)}^2} - 12{t_1}({t_1} - 12)}}{{144}}$,

$\begin{aligned} Y= & \frac{1}{b-a} x^{T}(a) W x(a)+\frac{2}{b-a} x^{T}(a) W x(b)+\frac{1}{b-a} x^{T}(b) W x(b) \\ & -\frac{4}{(b-a)^{2}} x^{T}(a) W \int_{a}^{b} x(u) \mathrm{d} u-\frac{4}{(b-a)^{2}} x^{T}(b) W \int_{a}^{b} x(u) \mathrm{d} u \\ & +\frac{4}{(b-a)^{3}} \int_{a}^{b} x^{T}(u) \mathrm{d} u W \int_{a}^{b} x(u) \mathrm{d} u \end{aligned}$

由于 Wirtinger 不等式是 Jensen 不等式的改进, 得 $Y > 0$. 欲得到 Wirtinger 不等式的精确估计, 只需研究${F_1}({t_1})$ 的取值. 经分析, ${F_1}({t_1})$ 在 ${t_1} = 6$ 取得最大值且与引理 2.2 一致, 结论得证.

2) 增加正项角度

证 给定任意一个对称正定矩阵 $W \in {\mathbb{R}^{n \times n}}$, 从添加正项 ${x^T}(\frac{{a + b}}{2})Wx(\frac{{a + b}}{2})$ 的角度来证明 Wirtinger 不等式, 对于有连续导数的函数 $x$, 变量 ${t_2}$, 构造定义在 $[a,b] \times \mathbb{R}$ 上的函数 ${Z_2}$,

$\begin{align*} {{Z}_{2}}(u;{{t}_{2}})=&-(u-a)\int_{a}^{b}{(u-\frac{a+b}{2})}\dot{x}(u){\rm d}u+\frac{{{(b-a)}^{2}}}{2}\int_{a}^{u}{\dot{x}(u){\rm d}u-(u-a)\int_{a}^{b}{x(u){\rm d}}}u \nonumber \\ & +(b-a)(u-a)x(a)+(u-a)(b-u)x(\frac{a+b}{2})+\frac{3}{2}(u-a)(b-u)x(a)\nonumber \\ & +\frac{3}{2}(u-a)(b-u)x(b)-\frac{{{t}_{2}}(b-a)}{2}(u-a)x(\frac{a+b}{2})\nonumber \\ & -\frac{3}{b-a}(u-a)(b-u)\int_{a}^{b}{x(u){\rm d}u}+{{t}_{2}}(u-a)(u-\frac{a+b}{2})x(\frac{a+b}{2}), \end{align*}$

显然, 上述构造满足 ${Z_2}(a) = {Z_2}(b) = 0$, 且

$\begin{equation} \int_a^b {{Z_2}(u)} {\rm d}u = (\frac{{{{(b - a)}^3}}}{6} + \frac{{{t_2}{{(b - a)}^3}}}{{12}} - \frac{{{t_2}{{(b - a)}^3}}}{4})x(\frac{{a + b}}{2}) = \frac{{{{(b - a)}^3}(1 - {t_2})}}{6}x(\frac{{a + b}}{2}), \end{equation}$

对 $\int_{a}^{b}{{{{\dot{Z}}}_{2}}^{T}(u)W{{{\dot{Z}}}_{2}}}(u){\rm d}u$ 进行求解, 可得

$\begin{align*} \int_{a}^{b}{{{{\dot{Z}}}_{2}}^{T}(u)W}{{{\dot{Z}}}_{2}}(u){\rm d}u=\ &\frac{{{(b-a)}^{4}}}{4}\int_{a}^{b}{{{{\dot{x}}}^{T}}}(u)W\dot{x}(u){\rm d}u-\frac{{{(b-a)}^{3}}}{4}\int_{a}^{b}{{{{\dot{x}}}^{T}}}(u){\rm d}uW\int_{a}^{b}{\dot{x}(u){\rm d}u} \nonumber\\ & -\frac{3{{(b-a)}^{3}}}{4}{{x}^{T}}(a)Wx(a)-\frac{3{{(b-a)}^{3}}}{2}{{x}^{T}}(a)Wx(b) \nonumber\\ & -\frac{3{{(b-a)}^{3}}}{4}{{x}^{T}}(b)Wx(b)+3{{(b-a)}^{2}}{{x}^{T}}(a)W\int_{a}^{b}{x(u){\rm d}u}\nonumber \\ & +3{{(b-a)}^{2}}{{x}^{T}}(b)W\int_{a}^{b}{x(u){\rm d}u}-3(b-a)\int_{a}^{b}{{{x}^{T}}(u){\rm d}u}W\int_{a}^{b}{x(u){\rm d}u}\nonumber \\ & +\frac{{{(b-a)}^{3}}{{({{t}_{2}}-1)}^{2}}}{3}{{x}^{T}}(\frac{a+b}{2})Wx(\frac{a+b}{2}), \end{align*}$

应用引理 2.1 以及引理 2.3 估计 $\int_a^b {\dot Z_2^T(u)W{{\dot Z}_2}(u)} {\rm d}u$, 然后移项有下述不等式成立

$\begin{align*} \int_{a}^{b}{{{{\dot{x}}}^{T}}}(u)W\dot{x}(u){\rm d}u\ge\ & \frac{1}{b-a}\int_{a}^{b}{{{{\dot{x}}}^{T}}}(u){\rm d}uW\int_{a}^{b}{\dot{x}(u){\rm d}u}+\frac{3}{b-a}{{x}^{T}}(a)Wx(a) \nonumber\\ & +\frac{6}{b-a}{{x}^{T}}(a)Wx(b)\!+\!\frac{3}{b-a}{{x}^{T}}(b)Wx(b)\!-\!\frac{12}{{{(b-a)}^{2}}}{{x}^{T}}(a)W\int_{a}^{b}{x(u){\rm d}u} \nonumber \\ & -\frac{12}{{{(b-a)}^{2}}}{{x}^{T}}(b)W\int_{a}^{b}{x(u){\rm d}u}+\frac{12}{{{(b-a)}^{3}}}\int_{a}^{b}{{{x}^{T}}(u){\rm d}u}W\int_{a}^{b}{x(u){\rm d}u} \nonumber\\ & +\frac{({{\pi }^{2}}-12){{({{t}_{2}}-1)}^{2}}}{9(b-a)}{{x}^{T}}(\frac{a+b}{2})Wx(\frac{a+b}{2}). \end{align*}$

式 (3.9) 与引理 2.2 中不等式的唯一区别在于不等式 (3.9) 中含有项 ${x^T}(\frac{{a + b}}{2})Wx(\frac{{a + b}}{2})$. 设 ${F_2}({t_2}) = ({\pi ^2} - 12){({t_2} - 1)^2}$, 对 ${x^T}(\frac{{a + b}}{2})Wx(\frac{{a + b}}{2})$ 项的系数取值进行分析. 经过分析, 当在实数域上时, ${F_2}({t_2})$ 为开口向下的抛物线, 当 ${t_2} = 1$ 时取得最大值, 即 ${F_2}({t_2}) = 0$, 说明正项未被引入, 此时 Wirtinger 不等式为局部最优; 而在复数域上, 当 ${t_2}$ 的取值使 ${F_2}({t_2})$ 为正值时, 说明正项可以被引入, 从而不等式 (3.9) 优于现有的 Wirtinger 不等式. 结论得证.

注 3.1 综合考虑 '估计精度' 以及 '运算简便性' 两因素, Wirtinger 不等式作为应用较为广泛的积分不等式之一需要被深入理解. 本文选择从单调性和增加正项两个角度出发进行了论证. 选择这两个角度的原因如下

1) 单调性角度: 借鉴文献 [18] 中 Wirtinger 不等式的构造函数方法, 我们选择采用含参构造方法, 从单调性角度进行论证; 采用单调性角度, 能够更为直观地衡量积分不等式的估计精度是否得到提升, 并且更容易进行推广.

2) 增加正项角度: 鉴于增加正项能提升积分不等式估计精度的直观观念以及时滞分解 LKF 的广泛应用, 我们选择增加正项 ${x^T}(\frac{{a + b}}{2})Wx(\frac{{a + b}}{2})$ 来论证 Wirtinger 不等式; 采用增加正项角度, 为理解 Wirtinger 不等式提供了一个新的视角.

4 扩展 Wirtinger 不等式

引理 4.1 给定任意一个对称正定矩阵 $W \in {\mathbb{R}^{n \times n}}$, 满足条件 $k_{1}^{2}\le 36$ 的常复数 ${k_1}$, 对于所有连续向量函数 $x:[a,b] \to {\mathbb{R}^n}$, 有

$\begin{equation} \int_{a}^{b}{{{{\dot{x}}}^{T}}(u)}W\dot{x}(u){\rm d}u\ge \frac{1}{b-a}\int_{a}^{b}{{{{\dot{x}}}^{T}}(u)}{\rm d}uW\int_{a}^{b}{\dot{x}(u)}{\rm d}u+{{G}_{1}}({{k}_{1}})Y, \end{equation}$

其中, ${{G}_{1}}({{k}_{1}})=\frac{432+k_{1}^{2}({{\pi }^{2}}-12)}{144}$, $Y$ 如 (3.5) 式所示.

证 对于有连续导数的函数 $x$, 定义在 $[a,b]$ 上的函数 ${Z_3}$,

$\begin{align*} {{Z}_{3}}(u;{{k}_{1}})=&-{{(u-a)}^{2}}\int_{a}^{b}{\dot{x}(u){\rm d}u+}{{(u-a)}^{2}}x(b)-(u-a)(b-a)x(a)+(u-a)(b-u)x(a) \nonumber\\ & -\frac{{{k}_{1}}{{(b-a)}^{2}}}{6}\int_{a}^{u}{\dot{x}(u){\rm d}u+}\frac{{{k}_{1}}(b-a)(u-a)}{6}x(b)-\frac{{{k}_{1}}(b-a)(u-a)}{6}x(a), \end{align*}$

依据式 (4.2) 进行简单的运算, 有

$\begin{array}{l} Z_{3}(a)=0, \\ Z_{3}(b)=-(b-a)^{2} \int_{a}^{b} \dot{x}(u) \mathrm{d} u+(b-a)^{2}(x(b)-x(a))-\frac{k_{1}(b-a)^{2}}{6} \int_{a}^{b} \dot{x}(u) \mathrm{d} u \\ +\frac{k_{1}(b-a)^{2}}{6}(x(b)-x(a))=0 \\ \int_{a}^{b} Z_{3}(u) \mathrm{d} u=\frac{k_{1}(b-a)^{3}}{12} x(a)+\frac{k_{1}(b-a)^{3}}{12} x(b)-\frac{k_{1}(b-a)^{2}}{6} \int_{a}^{b} x(u) \mathrm{d} u, \\ \int_{a}^{b} Z_{3}^{T}(u) \mathrm{d} u W \int_{a}^{b} Z_{3}(u) \mathrm{d} u=\frac{k_{1}^{2}(b-a)^{6}}{144} x^{T}(a) W x(a)+\frac{k_{1}^{2}(b-a)^{6}}{72} x^{T}(a) W x(b) \\ +\frac{k_{1}^{2}(b-a)^{6}}{144} x^{T}(b) W x(b)-\frac{k_{1}^{2}(b-a)^{5}}{36} x^{T}(a) W \int_{a}^{b} x(u) \mathrm{d} u \\ -\frac{k_{1}^{2}(b-a)^{5}}{36} x^{T}(b) W \int_{a}^{b} x(u) \mathrm{d} u \\ +\frac{k_{1}^{2}(b-a)^{4}}{36} \int_{a}^{b} x^{T}(u) \mathrm{d} u W \int_{a}^{b} x(u) \mathrm{d} u \\ \int_{a}^{b} \dot{Z}_{3}^{T}(u) W \dot{Z}_{3}(u) \mathrm{d} u=\frac{k_{1}^{2}(b-a)^{4}}{36} \int_{a}^{b} \dot{x}^{T}(u) W \dot{x}(u) \mathrm{d} u-\frac{k_{1}^{2}(b-a)^{3}}{36} x^{T}(a) W x(a) \\ +\frac{k_{1}^{2}(b-a)^{3}}{18} x^{T}(a) W x(b)-\frac{k_{1}^{2}(b-a)^{3}}{36} x^{T}(b) W x(b), \end{array}$

在 (4.3) 等式两边同时增加项 ${(b - a)^4}\int_a^b {{{\dot x}^T}(u)W\dot x(u){\rm d}u} $, 移项通分有

$\begin{align*} \int_{a}^{b}{{{{\dot{x}}}^{T}}(u)W\dot{x}(u){\rm d}u}=\ &\frac{36-k_{1}^{2}}{36}\int_{a}^{b}{{{{\dot{x}}}^{T}}(u)W\dot{x}(u){\rm d}u}+\frac{k_{1}^{2}}{36(b-a)}{{x}^{T}}(a)Wx(a) \nonumber\\ & -\frac{k_{1}^{2}}{18(b-a)}{{x}^{T}}(a)Wx(b) +\frac{k_{1}^{2}}{36(b-a)}{{x}^{T}}(b)Wx(b) \nonumber\\ & +\frac{1}{{{(b-a)}^{4}}}\int_{a}^{b}{\dot{Z}_{3}^{T}(u)W{{{\dot{Z}}}_{3}}(u){\rm d}u}, \end{align*}$

限定常复数 $k_{1}^{2}\le 36$, 对 (4.4) 式中的项 $\frac{{36 - k_1^2}}{{36}}\int_a^b {{{\dot x}^T}(u)W\dot x(u){\rm d}u} $ 使用引理 2.2 进行定界, 则有如下不等式成立

$\begin{aligned} & \frac{\left(36-k_{1}^{2}\right)}{36} \int_{a}^{b} \dot{x}^{T}(u) W \dot{x}(u) \mathrm{d} u \\ \geq & \frac{\left(36-k_{1}^{2}\right)}{36(b-a)} \int_{a}^{b} \dot{x}^{T}(u) \mathrm{d} u W \int_{a}^{b} \dot{x}(u) \mathrm{d} u+\frac{\left(36-k_{1}^{2}\right)}{12(b-a)} x^{T}(a) W x(a) \\ & +\frac{\left(36-k_{1}^{2}\right)}{6(b-a)} x^{T}(a) W x(b)+\frac{\left(36-k_{1}^{2}\right)}{12(b-a)} x^{T}(b) W x(b) \\ & -\frac{\left(36-k_{1}^{2}\right)}{3(b-a)^{2}} x^{T}(a) W \int_{a}^{b} x(u) \mathrm{d} u-\frac{\left(36-k_{1}^{2}\right)}{3(b-a)^{2}} x^{T}(b) W \int_{a}^{b} x(u) \mathrm{d} u \\ & +\frac{\left(36-k_{1}^{2}\right)}{3(b-a)^{3}} \int_{a}^{b} x^{T}(u) \mathrm{d} u W \int_{a}^{b} x(u) \mathrm{d} u, \end{aligned}$

运用引理 2.1, 引理 2.3 对式 (4.4) 中的项 $\frac{1}{{{{(b - a)}^4}}}\int_a^b {\dot Z_3^T(u)W{{\dot Z}_3}(u){\rm d}u} $ 进行定界, 则有如下不等式成立

$\begin{align*} &\frac{1}{{{(b-a)}^{4}}}\int_{a}^{b}{\dot{Z}_{3}^{T}(u)W{{{\dot{Z}}}_{3}}(u){\rm d}u}\\ \ge\ &\frac{{{\pi }^{2}}}{{{(b-a)}^{7}}}\int_{a}^{b}{Z_{3}^{T}(u)}{\rm d}uW\int_{a}^{b}{{{Z}_{3}}(u){\rm d}u} \nonumber\\ =\ &\frac{k_{1}^{2}{{\pi }^{2}}}{144(b-a)}{{x}^{T}}(a)Wx(a)+\frac{k_{1}^{2}{{\pi }^{2}}}{72(b-a)}{{x}^{T}}(a)Wx(b)\nonumber \\ & +\frac{k_{1}^{2}{{\pi }^{2}}}{144(b-a)}{{x}^{T}}(b)Wx(b)-\frac{k_{1}^{2}{{\pi }^{2}}}{36{{(b-a)}^{2}}}{{x}^{T}}(a)W\int_{a}^{b}{x(u){\rm d}u} \nonumber\\ & -\frac{k_{1}^{2}{{\pi }^{2}}}{36{{(b-a)}^{2}}}{{x}^{T}}(b)W\int_{a}^{b}{x(u){\rm d}u} +\frac{k_{1}^{2}{{\pi }^{2}}}{36{{(b-a)}^{3}}}\int_{a}^{b}{{{x}^{T}}(u){\rm d}uW\int_{a}^{b}{x(u){\rm d}u}}, \end{align*}$

将定界的式 (4.5) 以及式 (4.6) 代入式 (4.4) 中, 结论得证.

注 4.1 本文所提出的扩展 Wirtinger 不等式相较于现有的多种方法更具通用性. 例如, 当 ${k_1} = 0$ 时, 引理 4.1 与引理 2.2 是等价的; 当 ${k_1} = \pm 6$ 时, 下述引理 4.2 显然成立. 同样, 基于含参函数构造思想, 下述引理 4.3 也可以被证明成立. 因此, 引理 2.2, 引理 4.2 和引理 4.3 都可以视为引理 4.1 的特殊情况, 这表明引理 4.1 更具一般性.

引理 4.2 给定任意一个对称正定矩阵 $W \in {\mathbb{R}^{n \times n}}$, 对于任一连续向量函数 $x:[a,b] \to {\mathbb{R}^n}$, 有

$\begin{equation} \int_a^b {{{\dot x}^T}(u)} W\dot x(u){\rm d}u \ge \frac{1}{{b - a}}\int_a^b {{{\dot x}^T}(u)} {\rm d}uW\int_a^b {\dot x(u)} {\rm d}u + \frac{{{\pi ^2}}}{4}Y. \end{equation}$

其中, $Y$ 如 (3.5) 式所示.

引理 4.3 给定任意一个对称正定矩阵 $W \in {\mathbb{R}^{n \times n}}$, 常值 ${k_2} \in [0,6]$, 对于任一连续向量函数$x:[a,b] \to {\mathbb{R}^n}$, 有

$\begin{equation} \int_a^b {{{\dot x}^T}(u)} W\dot x(u){\rm d}u \ge \frac{1}{{b - a}}\int_a^b {{{\dot x}^T}(u)} {\rm d}uW\int_a^b {\dot x(u)} {\rm d}u + {G_2}({k_2})Y, \end{equation}$

其中 ${G_2}({k_2}) = \frac{{({\pi ^2} - 12)k_2^2 + (72 - 6{\pi ^2}){k_2} + 9{\pi ^2}}}{{36}}$, $Y$ 如 (3.5) 式所示.

注 4.2 引理 4.3 虽然被视为引理 4.1 的一个特例, 但它仍然具有更广泛的适用性, 相比现有的许多方法更加通用. 举例来说, 当 ${k_2} = 0$ 时, 引理 4.3 与引理 4.2 具有等价关系; 当 ${k_2} = 3$ 时, 引理 4.3 与引理 2.2 也具有等价关系.

注 4.3 本文提出的引理 4.3 为一种积分不等式, 能够在 $0 \le {k_2} \le 6$ 范围内给出上界. 引理 4.3 在引理 4.2 的基础上逐步增大积分不等式的上界, 但上界并不会一直增大, 当达到最大上界时将与引理 2.2 一致. 在引理 4.9 的推导中, 引理 2.2 被用于对项 $\frac{{(6{k_2} - k_2^2)}}{9}\int_a^b {{{\dot x}^T}(u)W\dot x(u){\rm d}u} $ 进行定界, 若使用引理 2.1 进行定界, 同样会增大 Jensen 积分不等式的上界, 结论如下

$\begin{align*} \int_a^b {{{\dot x}^T}(u)} W\dot x(u){\rm d}u \ge \frac{1}{{(b - a)}}\int_a^b {{{\dot x}^T}(u){\rm d}uW} \int_a^b {\dot x(u){\rm d}u} + \frac{{{\pi ^2}{{({k_2} - 3)}^2}}}{{36(b - a)}}Y, \end{align*}$

此时, 积分不等式的上界将在引理 2.1 的基础上逐步增大且最大上界与引理 4.2 相同.

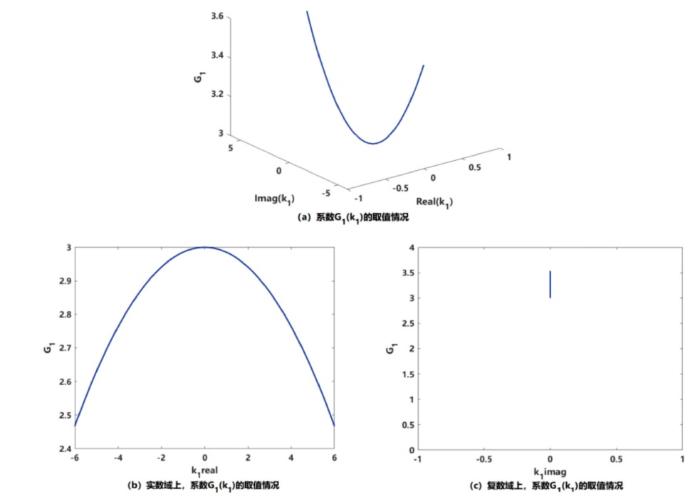
注 4.4 本文提出的扩展 Wirtinger 不等式在求解积分上界时, 能够比原有 Wirtinger 不等式获得更加精确的结果. 为了进一步说明其优越性, 我们对系数 ${G_1}({k_1})$ 的取值情况进行了详细的分析和可视化. 具体而言, 当 $k_1^2 \le 36$ 且${k_1}$ 取复数值时, 扩展 Wirtinger 不等式能够获得最优的积分上界. 我们绘制了系数 ${G_1}({k_1})$ 取值情况的图像, 其中图1(a) 展示了整体的取值情况, 而图1(b) 和图1(c) 分别展示了在实数域和复数域内的取值情况. 从图中可以清晰地观察到, 所提出的扩展 Wirtinger 不等式相较于原有 Wirtinger 不等式, 在积分上界的计算中具有更高的精度和优越性.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   系数 ${G_1}({k_1})$ 取值情况


注 4.5 为了凸显引理 4.1, 引理 4.2 和引理 4.3 之间的差异, 本文给出了各引理中下界 $Y$ 的不同系数的取值范围, 见表4.1 (鉴于复数域上的结果更为复杂, 这里仅展示引理 4.1 在实数域上的解). 易见, $Y$ 的系数是衡量积分不等式估计精度的一个指标, 系数值越大, 精度越高.由表4.1 可见, 引理 4.2 的系数取值范围是引理 4.1 在实数域上某一点的取值, 而引理 4.3 的系数取值范围与引理 4.1 在实数域上的系数取值范围相同.

表4.1   $Y$ 的系数对比

新窗口打开| 下载CSV


5 主要结论

在本节中, 我们将基于扩展不等式, 给出加性时变时滞系统的保守性较低的稳定性准则. 简单起见, 定义以下向量和矩阵

$\begin{array}{l} e_{j}=\left[0_{n \times(j-1) n} I_{n} 0_{n \times(9-j) n}\right],(j=1,2, \cdots, 9), \\ \tilde{e}_{j}=\left[0_{n \times(j-1) n} I_{n} 0_{n \times(8-j) n}\right],(j=1,2, \cdots, 8), \\ \xi(t)=\left[x^{T}(t), x^{T}\left(t-d_{1}(t)\right), x^{T}\left(t-d_{1}(t)-d_{2}(t)\right), x^{T}\left(t-d_{1}(t)-\bar{d}_{2}\right), x^{T}\left(t-\bar{d}_{1}-\bar{d}_{2}\right),\right. \end{array}$
$\begin{array}{l} \frac{1}{d_{1}(t)} \int_{t-d_{1}(t)}^{t} x^{T}(s) \mathrm{d} s, \frac{1}{d_{2}(t)} \int_{t-d_{1}(t)-d_{2}(t)}^{t-d_{1}(t)} x^{T}(s) \mathrm{d} s, \frac{1}{\bar{d}_{2}-d_{2}(t)} \int_{t-d_{1}(t)-\bar{d}_{2}}^{t-d_{1}(t)-d_{2}(t)} x^{T}(s) \mathrm{d} s, \\ \left.\frac{1}{\bar{d}_{1}-d_{1}(t)} \int_{t-\bar{d}_{1}-\bar{d}_{2}}^{t-d_{1}(t)-\bar{d}_{2}} x^{T}(s) \mathrm{d} s\right]^{T}, \end{array}$
$\begin{array}{l} \Gamma_{1}=\left[\begin{array}{c} x\left(t-d_{1}(t)-\bar{d}_{2}\right)-x\left(t-\bar{d}_{1}-\bar{d}_{2}\right) \\ x\left(t-d_{1}(t)-\bar{d}_{2}\right)+x\left(t-\bar{d}_{1}-\bar{d}_{2}\right)-\frac{2}{d_{1}-d_{1}(t)} \int_{t-\bar{d}_{1}-\bar{d}_{2}}^{t-d_{2}(t)-\bar{d}_{2}} x(s) \mathrm{d} s \end{array}\right], \\ \Gamma_{2}=\left[\begin{array}{c} x\left(t-d_{1}(t)-d_{2}(t)\right)-x\left(t-d_{1}(t)-\bar{d}_{2}\right) \\ x\left(t-d_{1}(t)-d_{2}(t)\right)+x\left(t-d_{1}(t)-\bar{d}_{2}\right)-\frac{2}{d_{2}-d_{2}(t)} \int_{t-d_{1}(t)-\bar{d}_{2}}^{t-d_{1}(t)-d_{2}(t)} x(s) \mathrm{d} s \end{array}\right], \\ \Gamma_{3}=\left[\begin{array}{c} x\left(t-d_{1}(t)\right)-x\left(t-d_{1}(t)-d_{2}(t)\right) \\ x\left(t-d_{1}(t)\right)+x\left(t-d_{1}(t)-d_{2}(t)\right)-\frac{2}{d_{2}(t)} \int_{t-d_{1}(t)-d_{2}(t)}^{t-d_{1}(t)} x(s) \mathrm{d} s \end{array}\right], \\ \Gamma_{4}=\left[\begin{array}{c} x(t)-x\left(t-d_{1}(t)\right) \\ x(t)+x\left(t-d_{1}(t)\right)-\frac{2}{d_{1}(t)} \int_{t-d_{1}(t)}^{t} x(s) \mathrm{d} s \end{array}\right], \\ \Gamma=\left[\begin{array}{l} \Gamma_{1} \\ \Gamma_{2} \\ \Gamma_{3} \\ \Gamma_{4} \end{array}\right]. \end{array}$

定理 5.1 给定标量 ${\bar d_j} > 0$, ${\mu _j} > 0,(j = 1,2)$ 以及满足条件 $k_1^2 \le 36$ 的常复数 ${k_1}$, 则满足(2.2) 式的时滞系统 (2.1) 是渐近稳定的, 如果存在 $2n \times 2n$ 的矩阵 $\left[ \begin{matrix} {{P}_{1}} & {{P}_{2}} \\ * & {{P}_{3}} \\ \end{matrix} \right]>0$, $n \times n$ 的矩阵 ${Q_j} > 0,\left({j = 1,2,3,4} \right)$, $W > 0$, $8n \times 8n$ 的矩阵 $M$, 使如下线性矩阵不等式 (5.1)-(5.4) 成立,

$\begin{align*} &\left[ \begin{matrix} {{\Xi }_{1}}+{{\Xi }_{2}}+{{\Xi }_{3}}+{{{\bar{d}}}_{1}}{{\Phi }_{1}}+{{{\bar{d}}}_{2}}{{\Phi }_{2}} & {{E}^{T}}{{M}^{T}}E_{4}^{T} & {{E}^{T}}{{M}^{T}}E_{3}^{T} \\ * & -\frac{1}{{{{\bar{d}}}_{1}}}\tilde{W} & 0 \\ * & * & -\frac{1}{{{{\bar{d}}}_{2}}}\tilde{W} \\ \end{matrix} \right]<0, \end{align*}$
$\begin{align*} &\left[ \begin{matrix} {{\Xi }_{1}}+{{\Xi }_{2}}+{{\Xi }_{3}}+{{{\bar{d}}}_{1}}{{\Phi }_{1}}+{{{\bar{d}}}_{2}}{{\Phi }_{3}} & {{E}^{T}}{{M}^{T}}E_{4}^{T} & {{E}^{T}}{{M}^{T}}E_{2}^{T} \\ * & -\frac{1}{{{{\bar{d}}}_{1}}}\tilde{W} & 0 \\ * & * & -\frac{1}{{{{\bar{d}}}_{2}}}\tilde{W} \\ \end{matrix} \right]<0, \end{align*}$
$\begin{align*} &\left[ \begin{matrix} {{\Xi }_{1}}+{{\Xi }_{2}}+{{\Xi }_{3}}+{{{\bar{d}}}_{1}}{{\Phi }_{4}}+{{{\bar{d}}}_{2}}{{\Phi }_{2}} & {{E}^{T}}{{M}^{T}}E_{1}^{T} & {{E}^{T}}{{M}^{T}}E_{3}^{T} \\ * & -\frac{1}{{{{\bar{d}}}_{1}}}\tilde{W} & 0 \\ * & * & -\frac{1}{{{{\bar{d}}}_{2}}}\tilde{W} \\ \end{matrix} \right]<0, \end{align*}$
$\begin{align*} &\left[ \begin{matrix} {{\Xi }_{1}}+{{\Xi }_{2}}+{{\Xi }_{3}}+{{{\bar{d}}}_{1}}{{\Phi }_{4}}+{{{\bar{d}}}_{2}}{{\Phi }_{3}} & {{E}^{T}}{{M}^{T}}E_{1}^{T} & {{E}^{T}}{{M}^{T}}E_{2}^{T} \\ * & -\frac{1}{{{{\bar{d}}}_{1}}}\tilde{W} & 0 \\ * & * & -\frac{1}{{{{\bar{d}}}_{2}}}\tilde{W} \\ \end{matrix} \right]<0, \end{align*}$

其中

$\begin{align*} & {{\Xi }_{1}}=Sym\{e_{1}^{T}({{P}_{1}}A+{{P}_{2}}){{e}_{1}}+e_{1}^{T}{{P}_{1}}B{{e}_{3}}-e_{1}^{T}{{P}_{2}}B{{e}_{5}}\}, \\ & {{\Xi }_{2}}=e_{1}^{T}({{Q}_{1}}+{{Q}_{2}}+{{Q}_{3}}+{{Q}_{4}}){{e}_{1}}-(1-{{\mu }_{1}})e_{2}^{T}{{Q}_{1}}{{e}_{2}}\\ & \hskip.8cm -(1-{{\mu }_{1}}-{{\mu }_{2}})e_{3}^{T}{{Q}_{2}}{{e}_{3}}-(1-{{\mu }_{1}})e_{4}^{T}{{Q}_{3}}{{e}_{4}}-e_{5}^{T}{{Q}_{4}}{{e}_{5}}, \\ & {{\Xi }_{3}}=({{{\bar{d}}}_{1}}+{{{\bar{d}}}_{2}})(e_{1}^{T}{{A}^{T}}WA{{e}_{1}}+e_{3}^{T}{{B}^{T}}WB{{e}_{3}}+Sym\{e_{1}^{T}{{A}^{T}}WB{{e}_{3}}+{{E}^{T}}ME\}), \\ & {{\Phi }_{j}}=Sym\{e_{1}^{T}({{A}^{T}}{{P}_{2}}+{{P}_{3}}){{e}_{j+5}}+e_{3}^{T}{{B}^{T}}{{P}_{2}}{{e}_{j+5}}-e_{5}^{T}{{P}_{3}}{{e}_{j+5}}\},(j=1,2,3,4),\\ & {{E}_{j}}=\left[ \begin{matrix} {{{\tilde{e}}}_{2j-1}} \\ {{{\tilde{e}}}_{2j}} \\ \end{matrix} \right],(j=1,2,3,4),&\\ &\tilde{W}=\left[ \begin{matrix} W & 0 \\ 0 & \frac{432+k_{1}^{2}({{\pi }^{2}}-12)}{144}W \\ \end{matrix} \right],&\\ &E=\left[ \begin{matrix} {{e}_{4}}-{{e}_{5}} \\ {{e}_{4}}+{{e}_{5}}-2{{e}_{9}} \\ {{e}_{3}}-{{e}_{4}} \\ \begin{matrix} {{e}_{3}}+{{e}_{4}}-2{{e}_{8}} \\ {{e}_{2}}-{{e}_{3}} \\ {{e}_{2}}+{{e}_{3}}-2{{e}_{7}} \\ \begin{matrix} {{e}_{1}}-{{e}_{2}} \\ {{e}_{1}}+{{e}_{2}}-2{{e}_{6}} \\ \end{matrix} \\ \end{matrix} \\ \end{matrix} \right].& \end{align*}$

证 构造以下 LKF,

$\begin{align*} V(t)={V_1}(t) + {V_2}(t) + {V_3}(t), \end{align*}$
$\begin{aligned} V_{1}(t)= & {\left[\begin{array}{c} x(t) \\ \int_{t-\bar{d}_{1}-\bar{d}_{2}}^{t} x(s) \mathrm{d} s \end{array}\right]^{T}\left[\begin{array}{ll} P_{1} & P_{2} \\ * & P_{3} \end{array}\right]\left[\begin{array}{c} x \\ \int_{t-\bar{d}_{1}-\bar{d}_{2}}^{t} x(t) \mathrm{d} s \end{array}\right] }, \\ V_{2}(t)= & \int_{t-d_{1}(t)}^{t} x^{T}(s) Q_{1} x(s) \mathrm{d} s+\int_{t-d_{1}(t)-d_{2}(t)}^{t} x^{T}(s) Q_{2} x(s) \mathrm{d} s \\ & +\int_{t-d_{1}(t)-\bar{d}_{2}}^{t} x^{T}(s) Q_{3} x(s) \mathrm{d} s+\int_{t-\bar{d}_{1}-\bar{d}_{2}}^{t} x^{T}(s) Q_{4} x(s) \mathrm{d} s, \\ V_{3}(t)= & \int_{-\bar{d}_{1}-\bar{d}_{2}}^{0} \int_{t+\theta}^{t} \dot{x}^{T}(s) W \dot{x}(s) \mathrm{d} s \mathrm{~d} \theta, \end{aligned}$

对 $V(t)$ 求导有以下结果

$\begin{align*} & {{{\dot{V}}}_{1}}(t)={{\xi }^{T}}(t)\left[ {{\Xi }_{1}}+{{d}_{1}}(t){{\Phi }_{1}}+{{d}_{2}}(t){{\Phi }_{2}}+({{{\bar{d}}}_{2}}-{{d}_{2}}(t)){{\Phi }_{3}}+({{{\bar{d}}}_{1}}-{{d}_{1}}(t)){{\Phi }_{4}} \right]\xi (t), \nonumber \\ & {{{\dot{V}}}_{2}}(t)={{\xi }^{T}}(t)\left[ e_{1}^{T}({{Q}_{1}}+{{Q}_{2}}+{{Q}_{3}}+{{Q}_{4}}){{e}_{1}}-(1-{{{\dot{d}}}_{1}}(t))e_{2}^{T}{{Q}_{1}}{{e}_{2}}-(1-{{{\dot{d}}}_{1}}(t)-{{{\dot{d}}}_{2}}(t))e_{3}^{T}{{Q}_{2}}{{e}_{3}}) \right. \nonumber\\ & \left. \hskip1.2cm -(1-{{{\dot{d}}}_{1}}(t))e_{4}^{T}{{Q}_{3}}{{e}_{4}}-e_{5}^{T}{{Q}_{4}}{{e}_{5}} \right]\xi (t) \le {{\xi }^{T}}(t){{\Xi }_{2}}\xi (t), \nonumber\\ &{{{\dot{V}}}_{3}}(t)=({{{\bar{d}}}_{1}}+{{{\bar{d}}}_{2}}){{{\dot{x}}}^{T}}(t)W\dot{x}(t)-\int_{t-{{{\bar{d}}}_{1}}-{{{\bar{d}}}_{2}}}^{t}{{{{\dot{x}}}^{T}}(s)W\dot{x}(s)}{\rm d}s \nonumber\\ & \hskip.8cm =({{{\bar{d}}}_{1}}+{{{\bar{d}}}_{2}}){{{\dot{x}}}^{T}}(t)W\dot{x}(t)-\int_{t-{{{\bar{d}}}_{1}}-{{{\bar{d}}}_{2}}}^{t-{{d}_{1}}(t)-{{{\bar{d}}}_{2}}}{{{{\dot{x}}}^{T}}(s)W\dot{x}(s)}{\rm d}s-\int_{t-{{d}_{1}}(t)-{{{\bar{d}}}_{2}}}^{t-{{d}_{1}}(t)-{{d}_{2}}(t)}{{{{\dot{x}}}^{T}}(s)W\dot{x}(s)}{\rm d}s \nonumber \\ & \hskip1.2cm -\int_{t-{{d}_{1}}(t)-{{d}_{2}}(t)}^{t-{{d}_{1}}(t)}{{{{\dot{x}}}^{T}}(s)W\dot{x}(s)}{\rm d}s-\int_{t-{{d}_{1}}(t)}^{t}{{{{\dot{x}}}^{T}}(s)W\dot{x}(s)}{\rm d}s, \end{align*}$

使用引理 4.1, 对上述积分项进行估计, 结果如下

$\begin{aligned} & -\int_{t-\bar{d}_{1}-\bar{d}_{2}}^{t-d_{1}(t)-\bar{d}_{2}} \dot{x}^{T}(s) W \dot{x}(s) \mathrm{d} s-\int_{t-d_{1}(t)-\bar{d}_{2}}^{t-d_{1}(t)-d_{2}(t)} \dot{x}^{T}(s) W \dot{x}(s) \mathrm{d} s \\ & -\int_{t-d_{1}(t)-d_{2}(t)}^{t-d_{1}(t)} \dot{x}^{T}(s) W \dot{x}(s) \mathrm{d} s-\int_{t-d_{1}(t)}^{t} \dot{x}^{T}(s) W \dot{x}(s) \mathrm{d} s \\ \leq & -\frac{1}{\bar{d}_{1}-d_{1}(t)} \Gamma_{1}^{T} \tilde{W} \Gamma_{1}-\frac{1}{\bar{d}_{2}-d_{2}(t)} \Gamma_{2}^{T} \tilde{W} \Gamma_{2}-\frac{1}{d_{2}(t)} \Gamma_{3}^{T} \tilde{W} \Gamma_{3}-\frac{1}{d_{1}(t)} \Gamma_{4}^{T} \tilde{W} \Gamma_{4} \\ = & {\left[\begin{array}{l} \Gamma_{1} \\ \Gamma_{2} \\ \Gamma_{3} \\ \Gamma_{4} \end{array}\right]\left[\begin{array}{cccc} T-\frac{1}{\bar{d}_{1}-d_{1}(t)} \tilde{W} & 0 & 0 \\ 0 & -\frac{1}{\bar{d}_{2}-d_{2}(t)} \tilde{W} & 0 & 0 \\ 0 & 0 & -\frac{1}{d_{2}(t)} \tilde{W} & 0 \\ 0 & 0 & 0 & -\frac{1}{d_{1}(t)} \tilde{W} \end{array}\right]\left[\begin{array}{l} \Gamma_{1} \\ \Gamma_{2} \\ \Gamma_{3} \\ \Gamma_{4} \end{array}\right] }, \end{aligned}$

接着, 运用引理 2.4 对上述式子进行处理

$\begin{aligned} & {\left[\begin{array}{l} \Gamma_{1} \\ \Gamma_{2} \\ \Gamma_{3} \\ \Gamma_{4} \end{array}\right]^{T}\left[\begin{array}{cccc} -\frac{1}{\bar{d}_{1}-d_{1}(t)} \tilde{W} & 0 & 0 & 0 \\ 0 & -\frac{1}{\bar{d}_{2}-d_{2}(t)} \tilde{W} & 0 & 0 \\ 0 & 0 & -\frac{1}{d_{2}(t)} \tilde{W} & 0 \\ 0 & 0 & 0 & -\frac{1}{d_{1}(t)} \tilde{W} \end{array}\right]\left[\begin{array}{l} \Gamma_{1} \\ \Gamma_{2} \\ \Gamma_{3} \\ \Gamma_{4} \end{array}\right] } \\ \leq & \Gamma^{T}\left[M+M^{T}+M^{T}\left[\begin{array}{cccc} \left(\bar{d}_{1}-d_{1}(t)\right) \tilde{W}^{-1} & 0 & 0 & 0 \\ 0 & \left(\bar{d}_{2}-d_{2}(t)\right) \tilde{W}^{-1} & 0 & 0 \\ 0 & 0 & d_{2}(t) \tilde{W}^{-1} & 0 \\ 0 & 0 & 0 & d_{1}(t) \tilde{W}^{-1} \end{array}\right] M\right] \Gamma, \end{aligned}$

可以获得

$\begin{aligned} \dot{V}_{3}(t) \leq & \left(\bar{d}_{1}+\bar{d}_{2}\right) \dot{x}^{T}(t) W \dot{x}(t) \\ & +\Gamma^{T}\left[M+M^{T}+M^{T}\left[\begin{array}{cccc} \left(\bar{d}_{1}-d_{1}(t)\right) \tilde{W}^{-1} & 0 & 0 & 0 \\ 0 & \left(\bar{d}_{2}-d_{2}(t)\right) \tilde{W}^{-1} & 0 & 0 \\ 0 & 0 & d_{2}(t) \tilde{W}^{-1} & 0 \\ 0 & 0 & 0 & d_{1}(t) \tilde{W}^{-1} \end{array}\right] M\right] \Gamma \end{aligned}$
$\begin{aligned} = & \xi^{T}(t)\left[\Xi_{3}+d_{1}(t) E^{T} M^{T} E_{4}^{T} \tilde{W}^{-1} E_{4} M E+d_{2}(t) E^{T} M^{T} E_{3}^{T} \tilde{W}^{-1} E_{3} M E\right. \\ & \left.+\left(\bar{d}_{2}-d_{2}(t)\right) E^{T} M^{T} E_{2}^{T} \tilde{W}^{-1} E_{2} M E+\left(\bar{d}_{1}-d_{1}(t)\right) E^{T} M^{T} E_{1}^{T} \tilde{W}^{-1} E_{1} M E\right] \xi(t), \end{aligned}$

综上所述, 有

$\begin{aligned} \dot{V}(t) \leq & \xi^{T}(t)\left[\Xi_{1}+\Xi_{2}+\Xi_{3}+d_{1}(t)\left(\Phi_{1}+E^{T} M^{T} E_{4}^{T} \tilde{W}^{-1} E_{4} M E\right)\right. \\ & +d_{2}(t)\left(\Phi_{2}+E^{T} M^{T} E_{3}^{T} \tilde{W}^{-1} E_{3} M E\right)+\left(\bar{d}_{2}-d_{2}(t)\right)\left(\Phi_{3}+E^{T} M^{T} E_{2}^{T} \tilde{W}^{-1} E_{2} M E\right) \\ & \left.+\left(\bar{d}_{1}-d_{1}(t)\right)\left(\Phi_{4}+E^{T} M^{T} E_{1}^{T} \tilde{W}^{-1} E_{1} M E\right)\right] \xi(t), \end{aligned}$

基于凸组合技术, 下式成立则保证了 $\dot V(t) < 0$ 成立

$\begin{array}{l} \Xi_{1}+\Xi_{2}+\Xi_{3}+\bar{d}_{1}\left(\Phi_{1}+E^{T} M^{T} E_{4}^{T} \tilde{W}^{-1} E_{4} M E\right)+\bar{d}_{2}\left(\Phi_{2}+E^{T} M^{T} E_{3}^{T} \tilde{W}^{-1} E_{3} M E\right)<0, \\ \Xi_{1}+\Xi_{2}+\Xi_{3}+\bar{d}_{1}\left(\Phi_{1}+E^{T} M^{T} E_{4}^{T} \tilde{W}^{-1} E_{4} M E\right)+\bar{d}_{2}\left(\Phi_{3}+E^{T} M^{T} E_{2}^{T} \tilde{W}^{-1} E_{2} M E\right)<0, \\ \Xi_{1}+\Xi_{2}+\Xi_{3}+\bar{d}_{1}\left(\Phi_{4}+E^{T} M^{T} E_{1}^{T} \tilde{W}^{-1} E_{1} M E\right)+\bar{d}_{2}\left(\Phi_{2}+E^{T} M^{T} E_{3}^{T} \tilde{W}^{-1} E_{3} M E\right)<0, \\ \Xi_{1}+\Xi_{2}+\Xi_{3}+\bar{d}_{1}\left(\Phi_{4}+E^{T} M^{T} E_{1}^{T} \tilde{W}^{-1} E_{1} M E\right)+\bar{d}_{2}\left(\Phi_{3}+E^{T} M^{T} E_{2}^{T} \tilde{W}^{-1} E_{2} M E\right)<0, \end{array}$

依据引理 2.5, 如果式 (5.1)-(5.4) 成立则成立, 结论得证.

注 5.1 在上述推导过程中, 我们使用了引理 4.1 对积分项进行了估计. 此外, 本文中的引理 2.1, 引理 2.2, 引理 4.2 和引理 4.3 等均可只改变 $\tilde W$ 项实现对积分项的估计. 因此, 本文所提出的扩展不等式并未增加计算量.

为验证引理 2.6 的优越性, 本文同样借鉴了文献 [11] 中的 LKF 构造方法和积分项估计技术, 利用基于三阶矩阵的扩展互凸矩阵不等式 (引理 2.6) 代替文献 [11] 中的引理 2 来对凸项进行估计, 从而得出满足式 (2.2) 的时滞系统 (2.1) 的稳定性准则, 该准则如下所示

定理 5.2 给定标量 ${\bar d_j} > 0$, ${\mu _j} > 0,(j = 1,2)$, 则满足 (2.2) 式的时滞系统 (2.1) 是渐近稳定的, 如果存在 $2n \times 2n$ 的矩阵$\left[\begin{matrix} {{P}_{1}} & {{P}_{2}} \\ * & {{P}_{3}} \\ \end{matrix} \right]>0$, $n \times n$ 的矩阵 ${Q_j} > 0,\left({j = 1,2,3,4} \right)$, $W > 0$, $8n \times 8n$ 的矩阵 $M,N$, 使如下线性矩阵不等式 (5.7)-(5.10) 成立

$\begin{align*} & \left[ \begin{matrix} {{\Xi }_{1}}+{{\Xi }_{2}}+{{\Xi }_{3}}+{{{\bar{d}}}_{1}}{{\Phi }_{1}}+{{{\bar{d}}}_{2}}{{\Phi }_{2}} & {{E}^{T}}{{M}^{T}}E_{4}^{T} & {{E}^{T}}{{N}^{T}}E_{4}^{T} & {{E}^{T}}{{M}^{T}}E_{3}^{T} & {{E}^{T}}{{N}^{T}}E_{3}^{T} \\ * & -\frac{2}{{{{\bar{d}}}_{1}}}\tilde{W} & 0 & 0 & 0 \\ * & * & -\frac{2}{{{{\bar{d}}}_{1}}}\tilde{W} & 0 & 0 \\ * & * & * & -\frac{2}{{{{\bar{d}}}_{2}}}\tilde{W} & 0 \\ * & * & * & * & -\frac{2}{{{{\bar{d}}}_{2}}}\tilde{W} \\ \end{matrix} \right]<0, \end{align*}$
$\begin{align*} &\left[ \begin{matrix} {{\Xi }_{1}}+{{\Xi }_{2}}+{{\Xi }_{3}}+{{{\bar{d}}}_{1}}{{\Phi }_{1}}+{{{\bar{d}}}_{2}}{{\Phi }_{3}} & {{E}^{T}}{{M}^{T}}E_{4}^{T} & {{E}^{T}}{{N}^{T}}E_{4}^{T} & {{E}^{T}}{{M}^{T}}E_{2}^{T} & {{E}^{T}}{{N}^{T}}E_{2}^{T} \\ * & -\frac{2}{{{{\bar{d}}}_{1}}}\tilde{W} & 0 & 0 & 0 \\ * & * & -\frac{2}{{{{\bar{d}}}_{1}}}\tilde{W} & 0 & 0 \\ * & * & * & -\frac{2}{{{{\bar{d}}}_{2}}}\tilde{W} & 0 \\ * & * & * & * & -\frac{2}{{{{\bar{d}}}_{2}}}\tilde{W} \\ \end{matrix} \right]<0, \end{align*}$
$\begin{align*} & \left[ \begin{matrix} {{\Xi }_{1}}+{{\Xi }_{2}}+{{\Xi }_{3}}+{{{\bar{d}}}_{1}}{{\Phi }_{4}}+{{{\bar{d}}}_{2}}{{\Phi }_{2}} & {{E}^{T}}{{M}^{T}}E_{1}^{T} & {{E}^{T}}{{N}^{T}}E_{1}^{T} & {{E}^{T}}{{M}^{T}}E_{3}^{T} & {{E}^{T}}{{N}^{T}}E_{3}^{T} \\ * & -\frac{2}{{{{\bar{d}}}_{1}}}\tilde{W} & 0 & 0 & 0 \\ * & * & -\frac{2}{{{{\bar{d}}}_{1}}}\tilde{W} & 0 & 0 \\ * & * & * & -\frac{2}{{{{\bar{d}}}_{2}}}\tilde{W} & 0 \\ * & * & * & * & -\frac{2}{{{{\bar{d}}}_{2}}}\tilde{W} \\ \end{matrix} \right]<0, \end{align*}$
$\begin{align*} & \left[ \begin{matrix} {{\Xi }_{1}}+{{\Xi }_{2}}+{{\Xi }_{3}}+{{{\bar{d}}}_{1}}{{\Phi }_{4}}+{{{\bar{d}}}_{2}}{{\Phi }_{3}} & {{E}^{T}}{{M}^{T}}E_{1}^{T} & {{E}^{T}}{{N}^{T}}E_{1}^{T} & {{E}^{T}}{{M}^{T}}E_{2}^{T} & {{E}^{T}}{{N}^{T}}E_{2}^{T} \\ * & -\frac{2}{{{{\bar{d}}}_{1}}}\tilde{W} & 0 & 0 & 0 \\ * & * & -\frac{2}{{{{\bar{d}}}_{1}}}\tilde{W} & 0 & 0 \\ * & * & * & -\frac{2}{{{{\bar{d}}}_{2}}}\tilde{W} & 0 \\ * & * & * & * & -\frac{2}{{{{\bar{d}}}_{2}}}\tilde{W} \\ \end{matrix} \right]<0. \end{align*}$

证 本定理的证明类似于定理 5.1, 此处只给出不同于定理 5.1 的部分, 即本定理利用引理 2.6 对式 (5.6) 进行估计, 估计如下

$\begin{align*} & {{\left[ \begin{matrix} {{\Gamma }_{1}} \\ {{\Gamma }_{2}} \\ {{\Gamma }_{3}} \\ {{\Gamma }_{4}} \\ \end{matrix} \right]}^{T}}\left[ \begin{matrix} -\frac{1}{{{{\bar{d}}}_{1}}-{{d}_{1}}(t)}\tilde{W} & 0 & 0 & 0 \\ 0 & -\frac{1}{{{{\bar{d}}}_{2}}-{{d}_{2}}(t)}\tilde{W} & 0 & 0 \\ 0 & 0 & -\frac{1}{{{d}_{2}}(t)}\tilde{W} & 0 \\ 0 & 0 & 0 & -\frac{1}{{{d}_{1}}(t)}\tilde{W} \\ \end{matrix} \right]\left[ \begin{matrix} {{\Gamma }_{1}} \\ {{\Gamma }_{2}} \\ {{\Gamma }_{3}} \\ {{\Gamma }_{4}} \\ \end{matrix} \right] \\ \le\ & {{\Gamma }^{T}}\left[ \frac{1}{2}{{M}^{T}}\left[ \begin{matrix} ({{{\bar{d}}}_{1}}-{{d}_{1}}(t)){{{\tilde{W}}}^{-1}} & 0 & 0 & 0 \\ 0 & ({{{\bar{d}}}_{2}}-{{d}_{2}}(t)){{{\tilde{W}}}^{-1}} & 0 & 0 \\ 0 & 0 & {{d}_{2}}(t){{{\tilde{W}}}^{-1}} & 0 \\ 0 & 0 & 0 & {{d}_{1}}(t){{{\tilde{W}}}^{-1}} \\ \end{matrix} \right]M \right. \\ & +\frac{1}{2}{{N}^{T}}\left[ \begin{matrix} ({{{\bar{d}}}_{1}}-{{d}_{1}}(t)){{{\tilde{W}}}^{-1}} & 0 & 0 & 0 \\ 0 & ({{{\bar{d}}}_{2}}-{{d}_{2}}(t)){{{\tilde{W}}}^{-1}} & 0 & 0 \\ 0 & 0 & {{d}_{2}}(t){{{\tilde{W}}}^{-1}} & 0 \\ 0 & 0 & 0 & {{d}_{1}}(t){{{\tilde{W}}}^{-1}} \\ \end{matrix} \right]N\\ &\left.+\frac{M+N+{{M}^{T}}+{{N}^{T}}}{2} \right]\Gamma, \end{align*}$

其余步骤与定理 5.1 相同, 从而证明完成.

6 数值实例

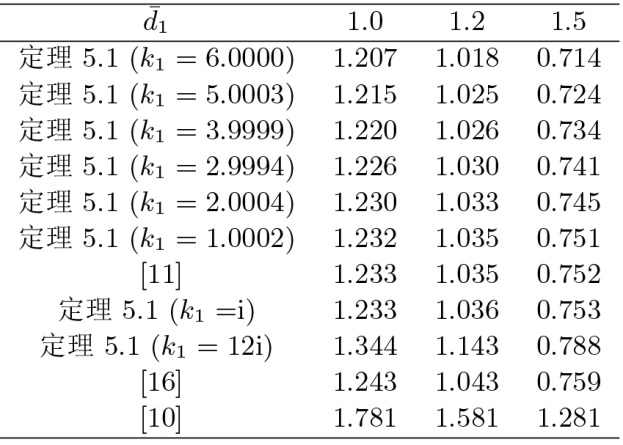
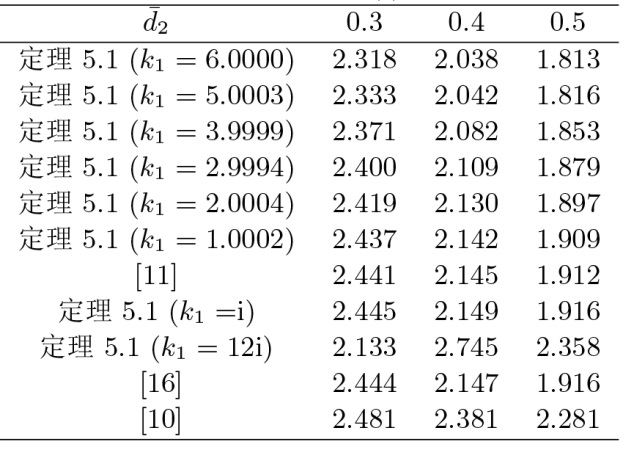
在本节中, 应用一个经常用到的数值例子来验证所提出的扩展不等式的优越性. 考虑具有以下参数的系统 (2.1)

$A = \left[ {\begin{array}{*{20}{c}} { - 2}&0\\ 0&{ - 0.9} \end{array}} \right]\begin{array}{*{20}{c}},&{B = } \end{array}\left[ {\begin{array}{*{20}{c}} { - 1}&0\\ { - 1}&{ - 1} \end{array}} \right],$

假设时滞导数上界 ${\mu _1}$ 和 ${\mu _2}$ 分别为 0.1 和 0.8. 本研究旨在找到时滞 ${d_1}(t)$ 的上界 ${\bar d_1}$ 或时滞 ${d_2}(t)$ 的上界 ${\bar d_2}$. 为了确保结果的可靠性, 将本文提出的准则与文献 [9,11,15] 中的稳定性准则进行比较. 在表6.1 和表6.2 中, 列出了相应的对比结果, 其中, i 为虚数. 结果表明: 1) 使用本文提出的定理 5.1 可以在不增加计算负担的情况下, 获得比文献 [11,15] 更大的时滞上界; 2) 当 ${\bar d_2=0.4,0.5}$ 时, 本文提出的定理 5.1 获得了比文献 [9] 更大的时滞 ${d_1}(t)$ 的上界 ${\bar d_1}$; 3) 由于时滞上界的获取不仅取决于积分不等式的估计精度, 还取决于 LKF 的构造, 因而, 本文提出的定理 5.1 没有获得比文献 [9] 更大的时滞${d_2}(t)$ 的上界 ${\bar d_2}$; 4) 鉴于 2), 3) 中 ${d_1}(t)$ 和 ${d_2}(t)$ 的取值上界并非在同一情况下取到, 侧面反映了时滞 ${d_1}(t)$ 和 ${d_2}(t)$ 是存在差异的, 故对加性时变时滞系统稳定性的研究是必要的.

表6.1   ${\bar d_1}$ 给定下的 ${d_2}(t)$ 的上界 ${\bar d_2}$

新窗口打开| 下载CSV


表6.2   ${\bar d_2}$ 给定下的 ${d_1}(t)$ 的上界 ${\bar d_1}$

新窗口打开| 下载CSV


注 6.1 关于 ${k_1}$ 的复数取值, 此处我们仅仅在纯虚数下进行了模拟仿真, 具体原因如下 1) 当 ${k_1}$ 取纯虚数值时, 仿真中的操作更为简便, 所涉及的运算主要是实数操作; 2) 仿真所应用的软件为 MATLAB, 其并不支持复数域运算.

为了验证引理 2.6 的优越性并增强实验结果的可信度, 采用了与文献 [11] 中相同的时滞系统进行仿真实验. 我们对定理 5.2 的结论与文献 [11] 中给出的加性时变时滞系统的稳定性准则进行稳定性分析比较, 并将实验结果汇总在表6.3 和表6.4 中进行展示. 通过对比表格数据, 可以得出结论: 定理 5.2 可以获得比文献 [11] 更大的时滞上界, 从而提高了系统的稳定性.

表6.3   ${\bar d_1}$ 给定下的 ${d_2}(t)$ 的上界 ${\bar d_2}$

新窗口打开| 下载CSV


表6.4   ${\bar d_2}$ 给定下的 ${d_1}(t)$ 的上界 ${\bar d_1}$

新窗口打开| 下载CSV


注 6.2 本节所采用的仿真实验平台为 MATLAB, 我们利用其内置的线性矩阵不等式 (LMI) 工具箱来求解线性矩阵不等式.

7 结语

本文首先从单调性和增加正项两个角度对 Wirtinger 不等式进行了论证. 接着, 提出了扩展不等式, 其中包括一个扩展 Wirtinger 不等式和一个基于三阶矩阵的扩展互凸不等式. 然后, 分别利用这两个扩展不等式, 给出了加性时变时滞系统的稳定性准则. 最后, 通过数值算例说明了扩展不等式的优越性. 在未来的研究工作中, 将试图从更多角度深入探讨以改进积分不等式来提高时滞系统的稳定性. 具体而言, 可从巧妙选择正项, 优化构造函数, 引入辅助不等式, 引入含参函数以及充分利用单调性等角度思考.

参考文献

Chen D, Liu X W, Song Y L.

Stability analysis of discrete-time system with slowly time-varying delays

Procedia Computer Science, 2022, 199: 1008-1015

DOI:10.1016/j.procs.2022.01.127      URL     [本文引用: 1]

Cai L, Xiong L L, Zhang H Y.

A generalized multiple integral inequality with application to time-varying delay systems

Procedia Computer Science, 2022, 199: 1268-1275

[本文引用: 1]

Fridman E.

New Lyapunov-Krasovskii functionals for stability of linear retarded and neutral type systems

Systems and Control Letters, 2001, 43(4): 309-319

[本文引用: 2]

Gong C, Zhang X, Wu L G.

Multiple-integral inequalities to stability analysis of linear time-delay systems

Journal of the Franklin Institute, 2017, 354(3): 1446-1463

[本文引用: 2]

González A.

Improved results on stability analysis of time-varying delay systems via delay partitioning method and Finsler's lemma

Journal of the Franklin Institute, 2022, 359(14): 7632-7649

[本文引用: 1]

Gouaisbaut F, Peaucelle D.

Delay-dependent stability analysis of linear time delay systems

IFAC Proceedings Volumes, 2006, 39(10): 54-59

[本文引用: 1]

Gyurkovics E.

A note on Wirtinger-type integral inequalities for time-delay systems

Automatica, 2015, 61: 44-46

Han Q L.

A discrete delay decomposition approach to stability of linear retarded and neutral systems

Automatica, 2009, 45(2): 517-524

[本文引用: 1]

Ji Y D, Ma X T, Wang L Y, et al.

Novel stability criterion for linear system with two additive time-varying delays using general integral inqualities

AIMS Mathematics, 2021, 6(8): 8667-8680

[本文引用: 3]

Jin L, He Y, Jiang L.

A novel integral inequality and its application to stability analysis of linear system with multiple time delays

Applied Mathematics Letters, 2022, 124: 107648

[本文引用: 1]

Jiao J M, Zhang R.

An extended reciprocally convex matrix inequality and its application to stability analysis of systems with additive time-varying delays

Journal of the Franklin Institute, 2020, 357(4): 2282-2294

[本文引用: 8]

Li H F, Zhou B, Hou M Z, et al.

On the time-varying Halanay inequality with applications to stability analysis of time-delay systems

Journal of the Franklin Institute, 2021, 358(10): 5488-5512

[本文引用: 1]

Liu K, Seuret A, Xia Y Q.

Stability analysis of systems with time-varying delays via the second-order Bessel-Legendre inequality

Automatica, 2017, 76: 138-142

[本文引用: 2]

Liu P L.

A delay decomposition approach to robust stability analysis of uncertain systems with time-varying delay

ISA Transactions, 2012, 51(6): 694-701

[本文引用: 1]

Park I, Lee J H, Park P G.

New free-matrix-based integral inequality: Application to stability analysis of systems with additive time-varying delays

IEEE Access, 2020, 8: 125680-125691

[本文引用: 2]

Park P G, Ko J W, Jeong C K.

Reciprocally convex approach to stability of systems with time-varying delays

Automatica, 2011, 47(1): 235-238

[本文引用: 2]

Seuret A, Gouaisbaut F.

Jensen's and Wirtinger's inequalities for time-delay systems

IFAC Proceedings Volumes, 2013, 46(3): 343-348

[本文引用: 5]

Seuret A, Gouaisbaut F.

Wirtinger-based integral inequality: Application to time-delay systems

Automatica, 2013, 49(9): 2860-2866

[本文引用: 2]

Tian J K, Ren Z R, Zhong S M.

A new integral inequality and application to stability of time-delay systems

Applied Mathematics Letters, 2020, 101: 106058

[本文引用: 1]

Wu M, He Y, She J H.

New delay-dependent stability criteria and stabilizing method for neutral systems

IEEE Transactions on Automatic Control, 2004, 49(12): 2266-2271

[本文引用: 1]

Wang C, Shen Y.

Improved delay-dependent robust stability criteria for uncertain time delay systems

Applied Mathematics and Computation, 2011, 218(6): 2880-2888

[本文引用: 1]

Yang B, Yan Z F, Pan X J, et al.

Improved stability criteria for linear systems with time-varying delays

Journal of the Franklin Institute, 2021, 358(15): 7804-7824

DOI:10.1016/j.jfranklin.2021.07.045      [本文引用: 1]

This paper is concerned with the stability analysis of linear systems with time-varying delays. First, by introducing the quadratic terms of time-varying delays and some integral vectors, a more suitable Lyapunov-Krasovskii functional (LKF) is constructed. Second, two new delay-dependent estimation methods are developed in the stability analysis of linear system with time-varying delays, which include a reciprocally convex matrix inequality and an integral inequality. More information about time-varying delays and more free matrices are introduced into the two estimation approaches, which play a key role for obtaining an accurate upper bound of the integral terms in time derivative of LKFs. Third, based on the novel LKFs and new estimation approaches, some less conservative criteria are derived in the form of linear matrix inequality (LMI). Finally, three numerical examples are applied to verify the advantages and effectiveness of the newly proposed methods. (c) 2021 The Franklin Institute. Published by Elsevier Ltd.

Zeng H B, Lin H C, He Y, et al.

Hierarchical stability conditions for time-varying delay systems via an extended reciprocally convex quadratic inequality

Journal of the Franklin Institute, 2020, 357(14): 9930-9941

[本文引用: 1]

Zhi Y L, He Y, Zhang C K, et al.

New method for stability of systems with time-varying delay via improved free-matrix-based integral inequality

IFAC-PapersOnLine, 2017, 50(1): 1281-1285

[本文引用: 1]

Zhao X, Lin C, Chen B, et al.

Stability analysis for linear time-delay systems using new inequality based on the second-order derivative

Journal of the Franklin Institute, 2019, 356(15): 8770-8784

DOI:10.1016/j.jfranklin.2019.03.038      [本文引用: 1]

This paper studies the stability problem of linear time-varying delay system. Firstly, a double integral inequality based on the second-order derivative is proposed in this paper. Secondly, novel Lyapunov-Krasovskii functional consisting of integral terms based on the second-order derivative is constructed to enhance the feasible region of delay-dependent stability. Based on the two aspects, new delay-dependent stability criteria which guarantee the asymptotic stability of linear systems with time-varying delay are given in the form of linear matrix inequality (LMI). Finally, several numerical examples are given to show the advantages of the proposed methods. (C) 2019 The Franklin Institute. Published by Elsevier Ltd.

Zhang C K, He Y, Jiang L, et al.

An improved summation inequality to discrete-time systems with time-varying delay

Automatica, 2016, 74: 10-15

[本文引用: 1]

Zhang H G, Liu Z W.

Stability analysis for linear delayed systems via an optimally dividing delay interval approach

Automatica, 2011, 47(9): 2126-2129

[本文引用: 1]

Zhang X M, Han Q L, Seuret A, et al.

An improved reciprocally convex inequality and an augmented Lyapunov-Krasovskii functional for stability of linear systems with time-varying delay

Automatica, 2017, 84: 221-226

[本文引用: 1]

/

〈 〉

版权所有 © 《数学物理学报》杂志社
地址： 武汉市71010号信箱(430071)　电话: 027-87199206(中文版)　027-87199087(英文版)
E-mail: actams@apm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发