数学物理学报, 2024, 44(5): 1282-1300

第二类 Volterra 型积分方程的数值算法研究

代雪飞, 于一康, 牛晶,*

哈尔滨师范大学数学科学学院 哈尔滨 150025

Numerical Algorithm for Volterra Type Integral Equation of the Second Kind

Dai Xuefei, Yu Yikang, Niu Jing,*

School of Mathematical and Sciences, Harbin Normal University, Harbin 150025

通讯作者: *牛晶, E-mail: njirwin@163.com

收稿日期: 2023-08-7   修回日期: 2024-04-16  

基金资助: 国家青年自然科学基金项目(12101164)
哈尔滨师范大学硕士研究生创新科研项目(HSDSSCX2023-12)

Received: 2023-08-7   Revised: 2024-04-16  

Fund supported: Youth Fund of NSFC(12101164)
Postgraduate Innovative Scientific Research Project of Harbin Normal University(HSDSSCX2023-12)

摘要

该文将最小二乘法与再生核法相结合, 提出了求解第二类 Volterra 型积分方程的新算法. 通过构造再生核空间的多尺度正交基, 得到了模型的解的表达式. 为了减少计算量, 简化计算过程, 文章利用最小二乘法将模型转化为线性代数方程进而得到 $\varepsilon$ 近似解. 此外, 为了验证算法的严谨性, 文章详细证明了新算法的一致收敛性和稳定性, 并对误差估计进行了讨论分析. 通过算例验证了该算法的可行性和适用性, 并与一些已知的方法相比, 所得结果更精准.

关键词： 最小二乘法; 再生核空间; Volterra 积分方程

Abstract

In this paper, a new algorithm for solving the second Volterra type integral equation is proposed by combining the least square method with the reproducing kernel method. By constructing the multi-scale orthogonal basis of the reproducing kernel space, the solution expression of the model is obtained. To reduce the amount of computation and simplify the calculation process, this paper transforms the model into linear algebraic equation by using least square method and obtains the approximate solution of $\varepsilon$. In addition, to verify the rigor of the algorithm, the uniform convergence and stability of the algorithm are proved in detail, and the error estimation is discussed and analyzed. The feasibility and applicability of the proposed algorithm are verified by numerical examples. Compared with some known methods, the results obtained in this paper are more accurate.

Keywords： Least square method; Reproducing kernel space; Volterra integral equation

PDF (795KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

代雪飞, 于一康, 牛晶. 第二类 Volterra 型积分方程的数值算法研究[J]. 数学物理学报, 2024, 44(5): 1282-1300

Dai Xuefei, Yu Yikang, Niu Jing. Numerical Algorithm for Volterra Type Integral Equation of the Second Kind[J]. Acta Mathematica Scientia, 2024, 44(5): 1282-1300

1 引言

随着科技水平的提升, 我们所面临的许多实际问题也变得相对复杂, 而有些问题转化为积分方程的表达形式更容易被解决. 例如：金融数学、医学领域、化学和电化学过程[1,2]、 电磁和电动力学、流体力学、生物学以及人口问题等等[3,4]. 其中 Volterra 型方程是积分方程的一种常见形式, 这类方程常被应用在流行病学的传播、种群遗传学、天线合成问题、人口动力学、半导体器件等[5⇓⇓-8] 相关领域. 因此, 深入研究 Volterra 型积分方程, 对于解决以上实际问题具有重要意义, 例如以下第二类线性 Volterra 积分方程[5]

$\begin{equation}\label{eq:1} g(x)-\mu \int^t_af(x,t)g(t){\rm d}t=w(x),\;\;x\in[a,b], \end{equation}$

其中 $\mu$ 是实数, $w(x)\in L^{2}[a,b]$ 是已知函数, $f(x,t) \in L^{2}([a,b])^{2}$ 是内核, $g(x)$ 是待确定的未知函数.

由于此类方程对于工程中许多问题的建模非常重要, 所以解析方法和数值方法在分析此类模型并获得近似解方面发挥着重要作用[9⇓⇓⇓⇓⇓⇓-16]. Abaoub 等人[9] 用定理证明了第二类线性和非线性 Volterra 积分方程解的存在唯一性. 曾[10] 理论分析了 Volterra 积分微分方程解的稳定性. 袁[11] 等人讨论了 Lotka-Volterra 竞争模型解的存在性. Chu[12] 给出了第二类线性 Volterra 积分方程解的存在性和唯一性的证明, 通过图像展示了所提出的最优同调渐近数值技术的可靠性和准确性. Khidir[13] 介绍了一种将 Volterra 积分方程转化为易于求解的代数方程组的切比雪夫谱配点法. Bulaic[14] 提供了一个 MatLab 工具箱，其主要目的是利用 MatLab 函数来求解第二类 Volterra 积分方程. 冯[15] 等人基于 Legendre 配置方法得到 Volterra 积分方程的数值解, 并给出严格的收敛性分析. Hesameddini 和 Shahbazi[16] 提出了一种基于移位标准正交 Bernstein 多项式的求解 Volterra-Fredholm 的可靠算法, 通过实例验证了该方法比 Legendre 配置法、泰勒配置法、泰勒多项式配置法和 Lagrange 配置法四种经典算法更有效.

本文将结合最小二乘法和再生核法来解决第二类 Volterra 型积分方程问题. 最小二乘法是计算数学中最基本的算法之一, 常常用来解决实际问题. 例如: Varah[17] 用最小二乘法来求解微分方程中出现参数的数值问题, 并从化学和生物建模的问题方面来说明该方法. Wang 等人[18] 利用最小二乘法估计指数律、对数律和复合函数模型的参数, 并进行各种拟合优度检验为小型风力发电机组的精确微观选址提供了依据. Rahman 等人[19] 采用稳健最小二乘法分析了各变量的边际效应, 来估计控制腐败对汇款流入有积极影响, 政府效率和政治稳定则会影响孟加拉国的汇款流入. 最小二乘法的其他应用详见文献 [20⇓⇓⇓⇓-25]. 近年来, 再生核方法的应用也很广泛. 例如: 一般的一维界面问题[26], 非局部分数阶边值问题[27], 线性边值问题[28], 三阶三点边值问题[29], 非线性奇异边值问题[30], 分数阶 Riccati 微分方程[31], 具有周期边界条件的二阶微分方程组[32], 非线性 Hamiltonian 系统[33], 分数阶非线性微分方程[34], 一维时滞传导方程[35], Allen-Cahn 方程[36] 等相关问题都可以由再生核数值算法来求解.

本文的主要目的是在再生核空间 ${W}^m_{2}[a,b]$ 中对第二类 Volterra 型积分方程设计一个稳定的高精度数值方法. 全文一共分为五部分, 具体结构如下: 第 1 节简单介绍了 Volterra 型积分方程, 最小二乘法, 以及再生核方法的研究现状. 第 2 节构造了再生核空间的多尺度标准正交基. 第 3 节基于最小二乘法设计了一个新算法, 还讨论了该方法所得 $\varepsilon$ 近似解的一致收敛性. 第 4 节数值实验验证了本文的理论结果. 最后, 第 5 节对本论文进行总结.

2 预备知识

本节介绍了再生核空间的相关知识点, 并且构造了一组再生核空间 ${W}^m_{2}[a,b]$ 的多尺度标准正交基.

定义 2.1[37] ${W}^m_{2}[a,b]=\{g(x)|g^{(m-1)}(x) \; \mbox{在}\; [a,b] \;\mbox{上是绝对连续的实值函数}, \;g^{(m)}(x) \in L^{2}[a,b]\}$ 是具有再生核 $K(x,y)$ 的再生核空间.

其内积和范数表示为

$\left\{\begin{array}{l} \langle g, h\rangle_{W_{2}^{m}[a, b]}=\sum_{j=1}^{m-1} g^{(j)}(a) h^{(j)}(a)+\int_{a}^{b} g^{(m)} h^{(m)} \mathrm{d} x, \quad g, h \in W_{2}^{m}[a, b] \\ \|g\|_{W_{2}^{m}[a, b]}=\sqrt{\langle g, g\rangle_{W_{2}^{m}[a, b]}}. \end{array}\right.$

为了方便, 把 $\langle \cdot,\cdot\rangle_{W^m_2[a,b]}$ 和 $\left\|\cdot\right\|_{W^m_{2}[a,b]}$ 缩写为 $\langle \cdot,\cdot\rangle_m$ 和 $\left\|\cdot\right\|_m$, 定义 $K_x^m(y)$ 为 ${W}^m_{2}[a,b]$ 的再生核, 用 $(\cdot,\cdot)$ 和 $\left\|\cdot\right\|_0$ 代表在 $L^{2}[a,b]$ 上的内积和范数.

引理 2.1[37] 设 $H$ 是 Hilbert 空间, $H$ 中的元素是集合 $X$ 上的复值函数, 则下述两条命题等价

(1) $\forall x \in X$, 存在正数 $C_x$, 使得

$\begin{equation*} | g(x)| \leq C_x\|g\|,\ g\in H. \end{equation*}$

(2) $\forall x \in X$, 存在唯一的函数 $K_x(y)\in H$, 使得

$\begin{equation*} \langle g,K_x\rangle = g(x),\ g\in H. \end{equation*}$

引理 2.2 对于 $\forall g \in W^m_{2}[a,b]$, 存在一个常数 $M$, 使得

$\begin{equation*} \left\|g\right\|_{0}\leq M\left\|g\right\|_m. \end{equation*}$

下面, 我们将给出 $W^1_{2}[a,b]$ 的一个标准正交基. 令

$\begin{equation} \varphi_{s,j}=2^{\frac{s-1}{2}}\sqrt{b-a} \begin{cases} \frac{x-a}{b-a}-\frac{j}{2^{s-1}}, & x\in [\frac{j}{2^{s-1}}(b-a)+a,\frac{j+1/2}{2^{s-1}}(b-a)+a],\\[3mm] \frac{j+1}{2^{s-1}}-\frac{x-a}{b-a}, & x\in [\frac{j+1/2}{2^{s-1}}(b-a)+a,\frac{j+1}{2^{s-1}}(b-a)+a],\\ \quad 0, & \text {其他}. \end{cases} \end{equation}$

其中 $s=1,2,3,\cdots, j=0,1,\cdots,2^{s-1}-1$.

引理 2.3 $\{1,\frac{x-a}{\sqrt{b-a}},\varphi_{1,0},\varphi_{2,0},\varphi_{2,1},\cdots,\varphi_{s,0},\varphi_{s,1},\cdots,\varphi_{s,2^{s-1}-1}, \cdots\}$ 是 $W^1_{2}[a,b]$ 的一组标准正交基.

证 首先, 证明这组基在 $W^1_{2}[a,b]$ 是正交的, 由于

$\begin{equation*} \langle 1,1\rangle_1=1,\langle 1,\frac{x-a}{\sqrt{b-a}}\rangle_1=0,\langle \frac{x-a}{\sqrt{b-a}},\frac{x-a}{\sqrt{b-a}}\rangle_1=1, \end{equation*}$
$\begin{equation*} \langle 1,\varphi_{s,j}\rangle_1=\langle \frac{x-a}{\sqrt{b-a}},\varphi_{s,j}\rangle_1=0,l=1,2,3,\cdots, j=0,1,\cdots,2^{s-1}-1, \end{equation*}$

且有

$\begin{equation*} \langle \varphi_{s,i},\varphi_{n,j}\rangle_1= \begin{cases} 1,\;s=n,j=i,\\ 0,\;s\neq n,j\neq i, \end{cases} \end{equation*}$

这组基的正交性证明完毕.

下面, 证明这组基在 $W^1_{2}[a,b]$ 是完全的. 假设 $g\in W^1_{2}[a,b]$, 并且

$\begin{equation*} \langle 1,g\rangle_1=\langle \frac{x-a}{\sqrt{b-a}},g\rangle_1=0,\langle \varphi_{s,j},g\rangle_1=0,s=1,2,3,\cdots, j=0,1,\cdots,2^{s-1}-1. \end{equation*}$

只需证 $g\equiv0$ 即可, 根据 $\left\|\cdot\right\|_m$ 的定义, 得到

$\begin{equation*} \langle 1,g\rangle_1=f(0)=0, \langle g,\frac{x-a}{\sqrt{b-a}}\rangle_1=\frac{1}{\sqrt{b-a}}g(1)=0, \end{equation*}$
$\begin{equation*} \langle g,\varphi_{s,j}\rangle_1=g(\frac{j}{2^{s-1}}(b-a)+a),s=1,2,3,\cdots, j=0,1,\cdots,2^{s-1}-1. \end{equation*}$

由 $\{\frac{j}{2^{s-1}}(b-a)+a\}_{s,j}$ 在 $[a,b]$ 上的稠密性和 $g$ 的连续性, 得到 $g\equiv0$. 基的完全性得证.

定义一个积分算子 $\mathcal{P}:L^{2}[a,b] \to C[a,b]$, 对 $\forall g\in L^{2}[a,b]$, 有 $\mathcal{P}g=\int^x_ag(t){\rm d} t$. 则有如下两个引理

引理 2.4 $\{1,x-a,\frac{1}{2\sqrt{b-a}}(x-a)^{2},\mathcal{P}{\varphi_{1,0}},\mathcal{P}{\varphi_{2,0}},\mathcal{P}{\varphi_{2,1}},\cdots,\mathcal{P}{\varphi_{s,0}}, \mathcal{P}{\varphi_{s,1}},\cdots,\mathcal{P}{\varphi_{s,2^{s-1}-1}},$$\cdots\}$ 是 $W^2_{2}[a,b]$ 的一组标准正交基.

证 由于

$\begin{equation*} \langle 1,1\rangle_2=1,\langle 1,x-a\rangle_2=0,\langle x-a,x-a\rangle_2=1, \end{equation*}$
$\begin{equation*} \langle 1,\frac{1}{2\sqrt{b-a}}(x-a)^{2} \rangle_{2}=0,\langle \frac{1}{2\sqrt{b-a}}(x-a)^{2},\frac{1}{2\sqrt{b-a}}(x-a)^{2} \rangle_{2}=1, \end{equation*}$
$\begin{equation*} \langle 1,\mathcal{P}{\varphi_{s,j}}\rangle_2=\langle x-a,\mathcal{P}{\varphi_{s,j}}\rangle_2=\langle \frac{1}{2\sqrt{b-a}}(x-a)^{2},\mathcal{P}{\varphi_{s,j}}\rangle_2=0, \end{equation*}$

且有

$\begin{equation*} \langle \mathcal{P}{\varphi_{s,j}},\mathcal{P}{\varphi_{n,i}}\rangle_2= \begin{cases} 1,\;s=n,j=i,\\ 0,\;s\neq n,j\neq i. \end{cases} \end{equation*}$

则这组基的正交的.

下证这组基的完全性, 由于

$\begin{equation*} \langle x-a,g\rangle_2=\langle \frac{(x-a)^{2}}{2\sqrt{b-a}},g\rangle_2=0,\langle \mathcal{P}{\varphi_{s,j}},g\rangle_2=0,l=1,2,3,\cdots, j=0,1,\cdots,2^{s-1}-1. \end{equation*}$

使得 $g'\equiv0$, 则 $g\equiv C$ (常数). 又由于 $\langle 1,g\rangle_2=0$, 则 $g\equiv0$, 基的完全性得证.

引理 2.5 $\{1,x-a,\frac{1}{2}(x-a)^{2},\frac{1}{6\sqrt{b-a}}(x-a)^{3},\mathcal{P}^{2}{\varphi_{1,0}},\mathcal{P}^{2}{\varphi_{2,0}},\mathcal{P}^{2}{\varphi_{2,1}},\cdots, \mathcal{P}^{2}{\varphi_{s,0}},\mathcal{P}^{2}{\varphi_{s,1}},$$\cdots,\mathcal{P}^{2}{\varphi_{s,2^{s-1}-1}}, \cdots\}$ 是 $W^3_{2}[a,b]$ 的一组标准正交基.

证 首先证明基的正交性.

$\begin{equation*} \langle x-a,x-a\rangle_3=\langle \frac{1}{2}(x-a)^{2},\frac{1}{2}(x-a)^{2} \rangle_{3}=\langle \frac{1}{6\sqrt{b-a}}(x-a)^{3},\frac{1}{6\sqrt{b-a}}(x-a)^{3}\rangle_{3}=1, \end{equation*}$
$\begin{equation*} \langle x-a,\frac{1}{2}(x-a)^{2} \rangle_{3}=\langle x-a, \frac{1}{6\sqrt{b-a}}(x-a)^{3}\rangle_{3}=\langle 1,x-a\rangle_3=0, \end{equation*}$
$\begin{equation*} \langle 1,\frac{1}{2}(x-a)^{2}\rangle_{3}=\langle \frac{1}{2}(x-a)^{2},\frac{1}{6\sqrt{b-a}}(x-a)^{3}\rangle_{3}=0, \end{equation*}$

以此类推

$\begin{equation*} \langle 1,\mathcal{P}^{2}{\varphi_{s,j}}\rangle_3=\langle x-a,\mathcal{P}^{2}{\varphi_{s,j}}\rangle_3=\langle \frac{1}{2}(x-a)^{2}, \mathcal{P}^{2}{\varphi_{s,j}}\rangle_3=0, \end{equation*}$
$\begin{equation*} \langle\frac{1}{6\sqrt{b-a}}(x-a)^{3},\mathcal{P}^{2}{\varphi_{s,j}}\rangle_3=0,s=1,2,3,\cdots, j=0,1,\cdots,2^{s-1}-1, \end{equation*}$

且有

$\begin{equation*} \langle \mathcal{P}^{2}{\varphi_{s,j}},\mathcal{P}^{2}{\varphi_{n,i}}\rangle_3= \begin{cases} 1,\;s=n,j=i,\\ 0,\;s\neq n,j\neq i. \end{cases} \end{equation*}$

下证基的完全性, 设 $g(x)\in W^3_{2}[a,b]$ 满足

$\begin{equation*} \langle \frac{1}{2}(x-a)^{2},g\rangle_3=\langle \frac{1}{6\sqrt{b-a}}(x-a)^{3},g\rangle_3=0,\langle \mathcal{P}^{2}{\varphi_{s,j}},g\rangle_3=0. \end{equation*}$

由上可得 $g''\equiv0$, 则 $g'\equiv C$ (常数). 又由于 $\langle 1,g\rangle_3=\langle x-a,g\rangle_3=0$, 则 $g(x)\equiv0$. 证毕.

由此可见, 可以将上述得到的 $W^m_{2}[a,b]$ 的标准正交基简化为

$\begin{equation}\label{eq:a5} \{\psi_{j}\}^m_{j=0}\cup \{\phi_{s,0},\phi_{s,1},\cdots,\phi_{s,2^{s-1}-1}\}^\infty_{s=1}, \end{equation}$

这里

$\begin{equation*} \{\psi_{j}\}^m_{j=0}= \begin{cases} \{1,\frac{x-a}{\sqrt{b-a}}\}, & m=1,\\[3mm] \{1,x-a,\frac{1}{2\sqrt{b-a}}(x-a)^{2}\}, & m=2,\\[3mm] \{1,x-a,\frac{1}{2}(x-a)^{2},\frac{1}{6\sqrt{b-a}}(x-a)^{3}\}, & m=3,\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdots, & \;\; \; \cdots. \end{cases} \end{equation*}$

且

$\begin{equation*} \{\phi_{s,0},\phi_{s,1},\cdots,\phi_{s,2^{s-1}-1}\}^\infty_{s=1}= \begin{cases} \{\varphi_{s,0},\varphi_{s,1},\cdots,\varphi_{s,2^{s-1}-1}\}^\infty_{s=1}, & m=1,\\ \{\mathcal{P}{\varphi_{s,0}}, \mathcal{P}{\varphi_{s,1}},\cdots,\mathcal{P}{\varphi_{s,2^{s-1}-1}}\}^\infty_{s=1}, & m=2,\\ \{\mathcal{P}^{2}{\varphi_{s,0}},\mathcal{P}^{2}{\varphi_{s,1}},\cdots, \mathcal{P}^{2}{\varphi_{s,2^{s-1}-1}}\}^\infty_{s=1}, & m=3,\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdots, & \;\; \; \cdots. \end{cases} \end{equation*}$

3 算法及其收敛性分析

在这一节中, 我们针对方程 (1.1) 提出了一种基于最小二乘的新的再生核算法, 应用该算法得到了方程 (1.1) 的 $\varepsilon$ 近似解, 并且对其进行了理论分析.

3.1 算子方程

定义一个算子 $\mathcal{A}:W^m_2[a,b] \to W^{m-2}_2[a,b]$, 假设 $f(x,t) \in C^{m}([a,b])^{2}$, 则关于 (1.1) 的算子方程为

$\begin{equation*} \mathcal{A}g=g(x)-\mu \int^x_af(x,t)g(t){\rm d} t,\;\;x\in[a,b]. \end{equation*}$

引理 3.1 算子 $\mathcal{A}$ 是线性有界算子.

证 显然, 算子 $\mathcal{A}$ 是线性的.

现令

$\mathcal{A}g=g(x)+u(x),$

其中

$u(x)=-\mu \int^x_af(x,t)g(t){\rm d} t,\;\;x\in[a,b],$

有

$\begin{align*} \|\mathcal{A}g\|^2_{m} &=\sum\limits_{j=1}^{m-1}[(\mathcal{A}g)^{(i)}(a)]^{2}+\int_{a}^{b} [(\mathcal{A}g)^{(m)}]^{2}{\rm d} x \\ &=\sum\limits_{j=1}^{m-1}[g^{(i)}(a)+u^{(i)}(a)]^{2}+\int_{a}^{b}[ g^{(m)} +u^{(m)}]^{2}{\rm d} x \\ &=\sum\limits_{j=1}^{m-1}[g^{(i)}(a)]^{2}+\sum\limits_{j=1}^{m-1}[u^{(i)}(a)][u^{(i)}(a)+2g^{(i)}(a)] \\ &~~~+\int_{a}^{b}[g^{(m)}]^{2}{\rm d} x +\int_{a}^{b} u^{(m)}[u^{(m)}+2g^{(m)}]{\rm d} x. \end{align*}$

根据 $\left\|\cdot\right\|_{m}$ 的定义, 有

$ \sum\limits_{j=1}^{m-1}[g^{(j)}(a)]^{2} \leq L_{1}\|g\|^2_{m},\sum\limits_{j=1}^{m-1}[u^{(i)}(a)][u^{(i)}(a)+2g^{(i)}(a)] \leq L_{2}\|g\|^2_{m} $

和

$ \int_{a}^{b}[g^{(m)}]^{2}{\rm d} x \leq L_{3}\|g\|^2_{m},\int_{a}^{b} u^{(m)}[u^{(m)}+2g^{(m)}]{\rm d} x\leq L_{4}\|g\|^2_{m}, $

其中 $L_{1},L_{2},L_{3},L_{4}$ 为常数, 由上可知

$ \|\mathcal{A}g\|_{m} \leq L\|g\|_{m}, $

其中 $L$ 为常数, 故 $\mathcal{A}$ 是有界的. 证毕.

定义 3.1 $\forall \varepsilon >0$, $\exists v(x) \in W^{m}_2[a,b]$, 若满足不等式

$\begin{equation*} \left\|\mathcal{A}v-w\right\|_{m}^{2}\leq \varepsilon^{2}, \end{equation*}$

则称 $v(x)$ 是方程 (1.1) 的 $\varepsilon$ 近似解.

引理 3.2 设 $g(x)$ 是方程 (1.1) 的精确解, 且 $g(x)\in W^{m}_2[a,b]$, 则 $\forall \varepsilon >0$, 方程 (1.1) 存在一个 $\varepsilon$ 近似解.

证 由于 $g(x)\in W^{m}_2[a,b]$, $g(x)$ 可以被表示为

$\begin{equation*} g(x)=\sum_{i=0}^{m}p_{i}^{\star}\psi_{i}+\sum_{s=1}^{\infty}\sum_{j=0}^{2^{s-1}-1}q_{s,j}^{\star}\phi_{s,j}, \end{equation*}$

这里 $p_{i}^{\star}=\langle \psi_{i},g\rangle_{m}$, $q_{s,j}^{\star}=\langle \phi_{s,j},g\rangle_{m}$.

对 $\forall \varepsilon >0$, $\exists N$, 当 $\forall n\geq N$ 时, 有

$\begin{equation*} \left\|g-\sum_{i=0}^{m}c_{i}^{\star}\psi_{i}-\sum_{s=1}^{n}\sum_{j=0}^{2^{s-1}-1}d_{s,j}^{\star}\phi_{s,j}\right\|^{2}_m \leq \frac{1}{\left\|\mathcal{A}\right\|^{2}}\;\varepsilon^{2}, \end{equation*}$

这里 $\left\|\mathcal{A}\right\|$ 是算子 $\mathcal{A}$ 的范数.

根据上面所述, 令

$\begin{equation*} g_{n}^{\star}=\sum_{i=0}^{m}p_{i}^{\star}\psi_{i}+\sum_{s=1}^{n}\sum_{j=0}^{2^{s-1}-1}q_{s,i}^{\star}\phi_{s,j}, \end{equation*}$

有

$\begin{equation*} \left\|\mathcal{A}g_{n}^{\star}-w\right\|^{2}_m=\left\|\mathcal{A}g_{n}^{\star}-\mathcal{A}g\right\|^{2}_m \leq \left\|\mathcal{A}\right\|^{2} \left\|g_{n}^{\star}-g\right\|^{2}_m \leq \left\|\mathcal{A}\right\|^{2}\frac{1}{\left\|\mathcal{A}\right\|^{2}}\;\varepsilon^{2}=\varepsilon^{2}, \end{equation*}$

故 $g_{n}^{\star}$ 是方程 (1.1) 的一个 $\varepsilon$ 近似解. 证毕.

3.2 算法

令

$\begin{equation*} g_{n}=\sum_{i=0}^{m}p_{i}\psi_{i}+\sum_{s=1}^{n}\sum_{j=0}^{2^{s-1}-1}q_{s,j}\phi_{s,j} \end{equation*}$

是方程 (1.1) 在 $W^{m}_2[a,b]$ 中的一个 $\varepsilon$ 近似解. 定义如下实值泛函

$\begin{equation*} J(p_{0},p_{1},p_{2},\cdots,p_{m},q_{1,0},q_{2,0},q_{2,1},\cdots,q_{n,0},q_{n,1},\cdots,q_{n,2^{n-1}-1})= \left\|\mathcal{A}g_{n}-w\right\|^{2}_m, \end{equation*}$

现要找到一组系数 $p_{0}^{\ast},p_{1}^{\ast},p_{2}^{\ast},\cdots,p_{m}^{\ast},q_{1,0}^{\ast},q_{2,0}^{\ast},q_{2,1}^{\ast}, \cdots,q_{n,0}^{\ast},q_{n,1}^{\ast},\cdots, q_{n,2^{n-1}-1}^{\ast}$, 使得

$\begin{equation}\label{eq:2} \left\|\mathcal{A}g_{n}^{\ast}-w\right\|^{2}_m=\left\|\sum_{i=0}^{m}p_{i}^{\ast}\mathcal{A}\psi_{i} +\sum_{s=1}^{n}\sum_{j=0}^{2^{s-1}-1}q_{s,j}^{\ast}\mathcal{A}\phi_{s,j}-w\right\|^{2}_m=\min J, \end{equation}$

求算法 (3.1) 中的 $J$ 的最小值等同于求解下列线性方程组

$\begin{equation}\label{eq:3} \begin{cases} \langle \mathcal{A}\psi_{i},\mathcal{A}g_{n}\rangle_m=\langle \mathcal{A}\psi_{i},w\rangle_m,\;i=0,1,2,\cdots,m,\\ \langle \mathcal{A}\phi_{s,j},\mathcal{A}g_{n}\rangle_m=\langle \mathcal{A}\phi_{s,j},w\rangle_m,\;s=1,2,\cdots,n, j=0,1,2,\cdots,2^{s-1}-1. \end{cases} \end{equation}$

由 (3.2) 式可得 $p_{0}^{\ast},p_{1}^{\ast},p_{2}^{\ast},\cdots,p_{m}^{\ast},q_{1,0}^{\ast},q_{2,0}^{\ast},q_{2,1}^{\ast}, \cdots,q_{n,0}^{\ast},q_{n,1}^{\ast},\cdots,q_{n,2^{n-1}-1}^{\ast}$, 即

$\begin{equation*} J(p_{0}^{\ast},p_{1}^{\ast},p_{2}^{\ast},\cdots,p_{m}^{\ast},q_{1,0}^{\ast},q_{2,0}^{\ast},q_{2,1}^{\ast},\cdots,q_{n,0}^{\ast},q_{n,1}^{\ast},\cdots, q_{n,2^{n-1}-1}^{\ast})=\min J. \end{equation*}$

定理 3.1 由 (3.1) 式得到的近似解 $g_{n}^{\ast}(x)$ 是 $\varepsilon$ 近似解.

证 由 (3.1) 式和引理 3.2 知

$\begin{equation*} \left\|\mathcal{A}g_{n}^{\ast}-w\right\|^{2}_m \leq \left\|\mathcal{A}g_{n}^{\star}-w\right\|^{2}_m \leq \varepsilon^{2}, \end{equation*}$

这表明由 (3.1) 式得到的近似解 $g_{n}^{\ast}(x)$ 是一个 $\varepsilon$ 近似解. 证毕.

定理 3.2 设 $\mathcal{A}$ 是 $W^m_2[a,b] \to W^{m-2}_2[a,b]$ 的一个可逆算子, 那么由 (3.1) 式得到的 $\varepsilon$ 近似解是存在且唯一的, 并且具有稳定性.

证 设 (3.2) 式的系数矩阵为 $G$. 由于 $G$ 是 $Gram$ 矩阵, 对称且正定. 因为

$\begin{equation*} \{\psi_{j}\}^m_{j=0}\cup \{\phi_{s,0},\phi_{s,1}, \cdots,\phi_{s,2^{s-1}-1}\}^n_{s=1} \end{equation*}$

是 $W^m_2[a,b]$的基, 则是线性无关的,进而

$\begin{equation*} \{\mathcal{A}\psi_{j}\}^m_{j=0}\cup \{\mathcal{A}\phi_{s,0},\\\mathcal{A} \phi_{s,1},\cdots, \mathcal{A}\phi_{s,2^{s-1}-1}\}^n_{s=1} \end{equation*}$

是线性无关的, 又由算子 $\mathcal{A}$ 的可逆性, 可得 (3.1) 式具有唯一可解性.

令 $\lambda$ 是 $G$ 的一个特征值, $H=(h_{1},h_{2},\cdots,h_{N})^{T}$ 是与 $\left\|H\right\|_{0}=1$ 对应的特征向量. 则

$\begin{equation*} Gh=\lambda h. \end{equation*}$

因此有

$ \lambda h_{j}=G(j,:)H, \;\left\|H\right\|^{2}_{0}=\sum\limits_{j=1}^{N}h_{j}^{2}=1, $

使得

$\begin{align*} \lambda=\lambda\sum\limits_{j=1}^{N}h_{j}^{2} &=\left\|\mathcal{A}(\sum_{i=1}^{m}h_{i}\psi_{i}+\sum_{s=1}^{n}\sum_{j=0}^{2^{s-1}-1}h_{s,j}\phi_{s,j})\right\|^{2}_m \\ & \leq \left\|\mathcal{A}\right\|^{2} \left\|\sum_{i=1}^{m}h_{i}\psi_{i}+\sum_{s=1}^{n}\sum_{j=0}^{2^{s-1}-1}h_{s,j}\phi_{s,j}\right\|^{2}_m =\left\|\mathcal{A}\right\|^{2} \end{align*}$

可知 $\lambda >0$.

另一方面, 我们有

$\begin{align*} 1=\left\|H\right\|^{2}_{0} &=\left\|\sum_{i=1}^{m}h_{i}\psi_{i}+\sum_{s=1}^{n}\sum_{j=0}^{2^{s-1}-1}h_{i,j}\phi_{s,j}\right\|^{2}_m\\ &=\left\|\mathcal{A}^{-1}\mathcal{A}(\sum_{i=1}^{m}h_{i}\psi_{i}+\sum_{s=1}^{n}\sum_{j=0}^{2^{s-1}-1}h_{s,j}\phi_{s,j}) \right\|^{2}_m \leq \left\|\mathcal{A}^{-1}\right\|^{2} \cdot \lambda \end{align*}$

这里 $\mathcal{A}^{-1}$ 是算子 $\mathcal{A}$ 的逆.

联立上式, 可得

$\begin{equation*} \lambda\leq \left\|\mathcal{A}\right\|^{2}, \; \lambda\geq \frac{1}{\left\|\mathcal{A}^{-1}\right\|^{2}}, \end{equation*}$

则有

$\begin{equation*} 1\leq\mbox{cond}(G)=\frac{\lambda_{\max}}{\lambda_{\min}} \leq \left\|\mathcal{A}\right\|^{2}\left\|\mathcal{A}^{-1}\right\|^{2}, \end{equation*}$

则 $G$ 的条件数是一致有界的, 故稳定性得证. 证毕.

3.3 算法分析

下面我们先给出算法的收敛性分析.

定理 3.3 设 $g^{\ast}_{n}(x)$ 是由 (3.1) 式得到的 $\varepsilon$ 近似解, 则 $g^{\ast}_{n}(x)$ 在 $[a,b]$ 上一致收敛于精确解 $g(x)$.

证 根据 $K^{m}_{x}$ 的再生性, 有

$\begin{equation*} | g(x)-g_{n}^{\ast}(x)| =\langle g-g_{n}^{\ast},K_x^m\rangle_m\leq \left\|g-g_{n}^{\ast}\right\|_m \left\|K_x^m\right\|_m\leq M_{1}\left\|g-g_{n}^{\ast}\right\|_m. \end{equation*}$

又由算子 $\mathcal{A}$ 和 $\mathcal{A}^{-1}$ 是有界的, 并且 $\left\|g-g_{n}^{\star}\right\|\rightarrow 0(n\rightarrow\infty)$, 则

$\begin{align*} \left\|g-g_{n}^{\ast}\right\|_m&=\left\|\mathcal{A}^{-1}\mathcal{A}(g-g_{n}^{\ast})\right\|_m\leq \left\|\mathcal{A}^{-1}\right\| \left\|\mathcal{A}(g-g_{n}^{\star})\right\|_m\\ & \leq\left\|\mathcal{A}^{-1}\right\|\left\|\mathcal{A}\right\|\left\|g-g_{n}^{\star}\right\|_m\rightarrow 0. \end{align*}$

证毕.

接下来给出算法的误差估计.

定理 3.4 设 $g(x)\in W^m_2[a,b]$ 是方程 (1.1) 的精确解, $g^{\ast}_{n}(x)$ 是由 (3.1) 式得到的 $\varepsilon$ 近似解, 则有

$\begin{equation*} \left\|g-g^{\ast}_{n}\right\|_{m} \leq 2^{-n}M. \end{equation*}$

证 根据前面所述, 有

$\begin{align*} \left\|g-g_{n}^{\star}\right\|_m^{2}&=\left\|\sum_{s=n+1}^{\infty}\sum_{j=0}^{2^{s-1}-1}q_{s,j}^{\star}\phi_{s,j}\right\|_m^{2}= \sum_{s=n+1}^{\infty}\sum_{j=0}^{2^{s-1}-1}(q_{s,j}^{\star})^{2}\\ &= \sum_{s=n+1}^{\infty}\sum_{j=0}^{2^{s-1}-1}\bigg(\int^b_ag^{(m)}\varphi'_{s,j}{\rm d} x\bigg)^{2}, \end{align*}$

由中值定理可得

$\begin{equation*} g^{(m)}(x)=g^{(m)}(\frac{b-a}{2^{s-1}}j+a)+g^{(m+1)}(\xi)(x-\frac{b-a}{2^{s-1}}j-a), \end{equation*}$

则有

$\begin{align*} | q_{s,j}^{\star}| & \leq \bigg| \int^{\frac{b-a}{2^{s-1}}(j+1)+a}_{\frac{b-a}{2^{s-1}}j+a}g^{(m)}(\frac{b-a}{2^{s-1}}j+a)\varphi'_{s,j}{\rm d} x \bigg| \\ &~~~+\bigg| \int^{\frac{b-a}{2^{s-1}}(j+1)+a}_{\frac{b-a}{2^{s-1}}j+a}g^{(m+1)}(\xi)(x-\frac{b-a}{2^{s-1}}j-a)\varphi'_{s,j}{\rm d} x \bigg| \\ &=Q_{1}+Q_{2}. \end{align*}$

这里

$\begin{equation*} \varphi'_{s,j}=2^{\frac{s-1}{2}}\sqrt{b-a} \begin{cases} \frac{1}{b-a}, & x\in [\frac{j}{2^{s-1}}(b-a)+a,\frac{j+1/2}{2^{s-1}}(b-a)+a],\\[3mm] \frac{-1}{b-a}, & x\in [\frac{j+1/2}{2^{s-1}}(b-a)+a,\frac{j+1}{2^{s-1}}(b-a)+a],\\ \quad 0, & \text {其他}. \end{cases} \end{equation*}$

可得 $Q_{1}=0$, 并且

$\begin{equation*} Q_{2}\leq\frac{2^{\frac{s-1}{2}}}{\sqrt{b-a}}| g^{(m+1)}| _{C}\cdot \bigg| \int^{\frac{b-a}{2^{s-1}}(j+1)+a}_{\frac{b-a}{2^{s-1}}j+a}(x-\frac{b-a}{2^{s-1}}j-a){\rm d} x\bigg | \leq 2^{-\frac{3}{2}j}M_{2}. \end{equation*}$

从而有

$\begin{equation*} \left\|g-g_{n}^{\star}\right\|_m^{2}\leq \sum_{s=n+1}^{\infty}\sum_{j=0}^{2^{s-1}-1}(2^{-\frac{3}{2}j}M_{2})^{2}\leq 4^{-n}M_{3}. \end{equation*}$

进而 $\left\|g-g^{\ast}_{n}\right\|_{m} \leq 2^{-n}M.$ 证毕.

在求解第二类非线性 Volterra 积分方程时, 需将第 3 节算法和拟牛顿法相结合. 首先, 利用拟牛顿法处理非线性模型中的非线性项, 将问题转化为线性模型. 再次, 应用最小二乘法将该线性模型转化为一个线性代数方程组进行求解, 进而得到原模型的 $\varepsilon$ 近似解. 通过第 4 节的数值实验结果验证了此方案的有效性和实用性.

4 数值算例

本节为了验证所提算法的精确性和适用性, 研究以下八个数值算例 (其中线性算例 1-4, 非线性算例 5-8), 并计算得到相应的误差和不同范数意义下的数值结果. 我们有如下定义

$\begin{equation*} e=| g(x)-g^{\ast}_{n}(x)|, \;\; \overline{e}=\frac{| g(x)-g^{\ast}_{n}(x)| }{ g(x)}, \;\; \|e\|_{L^\infty}=\max_{a\leq x\leq b}|g(x)-g^{\ast}_{n}(x)| \end{equation*}$
$\begin{equation*} \|e\|_{L^2}=\bigg(\int^b_a(g(x)-g^{\ast}_{n}(x))^{2}{\rm d} x\bigg)^{\frac{1}{2}},\;\;|e|_{1,\infty}=\|e'\|_{L^\infty},\;\; |e|_{H^{1}}=\|e'\|_{L^2}, \end{equation*}$
$\begin{equation*} r=\log_{2}\frac{\|e_{n-1}\|}{\|e_{n}\|}. \end{equation*}$

算例 1[38]

$\begin{equation*} g(x)-\mu \int^x_0 f(x,t)g(t){\rm d} t=w(x),\;\ x \in[0,1]. \end{equation*}$

其中

$\mu=1, f(x,t)=x-t, w(x)=1,$

精确解 $g(x)=\cosh x$.

算例 2[39]

$\begin{equation*} g(x)-\mu \int^x_0 f(x,t) g(t){\rm d} t=w(x),\;\ x \in[0,1]. \end{equation*}$

其中 $\mu=-1,$$f(x,t)= x,$$w(x)={\rm e}^{x}-x {\rm e}^{x} +\sin x+x \cos x,$

精确解 $g(x)={\rm e}^{x}+\sin x$.

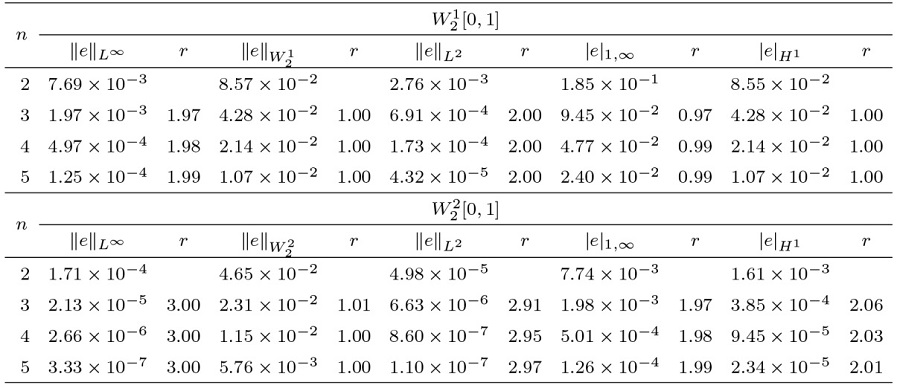
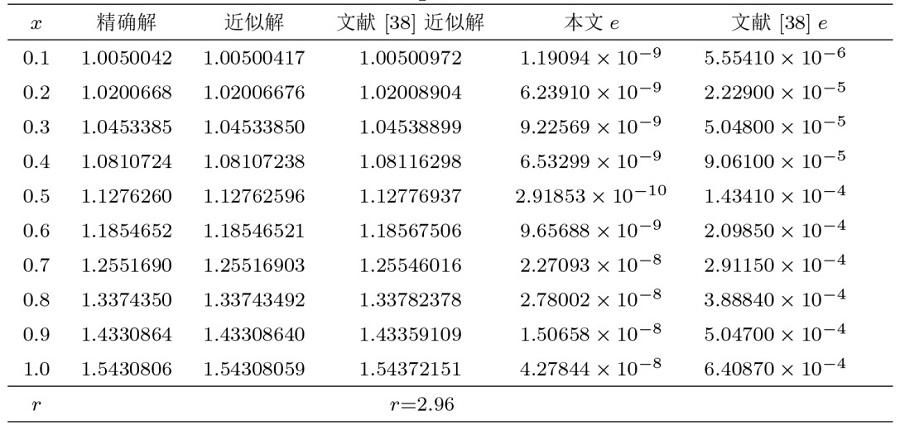
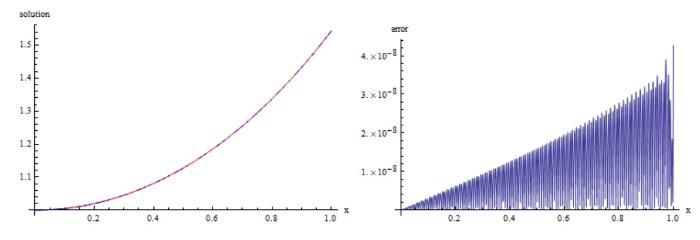
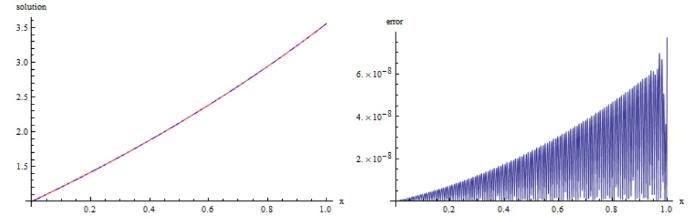
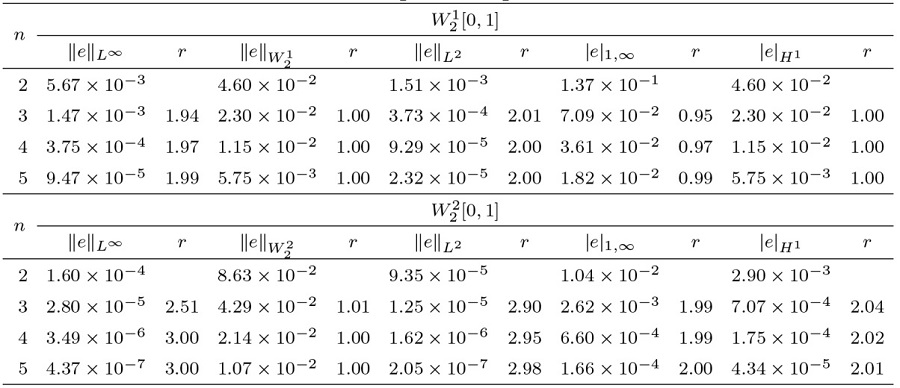
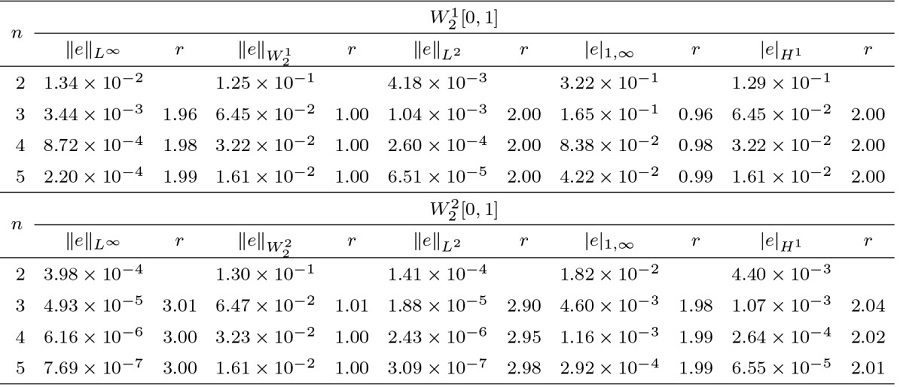
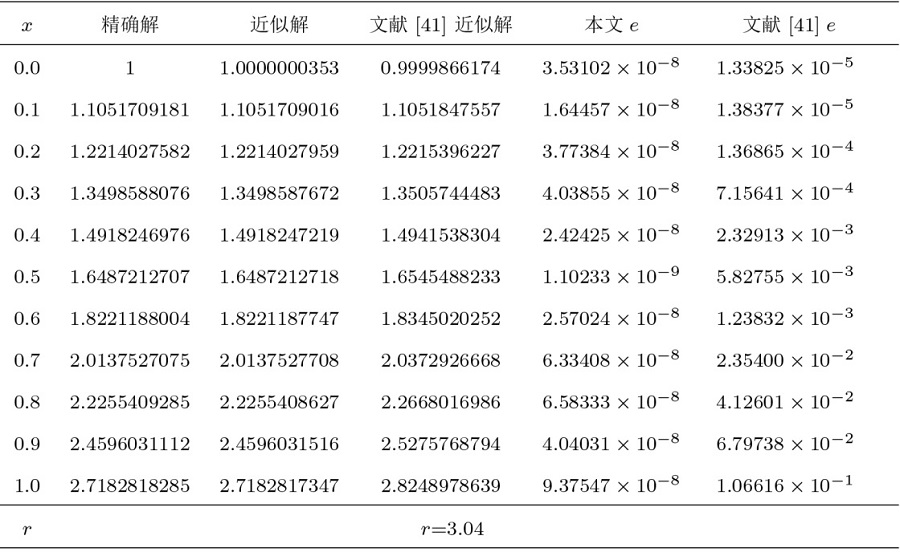
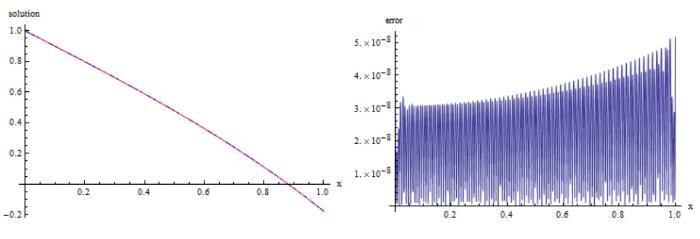
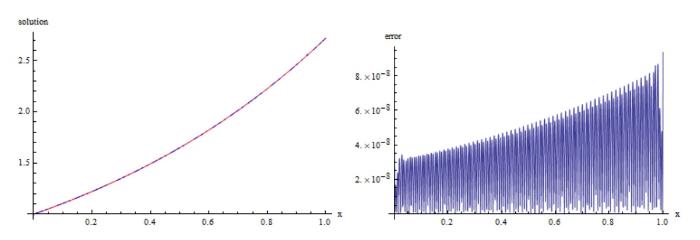
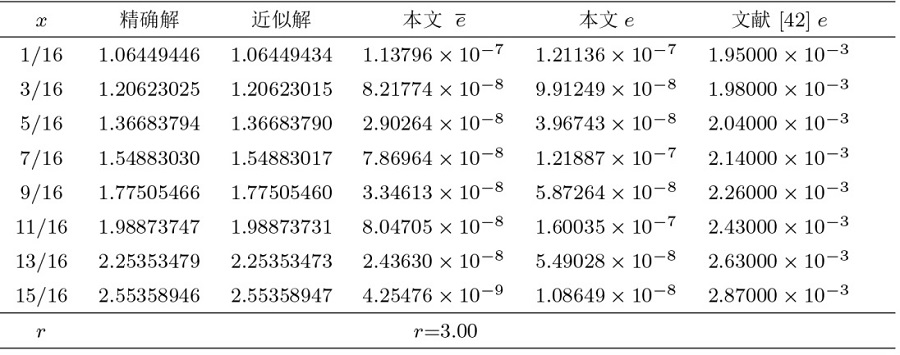
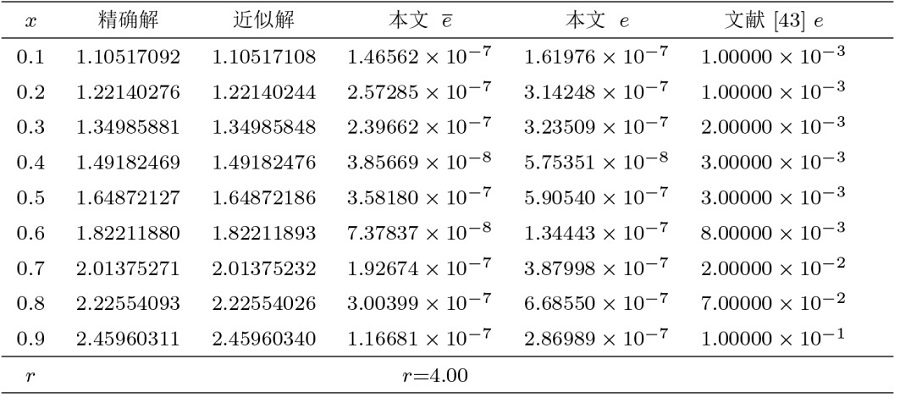
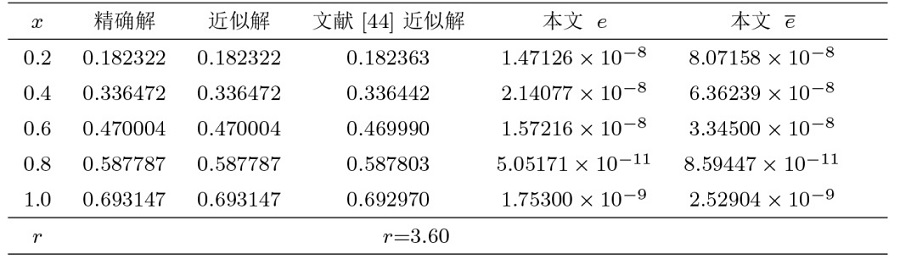
在表1、3 中, 分别给出了算例 1、2 的 $\|e\|_{L^\infty}$, $\|e\|_{W^m_2}$, $\|e\|_{L^2}$,$|e|_{1,\infty}$, $|e|_{H^{1}}$ 的收敛阶, 且 $\|e\|_{L^\infty}$ 和 $\|e\|_{L^2}$ 在同一个 $W^m_2[a,b]$ 下的收敛阶相同. 表2、4 展示了应用我们的方法得到的误差与文献 [38,39] 的方法进行比较, 数值结果表明我们的方法更接近精确解. 另外, 在图1、2 中展现了精确解和近似解及其误差.

表1   算例 1 中 ${W^1_2[0,1]}$ 和 ${W^2_2[0,1]}$ 下的数值结果

新窗口打开| 下载CSV


表2   算例 1 在 ${W^2_2[0,1]}(n=6)$ 下的数值结果

新窗口打开| 下载CSV


表3   算例 2 中 ${W^1_2[0,1]}$ 和 ${W^2_2[0,1]}$ 下的数值结果

新窗口打开| 下载CSV


表4   算例 2 在 ${W^2_2[0,1]}(n=6)$ 下的数值结果

新窗口打开| 下载CSV


图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   算例 1 左图: 红色为精确解, 蓝色为近似解; 右图: $|g(x)-g^{\ast}_{n}(x)|$


图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   算例 2 左图: 红色为精确解, 蓝色为近似解; 右图: $|g(x)-g^{\ast}_{n}(x)|$


算例 3[40]

$\begin{equation*} g(x)-\mu \int^x_0 f(x,t)g(t){\rm d} t=w(x),\;\ x \in[0,1]. \end{equation*}$

其中 $\mu=1$, $f(x,t)=x-t$, $w(x)=1-x-\frac{x^{2}}{2}$, 精确解 $g(x)=1-\sinh x$.

算例 4[41]

$\begin{equation*} g(x)- \mu \int^x_0 f(x,t)g(t){\rm d} t=w(x),\;\ x \in[0,1]. \end{equation*}$

其中 $\mu=2$,$f(x,t)=\sin (x-t)$, $w(x)=\sin x +\cos x$, 精确解 $g(x)=\sin x$.

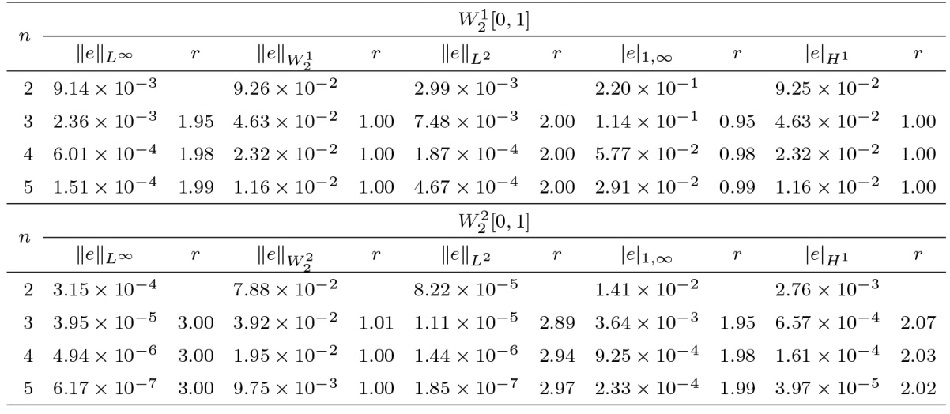
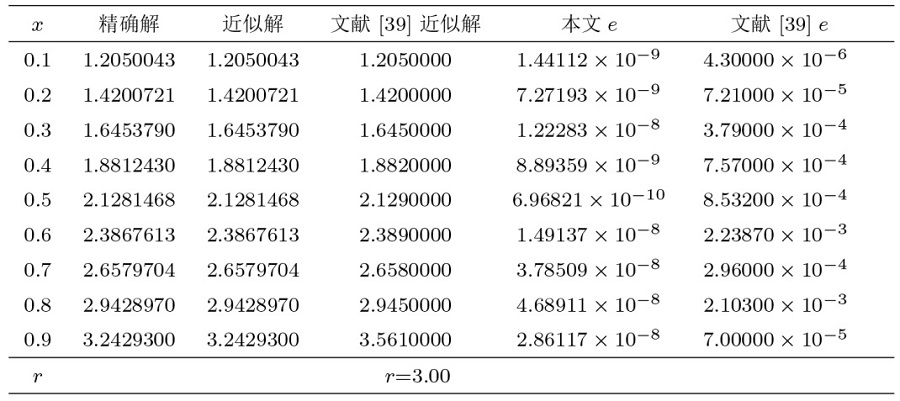
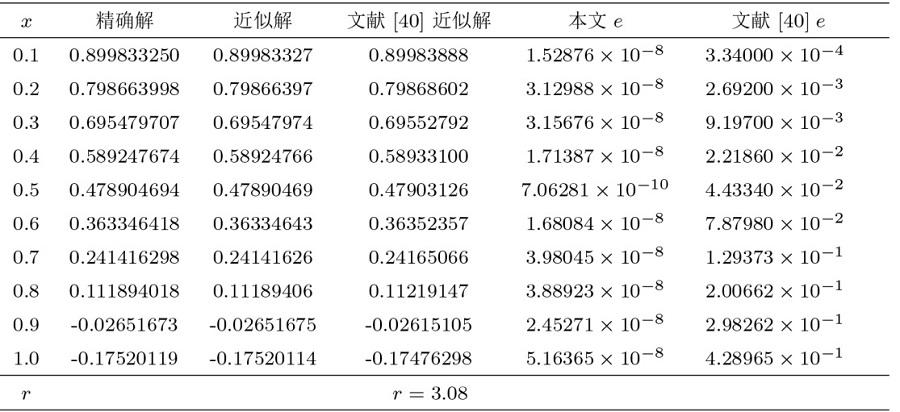
在表5、7 中, 分别展示了算例 3、4 在 $W^1_2[a,b]$ 和 $W^2_2[a,b]$ 下的 $\|e\|_{L^\infty}$ 的收敛阶仍然是 2, 3. 表6、8 表明应用我们的方法得到的结果, 并与文献 [40,41] 中方法进行比较, 数值结果验证了我们的方法更有效.

表5   算例 3 在 ${W^1_2[0,1]}$ 和 ${W^2_2[0,1]}$ 下的数值结果

新窗口打开| 下载CSV


表6   算例 3 在 ${W^2_2[0,1]}(n=6)$ 下的数值结果

新窗口打开| 下载CSV


表7   算例 4 在 ${W^1_2[0,1]}$ 和 ${W^2_2[0,1]}$ 下的数值结果

新窗口打开| 下载CSV


表8   算例 4 在 ${W^2_2[0,1]}(n=6)$ 下的数值结果

新窗口打开| 下载CSV


图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   算例 3 左图: 红色为精确解, 蓝色为近似解; 右图: $|g(x)-g^{\ast}_{n}(x)|$


图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   算例 4 左图: 红色为精确解, 蓝色为近似解; 右图: $|g(x)-g^{\ast}_{n}(x)|$


算例 5[42]

$\begin{equation*} g(x)-\mu \int^x_0 f(x,t) {g}^{2}(t){\rm d} t=w(x),\;\ x \in[0,1]. \end{equation*}$

其中 $\mu=-1$, $f(x,t)={\rm e}^{(x-t)}, w(x)={\rm e}^{2x}$, 精确解 $g(x)={\rm e}^{x}$.

算例 6[43]

$\begin{equation*} g(x)- \mu \int^x_0 {g}^{2}(t){\rm d} t=w(x),\;\ x \in[0,1]. \end{equation*}$

其中 $\mu=1$, $w(x)={\rm e}^{x}-\frac{1}{2}({\rm e}^{2x}-1)$, 精确解 $g(x)={\rm e}^{x}$.

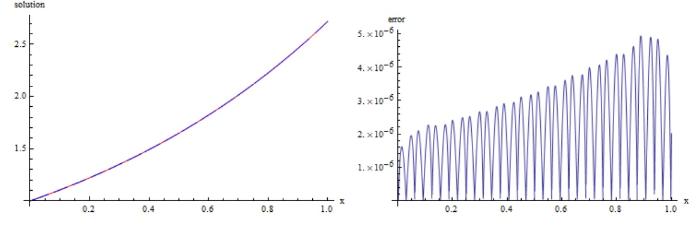
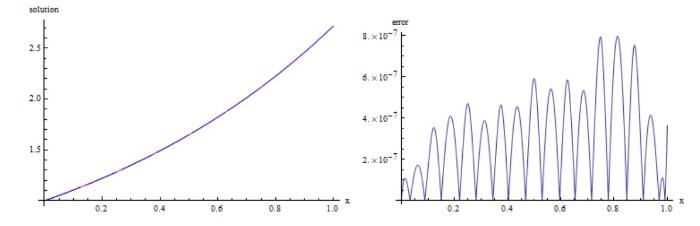
在表9、11 中, 分别展示了算例 5、6 在 $W^m_2[a,b]$ 下的数值结果. 表10、12 展示了应用我们的方法得到的误差与文献 [42,43] 中方法进行比较, 数值结果表明我们的方法更精确. 另外, 在图5、6 中展现了精确解和近似解的拟合程度.

表9   算例 5 在 ${W^m_2[0,1]}$ 下的数值结果

新窗口打开| 下载CSV


表10   算例 5 在 ${W^2_2[0,1]}(n=4)$ 下的数值结果

新窗口打开| 下载CSV


表11   算例 6 在 ${W^m_2[0,1]}$ 下的数值结果

新窗口打开| 下载CSV


表12   算例 6 在 ${W^3_2[0,1]}(n=3)$ 下的数值结果

新窗口打开| 下载CSV


图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   算例 5 左图: 红色为精确解, 蓝色为近似解; 右图: $|g(x)-g^{\ast}_{n}(x)|$


图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   算例 6 左图: 红色为精确解, 蓝色为近似解; 右图: $|g(x)-g^{\ast}_{n}(x)|$


算例 7[44]

$\begin{equation*} g(x)- \mu \int^x_0 f(x,t) {g}^{2}(t){\rm d} t=w(x),\;\ x \in[0,1]. \end{equation*}$

其中

$\mu=1, f(x,t)=x t^{2},$
$\begin{align*} w(x)&=(1+\frac{11}{9}x+\frac{2}{3}x^{2}-\frac{1}{3}x^{3}+\frac{2}{9}x^{4})\ln (x+1)\\ &~~~-\frac{1}{3}(x+x^{3})[\ln (x+1)]^{2}- \frac{11}{9}x^{2}+\frac{5}{18}x^{3}-\frac{2}{27}x^{4}, \end{align*}$

精确解 $g(x)=\ln (x+1).$

算例 8[45]

$\begin{equation*} g(x)-\mu \int^x_0 (1+{g}^{2}(t)){\rm d} t=w(x),\;\ x \in[0,1]. \end{equation*}$

其中

$\mu=-1, w(x)=\sec x + \tan x+x,$

精确解 $g(x)=\sec x$.

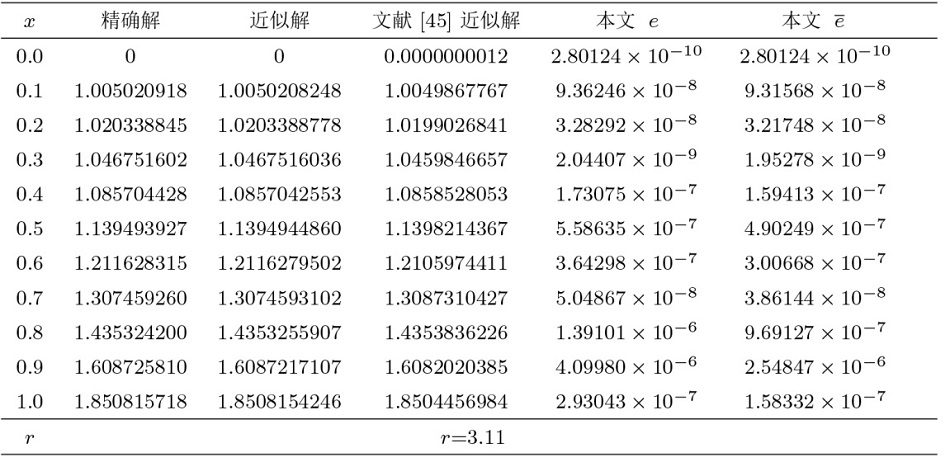
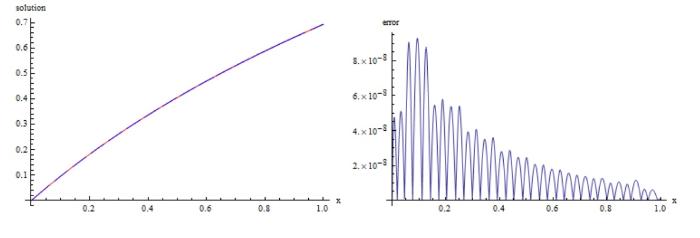
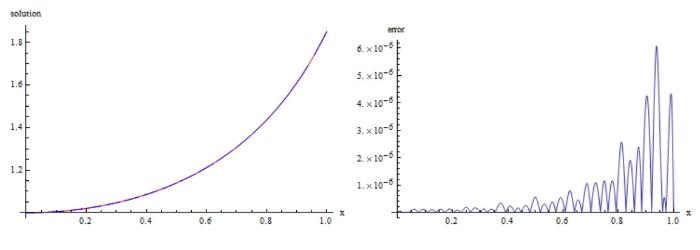
从表12、15 分别可以得到算例 7 和 8 在 $W^m_2[a,b]$ 下的数值结果. 表13、16 表明应用我们的方法得到的误差与文献 [44,45] 的方法进行比较, 数值结果验证了我们的方法是解决这类问题有效方法. 另外, 在图7、8 中展现了精确解和近似解以及相对应的误差图像.

表13   算例 7 在 ${W^m_2[0,1]}$ 下的数值结果

新窗口打开| 下载CSV


表14   算例 7 在 ${W^3_2[0,1]}(n=4)$ 下的数值结果

新窗口打开| 下载CSV


表15   算例 8 在 ${W^m_2[0,1]}$ 下的数值结果

新窗口打开| 下载CSV


表16   算例 8 在 ${W^3_2[0,1]}(n=4)$ 下的数值结果

新窗口打开| 下载CSV


图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   算例 7 左图: 红色为精确解, 蓝色为近似解; 右图: $|g(x)-g^{\ast}_{n}(x)|$


图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   算例 8 左图: 红色为精确解, 蓝色为近似解; 右图: $|g(x)-g^{\ast}_{n}(x)|$


5 结论

本文基于最小二乘法提出了一种求解第二类 Volterra 型积分方程的再生核算法, 并理论分析了此方法得到的 $\varepsilon$ 近似解的存在唯一性和稳定性. 文中还讨论了该方法的收敛阶, 并且数值结果也证明了我们的理论结果. 同时, 应用该方法和软件 Mathematica 9.0 求解了八个数值算例, 并与其他方法进行比较, 结果表明新方案在精度和计算量上都有着显著的优势, 图像和数据也都验证了该方法的有效性. 最后, 希望在已有的研究结果的支持下, 我们可以不断优化和改进算法, 将此方法进一步推广到多元或高维 Volterra 型积分问题中.

参考文献

Salon S, Chari M. Numerical Methods in Electromagnetism. Beijing: Academic Press, 1999

[本文引用: 1]

Cheng Z.

Quantum effects of thermal radiation in a Kerr nonlinear blackbody

J Opt Soc Amer B Opt Phys, 2002, 19(7): 1692-1705

DOI:10.1364/JOSAB.19.001692      URL     [本文引用: 1]

Chew W C, Tong M S, Hu B. Integral Equation Methods for Electromagnetic and Elastic Waves. Berlin: Springer Nature, 2022

[本文引用: 1]

Bloom F.

Asymptotic bounds for solutions to a system of damped integro-differential equations of electromagnetic theory

J Math Anal Appl, 1980, 73(2): 524-542

[本文引用: 1]

Wazwaz A M. Linear and Nonlinear Integral Equations. Berlin: Springer, 2011

[本文引用: 2]

Tang Q, Waxman D.

An integral equation describing an asexual population in a changing environment

Nonlinear Anal, 2003, 53(5): 683-699

[本文引用: 1]

Corduneanu C. Integral Equations and Applications. Cambridge: Cambridge University, Press, 1991

[本文引用: 1]

Schiavone P, Constanda C, Mioduchowski A. Integral Methods in Science and Engineering. Boston: Birkhäuser, 2012

[本文引用: 1]

Abaoub A E, Shkheam A S, Zali S M.

The Adomian decomposition method of Volterra integral equation of second kind

Am J Appl Math, 2018, 6(4): 142-148

[本文引用: 2]

曾志刚.

Volterra 积分微分方程的稳定性

数学物理学报, 2001, 21A(1): 48-54

[本文引用: 2]

Zeng Z G.

Stability of Volterra integro differential equations

Acta Math Sci, 2001, 21A(1): 48-54

[本文引用: 2]

袁海龙, 李艳玲.

一类具有 Lotka-Volterra 竞争模型共存解的存在性与稳定性

数学物理学报, 2017, 37A(1): 173-184

[本文引用: 2]

Yuan H L, Li Y L.

The existence and stability of coexistence solutions of a kind of Lotka-Volterra competition model

Acta Math Sci, 2017, 37A(1): 173-184

[本文引用: 2]

Chu Y M, Ullah S, Ali M, et al.

Numerical investigation of Volterra integral equations of second kind using optimal homotopy asymptotic method

Appl Math Comput, 2022, 430: 127304

[本文引用: 2]

Khidir A A.

A new numerical technique for solving Volterra integral equations using Chebyshev spectral method

Math Probl Eng, 2021, 2021: 1-11

[本文引用: 2]

Bulai I M, De Bonis M C, Laurita C, et al.

MatLab Toolbox for the numerical solution of linear Volterra integral equations arising in metastatic tumor growth models

Dolomites Research Notes on Approximation, 2022, 15(2): 13-24

[本文引用: 2]

冯立新, 杨晓旭.

解带有扰动数据的第一类 Volterra 积分方程的谱正则化方法

数学物理学报, 2020, 40A(3): 650-661

[本文引用: 2]

Feng L X, Yang X X.

Spectral regularization method for solving Volterra integral equation of the first kind with perturbed data

Acta Math Sci, 2020, 40A(3): 650-661

[本文引用: 2]

Hesameddini E, Shahbazi M.

A reliable algorithm based on the shifted orthonormal Bernstein polynomials for solving Volterra-Fredholm integral equations

Journal of Taibah University for Science, 2018, 12(4): 427-438

[本文引用: 2]

Varah J M.

A spline least squares method for numerical parameter estimation in differential equations

SIAM J Sci Comput, 1982, 3(1): 28-46

[本文引用: 1]

Wang W X, Xu Y, Han X L, Gao M L, et al.

A study of function-based wind profiles based on least squares method: A case in the suburbs of Hohho

Energy Reports, 2022, 8: 4303-4318

[本文引用: 1]

Rahman M H, Habib A.

Impact of economic and noneconomic factors on inflow of remittances into bangladesh: Application of robust least squares method

Finance and Economics Review, 2021, 3(1): 51-62

[本文引用: 1]

张晶, 余旌胡.

线性回归模型参数估计方法的分辨率

数学物理学报, 2020, 40A(5): 1381-1392

[本文引用: 1]

Zhang J, Yu J H.

Parameter resolution of estimation methods for linear regression models

Acta Math Sci, 2020, 40A(5): 1381-1392

[本文引用: 1]

马奕佳, 薛留根, 芦飞.

缺失数据下部分非线性变系数 EV 模型的统计推断

数学物理学报, 2020, 40A(2): 460-474

[本文引用: 1]

Ma Y J, Xue L g, Lu F.

Statistical inference in partially nonlinear varying-coefficient Errors-Variables models with missing responses

Acta Math Sci, 2020, 40A(2): 460-474

[本文引用: 1]

冯三营, 薛留根, 范承华.

非线性半参数回归模型中参数的经验似然置信域

数学物理学报, 2009, 29A(5): 1338-1349

[本文引用: 1]

Feng S Y, Xue L G, Fan C H.

Empirical likelihood confidence regions of the parameters in nonlinear semiparametric regression models

Acta math sci, 2009, 29A(5): 1338-1349

[本文引用: 1]

Salehi R, Dehghan M.

A generalized moving least square reproducing kernel method

J Comput Appl Math, 2013, 249: 120-132

[本文引用: 1]

Liu G, Han X, Lam K Y.

A combined genetic algorithm and nonlinear least squares method for material characterization using elastic waves

Comput Methods Appl. Mech Engrg, 2002, 191(17/18): 1909-1921

[本文引用: 1]

Fonken J M, Ramaswamy K R, Paul M J.

A scalable multi-step least squares method for network identification with unknown disturbance topology

Automatica, 2022, 141: 110295

[本文引用: 1]

Sun L X, Niu J, Hou J J.

A high order convergence collocation method based on the reproducing kernel for general interface problems

Appl Math Lett, 2021, 112: 106718

[本文引用: 1]

Geng F Z, Cui M G.

A reproducing kernel method for solving nonlocal fractional boundary value problems

Appl Math Lett, 2012, 25(5): 818-823

[本文引用: 1]

Li X Y, Wu B Y.

Error estimation for the reproducing kernel method to solve linear boundary value problems

J Comput Appl Math, 2013, 243: 10-15

[本文引用: 1]

Wu B Y, Li X Y.

Application of reproducing kernel method to third order three-point boundary value problems

Appl Math Comput, 2010, 217(7): 3425-3428

[本文引用: 1]

Niu J, Xu M Q, Lin Y Z, Xue Q.

Numerical solution of nonlinear singular boundary value problems

J Comput Appl Math, 2018, 331: 42-51

[本文引用: 1]

Xu M Q, Tohidi E, Niu J, Fang Y Z.

A new reproducing kernel-based collocation method with optimal convergence rate for some classes of BVPs

Appl Math Comput, 2022, 432: 127343

[本文引用: 1]

Al-Smadia M, Arqub O A, Shawagfeh N, Momanic S.

Numerical investigations for systems of second-order periodic boundary value problems using reproducing kernel method

Appl Math Comput, 2016, 291: 137-148

[本文引用: 1]

Niu J, Jia Y T, Sun J D.

A new piecewise reproducing kernel function algorithm for solving nonlinear Hamiltonian systems

Appl Math Lett, 2023, 136: 108451

[本文引用: 1]

Xu M Q, Niu J, Lin Y Z.

An efficient method for fractional nonlinear differential equations by quasi-Newton's method and simplified reproducing kernel method

Math Methods Appl Sci, 2018, 41(1): 5-14

[本文引用: 1]

Niu J, Sun L X, Xu M Q, Hou J J.

A reproducing kernel method for solving heat conduction equations with delay

Appl Math Lett, 2020, 100: 106036

[本文引用: 1]

Niu J, Xu M, Yao G M.

An efficient reproducing kernel method for solving the Allen-Cahn equation

Appl Math Lett, 2019, 89: 78-84

[本文引用: 1]

吴勃英, 林迎珍. 应用型再生核空间. 北京: 科学出版社, 2012

[本文引用: 2]

Wu B Y, Lin Y Z. Applied Regenerative Nuclear Space. Beijing: Science Press, 2012

[本文引用: 2]

Babolian E, Davari A.

Numerical implementation of Adomian decomposition method for linear Volterra integral equations of the second kind

Appl Math Comput, 2005, 165(1): 223-27

[本文引用: 2]

Dalal A M.

The modified decompositon method for solving Volterra integral equations of the second kind using Maple

Int J GEOMATE, 2019, 17(62): 23-28

[本文引用: 2]

Saad S, Mushtaq A K B.

Some new applications of Elzaki transform for solution of linear Volterra type integral equations

J Appl Math Phys, 2019, 7(8): 1877-1892

[本文引用: 2]

Ahmet A.

Application of the Bernstein polynomials for solving Volterra integral equations with convolution kernels

Faculty of Sciences and Mathematics, 2016, 30(4): 1045-1052

[本文引用: 2]

Singh I, Kumar S.

Haar wavelet method for some nonlinear Volterra integral equations of the first kind

J Comput Appl Math, 2016, 292: 541-552

[本文引用: 2]

Babolian E, Shahsavarani A.

Numerical solution of nonlinear Fredholm and Volterra integral equations of the second kind using Haar wavelets and collocation method

J Sci Tarbiat Moallem University, 2007, 7: 213-222

[本文引用: 2]

Mahmoudi Y.

Wavelet Galerkin method for numerical solution of nonlinear integral equation

Appl Math Comput, 2005, 167: 1119-1129

[本文引用: 2]

Ishola C Y, Taiwo O A, Adedokun K A, et al.

Solution of nonlinear Volterra integral equations by Chebyshev collocation approximation method

Pacific Journal of Science and Technology, 2022, 23(1): 34-39

[本文引用: 2]

/

〈 〉

版权所有 © 《数学物理学报》杂志社
地址： 武汉市71010号信箱(430071)　电话: 027-87199206(中文版)　027-87199087(英文版)
E-mail: actams@apm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发