1 引言
近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解.
特别地, 对于共轭问题, 引入复方程可在形式上降低问题的维数, 这允许我们在共轭的偶数阶问题中得到更加简明的计算方法与解的形式. 然而对奇数阶微分方程,引入复变量将导致实变量与复变量在方程中同时出现. 一般而言, 这很可能导致方程右端项出现实部与虚部的表示形式, 这对问题的解决产生了一定的困扰.
(1.1) $\begin{align*}\label{1} \begin{cases} \mu^2\dfrac {d^2u} {d x^2}=F(u,v,x,\mu),\\[0.2cm] \mu^2\dfrac {d^2v} {d x^2}=G(u,v,x,\mu),\quad 0<x<1,\\ u(0,\mu)=u^0,\quad v(0,\mu)=v^0,\quad u(1,\mu)=u^1,\quad v(1,\mu)=v^1, \end{cases} \end{align*}$
其中 $0<\mu\ll1$ $x_0\in(0,1)$ [19 ] 的讨论, 我们将 (1.1) 式写为实变量复方程
(1.2) $\begin{align*}\label{2} \begin{cases} \mu^2\dfrac {d^2z} {d x^2}=\Phi(z,x,\mu),\quad &0<x<1,\\ z(0,\mu)=z^0,\quad &z(1,\mu)=z^1, \end{cases} \end{align*}$
我们将在如下函数空间中寻找问题 (1.2) 的解 $z(x,\mu)$
假设 1.1 假设函数 $\Phi^{(-)}(z,x,\mu),\ \Phi^{(+)}(z,x,\mu)$
上解析, 其中 $l, \mu_0$
而$ \begin{aligned} 0=\Phi^{(+)}(z,x,0),\quad x_0\le x \le 1 \end{aligned} $
研究表明, 在假设 1.1, 1.2 下, 问题 (1.2) 在 $x=x_0$ $x=0$ $x=1$
(1.3) $\begin{align*} &\begin{cases} \dfrac {d\tilde z} {d\tau}=y,\\[0.2cm] \dfrac {d y} {d\tau}=\Phi^{(\mp)}(\tilde z,\bar x,0), \end{cases}\label{3} \end{align*}$
其中 $\bar x=x_0,0,1$ . 由于复微分方程中的自变量依然是实变量, 可类比实微分方程进行分析. 根据条件 1.2, 显然在 $y$ - $\tilde z$ $(0,\omega^{(\mp)}(x_0)),(0,\omega^{(-)}(0)),(0,\omega^{(+)}(1))$ $1^{\frac 1 2}=1$
引理 1.1 辅助系统 (1.3) 存在分别满足如下边值条件
(1.4) $\begin{align*}y^2\ &=2\int_{\omega^{(\mp)}(x_0)}^{\tilde z}\Phi^{(\mp)}(s,x_0,0)d s,\quad \bar x=x_0,\label{4}\end{align*}$
(1.5) $\begin{align*}y^2\ &=2\int_{\omega^{(-)}(0)}^{\tilde z}\Phi^{(\mp)}(s,0,0)d s,\quad \bar x=0,\label{5}\end{align*}$
(1.6) $\begin{align*}y^2\ &=2\int_{\omega^{(+)}(1)}^{\tilde z}\Phi^{(\mp)}(s,1,0)d s,\quad \bar x=1.\label{6}\end{align*}$
只要对 (1.3) 式分离变量即可得到上述首次积分.
对于首次积分 (1.4)-(1.6), 显然它对应于相平面上的分界轨道 (流形). 记
2 形式渐近解的构造
在上述条件之下, 下面我们将证明问题 (1.2) 存在具有内部层的光滑解, 并构造它在整个区间上一致有效的渐近展开式. 为此, 我们首先把原问题 (1.2) 分为子区间 $[x_0]$ $[x_0,1]$
(2.1) $\begin{align*}\label{8} \begin{cases} \mu^2\dfrac {d^2z^{(-)}} {d x^2}=\Phi^{(-)}(z^{(-)},x,\mu),\quad 0<x<x_0,\\ z^{(-)}(0,\mu)=z^0,\quad z^{(-)}(x_0,\mu)=w(\mu), \end{cases} \end{align*}$
(2.2) $\begin{align*}\label{9} \begin{cases} \mu^2\dfrac {d^2z^{(+)}} {d x^2}=\Phi^{(+)}(z^{(+)},x,\mu),\quad x_0<x<1,\\ z^{(+)}(1,\mu)=z^1,\quad z^{(+)}(x_0,\mu)=w(\mu), \end{cases} \end{align*}$
这里 $w(\mu)$ $w(\mu)$
其中 $w_k,\ k\ge 0$
假设左右问题的解 $z^{(\mp)}(x,\mu)$
(2.3) $\begin{align*}z^{(-)}(x,\mu)=\ &\bar z^{(-)}(x,\mu)+Lz(\tau_0,\mu)+Q^{(-)}z(\tau,\mu),\quad 0\le x\le x_0,\label{10}\end{align*}$
(2.4) $\begin{align*}z^{(+)}(x,\mu)=\ &\bar z^{(+)}(x,\mu)+Rz(\tau_1,\mu)+Q^{(+)}z(\tau,\mu),\quad x_0\le x\le 1,\label{11}\end{align*}$
其中 $\tau_0=\frac x \mu, \tau_1=\frac {x-1} \mu,\tau=\frac {x-x_0} \mu$
(2.5) $\begin{align*}\label{12} \bar z^{(\mp)}(x,\mu)=\bar z^{(\mp)}_0(x)+\mu\bar z^{(\mp)}_1(x)+\mu^2\bar z^{(\mp)}_2(x)+\cdots \end{align*}$
(2.6) $\begin{align*}\label{13} Q^{(\mp)}z(\tau,\mu)=Q_0^{(\mp)}z(\tau)+\mu Q_1^{(\mp)}z(\tau)+\mu^2Q_2^{(\mp)}z(\tau)+\cdots \end{align*}$
(2.7) $\begin{align*}\label{14} Lz(\tau_0,\mu)=L_0z(\tau_0)+\mu L_1z(\tau_0)+\mu^2 L_2z(\tau_0)+\cdots \end{align*}$
(2.8) $\begin{align*}\label{15} Rz(\tau_1,\mu)=R_0z(\tau_1)+\mu R_1z(\tau_1)+\mu^2 R_2z(\tau_1)+\cdots \end{align*}$
根据边界层函数法[20 ] , 可得各部分所满足的方程. 这里正则部分 $\bar z^{(\mp)}$
(2.9) $\begin{align*}\label{16} \mu^2\dfrac {d^2 \bar z^{(\mp)}} {d x^2}=\bar \Phi^{(\mp)}, \end{align*}$
内部层部分 $Q^{(\mp)}z$
(2.10) $\begin{align*}\label{17} \begin{cases} \dfrac {d^2 Q^{(\mp)}z} {d \tau^2}=\Pi^{(\mp)}\Phi,\\[3mm] Q^{(\mp)}z(0,\mu)=w(\mu)-\bar z^{(\mp)}(x_0,\mu),\quad Q^{(\mp)}z(\mp\infty,\mu)=0, \end{cases} \end{align*}$
(2.11) $\begin{align*}\label{18} \begin{cases} \dfrac {d^2 Lz} {d \tau_0^2}=L\Phi,\\[0.2cm] Lz(0,\mu)=z^0-\bar z^{(-)}(0,\mu),\quad Lz(+\infty,\mu)=0, \end{cases} \end{align*}$
(2.12) $\begin{align*}\label{19} \begin{cases} \dfrac {d^2 Rz} {d \tau_1^2}=R\Phi,\\[0.2cm] Rz(0,\mu)=z^1-\bar z^{(+)}(1,\mu),\quad Rz(-\infty,\mu)=0, \end{cases} \end{align*}$
把级数 (2.5) 代入 (2.9) 式, 将方程的右边项展开为 $\mu$
比较方程左右两边 $\mu$
确定正则部分零次项 $\bar z_0$
(2.13) $\begin{align*}\label{20} \Phi^{(\mp)}(\bar z_0(x),x,0)=0. \end{align*}$
方程 (2.13) 就是退化方程, 由假设 1.2, 它有解
确定 $k$ $\bar z^{(\mp)}_k,\ k\ge 1$
(2.14) $\begin{align*}\label{21} \Phi^{(\mp)}_z(\bar z^{(\mp)}_0(x),x,0)\bar z^{(\mp)}_k=\bar\varphi_k^{(\mp)}(x), \end{align*}$
其中 $\bar\varphi_k^{(\mp)}$ $\bar z^{(\mp)}_j(x),\ j\le k-1$
下面计算内部层的各阶项 $Q^{(\mp)}_k(\tau),\ k\ge 0$ . 将 (2.6) 式代入 (2.10) 式, 可得确定内部层零阶项 $Q^{(\mp)}_0z$
(2.15) $\begin{align*}\label{22} \begin{cases} \dfrac {d^2Q^{(\mp)}_0z} {d\tau^2}=\Phi^{(\mp)}(\bar z^{(\mp)}_0(x_0)+Q^{(\mp)}_0z(\tau),x_0,0),\\[3mm] Q^{(\mp)}_0z(0)=w_0-\bar z_0(x_0),\quad Q_0^{(\mp)}z(\mp\infty)=0, \end{cases} \end{align*}$
作变量替换并将正则部分零次项 $\bar z_0^{(\mp)}(x)=\omega^{(\mp)}(x)$
(2.16) $\begin{align*}\label{23} \Omega^{(\mp)}:\hat z^{(\mp)}=\left(2\int_{\omega^{(\mp)}(x_0)}^{\tilde z^{(\mp)}} \Phi^{(\mp)}(s,x_0,0)d s\right)^{\frac 1 2}. \end{align*} $
假设 2.1 假设 $w_0$ $z=w_0$ $\Omega^{(\mp)}$
根据假设 2.1, (2.15) 式的解存在, 记为 $Q_0^{(\mp)}z(\tau)$ . 由假设 1.2, 它满足指数估计
确定 $Q^{(\mp)}_1z(\tau)$
(2.17) $\begin{align*}\label{24} \begin{cases} \dfrac {d^2Q_1^{(\mp)}z} {d\tau^2}=\Phi^{(\mp)}_z(\bar z^{(\mp)}_0(x_0)+Q^{(\mp)}_0z(\tau),x_0,0)Q_1^{(\mp)}z(\tau)+h^{(\mp)}_1(\tau),\\[0.3cm] Q_1^{(\mp)}z(0)=w_1-\bar z^{(\mp)}_1(x_0),\quad Q_1^{(\mp)}z(\mp\infty)=0, \end{cases} \end{align*}$
是依赖于 $\bar z^{(\mp)}_0,\bar z^{(\mp)}_1,Q_0^{(\mp)}z$
(2.18) $\begin{align*}\label{25} Q^{(\mp)}_1z(\tau)=Q^{(\mp)}_1z(0)\dfrac {\hat z^{(\mp)}(\tau)} {\hat z^{(\mp)}(0)}+\hat z^{(\mp)}(\tau)\int_0^\tau(\hat z^{(\mp)})^{-2}(s)\int_{\mp\infty}^s\hat z^{(\mp)}(r)h_1^{(\mp)}(r)d r\!\!d s. \end{align*}$
根据假设 1.2 以及 (2.18) 式, 不失一般性, 可得指数估计式
确定内部层 $k$ $Q^{(\mp)}_kz(\tau),\ k\ge 1$
(2.19) $\begin{align*}\label{27} \begin{cases} \dfrac {d^2Q_k^{(\mp)}z} {d\tau^2}=\Phi^{(\mp)}_z(\bar z^{(\mp)}_0(x_0)+Q_0^{(\mp)}z(\tau),x_0,0)Q_k^{(\mp)}z(\tau)+h^{(\mp)}_k(\tau),\\[0.3cm] Q_k^{(\mp)}z(0)=w_k-\bar z^{(\mp)}_k(x_0),\quad Q_k^{(\mp)}z(\mp\infty)=0. \end{cases} \end{align*}$
其中 $h^{(\mp)}_k(\tau)$ $\bar z^{(\mp)}_j,\ j\le k,\ Q^{(\mp)}_lz,\ l\le k-1$
(2.20) $\begin{align*}\label{28} Q^{(\mp)}_kz(\tau)=Q^{(\mp)}_kz(0)\dfrac {\hat z^{(\mp)}(\tau)} {\hat z^{(\mp)}(0)}+\hat z^{(\mp)}(\tau)\int_0^\tau(\hat z^{(\mp)})^{-2}(s)\int_{\mp\infty}^s\hat z^{(\mp)}(r)h_k^{(\mp)}(r)d r\!\!d s. \end{align*}$
左边界层与右边界层所满足的问题 (2.11), (2.12) 与内部层满足的问题 (2.10) 类似, 可按上述方法类似解得 (2.7), (2.8) 式中的各阶项 $L_kz(\tau_0),R_kz(\tau_1),\ k\ge 0$ $L_0z,R_0z$
到此为止, 我们已构造出 (2.5)-(2.8) 式中的各阶项, 但仍有参数 $w_k$
(2.21) $\begin{align*} \mu\dfrac {d z^{(-)}(x_0,\mu)} {d x}=\mu\dfrac {d z^{(+)}(x_0,\mu)} {d x} \end{align*}$
将上式展开为 $\mu$ $\mu$
(2.22) $\begin{align*}\label{30} \dfrac d {d\tau} Q_0^{(-)}z(0)-\dfrac d {d\tau} Q_0^{(+)}z(0)=0. \end{align*}$
将 (2.16) 式代入 (2.22) 式, 由 $\frac d {d\tau} Q_0^{(\mp)}z=\hat z^{(\mp)}$
(2.23) $\begin{align*} \left(2\int_{\omega^{(-)}(x_0)}^{w_0}\Phi^{(-)}(z,x_0,0)d z\right)^{\frac 1 2}-\left(2\int_{\omega^{(+)}(x_0)}^{w_0}\Phi^{(+)}(z,x_0,0)d z\right)^{\frac 1 2}=0. \end{align*}$
(2.24) $\begin{align*} H(w)=\left(2\int_{\omega^{(-)}(x_0)}^w\Phi^{(-)}(z,x_0,0)d z\right)^{\frac 1 2}-\left(2\int_{\omega^{(+)}(x_0)}^w\Phi^{(+)}(z,x_0,0)d z\right)^{\frac 1 2}. \end{align*}$
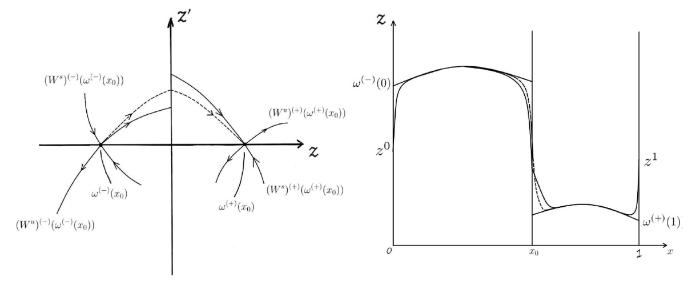
也就是 $(W^u)^{(-)}(\omega^{(-)}(x_0))\cap (W^s)^{(+)}(\omega^{(+)}(x_0))\ne\varnothing$ .
图1
图1
相平面示意图与解示意图. 所构造的解不但需要是连续的 (实线), 也是光滑的 (虚线).
(2.25) $\begin{align*}\label{31} \dfrac d {d x} \bar z_{k-1}^{(-)}(x_0)-\dfrac d {d x} \bar z_{k-1}^{(+)}(x_0)+\dfrac d {d\tau} Q_k^{(-)}z(0)-\dfrac d {d\tau} Q_k^{(+)}z(0)=0. \end{align*}$
将 (2.20) 式代入 (2.25) 式, 得到
整理可得缝接点 $w(\mu)$ $k$ $w_k$
(2.26) $\begin{align*} w_k=\ &\left(\dfrac {d H(w_0)} {d w}\right)^{-1}\left(\left(z_{k-1}^{(+)}\right)'(x_0)-\left(z_{k-1}^{(-)}\right)'(x_0)\right)\\ &+\left(\dfrac {d H(w_0)} {d w}\right)^{-1}\left(z^{(-)}\right)^{-1}(0)\bigg(\Phi^{(+)}(w_0,x_0)\bar z_k^{(+)}(0)-\Phi^{(-)}(w_0,x_0)\bar z_k^{(-)}(0)\\ & +\int_{+\infty}^0\hat z^{(+)}(r)h_k^{(+)}(r)d r-\int_{-\infty}^0\hat z^{(-)}(r)h_k^{(-)}(r)d r\bigg). \end{align*}$
到此为止, 我们已经完全确定了 (2.5)-(2.8) 式以及 $w(\mu)$
(2.27) $\begin{align*}\label{34} Z_n=\begin{cases} Z^{(-)}_n=\displaystyle\sum_{k=0}^n\mu^k\left(\bar z^{(-)}_k(x)+L_kz\left(\dfrac x \mu\right)+Q^{(-)}_kz\left(\dfrac {x-x_0} \mu\right)\right), &0\le x \le x_0,\\[0.4cm] Z^{(+)}_n=\displaystyle\sum_{k=0}^n\mu^k\left(\bar z^{(+)}_k(x)+R_kz\left(\dfrac {x-1} \mu\right)+Q^{(+)}_kz\left(\dfrac {x-x_0} \mu\right)\right),& x_0<x\le 1. \end{cases} \end{align*}$
3 解的存在性与余项估计
我们已经得到了问题 (1.2) 的形式渐近解 (2.27) 式, 但光滑解的存在性仍待证明. 为此, 我们回到原问题 (1.1) 和 (1.2) 与左右问题, 对函数 $z$ $x_0$
(3.1) $\begin{align*}\label{35} \begin{cases} \mu^2\dfrac {d^2z^{(-)}} {d x^2}=\Phi^{(-)}(z^{(-)},x,\mu),\quad 0<x<x_0,\\ z^{(-)}(0,\mu)=z^0,\quad z^{(-)}(x_0,\mu)=\bar w(\mu), \end{cases} \end{align*}$
(3.2) $\begin{align*}\label{36} \begin{cases} \mu^2\dfrac {d^2z^{(+)}} {d x^2}=\Phi^{(+)}(z^{(+)},x,\mu),\quad x_0<x<1,\\ z^{(+)}(1,\mu)=z^1,\quad z^{(+)}(x_0,\mu)=\bar w(\mu), \end{cases} \end{align*}$
需要特别指出的是, 这里 $w_k,\ 0\le k\le n+1$ $\delta$ $\delta$ $x_0$
(3.3) $\begin{align*}\label{37} \mu\dfrac d {d x}z^{(-)}(x_0,\mu)-\mu\dfrac d {d x}z^{(+)}(x_0,\mu)=0. \end{align*}$
注意到问题 (3.1), (3.2) 所对应的实问题的解都是存在的, 故对于固定的 $\delta$ [20 ]
(3.4) $\begin{equation}\label{38} \begin{aligned} \begin{cases} z^{(-)}(x,\mu)=\bar Z^{(-)}_{n+1}+O(\mu^{n+2}),\quad 0\le x \le x_0,\\ z^{(+)}(x,\mu)=\bar Z^{(+)}_{n+1}+O(\mu^{n+2}),\quad x_0\le x \le 1, \end{cases} \end{aligned} \end{equation}$
特别地, 这里的 $\bar Q_{n+1}^{(\mp)}z(\tau)$ $n$ $Q_{n+1}^{(\mp)}z(\tau)$ $Q_{n+1}^{(\mp)}z(0)=w_{n+1}-z_{n+1}^{(\mp)}(x_0)$ $Q_{n+1}^{(\mp)}z(0)=w_{n+1}+\delta-z_{n+1}^{(\mp)}(x_0)$
(3.5) $\begin{align*} \begin{cases} \dfrac d {d\tau}Q_0^{(-)}z(0)-\dfrac d {d\tau}Q_0^{(+)}z(0)=0,\\[0.3cm] \mu\dfrac d {d x}\bar z_{k-1}^{(-)}(x_0)-\mu\dfrac d {d x}\bar z_{k-1}^{(+)}(x_0)+\dfrac d {d\tau}Q_k^{(-)}z(0)-\dfrac d {d\tau}Q_k^{(+)}z(0)=0,\quad 1\le k\le n, \end{cases} \end{align*}$
(3.6) $\begin{align*} 0=\ &\mu\dfrac d {d x}z^{(-)}(x_0,\mu)-\mu\dfrac d {d x}z^{(+)}(x_0,\mu)\nonumber\\ =\ &\mu^{n+1}(\mu\dfrac d {d x}\bar z_{k-1}^{(-)}(x_0)-\mu\dfrac d {d x}\bar z_{k-1}^{(+)}(x_0)+\dfrac d {d\tau}\bar Q_k^{(-)}z(0)-\dfrac d {d\tau}\bar Q_k^{(+)}z(0))+O(\mu^{n+2})\nonumber\\ =\ &\mu^{n+1}\left(\dfrac {(\hat z^{(-)})'(0)-(\hat z^{(+)})'(0)} {\hat z^{(-)}(0)}\delta+O(\mu)\right).\label{41} \end{align*}$
与二阶的情况不同, (3.6) 式是复数形式, 往下将它写为实数形式进行讨论. 记
(3.7) $\begin{equation}\label{42} \begin{cases} ap-bq+O(\mu)=0,\\ aq+bp+O(\mu)=0. \end{cases} \end{equation}$
由于 $(\hat z^{(\mp)})'(0)=\frac {d^2 Q_0^{(\mp)}z(0)} {d\tau^2}=\Phi^{(\mp)}(w_0,x_0,0)$ $a+b{\rm i}\ne 0$
(3.8) $\begin{align*}\label{43} \begin{cases} p+O_1(\mu)=0,\\ q+O_2(\mu)=0, \end{cases} \end{align*}$
且 (3.8) 式中的 $O_{1,2}(\mu)$ $p,q$ $\mu$
在 $\mu$ $p,q$ $D>0$
下面仅讨论 $T_1(p,q,\mu)$ $p$ $L<\frac 1 \mu$ $-D\le q\le D$ $p+\mu T_1(p,q,\mu)$ $p$ $p=p^*(q)$ . 将它代入 $q+O_2(\mu)=0$ $q$
施介值定理, 得到该方程的解 $q=q^*$ . 最终, 我们解得 (3.8) 式的解为
(3.9) $\begin{align*} \begin{cases} p=p^*(q^*)=p^*,\\ q=q^*. \end{cases} \end{align*}$
故存在 $\delta=\delta^*=p^*+iq^*$ $x_0$
定理 3.1 如果问题 (1.2) 满足假设 1.1-3.1, 则它存在光滑解 $z(x,\mu)$
(3.10) $\begin{align*} z(x,\mu)=\begin{cases} \displaystyle\sum_{k=0}^n\mu^k\left(\bar z_i^{(-)}(x)+L_kz(\tau_0)+Q_k^{(-)}z(\tau)\right)+O\left(\mu^{n+1}\right),\quad 0\le x\le x_0,\\[4mm] \displaystyle\sum_{k=0}^n\mu^k\left(\bar z_i^{(+)}(x)+R_kz(\tau_1)+Q_k^{(+)}z(\tau)\right)+O\left(\mu^{n+1}\right),\quad x_0< x\le 1. \end{cases} \end{align*}$
至此, 我们证明了问题 (1.1), (1.2) 具有内部层的光滑解的存在性, 并给出了余项估计. 下面将以一个简单的例子加以验证.
4 算例
(4.1) $\begin{align*}\label{44} \begin{cases} \mu^2\dfrac {d^2u} {d x^2}=F(u,v,x,\mu),\\[0.2cm] \mu^2\dfrac {d^2v} {d x^2}=G(u,v,x,\mu),\quad 0<x<1,\\ u(0,\mu)=1,\quad v(0,\mu)=1,\quad u(1,\mu)=-1,\quad v(1,\mu)=-1, \end{cases} \end{align*}$
不难得到退化方程的解为 $\omega^{(-)}(x)=1+{\rm i},\ \omega^{(+)}(x)=-1-{\rm i}$ . 易得正则部分的解
(4.2) $\begin{align*} \begin{cases} \dfrac {d^2 Q^{(\mp)}z} {d\tau^2}=\Phi^{(\mp)}(\bar z^{(\mp)}+Q^{(\mp)}z(\tau),x_0+\tau\mu,\mu)-\Phi^{(\mp)}(\bar z^{(\mp)}(x_0+\tau\mu),x_0+\tau\mu,\mu),\\[2mm] Q^{(\mp)}z(0,\mu)=w-\omega^{(\mp)}(x_0),\quad Q^{(\mp)}z(\mp\infty,\mu)=0. \end{cases} \end{align*}$
(4.3) $\begin{align*} \Phi^{(-)}(z,x_0,0)=(1+{\rm i})z=\Phi^{(+)}(z,x_0,0),\quad x_0=\frac 1 2. \end{align*}$
(4.4) $\begin{align*} \int_{1+i}^{w_0}(1+{\rm i})zd z=\int_{-1-i}^{w_0}(1+{\rm i})zd z. \end{align*}$
取两个合适的积分路径, 解得 $w_0=p_0+iq_0=0$ . 故内部层的零次项满足方程
(4.5) $\begin{align*} \begin{cases} \dfrac {d^2 Q^{(\mp)}_0z} {d\tau^2}=(1+{\rm i})Q^{(\mp)}_0z,\\[3mm] Q_0^{(\mp)}z(0)=\mp(1+{\rm i}),\quad Q^{(\mp)}_0z(\mp\infty)=0. \end{cases} \end{align*}$
(4.6) $\begin{align*}Q_0^{(-)}z=\ &-(1+{\rm i})\exp\left(2^{\frac 1 4}\tau\cos\dfrac \pi 8\right)\left(\cos\left(2^{\frac 1 4}\tau\sin\dfrac \pi 8\right)+{\rm i}\tau\sin\left(2^{\frac 1 4}\tau\sin\dfrac \pi 8\right)\right),\end{align*}$
(4.7) $\begin{align*}Q_0^{(+)}z=\ &(1+{\rm i})\exp\left(-2^{\frac 1 4}\tau\cos\dfrac \pi 8\right)\left(\cos\left(2^{\frac 1 4}\tau\sin\dfrac \pi 8\right)-{\rm i}\tau\sin\left(2^{\frac 1 4}\tau\sin\dfrac \pi 8\right)\right).\end{align*}$
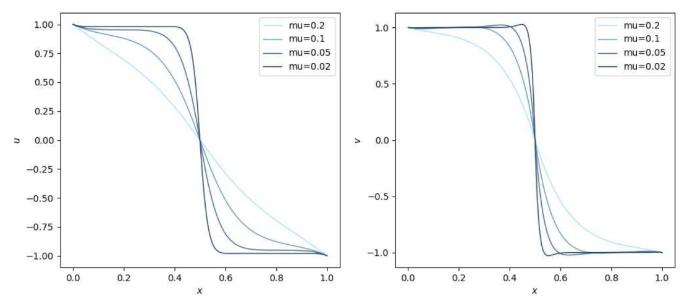
图2
图2
$\mu$
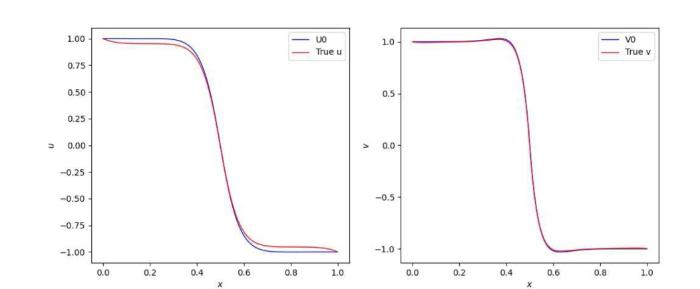
图3
图3
$\mu=0.05$
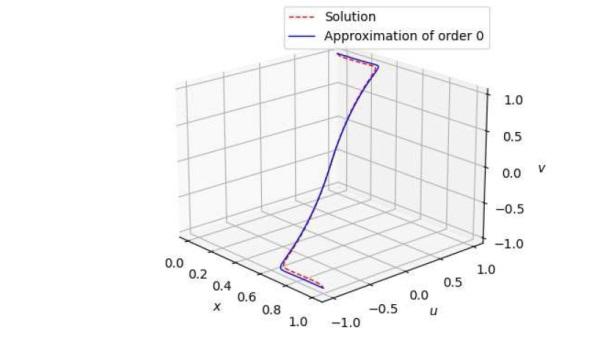
图4
图4
$\mu=0.05$
参考文献
View Option
[1]
Filippov A F Differential equations with discontinuous right-hand side
Matematicheskii Sbornik , 1960 , 93 1 ): 99 -128
[本文引用: 1]
[2]
Afsharnezhad Z Amaleh M K Continuation of the periodic orbits for the differential equation with discontinuous right hand side
Journal of Dynamics and Differential Equations , 2011 , 23 71 -92
[本文引用: 1]
[3]
Ni M Pang Y Levashova N T et al . Internal layers for a singularly perturbed second-order quasilinear differential equation with discontinuous right-hand side
Differential Equations , 2017 , 53 1567 -1577
[本文引用: 1]
[4]
Boykov I Roudnev V Boykova A Stability of solutions to systems of nonlinear differential equations with discontinuous right-hand sides: Applications to hopfield artificial neural networks
Mathematics , 2022 , 10 9 ): 1524
[本文引用: 1]
[5]
李迅 , 陶龙 . 右端不连续免疫对非线性出生率和医院容纳的影响
通化师范学院学报 , 2022 , 43 10 ): 31 -39
[本文引用: 1]
Li X Tao L Effects of right-end discontinuous treatment on nonliear birth rate and hospital capacity models
Journal of Tonghua Normal University , 2022 , 43 10 ): 31 -39
[本文引用: 1]
[6]
李子卉 . 几类不连续生物数学模型解渐近性质的研究 . 杭州 : 浙江工业大学 , 2020
[本文引用: 1]
Li Z H Asymptotic Properties of Discontinuous Biological Mathematical Models . Hangzhou : Zhejiang University of Technology , 2020
[本文引用: 1]
[7]
黄玉娇 . 具有广义分段线性激活函数的递归神经网络的多稳定性分析 . 沈阳 : 东北大学 , 2014
[本文引用: 1]
Huang Y J Multistability Analysis of Recurrent Neural Networks with Generalized Piecewise Linear Activation Functions . Shenyang : Northeastern University , 2014
[本文引用: 1]
[8]
Alvarez J Orlov I Acho L An invariance principle for discontinuous dynamic systems with application to a coulomb friction oscillator
J Dyn Sys Meas Control , 2000 , 122 4 ): 687 -690
[本文引用: 1]
[9]
Aase K K Continuous trading in an exchange economy under discontinuous dynamics: A resolution of the equity premium puzzle
Scandinavian Journal of Management , 1993 , 9 S3 -S28
[本文引用: 1]
[10]
倪明康 , 潘亚飞 , 吴潇 . 右端不连续奇异摄动问题的空间对照结构
上海大学学报 (自然科学版) , 2020 , 26 6 ): 853 -883
[本文引用: 1]
Ni M K Pan Y F Wu X Spatial contrast structure for singular perturbation problems with right end discontinuities
Journal of Shanghai University (Natural Science Edition) , 2020 , 26 6 ): 853 -883
[本文引用: 1]
[11]
Butuzov V F Simakov R E Asymptotics of the solution of a singularly perturbed system of equations with a multizone internal layer
Differential Equations , 2021 , 57 4 ): 415 -445
[本文引用: 1]
[12]
杨倩 . 具有重根的右端不连续奇摄动系统的渐近分析 . 上海 : 华东师范大学 , 2022
[本文引用: 1]
Yang Q Asymptotic Studies on Piecewise-Smooth Singularly Perturbed Dynamical Systems with Multiple Roots of the Degenerate Equations . Shanghai : East China Normal University , 2022
[本文引用: 1]
[13]
齐旭天 . 若干右端不连续奇摄动问题研究 . 上海 : 华东师范大学 , 2019
[本文引用: 1]
Qi X T On the Study of Some Discontinuous Singularly Perturbed Problems . Shanghai : East China Normal University , 2019
[本文引用: 1]
[14]
Vasily S 若干右端不连续奇摄动问题的研究 . 上海 : 华东师范大学 , 2018
[本文引用: 1]
Vasily S Investigation of Some Singularly Perturbed Problems with Discontinuous Right-side . Shanghai : East China Normal University , 2018
[本文引用: 1]
[15]
Rao S C S Chawla S Interior layers in coupled system of two singularly perturbed reaction-diffusion equations with discontinuous source term//Numerical Analysis and Its Applications: 5th International Conference, NAA 2012, Lozenetz, Bulgaria, June 15-20, 2012, Revised Selected Papers 5. Berlin Heidelberg: Springer , 2013 : 445 -453
[本文引用: 1]
[16]
Aleksei L 倪明康 , 杨倩 . 一类右端不连续的奇异摄动拟线性 Robin 边值问题的内部层解 (英文)
吉林大学学报 (理学版) , 2021 , 59 3 ): 451 -459
[本文引用: 1]
Aleksei L Ni M K Yang Q Solutions of internal layers for a class of singularly perturbed quasilinear robin boundary value problems with discontinuous right-hand side
Journal of Jilin University (Science Edition) , 2021 , 59 3 ): 451 -459
[本文引用: 1]
[17]
胡永生 . 一类四阶常微分方程两点边值问题的奇摄动
淮阴师范学院学报 (自然科学版) , 2022 , 21 2 ): 115 -120
[本文引用: 1]
Hu Y S A class of singularly perturbed two-point boundary values problem for fourth-order ordinary differential equation
Journal of Huaiyin Normal University (Science Edition) , 2022 , 21 2 ): 115 -120
[本文引用: 1]
[18]
Vasil'eva A B Butuzov V F Nefedov N N Singularly perturbed problems with boundary and internal layers
Proceedings of the Steklov Institute of Mathematics , 2010 , 268 1 ): 258 -273
[本文引用: 1]
[19]
倪明康 , 林武忠 . 奇异摄动问题中的渐近理论 . 北京 : 高等教育出版社 , 2009
[本文引用: 2]
Ni M K Lin W Z Asymptotic Theory in Singular Perturbation Problems . Beijing : Higher Education Press , 2009
[本文引用: 2]
[20]
Vasil'eva A B Butuzov V F Asymptotic Expansions of Solutions of Singularly Perturbed Equations (in Russian) . Moscow : Nauka , 1973
[本文引用: 3]
Differential equations with discontinuous right-hand side
1
1960
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
Continuation of the periodic orbits for the differential equation with discontinuous right hand side
1
2011
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
Internal layers for a singularly perturbed second-order quasilinear differential equation with discontinuous right-hand side
1
2017
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
Stability of solutions to systems of nonlinear differential equations with discontinuous right-hand sides: Applications to hopfield artificial neural networks
1
2022
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
右端不连续免疫对非线性出生率和医院容纳的影响
1
2022
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
右端不连续免疫对非线性出生率和医院容纳的影响
1
2022
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
1
2020
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
1
2020
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
1
2014
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
1
2014
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
An invariance principle for discontinuous dynamic systems with application to a coulomb friction oscillator
1
2000
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
Continuous trading in an exchange economy under discontinuous dynamics: A resolution of the equity premium puzzle
1
1993
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
右端不连续奇异摄动问题的空间对照结构
1
2020
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
右端不连续奇异摄动问题的空间对照结构
1
2020
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
Asymptotics of the solution of a singularly perturbed system of equations with a multizone internal layer
1
2021
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
1
2022
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
1
2022
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
1
2019
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
1
2019
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
1
2018
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
1
2018
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
1
2013
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
一类右端不连续的奇异摄动拟线性 Robin 边值问题的内部层解 (英文)
1
2021
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
一类右端不连续的奇异摄动拟线性 Robin 边值问题的内部层解 (英文)
1
2021
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
一类四阶常微分方程两点边值问题的奇摄动
1
2022
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
一类四阶常微分方程两点边值问题的奇摄动
1
2022
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
Singularly perturbed problems with boundary and internal layers
1
2010
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
2
2009
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
... 其中 $0<\mu\ll1$ $x_0\in(0,1)$ [19 ] 的讨论, 我们将 (1.1) 式写为实变量复方程 ...
2
2009
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
... 其中 $0<\mu\ll1$ $x_0\in(0,1)$ [19 ] 的讨论, 我们将 (1.1) 式写为实变量复方程 ...
3
1973
... 近年来, 对于右端不连续微分动力系统的研究已有很多的工作[1 ⇓ -3 ] , 这类系统在人工智能, 生物学, 机械工程, 经济学, 电磁学, 量子力学等领域有着广泛的应用[4 ⇓ ⇓ ⇓ ⇓ -9 ] . 与此同时, 针对右端不连续的奇摄动系统也已经有了不少的研究[10 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -18 ] . 但是, 多数的研究停留在二阶与三阶奇摄动方程上, 对更高阶方程的研究并不多见. 其原因在于高维动力系统在间断面上的动力学行为更加复杂, 特别是在求具有内层的光滑解时, 空间解的光滑缝接比平面上的困难的多. 在文献 [19 ] 中, 前苏联数学家 Vasil'eva 曾用复变量方法对一类四阶连续型空间对照结构进行了讨论. 本文将把复方法推广到一类右端不连续四阶奇摄动方程, 并通过边界层函数法与解的光滑缝接[20 ] 来给出其高精度的近似解. ...
... 根据边界层函数法[20 ] , 可得各部分所满足的方程. 这里正则部分 $\bar z^{(\mp)}$
... 注意到问题 (3.1), (3.2) 所对应的实问题的解都是存在的, 故对于固定的 $\delta$ [20 ] ...