一类三量子比特 X 态的几何量子失协

一类三量子比特 X 态的几何量子失协

卫佳宁^,¹, 段周波^,¹^,^*, 张钧^,¹^,²

¹太原理工大学数学学院太原 030024

²太原理工大学计算机科学与技术学院 (大数据学院) 太原 030024

Geometric Discord for a Class of Three-Qubit X States

Wei Jianing^,¹, Duan Zhoubo^,¹^,^*, Zhang Jun^,¹^,²

¹School of Mathematics, Taiyuan University of Technology, Taiyuan 030024

²College of Computer Science and Technology (College of Data Science), Taiyuan University of Technology, Taiyuan 030024

通讯作者: *段周波, E-mail: duanzhoubo@163.com

收稿日期: 2022-10-26 修回日期: 2024-04-29

基金资助:

国家自然科学基金(11771011)
山西省自然科学基金(201801D221032)
山西省自然科学基金(202303021211068)
山西省回国留学人员科研资助项目(2023-081)

Received: 2022-10-26 Revised: 2024-04-29

Fund supported:

National Natural Science Foundation of China(11771011)
Natural Science Foundation of Shanxi Province(201801D221032)
Natural Science Foundation of Shanxi Province(202303021211068)
Shanxi Scholarship Council of China(2023-081)

作者简介 About authors

卫佳宁,E-mail:weijianing21@163.com;

张钧,E-mail:zhang6347@163.com

摘要

基于 [Phys Rev Lett, 124, 110401 (2020)] 中提出的多体量子失协的定义, 该文通过测量诱导给出了依赖于四个实参数的一类三量子比特 X 态的几何量子失协解析表达式, 并给出了该类态几何量子失协的等高图. 作为应用, 该文研究了相位翻转信道下三量子比特 X 态几何量子失协的动力学行为.

关键词： 几何量子失协; 三量子比特 X 态; 相位翻转信道

Abstract

Based on the definition of multipartite quantum discord proposed in [Phys Rev Lett, 124, 110401(2020)], we give the analytic expression for the multipartite geometric quantum discord of one type of three-qubit X states which depend on four real parameters by measurement induction. And we present the level surfaces of the class of three-qubit X states. As an application, we investigate the dynamic behavior of multipartite geometric quantum discord for the three-qubit X states under the phase flip channel.

Keywords： Geometric quantum discord; Three-qubit X states; Phase flip channel

PDF (1607KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

卫佳宁, 段周波, 张钧. 一类三量子比特 X 态的几何量子失协[J]. 数学物理学报, 2024, 44(5): 1143-1151

Wei Jianing, Duan Zhoubo, Zhang Jun. Geometric Discord for a Class of Three-Qubit X States[J]. Acta Mathematica Scientia, 2024, 44(5): 1143-1151

1 引言

在量子信息的研究中, 纠缠是一种重要的物理资源, 是区分量子世界和经典世界的一种量子关联. 然而纠缠仅仅是量子关联的一个子集, 在量子信息处理过程中, 许多没有纠缠的量子态仍然可以表现出独特的量子特性. Ollivier, Zurek^[1]以及 Henderson, Vedral^[2]提出了区别于纠缠的量子关联—量子失协. 在量子任务中有极其重要的作用, 特别是在量子通信和计算任务中实现了量子优势^[3,4]. 最近, 量子失协得到了广泛的研究, 如量子关联的量化、量子失协的动力学行为以及其他量子特性等^{[5⇓⇓⇓⇓⇓⇓-12]}.

对于两体系统, 量子失协被定义为两个经典等效互信息表达式在量子世界中的最小差异^[13,14]. 两体量子态 $\rho_{AB}$ 的互信息(总关联) $I(\rho_{AB})=S(\rho_{A})+S(\rho_{B})-S(\rho_{AB})$ , 其中 $S(\rho)=-\mathrm{Tr}\rho\log_{2}\rho$ , 且 $\rho_{A(B)}=\mathrm{Tr}_{B(A)}\rho_{AB}$ . 若对子系统 $A$ 进行局部 Von Neumann 测量 $\{\Pi^{A}_{j}\}$ , 则测后量子态为 $\Pi^{A}(\rho_{AB})=\sum_{i}(\Pi^{A}_{i}\otimes \mathrm{I}_{B})\rho_{AB}(\Pi^{A}_{i}\otimes \mathrm{I}_{B})$ . 量子态 $\Pi^{A}(\rho_{AB})$ 的最大总关联(经典关联)定义为 $C(\rho_{AB})=\max_{\Pi^{A}}I(\Pi^{A}(\rho_{AB}))$ . 这样, 两体态 $\rho_{AB}$ 的量子失协表示为 $D_{A; B}(\rho)=I(\rho_{AB})-C(\rho_{AB})$ . 两体量子态量子失协得到了广泛研究. 最近, Radhakrishnan 等人^[15] 提出了多体量子失协. 多体量子失协问题激发了人们广泛的兴趣, 但由于优化过程复杂, 只能对一类特殊的态进行研究. 为此, Zhu 等人^[16] 基于两体量子几何失协度量提出了多体几何量子失协度量, 给出了一类含有三个实参变量的 X 态的几何量子失协.

在此基础上, 本文研究一类含有四个实参的三量子比特 X 态几何量子失协给出其解析表达式, 进一步研究在相位翻转信道下该类态几何量子失协的动力学行为.

2 预备知识

本节给出多体量子和几何失协的定义. 此外, 陈述一类三量子比特 X 态在条件测量下几何失协的结果.

Radhakrishnan 等人基于信息论提出多体量子失协. 这种方法的主要特征之一就是使用了条件测量, 其中每个连续的测量都与先前测量有条件地相关. 对于希尔伯特空间 $H=H_{A_{1}}\otimes H_{A_{2}}\otimes \cdots \otimes H_{A_{N}}$ 的量子态 $\rho$ , 我们进行 $N-1$ 次局部投影测量, 其中每个测量都取决于之前的测量结果. 设前 $k-1$ 次局部投影测量算子为

$\Pi^{({k-1})}_{j_{1}\cdots j_{k-1}}=\Pi^{A_{1}\cdots A_{k-1}}_{j_{1}\cdots j_{k-1}}=\Pi^{A_{1}}_{j_{1}}\otimes\Pi^{A_{2}}_{j_{2}|j_{1}}\otimes \cdots\otimes\Pi^{A_{k-1}}_{j_{k-1}|j_{1}\cdots j_{k-2}}\otimes \mathrm{I}_{A_kA_{k+1}\cdots A_N},$

其中,

$\sum_{j_1=1}^{d_1}\Pi^{A_{1}}_{j_{1}}=\mathrm{I}_{A_1}, \sum_{j_2=1}^{d_2}\Pi^{A_{2}}_{j_{2}|j_{1}}=\mathrm{I}_{A_2}(1\le j_1\le d_1),\cdots,$ $\sum_{j_{k-1}=1}^{d_{k-1}}\Pi^{A_{k-1}}_{j_{k-1}|j_{1}\cdots j_{k-2}}=\mathrm{I}_{A_{k-1}} (1\le j_{s}\le d_s(s=1,2,\cdots,{k-1})).$

记

$\begin{equation}\label{PM} \Pi^{A_{1}\ldots A_{k-1}}=\left\{\Pi^{A_{1}\cdots A_{k-1}}_{j_{1}\cdots j_{k-1}}:1\le j_{s}\le d_s(s=1,2,\cdots,{k-1})\right\}, \Pi=\Pi^{A_{1}\ldots A_{N-1}}.\end{equation}$

(2.1)

定义 $N$ 体量子态 $\rho$ 的多体量子失协为

$\begin{eqnarray*}\label{eq:1.1} D_{A_{1}; A_{2}; \cdots; A_{N}}(\rho) &=&\min_{\Pi^{A_{1}\cdots A_{k-1}}(1\le k\le N)}\Big[-S_{A_{2}\cdots A_{N}|A_{1}}(\rho)+S_{A_{2}|\Pi^{A_{1}}}(\rho)\nonumber\\ &&+S_{A_{3}|\Pi^{A_{1} A_{2}}}(\rho)+\cdots+S_{A_{N}|\Pi^{A_{1}\ldots A_{N-1}}}(\rho)\Big], \end{eqnarray*}$

(2.2)

其中 $S_{A_{2}\ldots A_{N}|A_{1}}(\rho)=S(\rho)-S(\rho_{A_{1}})$ , 且

$S_{A_{k}|\Pi^{A_{1}\cdots A_{k-1}}}(\rho)=\sum_{j_{1}\cdots j_{k-1}}p^{(k-1)}_{j_{1}\cdots j_{k-1}}S_{A_{1}\cdots A_{k}}\left(\Pi^{(k-1)}_{j_{1}\cdots j_{k-1}}\rho \Pi^{(k-1)}_{j_{1}\cdots j_{k-1}}/p^{(k-1)}_{j_{1}\cdots j_{k-1}}\right),$

$p^{(k-1)}_{j_{1}\cdots j_{k-1}}=\mathrm{Tr}\left(\Pi^{(k-1)}_{j_{1}\cdots j_{k-1}}\rho \Pi^{(k-1)}_{j_{1}\cdots j_{k-1}}\right).$

用符号 $D(H)$ 表示系统 $H$ 上所有量子态的集合, $\Omega$ 表示系统 $H$ 上所有零失协量子态的集合, 即

$\Omega=\left\{\chi\in D(H): D_{A_{1}; A_{2}; \cdots; A_{N}}(\chi)=0\right\}.$

设量子态 $\rho$ 经过投影测量方程 (2.1) 后得到的量子态为 $\Pi(\rho)$ , 则

$\Pi(\rho)=\sum_{j_1=1}^{d_1} \sum_{j_2=1}^{d_2} \cdots\sum_{j_{N-1}=1}^{d_{N-1}}P_{j_1j_2\cdots j_{N-1}}\rho P_{j_1j_2\cdots j_{N-1}},$

其中

$P_{j_1j_2\cdots j_{N-1}}=\Pi^{A_{1}}_{j_{1}}\otimes\Pi^{A_{2}}_{j_{2}|j_{1}}\otimes\cdots \otimes\Pi^{A_{N-1}}_{j_{N-1}|j_{1}\cdots j_{N-2}}\otimes \mathrm{I}_{A_N}.$

易见, 对任意的 $\rho\in D(H)$ , 有 $\Pi^2(\rho)=\Pi(\rho)$ , 且后测量态 $\Pi(\rho)$ 为零失协量子态. 反之, 任意零失协量子态 $\chi$ 都是某个量子态 $\rho$ 经过测量方程 (2.1) 后得到的量子态即为 $\chi=\Pi(\rho)$ . 因此

$\Omega=\left\{\Pi(\rho)\in D(H): \Pi^{A_{1}\cdots A_{k-1}}(1\le k\le N)\right\}.$

定义 2.1 几何量子失协定义为已知量子态 $\rho$ 和所有零失协态的集合之间最短的“距离”, 即

$\begin{equation}\label{eq:2.1} D_{G}^{(N)}(\rho)=\min_{\chi\in\Omega}\|\rho-\chi\|^{2} =\min_{\Pi^{A_{1}\cdots A_{k-1}}(1\le k\le N)}\|\rho-\Pi(\rho)\|^{2}, \end{equation}$

(2.3)

其中, $\|T\|=\sqrt{\mathrm{Tr}[(T^{\dagger}T)]}$ 为算子 $T$ 的希尔伯特—施密特范数.

希尔伯特空间 $H=H_{A}\otimes H_{B}\otimes H_{C}=\mathbb{C}^{2}\otimes \mathbb{C}^{2}\otimes \mathbb{C}^{2}$ 中一类含有四个实参 $s,c_{1},c_{2},c_{3}$ 的三量子比特 X 态 $\rho$ 表示为

$\begin{equation}\label{eq:www} \rho=\frac{1}{8}\bigg(\mathrm{I}+s\mathrm{I}\otimes \sigma_{3}\otimes \mathrm{I}+\sum^{3}_{i=1}c_{i}\sigma_{i}\otimes\sigma_{i}\otimes\sigma_{i}\bigg). \end{equation}$

(2.4)

其中 $\mathrm{I}$ 是单位算子, $\{{\sigma}_{i}\}^{3}_{i=1}$ 是 Pauli 矩阵. 为了计算该类态的几何量子失协 $D_{G}^{(3)}$ (2.3) 式, 需计算 $\|\rho\|^{2}$ , $-2\mathrm{Tr}(\rho \chi)$ , $\|\chi\|^{2}$ . 由定义可得

$\begin{equation}\label{eq:2.4} \|\rho\|^{2}=\mathrm{Tr}(\rho^{2})=\frac{1}{8}\left(1+c^{2}_{1}+c^{2}_{2}+c^{2}_{3}-s^{2}\right). \end{equation}$

(2.5)

对 $A$ 系统进行测量, 测量算子为 $A_{j}=V_{A}\Pi_{j}V^{\dagger}_{A},(j=0,1)$ , 其中 $\Pi_{0}=|0\rangle\langle 0|,\Pi_{1}=|1\rangle\langle 1|$ , 且 $V_{A}=t_{A}\mathrm{I}+i\vec{y}_{A}\cdot\vec{\sigma}$ 是酉算子, $t_{A}\in\mathbb{R}$ , $\vec{y}_{A}=(y_{A_1},y_{A_2},y_{A_3})\in\mathbb{R}^{3}$ , $\vec{\sigma}=(\sigma_{1},\sigma_{2},\sigma_{3})$ , $t^{2}_{A}+y_{A_1}^{2}+y_{A_2}^{2}+y_{A_3}^{2}=1$ . 若对子系统 $A$ 进行测量 $\{A_{j}\}^{1}_{j=0}$ , 则测后的量子态 $\tilde{\rho}=\sum_{i=0,1} p_{i}\rho_{i}$ , 其概率分布为 $p_{0}=p_{1}=\frac{1}{2}$ 以及对应的量子态

$\begin{align*} \rho_{0}&=\frac{1}{4}\left(V_{A}\Pi_{0}V^{\dagger}_{A}\right)\otimes\bigg(\mathrm{I}+\sum^{3}_{i=1}c_{i}z_{i}\sigma_{i}\otimes\sigma_{i}+s\sigma_{3}\otimes \mathrm{I}\bigg),\label{eq:A0} \end{align*}$

(2.6)

$\begin{align*} \rho_{1}&=\frac{1}{4}\left(V_{A}\Pi_{1}V^{\dagger}_{A}\right)\otimes\bigg(\mathrm{I}-\sum^{3}_{i=1}c_{i}z_{i}\sigma_{i}\otimes\sigma_{i}+s\sigma_{3}\otimes \mathrm{I}\bigg),\label{eq:A1} \end{align*}$

(2.7)

其中

$z_{1}=2(-t_{A}y_{A_2}+y_{A_1}y_{A_3}),$

(2.8)

$z_{2}=2(t_{A}y_{A_1}+y_{A_2}y_{A_3}),$

(2.9)

$z_{3}=t^{2}_{A}-y_{A_1}^{2}-y_{A_2}^{2}+y_{A_3}^{2}.$

(2.10)

显然 $z_{1}^{2}+z_{2}^{2}+z_{3}^{2}=1$ , 接下来根据子系统 $A$ 的测量结果考虑子系统 $B$ . 采用相同的方法, 子系统 $B$ 上的测量为 $\{{B_{k}^{j}=V_{B^{j}}\Pi_{k}V^{\dagger}_{B^{j}}: k=0,1}\} (j=0,1)$ , $V_{B^{j}}=t_{B^{j}}I+i\vec{y}_{B^{j}}\cdot\vec{\sigma}$ , $t_{B^{j}}\in\mathbb{R}$ , $\vec{y}_{B^{j}}=(y_{B^{j}_1},y_{B^{j}_2},y_{B^{j}_3})\in\mathbb{R}^{3}$ 且 $t^{2}_{B^{j}}+y_{B^{j}_1}^{2}+y_{B^{j}_2}^{2}+y_{B^{j}_3}^{2}=1$ . 子系统 $B$ 上的测量 $\{B_{k}^{j}\}$ 取决于子系统 $A$ 上的测量结果, 若子系统 $A$ 上的测量结果为 $0$ , 我们将对 $\rho_{0}$ 在子系统 $B$ 上进行测量 $\{B^{0}_{0},B^{0}_{1}\}$ , 则

$\begin{align*}&\rho_{00}=\frac{1}{2(1+sl_{3})}V_{A}\Pi_{0}V^{\dagger}_{A}\otimes V_{B^{0}}\Pi_{0}V^{\dagger}_{B^{0}}\otimes\bigg(\mathrm{I}+\sum^{3}_{i=1}c_{i}z_{i}l_{i}\sigma_{i}+sl_{3}\mathrm{I}\bigg),\end{align*}$

(2.11)

$\begin{align*}&\rho_{01}=\frac{1}{2(1-sl_{3})}V_{A}\Pi_{0}V^{\dagger}_{A}\otimes V_{B^{0}}\Pi_{1}V^{\dagger}_{B^{0}}\otimes\bigg(\mathrm{I}-\sum^{3}_{i=1}c_{i}z_{i}l_{i}\sigma_{i}-sl_{3}\mathrm{I}\bigg), \end{align*}$

(2.12)

与之对应的概率分布 $p_{00}=\frac{1+sl_{3}}{4}$ , $p_{01}=\frac{1-sl_{3}}{4}$ , 其中

$l_{1}=2(-t_{B^{0}}y_{B^{0}_2}+y_{B^{0}_1}y_{B^{0}_3}),$

(2.13)

$l_{2}=2(t_{B^{0}}y_{B^{0}_1}+y_{B^{0}_2}y_{B^{0}_3}),$

(2.14)

$l_{3}=t^{2}_{B^{0}}-y_{B^{0}_1}^{2}-y_{B^{0}_2}^{2}+y_{B^{0}_3}^{2}.$

(2.15)

若子系统 A 上的测量结果为 $1$ , 我们将对 $\rho_{1}$ 在子系统 $B$ 上进行测量 $\{{B^{1}_{0}},{B^{1}_{1}}\}$ , 则

$\begin{align*} &\rho_{10}=\frac{1}{2(1+sm_{3})}V_{A}\Pi_{1}V^{\dagger}_{A}\otimes V_{B^{1}}\Pi_{0}V^{\dagger}_{B^{1}}\otimes\bigg(\mathrm{I}-\sum^{3}_{i=1}c_{i}z_{i}m_{i}\sigma_{i}+sm_{3}\mathrm{I}\bigg),\end{align*}$

(2.16)

$\begin{align*} &\rho_{11}=\frac{1}{2(1-sm_{3})}V_{A}\Pi_{1}V^{\dagger}_{A}\otimes V_{B^{1}}\Pi_{1}V^{\dagger}_{B^{1}}\otimes\bigg(\mathrm{I}+\sum^{3}_{i=1}c_{i}z_{i}m_{i}\sigma_{i}-sm_{3}\mathrm{I}\bigg) \end{align*}$

(2.17)

与之对应的概率分布为 $p_{10}=\frac{1+sm_{3}}{4}$ , $p_{11}=\frac{1-sm_{3}}{4}$ , 其中

$m_{1}=2\left(-t_{B^{1}}y_{B^{1}_2}+y_{B^{1}_1}y_{B^{1}_3}\right)$

(2.18)

$m_{2}=2\left(t_{B^{1}}y_{B^{1}_1}+y_{B^{1}_2}y_{B^{1}_3}\right),$

(2.19)

$m_{3}=t^{2}_{B^{1}}-y_{B^{1}_1}^{2}-y_{B^{1}_2}^{2}+y_{B^{1}_3}^{2}.$

(2.20)

显然 $l_{1}^{2}+l_{2}^{2}+l_{3}^{2}=1$ , $m_{1}^{2}+m_{2}^{2}+m_{3}^{2}=1$ , 并且我们得到态

$\chi=\Pi(\rho)=p_{00}\rho_{00}+p_{01}\rho_{01}+p_{10}\rho_{10}+p_{11}\rho_{11}.$

那么

$\begin{equation} -2\mathrm{Tr}(\rho\chi)=-\frac{1}{4}\left[1+\frac{1}{2}\left(\sum^{3}_{i=1}c_{i}^{2}z_{i}^{2}l_{i}^{2} +\sum^{3}_{i=1}c_{i}^{2}z_{i}^{2}m_{i}^{2}+s^{2}l_{3}^{2}+s^{2}m_{3}^{2}\right)\right]. \end{equation}$

(2.21)

设 $q$ 为经过 $AB$ 系统测量之后 $C$ 系统的量子态, 则

$q_{00}=(1+sl_{3})\mathrm{I}+c_{1}z_{1}l_{1}\sigma_{1}+c_{2}z_{2}l_{2}\sigma_{2}+c_{3}z_{3}l_{3}\sigma_{3},$

(2.22)

$q_{01}=(1-sl_{3})\mathrm{I}-c_{1}z_{1}l_{1}\sigma_{1}-c_{2}z_{2}l_{2}\sigma_{2}-c_{3}z_{3}l_{3}\sigma_{3},$

(2.23)

$q_{10}=(1+sm_{3})\mathrm{I}-c_{1}z_{1}m_{1}\sigma_{1}-c_{2}z_{2}m_{2}\sigma_{2}-c_{3}z_{3}m_{3}\sigma_{3},$

(2.24)

$q_{11}=(1-sm_{3})\mathrm{I}+c_{1}z_{1}m_{1}\sigma_{1}+c_{2}z_{2}m_{2}\sigma_{2}+c_{3}z_{3}m_{3}\sigma_{3}.$

(2.25)

可知

$\mathrm{Tr}(q_{00}^{2})=2\left[(1+sl_{3})^{2}+c_{1}^{2}z_{1}^{2}l_{1}^{2}+c_{2}^{2}z_{2}^{2}l_{2}^{2}+c_{3}^{2}z_{3}^{2}l_{3}^{2}\right],$

(2.26)

$\mathrm{Tr}(q_{01}^{2})=2\left[(1-sl_{3})^{2}-c_{1}^{2}z_{1}^{2}l_{1}^{2}-c_{2}^{2}z_{2}^{2}l_{2}^{2}-c_{3}^{2}z_{3}^{2}l_{3}^{2}\right],$

(2.27)

$\mathrm{Tr}(q_{10}^{2})=2\left[(1+sm_{3})^{2}-c_{1}^{2}z_{1}^{2}m_{1}^{2}-c_{2}^{2}z_{2}^{2}m_{2}^{2}-c_{3}^{2}z_{3}^{2}m_{3}^{2}\right],$

(2.28)

$\mathrm{Tr}(q_{11}^{2})=2\left[(1-sm_{3})^{2}+c_{1}^{2}z_{1}^{2}m_{1}^{2}+c_{2}^{2}z_{2}^{2}m_{2}^{2}+c_{3}^{2}z_{3}^{2}m_{3}^{2}\right].$

(2.29)

由定义可得

$\begin{align*} \mathrm{Tr}(\chi^{2})&=\frac{1}{8^{2}}\mathrm{Tr}(V_{A}\Pi_{0}V^{\dagger}_{A})^{2} \mathrm{Tr}(V_{B^{0}}\Pi_{0}V^{\dagger}_{B^{0}})^{2}\mathrm{Tr}(q_{00}^{2})\notag\\ & ~~~ +\frac{1}{8^{2}}\mathrm{Tr}(V_{A}\Pi_{0}V^{\dagger}_{A})^{2} \mathrm{Tr}(V_{B^{0}}\Pi_{1}V^{\dagger}_{B^{0}})^{2}\mathrm{Tr}(q_{01}^{2})\notag\\ &~~~ +\frac{1}{8^{2}}\mathrm{Tr}(V_{A}\Pi_{1}V^{\dagger}_{A})^{2} \mathrm{Tr}(V_{B^{1}}\Pi_{0}V^{\dagger}_{B^{1}})^{2}\mathrm{Tr}(q_{10}^{2})\notag\\ &~~~ +\frac{1}{8^{2}}\mathrm{Tr}(V_{A}\Pi_{1}V^{\dagger}_{A})^{2} \mathrm{Tr}(V_{B^{1}}\Pi_{1}V^{\dagger}_{B^{1}})^{2}\mathrm{Tr}(q_{11}^{2})\notag\\ &=\frac{1}{16}\left(2+\sum^{3}_{i=1}c_{i}^{2}z_{i}^{2}l_{i}^{2}+ \sum^{3}_{i=1}c_{i}^{2}z_{i}^{2}m_{i}^{2}+s^{2}l_{3}^{2}+s^{2}m_{3}^{2}\right). \end{align*}$

(2.30)

综上所述我们可以得到

$\begin{align*}\label{eq:2.29} \|\rho-\chi\|^{2}&=\|\rho\|^{2}-2\mathrm{Tr}(\rho\chi)+\|\chi\|^{2}\notag\\ &=\frac{1}{8}\left\{c_{1}^{2}+c_{2}^{2}+c_{3}^{2}+s^{2}-\frac{1}{2}\left(\sum_{i=1}^{3} c_{i}^{2}z_{i}^{2}(l_{i}^{2}+m_{i}^{2})+s^{2}(l_{3}^{2}+m_{3}^{2})\right)\right\}. \end{align*}$

(2.31)

3 三量子比特 X 态的几何量子失协

本节运用拉格朗日乘数法解决优化问题, 获得几何量子失协的解析表达式.

定理 3.1 希尔伯特空间 $H=H_{A}\otimes H_{B}\otimes H_{C}=\mathbb{C}^{2}\otimes \mathbb{C}^{2}\otimes \mathbb{C}^{2}$ 中三量子比特 X 态 $\rho$ (2.4) 式的几何量子失协

$\begin{align*} D_{G}^{(3)}(\rho)=\frac{1}{8}(c_{1}^{2}+c_{2}^{2}+c_{3}^{2}+s^{2}-2c),\label{D} \end{align*}$

(3.1)

其中 $c=\max\left\{\frac{1}{2}c_{1}^{2},\frac{1}{2}c_{2}^{2},\frac{1}{2} (c_{3}^{2}+s^{2})\right\}$ .

证首先, 由 (2.31) 式得

$\begin{align*}\label{OOOO} \min_{\chi\in\Omega} \|\rho-\chi\|^{2} &=\min_{z_{i},l_{i},m_{i}}\Big\{\frac{1}{8}\left\{c_{1}^{2}+c_{2}^{2}+c_{3}^{2} +s^{2}-\frac{1}{2}\left[\sum_{i=1}^3 c_{i}^{2}z_{i}^{2}(l_{i}^{2}+m_{i}^{2})+s^{2}(l_{3}^{2}+m_{3}^{2})\right]\right\}\Big\}\notag\\ &=\frac{1}{8}\Big\{c_{1}^{2}+c_{2}^{2}+c_{3}^{2}+s^{2}- \max_{z_{i},l_{i},m_{i}}\left\{\frac{1}{2}\left[\sum_{i=1}^3 c_{i}^{2}z_{i}^{2}(l_{i}^{2}+m_{i}^{2})+s^{2}(l_{3}^{2}+m_{3}^{2})\right]\right\}\Big\}. \end{align*}$

(3.2)

现在我们只需考虑 $\max_{z_{i},l_{i},m_{i}}\left\{\frac{1}{2}[\sum_{i=1}^3 c_{i}^{2}z_{i}^{2}(l_{i}^{2}+m_{i}^{2})+s^{2}(l_{3}^{2}+m_{3}^{2})]\right\}$ . 由于子系统 $B$ 的测量由子系统 $A$ 决定, 我们需要优先考虑 $z_{1},z_{2},z_{3}$ . 同时我们也注意到 $l_{i}$ 与 $m_{i}$ 求解方法相同, 为了计算方便简化方程, 设目标函数

$\begin{align*} G(z_{1},z_{2},z_{3})=\frac{1}{2}\left(\sum_{i=1}^3 c_{i}^{2}z_{i}^{2}l_{i}^{2}+s^{2}l_{3}^{2}\right).\label{G} \end{align*}$

(3.3)

是关于 $z_{1},z_{2},z_{3}$ 的偶函数, 于是令 $z_{1},z_{2},z_{3} \in [0,1]$ .

由 $z_{1}^{2}+z_{2}^{2}+z_{3}^{2}=1$ , 可令条件函数

$\begin{align*} \varphi(z_{1},z_{2},z_{3})=z_{1}^{2}+z_{2}^{2}+z_{3}^{2}-1 \end{align*}$

(3.4)

设拉格朗日函数 $H(z_{1},z_{2},z_{3})=G(z_{1},z_{2},z_{3})+\lambda\varphi(z_{1},z_{2},z_{3})$ , 其中 $\lambda$ 是拉格朗日乘子, 可得

$\begin{align*} \left\{ \begin{aligned} &\frac{\partial H}{\partial z_{1} }=c_{1}^{2}l_{1}^{2}z_{1}+2\lambda z_{1}=0,\\ &\frac{\partial H}{\partial z_{2} }=c_{2}^{2}l_{2}^{2}z_{2}+2\lambda z_{2}=0,\\ &\frac{\partial H}{\partial z_{3} }=c_{3}^{2}l_{3}^{2}z_{1}+2\lambda z_{3}=0,\\ &\frac{\partial H}{\partial \lambda }z_{1}^{2}+z_{2}^{2}+z_{3}^{2}-1=0. \end{aligned} \right.\label{w6} \end{align*}$

(3.5)

由 (3.5) 式可得

$\begin{align*} \left\{ \begin{aligned} (c_{1}^{2}l_{1}^{2}-c_{2}^{2}l_{2}^{2})z_{1}z_{2}=0,\\ (c_{2}^{2}l_{2}^{2}-c_{3}^{2}l_{3}^{2})z_{2}z_{3}=0,\\ (c_{1}^{2}l_{1}^{2}-c_{3}^{2}l_{3}^{2})z_{1}z_{3}=0,\\ z_{1}^{2}+z_{2}^{2}+z_{3}^{2}-1=0. \end{aligned} \right. \end{align*}$

(3.6)

情况 1 若 $c_{1}^{2}l_{1}^{2}\neq c_{2}^{2}l_{2}^{2}\neq c_{3}^{2}l_{3}^{2}$ , 则 $z_{1},z_{2},z_{3}$ 至少有两个为 $0$ , 因为 $z_{1}^{2}+z_{2}^{2}+z_{3}^{2}-1=0$ , 所以 $z_{1},z_{2},z_{3}$ 不可能同时为零.

(a) 若 $z_{1}=1,z_{2}=z_{3}=0$ , 可得

$\begin{align*} F(l_{1},l_{3}):=G(1,0,0)=\frac{1}{2}(c_{1}^{2}l_{1}^{2}+s^{2}l_{3}^{2}).\label{w7} \end{align*}$

(3.7)

(b) 若 $z_{2}=1,z_{1}=z_{3}=0$ , 可得

$\begin{align*} F(l_{2},l_{3}):=G(0,1,0)=\frac{1}{2}(c_{2}^{2}l_{2}^{2}+s^{2}l_{3}^{2}).\label{w8} \end{align*}$

(3.8)

$\begin{align*} F(l_{3}):=G(0,0,1)=\frac{1}{2}(c_{3}^{2}l_{3}^{2}+s^{2}l_{3}^{2}).\label{w9} \end{align*}$

(3.9)

情况 2 若 $c_{1}^{2}l_{1}^{2}=c_{2}^{2}l_{2}^{2}\neq c_{3}^{2}l_{3}^{2}$ , 则 $z_{1}z_{3}=z_{2}z_{3}=0$ , 可得

(a) $z_{1}=z_{2}=0$ 且 $z_{3}=1$ , 那么可得与情况 1 (c) 相同的公式.

(b) $z_{3}=0$ 且 $z_{1}^{2}+z_{2}^{2}-1=0$ . 将 $c_{1}^{2}l_{1}^{2}=c_{2}^{2}l_{2}^{2}$ , 带入 (3.3) 式得到 $G(z_{1},z_{2},0)$ 与 (3.7) 式, (3.8) 式相同.

情况 3 若 $c_{1}^{2}l_{1}^{2}=c_{3}^{2}l_{3}^{2}\neq c_{2}^{2}l_{2}^{2}$ , 则 $z_{1}z_{2}=z_{2}z_{3}=0$ , 可得

(a) $z_{1}=z_{3}=0$ 且 $z_{2}=1$ , 那么可得与情况 1 (b) 相同的公式.

(b) $z_{2}=0$ 且 $z_{1}^{2}+z_{3}^{2}-1=0$ . 同理可得 $G(z_{1},0,z_{3})$ 与 (3.7) 式, (3.9) 式相同.

情况 4 若 $c_{2}^{2}l_{2}^{2}= c_{3}^{2}l_{3}^{2}\neq c_{1}^{2}l_{1}^{2}$ , 那么 $z_{1}z_{2}=z_{1}z_{3}=0$ , 可得

(a) $z_{2}=z_{3}=0$ 且 $z_{1}=1$ , 那么可得与情况 1 (a) 相同的公式.

(b) $z_{1}=0$ 且 $z_{2}^{2}+z_{3}^{2}-1=0$ . 同理可得 $G(0,z_{2},z_{3})$ 与 (3.8) 式, (3.9) 式相同.

情况 5 若 $c_{1}^{2}l_{1}^{2}=c_{3}^{2}l_{3}^{2}= c_{2}^{2}l_{2}^{2}$ , 带入 (3.3) 式可得 $G(z_{1},z_{2},z_{3})$ 与 (3.7) 式, (3.8) 式, (3.9) 式相同.

综上 $\max G(z_{1},z_{2},z_{3})$ , $z_{1},z_{2},z_{3}\in[0,1]$ 等价于 $\max\left\lbrace F(l_{1},l_{3}),F(l_{2},l_{3}),F(l_{3})\right\rbrace$ . 由 (3.7) 式, (3.8) 式, (3.9) 式, 知 $F$ 是关于 $l_{1},l_{2},l_{3}$ 的偶函数, 因此只考虑 $l_{1},l_{2},l_{3}\in[0,1]$ . 分为以下几种情况:

情况 6 对 $F(l_{1},l_{3})$ 求导, 可得

$\frac{\partial F(l_{1},l_{3})}{\partial l_{1}}=c_{1}^{2}l_{1},$

(3.10)

$\frac{\partial F(l_{1},l_{3})}{\partial l_{3}}=s_{1}^{2}l_{3}.$

(3.11)

由上可知 $F(l_{1},l_{3})$ 驻点为 $(0,0)$ , 边界点为 $(1,0)$ 与 $(0,1)$ . 分别带入 (3.7) 式可得

$\begin{equation} \max_{l_{1},l_{3}} F(l_{1},l_{3})=\max\left\{\frac{1}{2}c_{1}^{2},\frac{1}{2}s^{2}\right\}. \end{equation}$

(3.12)

情况 7 对 $F(l_{2},l_{3})$ 求导, 同理可得

$\begin{equation} \max_{l_{2},l_{3}} F(l_{2},l_{3})=\max\left\{\frac{1}{2}c_{2}^{2},\frac{1}{2}s^{2}\right\}. \end{equation}$

(3.13)

情况 8 对 $F(l_{3})$ 求导, 可得

$\begin{align*} \frac{\partial F(l_{3})}{\partial l_{3}}&=(c_{1}^{2}+s^{2})l_{3}. \end{align*}$

(3.14)

由上可知 $F(l_{3})$ 单调递增, 则

$\begin{equation} \max_{l_{3}} F(l_{3})=\frac{1}{2}(c_{3}^{2}+s^{2}). \end{equation}$

(3.15)

综上可知, c:= $\max\left\lbrace F(l_{1},l_{3}),F(l_{2},l_{3}),F(l_{3})\right\rbrace=\max\left \{\frac{1}{2}c_{1}^{2},\frac{1}{2}c_{2}^{2},\frac{1}{2}(c_{3}^{2}+s^{2})\right\}$ . 由于 $l_{i}$ 与 $m_{i}$ 讨论情况相同, 故由 (3.2) 式得

$\begin{align*} D_{G}^{(3)}(\rho)=\frac{1}{8}\left(c_{1}^{2}+c_{2}^{2}+c_{3}^{2}+s^{2}-2c\right). \end{align*}$

(3.16)

证毕.

记 $D_{G}^{(3)}(\rho)=D_{G}^{(3)}(c_{1},c_{2},c_{3},s)$ . 根据 (3.1) 式, 绘制了该类态几何量子失协等高图如图1 所示. 由图1可以看出与量子失协的等高图不同, 几何量子失协是由三个相交“圆柱体”组成, 并且表面收缩率会随着 $s$ 的增加而变大. 此外, 因为 $D_{G}^{(3)}(c_{1},c_{2},c_{3},s)=D_{G}^{(3)}(-c_{1},-c_{2},-c_{3},s)$ , 所以对于比较大的 $s$ 图形不会在平面 $c_{3}=0$ 上方移动, 如图1(b), 图1(d).

图1

新窗口打开| 下载原图ZIP| 生成PPT

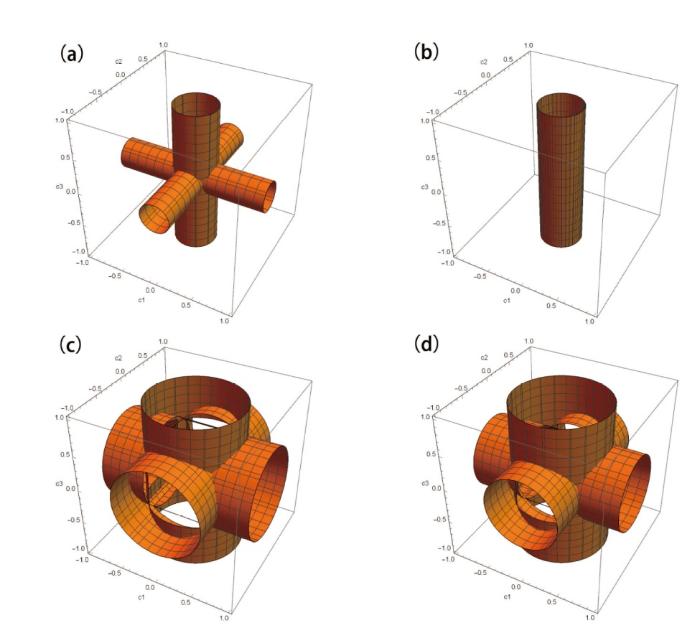
图1 几何量子失协等高图 $D_{G}^{(3)}(c_{1},c_{2},c_{3},s)=D$ : (a) $s=0.2$ , $D=0.01$ ; (b) $s=0.4$ , $D=0.01$ ; (c) $s=0.2$ , $D=0.05$ ; (d) $s=0.4$ , $D=0.05$ .

4 相位翻转下几何量子失协的动力学行为

假设 (2.4) 式给出的三量子比特 X 态 $\rho$ 经过相位翻转信道 $\varepsilon(\cdot)$ ^[17], 其中 Kraus 算子

$\Gamma^{(A_{1})}_{0}=\mathrm{diag}(\sqrt{1-p/2},\sqrt{1-p/2})\otimes {\mathrm{I_2}}\otimes{\mathrm{I_2}},$

(4.1)

$\Gamma^{(A_{1})}_{1}=\mathrm{diag}(\sqrt{p/2},-\sqrt{p/2})\otimes {\mathrm{I_2}}\otimes {\mathrm{I_2}},$

(4.2)

$\Gamma^{(A_{2})}_{0}={\mathrm{I_2}}\otimes \mathrm{diag}(\sqrt{1-p/2},\sqrt{1-p/2})\otimes{\mathrm{I_2}},$

(4.3)

$\Gamma^{(A_{2})}_{1}={\mathrm{I_2}}\otimes \mathrm{diag}(\sqrt{p/2},-\sqrt{p/2})\otimes {\mathrm{I_2}},$

(4.4)

$\Gamma^{(A_{3})}_{0}={\mathrm{I_2}}\otimes{\mathrm{I_2}}\otimes \mathrm{diag}(\sqrt{1-p/2},\sqrt{1-p/2}),$

(4.5)

$\Gamma^{(A_{3})}_{1}={\mathrm{I_2}}\otimes {\mathrm{I_2}}\otimes \mathrm{diag}(\sqrt{p/2},-\sqrt{p/2}),$

(4.6)

其中 $p=1-\exp(-\gamma t)$ , $\gamma$ 为相位阻尼率^[18].

若初始态 $\rho$ 经过相位翻转信道之后, 将演化成

$\begin{align*} \varepsilon(\rho)&=\frac{1}{8}\Big[{\mathrm{I_2}}\otimes {\mathrm{I_2}}\otimes {\mathrm{I_2}}+{\mathrm{I_2}}\otimes s\sigma_{3}\otimes {\mathrm{I_2}}+(1-p)^{3}c_{1}\sigma_{1}\otimes\sigma_{1}\otimes\sigma_{1} \notag\\ &~~~+(1-p)^{3}c_{2}\sigma_{2}\otimes\sigma_{2}\otimes\sigma_{2} +c_{3}\sigma_{3}\otimes\sigma_{3}\otimes\sigma_{3}\Big]. \end{align*}$

(4.7)

该类态 $\rho$ 通过相位翻转信道之后, 根据定理 3.1 可解析求解得到几何量子失协

$\begin{align*} D_{G}^{(3)}(\varepsilon(\rho))=\frac{1}{8}\left\{(1-p)^{6}(c_{1}^{2}+c_{2}^{2})+c_{3}^{2}+s^{2} -\max\left\{(1-p)^{6}c^{2}_{1},(1-p)^{6}c^{2}_{2},c^{2}_{3}+s^{2}\right\}\right\}. \end{align*}$

(4.8)

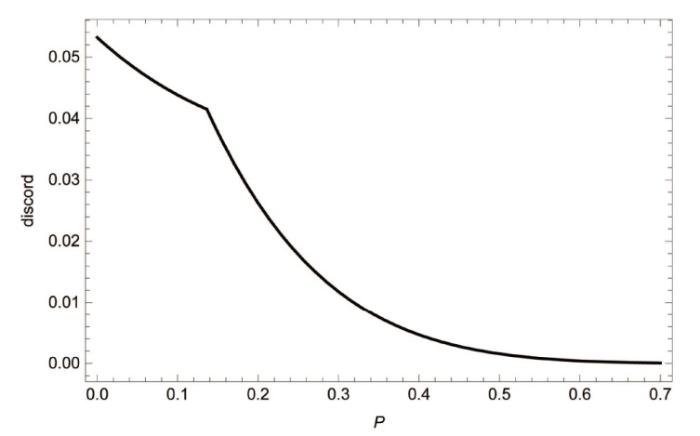
图2 给出了当参数 $s=\frac{1}{8}$ , $c_{1}=\frac{4}{5}$ , $c_{2}=\frac{c_{1}}{2}$ , $c_{3}=\frac{1}{2}$ , 此时三量子比特 X 态 $\rho$ 相位翻转下几何量子失协的动力学行为. 通过图形可以发现几何量子失协随着参数 $p$ 单调递减, 且在 $p=0.136329$ 处发生几何量子失协突变的现象.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 相位翻转下的几何量子失协: $s=\frac{1}{8}$ , $c_{1}=\frac{4}{5}$ , $c_{2}=\frac{c_{1}}{2}$ , $c_{3}=\frac{1}{2}$ .

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Ollivier

, Zurek

W H

Quantum discord: A measure of the quantumness of correlations

Physical Review Letters, 2001, 88(1): 017901