数学物理学报, 2024, 44(4): 994-1011

具有无穷分布时滞和反馈控制的周期阶段结构单种群模型

尹瑞霞1, 王泽东1, 张龙,1,2,*

1新疆大学数学与系统科学学院 乌鲁木齐 830017

2新疆维吾尔自治区应用数学重点实验室 乌鲁木齐 830017

A Periodic Stage Structure Single-Population Model with Infinite Delay and Feedback Control

Yin Ruixia1, Wang Zedong1, Zhang Long,1,2,*

1College of Mathematics and System Sciences, Xinjiang University, Urumqi 830017

2The Key Laboratory of Applied Mathematics of Xinjiang Uygur of Xinjiang, Urumqi 830017

通讯作者: *张龙, E-mail:longzhang_xj@sohu.com

收稿日期: 2023-07-3   修回日期: 2024-04-25  

基金资助: 新疆维吾尔自治区应用数学重点实验室开放课题(2021D04014)
新疆维吾尔自治区天山英才领军人才项目(2023TSYCLJ0054)
国家自然科学基金(12261087)
国家自然科学基金(12262035)
国家自然科学基金(12201540)
国家自然科学基金(11861065)
新疆维吾尔自治区自然科学基金(2022D01E41)
新疆维吾尔自治区高校科研项目(XJEDU2021I002)

Received: 2023-07-3   Revised: 2024-04-25  

Fund supported: Open Project of Key Laboratory of Applied Mathematics of XinjiangUygur Autonomous Region(2021D04014)
Leading Talents of Tianshan Mountains Project in Xinjiang Uygur Autonomous Region(2023TSYCLJ0054)
NSFC(12261087)
NSFC(12262035)
NSFC(12201540)
NSFC(11861065)
Natural Science Foundation of Xinjiang Province(2022D01E41)
Scientific Research Programmes of Colleges in Xinjiang(XJEDU2021I002)

摘要

该文研究了一类具有无穷分布时滞和反馈控制的周期阶段结构单种群模型. 首先得到了辅助系统-周期阶段结构单种群模型存在唯一全局渐近稳定周期解的充分性判别准则, 其次以积分形式建立了模型持久性和正周期解存在性的充分性判别准则. 最后通过数值模拟演示了文中的理论结果.

关键词： 持久性; 周期解; 无穷分布时滞; 反馈控制; 阶段结构

Abstract

In this paper, we investigate a periodic stage structure single-population model with infinitely distributed delay and feedback control. Firstly, a sufficient criterion for the existence of a unique globally asymptotically stable periodic solution for the auxiliary system-periodic stage structure single-population model is derived. Secondly, we establish sufficiency criteria on the permanence of the model and the existence of a positive periodic solution in the form of integral. Finally, we illustrate the results with numerical simulations.

Keywords： Permanence; Periodic solution; Infinite delay; Feedback control; Stage structure

PDF (956KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

尹瑞霞, 王泽东, 张龙. 具有无穷分布时滞和反馈控制的周期阶段结构单种群模型[J]. 数学物理学报, 2024, 44(4): 994-1011

Yin Ruixia, Wang Zedong, Zhang Long. A Periodic Stage Structure Single-Population Model with Infinite Delay and Feedback Control[J]. Acta Mathematica Scientia, 2024, 44(4): 994-1011

1 引言

种群动力学模型[1]是生物数学领域中的重要研究分支, 其中单种群模型[2]是其重要研究内容. 近年来, 具有阶段结构的单种群模型[3]受到大家的广泛关注. 崔景安等[4]研究了下列具有阶段结构的自治单种群模型

$\begin{equation}\left\{\begin{aligned}&\dot x{_{1}}(t)=\alpha x_{2}(t)-\gamma_1 x_{1}(t)-\beta x_{1}(t)-\eta_{1} x^2_{1}(t),\\&\dot x{_{2}}(t)=\beta x_{1}(t)-\eta_{2} x^2_{2}(t),\\\end{aligned}\right.\end{equation}$

其中 $x_i(t)\ (i=1,2)$ 分别表示 $t$ 时刻某物种幼年与成年的种群密度. $\alpha $ 和 $\beta$ 分别表示 $t$ 时刻幼年种群的出生率和幼年到成年的转化率; $\gamma_1$ 表示 $t$ 时刻幼年种群的自然死亡率; $\eta_1$ 和 $\eta_2$ 表示 $t$ 时刻幼年与成年种群的密度制约系数. 作者建立了模型正平衡点全局渐近稳定性的充分条件.

由于现实生态及环境参数受季节, 繁殖等因素的影响, 种群的增长呈现周期变化[5]. 陈兰荪等[3]研究了如下具有周期系数及阶段结构的单种群模型

$\begin{equation} \left\{\begin{aligned}&\dot x{_{1}}(t)=\alpha(t) x_{2}(t)-\gamma_{1}(t)x_{1}(t)-\beta(t) x_{1}(t)-\eta_{1}(t)x^2_{1}(t),\\&\dot x{_{2}}(t)=\beta(t) x_{1}(t)-\gamma_{2}(t)x_{2}(t)-\eta_{2}(t) x^2_{2}(t),\\\end{aligned}\right.\end{equation}$

其中 $\gamma_2(t) $ 表示 $t$ 时刻成年种群的死亡率. 作者们指出当 $\gamma_2(t)=0$ 时系统 (1.2) 存在全局渐近稳定的正周期解.

为了刻画在物种养殖与繁育中获取最大收益, Gopalsamy 和 Weng[6] 将反馈控制变量引入到模型中. 一些学者引入天敌作为控制变量, 通过人为干扰达到对系统的控制[7⇓-9]. 傅金波和陈兰荪[8] 讨论了下述具有反馈控制的非自治多种群模型

$\begin{equation} \left\{\begin{array}{l}\dot N_i(t) =N_{i}(t)[b_{i}(t)-h_{i}(t) N_{i}(t)- \displaystyle\sum_{j=1,i\neq j}^{n} a_{i j}(t) N_{j}(t)-c_{i}(t) N_{i}\left(t-\tau_{i}\right)-d_{i}(t) P_{i}(t)], \\\dot P_i(t) =P_{i}(t)\left[r_{i}(t) N_{i}(t)-D_{i}(t) P_{i}(t)\right],(i=1,2, \cdots, n),\end{array}\right.\end{equation}$

其中 $ N_i(t), P_i(t)$ 分别表示 $t$ 时刻第 $i$ 个食饵和天敌种群的密度. $b_i(t),h_i(t)$ 分别为第 $i$ 个食饵种群的内禀增长率和密度制约系数; $d_i(t)$ 和 $r_i(t)$ 分别代表第 $i$ 个天敌对第 $i$ 个食饵种群的捕获率以及营养转化率; $a_{ij}(t)$ 表示第 $i$ 个食饵种群与第 $j$ 个食饵种群间的竞争系数, $D_i(t)$ 是第 $i$ 个天敌的密度制约系数 $(i,j=1,2,\cdots, n)$.

然而控制变量 (天敌) 捕获 (食饵) 种群后生物量的转化过程不是瞬时完成的[9], 并且 (食饵) 种群被控制变量 (天敌) 捕获的过程受过去状态的影响[10]. 不少学者使用无穷分布时滞对其进行刻画[11⇓⇓-14], 例如: Pu[11] 考虑了一类具有无穷分布时滞以及反馈控制的非自治种群模型, 得到了系统持久性的充分条件; Chen 和 Li[12]研究了具有无穷分布时滞及反馈控制的两种群竞争模型, 得到了平衡点全局稳定性的判定条件.

受上述工作启发, 我们建立如下具有无穷分布时滞和反馈控制的周期阶段结构单种群模型

$\begin{equation} \left\{\begin{aligned} \dot x{_{1}}(t) &=\alpha(t)x_2(t)-\gamma_1(t)x_1(t)-\beta(t)x_1(t)-\eta_1(t)x^2_1(t),\\ \dot x{_{2}}(t) &=\beta(t)x_1(t)-\gamma_2(t)x_2(t)-\eta_2(t)x^2_2(t)-d(t)x_2(t)\int_{-\infty }^{0}k_1(s)u(t+s){\rm d}s,\\ \dot u(t) &=u(t)\left[-e(t)u(t)+f(t)\int_{-\infty }^{0}k_2(s)x_2(t+s){\rm d}s \right],\end{aligned}\right. \end{equation}$

这里 $e(t)$ 和 $f(t)$ 分别代表控制变量 (天敌) 的密度制约系数和营养转化率. 我们假设 $\alpha(t),\beta(t)$,$\gamma_i(t),\eta_i(t),d(t),e(t)$ 和 $f(t)$ 在 $\mathbb{R}_+=[0,+\infty)$ 上是 $w$-周期连续函数; $k_i(s)$ 是定义在 $\mathbb{R}_{-}=(-\infty,0]$ 上的非负可积函数并且 $\int_{-\infty }^{0} k_i(s){\rm d}s=1\ (i=1,2)$.

近来, 一些学者讨论了非自治模型[13⇓-15]得到了系统正周期解存在性的充分条件, 此外 Shi[14]也讨论了系统概周期解的存在性和一致渐近稳定性. 比如王等[15]以不等式的形式给出了模型持久性成立的条件. 为了使系统更易持久, 我们改进文献 [16,17] 的方法, 使用积分条件构建了模型 (1.4) 持久性以及正周期解存在性的充分性判别准则.

文章内容安排如下: 第 2 节中我们引入一些假设和引理; 在第 3 节, 我们得到系统 (1.4) 的持久性及正周期解存在性的充分性判别条件; 最后通过数值模拟演示了理论结果.

2 预备知识

为方便起见, 定义 $\mathbb{R}_+$ 上的连续 $w$-周期函数 $g(t)$ 的记号如下

$\begin{equation*}\begin{aligned}A_w(g)=w^{-1}\int_{0}^{w} g(t){\rm d}t, \quad g^M=\max_{t\in \mathbb{R}_+} g(t), \quad g^L=\min_{t\in \mathbb{R}_+} g(t).\end{aligned}\end{equation*}$

对于模型(1.4) 我们作以下假设

(H1) $\alpha^L \beta^L> \gamma_2^M(\gamma_1^M+\beta^M)$;

(H2) $\alpha^L \geq 0, \beta^L>0, A_w(\gamma_1)>0,A_w(\eta_1)>0, e^L \geq 0,f^L>0, d^L>0$, 对所有 $t \in [w]$ 成立.

令 $C_w(\mathbb{R})$ 表示 $\mathbb{R}$ 上连续向量函数 $\phi(\theta)=\{\phi_1(\theta),\phi_2(\theta),\phi_3(\theta)\}$ 构成的 Banach 空间, 且范数定义为 $\|\phi\|=\sup |\phi(\theta) |,\ \theta \in \mathbb{R}$. 令 $C_w^+(\mathbb{R})=\{\phi=(\phi_1,\phi_2,\phi_3) \in C_w(\mathbb{R}): \phi_i(0)>0, $$i=1,2,3\}$. 基于系统 (1.4) 的生物背景, 其任意解 $x(t)=(x_1(t),x_2(t),u(t))$ 满足以下初始条件

$\begin{align*} \begin{aligned}& x_i(s)=\phi_i(s), s\in (-\infty,0],\ i=1,2.\\& u(s)=\phi_3(s), s\in (-\infty,0].\end{aligned}\end{align*}$

这里 $\phi=(\phi_1,\phi_2,\phi_3) \in C^+_w(\mathbb{R})$.

接着引入一些定义以及引理便于后续证明.

定义 2.1[5] 称系统 (1.4) 是持久的, 若对系统 (1.4) 满足初始条件 (2.1) 的任意正解 $x(t)=(x_1(t),x_2(t),u(t))$, 存在正常数 $m,M$, 满足

$\begin{equation*}\begin{aligned}& m \leq \liminf_{t\rightarrow +\infty} x_i(t) \leq \limsup_{t\rightarrow +\infty} x_i(t) \leq M,\ (i=1,2),\\& m \leq \liminf_{t\rightarrow +\infty} u(t) \leq \limsup_{t\rightarrow +\infty} u(t) \leq M.\end{aligned}\end{equation*}$

考虑下列泛函微分方程

$\begin{equation} \begin{aligned} \dot x=f(t,x_t),\end{aligned}\end{equation}$

其中 $f(t,\phi)=(f_1(t,\phi),f_2(t,\phi),f_3(t,\phi)): \mathbb{R}\times C_w \rightarrow \mathbb{R}^3$ 是连续的且关于 $\phi$ 满足 Lipschitz 条件, 根据泛函微分方程理论[16]对于任意$ t_0 \in \mathbb{R} $ 和 $\phi \in C_w(\mathbb{R})$, 系统 (2.2) 存在唯一解 $x(t,t_0,\phi)=(x_1(t,t_0,\phi),x_2(t,t_0,\phi),x_3(t,t_0,\phi))$. 如果下列条件成立, 则称系统 (2.2) 为合作的[16]

$\begin{equation*}\begin{aligned}\text{对于任意} \phi,\ \varphi \in C_w(\mathbb{R}),\ \text{若} \phi < \varphi,\text{且} \phi_i(0)=\varphi_i(0),\ \text{那么} f_i(t,\phi)<f_i(t,\varphi).\end{aligned}\end{equation*}$

引理 2.1[16] 假设系统 (2.2) 是合作的, 若

$\begin{equation*}\begin{aligned}\dot y \geq (\text{或} \leq) f(t,y_t),\quad y_{t_0}\geq (\text{或} \leq) \phi, \quad t \in [t_0,T].\end{aligned}\end{equation*}$

则有

$\begin{equation*}\begin{aligned}y_i(t) \geq (\text{或} \leq) x_i(t,t_0,\phi), \quad t \in [t_0,T], \quad i=1,2,3.\end{aligned}\end{equation*}$

这里 $x(t,t_0,\phi)=(x_1(t,t_0,\phi),x_2(t,t_0,\phi),x_3(t,t_0,\phi))$ 是系统 (2.2) 定义在 $[t_0,T]$ 上的一个解; $y(t)=(y_1(t),y_2(t),y_3(t)): [t_0,T] \rightarrow \mathbb{R}^3 $ 是连续可微的.

继续考虑非自治 Logistic 方程

$\begin{equation} \begin{aligned}\dot x(t)=x(t)(a(t)-b(t)x(t)),\end{aligned}\end{equation}$

其中 $a(t), b(t)$ 在 $\mathbb{R}_+$ 上是连续有界的 $w$-周期函数, 则有以下结果.

引理 2.2[10] 若 $A_w(a),A_w(b)>0$, 则存在正数 $m,M$ 使得

$\begin{equation*}\begin{aligned}m \leq \liminf_{t\rightarrow \infty} x(t) \leq \limsup_{t\rightarrow \infty}x(t) \leq M.\end{aligned}\end{equation*}$

接着考虑下列非自治线性方程

$\begin{equation} \begin{aligned}\dot x(t)=a(t)-b(t)x(t),\end{aligned}\end{equation}$

这里 $a(t),b(t)$ 在 $\mathbb{R}_+$ 上是连续有界的 $w$-周期函数, 我们有下面的引理.

引理 2.3[17] 若 $A_w(a),A_w(b)>0$, 则存在正数 $m,M$ 使得方程 (2.4) 任意正解 $x(t)$ 满足

$\begin{equation*}\begin{aligned}m \leq \liminf_{t\rightarrow \infty} x(t) \leq \limsup_{t\rightarrow \infty}x(t) \leq M.\end{aligned}\end{equation*}$

引理 2.4[17] 令 $x(t):\mathbb{R}\rightarrow \mathbb{R}$ 是非负有界连续函数; $k(s):\mathbb{R}_{-}\rightarrow \mathbb{R}_{+}$ 上的可积函数且满足 $\int_{-\infty}^{0} k(s){\rm d}s=1$, 则有

$\begin{equation*}\begin{aligned}\liminf_{t \rightarrow \infty} x(t) & \leq \liminf _{t \rightarrow \infty} \int_{-\infty}^{0} k(s) x(t+s){\rm d}s \\& \leq \limsup _{t \rightarrow \infty} \int_{-\infty}^{0} k(s) x(t+s){\rm d}s\leq \limsup _{t \rightarrow \infty} x(t).\end{aligned}\end{equation*}$

引理 2.5 如果条件 (H1) 成立, 则模型 (1.2) 存在唯一全局渐近稳定的正周期解.

证 类似文献 [4,定理 6] 我们将分三部分证明. 首先证明系统 (1.2) 的持久性; 其次给出周期解的存在性; 最后证明系统 (1.2) 周期解的唯一性和全局渐近稳定性.

显然 $\mathbb{R}_+^2$ 是系统 (1.2) 的正不变集, 则对于其任意解 $\bar{x}(t)=(\bar{x}_1(t),\bar{x}_2(t))$ 有

$\begin{equation*}\begin{aligned} \left\{\begin{aligned}&\dot x{_{1}}(t) \geq \alpha^L x_{2}(t)-\gamma_1^M x_{1}(t)-\beta^M x_{1}(t)-\eta_{1}^M x^2_{1}(t),\\&\dot x{_{2}}(t) \geq \beta^L x_{1}(t)-\gamma_2^M x_{2}(t)-\eta_{2}^M x^2_{2}(t).\end{aligned}\right.\end{aligned}\end{equation*}$

Cui 等[4,引理 3] 已经证明了 $\alpha^L \beta^L> \gamma_2^M(\gamma_1^M+\beta^M)$ 成立时, 下列模型 (2.5) 有唯一全局渐近稳定的正平衡点 $(\hat{x}_1,\hat{x}_2)$

$\begin{equation}\begin{aligned} \left\{\begin{aligned}&\dot x{_{1}}(t)= \alpha^L x_{2}(t)-\gamma_1^M x_{1}(t)-\beta^M x_{1}(t)-\eta_{1}^M x^2_{1}(t),\\&\dot x{_{2}}(t) = \beta^L x_{1}(t)-\gamma_2^M x_{2}(t)-\eta_{2}^M x^2_{2}(t).\end{aligned}\right.\end{aligned}\end{equation}$

应用文献 [4, 引理 4, 定理 5] 易得

$\begin{equation*}\begin{aligned}\liminf_{t\rightarrow +\infty} \bar{x}_i(t) \geq \hat{x}_i\ \ (i=1,2).\end{aligned}\end{equation*}$

接着证明系统 (1.2) 的任意正解是最终有界的. 令 $\rho(t)=\bar{x}_1(t)+\bar{x}_2(t)$, 则对于任意的正数 $\epsilon < \gamma_1^L$, 沿系统 (1.2) 的任意正解 $(\bar{x}_1(t),\bar{x}_2(t))$ 对 $\rho (t)$ 求导有

$\begin{equation*}\begin{aligned}\dot{\rho}(t)+\epsilon \rho(t) & <-(\gamma_1^L-\epsilon)\bar{x}_1(t)+(\alpha^M+\epsilon)\bar{x}_2(t)-\eta^L_2 \bar{x}_2^2(t) \\& < (\alpha^M+\epsilon)\bar{x}_2(t)-\eta^L_2 \bar{x}_2^2(t) < c,\end{aligned}\end{equation*}$

易得 $c>0$, 此外 $\limsup\limits_{t \rightarrow +\infty} \rho(t) \leq \frac{c}{\epsilon}$.

因此,

$\begin{equation*}\begin{aligned}\limsup_{t\rightarrow +\infty} \bar{x}_i(t) \leq \frac{c}{\epsilon}\ \ (i=1,2),\end{aligned}\end{equation*}$

所以系统 (1.2) 是持久的. 其次微分方程解的存在性问题往往归结为算子方程不动点的存在性问题. 因此我们利用 Schauder 不动点定理[18]证明模型 (1.2) 周期解的存在性, 为此构造集合 $\Omega$ 作为模型 (1.2) 的正不变集.

由模型 (1.2) 可得

$\begin{equation*}\begin{aligned}\left\{\begin{aligned}&\dot x{_{1}}(t) \leq \alpha^M x_{2}(t)-\gamma_1^L x_{1}(t)-\beta^L x_{1}(t)-\eta_{1}^L x^2_{1}(t),\\&\dot x{_{2}}(t) \leq \beta^M x_{1}(t)-\gamma_2^L x_{2}(t)-\eta_{2}^L x^2_{2}(t),\end{aligned}\right.\end{aligned}\end{equation*}$

类似文献 [4, 引理 3] 的证明, 不难验证下列模型 (2.6) 在条件 $\alpha^M \beta^M> \gamma^L(\gamma_1^L+\beta^L)$ 成立时存在唯一全局渐近稳定的正平衡点的 $(\check{x}_1,\check{x}_2)$.

$\begin{equation} \begin{aligned}\left\{\begin{aligned}&\dot x{_{1}}(t)= \alpha^M x_{2}(t)-\gamma_1^L x_{1}(t)-\beta^L x_{1}(t)-\eta_{1}^L x^2_{1}(t),\\&\dot x{_{2}}(t) = \beta^M x_{1}(t)-\gamma_2^L x_{2}(t)-\eta_{2}^L x^2_{2}(t),\end{aligned}\right.\end{aligned}\end{equation}$

显然当 $\alpha^L \beta^L> \gamma_2^M(\gamma_1^M+\beta^M)$ 时有 $\alpha^M \beta^M> \gamma_2^L(\gamma_1^L+\beta^L)$ 成立, 因此模型 (2.5), (2.6) 分别存在唯一全局渐近稳定的正平衡点 $(\hat{x}_1,\hat{x}_2)$ 与 $(\check{x}_1,\check{x}_2)$. 接着选取正数 $p_i,q_i$ 且满足

$\begin{equation*}\begin{aligned}& p_{1}<\min \{\hat{x}_1,\check{x}_1\}; p_{2}>\max \{\hat{x}_1,\check{x}_1\},\\& \frac{p_1(\eta_1^M p_{1}+\gamma_1^{M}+\beta^{M})}{a^{L}}<q_{1}<\min \left\{\frac{-\gamma^M+\sqrt{(\gamma^M)^2+4\eta_1^M\beta^Lp_1}}{2\eta_2^M}, \hat{x}_{2}, \check{x}_{2}\right\}, \\& \max \left\{\frac{-\gamma^L+\sqrt{(\gamma^L)^2+4\eta_2^L\beta^Mp_2 }}{2\eta_2^L},\hat{x}_{2}, \check{x}_{2}\right\} <q_{2} <\frac{p_2(\eta_1^L p_{2}+\gamma_1^{L}+\beta^{L})}{a^{M}}. \\\end{aligned}\end{equation*}$

这里令 $A(p_1,q_2),B(p_2,q_2),C(p_2,q_1),D(p_1,q_1)$ 表示矩形区域的四个顶点, 显然任何与矩形区域 $ABCD$ 相交的轨迹都从外部进入内部, 由此得 $\Omega=\{(\bar{x}_1(t),\bar{x}_2(t))|(\bar{x}_1,\bar{x}_2 ) \in ABCD\}$ 是系统 (1.2) 的正不变集, 易得 $\Omega$ 是闭有界凸集.

定义 Poincare 周期映射 $\mathcal{A}: \Omega \rightarrow \Omega$, 如下

$\begin{equation*}\begin{aligned}\mathcal{A}X_0=X(w,X_0),\end{aligned}\end{equation*}$

这里 $X_0=(\bar{x}_{10},\bar{x}_{20})$ 是系统 (1.2) 的初始条件. 根据 $\Omega$ 是正不变集可得 $\mathcal{A}\Omega \subset \Omega$. 现证明算子 $\mathcal{A}$ 是全连续的. 由于系统 (1.2) 的解是连续函数因此对应的算子 $\mathcal{A}$ 也是连续的; 接着证明 $\mathcal{A}\Omega$ 是相对紧的, 由 Arzela-Ascoli 定理[19]仅需证明 $\mathcal{A}\Omega$ 是一致有界且是等度连续. 根据 $\Omega$ 的有界性易得 $\mathcal{A}\Omega \subset \Omega$ 是有界的; 又借助 $\frac{\mathrm{d} x_i(t)}{\mathrm{d} t}\ (i=1,2)$ 的有界性可得 $\mathcal{A}\Omega$ 是等度连续的. 所以根据 Schauder 不动点定理[18]得 $\mathcal{A}$ 在 $\Omega$ 内至少存在一个正不动点, 对应的系统 (1.2) 至少存在一个周期解 $x^*(t)=(x_1^*(t),x_2^*(t))$.

最后我们证明周期解的唯一性和稳定性. 将系统 (1.2) 改写成

$\begin{equation*}\begin{aligned}\left\{\begin{aligned}&\dot x{_{1}}(t)=f_1(t,x_1,x_2),\\&\dot x{_{2}}(t)=f_2(t,x_1,x_2),\end{aligned}\right.\end{aligned}\end{equation*}$

这里 $f_i(t,x_1,x_2)\ (i=1,2)$ 在 $\Omega \subset R^2_+$ 上关于 $x_i$ 满足 Lipschitz 条件, 同时范数定义为

$ \| (x_1,x_2) \|=\max\{|x_1|,|x_2|\},$

其中 $ (x_1,x_2)\in \Omega$.

不难证明上述系统定义在 $\Omega$ 上的解的存在唯一性问题等价于积分方程解的存在性问题, 显然算子 $\mathcal{A}$ 满足压缩映射, 因此根据压缩映射原理[19] 可以得到算子方程 $\mathcal{A}X_0=X(w,X_0)$ 存在唯一的不动点, 并且由于不动点具有正坐标, 所以对应的系统 (1.2) 有唯一的正周期解. 根据文献 [4, 定理 3] 的证明方法可以得到算子 $\mathcal{A}$ 是单调的, 正的和凹的, 因此系统 (1.2) 的周期解 $x^*(t)=(x^*_1(t),x^*_2(t))$ 是全局渐近稳定的, 即对于系统 (1.2) 满足 $X_0=(\bar{x}_{10},\bar{x}_{20}) \in \Omega $ 的任意解 $\bar{x}(t)=(\bar{x}_1(t),\bar{x}_2(t))$ 有 $\lim\limits_{t\rightarrow \infty} (\bar{x}_1(t),\bar{x}_2(t))=(x^*_{1}(t),x^*_{2}(t))$.

引理 2.5 证明完毕.

3 主要结果

下面我们分四个部分证明系统 (1.4) 的持久性, 并根据文献 [22, 定理 1] 得到系统 (1.4) 正周期解的存在性.

定理3.1 假设 (H1) 与 (H2) 成立, 则满足初始条件 (2.1) 的系统 (1.4) 在 $[0,+\infty)$ 上存在非负解 $x(t)=(x_1(t),x_2(t),x_3(t))$ 且其是最终有界的.

证 对于任意 $\phi \in C^+_w(\mathbb{R})$ 定义

$\begin{equation*}\begin{aligned}h(t, \phi)=\left(\begin{array}{c}\alpha(t)\phi_2(0)-\gamma_1(t)\phi_1(0)-\beta(t)\phi_1(0)-\eta_1(t)\phi_1^2(0) \\[2mm] \beta(t)\phi_1(0)-\gamma_2(t)\phi_2(0)-\eta_2(t)\phi_2^2(0)-d(t)\phi_2(0) \int_{-\infty}^{0} k_1(s)\phi_3(s){\rm d}s \\[3mm] \phi_3(0)(-e(t)\phi_3(0)+f(t) \int_{-\infty}^{0} k_2(s)\phi_2(s){\rm d}s)\end{array}\right).\end{aligned}\end{equation*}$

由于 $h(t, \phi)$ 在 $(t,\phi) \in \mathbb{R}\times C^+_w(\mathbb{R})$ 上连续, 且 $h(t, \phi)$ 关于 $\phi$ 在 $\mathbb{R}\times C^+_w(\mathbb{R})$ 上满足 Lipschitz 条件. 由泛函微分方程基本理论[20]易得系统 (1.4) 满足 $x_0=\phi$ 的解存在于它的最大存在区间 $[0,T_\phi)$ 上, 若 $\phi_i(0)=0\ (i=1,2,3)$, 那么 $h(t,\phi) \geq 0$, 此时根据文献 [21,定理 5.2.1] 可以得到模型 (1.4) 满足初始条件 (2.1) 的解在区间 $[0,T_\phi)$ 上是非负的.

首先证明解的最大存在区间是 $[0,\infty)$. 否则令解的最大存在区间是 $[0,T_\phi)$ 且 $T_\phi < \infty$, 则当 $t\rightarrow T_\phi$ 时解是无界的.

对于任意 $t \in [0,T_\phi)$, 由模型 (1.4) 及假设 (H2) 可得

$\begin{equation*}\begin{aligned}\left\{\begin{aligned}&\dot x{_{1}}(t)=\alpha(t) x_{2}(t)-\gamma_{1}(t)x_{1}(t)-\beta(t) x_{1}(t)-\eta_{1}(t)x^2_{1}(t),\\&\dot x{_{2}}(t) \leq \beta(t) x_{1}(t)-\gamma_{2}(t)x_{2}(t)-\eta_{2}(t) x^2_{2}(t).\\\end{aligned}\right.\end{aligned}\end{equation*}$

因此构造辅助系统

$\begin{equation*}\begin{aligned}\left\{\begin{aligned}&\dot x{_{1}}(t)=\alpha(t) x_{2}(t)-\gamma_{1}(t)x_{1}(t)-\beta(t) x_{1}(t)-\eta_{1}(t)x^2_{1}(t),\\&\dot x{_{2}}(t) = \beta(t) x_{1}(t)-\gamma_{2}(t)x_{2}(t)-\eta_{2}(t) x^2_{2}(t),\\\end{aligned}\right.\end{aligned}\end{equation*}$

根据引理 2.5 可得当假设 (H1) 成立时有 $\bar{x}_i(t) \rightarrow x_i^*(t)$, 其中 $\bar{x}(t)=(\bar{x}_1(t),\bar{x}_2(t))$ 是模型 (1.2) 满足初值 $\bar{x}(0)=x(0)$ 的解, 根据 $x_i^*(t)$ 的全局渐近稳定性, 所以 $\bar{x}_i(t)(i=1,2)$ 在 $\mathbb{R}_+$ 上有界.

接着根据引理 2.1 可得

$\begin{equation} \begin{aligned}x_i(t) \leq \bar{x}_i(t), i=1,2, \quad \text{对所有 $t \in [0,T_\phi)$ 成立},\end{aligned}\end{equation}$

因此 $x_i(t)\ (i=1,2)$ 在 $[0,T_\phi)$ 上有界. 此外对于 $t \in [0,T_\phi)$ 我们有

$\begin{equation*}\begin{aligned}u(t) < u(0) {\rm e}^{\int_{0}^{t} \left[f(u)\int_{-\infty}^{0}k_1(s)x_2(u+s){\rm d}s \right]{\rm d}u},\end{aligned}\end{equation*}$

由 $x_i(t)\ (i=1,2)$ 的有界性, 易得 $u(t)$ 在 $t \in [0,T_\phi)$ 上有界. 显然这与假设矛盾, 因此 $T_\phi=\infty$, 即系统解的最大存在区间是 $[0,\infty)$.

令 $ M_1 >\max_{t \in R} |x^*(t)|$, 其中 $|x^*(t)|=\sum\limits_{i=1}^{2} x_i^*(t)$. 由于 $t\rightarrow \infty$ 时 $\bar{x}_i(t) \rightarrow x_i^*(t)\ (i=1,2)$, 因此存在 $\tilde{T}>0$ 使得

$\begin{equation*}\begin{aligned}\bar{x}_i(t) < M_1, \quad i=1,2, \quad t \geq \tilde{T},\end{aligned}\end{equation*}$

因此, 由 (3.1) 式可得

$\begin{equation*}\begin{aligned}x_i(t) < M_1, \quad i=1,2, \quad t \geq \tilde{T},\end{aligned}\end{equation*}$

所以

$\begin{equation*}\begin{aligned}\limsup_{t\rightarrow \infty} x_i(t) \leq M_1, \quad i=1,2.\end{aligned}\end{equation*}$

由引理 2.4, 我们进一步得到对于任意 $\varepsilon>0$, 存在常数 $\bar{T}> \tilde{T}$ 使得 $t>\bar{T}$ 时有

$\begin{equation*}\begin{aligned}\int_{-\infty }^{0}k_2(s)x_2(t+s){\rm d}s \leq M_1+\varepsilon,\end{aligned}\end{equation*}$

对于模型 (1.4) 的第三个方程我们有

$\begin{equation*}\begin{aligned}\dot{u}(t) \leq u(t)[-e(t)u(t)+(M_1+\varepsilon) f(t)].\end{aligned}\end{equation*}$

此时构造辅助系统

$\begin{equation} \begin{aligned}\dot{\tilde{u}}(t) = \tilde{u}(t)[-e(t)\tilde{u}(t)+(M_1+\varepsilon) f(t)],\end{aligned}\end{equation}$

根据引理 2.2 以及假设 (H2) 可得存在正数 $\bar{u}$, 使得对于辅助系统 (3.2) 的任意解 $\tilde{u}(t)$ 有

$\begin{equation*}\begin{aligned}\limsup_{t\rightarrow \infty} \tilde{u}(t) \leq \bar{u},\end{aligned}\end{equation*}$

接着由引理 2.1, 易得

$\begin{equation} \begin{aligned}u(t) \leq \tilde{u}(t), \quad \text{对所有 $t \geq \bar{T}$ 成立}.\end{aligned}\end{equation}$

不妨令 $ M=\max\{M_1,\bar{u}\}$, 则有

$\begin{equation*}\begin{aligned}\limsup_{t\rightarrow +\infty} x_i(t)\leq M(i=1,2), \quad \limsup_{t\rightarrow +\infty} u(t)\leq M,\end{aligned}\end{equation*}$

且存在正数 $T>\bar{T}$, 当 $t>T$ 时有

$\begin{equation*}\begin{aligned}x_i(t)< M(i=1,2), \quad u(t) < M.\end{aligned}\end{equation*}$

综上定理 3.1 证毕.

定理 3.2 假设 (H1) 与 (H2) 成立, 令 $x^*(t)=(x_1^*(t),x_2^*(t))$ 是模型 (1.2) 的周期解, 若

$\begin{equation*}\begin{aligned}\int_{0}^{w} \left[-e(t) +f(t) \int_{-\infty}^{0} k_2(s)x_2^*(t+s){\rm d}s \right]{\rm d}t>0,\end{aligned}\end{equation*}$

则存在常数 $\sigma_3>0$ 使得对于系统 (1.4) 的任意正解 $x(t)=(x_1(t),x_2(t),u(t))$ 满足

$\begin{equation*}\begin{aligned}\liminf_{t\rightarrow +\infty} u(t) \geq \sigma_3.\end{aligned}\end{equation*}$

证 根据定理 3.2 的条件我们可以选择充分小的正数 $\epsilon_0>0$ 满足

$\begin{equation} \begin{aligned}\int_{0}^{w} \left[-e(t) +f(t) \int_{-\infty}^{0} k_2(s)x_2^*(t+s){\rm d}s -2f(t)\epsilon_0 \right]{\rm d}t> \epsilon_0.\end{aligned}\end{equation}$

对于任意正数 $\xi>0$, 考虑辅助系统

$\begin{equation} \begin{aligned}\left\{\begin{aligned}&\dot x{_{1}}(t)=\alpha(t) x_{2}(t)-\gamma_{1}(t)x_{1}(t)-\beta(t) x_{1}(t)-\eta_{1}(t)x^2_{1}(t),\\&\dot x{_{2}}(t)=\beta(t) x_{1}(t)-\gamma_{2}(t)x_{2}(t)-\eta_{2}(t) x^2_{2}(t)-2\xi d(t) x_2(t),\\\end{aligned}\right.\end{aligned}\end{equation}$

根据假设 (H1), 对于充分小的正常数 $\xi>0$ 使得

$\begin{equation*}\begin{aligned}\alpha^L \beta^L> (\gamma_2^M + 2\xi d^M) (\gamma_1^M+\beta^M),\end{aligned}\end{equation*}$

则由引理 2.5 可得模型 (3.5) 存在唯一全局渐近稳定的周期解 $x^*_\xi(t)$, 令 $x_\xi(t)$ 是模型 (3.5) 满足 $x_\xi(0)=x(0)$ 的任意正解, 那么对于上述 $\epsilon_0$, 存在正常数 $T_0$ 使得

$\begin{equation*}\begin{aligned}| x^*_{i\xi}(t)- x_{i\xi}(t) | < \frac{\epsilon_0}{2}, \quad t>T_0, \quad i=1,2.\end{aligned}\end{equation*}$

另外通过解关于参数的连续性可得当 $\xi\rightarrow 0$ 时, $x_\xi(t)$ 在 $[T_0,T_0+w]$ 上一致收敛于 $x^*(t)$, 因此存在 $0<\xi_0 <\epsilon_0$ 使得对于任意 $0 < \xi < \xi_0$ 有

$\begin{equation*}\begin{aligned}| x^*_{i\xi}(t)- x_i^*(t) | < \frac{\epsilon_0}{2}, \quad t \in [T_0,T_0+w], \quad i=1,2.\end{aligned}\end{equation*}$

接着由 $x^*_{\xi}(t)$ 和 $x^*(t)$ 的周期性, 则有

$\begin{equation} \begin{aligned}| x^*_{i\xi}(t)- x_i^*(t) | < \frac{\epsilon_0}{2}, \quad t \in R, \quad i=1,2.\end{aligned}\end{equation}$

下面我们分两部分讨论, 首先证明

$\begin{equation} \begin{aligned}\limsup_{t \to \infty} u(t) \geq \xi,\end{aligned}\end{equation}$

假设结论不成立, 则对于任意 $0<\xi< \xi_0$, 系统 (1.4) 存在一个正解 $x(t)=(x_1(t),x_2(t),u(t))$ 使得

$\begin{equation*}\begin{aligned}\limsup_{t \to \infty} u(t) < \xi,\end{aligned}\end{equation*}$

因此存在 $T_1>0$, 使得当 $t>T_1$ 时有 $u(t)<\xi < \epsilon_0$.

此外选择正数 $t_1$ 使得

$\begin{equation*}\begin{aligned}H \int_{-\infty }^{-t_1} k(s){\rm d}s<\xi,\end{aligned}\end{equation*}$

其中 $H=H_0+M_1, k(s)=k_1(s)+k_2(s)$, 且 $H_0=\sup\{x_2(t+s),u(t+s)\}$.

则对于 $t>T_1+t_1$ 我们有

$\begin{equation*}\left\{\begin{aligned}\dot x_1(t) &=\alpha(t)x_2(t)-r_1(t)x_1(t)-\beta(t)x_1(t)-\eta_1(t)x^2_1(t),\\\dot x_2(t) & = \beta(t)x_1(t)-r_2(t)x_2(t)-\eta_2(t)x^2_2(t)- d(t)x_2(t) \left\{ \int_{-\infty }^{-t_1}+\int_{-t_1}^{0} \right\} k_1(s)u(t+s){\rm d}s,\\&\geq \beta(t)x_1(t)-r_2(t)x_2(t)-\eta_2(t)x^2_2(t)-2\xi d(t)x_2(t),\end{aligned}\right.\end{equation*}$

根据引理 2.1 可得

$\begin{equation} \begin{aligned}x_i(t) \geq x_{i\xi}(t), \quad t \geq T_1+t_1,\end{aligned}\end{equation}$

其中 $x_{\xi}(t)=(x_{1\xi}(t),x_{2\xi}(t))$ 是模型 (3.5) 满足初值 $x_{\xi}(T_1+t_1)=x(T_1+t_1)$ 的任意解, 根据周期解 $x^*_{\xi}(t)$ 的全局渐近稳定性, 存在 $T_2>T_1+t_1$ 使得

$\begin{equation} \begin{aligned}| x_{i\xi}(t)- x^*_{i\xi}(t) | < \frac{\epsilon_0}{2}, \quad t>T_2, \quad i=1,2.\end{aligned}\end{equation}$

进一步由 (3.6), (3.8) 和 (3.9) 式可得

$\begin{equation*}\begin{aligned}x_i(t) \geq x^*_i(t)-\epsilon_0, \quad t>T_2, \quad i=1,2.\end{aligned}\end{equation*}$

此时存在 $T_3>T_2$ 使得当 $t>T_3+t_1$ 时有

$\begin{equation*}\begin{aligned}\dot u(t)& \geq u(t)\bigg[-e(t)\epsilon_0 +f(t)\int_{-t_1}^{0}k_2(s)x_2(t+s){\rm d}s \bigg] \\& \geq u(t) \bigg[-e(t)+ f(t)\int_{-t_1}^{0}k_2(s)(x^*_2(t+s)-\epsilon_0){\rm d}s \bigg] \\& \geq u(t) \bigg[-e(t) + f(t)\int_{-t_1}^{0}k_2(s)x^*_2(t+s){\rm d}s-f(t)\epsilon_0\int_{-\infty}^{0}k_2(s){\rm d}s \bigg] \\& = u(t) \bigg[-e(t)+ f(t)\int_{-\infty}^{0}k_2(s)x^*_2(t+s){\rm d}s-f(t)\epsilon_0-f(t)\int_{-\infty}^{-t_1}k_2(s)x^*_2(t+s){\rm d}s \bigg] \\& \geq u(t) \bigg[-e(t)+ f(t)\int_{-\infty}^{0}k_2(s)x^*_2(t+s){\rm d}s-2f(t)\epsilon_0 \bigg],\end{aligned}\end{equation*}$

对上式两边从 $T_3+t_1$ 到 $t$ 积分, 应用 (3.8) 式显然可得 $t \rightarrow \infty$ 时 $u(t)\rightarrow \infty$, 这与假设矛盾, 所以 (3.7) 式成立.

我们继续证明定理 3.3 的结果. 假设结论不成立, 则系统 (1.4) 存在一个初始函数序列 $\{ \Phi_k\} \subset C_w^+(\mathbb{R})$ 使得对于其任意解有

$\begin{equation*}\begin{aligned} \liminf_{t \to \infty} u(t,\Phi _k)<\frac{\xi}{k+1}, \quad k=1,2,\cdots.\end{aligned}\end{equation*}$

根据 (3.7) 式, 对于任意正整数 $k$ 存在时间序列 $\{s_q^{(k)}\},\{t_q^{(k)}\}$ 满足

$\begin{equation*}\begin{aligned} 0 < s_1^{(k)} < t_1^{(k)} < s_2^{(k)} < t_2^{(k)} < \cdots < s_q^{(k)} <t_q^{(k)} <\cdots,\end{aligned}\end{equation*}$
$\begin{equation*}\begin{aligned}s^{(k)}_q \rightarrow \infty, t^{(k)}_q \rightarrow \infty, \quad q \rightarrow \infty,\end{aligned}\end{equation*}$

使得

$\begin{equation*}\begin{aligned}u(s^{(k)}_q,\Phi_k)=\xi, \quad u(t^{(k)}_q,\Phi_k)=\frac{\xi}{k+1},\end{aligned}\end{equation*}$
$\begin{equation} \begin{aligned}\frac{\xi}{k+1} < u(t,\Phi_k) < \xi <\epsilon_0, \quad t \in (s^{(k)}_q,t^{(k)}_q).\end{aligned}\end{equation}$

由定理 3.1 可知, 对于任意正整数 $k$ 存在正数 $M,T_3^{(k)}>T^{(k)}$ 使得 $t>T_3^{(k)}$ 时有 $x_i(t,\Phi_k) < M$, $u(t,\Phi_k)<M$. 此外对于任一 $k$ 选择 $t_1^{(k)}$ 使得

$\begin{equation} \begin{aligned}H_0^{(k)} \int_{-\infty }^{-t^{(k)}_1} k(s){\rm d}s<\xi,\end{aligned}\end{equation}$

这里 $H_0^{(k)}=\sup\{x_2(t+s,\phi_k),u(t+s,\phi_k)\}$. 选择正整数 $K_1^{(k)}$ 使得当 $q \geq K_1^{(k)}$ 时有 $s^{(k)}_q >T_3^{(k)}+t_1^{(k)}$, 并且

$\begin{equation*}\begin{aligned}\dot u(t,\Phi_k) &=u(t,\Phi_k) \bigg[-e(t)u(t,\Phi_k)+f(t)\int_{-\infty }^{0}k_2(s)x_2(t+s,\Phi_k){\rm d}s \bigg]\\& \geq u(t,\Phi_k)( -e(t)M),\\\end{aligned}\end{equation*}$

对上式从 $s^{(k)}_q$ 到 $t^{(k)}_q$ 进行积分, 则有

$\begin{equation} \begin{aligned}t^{(k)}_q-s^{(k)}_q \geq \frac{\ln(k+1)}{r_1}, \quad q \geq K_1^{(k)},\end{aligned}\end{equation}$

这里 $r_1=\max\limits_{t \in R}\{|e(t)|M\}$.

接着根据 (3.11) 式, 对于任意正整数 $k$ 存在正整数 $K_2^{(k)}>K_1^{(k)}$ 使得 $q \geq K_2^{(k)}$ 时有

$\begin{equation*}\begin{aligned}H_0^{(k)} \int_{-\infty }^{T_3^{(k)}-s^{(k)}_q} k(s){\rm d}s < \frac{\xi}{2},\end{aligned}\end{equation*}$

以及存在常数 $t_1$ 使得

$\begin{equation*}\begin{aligned}M\int_{-\infty }^{-t_1} k(s){\rm d}s < \frac{\xi}{2},\end{aligned}\end{equation*}$

由 (3.12) 式, 存在正整数 $K_0$ 使得 $k \geq K_0, q \geq K_2^{(k)} $ 时有 $t^{(k)}_q-s^{(k)}_q > t_1$. 则对于任意 $t \in [s^{(k)}_q+t_1, t^{(k)}_q]$ 有

$\begin{equation*}\left\{\begin{aligned}\dot x_1(t,\Phi_k) &=\alpha(t)x_2(t,\Phi_k)-r_1(t)x_1(t,\Phi_k)-\beta(t)x_1(t,\Phi_k)-\eta_1(t)x^2_1(t,\Phi_k),\\\dot x_2(t,\Phi_k) & = \beta(t)x_1(t,\Phi_k)-r_2(t)x_2(t,\Phi_k)-\eta_2(t)x^2_2(t,\Phi_k)\\& -d(t)x_2(t,\Phi_k) \left\{\int_{-\infty }^{T_3^{(k)}}+\int_{T_3^{(k)}}^{s^{(k)}_q}+\int_{s^{(k)}_q}^{t} \right\} k_1(s-t)u(s,\Phi_k){\rm d}s\\&\geq \beta(t)x_1(t,\Phi_k)-r_2(t)x_2(t,\Phi_k)-\eta_2(t)x^2_2(t,\Phi_k)\\& -d(t)x_2(t,\Phi_k) \left\{H_0^{(k)}\int_{-\infty }^{T_3^{(k)}-t}+M \int_{-\infty}^{s^{(k)}_q-t}+\xi \int_{-\infty}^{0} \right\} k_1(s){\rm d}s\\&\geq \beta(t)x_1(t,\Phi_k)-r_2(t)x_2(t,\Phi_k)-\eta_2(t)x^2_2(t,\Phi_k)-2\xi d(t)x_2(t,\Phi_k),\end{aligned}\right.\end{equation*}$

根据引理 2.1 易得

$\begin{equation*}\begin{aligned}x_i(t,\Phi_k) \geq x_{i\xi}(t), \quad t \in [s^{(k)}_q+t_1,t^{(k)}_q], \quad i=1,2,\end{aligned}\end{equation*}$

其中 $x_{\xi}(t)=(x_{1\xi}(t),x_{2\xi}(t))$ 是模型 (3.5) 满足初值 $x_{i\xi}(s^{(k)}_q+t_1)=x_i(s^{(k)}_q+t_1,\Phi_k)$ 的任意解. 接着根据唯一正周期解 $x^*_{\xi}(t)$ 的全局渐近稳定性, 易得存在正数 $P_1$ 使得

$\begin{equation*}\begin{aligned}x_{i\xi}(t)>x^*_{i\xi}(t)-\frac{\epsilon_0}{2}, \quad t\geq s^{(k)}_q+t_1+P_1.\end{aligned}\end{equation*}$

由 (3.11) 式, 存在正数 $\bar{K}_0>K_0$ 使得 $k \geq \bar{K}_0, q \geq K_2^{(k)} $ 时有

$\begin{equation*}\begin{aligned}t^{(k)}_q-s^{(k)}_q >2L_1,\end{aligned}\end{equation*}$

其中 $L_1>P_1+t_1$, 则我们有

$\begin{equation*}\begin{aligned}x_i(t,\Phi_k) \geq x^*_i(t)-\epsilon_0, \quad t \in [s^{(k)}_q+L_1,t^{(k)}_q].\end{aligned}\end{equation*}$

因此对于 $t \in [s^{(k)}_q+L_1+t_1,t^{(k)}_q]$ 有

$\begin{equation*}\begin{aligned}\dot u(t,\Phi_k)& \geq u(t,\Phi_k) \bigg[-e(t)\epsilon_0+f(t)\int_{-t_1}^{0}k_2(s)x_2(t+s,\Phi_k){\rm d}s \bigg] \\& \geq u(t,\Phi_k) \bigg[-e(t)+ f(t)\int_{-t_1 }^{0}k_2(s)(x^*_2(t+s,\Phi_k)-\epsilon_0){\rm d}s \bigg]\\& \geq u(t,\Phi_k) \bigg[-e(t)+ f(t)\int_{-\infty }^{0}k_2(s)x^*_2(t+s,\Phi_k){\rm d}s-2f(t)\epsilon_0 \bigg],\\\end{aligned}\end{equation*}$

对上式从 $s^{(k)}_q+L_1+t_1$ 到 $t^{(k)}_q$ 积分易得

$\begin{equation*}\begin{aligned}u(t^{(k)}_q,\Phi_k)\geq u(s^{(k)}_q+L_1+t_1,\Phi_k){\rm e}^{\int_{s^{(k)}_q+L_1+t_1}^{t^{(k)}_q} \big[-e(t)+ f(t)\int_{-\infty }^{0}k_2(s)x_2(t+s,\Phi_k){\rm d}s- 2f(t)\epsilon_0 \big]{\rm d}t},\end{aligned}\end{equation*}$

因此应用 (3.4) 式易得

$\begin{equation*}\begin{aligned}\frac{\xi}{k+1} & \geq \frac{\xi}{k+1} {\rm e}^{\int_{s^{(k)}_q+L_1+t_1}^{t^{(k)}_q} \big[-e(t)+ f(t)\int_{-\infty }^{0}k_2(s)x_2(t+s,\Phi_k){\rm d}s- 2f(t)\epsilon_0 \big]{\rm d}t}& > \frac{\xi}{k+1},\end{aligned}\end{equation*}$

显然这是矛盾的, 所以定理 3.2 结论成立, 定理 3.2 证明完毕.

定理 3.3 若定理 $3.2$ 的所有条件成立, 则存在正数 $\sigma_2(\sigma_2<{M})$ 使得系统 (1.4) 满足初始条件 (2.1) 的任意正解 $(x_1(t),x_2(t),u(t))$ 有

$\begin{equation*}\begin{aligned}\liminf_{t\rightarrow +\infty} x_2(t) \geq \sigma_2.\end{aligned}\end{equation*}$

证 根据 $x^*(t)=(x_1^*(t),x^*_2(t))$ 的正性, 选择充分小的正常数 $0<\delta<\sigma_3$, 使得

$\begin{equation} \begin{aligned}x_i^*(t)-\delta > \delta (i=1,2),\end{aligned}\end{equation}$
$\begin{equation} \begin{aligned}\int_{0}^{w} \bigg[-e(t)\sigma_3 +2 \delta f(t)\bigg]{\rm d}t < -\delta.\end{aligned}\end{equation}$

对于任意正数 $ \tau $, 考虑辅助系统

$\begin{equation} \begin{aligned}\left\{\begin{aligned}&\dot x{_{1}}(t)=\alpha(t) x_{2}(t)-\gamma_{1}(t)x_{1}(t)-\beta(t) x_{1}(t)-\eta_{1}(t)x^2_{1}(t),\\&\dot x{_{2}}(t)=\beta(t) x_{1}(t)-\gamma_{2}(t)x_{2}(t)-\eta_{2}(t) x^2_{2}(t)-2 \tau d(t) x_2(t),\\\end{aligned}\right.\end{aligned} \end{equation}$

根据假设 (H1), 存在充分小的正数 $ \tau>0 $ 使得

$\begin{equation*}\begin{aligned}\alpha^L \beta^L> (\gamma_2^M + 2 \tau d^M) (\gamma_1^M+\beta^M),\end{aligned}\end{equation*}$

则由引理 2.5 可得模型 (3.15) 存在唯一全局渐近稳定的周期解 $x^*_\tau(t)$, 令 $x_\tau(t)$ 是模型 (3.15) 满足初始条件 $x_\tau(0)=x(0)$ 的任意正解. 另外通过解关于参数的连续性可得当 $ \tau \rightarrow 0$ 时, $x_\tau(t)$ 在 $[w]$ 上一致收敛于 $x^*(t)$, 因此存在 $0< \tau_0 < \delta$ 使得对于任意 $0 < \tau < \tau_0$ 有

$\begin{equation*}\begin{aligned}| x^*_{i \tau}(t)- x^*(t) | < \frac{\delta}{2}, \quad i=1,2, \quad t \in [w],\end{aligned}\end{equation*}$

进一步由 $x^*_{\tau}(t)$ 和 $x^*(t)$ 的周期性, 可得

$\begin{equation} \begin{aligned}| x^*_{i \tau}(t)- x^*(t) | < \frac{\delta}{2}, \quad t \in \mathbb{R}, \quad i=1,2.\end{aligned}\end{equation}$

类似于文献 [14, 定理 3] 的证明过程, 我们将分两部分完成. 首先证明

$\begin{equation} \begin{aligned}\limsup_{t \to \infty} x_2(t) \geq \tau,\end{aligned}\end{equation}$

假设结论不成立, 则对于系统 (1.4) 存在一个满足初始条件 (2.1) 的正解 $(x_1(t),x_2(t),u(t))$ 使得

$\begin{equation*}\begin{aligned}\limsup_{t \to \infty} x_2(t) \leq \tau,\end{aligned}\end{equation*}$

因此存在 $D_1>0$ 使得

$\begin{equation} \begin{aligned}x_2(t)< \tau < \delta, \quad t>D_1.\end{aligned}\end{equation}$

此外选择常数 $t_2>0$, 使得

$\begin{equation*}\begin{aligned} H_0 \int_{-\infty }^{-t_2} k(s){\rm d}s< \tau <\delta,\end{aligned}\end{equation*}$

这里 $H_0=\sup\{x_2(t+s),u(t+s)\}, k(s)=k_1(s)+k_2(s)$.

所以当 $t>D_1+t_2$ 时, 由模型 (1.4) 的第三式有

$\begin{equation*}\begin{aligned}\dot u(t) &= u(t)\Bigg[-e(t)u(t)+f(t)\left\{\int_{-\infty }^{-t_2} + \int_{-t_2}^{0} \right\} k_2(s)x_2(t+s){\rm d}s \Bigg], \\&\leq u(t)[-e(t)\sigma_3 + 2 \delta f(t)],\end{aligned}\end{equation*}$

由 (3.14) 式易得当 $ t\rightarrow \infty$ 时 $u(t) \rightarrow0$. 因此存在正数 $D_2>D_1+t_2$, 当 $t>D_2$ 时有 $u(t)< \tau < \delta$.

接着当 $t>D_2+t_2$ 时易得

$\begin{equation*}\left\{\begin{aligned}\dot x_1(t) &=\alpha(t)x_2(t)-r_1(t)x_1(t)-\beta(t)x_1(t)-\eta_1(t)x^2_1(t),\\\dot x_2(t) & = \beta(t)x_1(t)-r_2(t)x_2(t)-\eta_2(t)x^2_2(t)- d(t)x_2(t) \left\{\int_{-\infty }^{-t_2}+\int_{-t_2}^{0} \right\} k_1(s)u(t+s){\rm d}s \\&\geq \beta(t)x_1(t)-r_2(t)x_2(t)-\eta_2(t)x^2_2(t)-2 \tau d(t)x_2(t),\end{aligned}\right.\end{equation*}$

根据引理 2.1 易得

$\begin{equation} \begin{aligned}x_i(t) \geq x_{i\tau}(t), \quad i=1,2, \quad t>D_2+t_2,\end{aligned}\end{equation}$

这里 $x_{\tau}(t)=(x_{1 \tau}(t),x_{2 \tau}(t))$ 是系统 (3.15) 满足初值 $x_{\tau}(D_2+t_2)=x(D_2+t_2)$ 的解. 由周期解 $x_{\tau}^*(t)$ 的全局渐近稳定性, 可得存在 $D_3=\max\{D_2+t_2,T\}$ 使得 $t>D_3$ 时有

$\begin{equation} \begin{aligned}\left | x_{i \tau }(t)-x^*_{i \tau }(t) \right | < \frac{\delta}{2},\end{aligned}\end{equation}$

因此由 (3.16), (3.19) 和 (3.20) 式我们得到

$\begin{equation} \begin{aligned}x_i(t) \geq x_{i \tau}(t) \geq x^*(t)-\delta > \delta, \quad i=1,2.\end{aligned}\end{equation}$

这与 (3.18) 式矛盾, 因此 (3.17) 式成立.

我们继续证明定理 3.3, 假设结论不成立, 则模型 (1.4) 存在一个初始函数序列 $\{ \varphi_k\} \subset C_w^+(R)$ 使得对于其任意解 $x(t)=(x_1(t),x_2(t),u(t))$ 有

$\begin{equation*}\begin{aligned}\liminf_{t \to \infty} x_2(t,\varphi _k)<\frac{\tau}{2k^2}, k=1,2,\cdots.\end{aligned}\end{equation*}$

由 (3.17) 式易得对于每一个 $k$ 存在两个时间序列 $\{S^{(k)}_q\},\{V^{(k)}_q\}$ 满足

$\begin{equation*}\begin{aligned}0<S^{(k)}_1 < V^{(k)}_1 < S^{(k)}_2 < V^{(k)}_2 <\cdots < S^{(k)}_q < V^{(k)}_q <\cdots,\end{aligned}\end{equation*}$
$\begin{equation*}\begin{aligned}S^{(k)}_q \rightarrow \infty, V^{(k)}_q \rightarrow \infty, \quad q \rightarrow \infty,\end{aligned}\end{equation*}$
$\begin{equation*}\begin{aligned}x_2(S^{(k)}_q,\varphi_k)=\frac{\tau}{k}, \quad x_2(V^{(k)}_q,\varphi_k)=\frac{\tau}{k^2},\end{aligned}\end{equation*}$

且

$\begin{equation} \begin{aligned}\frac{\tau}{k^2} < x_2(t,\varphi_k) < \frac{\tau}{k}< \delta, \quad t \in (S^{(k)}_q,V^{(k)}_q).\end{aligned}\end{equation}$

由定理 3.1 可知, 对于任意正整数 $k$ 存在正数 $M, D_3^{(k)}>T^{(k)}$ 使得 $t>D_3^{(k)}$ 时有 $x_i(t,\varphi_k) < M, u(t,\varphi_k)<M$. 此外对于任一正整数 $k$ 取常数 $t^{(k)}_2>0$ 使得

$\begin{equation} \begin{aligned}H^{(k)}_0 \int_{-\infty }^{-t^{(k)}_2} k(s){\rm d}s<\xi,\end{aligned}\end{equation}$

这里 $H_0^{(k)}=\sup\{x_2(t+s,\varphi_k),u(t+s,\varphi_k)\}$. 因此存在正整数 $N^{(k)}_1>0$ 使得当 $q \geq N^{(k)}_1$ 有 $S_1^{(k)}>D^{(k)}_3+t^{(k)}_2$. 接着由模型 (1.4) 的第二个方程有

$\begin{equation*}\begin{aligned}\dot x_2(t,\varphi_k) & > -r_2(t)x_2(t,\varphi_k)-\eta_2(t)x^2_2(t,\varphi_k)\\& -d(t)x_2(t,\varphi_k) \left \{ \int_{-\infty }^{-t^{(k)}_2}+\int_{-t^{(k)}_2}^{0} \right\} k_1(s)u(t+s,\varphi_k){\rm d}s \\&\geq -(r_2(t)+\eta_2(t)M+2d(t)M)x_2(t,\Phi_k)\\&\geq -\Psi^m x_2(t,\Phi_k),\end{aligned}\end{equation*}$

这里 $ \Psi^m=\max_{t\in R } \{ |r_2(t)| +| \eta_2(t)| M+2 |d(t)| M \}$, 则通过积分运算可以得到

$\begin{equation} \begin{aligned}V^{(k)}_q-S^{(k)}_q \geq \frac{\ln k}{\Psi^m},\quad \forall q \geq N_1^{(k)},k=1,2,\cdots.\end{aligned}\end{equation}$

由 (3.14) 式, 选择常数 $P_2>0$ 使 $ t \geq 0, a\geq P_2$ 时有

$\begin{equation} \begin{aligned}M {\rm e}^{\int_{t}^{t+a} \big[-e(u)\sigma_3+2 \delta f(u)\big]{\rm d}u} < \tau < \delta.\end{aligned}\end{equation}$

对于任一正整数 $k=1,2,\cdots$, 由 (3.23) 式我们选择常数 $N_2^{(k)}>N_1^{(k)}$ 使得当 $q\geq N_2^{(k)}$ 时有

$\begin{equation} \begin{aligned}H_0^{(k)}\int_{-\infty}^{D_3^{(k)}-S_q^{(k)}}k(s){\rm d}s <\frac{\delta}{2},\end{aligned}\end{equation}$

以及存在正数 $t_2$ 使得

$\begin{equation} \begin{aligned}M\int_{-\infty}^{-t_2}k(s){\rm d}s <\frac{ \delta }{2}.\end{aligned}\end{equation}$

由 (3.24) 和 (3.25) 式可得存在正数 $L_2$ 和整数 $N_0>0$ 使得

$\begin{equation} \begin{aligned}V^{(k)}_q-S^{(k)}_q>P_2+L_2, \quad k\geq N_0, q\geq N^{(k)}_2.\end{aligned}\end{equation}$

其中 $L_2> P_2+t_2$, 在下面的讨论中令 $k\geq N_0, q\geq N^{(k)}_2$, 任意 $t \in [S^{(k)}_q+t_2,V^{(k)}_q]$, 由 (3.22) (3.26) (3.27) 式有

$\begin{equation*}\begin{aligned}\dot u(t,\varphi_k) &=u(t,\varphi_k)\Bigg[-e(t)u(t,\varphi_k)+f(t) \left\{\int_{-\infty }^{D_3^{(k)}}+\int_{D_3^{(k)}}^{S^{(k)}_q}+\int_{S^{(k)}_q}^{t} \right\} k_2(s-t)x_2(s,\varphi_k){\rm d}s \Bigg] \\& \leq u(t,\varphi_k) \Bigg[-e(t)\sigma_3+f(t) \left \{H_0^{(k)} \int_{-\infty }^{D_3^{(k)}-S^{(k)}_q}+ M \int_{-\infty}^{-t_2} + \delta \int_{-\infty}^{0} \right\}k_2(s){\rm d}s \Bigg]\\& \leq u(t,\varphi_k)[-e(t) \sigma_3 +2 \delta f(t)],\end{aligned}\end{equation*}$

由 (3.14) 式, 对上述不等式从 $S^{(k)}_q+t_2$ 到 $t$ 积分, 易得

$\begin{equation*}\begin{aligned}u(t,\varphi_k) \leq u(S^{(k)}_q+t_2) {\rm e}^{\int_{S^{(k)}_q+t_2}^{t} \big[-e(u)\sigma_3+2 \delta f(u)\big]{\rm d}u},\end{aligned}\end{equation*}$

根据 (3.25) 和 (3.28) 式可得, 当 $t \in [S^{(k)}_q+t_2+P_2,V^{(k)}_q]$ 有

$\begin{equation*}\begin{aligned}u(t,\varphi_k) \leq M {\rm e}^{\int_{S^{(k)}_q+t_2+p_2}^{t} \big[-e(u)\sigma_3+2 \delta f(u)\big]{\rm d}u} < \delta,\end{aligned}\end{equation*}$

所以对于 $t \in \big[S^{(k)}_q+t_2+P_2,V^{(k)}_q \big]$, 系统 (1.4) 的前两个方程有

$\begin{equation*}\left\{\begin{aligned}\dot x_1(t,\varphi_k) &=\alpha(t)x_2(t,\varphi_k)-r_1(t)x_1(t,\varphi_k)-\beta(t)x_1(t,\varphi_k)-\eta_1(t)x^2_1(t,\varphi_k),\\\dot x_2(t,\varphi_k) &= \beta(t)x_1(t,\varphi_k)-r_2(t)x_2(t,\varphi_k)-\eta_2(t)x^2_2(t,\varphi_k)\\& -d(t)x_2(t,\varphi_k) \left\{\int_{-\infty }^{D_3^{(k)}}+\int_{D_3^{(k)}}^{S^{(k)}_q+P_2}+\int_{{S^{(k)}_q+P_2}}^{t} \right\} k_1(s-t)u(s,\varphi_k){\rm d}s \\&\geq \beta(t)x_1(t,\varphi_k)-r_2(t)x_2(t,\varphi_k)-\eta_2(t)x^2_2(t,\varphi_k)\\& -d(t)x_2(t,\varphi_k) \left\{H_0^{(k)} \int_{-\infty }^{D_3^{(k)}-t} + M \int_{-\infty}^{S^{(k)}_q+P_2-t} + \delta \int_{-\infty}^{0}\right \}k_1(s){\rm d}s \\&\geq \beta(t)x_1(t,\varphi_k)-r_2(t)x_2(t,\varphi_k)-\eta_2(t)x^2_2(t,\varphi_k)-2 \tau d(t)x_2(t,\varphi_k).\end{aligned}\right.\end{equation*}$

因此根据引理 2.1 可以得到

$\begin{equation*}\begin{aligned}x_i(t,\varphi_k) \geq x_{i \tau}(t), \quad \forall t \in \big[S^{(k)}_q+t_2+P_2,V^{(k)}_q \big].\end{aligned}\end{equation*}$

此时, 我们令 $t_0=S^{(k)}_q+t_2+P_2, x_0=\left(x_{1\tau}(S^{(k)}_q+t_2+P_2),x_{2 \tau}(S^{(k)}_q+t_2+P_2)\right)$, 则

$\begin{equation*}\begin{aligned}|x_{i \tau}(t,t_0,x_0)-x^*_{i \tau}(t)|< \frac{\delta}{2}, \quad t\geq S^{(k)}_q+P_2+L_2,\end{aligned}\end{equation*}$

所以,

$\begin{equation*}\begin{aligned}x_i(t,\Phi_k) \geq x_{i \tau}(t,\Phi_k) \geq x^*(t,\Phi_k)-\delta > \delta,\end{aligned}\end{equation*}$

显然这与 (3.22) 式矛盾, 因此定理 3.3 得证. 证毕.

定理 3.4 假设 (H1) 与 (H2) 成立, 令 $x^*(t)=(x_1^*(t),x_2^*(t))$ 是模型 $(1.2)$ 的周期解, 若

$\begin{equation*}\begin{aligned}\int_{0}^{w} \left[-e(t) +f(t) \int_{-\infty}^{0} k_2(s)x_2^*(t+s){\rm d}s \right]{\rm d}t>0,\end{aligned}\end{equation*}$

则系统 (1.4) 是持久的.

证 结合定义 2.1 以及定理 3.1-3.3, 我们仅需证明存在正数 $\sigma_1<M $ 使得

$\begin{equation*}\begin{aligned}\liminf_{t\rightarrow +\infty} x_1(t) \geq \sigma_1.\end{aligned}\end{equation*}$

应用定理 3.1 和 3.3 的结论, 对于系统 (1.4) 的第一个方程有

$\begin{equation*}\begin{aligned}\dot x_1(t)&=\alpha(t)x_2(t)-\gamma_1(t)x_1(t)-\beta(t)x_1(t)-\eta_1(t)x^2_1(t) \\& \geq \alpha(t) \sigma_2 -(\gamma_1(t)+\beta(t)+\eta(t) M)x_1(t).\\\end{aligned}\end{equation*}$

构造辅助系统

$\begin{equation} \begin{aligned}\dot {\tilde{x}}_1(t)& = \alpha(t) \sigma_2 -(\gamma_1(t)+\beta(t)+\eta(t) M)\tilde{x}_1(t),\end{aligned}\end{equation}$

根据引理 2.3 以及假设 (H2) 可得对于辅助系统 (3.29) 的任意正解 $\tilde{x}_1(t)$ 存在正数 $\sigma_1>0$, 使得

$\begin{equation*}\begin{aligned}\liminf_{t\rightarrow \infty} \tilde{x}_1(t) \geq \sigma_1.\end{aligned}\end{equation*}$

由引理 2.1 易得

$\begin{equation*}\begin{aligned}x_1(t) \geq \tilde{x}_1(t),\end{aligned}\end{equation*}$

对所有 $t \in [0,+\infty)$ 成立.

此时令 $m=\min\{\sigma_1,\sigma_2,\sigma_3\}$, 则可以得到

$\begin{equation*}\begin{aligned}&\liminf_{t\rightarrow \infty} x_i(t) \geq m(i=1,2), \quad \liminf_{t\rightarrow \infty} u(t)>m.\end{aligned}\end{equation*}$

结合定理 3.1-3.3, 定理 3.4 证明完毕.

由周期系统周期解的存在性定理[22], 即: 若周期系统是持久的, 则至少存在一个正周期解. 我们有以下结果

推论 3.1 若定理 3.4 的条件成立, 则模型 (1.4) 至少存在一个正周期解.

4 数值模拟

本节我们选取一些具有生物意义的参数演示理论结果. 首先令

$\int_{-\infty}^{0} k_1(s){\rm d}s=\int_{-\infty}^{0} k_2(s){\rm d}s=\int_{-\infty}^{0} {\rm e}^{s}{\rm d}s $(参见文献 [11]).

接着类似于文献 [23] 的方法, 令连续 $w$-周期函数

$g(t)=g_0[1+g_j \sin(\frac{2 \pi t}{w})], $

其中 $g_0$ 表示不受季节, 繁殖等因素影响的参数值; $g_j (0< g_j<1)$ 为波动幅度. 参考文献 [11] 取 $\alpha_j,\gamma_{1j},\gamma_{2j},\eta_{1j},\eta_{2j},d_j,e_j=0.1$, 并假定 $\beta_j,f_j=0.3, w=365$.

最后基于文献 [24,25], 在表1中给出具体参数值.

表1   参数的具体值

新窗口打开| 下载CSV


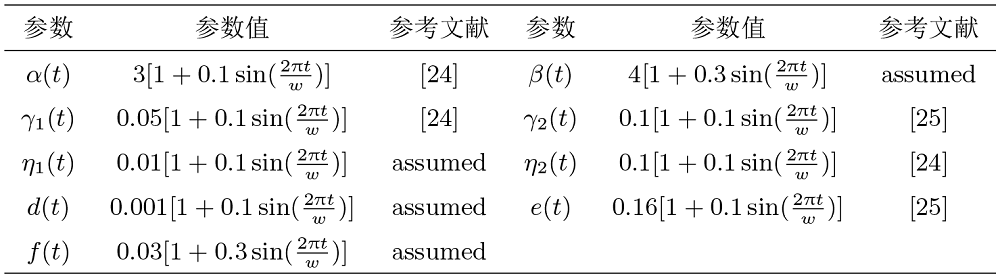
容易验证假设 (H1), (H2) 成立, 故由引理 2.5 可得系统 (1.2) 存在全局渐近稳定的周期解 $x^*(t)=(x^*_1(t),x^*_2(t))$, 由图1可知周期函数 $x_2^*(t)$ 的上下界分别为 27.7 和 26.4, 即 $26.4 \leq x^*_2(t) \leq 27.7$.

图1

新窗口打开| 下载原图ZIP| 生成PPT

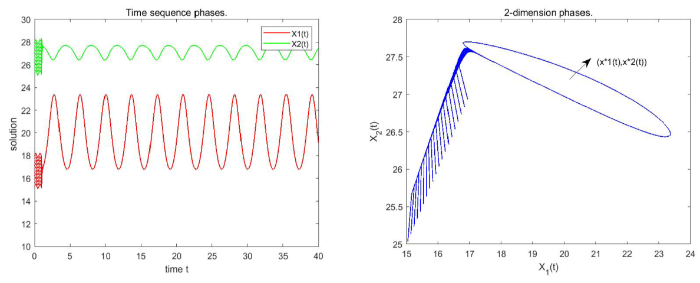
图1   辅助系统 (1.2) 的动力学行为. 左: 时间序列图; 右: 二维相图. 模型的初值为 $(\bar{x}_1(s),\bar{x}_2(s))=(15+0.1 \sin(s)+0.1 k,25+0.1 \sin(s)+0.1k)$, 其中 $k \in [0,20],s \in (-\infty,0]$.


不妨取 $M_1=500$, 根据引理 2.2 以及假设 (H2) 易得辅助系统 (3.2) 存在唯一全局渐近稳定的正周期解. 图2左图演示了该结果. 接着由

$\begin{equation*}\begin{aligned}&\int_{0}^{w} \Big[-e(t)+f(t) \int_{-\infty}^{0} k_2(s)x^*_2(t+s){\rm d}s \Big]{\rm d}t\\= \ & \int_{0}^{w} \Big[-0.16(1+0.1\sin(\frac{2\pi t}{365})+0.03(1+0.3\sin(\frac{2\pi t}{365}))*26.4 \Big]{\rm d}t\\> \ & 0.3944 >0,\end{aligned}\end{equation*}$

图2

新窗口打开| 下载原图ZIP| 生成PPT

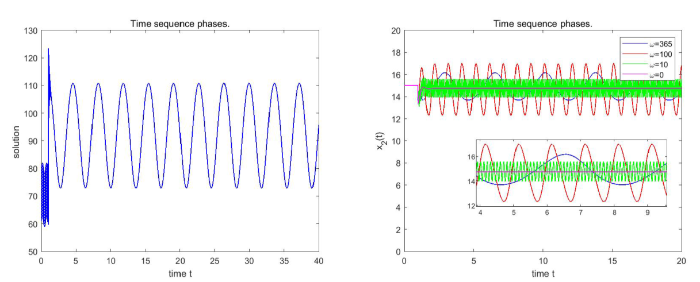
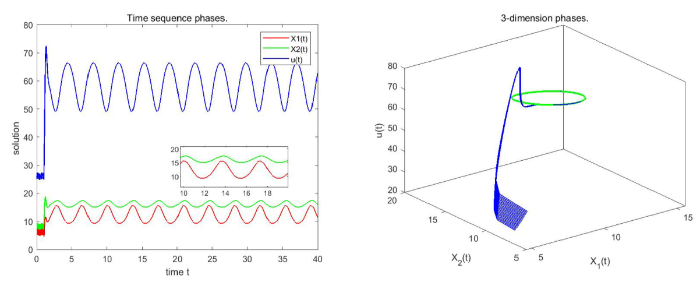
图2   左: 系统 (3.2) 的时间序列图. 模型的初值为 $(\tilde{u}(s))=(60+2\sin(s)+k) $, 其中 $k \in [0,20], s \in (-\infty,0]$. 右: 其他参数不变, 分别取不同 $w$ 值, $x_2(t)$ 的时间序列图.


可得定理 3.4 的条件成立, 因此, 根据定理 3.1-3.4 以及推论 3.1 可得模型 (1.4) 是持久的并且存在正周期解, 图3演示了上述结果.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   左: 系统 (1.4) 的时间序列图; 右: 系统 (1.4) 的三维空间相图. 模型的初值为 $(\phi_1(s),\phi_2(s),\phi_3(s))=(5+0.2 \sin(s)+0.1 k,7+0.2\sin(s)+0.1k,25+0.3\sin(s)+0.1k) $, 其中 $k \in [0,20], s \in (-\infty,0]$.


最后, 研究周期性对模型 (1.4) 的影响. 从图 2 右图中可以看到, 无周期时 $x_2(t)$ 趋于一条直线即达到正平衡点. 在模拟的情形中 $w=100$ 时峰值最大, $w=10$ 时波动最大. 因此考虑非自治模型与现实更吻合.

5 结论

具有无穷分布时滞和反馈控制的种群模型已经受到了广泛关注, 本文研究了一类具有反馈控制与无穷分布分布时滞的周期阶段结构单种群模型. 通过分析方法, 以积分的形式给出了系统持久性以及正周期解存在性的充分条件. 最后借助数值模拟演示了文中结果.

参考文献

Vance R R, Coddington E A.

A nonautonomous model of population growth

J Math Biol, 1989, 27(5): 491-506

PMID:2794800      [本文引用: 1]

With x = population size, the nonautonomous equation x = xf(t, x) provides a very general description of population growth in which any of the many factors that influence the growth rate may vary through time. If there is some fixed length of time (usually long) such that during any interval of this length the population experiences environmental variability representative of the variation that occurs in all time, then definite conclusions about the population's long-term behavior apply. Specifically, conditions that produce population persistence can be distinguished from conditions that cause extinction, and the difference between any pair of solutions eventually converges to zero. These attributes resemble corresponding features of the related autonomous population growth model x = xf(x).

Chen F D, Yang J H, Chen L J.

Note on the persistent property of a feedback control system with delays

Nonlinear Anal: Real World Appl, 2010, 11(2): 1061-1066

[本文引用: 1]

Liu S Q, Chen L S, Agarwal R.

Recent progress on stage-structured population dynamics

Math Comput Model, 2002, 36: 1319-1460

[本文引用: 2]

Cui J A, Chen L S, Wang W D.

The effect of dispersal on population growth with stage-structure

Comput Math Appl, 2000, 39(1/2): 91-102

[本文引用: 6]

Wang C Y, Li L R, Zhang Q Y.

Dynamical behaviour of a Lotka-Volterra competitive-competitive-cooperative model with feedback controls and time delays

J Biol Dyn, 2019, 13(1): 43-68

[本文引用: 2]

Gopalsamy K, Weng P X.

Feedback regulation of logistic growth

Internat J Math Sci, 1993, 16(1): 177-192

[本文引用: 1]

Jana S, Kar T K.

A mathematical study of a prey-predator model in relevance to pest control

Nonlinear Dyn, 2013, 74: 667-683

[本文引用: 1]

傅金波, 陈兰荪.

基于生态环境和反馈控制的多种群竞争系统的正周期解

数学物理学报, 2017, 37A(3): 553-561

[本文引用: 2]

Fu J B, Chen L S.

Positive periodic solution of multiple species comptition system with ecological environment and feedback controls

Acta Math Sci, 2017, 37A(3): 553-561

[本文引用: 2]

Basir F A, Noor M H.

A model for pest control using integrated approach: Impact of latent and gestation delays

Nonlinear Dyn, 2022, 108(2): 1805-1820

[本文引用: 2]

Teng Z D, Chen L S.

Permanence and extinction of periodic predator-prey systems in a patchy environment with delay

Nonlinear Anal: Real World Appl, 2003, 4(2): 335-364

[本文引用: 2]

Pu L Q, Adam B, Lin Z Q.

Extinction in a nonautonomous competitive system with toxic substance and feedback control

J Appl Anal Comput, 2019, 9(5): 1838-1854

[本文引用: 4]

Chen F D, Li Z, Huang Y J.

Note on the permanence of a competitive system with infinite delay and feedback controls

Nonlinear Anal: Real World Appl, 2007, 8(2): 680-687

[本文引用: 2]

Guo K, Song K Y, Ma W B.

Existence of positive periodic solutions of a delayed periodic Microcystins degradation model with nonlinear functional responses

Appl Math Lett, 2022, 131: 108056

[本文引用: 2]

王长有, 李楠, 蒋涛, 杨强.

一类具有时滞及反馈控制的非自治非线性比率依赖食物链模型

数学物理学报, 2022, 42A(1): 245-268

[本文引用: 4]

Wang C Y, Li N, Jiang T, Yang Q.

On a Nonlinear non-autonomous ratio-dependent food chain model with delays and feedback controls

Acta Math Sci, 2022, 42A(1): 245-268

[本文引用: 4]

Shi L, Qi L X, Zhai S L.

Periodic and almost periodic solutions for a non-autonomous respiratory disease model with a lag effect

Acta Math Sci, 2022, 42B(1): 187-211

[本文引用: 2]

Zhang L, Teng Z D.

Permanence for a delayed periodic predator-prey model with prey dispersal in multi-patches and predator density-independent

J Math Anal Appl, 2008, 338(1): 175-193

[本文引用: 4]

Hu H X, Teng Z D, Jiang H J.

Permanence of the nonautonomous competitive systems with infinite delay and feedback controls

Nonlinear Anal: Real World Appl, 2009, 10(4): 2420-2433

[本文引用: 3]

Liu Z Q, Kang S M.

Applications of Schauder's fixed-point theorem with respect to iterated functional equations

Appl Math Lett, 2001, 14(8): 955-962

[本文引用: 2]

张恭庆, 林源渠. 泛函分析讲义. 北京: 北京大学出版社, 2004

[本文引用: 2]

Zhang G Q, Lin Y Q. Lecture Notes on Functional Analysis. Beijing: Peking University Press, 2004

[本文引用: 2]

Hale J K. Introduction to Functional Differential Equations. New York: Springer, 1993

[本文引用: 1]

Smith H L.

Monotone Dynamical Systems: An Introduction to the Theory of Competitive and Cooperative Systems

Providence, RI: American Mathematical Society, 1995

[本文引用: 1]

滕志东, 陈兰荪.

高维时滞周期的 Kolmogorov 型系统的正周期解

应用数学学报, 1999, 22(3): 446-456

DOI:10.12387/C1999072      [本文引用: 2]

本文应用Banach空间中的Horn不动点定理得到了高维时滞的周期Kolmogorov型生态系统的正周期解存在性定理．作为这个定理的应用，讨论了几类时滞的周期Lotka-Volterra型系统的正周期解的存在性问题、建立了新的实用的判别准则.

Teng Z D, Chen L S.

The positive periodic solutions of periodic Kolmogorov type systems with delays

Acta Math Appl Sin, 1999, 22(3): 446-456

DOI:10.12387/C1999072      [本文引用: 2]

本文应用Banach空间中的Horn不动点定理得到了高维时滞的周期Kolmogorov型生态系统的正周期解存在性定理．作为这个定理的应用，讨论了几类时滞的周期Lotka-Volterra型系统的正周期解的存在性问题、建立了新的实用的判别准则.

Wu H, Chen W, Wang N, et al.

A delayed stage-structure brucellosis model with interaction among seasonality, time-varying incubation and density-dependent growth

Int J Biomath, 2023, 16(6): 2250114

[本文引用: 1]

Pandey S, Ghosh U, Das D, et al.

Rich dynamics of a delay-induced stage-structure prey-predator model with cooperative behaviour in both species and the impact of prey refuge

Math Comput Simul, 2024, 216: 49-76

[本文引用: 1]

Hu D P, Li Y Y, Liu M, et al.

Stability and Hopf bifurcation for a delayed predator-prey model with stage structure for prey and Ivlev-type functional response

Nonlinear Dynam, 2020, 99: 3323-3350

[本文引用: 1]

/

〈 〉

版权所有 © 《数学物理学报》杂志社
地址： 武汉市71010号信箱(430071)　电话: 027-87199206(中文版)　027-87199087(英文版)
E-mail: actams@apm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发