带干扰项的 ARZ 交通流模型的时滞控制与 ISS 稳定性

带干扰项的 ARZ 交通流模型的时滞控制与 ISS 稳定性

高彩霞^,, 赵东霞^,^*

中北大学数学学院太原 030051

The Delayed Control and Input-to-State Stability of ARZ Traffic Flow Model with Disturbances

Gao Caixia^,, Zhao Dongxia^,^*

School of Mathematics, North University of China, Taiyuan 030051

通讯作者: *赵东霞, E-mail: zhaodongxia6@sina.com

收稿日期: 2023-05-31 修回日期: 2024-01-30

基金资助:

山西省基础研究计划(20210302123046)
国家自然科学基金青年基金(12001343)

Received: 2023-05-31 Revised: 2024-01-30

Fund supported:

Fundamental Research Program of Shanxi Province(20210302123046)
National Natural Science Foundation of China(12001343)

作者简介 About authors

高彩霞,E-mail:1519546532@qq.com

摘要

针对线性化之后的 ARZ 交通流模型, 已有文献通常基于如下假设: 一是系统的平衡态恰好等于自由流的速度, 二是进入上游路段的交通量恰好等于交通需求的数学期望, 三是边界反馈不考虑时滞因素的影响. 该文抛开各类限制条件, 结合时滞边界控制策略, 建立了具有模型漂移项和边界扰动项的 PDE-PDE 无穷维耦合闭环系统. 具体地, 采用算子半群理论, 将闭环系统改写为抽象发展方程的形式; 结合线性系统解与控制算子的允许性理论, 证明了闭环系统的适定性; 构造加权 ISS-Lyapunov 函数, 证明了闭环系统的输入-状态稳定性 (ISS), 得到了反馈参数的耗散性条件. 通过数值仿真实验, 进一步验证本文设计的时滞控制器的有效性与参数条件的可行性.

关键词： ARZ 交通流模型; 时滞边界控制; ISS-Lyapunov 函数; ISS 稳定性

Abstract

For the linearized ARZ traffic flow model, the existing literatures are usually based on the following assumptions: First, the equilibrium state of the system is exactly equal to the speed of free flow; Second, the traffic flow entering the upstream section is exactly equal to the mathematical expectation of traffic demand; Third, the boundary feedback doesn't consider the impact of time delay factors. In this paper, a PDE-PDE infinite-dimensional coupled closed-loop system with model drift term and boundary disturbance term is established without these constraints by combining the time-delay boundary control strategy. Specifically, the closed-loop system is transformed into an abstract evolution equation by using operator semigroup theory. The well-posedness of the closed-loop system is proved by combining the admissible theory of linear system solutions and control operators. The weighting ISS-Lyapunov function is constructed, and the input-to-state stability(ISS) of the closed-loop system is proved. The dissipative conditions of the feedback parameters are obtained. The effectiveness of the proposed controller and the feasibility of the parameter conditions are further verified by numerical simulation experiments.

Keywords： ARZ traffic flow model; Time-delay boundary control; ISS-Lyapunov function; Input-to-state stability

PDF (1061KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

高彩霞, 赵东霞. 带干扰项的 ARZ 交通流模型的时滞控制与 ISS 稳定性[J]. 数学物理学报, 2024, 44(4): 960-977

Gao Caixia, Zhao Dongxia. The Delayed Control and Input-to-State Stability of ARZ Traffic Flow Model with Disturbances[J]. Acta Mathematica Scientia, 2024, 44(4): 960-977

1 引言

ARZ非平衡交通流模型能够较为准确地刻画城市快速路网车辆的运行, 在黎曼坐标变换和线性化处理后呈现为二阶双曲偏微分方程组的形式^[1⇓-3]. 近年来, 入口匝道控制和可变限速控制成为城市快速路网车辆交通流控制的两种有效方法^[4], 将其应用于 AR/ARZ 非平衡交通流模型, 取得了一系列研究成果^[5,6]. 对于线性/拟线性双曲系统柯西问题解的适定性, 文献 [7,定理 A.1,B.1] 采用 Lumer-Philipps 定理、不动点定理和能量估计等数学方法进行了证明. 在稳定性分析方面, 文献 [8] 研究了一维 $n\times n$ 线性双曲平衡律系统在比例-积分 (PI) 边界反馈控制下的稳定性, 结合 Lyapunov 函数和线性矩阵不等式 (LMI) 方法, 建立了系统指数稳定所满足的矩阵不等式条件. 进而, 将所得结论应用于 ARZ 交通流模型在入口匝道和可变限速反馈控制下的镇定问题中, 证明了反馈参数满足某种耗散条件时, 交通流状态以指数速率收敛到稳态. 为了处理由于不确定的交通需求导致进入上游路段的交通流量的振荡, 文献 [9] 考虑了闭环系统的输入-状态稳定性 (ISS). 文献 [10,11] 采用 Backstepping 方法设计完全状态反馈以抑制交通状况中的走走停停现象.

在自动控制中, 时滞的出现可能由控制器造成, 也可能是人为因素, 时滞现象可能使得系统的状态变得不稳定, 但合适的时滞取值亦有可能改善系统的性能. 于是, 时滞控制策略吸引了广大学者的关注. 文献 [12] 研究了一类扩散波方程的输入控制器具有时滞的情形, 结果表明无论时滞取值多少, 只要控制参数满足某个约束条件, 即可得到闭环系统的指数稳定性. 在此基础上, 文献 [13] 建立了扩散波方程在时滞控制器下的与时滞相关及与时滞无关的指数稳定性. 针对一阶线性双曲守恒律系统, 文献 [14] 采用特征根分析方法讨论了系统的与时滞无关的稳定性和不稳定性. 此外, 当波的传播时间与控制器的反馈时滞恰好是整数倍时, 采用 Schur-Cohn 准则建立了闭环系统稳定时参数所满足的充要条件.

本文针对线性化之后的 ARZ 交通流模型, 充分考虑三个因素: 一是系统的平衡态不一定等于自由流的速度, 二是进入上游路段的交通量在交通需求的数学期望附近不可避免地出现了有界振荡, 三是利用边界状态反馈和时滞边界状态反馈的线性组合设计控制器. 一般地, 若平衡态不等于自由流的速度, 方程中会出现模型漂移项; 若进入上游路段的交通量有振荡, 导致边界条件中产生一个不确定干扰, 为闭环系统适定性的证明带来了一定困难. 此外, 控制器的时滞效应对稳定性的影响也是本文探讨的一个重要内容. 本文的主要贡献有: (1) 将时滞项用一阶运输方程边值问题的解进行刻画, 构建具有模型漂移项和边界扰动项的 PDE-PDE 无穷维耦合闭环系统; (2) 结合线性系统解与控制算子的允许性等算子半群理论, 证明了闭环系统的适定性; (3) 求得反馈参数的耗散条件以及时滞参数 $\tau$ 的稳定域, 建立了闭环系统的输入-状态稳定性 (ISS).

2 模型建立和控制器设计

2.1 模型建立

高速公路路段的宏观交通流动态一般用 ARZ 模型描述

$\begin{equation} \begin{cases}\partial_t \rho+\partial_x (\rho v)=0,\\\partial_t v+(v-\rho p'(\rho))\partial_x v=\dfrac{V(\rho)-v}{\tau_0},\end{cases}\end{equation}$

(2.1)

其中, 密度 $\rho(x,t)$ 是某一时刻某一路段上的车辆数量, $v(x,t)$ 代表交通流的运动速度, $(x,t)\in[L]\times[0,\infty)$ , $L$ 为路段长度, $\tau_0>0$ 是速度松弛时间 (与驾驶员的反应时间有关), $p(\rho)$ 表示交通压力项, $V(\rho)$ 表示平衡速度-密度基本曲线, 且满足

$\begin{equation}p(\rho)=v_f-V(\rho),\end{equation}$

(2.2)

$\begin{equation}V(\rho)=v_f(1-(\dfrac{\rho}{\rho_m})^\gamma),\end{equation}$

(2.3)

其中, $v_f$ 为自由流速度, $\rho_m$ 为交通流的最大密度, 两者均为交通基础设施的固有属性, $\gamma>0$ 一般为 $1$ 左右的常数. 特别指出, 2.1 和 2.2 节的模型介绍详见参考文献 [8,9] 及其相关文献. 为保证论文内容的连贯性和完整性, 此处作简要叙述.

作黎曼坐标变换

$\begin{equation}\begin{cases}z=v,\\w=v+v_f(\dfrac{\rho}{\rho_m})^\gamma.\end{cases}\end{equation}$

(2.4)

则非线性方程 (2.1) 在黎曼坐标系下的特征形式为

$\begin{equation}\begin{cases}\partial_t w+\lambda_1\partial_x w=\dfrac{v_f-w}{\tau_0},\\[3mm]\partial_t z+\lambda_2\partial_x z=\dfrac{v_f-w}{\tau_0},\end{cases}\end{equation}$

(2.5)

其中

$\begin{equation}\lambda_1=z>0,\;\lambda_2=(1+\gamma)z-\gamma w,\end{equation}$

(2.6)

且 $\lambda_2$ 的正负分别代表交通流处于自由模态和拥堵模态^[15].

不妨设 $(\rho^*,v^*)$ 与 $(w^*,z^*)$ 分别为系统 (2.1) 和 (2.5) 的稳定状态. 定义偏差函数

$\begin{equation}\tilde{w}(x,t)=w(x,t)-w^*,\;\;\tilde{z}(x,t)=z(x,t)-z^*.\end{equation}$

(2.7)

则可得如下线性化的 ARZ 模型

$\begin{equation} \begin{cases}\partial_t \tilde{w}+\lambda_1^*\partial_x \tilde{w}=-c\tilde{w}+c(v_f-w^*),\\\partial_t \tilde{z}+\lambda_2^*\partial_x \tilde{z}=-c\tilde{w}+c(v_f-w^*),\end{cases}\end{equation}$

(2.8)

其中

$\begin{equation}\lambda_1^*=z^*,\;\; \lambda_2^*=(1+\gamma)z^*-\gamma w^*,\;\;c=\dfrac{1}{\tau_0}>0.\end{equation}$

(2.9)

注 2.1 显然, 当 $v_f-w^*\neq0$ , 即稳态 $w^*$ 不等于自由流速度 $v_f$ 时, 系统 (2.8) 存在模型漂移项 $c(v_f-w^*)$ , 可看作系统的一个有界扰动.

2.2 时滞边界控制器设计

在这一部分, 结合匝道控制和可变限速控制设计时滞反馈控制器.

不妨设快速路段处于自由模态, 即

$\begin{equation} (1+\gamma)z^*-\gamma w^*>0 \end{equation}$

(2.10)

的情形, 那么特征速度的传播方向是从上游传播到下游. 因此, 本文基于下游出口处交通流密度 ( $\rho(L,t),\rho(L,t-\tau)$ ) 和车流速度 ( $v(L,t),v(L,t-\tau)$ ) 的在线输出量测, 在快速路段的车辆入口处对匝道流量 $r(t)$ 和速度 $v(0,t)$ 进行反馈控制, 具体如下

$\begin{equation} \begin{cases} r(t)=r^*+k_p^r(\rho(L,t)-\rho^*)+k_d^r(\rho(L,t-\tau)-\rho^*),\\ v(0,t)=v^*+k_p^v(v(L,t)-v^*)+k_d^v(v(L,t-\tau)-v^*), \end{cases} \end{equation}$

(2.11)

其中, $k_p^r$ , $k_d^r$ , $k_p^v$ , $k_d^v$ 是调优增益系数, $\tau>0$ 表示时滞, $r^*$ 代表交通流达到稳态时入口匝道的车流量.

注 2.2 时滞控制器 (2.11) 由边界状态反馈和时滞边界状态反馈的线性组合构成, 考虑到从输出量测到输入控制往往具有滞后性, 因此, 可设边界条件 (2.11) 中瞬时反馈系数 $k_p^r=k_p^v=0,$ 即仅包含时滞反馈, 则得

$\begin{equation} \begin{cases} r(t)=r^*+k_d^r(\rho(L,t-\tau)-\rho^*),\\ v(0,t)=v^*+k_d^v(v(L,t-\tau)-v^*). \end{cases} \end{equation}$

(2.12)

定义偏差函数

$\begin{equation} \tilde{\rho}(x,t)=\rho(x,t)-\rho^*,\;\;\tilde{v}(x,t)=v(x,t)-v^*,\end{equation}$

(2.13)

则时滞控制器 (2.11) 可改写为

$\begin{equation} \begin{cases}r(t)=r^*+k_p^r\tilde{\rho}(L,t)+k_d^r\tilde{\rho}(L,t-\tau),\\\tilde{v\underline{}}(0,t)=k_p^v\tilde{v}(L,t)+k_d^v\tilde{v}(L,t-\tau).\end{cases}\end{equation}$

(2.14)

假设上游入口边界处交通流所满足的守恒条件和交通流稳态时的守恒条件分别为

$\begin{equation} p_{in}(t)+r(t)=\rho(0,t)v(0,t)I,\end{equation}$

(2.15)

$\begin{equation} p_{in}^*+r^*=\rho^*v^*I,\end{equation}$

(2.16)

其中, $p_{in}(t)=p_{in}^*+\tilde{p}_{in}(t),$ $p_{in}^*$ 表示该交通需求的数学期望, $\tilde{p}_{in}(t)$ 表示由于不确定的交通需求导致进入路段上游车流量的有界振荡, 两者相加所得的 $p_{in}(t)$ 表示从上游驶入路段入口处的交通量, $I$ 表示车道数. 将 (2.15) 式与 (2.16) 式相减, 结合 (2.14) 式, 并利用二元函数的一阶泰勒公式将 (2.15) 式右端的非线性项进行线性化处理, 可得

$\begin{equation} \tilde{p}_{in}(t)+k_p^r\tilde{\rho}(L,t)+k_d^r\tilde{\rho}(L,t-\tau)=\tilde{\rho}(0,t)v^*I+\rho^*Ik_p^v\tilde{v}(L,t)+\rho^*Ik_d^v\tilde{v}(L,t-\tau).\end{equation}$

(2.17)

在黎曼坐标系 (2.4) 下, 不妨令 $\gamma=1$ , $\alpha\doteq\frac{v_f}{\rho_m}$ , 并结合边界条件 (2.17) 可得

$\begin{align*} \tilde{w}(0,t)=\ &\tilde{v}(0,t)+\alpha\tilde{\rho}(0,t)\\=\ &k_p^v\tilde{v}(L,t)+k_d^v\tilde{v}(L,t-\tau)+\dfrac{\alpha k_p^r}{v^*I}\tilde{\rho}(L,t)+\dfrac{\alpha k_d^r}{v^*I}\tilde{\rho}(L,t-\tau)\\&-\dfrac{\alpha \rho^*k_p^v}{v^*}\tilde{v}(L,t)-\dfrac{\alpha \rho^*k_d^v}{v^*}\tilde{v}(L,t-\tau)+\dfrac{\alpha \tilde{p}_{in}(t)}{v^*I}\\=\ &(k_p^v-\dfrac{\alpha \rho^*k_p^v}{v^*}-\dfrac{k_p^r}{v^*I})\tilde{z}(L,t)+(k_d^v-\dfrac{\alpha \rho^*k_d^v}{v^*}-\dfrac{ k_d^r}{v^*I})\tilde{z}(L,t-\tau)\\&+\dfrac{k_p^r}{v^*I}\tilde{w}(L,t)+\dfrac{ k_d^r}{v^*I}\tilde{w}(L,t-\tau)+\dfrac{\alpha \tilde{p}_{in}(t)}{v^*I}.\end{align*}$

(2.18)

由 (2.14) 式第二个式子知

$\begin{equation} \tilde{z}(0,t)=k_p^v\tilde{z}(L,t)+k_d^v\tilde{z}(L,t-\tau).\end{equation}$

(2.19)

因此, 在黎曼坐标系下的时滞边界条件为

$\begin{equation} \begin{cases}\tilde{w}(0,t)=k_1\tilde{w}(L,t)+k_2\tilde{z}(L,t)+k_3\tilde{w}(L,t-\tau)+k_4\tilde{z}(L,t-\tau)+\dfrac{\alpha \tilde{p}_{in}(t)}{v^*I},\\\tilde{z}(0,t)=k_5\tilde{z}(L,t)+k_6\tilde{z}(L,t-\tau),\end{cases}\end{equation}$

(2.20)

其中

$\begin{equation} \begin{aligned}&k_1=\dfrac{k_p^r}{v^*I},\;k_2=k_p^v-\dfrac{\alpha \rho^*k_p^v}{v^*}-\dfrac{k_p^r}{v^*I},\;k_3=\dfrac{k_d^r}{v^*I},\\&k_4=k_d^v-\dfrac{\alpha \rho^*k_d^v}{v^*}-\dfrac{k_d^r}{v^*I},\;k_5=k_p^v,\;k_6=k_d^v.\end{aligned}\end{equation}$

(2.21)

2.3 PDE-PDE 闭环系统的重建

首先引入两个辅助函数 $u(x,t),\;g(x,t)$ 去刻画系统 (2.20) 中的时滞项, 将其进行形式上的无时滞化处理. 显然, 一阶运输方程初值问题

$\begin{equation} \begin{cases}\partial_t u(x,t)+\dfrac{L}{\tau}\partial_x u(x,t)=0,\\[3mm]u(x,0)=\tilde{w}(L,-\dfrac{\tau}{L}x)\end{cases}\end{equation}$

(2.22)

的解可表示为

$\begin{equation} u(x,t)=\tilde{w}(L,t-\dfrac{\tau}{L}x). \end{equation}$

(2.23)

同理

$\begin{equation} \begin{cases} \partial_t g(x,t)+\dfrac{L}{\tau}\partial_x g(x,t)=0,\\[3mm] g(x,0)=\tilde{z}(L,-\dfrac{\tau}{L}x) \end{cases} \end{equation}$

(2.24)

的解为

$\begin{equation} g(x,t)=\tilde{z}(L,t-\dfrac{\tau}{L}x). \end{equation}$

(2.25)

从而, 时滞系统 (2.8), (2.20) 可改写为如下 PDE-PDE 耦合闭环系统的形式

$\begin{equation}\begin{cases}\partial_t \tilde{w}(x,t)+\lambda_1^*\partial_x \tilde{w}(x,t)=-c\tilde{w}(x,t)+c(v_f-w^*),\\\partial_t \tilde{z}(x,t)+\lambda_2^*\partial_x \tilde{z}(x,t)=-c\tilde{w}(x,t)+c(v_f-w^*),\\[2mm]\partial_t u(x,t)+\dfrac{L}{\tau}\partial_x u(x,t)=0,\\[3mm]\partial_t g(x,t)+\dfrac{L}{\tau}\partial_x g(x,t)=0,\\[2mm]\tilde{w}(0,t)=k_1\tilde{w}(L,t)+k_2\tilde{z}(L,t)+k_3u(L,t)+k_4g(L,t)+\dfrac{\alpha \tilde{p}_{in}(t)}{v^*I},\\\tilde{z}(0,t)=k_5\tilde{z}(L,t)+k_6g(L,t),\\u(0,t)=\tilde{w}(L,t),\\g(0,t)=\tilde{z}(L,t).\end{cases}\end{equation}$

(2.26)

注 2.3 闭环系统 (2.26) 中存在模型漂移项 $c(v_f-w^*)$ 和边界条件的不确定扰动项 $\frac{\alpha \tilde{p}_{in}(t)}{v^*I}$ . 因此, 本文第三部分结合解与控制算子的允许性等算子半群理论证明系统的适定性, 第四部分构建 ISS 加权 Lyapunov 函数证明闭环系统的输入-状态稳定性.

3 系统 (2.26) 的适定性

设 Hilbert 状态空间为

$\begin{equation} \mathcal{H}=\big(L^2(0,L)\big)^4, \end{equation}$

(3.1)

其中的内积定义为

$\begin{equation} \langle X_1,X_2\rangle=\int_0^L\big[m_1(x)\overline{m_2(x)}+n_1(x)\overline{n_2(x)}\big]{\rm d}x+\tau\int_0^L\big[r_1(x)\overline{r_2(x)} +s_1(x)\overline{s_2(x)}\big]{\rm d}x, \end{equation}$

(3.2)

这里 $X_i=(m_i,n_i,r_i,s_i)\in \mathcal{H}(i=1,2),$ $\overline{m_2(x)}$ 表示 $m_2(x)$ 的共轭函数, 其他类似.

3.1 抽象发展方程形式

定义线性算子 $\mathcal{A}:\;D(\mathcal{A})\subseteq \mathcal{H}\rightarrow \mathcal{H}$ 如下

$\begin{equation} \mathcal{A} X=\left( \begin{array}{cccc} -\lambda_1^*\frac{\partial}{\partial{x}}-c & 0 & 0 & 0 \\[3mm] -c & -\lambda_2^*\frac{\partial}{\partial{x}} & 0 & 0 \\[3mm] 0 & 0 & -\frac{L}{\tau}\frac{\partial}{\partial{x}} & 0 \\[3mm] 0 & 0 & 0 & -\frac{L}{\tau}\frac{\partial}{\partial{x}} \\ \end{array}\right)\left( \begin{array}{ccccc} m \\ n \\ r \\ s \end{array}\right),\end{equation}$

(3.3)

$\begin{equation} \begin{aligned}D(\mathcal{A})=\Big\{&(m, n, r, s)^T\in(H^1(0,L))^4|(0)=k_1m(L)+k_2n(L)+k_3r(L)+k_4s(L),\\&n(0)=k_5n(L)+k_6s(L),\;\;r(0)=m(L),\;\; s(0)=n(L)\Big\}.\end{aligned}\end{equation}$

(3.4)

经过计算, 其伴随算子 $\mathcal{A}^*$ 为

$\begin{align*} &\mathcal{A^*} X=\left( \begin{array}{cccc} \lambda_1^*\frac{\partial}{\partial{x}}-c & -c & 0 & 0 \\[2mm] 0& \lambda_2^*\frac{\partial}{\partial{x}} & 0 & 0 \\[2mm] 0 & 0 & \frac{L}{\tau}\frac{\partial}{\partial{x}} & 0 \\[2mm] 0 & 0 & 0 & \frac{L}{\tau}\frac{\partial}{\partial{x}} \end{array}\right)\left( \begin{array}{ccccc} \varphi \\ \psi \\ \xi \\ \zeta \end{array}\right),\end{align*}$

(3.5)

$\begin{align*}\begin{aligned}D(\mathcal{A^*})=\Big\{&(\varphi, \psi, \xi, \zeta)^T\in(H^1(0,1))^4\mid\lambda_1^*\varphi(L)=\xi(0)+\lambda_1^*k_1\varphi(0),\\&\lambda_2^*\psi(L)=\lambda_1^*k_2\varphi(0)+\lambda_2^*k_5\psi(0)+\zeta(0),\;\;\xi(L)=\lambda_1^*k_3\varphi(0),\\ &\zeta(L)=\lambda_1^*k_4\varphi(0)+\lambda_2^*k_6\psi(0)\Big\}.\end{aligned}\end{align*}$

(3.6)

将系统 (2.26) 与 $(\varphi,\psi,\xi,\zeta)^T$ 做内积, 得

$\begin{align*} \dfrac{\rm d}{{\rm d}t} \langle (\tilde{w},\tilde{z},u,g)^T,(\varphi,\psi,\xi,\zeta)^T\rangle_\mathcal{H}=\ &\langle (\tilde{w},\tilde{z},u,g)^T,\mathcal{A}^*(\varphi,\psi,\xi,\zeta)^T\rangle_\mathcal{H}\\&+\langle (c,c,0,0)^T(v_f-w^*),(\varphi,\psi,\xi,\zeta)^T\rangle_{D(\mathcal{A}^*)'\times D(\mathcal{A}^*)}\\&+\langle (\delta(x),0,0,0)^T\dfrac{\alpha \tilde{p}_{in}(t)}{v^*I},(\varphi,\psi,\xi,\zeta)^T\rangle_{D(\mathcal{A}^*)'\times D(\mathcal{A}^*)},\end{align*}$

(3.7)

其中 $D(\mathcal{A}^*)'$ 是 $D(\mathcal{A}^*)$ 关于枢轴空间 $L^2$ 的对偶. 于是, 系统 (2.26) 可改写成抽象发展方程的形式

$\begin{equation} \begin{cases}\dot{X}(t)=\mathcal{A}X(t)+\mathcal{B}_1(v_f-w^*)+\mathcal{B}_2\dfrac{\alpha \tilde{p}_{in}(t)}{v^*I},\\X(0)=X_0,\\\end{cases}\end{equation}$

(3.8)

其中, $X(t)=(\tilde{w}(\cdot,t),\,\tilde{z}(\cdot,t),\,u(\cdot,t),\,g(\cdot,t))$ ,

$\begin{equation} \mathcal{B}_1=\begin{pmatrix} c \\ c \\ 0 \\ 0\end{pmatrix},\quad \mathcal{B}_2=\begin{pmatrix} \delta(x) \\ 0 \\ 0 \\ 0\end{pmatrix},\end{equation}$

(3.9)

且 $\delta(\cdot)$ 为狄拉克函数.

注 3.1 显然 $\mathcal{B}_1$ 可看作算子 $\mathcal{A}$ 的一个有界扰动, 而 $\mathcal{B}_2$ 是一个无界算子, 为建立系统的适定性, 需验证 $(\mathcal{A},\mathcal{B}_2)$ 是允许的. 不失一般性, 以下计算令 $L=1.$

3.2 算子 $\mathcal{A}$ 的性质

定理 3.1 设 $\mathcal{A}$ 由 (3.3) 和 (3.4) 式给出. 那么 $\mathcal{A}^{-1}$ 存在且为紧算子, 当且仅当参数满足条件

$\begin{equation} \left |\begin{array}{ccccc}1-k_1{\rm e}^\frac{-c}{\lambda_1^*}-k_2\dfrac{\lambda_1^*}{\lambda_2^*}\big({\rm e}^{\frac{-c}{\lambda_1^*}}-1\big) & -k_2 & -k_3 & -k_4\\[3mm]-k_5\dfrac{\lambda_1^*}{\lambda_2^*}\big({\rm e}^\frac{-c}{\lambda_1^*}-1\big) & 1-k_5 & 0 & -k_6\\[2mm]{\rm e}^\frac{-c}{\lambda_1^*} & 0 & -1 & 0\\[1mm]-\dfrac{\lambda_1^*}{\lambda_2^*}\big({\rm e}^{\frac{-c}{\lambda_1^*}}-1\big) & -1 & 0 & 1\end{array}\right|\neq0.\end{equation}$

(3.10)

从而, 算子 $\mathcal{A}$ 的谱 $\sigma(\mathcal{A})$ 仅由有穷代数重数的孤立特征值构成.

证任给 $X_1=(m_1,n_1,r_1,s_1)\in\mathcal{H},$ 求解

$\mathcal{A}X=X_1,\;X=(m,n,r,s)\in D(\mathcal{A}),$

即

$\begin{equation} \mathcal{A}\left( \begin{array}{cccc} m \\ n \\ r \\ s \\ \end{array}\right)=\left( \begin{array}{cccc} -\lambda_1^*m'-cm \\ -\lambda_2^*n'-cm \\[2mm] -\frac{1}{\tau}r' \\[3mm] -\frac{1}{\tau}s' \\ \end{array}\right)=\left( \begin{array}{c} m_1 \\ n_1 \\ r_1 \\ s_1 \\ \end{array}\right).\end{equation}$

(3.11)

于是,

$\begin{equation} \begin{cases} -\lambda_1^*m'-cm-m_1=0,\\ -\lambda_2^*n'-cm-n_1=0,\\[2mm] -\frac{1}{\tau}r'=r_1, \;-\frac{1}{\tau}s'=s_1,\\[2mm] m(0)=k_1m(1)+k_2n(1)+k_3r(1)+k_4s(1),\\ n(0)=k_5n(1)+k_6s(1),\; r(0)=m(1),\; s(0)=n(1).\end{cases}\end{equation}$

(3.12)

根据一阶线性微分方程求解公式可得方程组 (3.12) 的解为

$\begin{align*}&m(x)={\rm e}^{\frac{-c}{\lambda_1^*}x}\bigg[\int_{0}^{x} \frac{m_1(\sigma)}{-\lambda_1^*}{\rm e}^{\frac{c}{\lambda_1^*}\sigma}{\rm d}\sigma+m(0)\bigg],\end{align*}$

(3.13)

$\begin{align*}n(x)=n(0)-\displaystyle\int_{0}^{x}\frac{1}{\lambda_2^*}(n_1(\sigma)+cm(\sigma)){\rm d}\sigma,\end{align*}$

(3.14)

$\begin{align*}r(x)=r(0)-\tau\displaystyle\int_{0}^{x} r_1(\sigma){\rm d}\sigma,\end{align*}$

(3.15)

$\begin{align*}s(x)=s(0)-\tau\displaystyle\int_{0}^{x} s_1(\sigma){\rm d}\sigma.\end{align*}$

(3.16)

再将 (3.13) 式代入 (3.14) 式中, 得

$\begin{align*} n(x)&=n(0)-\dfrac{1}{\lambda_2^*}\displaystyle\int_{0}^{x}n_1(\sigma){\rm d}\sigma-\dfrac{c}{\lambda_2^*}\displaystyle\int_{0}^{x}\bigg[{\rm e}^{\frac{-c}{\lambda_1^*}\sigma}\bigg(\displaystyle\int_{0}^{\sigma}\frac{m_1(t)}{-\lambda_1^*}{\rm e}^{\frac{c}{\lambda_1^*}t}{\rm d}t+m(0)\bigg)\bigg]{\rm d}\sigma\\[4mm]&=n(0)-\dfrac{1}{\lambda_2^*}\displaystyle\int_{0}^{x}n_1(\sigma){\rm d}\sigma-\dfrac{c}{\lambda_2^*}\displaystyle\int_{0}^{x}{\rm e}^{\frac{-c}{\lambda_1^*}\sigma} \displaystyle\int_{0}^{\sigma}\dfrac{m_1(t)}{-\lambda_1^*}{\rm e}^{\frac{c}{\lambda_1^*}t}{\rm d}t{\rm d}\sigma-\dfrac{c}{\lambda_2^*}\displaystyle\int_{0}^{x}{\rm e}^{\frac{-c}{\lambda_1^*}\sigma} m(0){\rm d}\sigma\\[4mm]&=n(0)-\dfrac{1}{\lambda_2^*}\displaystyle\int_{0}^{x} n_1(\sigma){\rm d}\sigma-\dfrac{1}{\lambda_2^*}\displaystyle\int_{0}^{x}m_1(t)\big({\rm e}^{\frac{c}{\lambda_1^*}(t-x)}-1\big){\rm d}t+\frac{\lambda_1^*}{\lambda_2^*}\big({\rm e}^{\frac{-c}{\lambda_1^*}x}-1\big)m(0).\end{align*}$

(3.17)

将 (3.13)-(3.17) 式代入 (3.12) 式中的边界条件, 得到关于 $m(0),n(0),r(0),s(0)$ 的线性方程组

$\begin{equation} \begin{cases}\big(1-k_1{\rm e}^\frac{-c}{\lambda_1^*}-k_2\dfrac{\lambda_1^*}{\lambda_2^*}\big({\rm e}^{\frac{-c}{\lambda_1^*}}-1\big)\big)m(0)-k_2n(0)-k_3r(0)-k_4s(0)=k_1{\rm e}^\frac{-c}{\lambda_1^*}\displaystyle\int_0^1\frac{m_1(\sigma)}{-\lambda_1^*}{\rm e}^{\frac{c}{\lambda_1^*}\sigma}{\rm d}\sigma\\[3mm]-\dfrac{k_2}{\lambda_2^*}\displaystyle\int_0^1n_1(\sigma){\rm d}\sigma-\dfrac{k_2}{\lambda_2^*}\displaystyle\int_0^1m_1(t)\big({\rm e}^{\frac{c}{\lambda_1^*}(t-1)}-1\big){\rm d}t-k_3\tau\displaystyle\int_{0}^{1}r_1(\sigma){\rm d}\sigma-k_4\tau\displaystyle\int_{0}^{1}s_1(\sigma){\rm d}\sigma,\\[3mm]-k_5\dfrac{\lambda_1^*}{\lambda_2^*}\big({\rm e}^\frac{-c}{\lambda_1^*}-1\big)m(0)+\big(1-k_5\big)n(0)-k_6s(0)=-\dfrac{k_5}{\lambda_2^*}\displaystyle\int_{0}^{1}n_1(\sigma){\rm d}\sigma-k_6\tau\displaystyle\int_{0}^{1}s_1(\sigma){\rm d}\sigma\\[3mm]-\dfrac{k_5}{\lambda_2^*}\displaystyle\int_{0}^{1}m_1(t)\big({\rm e}^{\frac{c}{\lambda_1^*}(t-1)}-1\big){\rm d}t,\\[3mm]{\rm e}^{\frac{-c}{\lambda_1^*}}m(0)-r(0)=-{\rm e}^{\frac{-c}{\lambda_1^*}}\displaystyle\int_{0}^{1}\frac{m_1(\sigma)}{-\lambda_1^*}{\rm e}^{\frac{c}{\lambda_1^*}\sigma}{\rm d}\sigma,\\[3mm]-\dfrac{\lambda_1^*}{\lambda_2^*}\big({\rm e}^{\frac{-c}{\lambda_1^*}}-1\big)m(0)-n(0)+s(0)=-\dfrac{1}{\lambda_2^*}\displaystyle\int_{0}^{1}n_1(\sigma){\rm d}\sigma-\dfrac{1}{\lambda_2^*}\displaystyle\int_{0}^{1}m_1(t)\big({\rm e}^{\frac{c}{\lambda_1^*}(t-1)}-1\big){\rm d}t.\end{cases}\end{equation}$

(3.18)

根据线性方程组求解的克莱姆法则, 当且仅当系数行列式

$\begin{equation} D=\left |\begin{array}{cccc}1-k_1{\rm e}^\frac{-c}{\lambda_1^*}-k_2\dfrac{\lambda_1^*}{\lambda_2^*}\big({\rm e}^{\frac{-c}{\lambda_1^*}}-1\big) & -k_2 & -k_3 & -k_4\\[3mm]-k_5\dfrac{\lambda_1^*}{\lambda_2^*}\big({\rm e}^\frac{-c}{\lambda_1^*}-1\big) & 1-k_5 & 0 & -k_6\\[3mm]{\rm e}^\frac{-c}{\lambda_1^*} & 0 & -1 & 0\\[1mm]-\dfrac{\lambda_1^*}{\lambda_2^*}\big({\rm e}^{\frac{-c}{\lambda_1^*}}-1\big) & -1 & 0 & 1\end{array}\right|\neq0\end{equation}$

(3.19)

时, 方程组 (3.18) 有唯一解, 且

$\begin{equation} m(0)=\frac{D_1}{D},\;n(0)=\frac{D_2}{D},\;r(0)=\frac{D_3}{D},\\s(0)=\frac{D_4}{D},\end{equation}$

(3.20)

其中, $D_i$ 是把 $D$ 的第 $i$ 列各元素分别换成方程组 (3.18) 中相应的常数项所得到的行列式. 从而, 方程组 (3.12) 有唯一解

$\begin{equation} \begin{cases}m(x)={\rm e}^{\frac{-c}{\lambda_1^*}x}\bigg[\displaystyle\int_{0}^{x} \frac{m_1(\sigma)}{-\lambda_1^*}{\rm e}^{\frac{c}{\lambda_1^*}\sigma}{\rm d}\sigma+\dfrac{D_1}{D}\bigg],\\[3mm]n(x)=\dfrac{D_2}{D}-\dfrac{1}{\lambda_2^*}\displaystyle\int_{0}^{x} n_1(\sigma){\rm d}\sigma-\dfrac{1}{\lambda_2^*}\displaystyle\int_{0}^{x}m_1(t)\big({\rm e}^{\frac{c}{\lambda_1^*}(t-x)}-1\big){\rm d}t+\dfrac{\lambda_1^*}{\lambda_2^*}\big({\rm e}^{\frac{-c}{\lambda_1^*}x}-1\big)\dfrac{D_1}{D},\\[3mm]r(x)=\dfrac{D_3}{D}-\tau\displaystyle\int_{0}^{x} r_1(\sigma){\rm d}\sigma,\\[3mm]s(x)=\dfrac{D_4}{D}-\tau\displaystyle\int_{0}^{x} s_1(\sigma){\rm d}\sigma.\end{cases}\end{equation}$

(3.21)

因此, 根据 Sobolev 嵌入定理, $\mathcal{A}^{-1}$ 存在并且在 $\mathcal{H}$ 上是紧的. 从而 $\sigma(\mathcal{A})$ 仅由有穷代数重数的孤立特征值所构成. 证毕.

下面考虑系统算子 $\mathcal{A}$ 的特征值问题

$\begin{equation*}\mathcal{A}X=\lambda X,\;\;\forall\; X=(m,n,r,s)\in D(\mathcal{A}),\end{equation*}$

即

$\begin{equation*}\mathcal{A}\left( \begin{array}{cccc} m \\ n \\ r \\ s \\ \end{array}\right)=\left( \begin{array}{cccc} -\lambda_1^*m'-cm \\ -\lambda_2^*n'-cm \\[2mm] -\frac{1}{\tau}r' \\[3mm] -\frac{1}{\tau}s' \\ \end{array}\right)=\left( \begin{array}{c} \lambda m \\ \lambda n \\ \lambda r \\ \lambda s \\ \end{array}\right).\end{equation*}$

计算可得, $(m,n,r,s)\neq 0$ 当且仅当方程

$\begin{equation} \Delta(\lambda)\doteq\left |\begin{array}{cccc}q_1 & -k_2{\rm e}^{-\frac{\lambda}{\lambda_2^*}} & -k_3{\rm e}^{-\tau\lambda} & -k_4{\rm e}^{-\tau\lambda}\\q_2 & k_5{\rm e}^{-\frac{\lambda}{\lambda_2^*}}-1 & 0 & k_6{\rm e}^{-\tau\lambda}\\q_3 & 0 & -1 & 0\\q_4 & {\rm e}^{-\frac{\lambda}{\lambda_2^*}} & 0 & -1\end{array}\right|=0\end{equation}$

(3.22)

有解, 其中,

$\begin{equation*}\begin{cases}q_1=1-k_1{\rm e}^{-\frac{\lambda+c}{\lambda_1^*}}+\dfrac{k_2c\lambda_1^*}{\lambda\lambda_1^*-(\lambda+c)\lambda_2^*}\big({\rm e}^{-\frac{\lambda+c}{\lambda_1^*}}-{\rm e}^{-\frac{\lambda}{\lambda_2^*}}\big),\\[3mm]q_2=-\dfrac{k_5c\lambda_1^*}{\lambda\lambda_1^*-(\lambda+c)\lambda_2^*}\big({\rm e}^{-\frac{\lambda+c}{\lambda_1^*}}-{\rm e}^{-\frac{\lambda}{\lambda_2^*}}\big),\;\;q_3={\rm e}^{-\frac{\lambda+c}{\lambda_1^*}},\\[3mm]q_4=\dfrac{-c\lambda_1^*}{\lambda\lambda_1^*-(\lambda+c)\lambda_2^*}\big({\rm e}^{-\frac{\lambda+c}{\lambda_1^*}}-{\rm e}^{-\frac{\lambda}{\lambda_2^*}}\big).\end{cases}\end{equation*}$

从而可得关于算子 $\mathcal{A}$ 的如下结论.

定理 3.2 设 $\mathcal{A}$ 由 (3.3) 和 (3.4) 式给出, 则

$\begin{equation*}\sigma(\mathcal{A})=\sigma_p(\mathcal{A})=\{\lambda\in C|\triangle(\lambda)=0\},\end{equation*}$

且任一 $\lambda\in\sigma(\mathcal{A})$ 都是几何单的, 相应的本征函数 $\phi_\lambda=(m_\lambda,n_\lambda,r_\lambda,s_\lambda)$ 形式如下

$\begin{equation*}\begin{aligned}&m_\lambda(x)={\rm e}^{-\frac{\lambda+c}{\lambda_1^*}x},\;\;r_\lambda(x)=s_\lambda(x)={\rm e}^{-\tau\lambda x},\\&n_\lambda(x)={\rm e}^{-\frac{\lambda}{\lambda_2^*}x}-\dfrac{c\lambda_1^*}{\lambda\lambda_1^*-(\lambda+c)\lambda_2^*}{\rm e}^{-\frac{\lambda}{\lambda_2^*}x}\big({\rm e}^{\frac{\lambda\lambda_1^*-(\lambda+c)\lambda_2^*}{\lambda_1^*\lambda_2^*}x}-1\big).\end{aligned}\end{equation*}$

3.3 算子 $\mathcal{A}$ 生成 $\mathcal{H}$ 上的 $C_0$ 压缩半群

定义 3.1 设 $X$ 是 Banach 空间, $T(t)(0\leq t<\infty)$ 是 $X$ 上的有界线性算子半群. 如果

$\begin{equation*}\lim_{t\rightarrow0^+} T(t)x=x,\;\forall x\in X,\end{equation*}$

则称 $T(t)(0\leq t<\infty)$ 为 $X$ 上的有界线性算子强连续半群, 简称为 $C_0$ 半群.

定理 3.3 设 $\mathcal{A}$ 由 (3.3) 和 (3.4) 式给出, 在 $\mathcal{H}$ 上定义一个新内积

$\begin{align*} \langle X_1,X_2\rangle_1=&\int_0^1\big[\dfrac{p_1}{\lambda_1^*}{\rm e}^{-\frac{\mu x}{\lambda_1^*}}m_1(x)\overline{m_2(x)}+\dfrac{p_2}{\lambda_2^*}{\rm e}^{-\frac{\mu x}{\lambda_2^*}}n_1(x)\overline{n_2(x)}\big]{\rm d}x\\ &+\tau\int_0^1\big[{\rm e}^{-\tau x}p_3r_1(x)\overline{r_2(x)}+{\rm e}^{-\tau x}p_4s_1(x)\overline{s_2(x)}\big]{\rm d}x, \end{align*}$

(3.23)

其中, $\mu>0, p_i>0\ (i=1,2,3,4)$ .

那么由 (3.23) 式所诱导的范数等价于由 (3.2) 式所诱导的范数. 此外, 如果参数满足如下条件

$\begin{equation} \begin{cases}4p_1k_1^2-p_1{\rm e}^{\frac{-\mu}{\lambda_1^*}}+p_3\leq0,\\4p_1k_2^2-p_2{\rm e}^{\frac{-\mu}{\lambda_2^*}}+2p_2k_5^2+p_4\leq0,\\4p_1k_3^2-{\rm e}^{-\tau}p_3\leq0,\\4p_1k_4^2-{\rm e}^{-\tau}p_4+2p_2k_6^2\leq0,\\\mu(\mu+2c) p_1 \lambda_2^* {\rm e}^{-\mu(\frac{1}{\lambda_1^*}+\frac{1}{\lambda_2^*})}>c^2 p_2 \lambda_1^*,\end{cases}\end{equation}$

(3.24)

则

$\begin{equation} \langle \mathcal{A}X,X\rangle_1\leq 0,\;\forall X \in D(\mathcal{A}).\end{equation}$

(3.25)

因此, $\mathcal{A}$ 在 $\mathcal{H}$ 上是耗散的, 且 $\mathcal{A}$ 生成 $\mathcal{H}$ 上的一个 $C_0$ 压缩半群 ${\rm e}^{\mathcal{A}t}.$

证对任意的 $X=(m,n,r,s)\in D(\mathcal{A})$

$\begin{align*} \langle\mathcal{A}X,X\rangle_1&=\langle(-\lambda_1^*m'-cm,-\lambda_2^*n'-cm,-\dfrac{1}{\tau}r',-\dfrac{1}{\tau}s'),(m,n,r,s)\rangle_1\\&=\displaystyle\int_{0}^{1}\dfrac{p_1}{\lambda_1^*}{\rm e}^{-\frac{\mu x}{\lambda_1^*}}(-\lambda_1^*m'-cm)\bar{m}{\rm d}x+\displaystyle\int_{0}^{1}\dfrac{p_2}{\lambda_2^*}{\rm e}^{-\frac{\mu x}{\lambda_2^*}}(-\lambda_2^*n'-cm)\bar{n}{\rm d}x\\& -\displaystyle\int_{0}^{1}{\rm e}^{-\tau x}p_3r'\bar{r}{\rm d}x-\displaystyle\int_{0}^{1}{\rm e}^{-\tau x}p_4s'\bar{s}{\rm d}x,\end{align*}$

(3.26)

于是, 其实部

$\begin{align*} {\rm Re}\langle\mathcal{A}X,X\rangle_1=&-\dfrac{1}{2}p_1{\rm e}^{-\frac{\mu}{\lambda_1^*}}m^2(1)+\dfrac{1}{2}p_1m^2(0)-\dfrac{1}{2}p_2{\rm e}^{-\frac{\mu}{\lambda_2^*}}n^2(1)+\dfrac{1}{2}p_2n^2(0)\\&-\dfrac{\mu}{2\lambda_1^*}\displaystyle\int_{0}^{1}p_1{\rm e}^{-\frac{\mu x}{\lambda_1^*}}m^2{\rm d}x-\dfrac{\mu}{2\lambda_2^*}\displaystyle\int_{0}^{1}p_2{\rm e}^{-\frac{\mu x}{\lambda_2^*}}n^2{\rm d}x-\displaystyle\int_{0}^{1}\dfrac{p_1}{\lambda_1^*}{\rm e}^{-\frac{\mu x}{\lambda_1^*}}cm^2{\rm d}x\\&-\displaystyle\int_{0}^{1}\dfrac{p_2}{2\lambda_2^*}{\rm e}^{-\frac{\mu x}{\lambda_2^*}}c(m\bar{n}+\bar{m}n){\rm d}x-\dfrac{1}{2}{\rm e}^{-\tau}p_3r^2(1)+\dfrac{1}{2}p_3r^2(0)\\&-\dfrac{\tau}{2}\displaystyle\int_{0}^{1}{\rm e}^{-\tau x}p_3r^2{\rm d}x-\dfrac{1}{2}{\rm e}^{-\tau}p_4s^2(1)+\dfrac{1}{2}p_4s^2(0)-\dfrac{\tau}{2}\displaystyle\int_{0}^{1}{\rm e}^{-\tau x}p_4s^2{\rm d}x,\end{align*}$

(3.27)

其中, $f\bar{f}\doteq f^2.$ 令

$\begin{align*} K=&-\dfrac{\mu}{2\lambda_1^*}\displaystyle\int_{0}^{1}p_1{\rm e}^{-\frac{\mu x}{\lambda_1^*}}m^2{\rm d}x-\dfrac{\mu}{2\lambda_2^*}\displaystyle\int_{0}^{1}p_2{\rm e}^{-\frac{\mu x}{\lambda_2^*}}n^2{\rm d}x-\displaystyle\int_{0}^{1}\dfrac{p_1}{\lambda_1^*}{\rm e}^{-\frac{\mu x}{\lambda_1^*}}cm^2{\rm d}x\\&-\displaystyle\int_{0}^{1}\dfrac{p_2}{2\lambda_2^*}{\rm e}^{-\frac{\mu x}{\lambda_2^*}}c(m\bar{n}+\bar{m}n){\rm d}x\\\leq&-\Big(\frac{\mu p_1}{2\lambda_1^*}+\frac{p_1 c}{\lambda_1^*}\Big){\rm e}^{-\frac{\mu}{\lambda_1^*}}\displaystyle\int_{0}^{1}m^2{\rm d}x-\dfrac{\mu p_2}{2\lambda_2^*}{\rm e}^{-\frac{\mu}{\lambda_2^*}}\displaystyle\int_{0}^{1}n^2{\rm d}x-\displaystyle\int_{0}^{1}\dfrac{p_2 c}{2\lambda_2^*}{\rm e}^{-\frac{\mu x}{\lambda_2^*}}(m\bar{n}+\bar{m}n){\rm d}x \\=&-\displaystyle\int_{0}^{1}\bar{E}^TFE{\rm d}x,\end{align*}$

(3.28)

且

$\begin{equation*}E=\left( \begin{array}{c} m \\ n \end{array}\right),\;F=\left( \begin{array}{cc} \Big(\frac{\mu p_1}{2\lambda_1^*}+\frac{p_1 c}{\lambda_1^*}\Big){\rm e}^{-\frac{\mu}{\lambda_1^*}} & \frac{p_2 c}{2\lambda_2^*}{\rm e}^{\frac{-\mu x}{\lambda_2^*}} \\[3mm] \frac{p_2 c}{2\lambda_2^*}{\rm e}^{\frac{-\mu x}{\lambda_2^*}} & \frac{\mu p_2}{2\lambda_2^*}{\rm e}^{-\frac{\mu}{\lambda_2^*}} \end{array} \right).\end{equation*}$

下证 $K<0,$ 即 $F$ 为正定矩阵, 即证 $F$ 的各阶顺序主子式均大于 0

$\begin{equation} \begin{array}{ll} {\rm (a)} \Big(\frac{\mu p_1}{2\lambda_1^*}+\frac{p_1 c}{\lambda_1^*}\Big){\rm e}^{-\frac{\mu}{\lambda_1^*}}>0,\\[3mm] {\rm (b)} \Big(\frac{\mu p_1}{2\lambda_1^*}+\frac{p_1 c}{\lambda_1^*}\Big){\rm e}^{-\frac{\mu}{\lambda_1^*}}\frac{\mu p_2}{2\lambda_2^*}{\rm e}^{-\frac{\mu}{\lambda_2^*}}-\frac{p_2^2 c^2}{4{\lambda_2^*}^2}{\rm e}^{\frac{-2\mu x}{\lambda_2^*}}>0.\end{array}\end{equation}$

(3.29)

条件 (a) 显然成立. 考虑到在 $x=0$ 处, 函数 ${\rm e}^{\frac{-2\mu x}{\lambda_2^*}}$ 取到最大值 $1$ , 所以为使 (b) 成立, 仅需参数满足

$\begin{equation*}\mu(\mu+2c) p_1 \lambda_2^* {\rm e}^{-\mu(\frac{1}{\lambda_1^*}+\frac{1}{\lambda_2^*})}>c^2 p_2 \lambda_1^*.\end{equation*}$

因此, (3.27) 式放缩为

$\begin{align*} Re\langle\mathcal{A}X,X\rangle_1\leq&-\dfrac{1}{2}p_1{\rm e}^{-\frac{\mu}{\lambda_1^*}}m^2(1)+\dfrac{1}{2}p_1m^2(0)-\dfrac{1}{2}p_2{\rm e}^{-\frac{\mu}{\lambda_2^*}}n^2(1)+\dfrac{1}{2}p_2n^2(0)\\&-\dfrac{1}{2}{\rm e}^{-\tau}p_3r^2(1)+\dfrac{1}{2}p_3r^2(0)-\dfrac{1}{2}{\rm e}^{-\tau}p_4s^2(1)+\dfrac{1}{2}p_4s^2(0)\\&-\dfrac{\tau}{2}\displaystyle\int_{0}^{1}{\rm e}^{-\tau x}p_3r^2{\rm d}x-\dfrac{\tau}{2}\displaystyle\int_{0}^{1}{\rm e}^{-\tau x}p_4s^2{\rm d}x.\end{align*}$

(3.30)

再将边界条件 (3.4) 代入 (3.30) 式中, 利用均值不等式放缩为

$\begin{align*} Re\langle\mathcal{A}X,X\rangle_1\leq\ &\big(-\dfrac{1}{2}p_1{\rm e}^{-\frac{\mu}{\lambda_1^*}}+2p_1k_1^2+\dfrac{1}{2}p_3\big)m^2(1)+\big(2p_1k_2^2-\dfrac{1}{2}p_2{\rm e}^{-\frac{\mu}{\lambda_2^*}}+p_2k_5^2+\dfrac{1}{2}p_4\big)n^2(1)\\&+\big(2p_1k_3^2-\dfrac{1}{2}{\rm e}^{-\tau}p_3\big)r^2(1)+\big(2p_1k_4^2+p_2k_6^2-\dfrac{1}{2}{\rm e}^{-\tau}p_4\big)s^2(1)\\&-\dfrac{\tau}{2}\displaystyle\int_{0}^{1}{\rm e}^{-\tau x}p_3r^2{\rm d}x-\dfrac{\tau}{2}\displaystyle\int_{0}^{1}{\rm e}^{-\tau x}p_4s^2{\rm d}x.\end{align*}$

(3.31)

于是, 当所选参数满足约束条件 (3.24) 的前四个条件时, 可得

$\begin{equation} {\rm Re}\langle\mathcal{A}X,X\rangle_1\leq 0.\end{equation}$

(3.32)

因此, 系统算子 $\mathcal{A}$ 在 $\mathcal{H}$ 上是耗散的. 则由 Lumer-Phillips 定理 (详见文献 [16,定理 4.3]{A. Pazy}), $\mathcal{A}$ 生成 $\mathcal{H}$ 上的一个 $C_0$ 压缩半群. 证毕.

定理 3.4 假设 $\tilde{\rm d}(t)\doteq\frac{\alpha \tilde{p}_{in}(t)}{v^*I}$ 是关于 $t$ 的有界可测函数, 则对 $\forall (\tilde{\omega}(\cdot,0),\tilde{z}(\cdot,0),u(\cdot,0),$ $g(\cdot,0))\in\mathcal{H},$ 系统 (3.8) 是适定的.

证对于线性系统 (3.8) 的子系统

$\begin{equation} \begin{cases}\dot{X}(t)=\mathcal{A}X(t)+\mathcal{B}_2\dfrac{\alpha \tilde{p}_{in}(t)}{v^*I},\\X(0)=X_0.\\\end{cases}\end{equation}$

(3.33)

考虑其对偶系统的观测问题

$\begin{equation} \begin{cases}\dot{X}^*(t)=\mathcal{A}^*X^*(t),\;\; X^*(t)=(\tilde{w}^*,\tilde{z}^*,u^*,g^*)\in D(\mathcal{A}^*),\\y^*=\mathcal{B}_2^*X^*(t),\end{cases}\end{equation}$

(3.34)

其中, $\mathcal{B}_2^*=\mathcal{B}_2$ . 由定理 3.3 易知, $1\in \rho(\mathcal{A})$ , 且 $\int_{0}^{T}|y^*(t)|^2{\rm d}t=\int_{0}^{T}(\tilde{w}^*(0,t))^2{\rm d}t$ 有界. 于是可得, $\mathcal{B}_2^*(I-\mathcal{A}^*)^{-1}$ 在 $\mathcal{H}$ 上是有界的. 因此, $\mathcal{B}_2^*$ 对 $\mathcal{A}^*$ 生成的 $C_0$ 半群 ${\rm e}^{\mathcal{A}^*t}$ 是可允许的. 于是, 根据文献 [17,定理 4.4.3]{M.Tucsnak} 可知, $\mathcal{B}_2$ 对 $\mathcal{A}$ 生成的 $C_0$ 半群 ${\rm e}^{\mathcal{A}t}$ 也是可允许的. 又由于 $\mathcal{B}_1$ 是一个有界算子, 从而由 $C_0$ 半群有界扰动定理可知, 系统 (3.8) 是适定的. 证毕.

4 稳定性分析

由于系统 (2.26) 具有模型漂移项以及不确定的交通需求扰动项, 因此这一部分通过构造合适的 ISS-Lyapunov 函数来证明系统的 ISS 稳定性. 不失一般性, 为方便计算, 取 $L=1$ .

定义 4.1 如果存在一个 $\mathcal{K}\mathcal{L}$ 类函数 $\beta$ 和一个 $\mathcal{K}$ 类函数 $\gamma$ , 对于任意初始状态 $(\tilde{w}(0,t),$ $\tilde{z}(0,t))\in L^2(0,1)$ , 系统 (2.26) 的解 $(\tilde{w}(x,t),\tilde{z}(x,t))$ 满足

$\begin{equation*}\Vert(\tilde{w}(x,t),\tilde{z}(x,t))\Vert_{{L^2}(0,1)}\leq\beta(\Vert(\tilde{w}(0,t),\tilde{z}(0,t))\Vert_{{L^2}(0,1)})\\+\gamma(\sup\Vert(c(v_f-w^*),\dfrac{\alpha \tilde{p}_{in}(t)}{v^*I})\Vert_{{L^2}(0,1)}),\end{equation*}$

则系统 (2.26) 在干扰 $(c(v_f-w^*),\frac{\alpha \tilde{p}_{in}(t)}{v^*I})$ 下均是ISS稳定的.

定理 4.1 如果存在 $p_i>0\ (i=1,2,3,4)$ 使得控制参数 $k_i\ (i=1,2,\cdots,6)$ 和时滞 $\tau$ 满足如下条件

$\begin{equation} \begin{cases}5p_1k_1^2-p_1{\rm e}^{\frac{-\mu}{\lambda_1^*}}+p_3\leq0,\;\;5p_1k_2^2-p_2{\rm e}^{\frac{-\mu}{\lambda_2^*}}+2p_2k_5^2+p_4\leq0,\\5p_1k_3^2-{\rm e}^{-\tau}p_3\leq0,\;\;5p_1k_4^2-{\rm e}^{-\tau}p_4+2p_2k_6^2\leq0,\\\mu+2c>\dfrac{p_1}{\lambda_1^*}{\rm e}^{\frac{\mu}{\lambda_1^*}},\;\;(\mu {\rm e}^{\frac{-\mu}{\lambda_1^*}}+2c{\rm e}^{\frac{-\mu}{\lambda_1^*}}-\dfrac{p_1}{\lambda_1^*})(\mu {\rm e}^{\frac{-\mu}{\lambda_2^*}}-\dfrac{p_2}{\lambda_2^*})>\dfrac{p_2\lambda_1^*}{p_1\lambda_2^*}c^2,\end{cases}\end{equation}$

(4.1)

则系统 (2.26) 是 ISS 稳定的.

证构造 ISS-Lyapunov 函数如下

$\begin{equation} V(t)=V_1(t)+V_2(t),\end{equation}$

(4.2)

其中

$\begin{align*} &V_1(t)=\displaystyle\int_{0}^{1}\big(\dfrac{p_1}{\lambda_1^*}{\rm e}^{-\frac{\mu x}{\lambda_1^*}}\tilde{w}^2+\dfrac{p_2}{\lambda_2^*}{\rm e}^{-\frac{\mu x}{\lambda_2^*}}\tilde{z}^2\big){\rm d}x,\end{align*}$

(4.3)

$\begin{align*} V_2(t)=\tau \displaystyle\int_{0}^{1}{\rm e}^{-\tau x}(p_3u^2+p_4g^2){\rm d}x. \end{align*}$

(4.4)

沿系统 (2.26) 的解, 将 (4.3) 式对 $t$ 求导并进行分部积分得

$\begin{align*} \dot{V}_1(t)=&\displaystyle\int_{0}^{1}\big[\dfrac{p_1}{\lambda_1^*}{\rm e}^{\frac{-\mu x}{\lambda_1^*}}2\tilde{w}\partial_t\tilde{w}+\dfrac{p_2}{\lambda_2^*}{\rm e}^{\frac{-\mu x}{\lambda_2^*}}2\tilde{z}\partial_t\tilde{z}\big]{\rm d}x\\=&-p_1{\rm e}^{\frac{-\mu}{\lambda_1^*}}\tilde{w}^2(1,t)+p_1\tilde{w}^2(0,t)-p_2{\rm e}^{\frac{-\mu}{\lambda_2^*}}\tilde{z}^2(1,t)+p_2\tilde{z}^2(0,t)\\&-\dfrac{\mu}{\lambda_1^*}\displaystyle\int_{0}^{1}p_1{\rm e}^{\frac{-\mu x}{\lambda_1^*}}\tilde{w}^2{\rm d}x-\dfrac{\mu}{\lambda_2^*}\displaystyle\int_{0}^{1}p_2{\rm e}^{\frac{-\mu x}{\lambda_2^*}}\tilde{z}^2{\rm d}x-\displaystyle\int_{0}^{1}\dfrac{p_1}{\lambda_1^*}{\rm e}^{\frac{-\mu x}{\lambda_1^*}}2c\tilde{w}^2{\rm d}x\\&-\displaystyle\int_{0}^{1}\dfrac{p_2}{\lambda_2^*}{\rm e}^{\frac{-\mu x}{\lambda_2^*}}2c\tilde{w}\tilde{z}{\rm d}x+\displaystyle\int_{0}^{1}\dfrac{p_1}{\lambda_1^*}{\rm e}^{\frac{-\mu x}{\lambda_1^*}}2\tilde{w}c(v_f-w^*){\rm d}x\\&+\displaystyle\int_{0}^{1}\dfrac{p_2}{\lambda_2^*}{\rm e}^{\frac{-\mu x}{\lambda_2^*}}2\tilde{z}c(v_f-w^*){\rm d}x.\end{align*}$

(4.5)

运用 Cauchy-Schwarz 不等式和 Young 不等式将 (4.5) 式放缩为

$\begin{align*} \dot{V}_1(t)\leq&-p_1{\rm e}^{\frac{-\mu}{\lambda_1^*}}\tilde{w}^2(1,t)+p_1\tilde{w}^2(0,t)-p_2{\rm e}^{\frac{-\mu}{\lambda_2^*}}\tilde{z}^2(1,t)+p_2\tilde{z}^2(0,t)\\&-\dfrac{\mu}{\lambda_1^*}\displaystyle\int_{0}^{1}p_1{\rm e}^{\frac{-\mu x}{\lambda_1^*}}\tilde{w}^2{\rm d}x-\dfrac{\mu}{\lambda_2^*}\displaystyle\int_{0}^{1}p_2{\rm e}^{\frac{-\mu x}{\lambda_2^*}}\tilde{z}^2{\rm d}x-\displaystyle\int_{0}^{1}\dfrac{p_1}{\lambda_1^*}{\rm e}^{\frac{-\mu x}{\lambda_1^*}}2c\tilde{w}^2{\rm d}x\\&-\displaystyle\int_{0}^{1}\dfrac{p_2}{\lambda_2^*}{\rm e}^{\frac{-\mu x}{\lambda_2^*}}2c\tilde{w}\tilde{z}{\rm d}x+\displaystyle\int_{0}^{1}\dfrac{p_1^2}{(\lambda_1^*)^2}{\rm e}^{\frac{-2\mu x}{\lambda_1^*}}\tilde{w}^2{\rm d}x+\displaystyle\int_{0}^{1}\dfrac{p_2^2}{(\lambda_2^*)^2}{\rm e}^{\frac{-2\mu x}{\lambda_2^*}}\tilde{z}^2{\rm d}x\\&+2c^2(v_f-w^*)^2.\end{align*}$

(4.6)

令

$\begin{align*} W(t)=&-\dfrac{\mu}{\lambda_1^*}\displaystyle\int_{0}^{1}p_1{\rm e}^{\frac{-\mu x}{\lambda_1^*}}\tilde{w}^2{\rm d}x-\dfrac{\mu}{\lambda_2^*}\displaystyle\int_{0}^{1}p_2{\rm e}^{\frac{-\mu x}{\lambda_2^*}}\tilde{z}^2{\rm d}x-\displaystyle\int_{0}^{1}\dfrac{p_1}{\lambda_1^*}{\rm e}^{\frac{-\mu x}{\lambda_1^*}}2c\tilde{w}^2{\rm d}x\\&-\displaystyle\int_{0}^{1}\dfrac{p_2}{\lambda_2^*}{\rm e}^{\frac{-\mu x}{\lambda_2^*}}2c\tilde{w}\tilde{z}{\rm d}x+\displaystyle\int_{0}^{1}\dfrac{p_1^2}{(\lambda_1^*)^2}{\rm e}^{\frac{-2\mu x}{\lambda_1^*}}\tilde{w}^2{\rm d}x+\displaystyle\int_{0}^{1}\dfrac{p_2^2}{(\lambda_2^*)^2}{\rm e}^{\frac{-2\mu x}{\lambda_2^*}}\tilde{z}^2{\rm d}x\\\leq&-\displaystyle\int_{0}^{1}\big(\dfrac{\mu}{\lambda_1^*}{\rm e}^{\frac{-\mu }{\lambda_1^*}}p_1+{\rm e}^{\frac{-\mu }{\lambda_1^*}}\dfrac{p_1}{\lambda_1^*}2c-\dfrac{p_1^2}{(\lambda_1^*)^2}\big)\tilde{w}^2{\rm d}x-\displaystyle\int_{0}^{1}\dfrac{p_2}{\lambda_2^*}{\rm e}^{\frac{-\mu x}{\lambda_2^*}}2c\tilde{w}\tilde{z}{\rm d}x\\&-\displaystyle\int_{0}^{1}\big(\dfrac{\mu}{\lambda_2^*}{\rm e}^{\frac{-\mu}{\lambda_2^*}}p_2-\dfrac{p_2^2}{(\lambda_2^*)^2}\big)\tilde{z}^2{\rm d}x\\=&-\displaystyle\int_{0}^{1}A^TPA{\rm d}x,\end{align*}$

(4.7)

且

$\begin{equation*}A=\left( \begin{array}{c} \tilde{w} \\ \tilde{z} \end{array}\right),\;P=\left( \begin{array}{cc} \dfrac{\mu}{\lambda_1^*}{\rm e}^{\frac{-\mu}{\lambda_1^*}}p_1+{\rm e}^{\frac{-\mu}{\lambda_1^*}}\dfrac{p_1}{\lambda_1^*}2c-\dfrac{p_1^2}{(\lambda_1^*)^2} & \dfrac{p_2}{\lambda_2^*}{\rm e}^{\frac{-\mu x}{\lambda_2^*}}c \\[3mm] \dfrac{p_2}{\lambda_2^*}{\rm e}^{\frac{-\mu x}{\lambda_2^*}}c & \dfrac{\mu}{\lambda_2^*}{\rm e}^{\frac{-\mu}{\lambda_2^*}}p_2-\dfrac{p_2^2}{(\lambda_2^*)^2} \end{array} \right).\end{equation*}$

下证 $\forall t>0,\;W(t)<0,$ 即 $P$ 为正定矩阵, 即证 $P$ 的各阶顺序主子式均大于 0:

$\begin{equation} \begin{array}{ll}{\rm (a)} \mu+2c>\dfrac{p_1}{\lambda_1^*}{\rm e}^{\frac{\mu}{\lambda_1^*}},\\[3mm]{\rm (b)} (\mu {\rm e}^{\frac{-\mu}{\lambda_1^*}}+2c{\rm e}^{\frac{-\mu}{\lambda_1^*}}-\dfrac{p_1}{\lambda_1^*})\cdot(\mu {\rm e}^{\frac{-\mu}{\lambda_2^*}}-\dfrac{p_2}{\lambda_2^*})>\dfrac{p_2\lambda_1^*}{p_1\lambda_2^*}{\rm e}^{\frac{-2\mu x}{\lambda_2^*}}c^2.\end{array}\end{equation}$

(4.8)

考虑到当 $x=0$ 时, ${\rm e}^{\frac{-2\mu x}{\lambda_2^*}}$ 取到最大, 所以为使 (b) 成立, 仅需

$\begin{equation} (\mu {\rm e}^{\frac{-\mu}{\lambda_1^*}}+2c{\rm e}^{\frac{-\mu}{\lambda_1^*}}-\dfrac{p_1}{\lambda_1^*})(\mu {\rm e}^{\frac{-\mu}{\lambda_2^*}}-\dfrac{p_2}{\lambda_2^*})>\dfrac{p_2\lambda_1^*}{p_1\lambda_2^*}c^2.\end{equation}$

(4.9)

沿系统 (2.26) 的解, 将 (4.4) 式对 $t$ 求导得

$\begin{align*} \dot{V_2}(t)=&\tau\displaystyle\int_{0}^{1}{\rm e}^{-\tau x}\big(p_3 2u\partial_t u+p_4 2g\partial_t g\big){\rm d}x\\=&-p_3{\rm e}^{-\tau}u^2(1,t)+p_3u^2(0,t)-p_4{\rm e}^{-\tau}g^2(1,t)+p_4g^2(0,t)\\&-\tau\displaystyle\int_{0}^{1}{\rm e}^{-\tau x}\big(p_3u^2+p_4g^2\big){\rm d}x.\end{align*}$

(4.10)

将系统 (2.26) 的边界条件代入 (4.5) 和 (4.10) 式中, 并利用均值不等式整理得

$\begin{align*} \dot{V}(t)=&\ \dot{V_1}(t)+\dot{V_2}(t)\\\leq&-p_1{\rm e}^{\frac{-\mu}{\lambda_1^*}}\tilde{w}^2(1,t)+p_1\tilde{w}^2(0,t)-p_2{\rm e}^{\frac{-\mu}{\lambda_2^*}}\tilde{z}^2(1,t)+p_2\tilde{z}^2(0,t)-{\rm e}^{-\tau}p_3u^2(1,t)\\&+p_3u^2(0,t)-{\rm e}^{-\tau}p_4g^2(1,t)+p_4g^2(0,t)-\mu\displaystyle\int_{0}^{1}\dfrac{p_1}{\lambda_1^*}{\rm e}^{\frac{-\mu x}{\lambda_1^*}}\tilde{w}^2{\rm d}x\\&-\mu\displaystyle\int_{0}^{1}\dfrac{p_2}{\lambda_2^*}{\rm e}^{\frac{-\mu x}{\lambda_2^*}}\tilde{z}^2{\rm d}x-\tau\displaystyle\int_{0}^{1}{\rm e}^{-\tau x}\big(p_3u^2+p_4g^2\big){\rm d}x+2c^2(v_f-w^*)^2\\\leq &\ \big[-p_1{\rm e}^{-\frac{\mu}{\lambda_1^*}}+5p_1k_1^2+p_3\big]\tilde{w}^2(1,t)+\big[5p_1k_2^2-p_2{\rm e}^{-\frac{\mu}{\lambda_2^*}}+2p_2k_5^2+p_4\big]\tilde{z}^2(1,t)\\&+\big[5p_1k_3^2-{\rm e}^{-\tau}p_3\big]u^2(1,t)+\big[5p_1k_4^2-{\rm e}^{-\tau}p_4+2p_2k_6^2\big]g^2(1,t)\\&-\mu\displaystyle\int_{0}^{1}\dfrac{p_1}{\lambda_1^*}{\rm e}^{\frac{-\mu x}{\lambda_1^*}}\tilde{w}^2{\rm d}x-\mu\displaystyle\int_{0}^{1}\dfrac{p_2}{\lambda_2^*}{\rm e}^{\frac{-\mu x}{\lambda_2^*}}\tilde{z}^2{\rm d}x-\tau\displaystyle\int_{0}^{1}{\rm e}^{-\tau x}\big(p_3u^2+p_4g^2\big){\rm d}x\\&+2c^2(v_f-w^*)^2+5p_1\dfrac{\alpha^2 \tilde{p}_{in}^2(t)}{(v^*I)^2}.\end{align*}$

(4.11)

于是, 由约束条件 (4.1) 的前四个条件可得

$\begin{align*} \dot{V}(t)\leq&-\mu\displaystyle\int_{0}^{1}\dfrac{p_1}{\lambda_1^*}{\rm e}^{\frac{-\mu x}{\lambda_1^*}}\tilde{w}^2{\rm d}x-\mu\displaystyle\int_{0}^{1}\dfrac{p_2}{\lambda_2^*}{\rm e}^{\frac{-\mu x}{\lambda_2^*}}\tilde{z}^2{\rm d}x-\tau\displaystyle\int_{0}^{1}{\rm e}^{-\tau x}\big(p_3u^2+p_4g^2\big){\rm d}x\\&+2c^2(v_f-w^*)^2+5p_1\dfrac{\alpha^2 \tilde{p}_{in}^2(t)}{(v^*I)^2}\\\leq&-\varepsilon V(t)+\nu\Vert(c(v_f-w^*),\dfrac{\alpha \tilde{p}_{in}(t)}{v^*I})\Vert^2,\end{align*}$

(4.12)

其中

$\begin{equation} \varepsilon=\min\{\mu,1\},\;\nu=\max\{2,5p_1\}.\end{equation}$

(4.13)

在 (4.12) 式两边从 0 到 $t$ 取积分得

$\begin{align*} V(t)&\leq{\rm e}^{-\varepsilon t}V(0)+\displaystyle\int_{0}^{t}{\rm e}^{-\varepsilon(t-s)}\nu\Vert(c(v_f-w^*),\dfrac{\alpha \tilde{p}_{in}(t)}{v^*I})\Vert^2{\rm d}s\\&\leq{\rm e}^{-\varepsilon t}V(0)+\nu\Vert(c(v_f-w^*),\dfrac{\alpha \tilde{p}_{in}(t)}{v^*I})\Vert^2.\end{align*}$

(4.14)

因此, 带有时滞控制器的系统 (2.26) 在有界干扰 $(c(v_f-w^*),\frac{\alpha \tilde{p}_{in}(t)}{v^*I})$ 下是 ISS 稳定的. 证毕.

注 4.1 根据定理 4.1 可知, 要使系统 (2.26) ISS 稳定, 控制器中的时滞参数 $\tau$ 需满足

$\begin{equation*}\tau\leq\min\Big\{\ln\dfrac{p_3}{5p_1k_3^2},\;\ln\dfrac{p_4}{5p_1k_4^2+2p_2k_6^2}\Big\}.\end{equation*}$

也就是说, 定理 4.1 建立的是与时滞相关的稳定性结论.

注 4.2 当不考虑漂移项 $c(v_f-w^*)$ 和交通需求扰动项 $\frac{\alpha \tilde{p}_{in}(t)}{v^*I}$ 时, 通过类似定理 4.1 的证明过程, 可以得到系统 (2.26) 在时滞控制器 (2.11) 的作用下达到指数稳定.

5 与时滞无关的稳定性分析结果

在这一部分, 不妨设 $\lambda_1^*=\lambda_2^*\doteq\lambda^*$ , 我们考虑系统 (2.8) 在单纯时滞反馈 (2.12) 下的特征方程. 此时, $k_1=k_2=k_5=0,$ 且

$\begin{equation} \Delta(\lambda)\doteq\left |\begin{array}{cccc}1 & 0 & -k_3{\rm e}^{-\tau\lambda} & -k_4{\rm e}^{-\tau\lambda}\\0 & -1 & 0 & k_6{\rm e}^{-\tau\lambda}\\{\rm e}^{-\frac{\lambda+c}{\lambda^*}} & 0 & -1 & 0\\{\rm e}^{-\frac{\lambda+c}{\lambda^*}}-{\rm e}^{-\frac{\lambda}{\lambda^*}} & {\rm e}^{-\frac{\lambda}{\lambda^*}} & 0 & -1\end{array}\right|=0,\end{equation}$

(5.1)

i.e.

$\begin{equation} {\rm e}^{2\lambda\sigma}+(k_4-k_6-a(k_3+k_4)){\rm e}^{\lambda\sigma}+ak_3k_6=0,\end{equation}$

(5.2)

其中,

$\begin{equation} a={\rm e}^{-\frac{c}{\lambda^*}}(0<a<1),\;\; \sigma=\tau+\dfrac{1}{\lambda^*}>0.\end{equation}$

(5.3)

令 $y={\rm e}^{\lambda\sigma}$ , 则 (5.2) 式可转化为关于 $y$ 的一元二次方程

$\begin{equation} F(y)\doteq y^2+(k_4-k_6-a(k_3+k_4))y+ak_3k_6=0.\end{equation}$

(5.4)

显然, 特征值的实部 Re $\lambda<0$ 当且仅当方程 (5.4) 的根位于单位圆内 $(|y|<1).$ 为此, 首先给出 Schur-Cohn 准则 (参见文献 [18,p34-36]).

命题 5.1 实系数多项式

$F(\mu)=a_{n} \mu^{n}+a_{n-1}\mu^{n-1}+\cdots+a_{1} \mu+a_{0},\; a_{n}>0$

的全体根位于单位圆内, 当且仅当

$F(1)>0, \ (-1)^{n}F(-1)>0,$

且 $(n-1)\times (n-1)$ Jury 矩阵

$\Delta_{n-1}^{\pm}=\left( \begin{array}{ccccc} a_{n} & 0 & 0 & \cdots & 0 \\ a_{n-1} & a_{n} & 0 & \cdots & 0 \\ a_{n-2} & a_{n-1} & a_{n} & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{2} & a_{3} & a_{4} & \cdots & a_{n} \\ \end{array} \right)\pm\left( \begin{array}{ccccc} 0 & 0 & \cdots & 0 & a_{0} \\ 0 & 0 & \cdots & a_{0} & a_{1} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & a_{0} & \cdots & a_{m-4} & a_{m-3} \\ a_{0} & a_{1} & \cdots & a_{m-3} & a_{m-2} \\ \end{array} \right)$

的内子矩阵的行列式均大于 0.

根据命题 5.1, 易得如下结论

定理 5.1 无论时滞 $\tau$ 取值如何, 系统算子 $\mathcal{A}$ 的特征值具有负实部, 当且仅当反馈参数满足

$\begin{equation} 1-ak_3k_6>0,\;\;1+ak_3k_6>|k_4-k_6-a(k_3+k_4)|.\end{equation}$

(5.5)

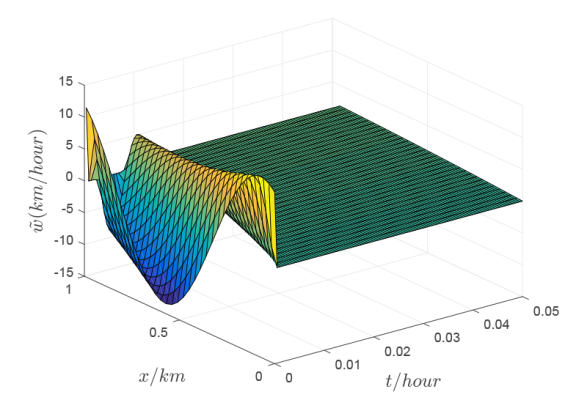
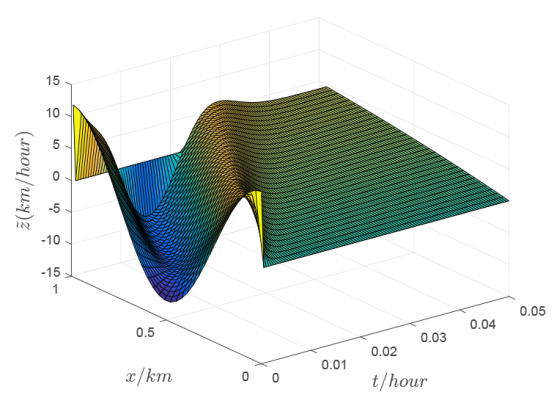
6 数值模拟

本节通过 MATLAB 数值仿真实例来验证所设计的时滞控制器的有效性和可行性. 考虑自由模态下的快速路段, 其道路参数为

$\bullet$ $\rho_m=200veh/{\rm km},\;v_f=150{\rm km/h};$

$\bullet$ 道路长度为: $L={\rm 1km}$ ;

$\bullet$ 速度松弛时间为: $\tau_0=\dfrac{1}{60}{\rm h}$ ;

$\bullet$ 车道数为: $I=4$ ;

$\bullet$ 交通需求扰动: $|\tilde{p}_{in}(t)|\leq50veh/{\rm h}$ ;

$\bullet$ 稳态 $(\rho^*,v^*)=(75,90)$ .

由 (2.4) 和 (2.9) 式计算可得

$\begin{equation} \lambda_1^*=90, \;\; \lambda_2^*=33.75.\end{equation}$

(6.1)

进而, 选取参数

$\begin{equation} p_1=3,\;p_2=0.0002,\;p_3=1,\;p_4=0.0001,\;\mu=0.01,\end{equation}$

(6.2)

控制器的时滞参数

$\begin{equation} \tau=0.01{\rm h},\end{equation}$

(6.3)

则根据定理 4.1, 反馈参数 $k_i\ (1\leq i\leq 6)$ 需满足条件

$\begin{equation} k_1^2\leq0.13,\;15k_2^2+0.0004k_5^2\leq0.0001,\;\;k_3^2\leq0.066,\;15k_4^2+0.0004k_6^2\leq0.0001.\end{equation}$

(6.4)

不妨取满足上述条件的 $k_i$ 为

$\begin{equation} k_1=0.3,\;k_2=0.002,\;k_3=0.24,\;k_4=0.002,\;k_5=0.2,\;k_6=0.2.\end{equation}$

(6.5)

图1和图2分别展示了系统 (2.26) 的状态 $\tilde{w}$ 与 $\tilde{z}$ 的收敛性, 初始条件为 $\tilde{w}(x,0)=12\cos(2\pi x)+6\sin(2\pi x), \tilde{z}(x,0)=12\cos(2\pi x), u(x,0)=12\cos(2\pi x)+22x, g(x,0)=12\cos(2\pi x)+36x.$ 根据图1和图2可以看出, 漂移项和边界扰动的存在使系统状态在平衡态附近出现轻微波动, 并未收敛到 0, 此时系统 (2.26) 达到 ISS 稳定.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 系统 (2.26) 中 $\tilde{w}(x,t)$ 的收敛性

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 系统 (2.26) 中 $\tilde{z}(x,t)$ 的收敛性

注 6.1 从定理 $4.1$ 的条件 (4.1) 式可以看出, 取定参数 $k_i$ 和 $p_i$ 后, 可以求得时滞参数 $\tau$ 的稳定域. 如果参数 $k_i$ , $p_i$ 的选取如 (6.2) 和 (6.5) 式所示, 那么, 易求得: $\tau\leq0.15{\rm h}$ . 这一结果表明, 只要时滞控制器中的时滞参数 $\tau$ 不超过 9 分钟, 则闭环系统 (2.26) 必可达到 ISS 稳定.

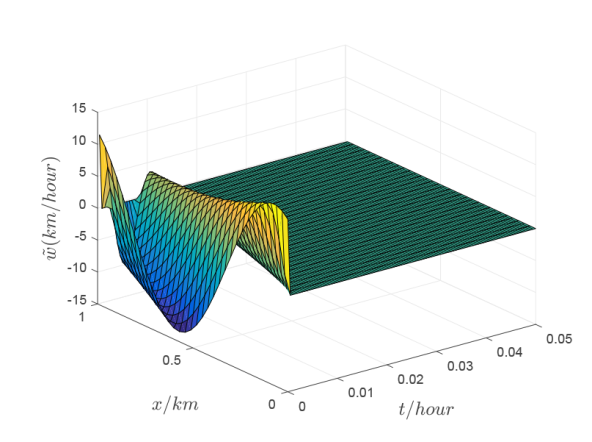
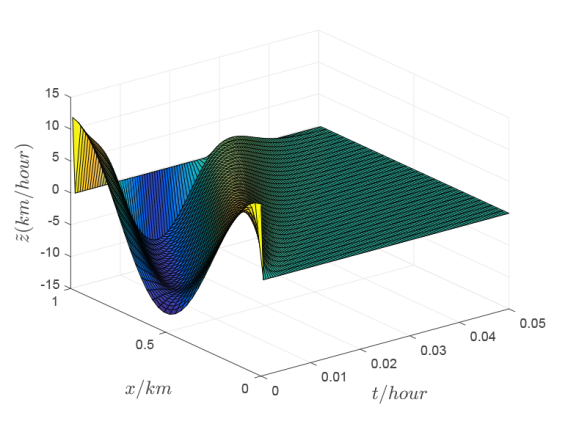
特别地, 当不考虑漂移项, 即 $v_f=w^*$ , 且边界处不存在交通需求扰动项时, 此时取稳态 $(\rho^*,v^*)=(80,90)$ , $\lambda_1^*=90,$ $\lambda_2^*=30$ , 其余参数选取同上. 图3与图4分别展示了系统 (2.26) 的状态 $\tilde{w}$ 与 $\tilde{z}$ 的收敛性, 其中初始条件为 $\tilde{w}(x,0)=12\cos(2\pi x)+6\sin(2\pi x)$ , $\tilde{z}(x,0)=12\cos(2\pi x)$ , $u(x,0)=12\cos(2\pi x)+22.5x, g(x,0)=12\cos(2\pi x)+36x.$ 可以看出, 不考虑系统的漂移项以及边界交通需求扰动项, 系统状态在较短时间内以指数形式收敛到稳态, 此时系统 (2.26) 达到指数稳定.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 当漂移项和交通需求扰动项不存在时, 系统 (2.26) 中 $\tilde{w}(x,t)$ 的收敛性

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 当漂移项和交通需求扰动项不存在时, 系统 (2.26) 中 $\tilde{z}(x,t)$ 的收敛性

7 结论

本文首先对宏观 ARZ 交通流模型进行黎曼坐标变换及线性化处理, 在自由模态下, 结合匝道控制和可变限速控制建立了状态反馈与时滞状态反馈相结合的控制策略. 其次, 将时滞项用一阶运输方程初值问题的解进行刻画, 构建了 PDE-PDE 无穷维耦合闭环系统. 然后, 结合线性系统解与控制算子的允许性理论, 证明了闭环系统的适定性. 通过构建加权 Lyapunov 函数证明了系统的 ISS 稳定性, 并得到了与时滞相关的稳定性条件. 最后, 若仅考虑时滞反馈, 在特征速度 $\lambda_1^*=\lambda_2^*$ 的情形下, 建立了与时滞无关的稳定性条件. 特别指出, 第 3.3 节中验证算子 $\mathcal{A}$ 的耗散性时, 构造了一个等价内积, 与第 4 节构建的 ISS 加权 Lyapunov 函数类似, 其中的证明思路也相似, 唯一不同之处在于放缩的要求, 3.3 节只需要 $\langle\mathcal{A}X,X\rangle\leq0,$ 而第 4 节需要做到 $\langle\mathcal{A}X,X\rangle\leq -\varepsilon\langle X,X\rangle (\varepsilon>0).$

此外, 若系统处于拥堵模态的情形, 即 $(1+\gamma)z^*-\gamma w^*<0,$ 类似地, 亦可建立系统的适定性和 ISS 稳定性. 在下一步研究工作中, 期望将结论推广至多段路段串联而成的城市快速路网的情形. 一般地, 若系统的平衡状态并非常量, 而是关于位置变量 $x$ 的函数, 系统将转化为一阶变系数双曲型偏微分方程组, 其控制器设计, 适定性和指数稳定性等也是很有意义的研究工作.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

, Rascle

Resurrection of “second order” models of traffic flow

SIAM Journal on Applied Mathematics, 2000, 60(3): 916-938

[本文引用: 1]

[2]

Zhang

H M

A non-equilibrium traffic model devoid of gas-like behavior

Transportation Research Part B: Methodological, 2002, 36(3): 275-290

[本文引用: 1]

[3]

Francois

, Mandy

, Xavier

, et al.

Prediction of traffic convective instability with spectral analysis of the Aw-Rascle-Zhang model

Physics Letters A, 2015, 379: 2319-2330

[本文引用: 1]

[4]

Z B

, Xu

C C

, Li

D W

, et al.

Comparing the effects of ramp metering and variable speed limit on reducing travel time and crash risk at bottlenecks

IET Intelligent Transport Systems, 2018, 12: 120-126

[本文引用: 1]

[5]

Zhang

L G

, Prieur

Necessary and sufficient conditions on the exponential stability of positive hyperbolic systems

IEEE Transactions on Automatic Control, 2017, 62(7): 3610-3617

[本文引用: 1]

[6]

, Krstic

. Traffic Congestion Control by PDE Backstepping. Switzerland: Springer, 2022

[本文引用: 1]

[7]

Bastin

, Coron

J M

. Stability and Boundary Stabilization of 1-D Hyperbolic Systems. Switzerland: Springer, 2016

[本文引用: 1]

[8]

Zhang

L G

, Prieur

, Qiao

J F

PI boundary control of linear hyperbolic balance laws with stabilization of ARZ traffic flow models

Systems

$\&$

Control Letters, 2019, 123: 85-91

[本文引用: 2]

[9]

Zhang

L G

, Luan

H R

, Lu

Y S

, et al.

Boundary feedback stabilization of freeway traffic networks: ISS control and experiments

IEEE Transactions on Control Systems Technology, 2022, 30(3): 997-1008

[本文引用: 2]

[10]

, Krstic

Traffic congestion control for Aw-Rascle-Zhang Model

Automatica, 2019, 100: 38-51

DOI:10.1016/j.automatica.2018.10.040 [本文引用: 1]

This paper develops boundary feedback control laws to reduce stop-and-go oscillations in congested traffic. The macroscopic traffic dynamics are governed by Aw-Rascle-Zhang (ARZ) model, consisting of second-order nonlinear partial differential equations (PDEs). A criterion to distinguish free and congested regimes for the ARZ traffic model leads to the study of hetero-directional hyperbolic PDE model of congested traffic regime. To stabilize the oscillations of traffic density and speed in a freeway segment, a boundary input through ramp metering is considered. We discuss the stabilization problem for freeway segments respectively, upstream and downstream of the ramp. For the more challenging upstream control problem, our full-state feedback control law employs a backstepping transformation. Both collocated and anti-collocated boundary observers are designed. The exponential stability in L-2 sense and finite time convergence to equilibrium are achieved and validated with simulation. In the absence of relaxation time and boundary parameters' knowledge, we propose adaptive output feedback control design. Control is applied at outlet and the measurement is taken from inlet of the freeway segment. We use the backstepping method to obtain an observer canonical form in which unknown parameters multiply with measured output. A parametric model based on this form is derived and gradient-based parameter estimators are designed. An explicit state observer involving the delayed values of the input and the output is introduced for state estimation. Using the parameter and state estimates, we develop an adaptive output feedback control law which achieves convergence to the steady regulation in the L-2 sense. (C) 2018 Published by Elsevier Ltd.

[11]

Burkhardt

, Yu

, Krstic

Stop-and-go suppression in two-class congested traffic

Automatica, 2021, 125: 109381

[本文引用: 1]

[12]

Chentouf

, Smaoui

Time-Delayed feedback control of a hydraulic model governed by a diffusive wave system

Complexity, 2020, 2020: 1-15

[本文引用: 1]

[13]

范东霞, 赵东霞, 史娜, 等.

一类扩散波方程的PDP反馈控制和稳定性分析

数学物理学报, 2021, 41A(4): 1088-1096

[本文引用: 1]

Fan

D X

, Zhao

D X

, Shi

, et al.

The PDP feedback control and stability analysis of a diffusive wave equation

Acta Mathematica Scientia, 2021, 41A(4): 1088-1096

[本文引用: 1]

[14]

Zhao

D X

, Bao

F X

The stability analysis for a 2 × 2 conservation law with PI controller and PDP Controller

Journal of Mathematics, 2023, Article 4382517

[本文引用: 1]

[15]

陆宇晟

. 城市快速路网的分布式边界观测器设计与边界反馈控制. 北京: 北京工业大学, 2020

[本文引用: 1]

Y S

. Distributed boundary observer design and boundary feedback control for urban rapid road network. Beijing: Beijing University of Technology, 2020

[本文引用: 1]

[16]

Pazy

. Semigroups of Linear Operators and Applications to Partial Differential Equations. New York: Springer-Verlag, 1983

[本文引用: 1]

[17]

Tucsnak

, Weiss

. Observation and Control for Operator Semi-groups. Switzerland: Birkhäuser, 2000

[本文引用: 1]

[18]

Jury

E I

. Inners and Stability of Dynamic Systems. New York: John Wiley Sons, 1974

[本文引用: 1]

Resurrection of “second order” models of traffic flow

2000

... ARZ非平衡交通流模型能够较为准确地刻画城市快速路网车辆的运行, 在黎曼坐标变换和线性化处理后呈现为二阶双曲偏微分方程组的形式^[1⇓-3]. 近年来, 入口匝道控制和可变限速控制成为城市快速路网车辆交通流控制的两种有效方法^[4], 将其应用于 AR/ARZ 非平衡交通流模型, 取得了一系列研究成果^[5,6]. 对于线性/拟线性双曲系统柯西问题解的适定性, 文献 [7,定理 A.1,B.1] 采用 Lumer-Philipps 定理、不动点定理和能量估计等数学方法进行了证明. 在稳定性分析方面, 文献 [8] 研究了一维

$n\times n$

线性双曲平衡律系统在比例-积分 (PI) 边界反馈控制下的稳定性, 结合 Lyapunov 函数和线性矩阵不等式 (LMI) 方法, 建立了系统指数稳定所满足的矩阵不等式条件. 进而, 将所得结论应用于 ARZ 交通流模型在入口匝道和可变限速反馈控制下的镇定问题中, 证明了反馈参数满足某种耗散条件时, 交通流状态以指数速率收敛到稳态. 为了处理由于不确定的交通需求导致进入上游路段的交通流量的振荡, 文献 [9] 考虑了闭环系统的输入-状态稳定性 (ISS). 文献 [10,11] 采用 Backstepping 方法设计完全状态反馈以抑制交通状况中的走走停停现象. ...

A non-equilibrium traffic model devoid of gas-like behavior

2002

$n\times n$

Prediction of traffic convective instability with spectral analysis of the Aw-Rascle-Zhang model

2015

$n\times n$

Comparing the effects of ramp metering and variable speed limit on reducing travel time and crash risk at bottlenecks

2018

$n\times n$

Necessary and sufficient conditions on the exponential stability of positive hyperbolic systems

2017

$n\times n$

2022

$n\times n$

2016

$n\times n$

PI boundary control of linear hyperbolic balance laws with stabilization of ARZ traffic flow models

2019

$n\times n$

... 其中,

$v_f$

为自由流速度,

$\rho_m$

为交通流的最大密度, 两者均为交通基础设施的固有属性,

$\gamma>0$

一般为

$1$

左右的常数. 特别指出, 2.1 和 2.2 节的模型介绍详见参考文献 [8,9] 及其相关文献. 为保证论文内容的连贯性和完整性, 此处作简要叙述. ...

Boundary feedback stabilization of freeway traffic networks: ISS control and experiments

2022

$n\times n$

... 其中,

$v_f$

为自由流速度,

$\rho_m$

为交通流的最大密度, 两者均为交通基础设施的固有属性,

$\gamma>0$

一般为

$1$

左右的常数. 特别指出, 2.1 和 2.2 节的模型介绍详见参考文献 [8,9] 及其相关文献. 为保证论文内容的连贯性和完整性, 此处作简要叙述. ...

Traffic congestion control for Aw-Rascle-Zhang Model

2019

$n\times n$

Stop-and-go suppression in two-class congested traffic

2021

$n\times n$

Time-Delayed feedback control of a hydraulic model governed by a diffusive wave system

2020

... 在自动控制中, 时滞的出现可能由控制器造成, 也可能是人为因素, 时滞现象可能使得系统的状态变得不稳定, 但合适的时滞取值亦有可能改善系统的性能. 于是, 时滞控制策略吸引了广大学者的关注. 文献 [12] 研究了一类扩散波方程的输入控制器具有时滞的情形, 结果表明无论时滞取值多少, 只要控制参数满足某个约束条件, 即可得到闭环系统的指数稳定性. 在此基础上, 文献 [13] 建立了扩散波方程在时滞控制器下的与时滞相关及与时滞无关的指数稳定性. 针对一阶线性双曲守恒律系统, 文献 [14] 采用特征根分析方法讨论了系统的与时滞无关的稳定性和不稳定性. 此外, 当波的传播时间与控制器的反馈时滞恰好是整数倍时, 采用 Schur-Cohn 准则建立了闭环系统稳定时参数所满足的充要条件. ...

一类扩散波方程的PDP反馈控制和稳定性分析

2021

一类扩散波方程的PDP反馈控制和稳定性分析

2021

The stability analysis for a 2 × 2 conservation law with PI controller and PDP Controller

2023

2020

... 且

$\lambda_2$

的正负分别代表交通流处于自由模态和拥堵模态^[15]. ...

2020

... 且