具有局部阻尼的二维 Mindlin-Timoshenko 板系统的镇定

具有局部阻尼的二维 Mindlin-Timoshenko 板系统的镇定

章春国^,¹^,^*, 孙宝楠¹, 付煜之¹, 于欣²

¹杭州电子科技大学数学系杭州 310018

²浙大宁波理工学院计算机与数据工程学院浙江宁波 315100

Stabilization of 2-D Mindlin Timoshenko Plate Systems with Local Damping

Zhang Chunguo^,¹^,^*, Sun Baonan¹, Fu Yuzhi¹, Yu Xin²

¹Department of Mathematics, Hangzhou Dianzi University, Hangzhou 310018

²School of Computer and Data Engineering, Ningbo Tech University, Zhejiang Ningbo 315100

通讯作者: *章春国, E-mail: cgzhang@hdu.edu.cn

收稿日期: 2023-04-29 修回日期: 2023-10-7

基金资助:

国家自然科学基金(61503103)
浙江省自然科学基金重点项目(LZ21A010001)

Received: 2023-04-29 Revised: 2023-10-7

Fund supported:

NSFC(61503103)
key project of Zhejiang Provencial Natural Science Foundation(LZ21A010001)

摘要

该文研究了具有局部阻尼的二维 Mindlin-Timoshenko 板系统, 首先将原系统转化成抽象柯西问题, 运用算子半群理论得到了系统的适定性. 借助系统频域稳定性结果, 通过引入几何光学条件结合乘子技巧得到了系统的一致指数稳定性.

关键词： Mindlin-Timoshenko 板系统; 局部阻尼; 分片乘子法; 一致指数稳定性

Abstract

In this paper, the two-dimensional Mindlin-Timoshenko plate system with local damping is studied. First, the original system is transformed into an abstract Cauchy problem, and the well posedness of the system is obtained by using operator semigroup theory. With the help of the frequency domain stability results of the linear system, the uniform exponential stability of the system is obtained by introducing geometric optical conditions and multiplier techniques.

Keywords： Mindlin-Timoshenko plate system; Local damping; Piecewise multiplier method; Uniform exponential stability.

PDF (610KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

章春国, 孙宝楠, 付煜之, 于欣. 具有局部阻尼的二维 Mindlin-Timoshenko 板系统的镇定[J]. 数学物理学报, 2024, 44(4): 946-959

Zhang Chunguo, Sun Baonan, Fu Yuzhi, Yu Xin. Stabilization of 2-D Mindlin Timoshenko Plate Systems with Local Damping[J]. Acta Mathematica Scientia, 2024, 44(4): 946-959

1 引言

众所周知, 弹性薄板具有广泛的工程应用背景, 如航天器、太阳帆板、旋转机翼以及螺旋桨桨叶等. 以弹性薄板为构件的柔性体, 用刚体动力学的理论和方法来研究弹性板的变形与振动. 在经典弹性板振动理论中, Kirchhoff 板模型是最为重要的经典薄板振动模型之一. 如果当弹性板具有一定的厚度且在板振动过程中考虑横向剪切效应时, 得到相应的板振动模型即为 Mindlin-Timoshenko 板模型 (系统), 因此 Mindlin-Timoshenko 板模型 (系统) 能更准确地描述具有一定厚度弹性板的振动.

近几年来, Mindlin-Timoshenko 系统的研究取得了许多成果. 文献 [1] 研究了具有边界阻尼的二维 Mindlin-Timoshenko 板系统的指数稳定性, Nicaise^[2] 研究了具有全局阻尼的 Mindlin-Timoshenko 系统的指数衰减性, 进一步, 当只有阻尼作用时, 该系统是多项式衰减的. 文献 [3 ⇓⇓⇓⇓-8] 研究了具有各种阻尼的 Mindlin-Timoshenko 系统或 Mindlin-Timoshenko 热弹性板系统的稳定性问题.

在工程技术应用中, 利用局部分布阻尼器对弹性振动系统进行抑振更为普遍. 因此, 分片乘子法作为有效的手段来解决问题. 文献 [9 ⇓⇓⇓-13] 的作者应用分片乘子法和应用 Liyapunov 函数法研究了弹性系统和粘弹性系统的稳定性.

本文将文献 [2] 推广到更一般情形, 更精确地说, 考虑如下的具有局部内部阻尼的二维 Mindlin-Timoshenko 板方程的初边值问题

(1.1)$\begin{equation} \left\{\begin{array}{lll} \rho_{1}\psi_{tt}-D(\psi_{xx}+\frac{1-\mu}{2}\psi_{yy} +\frac{1+\mu}{2}\varphi_{xy}) +K(\psi+\omega_{x})+\chi_{\Omega_{0}}\psi_{t}=0, & \Omega\times\left (0, + \infty \right), \\[2mm] \rho_{1}\varphi_{tt}-D(\varphi_{yy}+\frac{1-\mu}{2}\varphi_{xx} +\frac{1+\mu}{2}\psi_{xy}) +K(\varphi+\omega_{y})+\chi_{\Omega_{0}}\varphi_{t}=0,& \Omega\times\left ( 0, + \infty \right ), \\[1mm] \rho_{2}\omega_{tt}-K(\psi_{x}+\omega_{xx}+\varphi_{y}+\omega_{yy})+\chi_{\Omega_{0}}\omega_{t} =0, \quad \quad\quad\quad\quad\quad\quad\quad & \Omega\times\left ( 0, + \infty \right ), \\ \psi=\varphi=\omega=0, & \Gamma\times(0, +\infty), \\[1mm] D(\psi_{x}+\mu\varphi_{y}, \frac{1-\mu}{2}(\psi_{y}+\varphi_{x}))\cdot{\nu} =0, & \Gamma\times(0, +\infty), \\[2mm] D(\frac{1-\mu}{2}(\psi_{y}+\varphi_{x}), \varphi_{y}+\mu\psi_{x})\cdot{\nu}=0,& \Gamma\times(0, +\infty), \\[2mm] K[\frac{\partial\omega}{\partial\mathbf{{\nu}}}+(\psi, \varphi)\cdot{\nu}] =0, & \Gamma\times(0, +\infty), \\[2mm] (\psi(x, y, 0), \varphi(x, y, 0), \omega(x, y, 0))^T=(\psi_{01}, \varphi_{01}, \omega_{01})^T, & (x, y)\in\Omega, \\ (\psi_{t}(x, y, 0), \varphi_{t}(x, y, 0), \omega_{t}(x, y, 0))^T=(\psi_{02}, \varphi_{02}, \omega_{02})^T, & (x, y)\in\Omega, \end{array}\right. \end{equation}$

其中 $ \Omega $ 是 $ \mathbb{R}^2 $ ( ($x$, $y$) 平面) 中的有界区域, $ \Omega_0(\subset\Omega) $ 是 $ \Omega $ 中一个凸的子区域, 且 $ \Omega $ 具有光滑的边界 $ \Gamma=\partial \Omega $, $ \Omega_{0} $ 具有边界 $ \Gamma_0 $, 正常数 $ \rho_{1} $, $ \rho_{2} $ 分别表示单位质量, $ \mu(0<\mu<\frac{1}{2}) $ 是 Poisson's 比, $ D $, $ K $ 分别为柔性弹性模量与剪切模量. $ \psi $, $ \varphi $ 分别表示 $ xz $ 平面与 $ yz $ 平面的全转角, $ \omega $ 表示横向位移, $ \chi_{\Omega_{0}} $ 表示 $ \Omega_0 $ 上的特征函数, $ {\nu}=(\nu_{1}, \nu_{2}) $ 表示 $ \Gamma $ 的单位外法向量.

本文应用线性算子半群理论、分片乘子法以及 Hilbert 空间中线性系统指数稳定的频域结果, 得到了系统的适定性以及指数稳定性. 本文的安排如下: 在第 2 节中, 通过适当的假设将系统转换为抽象 Cauchy 问题. 在第 3 节中, 应用 Pazy^[14] 的 Lumer-Phillips 定理证明了系统的适定性. 在第 4 节中, 运用分片乘子法以及系统稳定性的频域结果结合矛盾讨论, 证明了系统是指数稳定的.

2 预备知识

定义系统 (1.1) 在 $ t $ 时刻的能量为

$\begin{align*} E(t)={}&\frac{1}{2}\int_{\Omega}^{}[D(|\psi_{x}|^{2}+|\varphi_{y}|^{2}+2\mu\psi_{x}\varphi_{y}+\frac{1-\mu}{2}|\psi_{y}+\varphi_{x}|^{2})\nonumber\\ &+K(|\psi+\omega_{x}|^{2}+|\varphi+\omega_{y}|^{2})]{\rm d}x{\rm d}y+\int_{\Omega}^{}[\rho_{1}(|\psi_{t}|^{2}+|\varphi_{t}|^{2})+\rho_{2}|\omega_{t}|^{2}]{\rm d}x{\rm d}y. \end{align*}$

对于充分光滑的 $ (\psi, \varphi, \omega) $ 和 $ (\widehat{\psi}, \widehat{\varphi}, \widehat{\omega}) $, 定义如下线性泛函

(2.1)$\begin{equation} \left\{\begin{array}{lll} L_{1}=L_{1}\{\psi, \varphi, \omega\}=D(\psi_{xx}+\frac{1-\mu}{2}\psi_{yy} +\frac{1+\mu}{2}\varphi_{xy})-K(\psi+\omega_{x}), \\[3mm] L_{2}=L_{2}\{\psi, \varphi, \omega\}=D(\varphi_{yy}+\frac{1-\mu}{2}\varphi_{xx} +\frac{1+\mu}{2}\psi_{xy})-K(\varphi+\omega_{y}), \\[1mm] L_{3}=L_{3}\{\psi, \varphi, \omega\}=K(\psi_{x}+\omega_{xx}+\varphi_{y}+\omega_{yy}), \\[1mm] B_{1}=B_{1}\{\psi, \varphi, \omega\}=D(\psi_{x}+\mu\varphi_{y}, \frac{1-\mu}{2}(\psi_{y}+\varphi_{x}))\cdot{\nu}, \\[3mm] B_{2}=B_{2}\{\psi, \varphi, \omega\}=D(\frac{1-\mu}{2}(\psi_{y}+\varphi_{x}), \varphi_{y}+\mu\psi_{x})\cdot{\nu}, \\[3mm] B_{3}=B_{3}\{\psi, \varphi, \omega\}=K[\frac{\partial \omega }{\partial {\nu}} +(\psi, \varphi)\cdot{\nu}] \end{array}\right. \end{equation}$

和双线性泛函

(2.2)$\begin{align*} a({\psi, \varphi, \omega};{\widehat{\psi}, \widehat{\varphi}, \widehat{\omega}})= {}&D\int_{\Omega}[\psi_{x}\overline{\widehat{\psi}}_{x}+\varphi_{y}\overline{\widehat{\varphi}}_{y} +\mu\psi_{x}\overline{\widehat{\varphi}}_{y}+\mu\overline{\widehat{\psi}}_{x}\varphi_{y} \\ & +\frac{1-\mu}{2}(\psi_{y}+\varphi_{x})(\overline{\widehat{\psi}}_{y}+\overline{\widehat{\varphi}}_{x})]{\rm d}x{\rm d}y\\&+K\int_{\Omega}^{}[(\psi+\omega_{x})(\overline{\widehat{\psi}}+\overline{\widehat{\omega}}_{x})+(\varphi+\omega_{y})(\overline{\widehat{\varphi}}+\overline{\widehat{\omega}}_{y})]{\rm d}x{\rm d}y, \end{align*}$

经过简单计算, 我们得到

(2.3)$\begin{equation} a({\psi, \varphi, \omega};{\widehat{\psi}, \widehat{\varphi}, \widehat{\omega}})=\overline{a(\widehat{\psi}, \widehat{\varphi}, \widehat{\omega};{\psi, \varphi, \omega})}. \end{equation}$

进一步, 对所有充分光滑的 $ (\psi, \varphi, \omega) $ 和 $ (\widehat{\psi}, \widehat{\varphi}, \widehat{\omega}) $, 应用格林公式, 我们得到如下恒等式

$\begin{align*}&\ \int_{\Omega}(\overline{\widehat{\psi}}L_1+\overline{\widehat{\varphi}}L_2+\overline{\widehat{\omega}}L_3){\rm d}x{\rm d}y\nonumber\\ &=\int_{\Omega}[D\overline{\widehat{\psi}}\mathrm{div}(\psi_{x}+\mu\varphi_{y}, \frac{1-\mu}{2}(\psi_{y}+\varphi_{x}))+D\overline{\widehat{\varphi}}\mathrm{div}(\frac{1-\mu}{2}(\psi_{y}+\varphi_{x}), \mu\psi_{x}+\varphi_{y})\\ &\quad\ +K\overline{\widehat{\omega}}\mathrm{div}(\psi+\omega_{x}, \varphi+\omega_{y})]{\rm d}x{\rm d}y-K\int_{\Omega}\overline{\widehat{\psi}}(\psi+\omega_{x})+\overline{\widehat{\varphi}}(\varphi+\omega_{y}){\rm d}x{\rm d}y\\ &=-\int_{\Omega}[D(\overline{\widehat{\psi}}_{x}, \overline{\widehat{\psi}}_{y})\cdot(\psi_{x}+\mu\varphi_{y}, \frac{1-\mu}{2}(\psi_{y}+\varphi_{x}))+D(\overline{\widehat{\varphi}}_{x}, \overline{\widehat{\varphi}}_{y})\cdot(\frac{1-\mu}{2}(\psi_{y}+\varphi_{x}), \mu\psi_{x}+\varphi_{y})\\ &\quad\ +K(\overline{\widehat{\omega}}_{x}, \overline{\widehat{\omega}}_{y})\cdot(\psi+\omega _{x}, \varphi+\omega_{y})]{\rm d}x{\rm d}y-K\int_{\Omega}[\overline{\widehat{\psi}}(\psi+\omega_{x})+\overline{\widehat{\varphi}}(\varphi+\omega_{y})]{\rm d}x{\rm d}y\\ &\quad\ +\int_{\Gamma}[D\overline{\widehat{\psi}}(\psi_{x}+\mu\varphi_{y}, \frac{1-\mu}{2}(\psi_{y}+\varphi_{x}))\cdot{\nu}]{\rm d}S+\int_{\Gamma}[D\overline{\widehat{\varphi}}(\frac{1-\mu}{2}(\psi_{y}+\varphi_{x}), \mu\psi_{x}+\varphi_{y})\cdot{\nu}]{\rm d}S\\ &\quad\ +\int_{\Gamma}[k\overline{\widehat{\omega}}(\psi+\omega_{x}, \varphi+\omega_{y})\cdot{\nu}]{\rm d}S\\ &=-a(\psi, \varphi, \omega;\widehat{\psi}, \widehat{\varphi}, \widehat{\omega}), \end{align*}$

即有以下等式成立

(2.4)$\begin{equation} a(\psi, \varphi, \omega;\widehat{\psi}, \widehat{\varphi}, \widehat{\omega})+\int_{\Omega}(\widehat{\psi}L_1+\widehat{\varphi}L_2+\widehat{\omega}L_3){\rm d}x{\rm d}y=0. \end{equation}$

由 (2.1)式, 我们将系统 (1.1) 改写为

(2.5)$\begin{equation} \left\{\begin{array}{lll} \rho_{1}\psi_{tt}-L_1=-\chi_{\Omega_{0}}\psi_{t},& \Omega\times\left ( 0, + \infty \right ), \\ \rho_{1}\varphi_{tt}-L_2=-\chi_{\Omega_{0}}\varphi_{t}, & \Omega\times\left ( 0, + \infty \right ), \\ \rho_{2}\omega_{tt}-L_3=-\chi_{\Omega_{0}}\omega_{t}, & \Omega\times\left ( 0, + \infty \right ), \\ \psi=\varphi=\omega=0,& \Gamma\times\left ( 0, + \infty \right ), \\ B_1=B_2=B_3=0, & \Gamma\times\left ( 0, + \infty \right ), \\ (\psi(x, y, 0), \varphi(x, y, 0), \omega(x, y, 0))^T=(\psi_{01}, \varphi_{01}, \omega_{01})^T, & (x, y)\in\Omega, \\ (\psi_{t}(x, y, 0), \varphi_{t}(x, y, 0), \omega_{t}(x, y, 0))^T=(\psi_{02}, \varphi_{02}, \omega_{02})^T, & (x, y)\in\Omega. \end{array}\right. \end{equation}$

引入函数空间

$ W=\left \{ (\psi, \varphi, \omega)\in[H^1(\Omega)]^3\vert \psi=\varphi=\omega =0, B_j\left \{ \psi, \varphi, \omega\right \} =0(j=1, 2, 3), \text{在}\ \Gamma\ \text{上} \right \}, $

其中 $ H^1(\Omega) $ 是一阶 Sobolev 空间^[15], 赋予范数

$\begin{align*} \left \| (\psi, \varphi, \omega)^T\right \| _{W}^{2} ={}&\int_{\Omega}[D(|\psi_{x}|^2+|\varphi_{y}|^2+\mu\psi_{x}\overline{\varphi}_{y}+\mu\overline{\psi}_{x}\varphi_{y}+\frac{1-\mu}{2}|\psi_{y}+\varphi_{x}|^2)]{\rm d}x{\rm d}y\nonumber\\ &+K\int_{\Omega}(|\psi+\omega_{x}|^2+|\varphi+\omega_{y}|^2){\rm d}x{\rm d}y, \nonumber\end{align*}$

具有内积 $ (\cdot, \cdot)_{W} $.

设空间 $ H=L^2_{\rho_{1}}(\Omega)\times{L^2_{\rho_{1}}(\Omega)}\times{L^2_{\rho_{2}}(\Omega)} $, $ \psi_{t}=p, \varphi_t=q, \omega_t=r $, 并赋予范数

$\left \| (p, q, r)^T \right \| ^{2}_{H}=\int _{\Omega}[\rho_1(|p|^2+|q|^2)+\rho_2|r|^2]{\rm d}x{\rm d}y, $

具有内积 $ (\cdot, \cdot)_{H} $, 则 $ W $ 和 $ H $ 都是 (复) Hilbert 空间.

记 $ \mathcal{H}=W\times{H} $, 其范数为

$\left \| (\psi, \varphi, \omega, p, q, r)^T \right \|^{2}_{\mathcal{H}}=\left \| (\psi, \varphi, \omega ) ^T\right \|^{2}_{W}+\left \| (p, q, r)^T \right \|^{2}_{H}, $

具有内积 $ (\cdot, \cdot)_{\mathcal{H}} $, 因此 $ \mathcal{H} $ 也是一个 (复) Hilbert 空间.

定义 $ \mathcal{H} $ 上的线性算子 $ \mathcal{A} $

$D(\mathcal{A})=\left\{\begin{array}{lll}(\psi, \varphi, \omega, p, q, r)\in{\mathcal{H}}\vert(p, q, r)\in W, \\ (\rho_{1}^{-1}(L_{1}-\chi_{\Omega_{0}}p), \rho_{1}^{-1}(L_2-\chi_{\Omega_{0}}q), \rho_{2}^{-1}(L_3-\chi_{\Omega_{0}}r))\in{H}\end{array}\right\}, $

(2.6)$\begin{equation} \mathcal{A}(\psi, \varphi, \omega, p, q, r)=(p, q, r, \rho_{1}^{-1}(L_{1}-\chi_{\Omega_{0}}p), \rho_{1}^{-1}(L_2-\chi_{\Omega_{0}}q), \rho_{2}^{-1}(L_3-\chi_{\Omega_{0}}r)). \end{equation}$

于是系统 (1.1) 改写为 $ \mathcal{H} $ 中的抽象 Cauchy 问题

(2.7)$\begin{equation} \frac{\mathrm{d} U}{\mathrm{d} t} =\mathcal{A}U, U(0)=U_0, \end{equation}$

其中, $ U=(\psi, \varphi, \omega, p, q, r) $, $ U_0=U(0)=(\psi_{01}, \varphi_{01}, \omega_{01}, \psi_{02}, \varphi_{02}, \omega_{02}). $

3 适定性

定理 3.1 线性算子 $ \mathcal{A} $ 生成 $ \mathcal{H} $ 上一个压缩 $ C_0$-半群 $ {\rm e}^{t\mathcal{A}}. $

证首先, 由算子 $ \mathcal{A} $ 和空间 $ \mathcal{H} $ 的定义, 对任意的 $ U=(\psi, \varphi, \omega, p, q, r) $ 有

$\begin{align*}&\ \mathrm{Re}(\mathcal{A}U, U)_{\mathcal{H}}\\ &= \mathrm{Re}\Big[\int_{\Omega_{0}}(\overline{p}(L_{1}-p)+\overline{q}(L_{2}-q)+\overline{r}(L_{3}-r)){\rm d}x{\rm d}y\Big] +\mathrm{Re}\Big[\int_{\Omega\setminus\Omega_{0}}(\overline{p}L_{1}+\overline{q}L_{2}+\overline{r}L_{3}){\rm d}x{\rm d}y\Big] \nonumber\\ &\quad \ +\mathrm{Re}\Big[D\int_{\Omega_{0}}(p_{x}\overline{\psi}_{x}+q_{y}\overline{\varphi}_{y}+\mu{p_{x}}\overline{\varphi}_{y}+\mu{q_y\overline{\psi}_x}+\frac{1-\mu}{2}(p_y+q_x)(\overline{\psi}_y+\overline{\varphi}_x)){\rm d}x{\rm d}y\Big] \nonumber\\ &\quad\ +\mathrm{Re}\left \{ K\int_{\Omega_{0}}\Big[(p+r_x)(\overline{\psi}+\overline{\omega}_{x})+(q+r_y)(\overline{\varphi}+\overline{\omega}_{y})\Big]{\rm d}x{\rm d}y \right \} \nonumber\\ &\quad\ +\mathrm{Re}\Big[D\int_{\Omega\setminus\Omega_{0}}(p_x\overline{\psi}_{x}+q_y\overline{\varphi}_{y}+\mu{p_x\overline{\varphi}_y}+\mu{q_y\overline{\psi}_x}+\frac{1-\mu}{2}(p_y+q_x)(\overline{\psi}_{y}+\overline{\varphi}_{x})){\rm d}x{\rm d}y\Big]\nonumber\\ &\quad\ +\mathrm{Re}\left \{ K\int_{\Omega\setminus\Omega_{0}}[(p+r_x)(\overline{\psi}+\overline{\omega}_{x})+(q+r_y)(\overline{\varphi}+\overline{\omega}_{y})]{\rm d}x{\rm d}y \right \} \nonumber\\ &=\mathrm{Re}[-a(\psi, \varphi, \omega;p, q, r)+a(p, q, r;\psi, \varphi, \omega)]-\mathrm{Re}\int_{\Omega_{0}}(\overline{p}p+\overline{q}q+\overline{r}r){\rm d}x{\rm d}y\nonumber\\ &=-\int_{\Omega_{0}}(|p|^2+|q|^2+|r|^2){\rm d}x{\rm d}y\le0. \nonumber \end{align*}$

因此, 我们有

(3.1)$\begin{equation} \mathrm{Re}(\mathcal{A}U, {U})_{\mathcal{H}}=-\int_{\Omega_{0}}(|p|^2+|q|^2+|r|^2){\rm d}x{\rm d}y\le0. \end{equation}$

这就说明了线性算子 $ \mathcal{A} $ 是耗散的.

接着, 我们将证明: 存在充分小的 $ \lambda >0 $, 使得 $ \lambda{I-\mathcal{A}} $ 是满射.

即对给定的 $ \lambda>0 $ 以及任意的 $ G=({g}_{1}, {g}_2, {g}_3, g_4, {g}_5, {g}_{6})\in\mathcal{A} $, 存在 $ (\psi, \varphi, \omega, p, q, r)\in{D(\mathcal{A})} $ 使得

$(\lambda{I}-\mathcal{A})(\psi, \varphi, \omega, p, q, r)=({g}_{1}, {g}_2, {g}_3, g_4, {g}_5, {g}_{6}), $

即

(3.2)$\begin{equation} \left\{\begin{array}{lll} \lambda(\psi, \varphi, \omega)-(p, q, r)=({g}_{1}, {g}_2, {g}_3), \\ \lambda(p, q, r)-[\rho_{1}^{-1}(L_1-\chi_{\Omega_{0}}p), \rho_{1}^{-1}(L_2-\chi_{\Omega_{0}}q), \rho_{2}^{-1}(L_3-\chi_{\Omega_{0}}r)]=(g_4, {g}_5, {g}_{6}). \end{array}\right. \end{equation}$

因此, $ (\psi, \varphi, \omega)\in{W} $ 满足

(3.3)$\begin{align*}&(\lambda^{2}+\lambda{\rho_{1}^{-1}\chi_{\Omega_{0}}}, \lambda^{2}+\lambda{\rho_{1}^{-1}\chi_{\Omega_{0}}}, \lambda^{2}+\lambda{\rho_{2}^{-1}\chi_{\Omega_{0}}})(\psi, \varphi, \omega)^T-(\rho_{1}^{-1}L_1, \rho_{1}^{-1}L_2, \rho_{2}^{-1}L_3)^T\\ =\ &(\lambda+\rho_{1}^{-1}\chi_{\Omega_{0}}, \lambda+\rho_{1}^{-1}\chi_{\Omega_{0}}, \lambda+\rho_{2}^{-1}\chi_{\Omega_{0}})(g_1, g_2, g_3)^T+(g_4, g_5, g_6)^T. \end{align*}$

为得到结果, 我们将运用 Lax-Milgram 定理证明 (3.2) 式存在唯一弱解.

对于任意 $ (\psi_1, \varphi_1, \omega_1)\in{W} $ 与 (3.2)式在 $ \mathcal{H} $ 中作内积, 有

(3.4)$\begin{equation} a_{\lambda}(\psi, \varphi, \omega;\psi_1, \varphi_1, \omega_1)=L_{G}(\psi_1, \varphi_1, \omega_1), \end{equation}$

其中

$\begin{align*} &\ a_{\lambda}(\psi, \varphi, \omega;\psi_1, \varphi_1, \omega_1)\\&=\int_{\Omega}[(\lambda^2\rho_{1}+\lambda\chi_{\Omega_{0}})(\psi\overline{\psi}_1+\varphi\overline{\varphi}_1)+(\lambda^2\rho_{2}+\lambda\chi_{\Omega_{0}})\omega\overline{\omega}_1]{\rm d}x{\rm d}y+a(\psi, \varphi, \omega;\psi_1, \varphi_1, \omega_1), \nonumber \end{align*}$

以及

$\begin{align*} L_{G}(\psi_1, \varphi_1, \omega)=&\int_{\Omega} \left \{ \rho_{1}[(\lambda +\rho_{1}^{-1}\chi_{\Omega _{0}})g_1+{g_4}]\overline{\psi}_{1}+ \rho_{1}[(\lambda +\rho_{1}^{-1}\chi_{\Omega _{0}})g_2+{g_5}]\overline{\varphi}_{1}\right. \nonumber \\ &\left. + \rho_{2}[(\lambda +\rho_{2}^{-1}\chi_{\Omega _{0}})g_3+{g_6}]\overline{\omega}_{1} \right \}{\rm d}x{\rm d}y. \nonumber \end{align*}$

显然, $ L_{G}(\psi_1, \varphi_1, \omega_1) $ 是空间 $ W $ 上的连续线性泛函, 且 $ a_{\lambda}(\psi, \varphi, \omega;\psi_1, \varphi_1, \omega_1) $ 是空间 $ W $ 上的共轭双线性连续泛函. 接下来验证 $ a_{\lambda}(\psi, \varphi, \omega;\psi_1, \varphi_1, \omega_1) $ 在 $ W $ 上满足强制性. 事实上, 对任意的 $ (\psi, \varphi, \omega)\in{W} $, 有

(3.5)$\begin{align*} &a_{\lambda}(\psi, \varphi, \omega;\psi_1, \varphi_1, \omega_1)\nonumber\\ =&\int_{\Omega_{0}}[(\lambda^2\rho_1+\lambda\chi_{\Omega _{0}})(\psi\overline{\psi}_{1}+\varphi\overline{\varphi}_{1})+(\lambda^2\rho_{2}+\lambda\chi_{\Omega _{0}})\omega\overline{\omega}_{1}]{\rm d}x{\rm d}y+a(\psi, \varphi, \omega;\psi_1, \varphi_1, \omega_{1}), \end{align*}$

因此, 由式 (3.5) 得

(3.6)$\begin{equation} \mathrm{Re}a_{\lambda}(\psi, \varphi, \omega;\psi, \varphi, \omega)\ge{a(\psi, \varphi, \omega;\psi, \varphi, \omega)}=\left \| (\psi, \varphi, \omega ) \right \|^{2}_{W}, \end{equation}$

故 $ a_{\lambda}(\psi, \varphi, \omega;\psi, \varphi, \omega) $ 是强制的, 由 Lax-Milgram 定理知系统(3.2) 存在唯一解.

特别地, 我们取 $ (\psi_1, \varphi_1, \omega_{1})\in(D(\Omega_{0}))^3 $, 则由(3.4) 式, 在 $ (D^{'}(\Omega_{0}))^3 $ 中分部积分得

(3.7)$\begin{align*}&(\lambda^2+\lambda{\rho_{1}^{-1}\chi_{\Omega_{0}}}, \lambda^2+\lambda{\rho_{1}^{-1}\chi_{\Omega _{0}}}, \lambda^2+\lambda{\rho_{2}^{-1}\chi_{\Omega _{0}}})(\psi, \varphi, \omega)^T-(\rho_{1}^{-1}L_1, \rho_{1}^{-1}L_2, \rho_{2}^{-1}L_3)^T\\=\ &(\lambda+\rho_{1}^{-1}\chi_{\Omega_{0}}, \lambda+\rho_{1}^{-1}\chi_{\Omega_{0}}, \lambda+\rho_{2}^{-1}\chi_{\Omega_{0}})(g_1, {g_2}, g_3)^T+(g_4, {g_5}, g_6)^T, \end{align*}$

从而

$(\rho_{1}^{-1}(L_1-\chi_{\Omega _{0}}p), (\rho_{1}^{-1}(L_2-\chi_{\Omega _{0}}q), (\rho_{2}^{-1}(L_3-\chi_{\Omega _{0}}r))\in{H}, $

取 $ (p, q, r)=\lambda(\psi, \varphi, \omega)-(g_1, g_2, g_3) $, 即得 $ \lambda{I}-\mathcal{A} $ 是满射.

因此, 对于任意的 $ (x, y)\in{\Omega_{0}} $, $ \mathcal{A} $ 是双射且 $ \mathcal{A}^{-1}\in{\mathcal{L}(\mathcal{H})} $, 则由 Lumer-Phillips 定理可得 $ \mathcal{A} $ 是 $ \mathcal{H} $ 上 $ C_0$-压缩半群 $ {\rm e}^{t\mathcal{A}} $ 的无穷小生成元. 证毕.

定理 3.2 对于任意的 $ (\psi_{01}, \varphi_{01}, \omega_{01}, \psi_{02}, \varphi_{02}, \omega_{02})\in{\mathcal{H}} $, 则控制系统 (1.1) 存在唯一的弱解

$(\psi, \varphi, \omega, p, q, r)={\rm e}^{t\mathcal{A}}(\psi_{01}, \varphi_{01}, \omega_{01}, \psi_{02}, \varphi_{02}, \omega_{02}), $

且 $ (\psi, \varphi, \omega)\in{C([0, +\infty);W)\cap{C^1([0, +\infty);H)}} $;

若 $ (\psi_{01}, \varphi_{01}, \omega_{01}, \psi_{02}, \varphi_{02}, \omega_{02})\in{D(\mathcal{A})} $, 则控制系统 (1.1) 存在唯一的强解

$(\psi, \varphi, \omega)\in{C^1([0, +\infty);W)\cap{C^2([0, +\infty);H)}}. $

4 指数稳定

注意到边界 $ \partial (\Omega\setminus \Omega_{0})=\Gamma_{0}\cup\Gamma $, 为了得到系统的指数稳定性, 我们需要引入如下几何光学条件.

假设 1 (几何光学条件) 设 $ {\nu_{0}} $ 是 $ \Gamma_{0} $ ($ \Omega\setminus\Omega_0 $ 的部分边界) 的单位外法向量, 在 $ \mathbb{R}^{2} $ 中, 设点 $ (x_0, y_0) $ 是 $ {\Omega_{0}} $ 内任一固定点, 对于任意的 $ (x, y)\in\Gamma_{0} $, 及向量

${m}{(x, y)=(x, y)-(x_0, y_0)}, $

都有

${m}\cdot{{\nu}}_{0}\le{0}. $

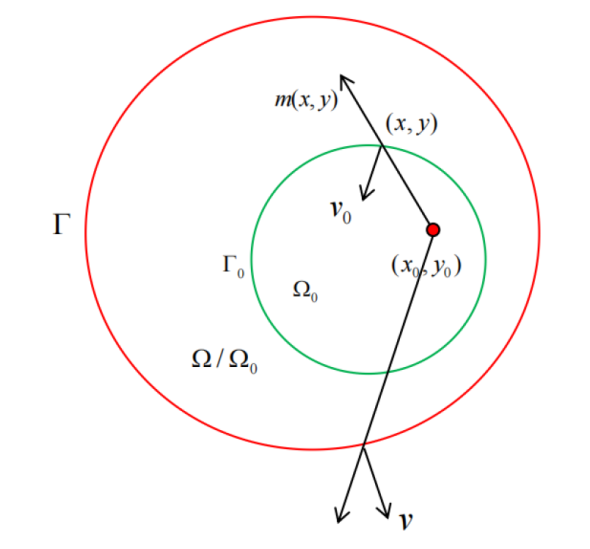
“几何光学条件”指的是区域 (其强调的是区域的边界). 例子示意如图1所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 示意图

引理 4.1 线性算子 $ \mathcal{A} $ 具有紧的预解式.

证定义算子 $ \mathcal{A}_{1}, \mathcal{A}_{2}, A $ 如下

$\begin{array}{c} D\left(\mathcal{A}_{1}\right)=\left\{\begin{array}{l} (\psi, \varphi, \omega, p, q, r) \in \mathcal{H} \mid(p, q, r) \in W,\left(\rho_{1}^{-1} L_{1}, \rho_{1}^{-1} L_{2}, \rho_{2}^{-1} L_{3}\right) \in H, \\ \psi=\varphi=\omega=0, \text { 在 } \Gamma \text { 上, }\left(B_{1}, B_{2}, B_{3}\right)=(0,0,0), \text { 在 } \Gamma \text { 上. } \end{array}\right\}, \\ \mathcal{A}_{1}(\psi, \varphi, \omega, p, q, r)=\left(p, q, r, \rho_{1}^{-1} L_{1}, \rho_{1}^{-1} L_{2}, \rho_{2}^{-1} L_{3}\right), \end{array}$

和

$\begin{array}{c} D\left(\mathcal{A}_{2}\right)=\left\{\begin{array}{l} (\psi, \varphi, \omega, p, q, r) \in \mathcal{H} \mid(p, q, r) \in W,\left(-\rho_{1}^{-1} \chi_{\Omega_{0}} p,-\rho_{1}^{-1} \chi_{\Omega_{0}} q,-\rho_{2}^{-1} \chi_{\Omega_{0}} r\right) \in H \\ \psi=\varphi=\omega=0 \text { 在 } \Gamma \text { 上. } \end{array}\right\}, \\ \mathcal{A}_{2}(0,0,0, p, q, r)=\left(0,0,0, \rho_{1}^{-1} \chi_{\Omega_{0}} p, \rho_{1}^{-1} \chi_{\Omega_{0}} q, \rho_{2}^{-1} \chi_{\Omega_{0}} r\right), \end{array}$

以及

$D(A)=\left \{ (\psi, \varphi, \omega)\in(H^2(\Omega))^3\vert(\rho_{1}^{-1}L_1, \rho_{1}^{-1}L_2, \rho_{2}^{-1}L_3)\in{H}, \psi=\varphi=\omega=0,\, \ \text{在}\ \Gamma\ \text{上}.\right \}, $

$A(\psi, \varphi, \omega)=-(\rho_{1}^{-1}L_1, \rho_{1}^{-1}L_2, \rho_{2}^{-1}L_3), $

因此

$\mathcal{A}=\mathcal{A}_1+\mathcal{A}_2, \mathcal{A}_1=\begin{pmatrix} 0& I\\ -A &0 \end{pmatrix}, $

这里 $ I $ 是恒等算子.

类似于文献 [9,引理 3.2] 的证明, 容易验证算子 $ A $ 是正定自伴随算子, 所以算子 $ \mathcal{A}_1 $ 是斜自伴的, 即 $ 1\in{\rho(\mathcal{A}_1)} $, ($ \rho(\mathcal{A}_1) $ 表示算子 $ \mathcal{A}_1 $ 的预解集). 假设 $ \left \{ X_n \right \}\subset \mathcal{H} $ 有界, 则存在正常数 $ M $, 使得 $ \left \| X_n \right \| _\mathcal{H}\le M $, 令$ Y_n=(I-\mathcal{A}_1)X_n $, 则

$\left \| (I-\mathcal{A}_1)Y_n \right \| ^{2}_{\mathcal{H}}\le M, $

即

$\begin{align*} \left \| (I-\mathcal{A}_1)Y_n \right \| ^{2}_{\mathcal{H}}\nonumber &=(Y_n-\mathcal{A}_1Y_n, Y_n-\mathcal{A}_1Y_n)_\mathcal{H}\nonumber\\ &=(Y_n-\mathcal{A}_1Y_n, Y_n)_{\mathcal{H}}-(Y_n-\mathcal{A}_1Y_n, \mathcal{A}_1Y_n)_{\mathcal{H}}\nonumber\\ &=(Y_n, Y_n)_{\mathcal{H}}-(\mathcal{A}_1Y_n, Y_n)_{\mathcal{H}}-(Y_n, \mathcal{A}_1Y_n)_\mathcal{H}+(\mathcal{A}_1Y_n, \mathcal{A}_1Y_n)_\mathcal{H}\nonumber\\ &=(Y_n, Y_n)_{\mathcal{H}}+(\mathcal{A}_1Y_n, \mathcal{A}_1Y_n)_\mathcal{H}\nonumber\\ &\le{M}, \nonumber \end{align*}$

根据 Sobolev 嵌入定理知 $ W $ 紧嵌入 $ \mathcal{H} $, 故 $ \left \{ Y_n\right \} $ 具有收敛子列, 这就证明了$ (I-\mathcal{A}_{1})^{-1} $ 是紧的, 则对于任意的 $ \lambda\in{\rho(\mathcal{A}_1)} $, 当 $ \mathrm{Re}\lambda\ge0 $ 时, 有

$\left \| (\lambda I-\mathcal{A}_1)^{-1} \right \| \le\frac{1}{\mathrm{Re}\lambda }, $

且

$(\lambda I-\mathcal{A}_1)^{-1}=[I-(1-\lambda)(I-\mathcal{A}_1)^{-1}]^{-1}(I-\mathcal{A}_{1})^{-1}, $

$\lambda I-\mathcal{A}=(\lambda {I}-\mathcal{A}_1)[I-(\lambda{I}-\mathcal{A}_1)^{-1}\mathcal{A}_2], $

所以, 当 $ \mathrm{Re}\lambda\ge3\left \| \mathcal{A}_2 \right \| $ 时, $ [I-(\lambda{I}-\mathcal{A}_1)^{-1}\mathcal{A}_2] $ 存在且有界, 这就说明了 $ \mathcal{A} $ 的预解式是紧的.

引理 4.2 $ \rho(\mathcal{A})\supset \left \{ {\rm i}\lambda \vert\lambda\in{\mathbb{R}} \right \}. $

证若结论不成立, 由于 $ 0\in{\rho(\mathcal{A})} $, 则存在 $ \lambda\ne0, \lambda\in{\mathbb{R}} $, 使得 $\rm i\lambda\notin\rho(\mathcal{A}) $, 由引理 4.1 知 $ \mathcal{A} $ 只有点谱. 如果 $ {\rm i}\lambda\in\sigma_p(\mathcal{A}) $ ($ \sigma_p(\mathcal{A}) $ 为 $ \mathcal{A} $ 的点谱), 则存在 $ (\psi, \varphi, \omega, p, q, r)\in{D(\mathcal{A})} $, 且 $ (\psi, \varphi, \omega, p, q, r)\ne0 $, 使得 $ ({\rm i}\lambda-\mathcal{A})(\psi, \varphi, \omega, p, q, r)=0 $, 即

(4.1)$\begin{equation} \left\{\begin{array}{lll} {\rm i}\lambda\psi=p,\ {\rm i}\lambda\varphi=q,\ {\rm i}\lambda\omega=r, \\ {\rm i}\lambda{p}=\rho_{1}^{-1}(L_1-\chi_{\Omega_{0}}p), {\rm i}\lambda{q}=\rho_{1}^{-1}(L_2-\chi_{\Omega_{0}}q), {\rm i}\lambda{r}=\rho_{2}^{-1}(L_3-\chi_{\Omega_{0}}r). \end{array}\right. \end{equation}$

由 (3.1) 式有

$\begin{align} 0&=\mathrm{Re}(({\rm i}\lambda-\mathcal{A})(\psi, \varphi, \omega, p, q, r), (\psi, \varphi, \omega, p, q, r))_{\mathcal{H}}\nonumber\\ &=-\mathrm{Re}(\mathcal{A}(\psi, \varphi, \omega, p, q, r), (\psi, \varphi, \omega, p, q, r))_{\mathcal{H}}\nonumber\\ &=\int_{\Omega}(\chi_{\Omega _{0}}|p|^2+\chi_{\Omega _{0}}|q|^2+\chi_{\Omega _{0}}|r|^2){\rm d}x{\rm d}y\nonumber\\ &=\int_{\Omega_{0}}(|p|^2+|q|^2+|r|^2){\rm d}x{\rm d}y, \nonumber \end{align}$

因而在 $ L^2(\Omega_0) $ 中 $ p=q=r=0 $, 又由 (4.1)式第一式可得, 在 $ L^2(\Omega_0) $ 中 $ \psi=\varphi=\omega=0 $. 根据常微分方程初值问题的唯一性, 可以得到结论: 在 $ L^2(\Omega) $ 中 $ (\psi, \varphi, \omega, p, q, r)=0 $. 故得矛盾, 则引理 4.2 得证.

引理 4.3^[16] Hilbert 空间 $ \mathcal{H} $ 上的压缩 $ C_0$-半群 $ {\rm e}^{t\mathcal{A}} $ 指数稳定的充要条件是

(4.2)$\begin{equation} \rho(\mathcal{A})\supset {\left \{ {\rm i}{\lambda} \vert\lambda \in{\mathbb{R}} \right \}}, \end{equation}$

(4.3)$\begin{equation} \mathrm{sup}\left \{ \left \| (\rm i\lambda -\mathcal{A})^{-1} \right \| \vert\lambda \in{\mathbb{R}} \right \}<+\infty. \end{equation}$

定理 4.4 在假设1下, $ \mathcal{A} $ 生成压缩 $ C_0$-半群 $ {\rm e}^{t\mathcal{A}} $ 指数稳定.

证由引理 4.2, 故只需证明式 (4.3). 下面将采用反证法.

假设式 (4.3) 不成立, 即

$\mathrm{sup}\left \{ \left \| ({\rm i}\lambda -\mathcal{A})^{-1} \right\| \vert\lambda \in{\mathbb{R}} \right \} =+\infty. $

由共鸣性定理和预解式的连续性可知, 存在 $ \lambda_n \in{\mathbb{R}} $ 及

$ (\psi_n, \varphi_{n}, \omega_n, p_n, q_n, r_n)\subset{D(\mathcal{A})} $, 使得当 $ |\lambda _n|\to\infty $ 时, 有

(4.4)$\begin{align*} &\left \| (\psi_n, \varphi_{n}, \omega_n, p_n, q_n, r_n) \right \| _{\mathcal{H}}\\ =\ &a(\psi_n, \varphi_{n}, \omega_n;\psi_{n}, \varphi_{n}, \omega_n)+\int_{\Omega}(\rho_1|p_n|^2+\rho_1|q_n|^2+\rho_2|r_n|^2){\rm d}x{\rm d}y=1, \end{align*}$

在 $ \mathcal{H} $ 中, 有

(4.5)$\begin{equation} ({\rm i}\lambda_n-\mathcal{A})(\psi_n, \varphi_{n}, \omega_n, p_n, q_n, r_n)=(h_{1, n}, {h}_{2, n}, h_{3, n}, {h}_{4, n}, {h}_{5, n}, {h}_{6, n})\longrightarrow0, \end{equation}$

其中, 在 $ [H^1(\Omega)]^3 $ 中, 有

(4.6)$\begin{equation} {\rm i}\lambda_n(\psi_{n}, \varphi_{n}, \omega_n)-(p_n, q_n, r_n)=(h_{1, n}, {h}_{2, n}, h_{3, n})\longrightarrow0, \end{equation}$

在 $ [L^2(\Omega)]^3 $ 中, 有

(4.7)$\begin{align*} &\ {\rm i}\lambda_n(p_n, q_n, r_n)-(\rho_{1}^{-1}(L_1-\chi_{\Omega _{0}}p_n), \rho_{1}^{-1}(L_2-\chi_{\Omega _{0}}q_n), \rho_{2}^{-1}( L_3-\chi_{\Omega _{0}}r_n))\\ &=({h}_{4, n}, {h}_{5, n}, {h}_{6, n})\longrightarrow0, \end{align*}$

且

(4.8)$\begin{align*} &\ \mathrm{Re}(({\rm i}\lambda_n-\mathcal{A})(\psi_n, \varphi_{n}, \omega_{n}, p_n, q_n, r_n), (\psi_n, \varphi_{n}, \omega_{n}, p_n, q_n, r_n))_\mathcal{H}\\ &=-\mathrm{Re}(\mathcal{A}(\psi_n, \varphi_{n}, \omega_{n}, p_n, q_n, r_n), (\psi_n, \varphi_{n}, \omega_{n}, p_n, q_n, r_n))_\mathcal{H}\\ &=\int_{\Omega_{0}}(|p_n|^2+|q_n|^2+|r_n|^2){\rm d}x{\rm d}y\\ &=o(1), \end{align*}$

因此, 在 $ L^2(\Omega_{0}) $ 中, 有

(4.9)$\begin{equation} p_n\to0,\ q_n\to0,\ r_n\to0. \end{equation}$

由于 $ W $ 嵌入 $ H $ 是稠的, 则在空间 $ H $ 中, 对 (4.6) 式用 $ (p_n, q_n, r_n) $ 做内积得

(4.10)$\begin{equation} \int_{\Omega_{0}}{\rm i}\lambda_n(\rho_{1}\psi_n\overline{p}_n, \rho_{1}\varphi_n\overline{q}_n, \rho_{2}\omega_{n}\overline{r}_n)-(\rho_{1}|p_n|^2+\rho_{1}|q_n|^2+\rho_{2}|r_n|^2){\rm d}x{\rm d}y=o(1), \end{equation}$

在 $ H $ 中, 对 (4.7)式用 $ (\psi_n, \varphi_n, \omega_n) $ 作内积得

$\begin{align*} &\ ((p_n({\rm i}\lambda_n+\rho_{1}^{-1}\chi_{\Omega _{0}})-\rho_{1}^{-1}L_1, q_n({\rm i}\lambda_n+\rho_{1}^{-1}\chi_{\Omega _{0}})-\rho_{1}^{-1}L_2, r_n({\rm i}\lambda_n+\rho_{2}^{-1}\chi_{\Omega _{0}})-\rho_{2}^{-1}L_3), \nonumber\\&\ (\psi_n, \varphi_n, \omega_{n}))_H\nonumber\\&=\int_{\Omega}{\rm i}\lambda_n(\rho_{1}p_n\overline{\psi}_{n}+\rho_{1}q_n\overline{\varphi}_{n}+\rho_{2}r_n\overline{\omega}_{n})+\chi_{\Omega _{0}}(p_n\overline{\psi}_{n}+q_n\overline{\varphi}_{n}+r_n\overline{\omega}_n)\nonumber\\&\quad-(L_1\overline{\psi}_n+L_2\overline{\varphi}_n+L_3\overline{\omega}_n){\rm d}x{\rm d}y\\ &=\int_{\Omega}{\rm i}\lambda_n(\rho_{1}p_n\overline{\psi}_{n}+\rho_{1}q_n\overline{\varphi}_{n}+\rho_{2}r_n\overline{\omega}_{n})-(\rho_{1}p_n\overline{\psi}_{n}+\rho_{1}q_n\overline{\varphi}_{n}+\rho_{2}r_n\overline{\omega}_{n}){\rm d}x{\rm d}y\\ &\quad\ +\int_{\Omega}\chi_{\Omega _{0}}(p_n\overline{\psi}_{n}+q_{n}\overline{\varphi}_{n}+r_n\overline{\omega}_{n}){\rm d}x{\rm d}y\\ &={\rm i}\lambda_n\int_{\Omega}(\rho_{1}p_n\overline{\psi}_{n}+\rho_{1}q_n\overline{\varphi}_{n}+\rho_{2}r_n\overline{\omega}_{n}){\rm d}x{\rm d}y+a(\psi_n, \varphi_{n}, \omega_{n};\psi_n, \varphi_{n}, \omega_{n})\\ &=o(1), \end{align*}$

即

(4.11)$\begin{equation} {\rm i}\lambda_{n}\int_{\Omega}(\rho_{1}\psi_{n}\overline{p}_n+\rho_{1}\varphi_{n}\overline{q}_n+\rho_{2}\omega\overline{r}_{n}){\rm d}x{\rm d}y+a(\psi_n, \varphi_{n}, \omega_{n};\psi_n, \varphi_{n}, \omega_{n})=o(1), \end{equation}$

故由 (4.10) 和 (4.11)式相加并取实部得

(4.12)$\begin{equation} a(\psi_n, \varphi_{n}, \omega_{n};\psi_n, \varphi_{n}, \omega_{n})-\int_{\Omega}(\rho_{1}|p_n|^2+\rho_{1}|q_n|^2+\rho_{2}|r_n|^2){\rm d}x{\rm d}y=o(1), \end{equation}$

由 (4.4) 和 (4.12)式可得

(4.13)$\begin{equation} \lim_{n \to \infty} \int_{\Omega}(\rho_{1}|p_n|^2+\rho_{1}|q_n|^2+\rho_{2}|r_n|^2){\rm d}x{\rm d}y=\frac{1}{2}, \end{equation}$

(4.14)$\begin{equation} \lim_{n \to \infty} a(\psi_n, \varphi_{n}, \omega_{n};\psi_n, \varphi_{n}, \omega_{n})=\frac{1}{2}. \end{equation}$

由 (4.6) 和 (4.13)式得到

(4.15)$\begin{equation} \psi_{n}\to0, \varphi_{n}\to0, \omega_{n}\to0, \text{在}\ L^2(\Omega)\text{中}. \end{equation}$

将(4.6)式代入 (4.7)式, 并消去 $ (p_n, q_n, r_n) $ 得

(4.16)$\begin{equation} \rho_{1}\lambda_{n}^{2}\psi_n+L_1=-{\rm i}\lambda_{n}h_{1, n}-{h}_{4, n}, \end{equation}$

同理有

(4.17)$\begin{equation} \rho_{1}\lambda_{n}^{2}\varphi_n+L_2=-{\rm i}\lambda_{n}h_{2, n}-{h}_{5, n}, \end{equation}$

(4.18)$\begin{equation} \rho_{2}\lambda_{n}^{2}\omega_n+L_3=-{\rm i}\lambda_{n}h_{3, n}-{h}_{6, n}. \end{equation}$

接下来, 我们将运用分片乘子法证明预期的结果.

取 $ h=h(x, y)\in{C^1(\Omega)} $, $ 0\le{h}\le{1} $ 且

$h(x, y)=\begin{cases} 1, & \text (x, y)\in{\Omega\setminus \Omega_0}, \\ 0, & \text (x, y)\in{\overline{\Omega}_0. } \end{cases}$

用 $ h(x, y){m}(x, y)\cdot\nabla \overline{\psi}_n $ 乘以 (4.16)式, 并在 $ \Omega $ 上积分得

(4.19)$\begin{equation} \int_{\Omega}h{m}(x, y)\cdot\nabla \overline{\psi}_n(\rho_{1}\lambda_{n}^{2}\psi_n+L_1){\rm d}x{\rm d}y=o(1), \end{equation}$

同理有

(4.20)$\begin{equation} \int_{\Omega}h{m}(x, y)\cdot\nabla \overline{\varphi}_n(\rho_{1}\lambda_{n}^{2}\varphi_n+L_2){\rm d}x{\rm d}y=o(1), \end{equation}$

(4.21)$\begin{equation} \int_{\Omega}h{m}(x, y)\cdot\nabla \overline{\omega}_n(\rho_{2}\lambda_{n}^{2}\omega_n+L_3){\rm d}x{\rm d}y=o(1). \end{equation}$

为了书写方便起见, 置

(4.22)$\begin{equation} \int_{\Omega}\rho_{1}\lambda_{n}^{2}h{m}(x, y)\cdot\nabla \overline{\psi}_n\psi_{n}{\rm d}x{\rm d}y=I_1, \end{equation}$

(4.23)$\begin{equation} \int_{\Omega}L_{1}h{m}(x, y)\cdot\nabla \overline{\psi}_n{\rm d}x{\rm d}y=I_2, \end{equation}$

(4.24)$\begin{equation} \int_{\Omega}\rho_{1}\lambda_{n}^{2}h{m}(x, y)\cdot\nabla \overline{\varphi}_n\varphi_{n}{\rm d}x{\rm d}y=I_1^{'}, \end{equation}$

(4.25)$\begin{equation} \int_{\Omega}L_{2}h{m}(x, y)\cdot\nabla \overline{\varphi}_n{\rm d}x{\rm d}y=I_2^{'}, \end{equation}$

(4.26)$\begin{equation} \int_{\Omega}\rho_{2}\lambda_{n}^{2}h{m}(x, y)\cdot\nabla\overline{\omega}_n\omega_{n}{\rm d}x{\rm d}y=I_1^{''}, \end{equation}$

(4.27)$\begin{equation} \int_{\Omega}L_{3}h{m}(x, y)\cdot\nabla \overline{\omega}_n{\rm d}x{\rm d}y=I_2^{''}, \end{equation}$

其中

$\begin{align*} I_1={}&-\int_{\Omega\setminus\Omega_{0}}\mathrm{div}(\rho_{1}\lambda_{n}^{2}\psi_{n}{m})\overline{\psi}_{n}{\rm d}x{\rm d}y+\int_{\Gamma_0}\rho_{1}\lambda_{n}^{2}|\psi_{n}|^{2}{m}\cdot{\nu_0}{\rm d}S+\int_{\Gamma}\rho_{1}\lambda_{n}^{2}|\psi_{n}|^{2}{m}\cdot{\nu}{\rm d}S\nonumber\\ ={}&-\int_{\Omega\setminus\Omega_{0}}[\rho_{1}\lambda_{n}^{2}|\psi_n|^2\mathrm{div}{m}+{m}\cdot\nabla (\rho_{1}\lambda_{n}^{2}\psi_n)\overline{\psi}_{n}]{\rm d}x{\rm d}y\\ &+\int_{\Gamma_0}\rho_{1}\lambda_{n}^{2}|\psi_{n}|^{2}{m}\cdot{\nu_{0}}{\rm d}S+\int_{\Gamma}\rho_{1}\lambda_{n}^{2}|\psi_{n}|^{2}{m}\cdot{\nu}{\rm d}S\\ ={}&-\rho_{1}\int_{\Omega\setminus\Omega_{0}}(|\lambda_{n}\psi_{n}|^{2}\mathrm{div}{m}+\lambda_{n}^{2}\overline{\psi}_{n}{m}\cdot\nabla \psi_{n}){\rm d}x{\rm d}y\\ &+\rho_{1}\int_{\Gamma_0}|\lambda_{n}\psi_{n}|^{2}{m}\cdot{\nu_0}{\rm d}S+\rho_{1}\int_{\Gamma}|\lambda_{n}\psi_{n}|^{2}{m}\cdot{\nu}{\rm d}S\\ ={}&\rho_{1}\int_{\Omega\setminus\Omega_{0}}(|p_{n}|^{2}\mathrm{div}{m}-\lambda_{n}^{2}\overline{\psi}_n{m}\cdot\nabla \psi_{n}){\rm d}x{\rm d}y-\rho_{1}\int_{\Gamma_0}|p_{n}|^{2}{m}\cdot{\nu_0}{\rm d}S-\rho_{1}\int_{\Gamma}|p_{n}|^{2}{m}\cdot{\nu}{\rm d}S\\ ={}&\rho_{1}\int_{\Omega\setminus\Omega_{0}}(|p_{n}|^{2}\mathrm{div}{m}-\lambda_{n}^{2}\overline{\psi}_{n}{m}\cdot\nabla \psi_{n}){\rm d}x{\rm d}y-\rho_{1}\int_{\Gamma_0}|p_{n}|^{2}{m}\cdot{\nu_0}{\rm d}S, \end{align*}$

即

$\begin{align*} &\int_{\Omega\setminus\Omega_{0}}\rho_{1}\lambda_{n}^{2}{m}\cdot\nabla\overline{\psi}_n\psi_{n}{\rm d}x{\rm d}y+\int_{\Omega\setminus\Omega_{0}}\rho_{1}\lambda_{n}^{2}{m}\cdot\nabla\psi_{n} \overline{\psi}_{n}{\rm d}x{\rm d}y\nonumber\\ =\ &\rho_{1}\int_{\Omega\setminus\Omega_{0}}|p_{n}|^{2}\mathrm{div}{m}{\rm d}x{\rm d}y-\rho_{1}\int_{\Gamma_0}|p_{n}|^{2}{m}\cdot{\nu_0}{\rm d}S, \end{align*}$

两边取实部得

(4.28)$\begin{equation} \mathrm{Re}I_{1}=\frac{1}{2}\rho_{1}\bigg(\int_{\Omega\setminus\Omega_{0}}|p_{n}|^{2}\mathrm{div}{m}{\rm d}x{\rm d}y-\int_{\Gamma_0}|p_{n}|^{2}{m}\cdot{\nu_0}{\rm d}S\bigg), \end{equation}$

同理, 对 (4.24) 和 (4.26)式采用相同的方法, 有

(4.29)$\begin{equation} \mathrm{Re}I_{1}^{'}=\frac{1}{2}\rho_{1}\bigg(\int_{\Omega\setminus\Omega_{0}}|q_{n}|^{2}\mathrm{div}{m}{\rm d}x{\rm d}y-\int_{\Gamma_0}|q_{n}|^{2}{m}\cdot{\nu_0}{\rm d}S\bigg), \end{equation}$

(4.30)$\begin{equation} \mathrm{Re}I_{1}^{''}=\frac{1}{2}\rho_{2}\bigg(\int_{\Omega\setminus\Omega_{0}}|r_{n}|^{2}\mathrm{div}{m}{\rm d}x{\rm d}y-\int_{\Gamma_0}|r_{n}|^{2}{m}\cdot{\nu_0}{\rm d}S\bigg), \end{equation}$

由 (4.28), (4.29) 和 (4.30)式得

(4.31)$\begin{align*} \mathrm{Re}(I_1+I_{1}^{'}+I_{1}^{''})=&\frac{1}{2}\bigg\{ \int_{\Omega\setminus\Omega_{0}}[(\rho_{1}|p|^2+\rho_{1}|q|^2+\rho_{2}|r|^2)\mathrm{div}{m}]{\rm d}x{\rm d}y \\ & -\int_{\Gamma_0}[(\rho_{1}|p|^2+\rho_{1}|q|^2+\rho_{2}|r|^2){m}\cdot{\nu_0}]{\rm d}S \bigg \}. \end{align*}$

另一方面, 对 (4.23) 式应用 Green 公式

(4.32)$\begin{align*} I_{2}={}&\int_{\Omega\setminus\Omega_{0}}D\mathrm{div}(\psi_{n, x}+\mu\varphi_{n, y}, \frac{1-\mu}{2}(\psi_{n, y}+\varphi_{n, x}))h{m}\cdot\nabla \overline{\psi}_{n}{\rm d}x{\rm d}y\\ &-\int_{\Omega\setminus\Omega_{0}}K(\psi_{n}+\omega_{n, x})\cdot\nabla (h{m}\cdot\nabla \overline{\psi}_n){\rm d}x{\rm d}y\\ ={}&-\int_{\Omega\setminus\Omega_{0}}D(\psi_{n, x}, +\mu\varphi_{n, y}, \frac{1-\mu}{2}(\psi_{n, y}+\varphi_{n, x}))\nabla (h{m}\cdot\nabla \overline{\psi}_{n}){\rm d}x{\rm d}y\\ &+\int_{\Gamma_0}Dh({m}\cdot\nabla \overline{\psi}_{n})[(\psi_{n, x}+\mu\varphi_{n, y}, \frac{1-\mu}{2}(\psi_{n, y}+\varphi_{n, x}))\cdot{\nu_0}]{\rm d}S\\ &+\int_{\Gamma}Dh({m}\cdot\nabla \overline{\psi}_{n})[(\psi_{n, x}+\mu\varphi_{n, y}, \frac{1-\mu}{2}(\psi_{n, y}+\varphi_{n, x}))\cdot{\nu}]{\rm d}S\\ &-\int_{\Omega\setminus\Omega_{0}}K(\psi_{n}+\omega_{n, x})(h{m}\cdot\nabla \overline{\psi}_{n}){\rm d}x{\rm d}y, \end{align*}$

由边界条件以及函数 $ h $ 的定义, 则

(4.33)$\begin{align*} I_{2}={}&-\int_{\Omega\setminus\Omega_{0}}D(\psi_{n, x}+\mu\varphi_{n, y}, \frac{1-\mu}{2}(\psi_{n, y}+\varphi_{n, x}))\cdot\nabla ({m}\cdot\nabla \overline{\psi}_{n}){\rm d}x{\rm d}y\\ &-\int_{\Omega\setminus\Omega_{0}}K(\psi_{n}+\omega_{n, x})({m}\cdot\nabla \overline{\psi}_{n}){\rm d}x{\rm d}y, \end{align*}$

同理

(4.34)$\begin{align*} I_{2}^{'}={}&-\int_{\Omega\setminus\Omega_{0}}D(\frac{1-\mu}{2}(\psi_{n, y}+\varphi_{n, x}), \varphi_{n, y}+\mu\psi_{n, x})\cdot\nabla ({m}\cdot\nabla \overline{\varphi}_{n}){\rm d}x{\rm d}y\\ &-\int_{\Omega\setminus\Omega_{0}}K(\varphi_{n}+\omega_{n, y})({m}\cdot\nabla \overline{\varphi}_{n}){\rm d}x{\rm d}y, \end{align*}$

以及

(4.35)$\begin{equation} I_{2}^{''}=-K\int_{\Omega\setminus\Omega_{0}}(\psi_{n}+\omega_{n, x}, \varphi_{n}+\omega_{n, y})\cdot\nabla ({m}\cdot\nabla \overline{\omega}_{n}){\rm d}x{\rm d}y, \end{equation}$

所以

(4.36)$\begin{align*} I_2+I_2^{'}+I_{2}^{''}={}&\int_{\Omega}(L_1h{m}\cdot\nabla \overline{\psi}_{n}+L_2h{m}\cdot\nabla\overline{\varphi}_{n}+L_3h{m}\cdot\nabla\overline{\omega}_{n}){\rm d}x{\rm d}y\\ ={}&-\int_{\Omega\setminus\Omega_{0}}D(\psi_{n, x}+\mu\varphi_{n, y}, \frac{1-\mu}{2}(\psi_{n, y}+\varphi_{n, x}))\cdot\nabla({m}\cdot\nabla\overline{\psi}_{n}){\rm d}x{\rm d}y\\ &-\int_{\Omega\setminus\Omega_{0}}D(\frac{1-\mu}{2}(\psi_{n, y}+\varphi_{n, x}), \varphi_{n, y}+\mu\psi_{n, x})\cdot\nabla ({m}\cdot\nabla \overline{\varphi}_{n}){\rm d}x{\rm d}y\\ &-\int_{\Omega\setminus\Omega_{0}}K[(\psi_{n}+\omega_{n, x})({m}\cdot\nabla\overline{\psi}_{n})+(\psi_{n}+\omega_{n, y})({m}\cdot\nabla\overline{\varphi}_{n})]{\rm d}x{\rm d}y\\ &-\int_{\Omega\setminus\Omega_{0}}K(\psi_{n}+\omega_{n, x}, \varphi_{n}+\omega_{n, y})\cdot\nabla({m}\cdot\nabla\overline{\omega}_{n}){\rm d}x{\rm d}y\\ ={}&-a(\psi_{n}, \varphi_{n}, \omega_{n};h{m}\cdot\nabla\psi_{n}, h{m}\cdot\nabla\varphi_{n}, h{m}\cdot\nabla\omega_{n}). \end{align*}$

其中

$\begin{align*} &-a(\psi_{n}, \varphi_{n}, \omega_{n};h{m}\cdot\nabla\psi_{n}, h{m}\cdot\nabla\varphi_{n}, h{m}\cdot\nabla\omega_{n})\nonumber\\ =&-\int_{\Omega} \Bigg\{Dh\Bigg[\nabla \overline{\psi}_n\begin{pmatrix} m_{1, x} &m_{1, y} \\ m_{2, x} &m_{2, y} \end{pmatrix}\begin{pmatrix} \psi_{n, x}+\mu\varphi_{n, y}\\\frac{1-\mu}{2}(\psi_{n, y}+\varphi_{n, x}) \end{pmatrix}\\&+\nabla \overline{\varphi}_{n}\begin{pmatrix} m_{1, x} &m_{1, y} \\ m_{2, x} &m_{2, y} \end{pmatrix}\begin{pmatrix}\frac{1-\mu}{2}(\psi_{n, y}+\varphi_{n, x})\\ \mu\psi_{n, x}+\varphi_{n, y} \end{pmatrix}\Bigg]{\rm d}x{\rm d}y \\ &+Kh\nabla \overline{\omega}_n\begin{pmatrix} m_{1, x} &m_{1, y} \\ m_{2, x} &m_{2, y} \end{pmatrix}\begin{pmatrix} \psi_{n}+\omega_{n, x}\\ \varphi_{n}+\omega_{n, y} \end{pmatrix}\Bigg\}{\rm d}x{\rm d}y\\ &-\int_{\Omega}\left[Dh(m_1, m_{2})\begin{pmatrix} \overline{\psi}_{n, xx} &\overline{\psi}_{n, xy} \\ \overline{\psi}_{n, xy} &\overline{\psi}_{n, yy} \end{pmatrix}\begin{pmatrix} \psi_{n, x}+\mu\varphi_{n, y}\\ \frac{1-\mu}{2}(\psi_{n, y}+\varphi_{n, x}) \end{pmatrix}\right]{\rm d}x{\rm d}y\\ &-\int_{\Omega}\left[Dh(m_1, m_{2})\begin{pmatrix} \overline{\varphi}_{n, xx} &\overline{\varphi}_{n, xy} \\ \overline{\varphi}_{n, xy} &\overline{\varphi}_{n, yy} \end{pmatrix}\begin{pmatrix} \frac{1-\mu}{2}(\psi_{n, y}+\varphi_{n, x})\\ \mu\psi_{n, x}+\varphi_{n, y} \end{pmatrix}\right]{\rm d}x{\rm d}y\\ &-K\int_{\Omega}(\psi_{n}+\omega_{n, x})(h{m}\cdot\nabla\overline{\psi}_{n}){\rm d}x{\rm d}y-K\int_{\Omega}(\varphi_{n}+\omega_{n, y})(h{m}\cdot\nabla\overline{\varphi}_{n}){\rm d}x{\rm d}y\\ &-K\int_{\Omega}h(m_1, m_2)\begin{pmatrix} \overline{\omega}_{n, xx} &\overline{\omega}_{n, xy} \\ \overline{\omega}_{n, xy} &\overline{\omega}_{n, yy} \end{pmatrix}\begin{pmatrix} \psi_n+\omega_{n, x}\\ \varphi_n+\omega_{n, y} \end{pmatrix}{\rm d}x{\rm d}y. \end{align*}$

将 $ I_2+I_2^{'}+I_{2}^{''} $ 取实部得

(4.37)$\begin{align*}\mathrm{Re}(I_2+I_2^{'}+I_{2}^{''})={}&\frac{1}{2}\mathrm{Re}[(I_2+I_2^{'}+I_{2}^{''})+(\overline{I}_2+\overline{I_2^{'}}+\overline{I_{2}^{''}})]\\ ={}&\frac{1}{2}\mathrm{Re}[a(h{m}\cdot\nabla\psi_{n}, h{m}\cdot\nabla\varphi_{n}, h{m}\cdot\nabla\omega_{n};\psi_{n}, \varphi_{n}, \omega_{n})\\ &-a(\psi_{n}, \varphi_{n}, \omega_{n};h{m}\cdot\nabla\psi_{n}, h{m}\cdot\nabla\varphi_{n}, h{m}\cdot\nabla\omega_{n})]\\ ={}&0, \end{align*}$

结合 (4.28)-(4.31) 和 (4.37) 式, 我们有

(4.38)$\begin{align*} o(1)={}&\frac{1}{2}\bigg \{ \int_{\Omega\setminus\Omega_{0}}\mathrm{div}{m}(\rho_{1}|p_n|^2+\rho_{1}|q_n|^2+\rho_{2}|r_n|^2){\rm d}x{\rm d}y \\ & -\int_{\Gamma_0}(\rho_{1}|p_n|^2+\rho_{1}|q_n|^2+\rho_{2}|r_n|^2){m}\cdot{\nu_0}{\rm d}S\bigg\}, \end{align*}$

根据几何光学条件${m}\cdot{\nu_0}\le0, $有

(4.39)$\begin{equation} p_n\to0, q_n\to0, r_n\to0,\ \text{在}\ L^2(\Omega \setminus \Omega _0)\ \text{中}, \end{equation}$

故由 (4.9) 与 (4.39) 式推得

$\lim_{n \to \infty} \int_{\Omega}(\rho_{1}|p_n|^2+\rho_{1}|q_n|^2+\rho_{2}|r_n|^2){\rm d}x{\rm d}y=0. $

与 (4.13) 式矛盾, 从而完成定理 4.4 证明.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Lagnese

J E

. Boundary Stabilization of Thin Plates. Philadelhia, PA: Society for Industrial and Applied Mathematics, 1989