1 引言
流体模型研究的是一个输入输出系统, 流体的流入和流出情况受外部驱动系统控制. 随着高新科技的迅速发展, 传统离散排队模型表现出很大的不便性, 这时关于流体模型的研究逐渐兴起, 并已在信息网络、数字化智慧工厂等方面有着广泛应用.
Virtamo 和 Norros[1]研究了由 M/M/1 排队模型驱动的流体模型, 运用谱分析方法和第二类切比雪夫多项式得到无限状态环境中库存量的平稳分布. Anda 和 Resing[2]使用嵌入点研究了由 M/M/1 队列驱动的流体模型, 并运用第一类修正 Bessel 函数给出库存量稳态分布的表达式. Kulkarni[3]分析了具有单个缓冲器的流体模型, 但是由于计算量大, 不能得到较稳定的数值解. 除谱分析方法外, 出现了更加多样的研究方法. Sericola 和 Tuffin[4]利用递归法研究并给出了一般分布的流体模型库存量的平稳分布函数. Lierde 等[5] 使用迭代方法, 不仅解决了谱分析方法不能得到较稳定数值解的问题, 还可以用来研究更多更复杂的流体排队模型. Ammar 和 Sherif[6]分析了由 M/M/1 灾难队列驱动的流体模型, 并利用生成函数技术和一阶修正 Bessel 函数得到缓冲器库存量平稳分布函数的显性表达式. Wang 和 Mao[7] 将启动-关闭期引入到流体排队模型中, 运用矩阵几何解方法给出了稳态条件下库存量分布函数的 LST 及均值的表达式. 徐秀丽等[8]将可选服务策略引入到流体模型的外部驱动系统中, 并利用 LT 得到了稳态时库存量分布函数的 LST 和平均库存量. 考虑服务台出现故障的情形, 孙红霜[9]研究了具有工作故障策略 M/M/1 排队系统驱动的流体模型, 使用矩阵几何解、 LT 和 LST 得到了库存量平稳分布函数和均值的显性表达式.
现实生活中, 系统为减少运行成本或降低服务台发生故障的概率, 没有顾客时系统中的服务台会停止运行或以低服务速率运行, 此时将服务台的行为称为休假. 目前基于各类休假策略的流体模型的研究已有大量研究成果. Sherif 和 Ammar[10]使用母函数法分析了多重休假 M/M/1 排队系统驱动的流体模型, 得到了缓冲器库存量平稳分布函数的显式解. Mao 等[11]研究了基于多重休假和有限状态空间的排队系统驱动的流体模型, 得到了库存量均值的表达式. Vijayashree 和 Anjuka[12]分析了具有多重工作休假策略的 M/M/1/
风力发电路灯作为将风能转化为电能的照明设备, 由于具有节能环保、低成本、方便安装维修等优势, 目前在海边城市及风力资源丰富的地区已有着广泛的应用. 考虑风力发电路灯的能量转化过程, 转化成的电流看作流体, 风力发电机看作流体缓冲器, 风能通过风力发电机转化成电流, 并贮存于蓄电池中. 风力变化影响着转化速率的高低. 当风力较大时, 转化速率较快, 类似于驱动系统处于忙期. 当风力较小时, 转化速率较慢, 类似于驱动系统处于工作休假期. 当风力大小无法带动风轮转动时, 此时无法进行能量转化, 类似于驱动系统处于休假期. 在此基础上, 本文研究了具有启动时间和完全故障的双阶段休假 M/M/1 排队系统驱动的流体模型, 通过建立稳态下系统的平衡方程, 得到了库存量平稳分布函数的 LST 及均值等性能指标, 并将其应用到风力发电路灯的能量转化过程中, 在数值分析中验证了参数变化对性能指标的影响. 根据实际情况构建了费用函数, 最终通过数值分析得到了系统参数对成本费用的影响.
2 驱动系统描述
考虑一个具有启动时间、多重休假、单重工作休假及工作中完全故障等策略的 M/M/1 排队系统, 模型假设如下
1) 顾客的到达率为
2) 正规忙期内, 服务台的服务速率为
3) 服务台在工作休假期内会发生完全故障, 服务台发生故障的概率服从参数为
4) 假设顾客的到达间隔时间、服务台的启动时间、服务时间、维修时间、故障时间、休假时间和工作休假时间均相互独立. 假设该排队系统的服务规则为先到先服务 (FIFO).
设
其中
现在证明拟生灭过程
引理 2.1 若系统负载
其中
定理 2.1 拟生灭过程
证 拟生灭过程
这里
由 (2.1) 式可知
当
为方便给出稳态分布的表达式, 构建以下两个数列
利用矩阵几何解方法, 借助于式 (2.2) 和 (2.3), 导出拟生灭过程
其中
证毕.
3 流体模型稳态分析
设
其中
流体模型即为具有净输入率结构 (3.1) 的三维随机过程
由文献 [16] 知, 当
则由全概率公式得到流体模型库存量的平稳分布函数
记流体模型稳态概率向量为
运用概率分析方法, 得到
且满足边界条件
其中
记
对 (3.2) 式的两边取 Laplace 变换, 结合边界条件得到
其中
为给出稳态分布直观的数学表达式, 构建函数矩阵
其中
引理 3.1 对任意
其中
特别的
为了方便, 构建以下函数序列
利用式 (3.4) 和 (3.5) 得到下述结论.
定理 3.1 当
其中
证 对矩阵方程 (3.3) 使用矩阵几何解法可以得到
其中
将 (3.6) 式展开, 整理得到
求解方程组 (3.8)式, 得到以下结果
求解 (3.7) 式, 得到以下结果
将 (3.9) 式中的结果代入到 (3.10) 式, 定理 3.1 得证.
下面计算流体模型稳态时库存量的 LST, 由 (3.7) 式得到
这里
由于矩阵
则矩阵
其中
引入
对 (3.12) 式运用洛必达法则, 得到库存量在稳态时的空库概率为
其中
进一步得到流体模型稳态时库存量均值的表达式
其中
4 数值分析
风力发电路灯为在蓄电池中储存更多的电流, 则需要提高风能转化效率以及减少转化过程中的能量损失. 下面给出系统参数变化对性能指标和费用函数的影响. 本节考虑净流入率
4.1 参数敏感性分析
为直观给出系统参数对性能指标的影响, 下面假设
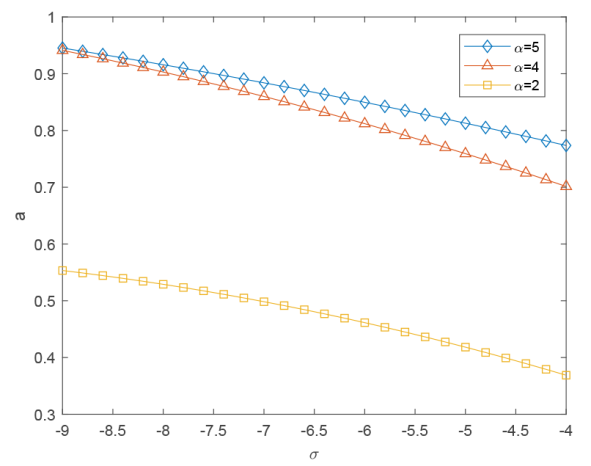
通过图1可以看出, 当
图1
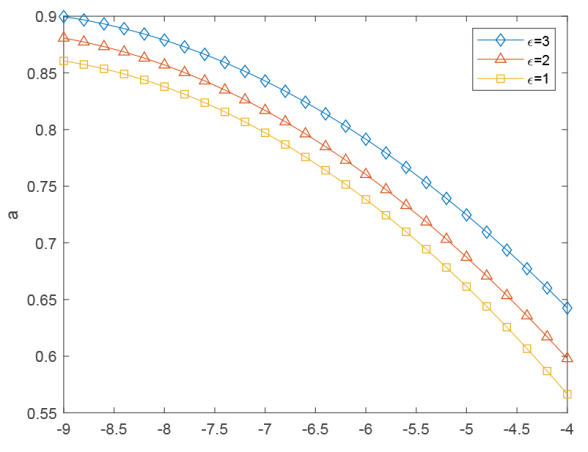
图2
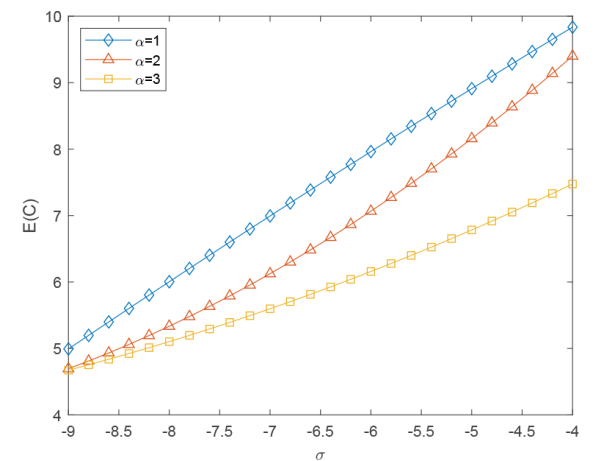
通过图3可以看出, 当
图3
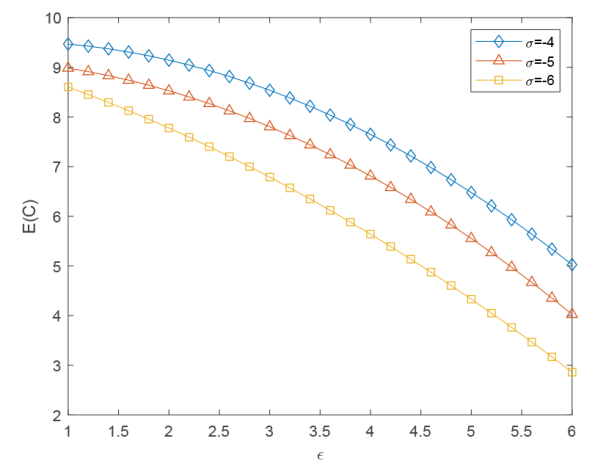
图4
4.2 费用分析
根据给出的性能指标, 记
假设
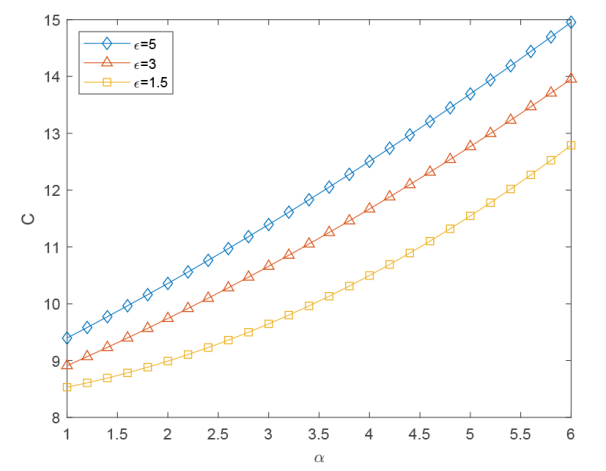
通过图5可以看出, 当
图5
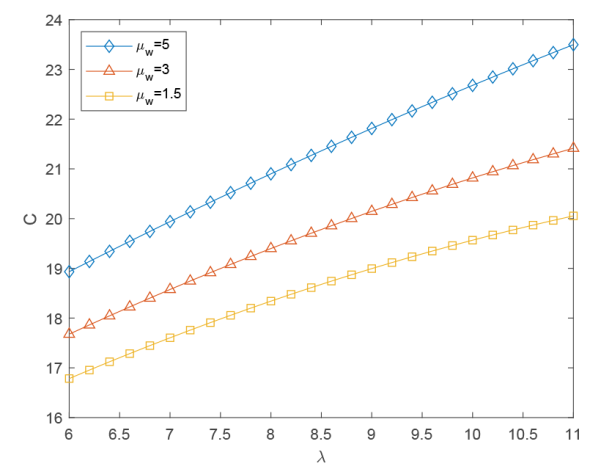
通过图6可以看出, 当
图6
5 总结
本文研究了具有启动时间, 完全故障和双阶段休假 M/M/1 排队系统驱动的流体模型, 利用拟生灭过程和矩阵几何解方法给出流体模型在稳态条件下的空库概率及均值等性能指标. 并结合风力发电路灯的能量转化系统, 通过数值分析得到了系统参数变化对性能指标和费用函数的影响, 以减少能源损耗, 获得更多的电流, 提高风能的利用效率.
参考文献
Fluid queue driven by an M/M/1 queue
Simple analysis of a fluid queue driven by an M/M/1 queue
A fluid queue driven by a Markovian queue
Invariant measures for fluid queues
Fluid queue driven by an M/M/1 disasters queue
Fluid model driven by an M/M/1 queue with set-up and close-down period
具有可选服务的 M/M/1 排队驱动的流模型
Fluid model driven by an M/M/1 queue with optional service
Analysis of an M/M/1 driven fluid queue with multiple exponential vacations
Fluid model driven by an M/M/1/N queue with exponential vacations
Fluid queue modulated by an M/M/1/N queue subject to multiple exponential working vacation
可选服务的 M/M/1 多重休假排队系统驱动的流模型
A fluid model driven by an M/M/1 vacations queue with optional service
Fluid model modulated by an M/M/ 1 working vacation queue with negative customer
基于矩阵分析方法的具有双阶段休假的排队系统驱动的流模型性能分析
Performance analysis of the fluid model driven by M/M/1 queuing system with two-stage vacation based on matrix analysis method
单重工作休假 M/M/c 排队驱动的流体模型分析
Analysis of the fluid model driven by M/M/c queue with single working vacation