1 引言
分裂可行问题 (Split Feasibility Problem, 记作 SFP) 是最优化领域的一个研究热点, 并在 LASSO 问题、信号处理、图像去噪问题等领域有着广泛的应用[2,9,10,16,19,27,32,37]. 因此, 该问题的理论算法及应用得到了广泛的关注和研究[3,4,6,11,14,17,20,25,27,28,31]. 1994 年, Censor 和 Elfving[5] 首次介绍了分裂可行问题模型, 其用于模拟反问题. 此后, 文献 [3,4] 建立了求解该模型的经典算法称之为 Byrne CQ 算法, 并将其推广到求解分裂可行问题更广义的临近分裂可行问题[22] (Proximal Split Feasibility Problem, 记作 PSFP). 针对 PSFP, 文献 [1,22,29⇓-31,35] 给出了相关的算法及其收敛性的推证. 即展开来讲, Moudafi 和 Thakur[22]构造了无需 Armijo 搜索[12,13,18,24,28,34] (该搜索常常计算额外的临近算子) 的自适应步长策略, 并讨论了分裂临近算法的弱收敛性. 基于惯性思想 (其用于加速算法的收敛性[2,16,20,27,28,32]), Shehu 等[31]修正了 Moudafi 等人的算法, 并证明了其弱收敛性. 为了研究其强收敛性, 众多学者给出了经典的强收敛算法, 例如, Abbas 等[1]设计了两种不同的一步迭代算法;随后, Shehu 等[29,30]结合 Mann-type, 加速混合粘滞类算法[21], 并提出了最速下降法; Wang 和 Xu[35]提出了分裂临近梯度法; Ma 和 Liu[20]构造了一种惯性分裂临近算法. 以上算法存在一个共同点: 在单调算子的 Lipschitz 连续的条件下, 步长趋近于零, 导致算法的效率较差. 此外, 算法的强收敛性证明需要较强的条件如临近算子的完全非扩张性. 针对这些因素, 本文提出了如下问题.
如何在算法[31]的基础上, 提出一个有界远离零的步长策略, 并通过弱化临近算子的完全非扩张性和单调算子的 Lipschitz 连续性来获得算法的强收敛性?
文章的结构如下. 第 2 节给出了一些基本概念和结论; 第 3 节给出了本文的主要结论; 第 4 节考虑了算法的应用; 第 5 节提供了数值实验.
2 预备知识
符号“
其中
另外, 示性函数定义为
定义 2.1 令
(i)
(ii)
(iii) 令
引理 2.1 令
(i)
(ii)
(iii)
引理 2.2[15] 令
(i)
(ii)
引理 2.3[26] 令
其中
(i)
(ii) 若对于序列
则
引理 2.4[23] 令
其中
3 惯性粘滞类算法及其强收敛性
在本节, 首先, 令
现在, 本节引入如下 PSFP[22]
任给
则上述函数的 Lipschitz 梯度分别为
其 Lipschitz 常数分别为
(A1) 问题 PSFP 的解集是非空的, 即
(A2) 令
(A3) 映射
本节的算法框架如下:
算法 1
步骤 0 固定
步骤 1 给定
其中步长
其中
步骤 2 若
注 3.1 若
注 3.2 在算法 1 中, 惯性参数
接下来, 本节的引理和定理的证明无需映射
引理 3.1 令步长序列
证 假设情形
进一步推出
同理, 可得
上式整理后, 即得
由数学归纳法知, 序列
由引理 2.4 知,
由于序列
现在, 在无需梯度算子
定理 3.1 假设条件 (A1)-(A3) 成立. 则由算法 {1} 产生的序列
证 令
同理, 可得
其中
其中
由上式可知,
根据
依据 (3.3) 式, 则有
那么存在一个常数
上式结合 (3.5) 和 (3.6) 式, 可知
上式结合 (3.1) 式, 可知
上式表明序列
再结合 (3.5) 式上面的式子, 可得
把 (3.7) 式代入上式, 则存在
即,
运用引理 2.1(i)-(ii) 和 (3.7) 式, 即证
由
令
接下来, 需证
假设
上式结合
故
由迭代公式 (3.1) 和 (3.2) 可知
其中
依据
利用 (3.13) 和 (3.14) 式, 可知
由 (3.1) 式和
上式可推出
由于序列
此外, 由 (3.14) 式, 可得
利用函数
上式意味着
进一步可知,
结合 (3.16) 式, 即证
因此
运用引理 2.3, 可证
若
进一步, 由定理 3.1 获得如下强收敛推论.
推论 3.1 令
其中
则上式生成的迭代序列
4 应用于分裂均衡问题
文献 [31] 介绍了分裂均衡问题属于变分包含问题, 并且, 其是临近分裂可行问题的特例. 接下来, 本节给出的分裂均衡问题 (Split Equilibrium Problem, 记作 SEP) 是指
其中
对于双边函数
(i)
(ii)
(iii) 对每一个
(iv) 对每一个
推论 4.1 令
其中
则如上方案生成的迭代序列
5 数值实验
在下面算例中, 本节主要研究 PSFP 的情形为
其中
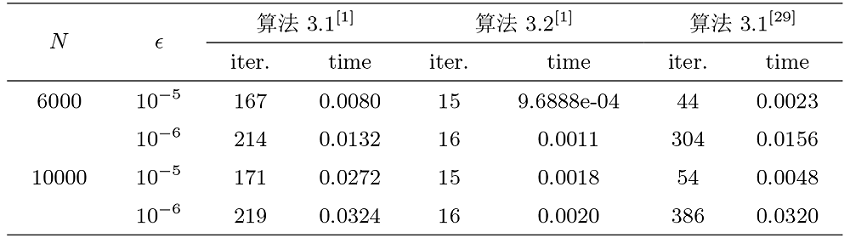
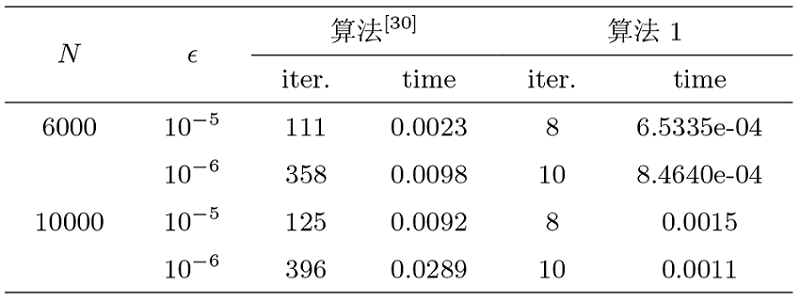
例 5.1[9] 设
其中
函数
对于算法 1, 固定
对于所有算法, 选择初始点
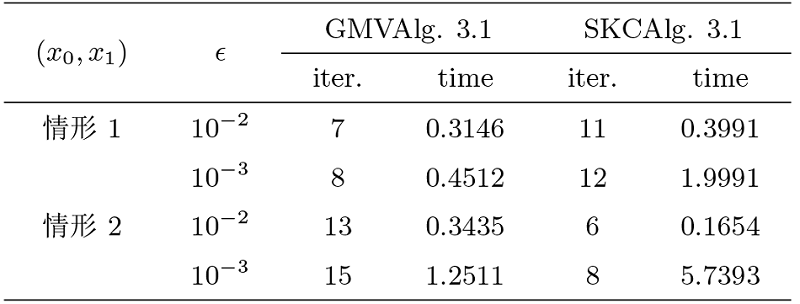
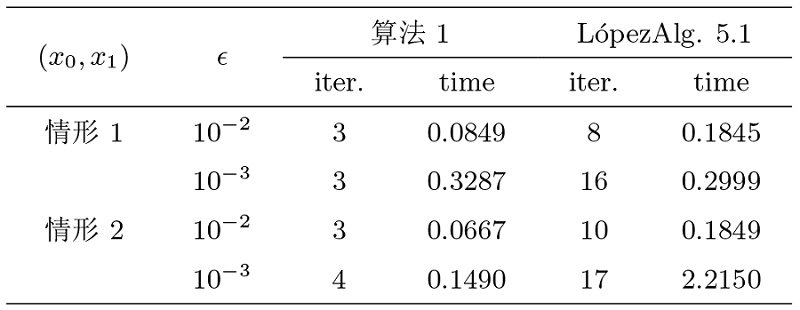
例 5.2[9] 设
对于算法 1, 选取
对于 LópezAlg. 5.1, 采取
所有算法的准止条件为
情形 1
情形 2
接下来, 集合
参考文献
Iterative methods for solving proximal split minimization problems
A new self-adaptive CQ algorithm with an application to the lasso problem
Iterative oblique projection onto convex sets and the split feasibility problem
A unified treatment of some iterative algorithms in signal processing and image reconstruction
A multiprojection algorithm using Bregman projection in a product space
The multiple-sets split feasibility problem and its applications for inverse problems
Hybrid inertial proximal algorithm for the split variational inclusion problem in Hilbert spaces with applications
Equilibrium programming in Hilbert spaces
Signal recovery by proximal forward-backward splitting
General splitting methods with linearization for the split feasibility problem
“Optimal” choice of the step length of the projection and contraction methods for solving the split feasibility problem
Note on the modified relaxation CQ algorithm for the split feasibility problem
A new relaxed CQ algorithm for solving split feasibility problems in Hilbert spaces and its applications
DOI:10.3934/jimo.2018080
[本文引用: 3]

Inspired by the works of Lopez et al. [21] and the recent paper of Dang et al. [15], we devise a new inertial relaxation of the CQ algorithm for solving Split Feasibility Problems (SFP) in real Hilbert spaces. Under mild and standard conditions we establish weak convergence of the proposed algorithm. We also propose a Mann-type variant which converges strongly. The performances and comparisons with some existing methods are presented through numerical examples in Compressed Sensing and Sparse Binary Tomography by solving the LASSO problem.
Proximal type algorithms involving linesearch and inertial technique for split variational inclusion problem in hilbert spaces with applications
On the convergence analysis of the gradient-CQ algorithms for the split feasibility problem
Splitting algorithms for the sum of two nonlinear operators
Solving the split feasibility problem without prior knowledge of matrix norms
The iterative method for solving the proximal split feasibility problem with an application to LASSO problem
Viscosity approximation methods for fixed points problems
Solving proximal split feasibility problems without prior knowledge of operator norms
Weak and strong convergence theorems for fixed points of asymptotically nonexpansive mappings
A note on the CQ algorithm for the split feasibility problem
An optimization approach to solving the split feasibility problem in Hilbert spaces
Approximation of zeros of inverse strongly monotone operators in Bachna spaces
Inertial relaxed CQ algorithms for solving a split feasibility problem in Hilbert spaces
New inertial relaxed method for solving split feasibilities
Strong convergence result for proximal split feasibility problem in Hilbert spaces
Accelerated hybrid viscosity and steepest-descent method for proximal split feasibility problems
Convergence analysis for the proximal split feasibility problem using an inertial extrapolation term method
The modified inertial relaxed CQ algorithm for solving the split feasibility problems
A new strong convergence for solving split variational inclusion problems
A modified forward-backward splitting method for maximal monotone mappings
Strong convergence for the proximal gradient method
A subgradient algorithm for a class of nonlinear split feasibility problems: Application to jointly constrained Nash equilibrium models
An algorithm for a class of split feasibility problems: Application to a model in electricity production