1 引言
在非 Hermitian 量子力学中存在一种带周期性约束条件的哈密尔顿方程
$\mathcal{H}=\frac{1}{2}\sum\limits_{k=1}^{n} p_{k}^{2}+\alpha \sum\limits_{k=1}^{n} \delta_{k} \delta_{k+1} \exp (q_{k}-q_{k+1}),$
其中参数 $\alpha>0$ $\delta_{1}=1, \delta_{i}=\prod\limits_{j=1}^{i-1}\epsilon_{j}, i=2,\cdots,n, \epsilon_{j} \in\{1,-1\}$ . 该方程考虑沿直线排列在位置 $q_{1}, q_{2},\cdots, q_{n}$ $n$ $1$ $q_{k}=q_{k}(t)$ $k$ $p_{k}=\dot{q}_{k}$ $\exp(q_{k}-q_{k-1})$ $t$
$\left\{ \begin{aligned} \frac{{\rm d}q_{k}}{{\rm d}t} & = \frac{\partial \mathcal H}{\partial p_{k}}, k=1,2,\cdots,n, \\ \frac{{\rm d}p_{k}}{{\rm d}t} & = -\frac{\partial \mathcal H}{\partial q_{k}}, k=1,2,\cdots,n. \\ \end{aligned} \right. $
使用文献[1 ]中著名的 Flaschka 变量替换
$a_{k}=-\frac{1}{2} p_{k}, b_{k}=\frac{\alpha}{2} \exp(\frac{1}{2}(q_{k}-q_{k+1})), k=1,2,\cdots,n,$
$\left\{ \begin{aligned} \frac{{\rm d}a_{k}}{{\rm d}t} & = 2(\epsilon_{k} b_{k}^{2}-\epsilon_{k-1} b_{k-1}^2), k=1,2,\cdots,n, \\ \frac{{\rm d}b_{k}}{{\rm d}t} & = b_{k}(a_{k+1}-a_{k}), k=1,2,\cdots,n. \\ \end{aligned} \right.$
约定 $a_{n+1}=a_{1}, b_{n}=b_{0}, \prod\limits_{k=1}^{n} b_{k}=(\frac{\alpha}{2})^{n}$ . 此时, 上述系统可以用矩阵方程形式表示, 即如下的 Lax 形式
$\dot{L}=\frac{{\rm d}L}{{\rm d}t}=[B,L],$
（1.1） $\begin{equation}L=\begin{pmatrix} a_{1} & \epsilon b_{1} & 0 &\cdots & 0 & b_{n}\\ b_{1} & a_{2} &\epsilon_{2} b_{2} & \cdots & \cdots & 0\\ 0 & b_{2} & a_{3}& & \vdots & \vdots\\ 0 & 0 & 0 & \cdots & a_{n-1} & \epsilon_{n-1} b_{n-1}\\ \delta_{n} b_{n} & 0 & 0 & \cdots & b_{n-1} & a_{n}\\ \end{pmatrix}. \end{equation}$
这样该方程的求解问题, 就转化为一个形如(1.1)的矩阵 $L$ $H L^T H=L$ $b_{k}>0, k=1,2,\cdots,n$ $H=\textrm{diag}(\delta_{1},\delta_{2},\cdots,\delta_{n})$ .
本文研究矩阵 $L$ $H=I_{r-1}\oplus(\epsilon)$ $\epsilon\in \{1,-1\}$ . 该类矩阵记为 $J_{n}$ . 当 $\epsilon=1$ $J_{n}$ [2 ] ; 当 $\epsilon=-1$ $J_{n}$ [3 ] . 对于周期 Jacobi 矩阵, 已经有了成熟的研究; 但对于周期伪 Jacobi 矩阵, 研究没有那么广泛. 然而其来源十分广泛, 经常出现在具有周期性边界条件的一维薛定谔方程的离散化和截断化中, 或者与非均匀环的振动有关[4 ] . 本文将考虑周期伪 Jacobi 矩阵 $J_{n}$
Ferguson[2 ] 、 Boley 和 Golub[4 ] 、 徐树方[5 ] 、徐映红和蒋尔雄[6 ] 等学者分别对周期 Jacobi 矩阵逆特征值问题的数值解法进行了研究, 主要考虑从整个矩阵及其最大顺序主子矩阵的特征值和一个给定的正数来对周期 Jacobi 矩阵进行了重构. 目前, 对该问题的研究取得了丰富的成果.随着研究的不断发展, 周期伪 Jacobi 矩阵的逆特征值问题也逐渐引起了众多学者的兴趣. 相比于周期 Jacobi 矩阵而言, 周期伪 Jacobi 矩阵的研究成果较少. 为了推广在周期 Jacobi 矩阵情况下的一些经典理论, 周期伪 Jacobi 矩阵的逆特征值问题也值得关注. 目前, 该问题也取得了一定的进展 (参见文献[3 ,7 ⇓ ⇓ -10 ]). 本文是这一领域研究的延续. 主要研究如下的周期伪 Jacobi 矩阵的逆特征值问题.
问题: 给定一个正数 $\beta$ $\boldsymbol{\lambda}=\left\{\lambda_{1},\lambda_{2},\cdots,\lambda_{n}\right\}$ $\boldsymbol{\mu}=\left\{\mu_{1},\mu_{2},\cdots,\mu_{n-1}\right\}$ $J_{n}$ $\sigma(J_{n})=\boldsymbol{\lambda}, \sigma(J_{n-1})=\boldsymbol{\mu}$ $\beta= \prod\limits_{j=1}^{n} b_{i}$ . 其中 $J_{n-1}$ $J_{n}$ $n-1$ $\sigma(J_{n}), \sigma(J_{n-1})$ $J_{n}$ $J_{n-1}$
2 矩阵的谱分布
在讨论矩阵 $J_{n}$ $J_{n-1}$
引理 2.1 [5 ] 已知 $\mu_{1}<\cdots<\mu_{n-1}$ $J_{n-1}$ $v_{i}=(v_{i1},v_{i2},\cdots,v_{i,n-1})^\mathrm{T}$ $\mu_{i}$
$v_{i1}v_{i,n-1}=\frac{b_{1} \cdots b_{n-2}}{\chi^{\prime}(\mu_{i})}, i=1,\cdots,n-1, $
其中 $\chi(\mu_{j})=\det(\mu_{j} I-J_{n-1})$ .
引理 2.2 [8 ] 已知一个在复共轭下封闭的集合 $\boldsymbol{\lambda}=\left\{\lambda_{1},\lambda_{2},\cdots,\lambda_{n}\right\}$ $\boldsymbol{\mu}=\left\{\mu_{1},\mu_{2},\cdots,\mu_{n-1}\right\}$ $\mu_{i} \notin \boldsymbol{\lambda}$
$\frac{x_{1}}{\lambda_{i}-\mu_{1}}+\frac{x_{2}}{\lambda_{i}-\mu_{2}}+\cdots+ \frac{x_{n-1}}{\lambda_{i}-\mu_{n-1}}=\lambda_{i}-a_{n}, i=1,2,\cdots,n $
$x_{j}=-\prod\limits_{i=1}^{n}(\lambda_{i}-\mu_{j})\prod\limits_{i=1,i\neq j}^{n-1}(\mu_{i}-\mu_{j})^{-1}, j=1,2,\cdots,n-1,$
$a_{n}=\sum\limits_{i=1}^{n}\lambda_{i}-\sum\limits_{i=1}^{n-1}\mu_{i}.$
引理 2.3 [3 ,6 ] 假设引理2.1的前提条件成立, 则 $\mu_{i}$ $J_{n}$
$b_{n} v_{i1} +\epsilon b_{n-1} v_{i,n-1}=0, i=1,\cdots,n-1.$
证 设 $y=(b_{n},0,\cdots,0,\epsilon b_{n-1})^\mathrm{T}, z=(\epsilon b_{n},0,\cdots,0,b_{n-1})$ $J_{n}$
$J_{n}= \begin{pmatrix} J_{n-1} & y\\ z & a_{n}\\ \end{pmatrix}.$
令 $V=(v_{1},v_{2},\cdots,v_{n-1})$ $n$ $U=V\oplus(1)$ $\widehat{U}=V^{\mathrm{T}}\oplus(1)$ $\widehat{U} U=I$ .
$\widehat{U} J_{n} U= \begin{pmatrix} V^{\mathrm{T}} J_{n-1} V & V^{\mathrm{T}} y\\ z V & a_{n}\\ \end{pmatrix}.$
令 $V^{\mathrm{T}} y=(\alpha_{1}+\epsilon \beta_{1},\cdots,\alpha_{n-1}+\epsilon \beta_{n-1})^\mathrm{T}$ $zV=(\epsilon \alpha_{1}+\beta_{1},\cdots, \epsilon \alpha_{n-1}+\beta_{n-1})$ $\alpha_{i}=b_{n} v_{i1}, \beta_{i}=b_{n-1} v_{i,n-1}$ . 再利用矩阵 $\lambda I-\hat{U}J_{n}U$
$\det(\lambda I-\hat{U} J_{n} U) = (\lambda-a_{n}) \prod\limits_{j=1}^{n-1} (\lambda-\mu_{j})-\sum\limits_{i=1}^{n-1}\epsilon (\alpha_{i} + \epsilon \beta_{i})^{2} \prod\limits_{j=1,j\neq i}^{n-1} (\lambda-\mu_{j}). $
倘若 $J_{n}$ $J_{n-1}$ $\mu_{i}$ $\det(\mu_{i} I-\hat{U} J_{n} U)=0$ . 又
$\det(\mu_{i} I-\hat{U} J_{n} U)=\epsilon (\alpha_{i} + \epsilon \beta_{i})^{2} \prod\limits_{j=1,j\neq i}^{n-1} (\mu_{i}-\mu_{j}),$
且 $\prod\limits_{j=1,j\neq i}^{n-1} (\mu_{i}-\mu_{j}) \neq 0$ $\mu_{i}\in\sigma(J_{n})$ $\alpha_{i}+\epsilon \beta_{i}=0$ $b_{n}v_{i1}+\epsilon b_{n-1}v_{i,n-1}=0$ .
定理 2.1 已知 $b_{n}v_{i1}+ \epsilon b_{n-1} v_{i,n-1}\neq 0$ $i=1,2,\cdots,n-1$ $J_{n}$ $f_{1}(\lambda)=0$
$f_{1}(\lambda)= \lambda-a_{n}-\sum\limits_{i=1}^{n-1}\frac{\epsilon (\alpha_{i}+ \epsilon\beta_{i})^{2}}{\lambda-\mu_{i}}.$
证 因为 $b_{n} v_{i1}+\epsilon b_{n-1} v_{i,n-1}\neq 0$ $J_{n}$ $J_{n-1}$ $\lambda \cap \mu =\emptyset$ . 故 $\prod\limits_{j=1}^{n-1} (\lambda-\mu_{j}) \neq 0$ . 从而
$\det(\lambda I-\hat{U} J_{n} U)= \prod\limits_{j=1}^{n-1} (\lambda-\mu_{j}) \left[\lambda-a_{n}-\sum\limits_{i=1}^{n-1} \frac{\epsilon (\alpha_{i} + \epsilon \beta_{i})^{2}}{\lambda-\mu_{i}}\right]=0 $
当且仅当 $f_{1}(\lambda)=0$ . 又因为 $f_{1}(\lambda)$ $n$ $f(\lambda)$ $n$ $J_{n}$ $n$
根据定理2.1的结论, 我们开始讨论 $J_{n}$ $J_{n-1}$
定理 2.2 已知 $\mu_{1}<\cdots<\mu_{n-1}$ $J_{n-1}$ $\lambda_{1},\lambda_{2},\cdots,\lambda_{n}$ $J_{n}$ $J_{n} $ $J_{n-1}$
(1) 当 $\epsilon=1$ $\lambda_{1} < \mu_{1} < \lambda_{2} < \cdots < \mu_{n-1} < \lambda_{n}$ .
(2) 当 $\epsilon=-1$
(a) $\mu_{1} < \lambda_{1} < \mu_{2} < \cdots < \mu_{n-1} <\lambda_{n-1} \le \lambda_{n}$
(b) $\lambda_{1} \le \lambda_{2} < \mu_{1} < \cdots < \lambda_{n} < \mu_{n-1}$
(c) $\mu_{1} < \lambda_{1} < \mu_{2} < \cdots < \lambda_{n-2} < \mu_{n-1}$ $\lambda_{n-1}$ $\lambda_{n}$
(d) $\mu_{1} < \lambda_{1} <\mu_{2} < \cdots < \mu_{j} <\lambda_{j} \le \lambda_{j+1} \le \lambda_{j+2} < \mu_{j+1} < \cdots < \lambda_{n} < \mu_{n-1}$ .
证 令 $f_{1}(\lambda)=h(\lambda)-g(\lambda)$ $h(\lambda)=\lambda-a_{n}, g(\lambda)=\sum\limits_{i=1}^{n-1} \frac{\epsilon (\alpha_{i} + \epsilon \beta_{i})^{2}}{\lambda-\mu_{i}}$ .
显然, $h(\lambda)$ $\mu_{i}$ $g(\lambda)$
(i) 当 $\epsilon=1$ $g^{\prime}(\lambda)<0$ $g(\lambda)$ $(\mu_{i}, \mu_{i+1}), i=1,2, \cdots,n-2$ $(-\infty, \mu_{1}), (\mu_{n-1}, +\infty)$ $\displaystyle\lim_{\lambda \rightarrow -\infty}g(\lambda)=-0$ $\displaystyle\lim_{\lambda \rightarrow +\infty}g(\lambda)=+0$ $\displaystyle\lim_{\lambda \rightarrow \mu_{i}^{-}}g(\lambda)=-\infty$ $\displaystyle\lim_{\lambda \rightarrow \mu_{i}^{+}}g(\lambda)=+\infty$ $i=1,2,\cdots,n-1$ . 故 $h(\lambda)$ $g(\lambda)$ $n$ $\mu_{i}$
(ii) 当 $\epsilon=-1$ $g^{\prime}(\lambda)>0$ $g(\lambda)$ $(\mu_{i}, \mu_{i+1}), i=1,2, \cdots,n-2$ $(-\infty, \mu_{1}), (\mu_{n-1}, +\infty)$ $\displaystyle\lim_{\lambda \rightarrow -\infty}g(\lambda)=+0$ $\displaystyle\lim_{\lambda \rightarrow +\infty}g(\lambda)=-0$ $\displaystyle\lim_{\lambda \rightarrow \mu_{i}^{-}}g(\lambda)=+\infty$ $\displaystyle\lim_{\lambda \rightarrow \mu_{i}^{+}}g(\lambda)=-\infty$ $i=1,2,\cdots,n-1$ . 故 $h(\lambda)$ $g(\lambda)$ $(\mu_{1}, \mu_{n-1})$ $n-2$
当其余两个交点全为实数时, 这两个交点只可能位于区间 $(\mu_{n-1},+\infty)$ $(-\infty,\mu_{1})$ $(\mu_{i},\mu_{i+1})$
当其余两个交点为一对共轭复数时, $h(\lambda)$ $g(\lambda)$ $(\mu_{1}, \mu_{n-1})$ $n-2$
定理 2.3 已知 $\lambda_{i}=\mu_{i}, i\in S=\left\{1,2, \cdots,s\right\}$ $\lambda_{s+1}, \cdots,\lambda_{n}$ $J_{n-1}$ $J_{n}$ $J_{n-1}$
(1) 当 $\epsilon=1$ $\lambda_{s+1}<\mu_{s+1}<\cdots<\mu_{n-1}<\lambda_{n}$
(2) 当 $\epsilon=-1$
(a) $\mu_{s+1} < \lambda_{s+1} < \mu_{s+2} < \cdots < \mu_{n-1} <\lambda_{n-1} \le \lambda_{n}$
(b) $\lambda_{s+1} \le \lambda_{s+2} < \mu_{s+1} < \cdots < \lambda_{n} < \mu_{n-1}$
(c) $\mu_{s+1} < \lambda_{s+1} < \mu_{s+2} < \cdots < \lambda_{n-2} < \mu_{n-1}$ $\lambda_{n-1}$ $\lambda_{n}$
(d) $\mu_{s+1} < \lambda_{s+1} <\mu_{s+2} < \cdots < \mu_{s+j} <\lambda_{s+j} \le \lambda_{s+j+1} \le \lambda_{s+j+2} < \mu_{j+1} < \cdots < \lambda_{n} < \mu_{n-1}$ .
证 由引理2.3和定理2.1可知, 当 $\lambda_{i}=\mu_{i}, i\in S=\left\{1,2, \cdots,s\right\}$ $\mu_{1}, \mu_{2},\cdots,\mu_{s}$ $J_{n}$ $s$
$f_{2}(\lambda)=\lambda-a_{n}-\sum\limits_{i=1, i \notin S}^{n-1} \frac{\epsilon (\alpha_{i} + \epsilon \beta_{i})^{2}}{\lambda-\mu_{i}}$
的 $n-s$
定理 2.4 假设问题 {PJIEP} 中的数集 $\boldsymbol{\lambda}$ $\boldsymbol{\mu}$ $\epsilon$
证 若已知 $\sigma(J_{n})=\boldsymbol{\lambda}$ $\sigma(J_{n-1})=\boldsymbol{\mu}$ $\epsilon$
当 $\boldsymbol{\lambda}$ $\boldsymbol{\mu}$ $\epsilon=-1$ $g(\lambda)$ $h(\lambda)$ $(-\infty,\mu_{1})$ $(\mu_{n-1},\infty)$ $\epsilon=1$ .
当 $\boldsymbol{\lambda}$ $\boldsymbol{\mu}$ $\epsilon=1$ $g(\lambda)$ $h(\lambda)$ $(-\infty,\mu_{1})$ $(\mu_{n-1},\infty)$ $\epsilon=-1$ .
3 问题 PJIEP 的可解性
根据矩阵 $J_{n}$ $J_{n-1}$
定理 3.1 已知 $\boldsymbol{\lambda}$ $\boldsymbol{\mu}$
(3.1) $\begin{equation}\prod_{i=1}^n\left|\mu_{j}-\lambda_{i}\right|-4 \epsilon \beta (-1)^{n+j-1} \ge 0, j=1,2,\cdots,n-1.\end{equation}$
证 本文只证明 $\boldsymbol{\lambda}\cap\boldsymbol{\mu}=\{\mu_{1},\mu_{2},\cdots,\mu_{s}\}$
先证明必要性. 假设存在一个周期伪 Jacobi 矩阵 $J_{n}$
$\sigma(J_{n})=\left\{\lambda_{1},\lambda_{2},\cdots,\lambda_{n}\right\},\sigma (J_{n-1})=\left\{\mu_{1},\mu_{2},\cdots,\mu_{n-1}\right\},$
其中 $\lambda_{i}=\mu_{i}, i\in S=\left\{1,2, \cdots,s\right\}$ .
(3.2) $\begin{equation} \left\{ \begin{aligned} b_{n} v_{i1} +\epsilon b_{n-1} v_{i,n-1} =0 &, i=1,2,\cdots,s, \\ b_{n} v_{i1} +\epsilon b_{n-1} v_{i,n-1} \neq 0&, i=s+1,s+2,,\cdots,n-1. \\ \end{aligned} \right. \end{equation}$
从定理2.1和定理2.3可知, $J_{n}$ $ f(\lambda)=\lambda-a_{n}-\sum\limits_{k=1}^{n-1} \frac{x_{k}}{\lambda-\mu_{k}}$
(3.3) $\begin{equation}x_{k}=0, k=1,2,\cdots,s; x_{k}=\epsilon (\alpha_{k}+\epsilon \beta_{k})^{2}, k=s+1,s+2,\cdots,n-1. \end{equation}$
(3.4) $\begin{equation}x_{1}=\cdots=x_{s}=0; x_{j}=-\prod\limits_{i=1}^{n}(\lambda_{i}-\mu_{j}) \prod\limits_{i=1,i \neq j}^{n-1} (\mu_{i}-\mu_{j})^{-1}, j=s+1,s+2,\cdots,n-1. \end{equation}$
(3.5) $\begin{equation}\alpha_{j}+\epsilon \beta_{j}=b_{n} v_{j1} +\epsilon b_{n-1} v_{j,n-1}=\pm \sqrt{\epsilon x_{j}}, j=1,2,\cdots,n-1.\end{equation}$
(3.6) $\begin{equation}(b_{n} v_{j1})(b_{n-1} v_{j,n-1})=\frac{ \beta}{\chi^{\prime}(\mu_j)}, j=1,2,\cdots,n-1.\end{equation}$
(3.7) $\begin{equation}b_{n} v_{j1}=\frac{1}{2}\left(\pm \sqrt{\epsilon x_{j}} \pm \sqrt{\epsilon x_{j}-4 \epsilon \beta /\chi^{\prime}(\mu_{j})}\right), j=1,2,\cdots,n-1.\end{equation}$
由 $\mu_{1}<\cdots<\mu_{n-1}$
(3.8) $\begin{equation}\chi^{\prime}(\mu_{j})=\prod\limits_{i=1,i \neq j}^{n-1}(\mu_{i}-\mu_{j})=(-1)^{n+j-1}\lvert \prod\limits_{i=1,i \neq j}^{n-1}(\mu_{i}-\mu_{j}) \rvert.\end{equation}$
(3.9) $\begin{equation}\prod\limits_{i=1}^{n}(\lambda_{i}-\mu_{j})=\left\{\begin{array}{ll} (-1)^{n+j}\lvert\prod\limits_{i=1}^{n}(\lambda_{i}-\mu_{j})\rvert, & \epsilon=1 \\[4mm] (-1)^{n+j-1}\lvert\prod\limits_{i=1}^{n}(\lambda_{i}-\mu_{j})\rvert, & \epsilon=-1.\end{array} \right. \end{equation}$
在公式(3.7)中, 令 $\Delta_{j}=\epsilon x_{j}-4 \epsilon \beta /\chi^{\prime}(\mu_{j})$ . 于是由公式(3.8)和(3.9)可得
$\begin{split} \Delta_{j} & =-\frac{\epsilon \prod\limits_{i=1}^{n}(\lambda_{i}-\mu_{j})}{\prod\limits_{i=1,i \neq j}^{n-1}(\mu_{i}-\mu_{j})}-\frac{4 \epsilon \beta}{\prod\limits_{i=1,i \neq j}^{n-1}(\mu_{i}-\mu_{j})} \\ & =\frac{\lvert \prod\limits_{i=1}^{n}(\lambda_{i}-\mu_{j}) \rvert}{\lvert \prod\limits_{i=1,i \neq j}^{n-1}(\mu_{i}-\mu_{j}) \rvert}-\frac{4 \epsilon \beta (-1)^{n+j-1}}{\lvert \prod\limits_{i=1,i \neq j}^{n-1}(\mu_{i}-\mu_{j})\rvert}, j=s+1,\cdots,n-1. \end{split} $
又因为公式(3.7)中的 $v_{j1}$ $b_{n}$ $\Delta_{j} \ge 0$
再证充分性. 假设公式 (3.1) 成立. 注意到 $\lambda_{i}=\mu_{i}, i\in S=\left\{1,2, \cdots,s\right\}$ $J_{n}$ $x_{j}, j=1,2,\cdots,n-1$ $\epsilon x_{j}=0, j=1,2,\cdots,s$ . 再由公式(3.8)和(3.9)可知 $\epsilon x_{j}>0, j=s+1,s+2,\cdots,n-1$ . 定义
(3.10) $\begin{equation}b_{n}=\frac{1}{2}\sqrt{\sum\limits_{j=1}^{n-1}\left(\sqrt{\epsilon x_{j}} \pm \sqrt{\epsilon x_{j}-4 \epsilon \beta /\chi^{\prime}(\mu_{j})}\right)^{2}}.\end{equation}$
当 $j=1,2,\cdots,s$ $\Delta_{j}$ $b_{n}>0$ . 再定义
(3.11) $\begin{equation} v_{j1}=\left\{ \begin{array}{ll} \displaystyle \frac{\sqrt{-\epsilon \beta /\chi^{\prime}(\mu_{j})}}{b_{n}}, & j=1,2,\cdots,s, \\[3mm] \displaystyle \frac{\sqrt{\epsilon x_{j}} \pm \sqrt{\epsilon x_{j}-4 \epsilon \beta /\chi^{\prime}(\mu_{j})}}{2b_{n}}, & j=s+1,s+2,\cdots,n-1. \end{array} \right. \end{equation}$
不难发现 $v_{j1}$ $\sum\limits_{j=1}^{n-1}v_{j1}^{2}=1$ . 于是 $(v_{11},v_{21},\cdots,v_{n-1,1})^{\mathrm{T}}$ 2 ]中的 Lanczos 算法, 可以通过初始值 $\mu_{1},\mu_{2},\cdots,\mu_{n-1}$ $(v_{11},v_{21},\cdots,v_{n-1,1})^{\mathrm{T}}$ $J_{n-1}$ . 从而有
$b_{n-1}=\frac{\beta}{b_{1} \cdots b_{n-2} b_{n}}, a_{n}=\sum\limits_{j=1}^{n}\lambda_{j}-\sum\limits_{j=1}^{n-1}\mu_{j}. $
于是就构造出了$J_{n}$ . 由定理2.3可知, 所得矩阵 $J_{n}$ $\lambda_{1},\lambda_{2},\cdots,\lambda_{n}$ . 充分性得证.
在上述定理充分性的证明中, 当 $\mu_{j}, j=1,2,\cdots,s$ $J_{n}$ $v_{j1}$ $\mu_{j}, j=s+1,s+2,\cdots,n-1$ $J_{n}$ $v_{j1}$ $(v_{11},v_{21},\cdots,v_{n-1,1})^{\mathrm{T}}$ $2^{n-1-s}$ $2^{n-s-1}$ $J_{n}$ . 若所有的 $\mu_{j}$ $J_{n}$ $2^{n-1}$ $J_{n}$ . 但需要注意的是, 对于某个指数 $j$ $v_{j1}$
4 构造算法及算例
根据定理2.4和定理3.1的证明过程, 本文可以给出如下构造算法.
算法 1 输入集合 $\boldsymbol{\lambda}$ $\boldsymbol{\mu}$ $\beta$ .
(1) 对 $\boldsymbol{\lambda}$ $\boldsymbol{\mu}$
若不满足定理2.2或定理2.3中的五种不等式序列, 则算法终止;
若满足定理2.2或定理2.3中的第一种不等式序列, 则 $\epsilon=1$ $\epsilon=-1$ .
(2) 若 $\boldsymbol{\lambda}$ $\boldsymbol{\mu}$
(3) 令 $\chi^{\prime}(\mu_{j})=(-1)^{n+j-1}\prod\limits^{n-1}_{i=1,i \neq j}\left|\mu_{i}-\mu_{j}\right|, j=1,2,\cdots,n-1$ .
(4) 对于 $j=1,2,\cdots,s$ $x_{j}=0$ .
(5) 对于 $j=s+1,s+2,\cdots,n-1$ $x_{j}=-\prod\limits_{i=1}^{n}(\lambda_{i}-\mu_{j})\prod\limits_{i=1,i\neq j}^{n-1}(\mu_{i}-\mu_{j})^{-1}$ .
$b_{n}=\displaystyle\frac{1}{2}\sqrt{\sum\limits_{j=1}^{n-1}\left(\sqrt{\epsilon x_{j}} \pm \sqrt{\epsilon x_{j}-4 \epsilon \beta /\chi^{\prime}(\mu_{j})}\right)^{2}},$
$v_{j1}=\left\{ \begin{array}{ll} \displaystyle \frac{\sqrt{-\epsilon \beta /\chi^{\prime}(\mu_{j})}}{b_{n}}, & j=1,2,\cdots,s, \\[3mm] \displaystyle \frac{\sqrt{\epsilon x_{j}} \pm \sqrt{\epsilon x_{j}-4 \epsilon \beta /\chi^{\prime}(\mu_{j})}}{2b_{n}}, & j=s+1,s+2,\cdots,n-1. \end{array} \right.$
(b) $u_{j0}=0,j=1,2,\cdots,n-1$ .
(c) $u_{j1}=v_{j1},j=1,2,\cdots,n-1$ .
(d) 对 $i=1,2,\cdots,n-2$
(i) $a_{i}=\sum\limits_{j=1}^{n-1}\mu_{j} u_{ji}^{2}$
(ii) $b_{i}=\sqrt{\sum\limits_{j=1}^{n-1}((\mu_{j}-a_{i}) u_{ji}-b_{i-1} u_{j,i-1})^2}$
(iii) 对于 $j=1,2,\cdots,n-1$ $u_{j,i+1}=((\mu_{j}-a_{i})u_{ji}-b_{i-1}u_{j,i-1})/b_{i}$
(e) $a_{n-1}=\sum\limits_{j=1}^{n-1}\mu_{j}u_{j,n-1}^{2}$ .
(8) $b_{n-1}=\frac{\beta}{b_{1} \cdots b_{n-2}b_{n}}$ $a_{n}=\sum\limits_{j=1}^{n}\lambda_{j}-\sum\limits_{j=1}^{n-1}\mu_{j}.$
注意上述过程中 $v_{j1}$ $b_{n}$
例 4.1 给定一个复数集合 $\boldsymbol{\lambda}=\big\{-\sqrt{3}, 0, \sqrt{3}, 0, -\textrm{i}, \textrm{i} \big\}$ $\boldsymbol{\mu}=\big\{-\sqrt{3}, -1, $ $0, 1, \sqrt{3} \big\}$ $\beta=1$ $J_{n}$ .
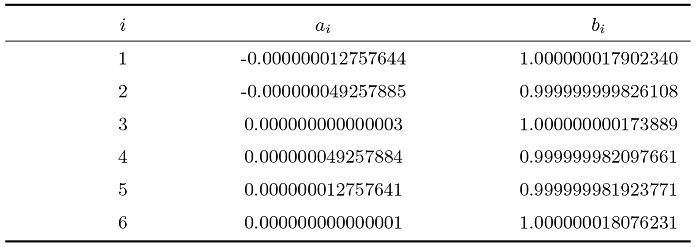
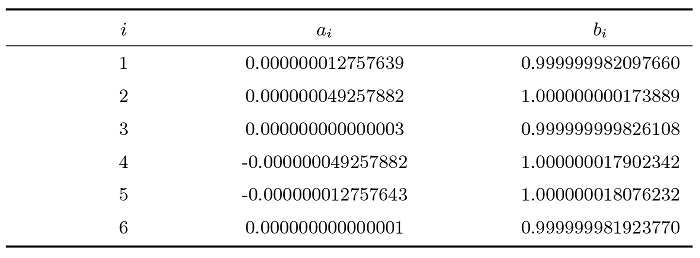
根据 $\boldsymbol{\lambda}$ $\boldsymbol{\mu}$ $\epsilon=-1$ . 由定理3.1可知, 公式3.1成立, 故该问题有解. 比较给出的数据可知, $v_{41}$ $v_{51}$ $2^2$ ${J}_{6}$ . 其非零元素如表1 -4 所示. 再计算 ${J}_{6}$ ${J}_{5}$ $\boldsymbol{\lambda}^{'}$ $\boldsymbol{\mu}^{'}$ $\boldsymbol{\lambda}$ $\boldsymbol{\mu}$ 表5 所示.
例 4.2 给定一个 $n$ $J_{n}$ $a_{i}=2, b_{i}=1$ $\epsilon=-1$ $n=10,20,50,100,500$ $\widehat{J}_{n}$ .
通过 Matlab 中的eig函数我们可以得出 $J_{n}$ $J_{n-1}$ $\widehat{J}_{n}$ $v_{j1}$ $\widehat{J}_{n}$ $\widehat{J}_{n-1}$ $\boldsymbol{\lambda}^{'}$ $\boldsymbol{\mu}^{'}$ $J_{n}$ $J_{n-1}$ $\boldsymbol{\lambda}$ $\boldsymbol{\mu}$ 表 6 所示. 数值结果表明所给算法对解决问题 PJIEP 是可行的.
5 结论
本文对依赖符号算子 $H=I_{r-1}\oplus(\epsilon)$ $J_{n}$ $J_{n}$ $J_{n-1}$ $\epsilon=\pm1$ $\boldsymbol{\lambda}$ $\boldsymbol{\mu}$ $\epsilon$
参考文献
View Option
[1]
Kodama Y Shipman B A . Fifty years of the finite nonperiodic Toda lattice: A geometric and topological viewpoint
J Phys A: Math Theor , 2018 , 51 35 ): 353001
[本文引用: 1]
[2]
Ferguson W E . The construction of Jacobi and periodic Jacobi matrices with prescribed spectra
Math Comp , 1980 , 35 1203 -1220
[本文引用: 3]
[3]
Bebiano N da Fonseca C M da Providência J . An inverse eigenvalue problem for periodic Jacobi matrices in Minkowski spaces
Linear Algebra Appl , 2011 , 435 2033 -2045
[本文引用: 3]
[4]
Boley D Golub G H . A modified method for reconstructing periodic Jacobi matrices
Math Comp , 1984 , 42 165 ): 143 -150
[本文引用: 2]
[5]
Xu S F . An introduction to inverse algebraic eigenvalue problems
Beijing: Peking University Press/Wiesbaden: Vieweg , 1998
[本文引用: 2]
[6]
Xu Y H Jiang E X . An inverse eigenvalue problem for periodic Jacobi matrices
Inverse Prob , 2007 , 23 1 ): 165 -181
[本文引用: 2]
[7]
Bebiano N da Providência J . Inverse spectral problems for structured pseudo-symmetric matrices
Linear Algebra Appl , 2013 , 438 10 ): 4062 -4074
[本文引用: 1]
[8]
Xu W R Bebiano N Chen G L . An inverse eigenvalue problem for modified pseudo-Jacobi matrices
J Comput Appl Math , 2021 , 389 113361
[本文引用: 2]
[9]
Xu W R Bebiano N Chen G L . An inverse eigenvalue problem for doubly periodic pseudo-Jacobi matrices
J Comput Appl Math , 2022 , 405 113957
[本文引用: 1]
[10]
Xu W R Bebiano N Chen G L . A reduction algorithm for reconstructing periodic Jacobi matrices in Minkowski spaces
Appl Math Comput , 2022 , 419 126853
[本文引用: 1]
Fifty years of the finite nonperiodic Toda lattice: A geometric and topological viewpoint
1
2018
... 使用文献[1 ]中著名的 Flaschka 变量替换 ...
The construction of Jacobi and periodic Jacobi matrices with prescribed spectra
3
1980
... 本文研究矩阵 $L$ $H=I_{r-1}\oplus(\epsilon)$ $\epsilon\in \{1,-1\}$ . 该类矩阵记为 $J_{n}$ . 当 $\epsilon=1$ $J_{n}$ [2 ] ; 当 $\epsilon=-1$ $J_{n}$ [3 ] . 对于周期 Jacobi 矩阵, 已经有了成熟的研究; 但对于周期伪 Jacobi 矩阵, 研究没有那么广泛. 然而其来源十分广泛, 经常出现在具有周期性边界条件的一维薛定谔方程的离散化和截断化中, 或者与非均匀环的振动有关[4 ] . 本文将考虑周期伪 Jacobi 矩阵 $J_{n}$
... Ferguson[2 ] 、 Boley 和 Golub[4 ] 、 徐树方[5 ] 、徐映红和蒋尔雄[6 ] 等学者分别对周期 Jacobi 矩阵逆特征值问题的数值解法进行了研究, 主要考虑从整个矩阵及其最大顺序主子矩阵的特征值和一个给定的正数来对周期 Jacobi 矩阵进行了重构. 目前, 对该问题的研究取得了丰富的成果.随着研究的不断发展, 周期伪 Jacobi 矩阵的逆特征值问题也逐渐引起了众多学者的兴趣. 相比于周期 Jacobi 矩阵而言, 周期伪 Jacobi 矩阵的研究成果较少. 为了推广在周期 Jacobi 矩阵情况下的一些经典理论, 周期伪 Jacobi 矩阵的逆特征值问题也值得关注. 目前, 该问题也取得了一定的进展 (参见文献[3 ,7 ⇓ ⇓ -10 ]). 本文是这一领域研究的延续. 主要研究如下的周期伪 Jacobi 矩阵的逆特征值问题. ...
... 不难发现 $v_{j1}$ $\sum\limits_{j=1}^{n-1}v_{j1}^{2}=1$ . 于是 $(v_{11},v_{21},\cdots,v_{n-1,1})^{\mathrm{T}}$ 2 ]中的 Lanczos 算法, 可以通过初始值 $\mu_{1},\mu_{2},\cdots,\mu_{n-1}$ $(v_{11},v_{21},\cdots,v_{n-1,1})^{\mathrm{T}}$ $J_{n-1}$ . 从而有 ...
An inverse eigenvalue problem for periodic Jacobi matrices in Minkowski spaces
3
2011
... 本文研究矩阵 $L$ $H=I_{r-1}\oplus(\epsilon)$ $\epsilon\in \{1,-1\}$ . 该类矩阵记为 $J_{n}$ . 当 $\epsilon=1$ $J_{n}$ [2 ] ; 当 $\epsilon=-1$ $J_{n}$ [3 ] . 对于周期 Jacobi 矩阵, 已经有了成熟的研究; 但对于周期伪 Jacobi 矩阵, 研究没有那么广泛. 然而其来源十分广泛, 经常出现在具有周期性边界条件的一维薛定谔方程的离散化和截断化中, 或者与非均匀环的振动有关[4 ] . 本文将考虑周期伪 Jacobi 矩阵 $J_{n}$
... Ferguson[2 ] 、 Boley 和 Golub[4 ] 、 徐树方[5 ] 、徐映红和蒋尔雄[6 ] 等学者分别对周期 Jacobi 矩阵逆特征值问题的数值解法进行了研究, 主要考虑从整个矩阵及其最大顺序主子矩阵的特征值和一个给定的正数来对周期 Jacobi 矩阵进行了重构. 目前, 对该问题的研究取得了丰富的成果.随着研究的不断发展, 周期伪 Jacobi 矩阵的逆特征值问题也逐渐引起了众多学者的兴趣. 相比于周期 Jacobi 矩阵而言, 周期伪 Jacobi 矩阵的研究成果较少. 为了推广在周期 Jacobi 矩阵情况下的一些经典理论, 周期伪 Jacobi 矩阵的逆特征值问题也值得关注. 目前, 该问题也取得了一定的进展 (参见文献[3 ,7 ⇓ ⇓ -10 ]). 本文是这一领域研究的延续. 主要研究如下的周期伪 Jacobi 矩阵的逆特征值问题. ...
... 引理 2.3 [3 ,6 ] 假设引理2.1的前提条件成立, 则 $\mu_{i}$ $J_{n}$
A modified method for reconstructing periodic Jacobi matrices
2
1984
... 本文研究矩阵 $L$ $H=I_{r-1}\oplus(\epsilon)$ $\epsilon\in \{1,-1\}$ . 该类矩阵记为 $J_{n}$ . 当 $\epsilon=1$ $J_{n}$ [2 ] ; 当 $\epsilon=-1$ $J_{n}$ [3 ] . 对于周期 Jacobi 矩阵, 已经有了成熟的研究; 但对于周期伪 Jacobi 矩阵, 研究没有那么广泛. 然而其来源十分广泛, 经常出现在具有周期性边界条件的一维薛定谔方程的离散化和截断化中, 或者与非均匀环的振动有关[4 ] . 本文将考虑周期伪 Jacobi 矩阵 $J_{n}$
... Ferguson[2 ] 、 Boley 和 Golub[4 ] 、 徐树方[5 ] 、徐映红和蒋尔雄[6 ] 等学者分别对周期 Jacobi 矩阵逆特征值问题的数值解法进行了研究, 主要考虑从整个矩阵及其最大顺序主子矩阵的特征值和一个给定的正数来对周期 Jacobi 矩阵进行了重构. 目前, 对该问题的研究取得了丰富的成果.随着研究的不断发展, 周期伪 Jacobi 矩阵的逆特征值问题也逐渐引起了众多学者的兴趣. 相比于周期 Jacobi 矩阵而言, 周期伪 Jacobi 矩阵的研究成果较少. 为了推广在周期 Jacobi 矩阵情况下的一些经典理论, 周期伪 Jacobi 矩阵的逆特征值问题也值得关注. 目前, 该问题也取得了一定的进展 (参见文献[3 ,7 ⇓ ⇓ -10 ]). 本文是这一领域研究的延续. 主要研究如下的周期伪 Jacobi 矩阵的逆特征值问题. ...
An introduction to inverse algebraic eigenvalue problems
2
1998
... Ferguson[2 ] 、 Boley 和 Golub[4 ] 、 徐树方[5 ] 、徐映红和蒋尔雄[6 ] 等学者分别对周期 Jacobi 矩阵逆特征值问题的数值解法进行了研究, 主要考虑从整个矩阵及其最大顺序主子矩阵的特征值和一个给定的正数来对周期 Jacobi 矩阵进行了重构. 目前, 对该问题的研究取得了丰富的成果.随着研究的不断发展, 周期伪 Jacobi 矩阵的逆特征值问题也逐渐引起了众多学者的兴趣. 相比于周期 Jacobi 矩阵而言, 周期伪 Jacobi 矩阵的研究成果较少. 为了推广在周期 Jacobi 矩阵情况下的一些经典理论, 周期伪 Jacobi 矩阵的逆特征值问题也值得关注. 目前, 该问题也取得了一定的进展 (参见文献[3 ,7 ⇓ ⇓ -10 ]). 本文是这一领域研究的延续. 主要研究如下的周期伪 Jacobi 矩阵的逆特征值问题. ...
... 引理 2.1 [5 ] 已知 $\mu_{1}<\cdots<\mu_{n-1}$ $J_{n-1}$ $v_{i}=(v_{i1},v_{i2},\cdots,v_{i,n-1})^\mathrm{T}$ $\mu_{i}$
An inverse eigenvalue problem for periodic Jacobi matrices
2
2007
... Ferguson[2 ] 、 Boley 和 Golub[4 ] 、 徐树方[5 ] 、徐映红和蒋尔雄[6 ] 等学者分别对周期 Jacobi 矩阵逆特征值问题的数值解法进行了研究, 主要考虑从整个矩阵及其最大顺序主子矩阵的特征值和一个给定的正数来对周期 Jacobi 矩阵进行了重构. 目前, 对该问题的研究取得了丰富的成果.随着研究的不断发展, 周期伪 Jacobi 矩阵的逆特征值问题也逐渐引起了众多学者的兴趣. 相比于周期 Jacobi 矩阵而言, 周期伪 Jacobi 矩阵的研究成果较少. 为了推广在周期 Jacobi 矩阵情况下的一些经典理论, 周期伪 Jacobi 矩阵的逆特征值问题也值得关注. 目前, 该问题也取得了一定的进展 (参见文献[3 ,7 ⇓ ⇓ -10 ]). 本文是这一领域研究的延续. 主要研究如下的周期伪 Jacobi 矩阵的逆特征值问题. ...
... 引理 2.3 [3 ,6 ] 假设引理2.1的前提条件成立, 则 $\mu_{i}$ $J_{n}$
Inverse spectral problems for structured pseudo-symmetric matrices
1
2013
... Ferguson[2 ] 、 Boley 和 Golub[4 ] 、 徐树方[5 ] 、徐映红和蒋尔雄[6 ] 等学者分别对周期 Jacobi 矩阵逆特征值问题的数值解法进行了研究, 主要考虑从整个矩阵及其最大顺序主子矩阵的特征值和一个给定的正数来对周期 Jacobi 矩阵进行了重构. 目前, 对该问题的研究取得了丰富的成果.随着研究的不断发展, 周期伪 Jacobi 矩阵的逆特征值问题也逐渐引起了众多学者的兴趣. 相比于周期 Jacobi 矩阵而言, 周期伪 Jacobi 矩阵的研究成果较少. 为了推广在周期 Jacobi 矩阵情况下的一些经典理论, 周期伪 Jacobi 矩阵的逆特征值问题也值得关注. 目前, 该问题也取得了一定的进展 (参见文献[3 ,7 ⇓ ⇓ -10 ]). 本文是这一领域研究的延续. 主要研究如下的周期伪 Jacobi 矩阵的逆特征值问题. ...
An inverse eigenvalue problem for modified pseudo-Jacobi matrices
2
2021
... Ferguson[2 ] 、 Boley 和 Golub[4 ] 、 徐树方[5 ] 、徐映红和蒋尔雄[6 ] 等学者分别对周期 Jacobi 矩阵逆特征值问题的数值解法进行了研究, 主要考虑从整个矩阵及其最大顺序主子矩阵的特征值和一个给定的正数来对周期 Jacobi 矩阵进行了重构. 目前, 对该问题的研究取得了丰富的成果.随着研究的不断发展, 周期伪 Jacobi 矩阵的逆特征值问题也逐渐引起了众多学者的兴趣. 相比于周期 Jacobi 矩阵而言, 周期伪 Jacobi 矩阵的研究成果较少. 为了推广在周期 Jacobi 矩阵情况下的一些经典理论, 周期伪 Jacobi 矩阵的逆特征值问题也值得关注. 目前, 该问题也取得了一定的进展 (参见文献[3 ,7 ⇓ ⇓ -10 ]). 本文是这一领域研究的延续. 主要研究如下的周期伪 Jacobi 矩阵的逆特征值问题. ...
... 引理 2.2 [8 ] 已知一个在复共轭下封闭的集合 $\boldsymbol{\lambda}=\left\{\lambda_{1},\lambda_{2},\cdots,\lambda_{n}\right\}$ $\boldsymbol{\mu}=\left\{\mu_{1},\mu_{2},\cdots,\mu_{n-1}\right\}$ $\mu_{i} \notin \boldsymbol{\lambda}$
An inverse eigenvalue problem for doubly periodic pseudo-Jacobi matrices
1
2022
... Ferguson[2 ] 、 Boley 和 Golub[4 ] 、 徐树方[5 ] 、徐映红和蒋尔雄[6 ] 等学者分别对周期 Jacobi 矩阵逆特征值问题的数值解法进行了研究, 主要考虑从整个矩阵及其最大顺序主子矩阵的特征值和一个给定的正数来对周期 Jacobi 矩阵进行了重构. 目前, 对该问题的研究取得了丰富的成果.随着研究的不断发展, 周期伪 Jacobi 矩阵的逆特征值问题也逐渐引起了众多学者的兴趣. 相比于周期 Jacobi 矩阵而言, 周期伪 Jacobi 矩阵的研究成果较少. 为了推广在周期 Jacobi 矩阵情况下的一些经典理论, 周期伪 Jacobi 矩阵的逆特征值问题也值得关注. 目前, 该问题也取得了一定的进展 (参见文献[3 ,7 ⇓ ⇓ -10 ]). 本文是这一领域研究的延续. 主要研究如下的周期伪 Jacobi 矩阵的逆特征值问题. ...
A reduction algorithm for reconstructing periodic Jacobi matrices in Minkowski spaces
1
2022
... Ferguson[2 ] 、 Boley 和 Golub[4 ] 、 徐树方[5 ] 、徐映红和蒋尔雄[6 ] 等学者分别对周期 Jacobi 矩阵逆特征值问题的数值解法进行了研究, 主要考虑从整个矩阵及其最大顺序主子矩阵的特征值和一个给定的正数来对周期 Jacobi 矩阵进行了重构. 目前, 对该问题的研究取得了丰富的成果.随着研究的不断发展, 周期伪 Jacobi 矩阵的逆特征值问题也逐渐引起了众多学者的兴趣. 相比于周期 Jacobi 矩阵而言, 周期伪 Jacobi 矩阵的研究成果较少. 为了推广在周期 Jacobi 矩阵情况下的一些经典理论, 周期伪 Jacobi 矩阵的逆特征值问题也值得关注. 目前, 该问题也取得了一定的进展 (参见文献[3 ,7 ⇓ ⇓ -10 ]). 本文是这一领域研究的延续. 主要研究如下的周期伪 Jacobi 矩阵的逆特征值问题. ...
