1 引言
u t − u x x t − 2 u 2 u x + 3 u x u x x − u u x x x = 0 ,
(1.1)
u t + 2 k u x − u x x t + ( b + 1 ) u n u x − b u x u x x − u u x x x = 0
(1.2)
的特殊情况, 即方程(1.2)中参数 b = − 3 k = 0 n = 2 .
当 b = 2 n = 1 [1 ] 在 1993 年提出的著名浅水波方程 CH 方程.当 k = 0 [1 ] 提出 CH 方程具有可积性并且有孤立尖波解.Cooper 和 Shepard[2 ] 研究了 CH 方程的近似孤立波解.Constantin 和 Strauss[3 ] 给出了 CH 方程孤立波的存在性及其数学解释, 并证明了 k = 0 b = 3 n = 1 [4 ] 提出的 DP 方程.Lundmark 和 Szmigielski[5 ] 利用反散射法计算出 DP 方程 3 次孤立尖波解的精确表达式. Chen 和 Tang[6 ] 得到了 DP 方程的扭波解.
CH 方程和 DP 方程引起了学者们广泛的兴趣, 在这两个方程的研究基础上,针对不同的参数 b n c b > 1 n = 1 [7 ] 证明了方程(1.2)具有周期性尖波解,Li[8 ] 讨论了方程(1.2)Cauchy 问题的非均匀依赖性,Freire[9 ] 给出了方程(1.2)在 Sobolev 空间中强解的全局存在性.对于给定 b = 2 n = 2 [10 ] 给出了方程(1.2)的一些物理解释,Liu 和 Ouyang[11 ] 得到了 c = 2 c = 1 [12 ] 给出了由三角函数组成的奇异波解,Daros 和 Arruda[13 ] 研究了椭圆行波解的不稳定性.当 b = 2 n = 3 [14 ] 得到了三次 CH 方程多种行波解的精确表达式.当 b = 3 n = 2 [11 ] 得到了 c = 5 2 [15 ] 研究了周期波解及其分支.当 b ≠ 2 c = b + 2 2 [16 ] 得到了两种孤立波解及其表达式.当 b ≠ 0 , − 2 , − 3 [17 ] 研究了显式周期波及其极限形式.当 b = 0 n = 2 [18 ] 研究了方程(1.2)的孤立波解及周期波解, 并给出了解之间的相关联系.当 k = 0 b > 1 n [19 ] 考虑了方程(1.2)孤立尖波解的存在性及其分支.当 k = 0 b = 0 n = 2 [21 ] 研究了方程(1.2)的精确解及其分支,Li 和 Liu[21 ] 得到了方程五种类型的爆破波解并发现了它们之间的关系.
本文利用定性分析及分支方法研究了方程(1.1)孤立波和周期波的存在性及其显式表达式, 并发现了不同于 b > 0
2 行波系统和分支相图
在本节中, 先利用行波变换推导出方程(1.1)的行波系统, 再研究了该系统的奇点性质及分支曲线, 最后得到了系统的分支相图.
2.1 行波系统及其动力学分析
假设波速 c u = φ ( ξ ) ξ = x − c t
− c φ ′ + c φ ‴ − 2 φ 2 φ ′ + 3 φ ′ φ ″ − φ φ ‴ = 0.
(2.1)
( φ − c ) φ ″ = g − c φ − 2 3 φ 3 + 2 ( φ ′ ) 2 ,
其中 g y = φ ′
{ d φ d ξ = y , d y d ξ = g − c φ − 2 3 φ 3 + 2 y 2 φ − c .
(2.2)
行波系统(2.2)具有一条奇异直线 φ = c d τ = d ξ φ − c
{ d φ d τ = ( φ − c ) y , d y d τ = g − c φ − 2 3 φ 3 + 2 y 2 .
(2.3)
显而易见, 行波系统 (2.2) 和 (2.3) 具有相同的首次积分
H ( φ , y ) = h = ( φ − c ) − 4 { y 2 − 4 3 [ ( φ − c ) 3 + ˉ a 2 2 ( φ − c ) 2 + ˉ a 1 3 ( φ − c ) + ˉ a 0 4 ] } ,
(2.4)
ˉ a 2 = 3 c , ˉ a 1 = 3 2 ( 2 c 2 + c ) , ˉ a 0 = 1 2 ( 2 c 3 + 3 c 2 − 3 g ) ,
相同的首次积分 H ( φ , y ) φ = c
根据系统 (2.3) 的第一个方程, 易得该系统的奇点在 φ φ = c
f ( φ ) = g − c φ − 2 3 φ 3 , f 0 ( φ ) = − c φ − 2 3 φ 3 .
f ′ 0 ( φ ) = − c − 2 φ 2
易知, f ′ 0 ( φ ) ( ± φ 0 , 0 ) φ 0 = √ − c 2 ( ± φ 0 , f ( ± φ 0 ) ) f ( φ )
由系统 (2.3) 的奇点个数及性质, 可得该系统有四条分支曲线 g 1 ( c ) − g 1 ( c ) g 2 ( c ) g 3 ( c )
g 1 ( c ) = 1 6 ( − 2 c ) 3 2 , g 2 ( c ) = 2 3 c 3 + c 2 , g 3 ( c ) = 1 24 ( 12 c 2 − 8 c 3 + 9 c 2 √ c 2 − 4 c − ( c 2 − 4 c ) 3 2 ) .
分支曲线 g 2 ( c ) g 1 ( c ) ( c 1 , g 1 ( c 1 ) ) ( 0 , 0 ) g 2 ( c ) − g 1 ( c ) ( c 2 , g 2 ( c 2 ) ) ( 0 , 0 ) g 3 ( c ) g 1 ( c ) ( c 1 , g 1 ( c 1 ) ) ( 0 , 0 ) g 3 ( c ) g 2 ( c ) ( c 1 , g 1 ( c 1 ) ) ( 0 , 0 ) c 1 = − 1 2 , c 2 = − 2 .
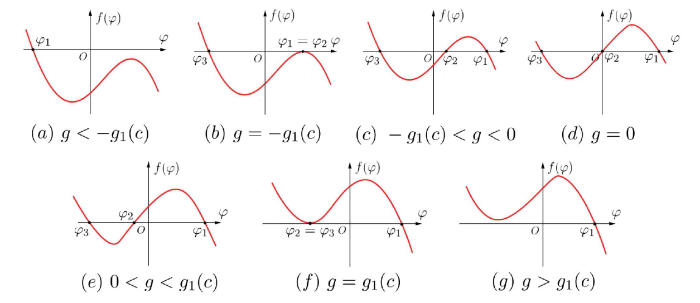
为了说明系统 (2.3) 的奇点情况, 首先计算在 φ f ( φ ) φ 1 φ 2 φ 3 φ 3 ≤ φ 2 ≤ φ 1 ) ,
1) 当 g > g 1 ( c ) g < − g 1 ( c ) f ( φ ) = 0
φ 1 = ( 6 g − √ Δ ) 1 3 + ( 6 g + √ Δ ) 1 3 2 ,
2) 当 g = g 1 ( c ) f ( φ ) = 0
φ 1 = − 3 g c , φ 2 = φ 3 = 3 g 2 c .
3) 当 g = − g 1 ( c ) f ( φ ) = 0
φ 3 = − 3 g c , φ 1 = φ 2 = 3 g 2 c .
4) 当 − g 1 ( c ) < g < g 1 ( c ) f ( φ ) = 0
φ 1 = √ − 2 c cos θ 3 , φ 2 = − √ − c 2 ( cos θ 3 − √ 3 sin θ 3 ) , φ 3 = − √ − c 2 ( cos θ 3 + √ 3 sin θ 3 ) ,
事实上, 由上述奇点分析可得 f ( φ ) 图1 所示).
图1
此外, 当 g ≤ g 2 ( c ) φ = c ( c , ± y 0 )
y 0 = √ 1 3 c 3 + 1 2 c 2 − 1 2 g .
因此, ( φ i , 0 ) ( i = 1 , 2 , 3 ) ( c , ± y 0 )
下面研究系统 (2.3) 的奇点性质. 系统 (2.3) 的线性化系统有如下 Jacobi 矩阵
J ( φ , y ) = ( y φ − c f ′ ( φ ) 4 y ) ,
| J − λ I | = | y − λ φ − c f ′ ( φ ) 4 y − λ | = λ 2 − y 2 − ( φ − c ) f ′ ( φ ) = 0.
因此, 在 φ ( φ i , 0 )
λ ± ( φ i , 0 ) = ± √ ( φ i − c ) f ′ ( φ i ) ( i = 1 , 2 , 3 ) .
同时, 在奇直线 φ = c ( c , ± y 0 )
λ 1 ( c , y 0 ) = y 0 , λ 2 ( c , y 0 ) = 4 y 0 , λ 1 ( c , − y 0 ) = − y 0 , λ 2 ( c , − y 0 ) = − 4 y 0 .
通过系统 (2.3) 奇点的特征值分析, 由平面定性理论可知, 当 ( φ i − c ) f ′ ( φ i ) > 0 ( φ i , 0 ) ( φ i − c ) f ′ ( φ i ) = 0 ( φ i , 0 ) ( φ i − c ) f ′ ( φ i ) < 0 ( φ i , 0 ) ( c , y 0 ) ( c , − y 0 )
2.2 系统 (2.3) 的分支相图
由 2.1 小节中系统 (2.3) 的动力学分析, 本小节给出了系统奇点的具体分类, 并进一步得到了在 c − g
(1) 当 g > g 1 ( c ) f ( φ ) φ 1 φ 1 > c ( φ 1 , 0 )
(2) 当 g = g 1 ( c ) f ( φ ) φ 1 φ 2 = φ 3
若 0 < c < c 1 , φ 3 = φ 2 < c < φ 1 , 若 c = c 1 , φ 3 = φ 2 = c < φ 1 , 若 c > c 1 , c < φ 3 = φ 2 < φ 1 .
所以, 在系统 (2.3)中 ( φ 1 , 0 ) ( φ 2 , 0 )
(3) 当 − g 1 ( c ) < g < g 1 ( c ) g > g 2 ( c ) f ( φ ) φ 1 φ 2 φ 3
若 0 > c > c 1 , φ 3 < φ 2 < c < φ 1 , 若 c < c 1 , φ 1 < φ 2 < φ 3 < c .
因此, 若 0 > c > c 1 ( φ 1 , 0 ) ( φ 2 , 0 ) ( φ 3 , 0 ) c < c 1 ( φ 1 , 0 ) ( φ 3 , 0 ) ( φ 2 , 0 )
(4) 当 − g 1 ( c ) < g < g 1 ( c ) g = g 2 ( c ) f ( φ ) φ 1 φ 2 φ 3
若 c 1 < c < 0 , φ 3 < φ 2 = c < φ 1 , 若 c 2 < c < c 1 , φ 3 = c < φ 2 < φ 1 .
所以, 我们可以得到结论: 若 c 1 < c < 0 ( φ 1 , 0 ) ( φ 2 , 0 ) ( φ 3 , 0 ) c 2 < c < c 1 ( φ 1 , 0 ) ( φ 2 , 0 ) ( φ 3 , 0 )
(5) 当 g 3 ( c ) < g < g 2 ( c ) c 1 < c < 0 f ( φ ) φ 1 φ 2 φ 3
φ 3 < c < φ 2 < φ 1 ,
这意味着, 在系统 (2.3)中 ( φ 1 , 0 ) ( φ 2 , 0 ) ( φ 3 , 0 )
(6) 当 g = g 3 ( c ) c 1 < c < 0 f ( φ ) φ 1 φ 2 φ 3 φ 3 < c < φ 2 < φ 1 ( φ 1 , 0 ) ( φ 2 , 0 ) ( φ 3 , 0 )
当 g = g 3 ( c ) c < c 1 f ( φ ) φ 1 φ 1 > c ( φ 1 , 0 )
(7) 当 − g 1 ( c ) < g < g 3 ( c ) g < g 2 ( c ) f ( φ ) φ 1 φ 2 φ 3
若 c 2 < c < 0 , φ 1 < φ 2 < c < φ 3 .
这意味着, 在系统 (2.3)中 (\varphi_1,0) (\varphi_2,0) (\varphi_3,0)
(8) 当 g=-g_1(c) f(\varphi) \varphi_1=\varphi_2 \varphi_3
\begin{align*}&\mbox{若}\ c_2<c<0,\ \ \varphi_1<c<\varphi_2=\varphi_1,\\&\mbox{若}\ c=c_2,\ \ \varphi_3=c<\varphi_2=\varphi_1,\\&\mbox{若}\ c<c_2,\ \ c<\varphi_3<\varphi_2=\varphi_1.\end{align*}
通过不等式和对应特征值, 可知若 c_2<c<0 (\varphi_1,0) (\varphi_3,0) c=c_2 (\varphi_1,0) (\varphi_3,0) c<c_2 (\varphi_1,0) (\varphi_3,0)
(9) 当 g<-g_1(c) f(\varphi) \varphi_1
\begin{align*}&\mbox{若}\ g<g_2(c),\ \ \varphi_1<c,\\&\mbox{若}\ g=g_2(c),\ \ \varphi_1=c,\\&\mbox{若}\ g>g_2(c),\ \ \varphi_1>c.\end{align*}
因此, 奇点 (\varphi_1,0) g<-g_1(c) g<g_2(c) (\varphi_1,0) g=g_2(c)<-g_1(c) (\varphi_1,0) g_2(c)<g<-g_1(c) (\varphi_1,0)
(10) 当 g\le g_2(c) (c, \pm y_0) (c, y_0) (c, -y_0)
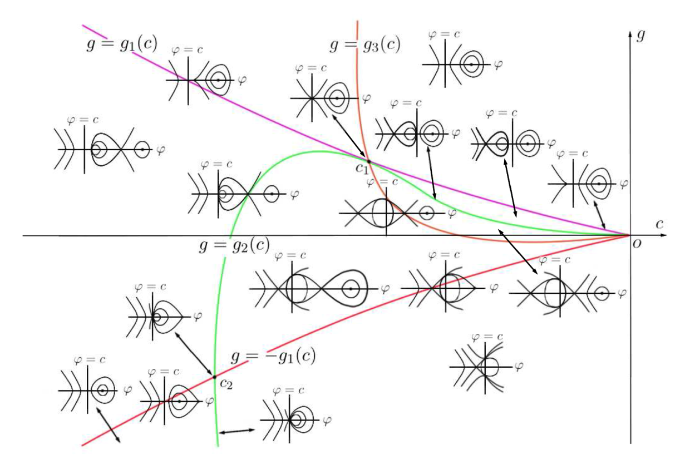
根据系统 (2.3) 的奇点性质 (1)-(10) 以及分支曲线 g_1(c) -g_1(c) g_2(c) c-g 图2 所示. 从奇点性质 (4)-(10) 和分支相图, 不难看出系统 (2.3) 有无限多闭轨穿过奇异直线 \varphi=c .
图 2
3 孤立波的存在性与表达式
本节讨论系统 (2.3) 中孤立波的存在性, 并给出了存在的参数条件及表达式. 由分支相图以及动力系统分支理论中同宿轨对应方程(1.1)的孤立波, 可以得到以下命题.
命题 3.1 对于给定波速 c (c<0) g
情形 A g_2(c)<g<g_1(c) c_1<c<0 .
情形 C g_3(c)<g<g_2(c) c_1<c<0 .
情形 D -g_1(c)<g<g_3(c) g<g_2(c) c_2<c<0 .
情形 E g_2(c)<g<g_1(c) g>-g_1(c) c<c_1 .
情形 F g=g_2(c) c_2<c<c_1 .
情形 H -g_1(c)<g<g_3(c) g<g_2(c) c_2<c<0 .
不难看出, 当 -g_1(c)<g<g_3(c) g<g_2(c) c_2<c<0
\begin{align*}& H_1=H(\varphi_1,0),\ H_2=H(\varphi_2,0),\ H_3=H(\varphi_3,0),\\& w_1=\sqrt{4-6\bar{a}_2H_3-18c^2H_3^2-12H_3\varphi_3-18H_3^2\varphi_3^2+12cH_3+36cH_3^2\varphi_3^2},\\& w_2=\sqrt{4-6\bar{a}_2H_2-18c^2H_2^2-12H_2\varphi_2-18H_2^2\varphi_2^2+12cH_2+36cH_2^2\varphi_2^2},\\&\alpha_1=\alpha_4=\frac{-2+6cH_3-3H_3\varphi_3+w_1}{3H_3},\ \alpha_2=\alpha_5=\frac{-2+6cH_3-3H_3\varphi_3-w_1}{3H_3},\\ & \alpha_3=\frac{-4+9cH_3-6H_3\varphi_3}{3H_3},\ \alpha_6=\alpha_8=\frac{-2+6cH_2-3H_2\varphi_2+w_2}{3H_2}, \\& \alpha_7=\alpha_9=\frac{-2+6cH_3-3H_2\varphi_2-w_2}{3H_2},\ \alpha_{10}=\frac{-4+9cH_2-6H_2\varphi_2}{3H_2}.\end{align*}
命题 3.2 对于不同的波速 c (c<0) g
(1) 当 g_2(c)<g<g_1(c) c_1<c<0
\begin{equation}u_1(\xi)=\varphi_3+\frac{4\mu_1 a_1 {\rm e}^{-\eta_1 \xi}}{\mu_1^2 {\rm e}^{-2\eta_1 \xi}+b_1^2-2\mu_1 b_1 {\rm e}^{-\eta_1 \xi}-4a_1},\end{equation}
(3.1)
\begin{align*}&a_1=(\alpha_1-\varphi_3)(\alpha_2-\varphi_3), \ b_1=2\varphi_3-\alpha_1-\alpha_2,\\&\eta_1=\sqrt{a_1H_3},\ \chi_1=(\alpha_2-\varphi_3)^2+b_1(\alpha_2-\varphi_3)+a_1, \\&\mu_1=\frac{2\sqrt{a_ 1\chi_1}+b_1(\alpha_2-\varphi_3)+2a_1}{\alpha_2-\varphi_3}.\end{align*}
(2) 当 g=g_2(c) c_1<c<0
\begin{equation}u_2(\xi)=\varphi_3+\frac{4\mu_2 a_2 {\rm e}^{-\eta_2 \xi}}{\mu_2^2 {\rm e}^{-2\eta_2 \xi}+b_2^2-2\mu_2 b_2 {\rm e}^{-\eta_2 \xi}-4a_2},\end{equation}
(3.2)
\begin{align*}&a_2=(c-\varphi_3)(\alpha_3-\varphi_3), \ b_2=2\varphi_3-c-\alpha_3,\\&\eta_2=\sqrt{a_2H_3},\ \chi_2=(c-\varphi_3)^2+b_2(c-\varphi_3)+a_2, \\&\mu_2=\frac{2\sqrt{a_ 2\chi_2}+b_2(c-\varphi_3)+2a_2}{c-\varphi_3}.\end{align*}
(3) 当 g_3(c)<g<g_2(c) c_1<c<0
\begin{equation}u_3(\xi)=\varphi_3+\frac{4\mu_3 a_3 {\rm e}^{-\eta_3 \xi}}{\mu_3^2 {\rm e}^{-2\eta_3 \xi}+b_3^2-2\mu_3 b_3 {\rm e}^{-\eta_3 \xi}-4a_3},\end{equation}
(3.3)
\begin{align*}&a_3=(\varphi_3-\alpha_4)(\varphi_3-\alpha_5), \ b_3=2\varphi_3-\alpha_4-\alpha_5,\\&\eta_3=\sqrt{a_3H_3},\ \chi_3=(\alpha_5-\varphi_3)^2+b_3(\alpha_5-\varphi_3)+a_3, \\&\mu_3=\frac{2\sqrt{a_ 3\chi_3}+b_3(\alpha_5-\varphi_3)+2a_3}{\alpha_5-\varphi_3}.\end{align*}
(4) 当 -g_1(c)<g<g_3(c) g<g_2(c) c_2<c<0
\begin{equation}u_4(\xi)=\varphi_2+\frac{4\mu_4 a_4 {\rm e}^{\eta_4 \xi}}{\mu_4^2 {\rm e}^{2\eta_4 \xi}+b_4^2+4a_4-2\mu_4 b_4 {\rm e}^{\eta_4 \xi}},\end{equation}
(3.4)
\begin{align*}&a_4=(\alpha_6-\varphi_2)(\varphi_2-\alpha_7), \ b_4=\alpha_6+\alpha_7-2\varphi_2,\\&\eta_4=\sqrt{-a_4H_2},\ \chi_4=-(\alpha_6-\varphi_2)^2+b_4(\alpha_6-\varphi_2)+a_4, \\&\mu_4=\frac{2\sqrt{a_4\chi_4}+b_4(\alpha_6-\varphi_2)+2a_4}{\alpha_6-\varphi_2}.\end{align*}
(5) 当 g_2(c)<g<g_1(c) g>-g_1(c) c<c_1
\begin{equation}u_5(\xi)=\varphi_2-\frac{4\mu_5 a_5 {\rm e}^{\eta_5 \xi}}{\mu_5^2 {\rm e}^{2\eta_5 \xi}+b_5^2-2\mu_5 b_5 {\rm e}^{\eta_5 \xi}-4a_5},\end{equation}
(3.5)
\begin{align*}&a_5=(\varphi_2-\alpha_8)(\varphi_2-\alpha_9), \ b_5=\alpha_8+\alpha_9-2\varphi_2,\\&\eta_5=\sqrt{a_5H_2},\ \chi_5=(\varphi_2-\alpha_9)^2+b_5(\varphi_2-\alpha_9)+a_5, \\&\mu_5=\frac{2\sqrt{a_5\chi_5}+b_5(\varphi_2-\alpha_9)+2a_5}{\varphi_2-\alpha_9}.\end{align*}
(6) 当 g=g_2(c) c_2<c<c_1
\begin{equation}u_6(\xi)=\varphi_2-\frac{4\mu_6 a_6 {\rm e}^{\eta_6 \xi}}{\mu_6^2 {\rm e}^{2\eta_6 \xi}+b_6^2-2\mu_6 b_6 {\rm e}^{\eta_6 \xi}-4a_6},\end{equation}
(3.6)
\begin{align*}&a_6=(\varphi_2-c)(\varphi_2-\alpha_{10}), \ b_6=c+\alpha_{10}-2\varphi_2,\\&\eta_6=\sqrt{a_6 H_2},\ \chi_6=(\varphi_2-c)^2+b_6(\varphi_2-c)+a_6, \\&\mu_6=\frac{2\sqrt{a_6\chi_6}+b_6(\varphi_2-c)+2a_6}{\varphi_2-c}.\end{align*}
(7) 当 g=g_2(c) c=c_2=-2
\begin{equation}u_7(\xi)=1-\frac{12}{4-9H_1 \xi^2}.\end{equation}
(3.7)
(8) 当 -g_1(c)<g<g_2(c) c_2<c<0
\begin{equation}u_8(\xi)=\varphi_2-\frac{4\mu_8 a_8 {\rm e}^{\eta_8 \xi}}{\mu_8^2 {\rm e}^{2\eta_8 \xi}+b_8^2+4a_8-2\mu_8b_8 {\rm e}^{\eta_8 \xi}},\end{equation}
(3.8)
\begin{align*}&a_8=(\varphi_2-\alpha_6)(\alpha_7-\varphi_2), \ b_8=2\varphi_2-\alpha_6-\alpha_7,\\&\eta_8=\sqrt{-a_8H_2},\ \chi_8=(\varphi_2-\alpha_7)^2+b_8(\varphi_2-\alpha_7)+a_8, \\&\mu_8=\frac{2\sqrt{a_8\chi_8}+b_8(\varphi_2-\alpha_7)+2a_8}{\varphi_2-\alpha_7}.\end{align*}
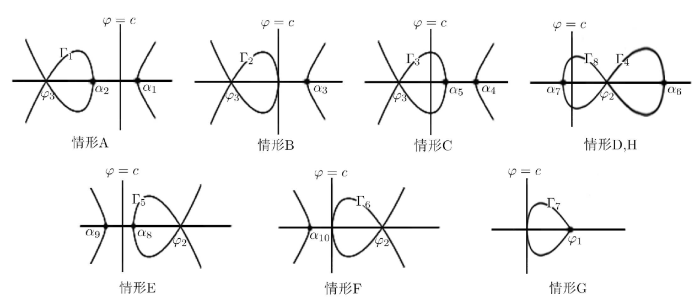
为了方便给出命题3.2中孤立波解的推导过程, 我们做出情形 A-H 下行波系统 (2.3) 的同宿轨道相图, 如图3 .
图3
(1) 当 g_2(c)<g<g_1(c) c_1<c<0 \Gamma_1 图3A ), \Gamma_1
\begin{equation*}y^2=H(\varphi_3,0)(\alpha_1-\varphi)(\alpha_2-\varphi)(\varphi-\varphi_3)^2,\ \mbox{且}\ \varphi_3<\varphi<\alpha_2<\alpha_1.\end{equation*}
易得 y \frac{\mathrm{d}\varphi}{y}=\mathrm{d}\xi \Gamma_1
\begin{equation}\int_{\alpha_2}^{\varphi}\frac{\mathrm{d}s}{(s-\varphi_3)\sqrt{(\alpha_1-s)(\alpha_2-s)}}=\sqrt{H(\varphi_3,0)}|\xi|.\end{equation}
(3.9)
在(3.9)式中, 计算积分并关于 \varphi
\begin{equation*}\varphi=\varphi_3+\frac{4\mu_1 a_1 {\rm e}^{-\eta_1 \xi}}{\mu_1^2 {\rm e}^{-2\eta_1 \xi}+b_1^2-2\mu_1 b_1 {\rm e}^{-\eta_1 \xi}-4a_1},\end{equation*}
由 u=\varphi(\xi) u_1(\xi)
(2) 当 g=g_2(c) c_1<c<0 \Gamma_2 图3B ), \Gamma_2
\begin{equation*}y^2=H(\varphi_3,0)(\alpha_3-\varphi)(c-\varphi)(\varphi-\varphi_3)^2,\ \mbox{且}\ \varphi_3<\varphi<c<\alpha_3.\end{equation*}
计算可得 y \frac{\mathrm{d}\varphi}{y}=\mathrm{d}\xi \Gamma_2
\begin{equation}\int_{c}^{\varphi}\frac{\mathrm{d}s}{(s-\varphi_3)\sqrt{(\alpha_3-s)(c-s)}}=\sqrt{H(\varphi_3,0)}|\xi|.\end{equation}
(3.10)
在 (3.10) 式中, 计算积分并关于 \varphi u_2(\xi)
(3) 当 g_3(c)<g<g_2(c) c_1<c<0 \Gamma_3 图3C ), \Gamma_3
\begin{equation*}y^2=H(\varphi_3,0)(\alpha_4-\varphi)(\alpha_5-\varphi)(\varphi-\varphi_3)^2,\ \mbox{且}\ \varphi_3<\varphi<\alpha_5<\alpha_4.\end{equation*}
由上式可知 y \frac{\mathrm{d}\varphi}{y}=\mathrm{d}\xi \Gamma_3
\begin{equation}\int_{\alpha_5}^{\varphi}\frac{\mathrm{d}s}{(s-\varphi_3)\sqrt{(\alpha_4-s)(\alpha_5-s)}}=\sqrt{H(\varphi_3,0)}|\xi|.\end{equation}
(3.11)
在(3.11)式中, 计算积分并关于 \varphi u_3(\xi)
(4) 当-g_1(c)<g<g_3(c) g<g_2(c) c_2<c<0 \Gamma_4 图3D ) 和\Gamma_8 图3H ), 分别有如下表达式
\begin{equation*}\Gamma_4:\ y^2=-H(\varphi_2,0)(\alpha_6-\varphi)(\varphi-\alpha_7)(\varphi-\varphi_2)^2,\ \mbox{且}\ \alpha_7<\varphi_2<\varphi<\alpha_6,\end{equation*}
\begin{equation*}\Gamma_8:\ y^2=-H(\varphi_2,0)(\varphi_2-\varphi)^2(\alpha_6-\varphi)(\varphi-\alpha_7),\ \mbox{且}\ \alpha_7<\varphi<\varphi_2<\alpha_6.\end{equation*}
同理, 分别将 y \frac{\mathrm{d}\varphi}{y}=\mathrm{d}\xi \Gamma_4 \Gamma_8
\begin{equation}\int_{\varphi}^{\alpha_6}\frac{\mathrm{d}s}{(s-\varphi_2)\sqrt{(\alpha_6-s)(s-\alpha_7)}}=\sqrt{-H(\varphi_2,0)}|\xi|,\end{equation}
(3.12)
\begin{equation}\int_{\alpha_7}^{\varphi}\frac{\mathrm{d}s}{(\varphi_2-s)\sqrt{(\alpha_6-s)(s-\alpha_7)}}=\sqrt{-H(\varphi_2,0)}|\xi|,\end{equation}
(3.13)
关于 \varphi u_4(\xi) u_8(\xi)
(5) 当 g_2(c)<g<g_1(c) g>-g_1(c) c<c_1 \Gamma_5 图3E ), \Gamma_5
\begin{equation*}y^2=H(\varphi_2,0)(\varphi-\varphi_2)^2(\varphi-\alpha_8)(\varphi-\alpha_9),\ \mbox{且}\ \alpha_9<\alpha_8<\varphi<\varphi_3.\end{equation*}
易得 y \frac{\mathrm{d}\varphi}{y}=\mathrm{d}\xi \Gamma_5
\begin{equation}\int_{\alpha_8}^{\varphi}\frac{\mathrm{d}s}{(\varphi_2-s)\sqrt{(s-\alpha_8)(s-\alpha_9)}}=\sqrt{H(\varphi_2,0)}|\xi|.\end{equation}
(3.14)
在 (3.14) 式中, 计算积分并关于 \varphi u_5(\xi)
(6) 当 g=g_2(c) c_2<c<c_1 \Gamma_6 图3F ), \Gamma_6
\begin{equation*}y^2=H(\varphi_2,0)(\varphi_2-\varphi)^2(\varphi-c)(\varphi-\alpha_{10}),\ \mbox{且}\ \alpha_{10}<c<\varphi<\varphi_2.\end{equation*}
计算上式可得 y \frac{\mathrm{d}\varphi}{y}=\mathrm{d}\xi \Gamma_6
\begin{equation}\int_{c}^{\varphi}\frac{\mathrm{d}s}{(\varphi_2-s)\sqrt{(s-c)(s-\alpha_{10})}}=\sqrt{H(\varphi_2,0)}|\xi|.\end{equation}
(3.15)
在 (3.15) 式中, 计算积分并关于 \varphi u_6(\xi)
(7) 当 g=g_2(c) c=c_2=-2 \Gamma_7 图3G ), \Gamma_7
\begin{equation*}y^2=-H(\varphi_1,0)(\varphi_1-\varphi)^2(\varphi-c)(1-\varphi),\ \mbox{且}\ c<\varphi<\varphi_1=1.\end{equation*}
易得 y \frac{\mathrm{d}\varphi}{y}=\mathrm{d}\xi \Gamma_7
\begin{equation}\int_{-2}^{\varphi}\frac{\mathrm{d}s}{(1-s)\sqrt{-s^2-s+2}}=\sqrt{-H(\varphi_1,0)}|\xi|.\end{equation}
(3.16)
在 (3.16) 式中, 计算积分并关于 \varphi u_7(\xi)
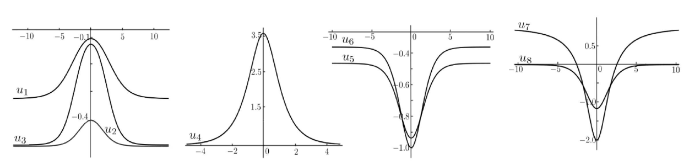
对于给定的波速 c (c<0) g u_1(\xi) - u_8(\xi) 图. 例如, 情形 A 的u_1(\xi) c=-0.1 g=0.01 u_2(\xi) c=-0.4 g=g_2(c) u_3(\xi) c=-0.2 g=0.02 u_4(\xi) c=-1.5 g=-0.5 u_5(\xi) c=-1 g=0.4 u_6(\xi) c=-1 g=g_2(c) u_7(\xi) c=-2 g=g_2(c) u_8(\xi) c=-1 g=0 图4 .
图4
图4
方程 (1.1) 孤立波解 u_1(\xi) - u_8(\xi)
4 周期波的表达式
本节研究了系统 (2.3) 在情形 A-G 中周期波的存在性及其显式表达式. 根据动力系统分支理论中封闭轨道对应方程 (1.1) 的光滑周期波, 可以得到命题 4.1. 为了方便说明命题 4.1, 给出以下记号
\begin{align*}&w_3=\sqrt{4-6\bar{a}_2H_1-18c^2H_1^2-12H_1\varphi_1-18H_1^2\varphi_1^2+12cH_1+36cH_1^2\varphi_1^2},\\ &\alpha_{11}=\alpha_{14}=\alpha_{16}=\alpha_{18}=\frac{-2+6cH_1-3H_1\varphi_1-w_3}{3H_1},\\ &\alpha_{12}=\alpha_{15}=\alpha_{17}=\alpha_{19}=\frac{-2+6cH_1-3H_1\varphi_1+w_3}{3H_1},\\ &\alpha_{13}=\alpha_{20}=\frac{-4+9cH_1-6H_1\varphi_1}{3H_1},\ H=H(\alpha_{21},0),\\ \ & \rho=-216H-32,\ \alpha_{21}=\frac{1}{18H}\left((-8-36H)\frac{2^{\frac{8}{3}}(27H+4)}{\rho^{\frac{1}{3}}}+2^{\frac{4}{3}}\rho^{\frac{1}{3}} \right).\end{align*}
命题 4.1 对于不同的波速 c (c<0) g
(1) 当 g_2(c)<g<g_1(c) c_1<c<0
\begin{equation}u_9(\xi)=\varphi_1-\frac{2a_9}{\sqrt{q_1} \sin{(\mu_9-\eta_9 \xi)}-b_9},\end{equation}
(4.1)
\begin{align*}&a_9=(\alpha_{11}-\varphi_1)(\varphi_1-\alpha_{12}), \ b_9=2\varphi_1-\alpha_{11}-\alpha_{12},\\&\eta_9=\sqrt{a_9H_1},\ q_1=b_9^2+4a_9, \\&\mu_9=\arcsin\left(\frac{b_9(\varphi_1-\alpha_{11})+2a_9}{\sqrt{q_1}(\varphi_1-\alpha_{11})}\right).\end{align*}
(2) 当 g=g_2(c) c_1<c<0
\begin{equation}u_{10}(\xi)=\varphi_1-\frac{2a_{10}}{\sqrt{q_2} \sin{(\mu_{10}-\eta_{10} \xi)}-b_{10}},\end{equation}
(4.2)
\begin{align*}&a_{10}=(c-\varphi_1)(\varphi_1-\alpha_{13}), \ b_{10}=2\varphi_1-c-\alpha_{13},\\&\eta_{10}=\sqrt{a_{10}H_1},\ q_2=b_{10}^2+4a_{10}, \\&\mu_{10}=\arcsin\left(\frac{b_{10}(\varphi_1-c)+2a_{10}}{\sqrt{q_2}(\varphi_1-c)}\right).\end{align*}
(3) 当 g_3(c)<g<g_2(c) c_1<c<0
\begin{equation}u_{11}(\xi)=\varphi_1-\frac{2a_{11}}{\sqrt{q_3} \sin{(\mu_{11}-\eta_{11} \xi)}-b_{11}},\end{equation}
(4.3)
\begin{align*}&a_{11}=(\alpha_{15}-\varphi_1)(\varphi_1-\alpha_{14}), \ b_{11}=2\varphi_1-\alpha_{14}-\alpha_{15},\\&\eta_{11}=\sqrt{a_{11} H_1},\ q_3=b_{11}^2+4a_{11}, \\&\mu_{11}=\arcsin\left(\frac{b_{11}(\varphi_1-\alpha_{14})+2a_{11}}{\sqrt{q_2}(\varphi_1-\alpha_{14})}\right).\end{align*}
(4) 当 -g_1(c)<g<g_3(c) g<g_2(c) c_2<c<0
\begin{equation}u_{12}(\xi)=\varphi_1-\frac{2a_{12}}{\sqrt{q_4} \sin{(\mu_{12}-\eta_{12} \xi)}-b_{12}},\end{equation}
(4.4)
\begin{align*}&a_{12}=(\alpha_{16}-\varphi_1)(\varphi_1-\alpha_{17}), \ b_{12}=2\varphi_1-\alpha_{16}-\alpha_{17},\\&\eta_{12}=\sqrt{a_{12}H_1},\ q_4=b_{12}^2+4a_{12}, \\&\mu_{12}=\arcsin\left(\frac{b_{12}(\varphi_1-\alpha_{16})+2a_{12}}{\sqrt{q_4}(\varphi_1-\alpha_{16})}\right).\end{align*}
(5) 当 g_2(c)<g<g_1(c) g>-g_1(c) c<c_1
\begin{equation}u_{13}(\xi)=\varphi_1-\frac{2a_{13}}{\sqrt{q_5} \sin{(\mu_{13}-\eta_{13} \xi)}-b_{13}},\end{equation}
(4.5)
\begin{align*}&a_{13}=(\alpha_{18}-\varphi_1)(\varphi_1-\alpha_{19}), \ b_{13}=2\varphi_1-\alpha_{18}-\alpha_{19},\\&\eta_{13}=\sqrt{a_{13}H_1},\ q_4=b_{13}^2+4a_{13}, \\&\mu_{13}=\arcsin\left(\frac{b_{13}(\varphi_1-\alpha_{19})+2a_{13}}{\sqrt{q_5}(\varphi_1-\alpha_{19})}\right).\end{align*}
(6) 当 g=g_2(c) c_2<c<c_1
\begin{equation}u_{14}(\xi)=\varphi_1-\frac{2a_{14}}{\sqrt{q_5} \sin{(\mu_{14}-\eta_{14} \xi)}-b_{14}},\end{equation}
(4.6)
\begin{align*}&a_{14}=(c-\varphi_1)(\varphi_1-\alpha_{20}), \ b_{14}=2\varphi_1-c-\alpha_{20},\\&\eta_{14}=\sqrt{a_{14}H_1},\ q_5=b_{14}^2+4a_{14}, \\&\mu_{14}=\arcsin\left(\frac{b_{14}(\varphi_1-c)+2a_{14}}{\sqrt{q_4}(\varphi_1-c)}\right).\end{align*}
(7) 当 g=g_2(c) c=c_2
\begin{equation}u_{15}(\xi)=\frac{\alpha_{21}B-2A-(\alpha_{21}B+2A) \mathrm{cn}(\sqrt{-ABH},l)}{A+B+(A-B) \mathrm{cn}(\sqrt{-ABH},l)},\end{equation}
(4.7)
\begin{align*}&H=H(\alpha_{21},0),\\&l^2=\frac{(\alpha_{21}-c)^2-(A-B)^2}{4 A B},\\&a_1^2=-\frac{(\beta_1-\beta_2)^2}{4},\ b_1=\frac{\beta_1+\beta_2}{2},\\&A^2=(\alpha_{21}-b_1)^2+a_1^2, \ B^2=(c-b_1)^2+a_1^2, \\\end{align*}
并且 \alpha_{21} \beta_1 \beta_2
\begin{equation*}(\varphi-c)^4+\frac{4(\varphi-c)^3}{3H}+\frac{4\bar{a}_2(\varphi-c)^2}{3H}+\frac{9\bar{a}_1(\varphi-c)}{9H}+\frac{\bar{a}_0}{3H}=(\varphi-\alpha_{21})(\varphi-c)(\varphi-\beta_1)(\varphi-\beta_2)\end{equation*}
所确定, 计算可得 \beta_1 \beta_2
\begin{align*}\beta_1=&\frac{729\cdot2^{\frac{1}{3}}H^3-18\left(3\cdot2^{\frac{2}{3}}\rho^{\frac{1}{3}}+2\rho^{\frac{2}{3}}-18\cdot2^{\frac{1}{3}}\right)H^2-\left(27\cdot2^{\frac{1}{3}}\rho_1+2^{\frac{11}{3}}\rho^{\frac{1}{3}}+8\rho^{\frac{2}{3}}-2^{\frac{16}{3}}\right)H}{18H^2\rho^{\frac{2}{3}}}\\&+\frac{\sqrt{-6\rho_1H\left(19683\cdot2^{\frac{2}{3}}H^3+2916\left(\rho^{\frac{1}{3}}+3\cdot2^{\frac{2}{3}}\right)H^2-27\rho_2H-4\rho_3\right)}}{18H^2\rho^{\frac{2}{3}}},\\\beta_2=&\frac{729\cdot2^{\frac{1}{3}}H^3-18\left(3\cdot2^{\frac{2}{3}}\rho^{\frac{1}{3}}+2\rho^{\frac{2}{3}}-18\cdot2^{\frac{1}{3}}\right)H^2-\left(27\cdot2^{\frac{1}{3}}\rho_1+2^{\frac{11}{3}}\rho^{\frac{1}{3}}+8\rho^{\frac{2}{3}}-2^{\frac{16}{3}}\right)H}{18H^2\rho^{\frac{2}{3}}}\\&-\frac{\sqrt{-6\rho_1H\left(19683\cdot2^{\frac{2}{3}}H^3+2916\left(\rho^{\frac{1}{3}}+3\cdot2^{\frac{2}{3}}\right)H^2-27\rho_2H-4\rho_3\right)}}{18H^2\rho^{\frac{2}{3}}},\\\end{align*}
\begin{align*} & \rho=-216H-32, \ \rho_1=27H^2+4H, \\ & \rho_2=27\cdot2^{\frac{2}{3}}\rho_1-48\rho^{\frac{1}{3}}-2^{\frac{7}{3}}\rho^{\frac{2}{3}}-2^{\frac{20}{3}},\\ & \rho_3=27\rho^{\frac{1}{3}}\rho_1+54\cdot2^{\frac{2}{3}}\rho_1-32\rho^{\frac{1}{3}}-2^{\frac{7}{3}}\rho^{\frac{2}{3}}-2^{\frac{17}{3}}.\end{align*}
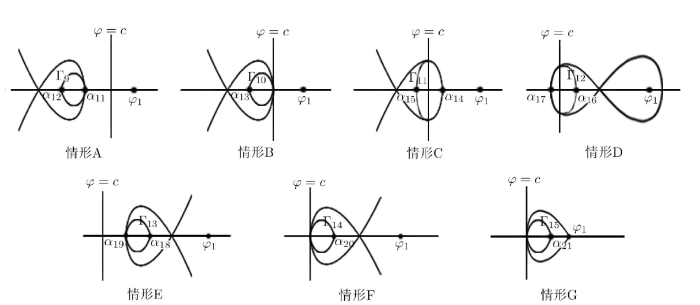
下面给出命题 4.1 的推导过程. 为了方便求出命题中周期波解, 给出七种情形下行波系统 (2.3) 的封闭轨道相图, 如图5 .
图5
(1) 当 g_2(c)<g<g_1(c) c_1<c<0 \Gamma_9 图5A ), \Gamma_9
\begin{equation*}y^2=-H(\varphi_1,0)(\varphi_1-\varphi)^2(\alpha_{11}-\varphi)(\varphi-\alpha_{12}),\ \mbox{且}\ \alpha_{12}<\varphi<\alpha_{11}<\varphi_1.\end{equation*}
由上式可解得 y \frac{\mathrm{d}\varphi}{y}=\mathrm{d}\xi \Gamma_9
\begin{equation}\int_{\alpha_{11}}^{\varphi}\frac{\mathrm{d}s}{(\varphi_1-s)\sqrt{(\alpha_{11}-s)(s-\alpha_{12})}}=\sqrt{-H(\varphi_1,0)}|\xi|.\end{equation}
(4.8)
在 (4.8) 式中, 计算积分并关于 \varphi u_9(\xi)=\varphi
(2) 当 g=g_2(c) c_1<c<0 \Gamma_{10} 图5B ), \Gamma_{10}
\begin{equation*}y^2=-H(\varphi_1,0)(\varphi_1-\varphi)^2(c-\varphi)(\varphi-\alpha_{13}),\ \mbox{且}\ \alpha_{13}<\varphi<c<\varphi_1.\end{equation*}
(4.9)
计算可得 y \frac{\mathrm{d}\varphi}{y}=\mathrm{d}\xi \Gamma_{10}
\begin{equation}\int_{c}^{\varphi}\frac{\mathrm{d}s}{(\varphi_1-s)\sqrt{(c-s)(s-\alpha_{13})}}=\sqrt{-H(\varphi_1,0)}|\xi|.\end{equation}
在 (4.9) 式中, 计算积分并关于 \varphi u_{10}(\xi)
(3) 当 g_3(c)<g<g_2(c) c_1<c<0 \Gamma_{11} 图5C ), \Gamma_{11}
\begin{equation*}y^2=-H(\varphi_1,0)(\varphi_1-\varphi)^2(\alpha_{14}-\varphi)(\varphi-\alpha_{15}),\ \mbox{且}\ \alpha_{15}<\varphi<\alpha_{14}<\varphi_1.\end{equation*}
易得 y \frac{\mathrm{d}\varphi}{y}=\mathrm{d}\xi \Gamma_{11}
\begin{equation}\int_{\alpha_{14}}^{\varphi}\frac{\mathrm{d}s}{(\varphi_1-s)\sqrt{(\alpha_{14}-s)(s-\alpha_{15})}}=\sqrt{-H(\varphi_1,0)}|\xi|.\end{equation}
(4.10)
在 (4.10) 式中, 计算积分并关于 \varphi u_{11}(\xi)
(4) 当 -g_1(c)<g<g_2(c) c_2<c<0 \Gamma_{12} 图5D ), \Gamma_{12}
\begin{equation*}y^2=-H(\varphi_1,0)(\varphi_1-\varphi)^2(\alpha_{16}-\varphi)(\varphi-\alpha_{17}),\ \mbox{且}\ \alpha_{17}<\varphi<\alpha_{16}<\varphi_1.\end{equation*}
计算可得 y \frac{\mathrm{d}\varphi}{y}=\mathrm{d}\xi \Gamma_{12}
\begin{equation}\int_{\varphi}^{\alpha_{16}}\frac{\mathrm{d}s}{(\varphi_1-s)\sqrt{(\alpha_{16}-s)(s-\alpha_{17})}}=\sqrt{-H(\varphi_1,0)}|\xi|.\end{equation}
(4.11)
在 (4.11) 式中, 计算积分并关于 \varphi u_{12}(\xi)
(5) 当 g_2(c)<g<g_1(c) g>-g_1(c) c<c_1 \Gamma_{13} 图5E ), \Gamma_{13}
\begin{equation*}y^2=-H(\varphi_1,0)(\varphi_1-\varphi)^2(\alpha_{18}-\varphi)(\varphi-\alpha_{19}),\ \mbox{且}\ \alpha_{19}<\varphi<\alpha_{18}<\varphi_1.\end{equation*}
由上式可得 y \frac{\mathrm{d}\varphi}{y}=\mathrm{d}\xi \Gamma_{13}
\begin{equation}\int_{\alpha_{19}}^{\varphi}\frac{\mathrm{d}s}{(\varphi_1-s)\sqrt{(\alpha_{18}-s)(s-\alpha_{19})}}=\sqrt{-H(\varphi_1,0)}|\xi|.\end{equation}
(4.12)
在 (4.13) 式中, 计算积分并关于 \varphi u_{13}(\xi)
(6) 当 g=g_2(c) c_2<c<c_1 \Gamma_{14} 图5F ), \Gamma_{14}
\begin{equation*}y^2=-H(\varphi_1,0)(\varphi_1-\varphi)^2(\alpha_{20}-\varphi)(\varphi-c),\ \mbox{且}\ c<\varphi<\alpha_{20}<\varphi_1.\end{equation*}
易得 y \frac{\mathrm{d}\varphi}{y}=\mathrm{d}\xi \Gamma_{14}
\begin{equation}\int_{c}^{\varphi}\frac{\mathrm{d}s}{(\varphi_1-s)\sqrt{(\alpha_{20}-s)(s-c)}}=\sqrt{-H(\varphi_1,0)}|\xi|.\end{equation}
(4.13)
在 (4.13) 式中, 计算积分并关于 \varphi u_{14}(\xi)
(7) 当 g=g_2(c) c=c_2 \Gamma_{15} 图5G ), \Gamma_{15}
\begin{equation*}y^2=-H(\alpha_{21},0)(\alpha_{21}-\varphi)(\varphi-c)(\varphi-\beta_1)(\varphi-\beta_2),\ \mbox{且}\ c<\varphi<\alpha_{21},\ \beta_1 \mbox{和} \beta_2 \mbox{为虚根}.\end{equation*}
同理可得 y \frac{\mathrm{d}\varphi}{y}=\mathrm{d}\xi \Gamma_{15}
\begin{equation}\int_{c}^{\varphi}\frac{\mathrm{d}s}{(\alpha_{21}-s)(s-c)(s-\beta_1)(s-\beta_2))}=\sqrt{-H(\alpha_{21},0)}|\xi|.\end{equation}
(4.14)
在 (4.14) 式中, 计算积分并关于 \varphi u_{15}(\xi)
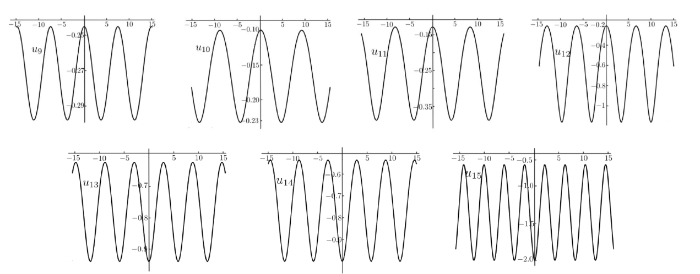
对于给定的波速 c (c<0) g u_9(\xi) - u_{15}(\xi) u_9(\xi) c=-0.2 g=0.04 u_{10}(\xi) c=-0.1 g=g_2(c) u_{11}(\xi) c=-0.2 g=0.02 u_{12}(\xi) c=-1 g=0 u_{13}(\xi) c=-1 g=0.4 u_{14}(\xi) c=-1 g=g_2(c) u_{15}(\xi) c=-2 g=g_2(c) H=-0.5 图6 .
图6
图6
方程 (1.1) 周期波解 u_9(\xi) - u_{15}(\xi)
5 总结
本文利用动力系统分支方法研究了方程 (1.1) 的分支、非线性波解及动力学特征, 并给出了孤立波解和周期波解的存在性及其精确表达式.由于方程 (1.1) 对应的奇异行波系统 (2.2) 具有一条奇异直线 \varphi=c \varphi=c b>0
参考文献
View Option
[2]
Cooper F Shepard H . Solitons in the Camassa-Holm shallow water equation
Phys Lett A, 1994 , 194 246 -250
[本文引用: 1]
[3]
Constantin A Strauss W A . Stability of peakons
Commun Pur Appl Math, 2000 , 53 603 -610
[本文引用: 1]
[4]
Degasperis A Procesi M . Asymptotic integrability
Symmetry and Perturbation Theory, 1999 , 1 23 -37
[本文引用: 1]
[5]
Lundmark H Szmigielski J . Multi-peakon solutions of the Degasperis-Procesi equation
Inverse Prob, 2003 , 19 1241 -1245
[本文引用: 1]
[6]
Chen C Tang M Y . A new type of bounded waves for Degasperis-Procesi equations
Chaos Solit Fract, 2006 , 27 698 -704
[本文引用: 1]
[7]
Guo B L Liu Z R . Periodic cusp wave solutions and single-solitons for the b - equation
Chaos Solit Fract, 2005 , 23 1451 -1463
[本文引用: 1]
[8]
Li Y . Nonunfiorm dependence for the Cauchy problem of the general b - equation
J Math Phys, 2001 , 52 033101
[本文引用: 1]
[9]
Freire I L . Remarks on strong global solutions of the b-equation
Appl Math Lett, 2023 , 146 108820
[本文引用: 1]
[10]
Tian L X Song X Y . New peaked solitary wave solutions of the generalized Camassa-Holm equation
Chaos Solit Fract, 2004 , 21 621 -637
[本文引用: 1]
[11]
Liu Z R Ouyang Z Y . A note on solitary waves for modified forms of Camassa-Holm and Degasperis-Procesi equations
Phys Lett A, 2007 , 366 377 -381
[本文引用: 2]
[12]
Khuri S A . New ansatz for obtaining wave solutions of the generalized Camassa-Holm equation
Chaos Solit Fract. 2005 , 25 705 -710
[本文引用: 1]
[13]
Daros A Arruda L K . On the instability of elliptic traveling wave solutions of the modified Camassa-Holm equation
J Differ Equations, 2019 , 266 1946 -1968
[本文引用: 1]
[14]
Zhou Y Q Chen G R Li J B . Bifurcations, exact peakon, periodic peakons and solitary wave solutions of the cubic Camassa-Holm type equation
Int J Bifurcat Chaos, 2023 , 33 2350014
[本文引用: 1]
[15]
Liu Z R Tang H . Explicit periodic wave solutions and their bifurcations for generalized Camassa-Holm equation
Int J Bifurcat Chaos, 2010 , 20 2507 -2519
[本文引用: 1]
[16]
Wazwaz A M . New solitary wave solutions to the modified forms of Degasperis-Procesi and Camassa-Holm equations
Appl Math Comput, 2007 , 186 130 -141
[本文引用: 1]
[17]
Chen Y R Ye W B Liu R . The explicit periodic wave solutions and their limit forms for a generalized b - equation
Acta Math Appl Sin, 2016 , 32 513 -528
[本文引用: 1]
[18]
Yang J P Liu R Chen Y R . Bifurcations of solitary waves of a simple equation
Int J Bifurcat Chaos, 2020 , 30 2050138
[本文引用: 1]
[19]
Yang J P Li Z G Liu Z R . The existence and bifurcation of peakon and anti-peakon to the n - degree b - equation
Int J Bifurcat Chaos, 2018 , 28 1850014
[本文引用: 1]
[20]
Li Z G Liu R . Bifurcations and exact solutions in a nonlinear wave equation
Int J Bifurcat Chaos, 2019 , 29 1950098
[21]
Li Z G Liu R . Blow-up solutions for a case of b - family equations
Acta Math Sci, 2020 , 40B 4 ): 910 -920
[本文引用: 2]
An integrable shallow water equation with peaked solitons
2
1993
... 当 b=2 n=1 [1 ] 在 1993 年提出的著名浅水波方程 CH 方程.当 k=0 [1 ] 提出 CH 方程具有可积性并且有孤立尖波解.Cooper 和 Shepard[2 ] 研究了 CH 方程的近似孤立波解.Constantin 和 Strauss[3 ] 给出了 CH 方程孤立波的存在性及其数学解释, 并证明了 k=0 b=3 n=1 [4 ] 提出的 DP 方程.Lundmark 和 Szmigielski[5 ] 利用反散射法计算出 DP 方程 3 次孤立尖波解的精确表达式. Chen 和 Tang[6 ] 得到了 DP 方程的扭波解. ...
... [1 ]提出 CH 方程具有可积性并且有孤立尖波解.Cooper 和 Shepard[2 ] 研究了 CH 方程的近似孤立波解.Constantin 和 Strauss[3 ] 给出了 CH 方程孤立波的存在性及其数学解释, 并证明了 k=0 b=3 n=1 [4 ] 提出的 DP 方程.Lundmark 和 Szmigielski[5 ] 利用反散射法计算出 DP 方程 3 次孤立尖波解的精确表达式. Chen 和 Tang[6 ] 得到了 DP 方程的扭波解. ...
Solitons in the Camassa-Holm shallow water equation
1
1994
... 当 b=2 n=1 [1 ] 在 1993 年提出的著名浅水波方程 CH 方程.当 k=0 [1 ] 提出 CH 方程具有可积性并且有孤立尖波解.Cooper 和 Shepard[2 ] 研究了 CH 方程的近似孤立波解.Constantin 和 Strauss[3 ] 给出了 CH 方程孤立波的存在性及其数学解释, 并证明了 k=0 b=3 n=1 [4 ] 提出的 DP 方程.Lundmark 和 Szmigielski[5 ] 利用反散射法计算出 DP 方程 3 次孤立尖波解的精确表达式. Chen 和 Tang[6 ] 得到了 DP 方程的扭波解. ...
Stability of peakons
1
2000
... 当 b=2 n=1 [1 ] 在 1993 年提出的著名浅水波方程 CH 方程.当 k=0 [1 ] 提出 CH 方程具有可积性并且有孤立尖波解.Cooper 和 Shepard[2 ] 研究了 CH 方程的近似孤立波解.Constantin 和 Strauss[3 ] 给出了 CH 方程孤立波的存在性及其数学解释, 并证明了 k=0 b=3 n=1 [4 ] 提出的 DP 方程.Lundmark 和 Szmigielski[5 ] 利用反散射法计算出 DP 方程 3 次孤立尖波解的精确表达式. Chen 和 Tang[6 ] 得到了 DP 方程的扭波解. ...
Asymptotic integrability
1
1999
... 当 b=2 n=1 [1 ] 在 1993 年提出的著名浅水波方程 CH 方程.当 k=0 [1 ] 提出 CH 方程具有可积性并且有孤立尖波解.Cooper 和 Shepard[2 ] 研究了 CH 方程的近似孤立波解.Constantin 和 Strauss[3 ] 给出了 CH 方程孤立波的存在性及其数学解释, 并证明了 k=0 b=3 n=1 [4 ] 提出的 DP 方程.Lundmark 和 Szmigielski[5 ] 利用反散射法计算出 DP 方程 3 次孤立尖波解的精确表达式. Chen 和 Tang[6 ] 得到了 DP 方程的扭波解. ...
Multi-peakon solutions of the Degasperis-Procesi equation
1
2003
... 当 b=2 n=1 [1 ] 在 1993 年提出的著名浅水波方程 CH 方程.当 k=0 [1 ] 提出 CH 方程具有可积性并且有孤立尖波解.Cooper 和 Shepard[2 ] 研究了 CH 方程的近似孤立波解.Constantin 和 Strauss[3 ] 给出了 CH 方程孤立波的存在性及其数学解释, 并证明了 k=0 b=3 n=1 [4 ] 提出的 DP 方程.Lundmark 和 Szmigielski[5 ] 利用反散射法计算出 DP 方程 3 次孤立尖波解的精确表达式. Chen 和 Tang[6 ] 得到了 DP 方程的扭波解. ...
A new type of bounded waves for Degasperis-Procesi equations
1
2006
... 当 b=2 n=1 [1 ] 在 1993 年提出的著名浅水波方程 CH 方程.当 k=0 [1 ] 提出 CH 方程具有可积性并且有孤立尖波解.Cooper 和 Shepard[2 ] 研究了 CH 方程的近似孤立波解.Constantin 和 Strauss[3 ] 给出了 CH 方程孤立波的存在性及其数学解释, 并证明了 k=0 b=3 n=1 [4 ] 提出的 DP 方程.Lundmark 和 Szmigielski[5 ] 利用反散射法计算出 DP 方程 3 次孤立尖波解的精确表达式. Chen 和 Tang[6 ] 得到了 DP 方程的扭波解. ...
Periodic cusp wave solutions and single-solitons for the b
1
2005
... CH 方程和 DP 方程引起了学者们广泛的兴趣, 在这两个方程的研究基础上,针对不同的参数 b n c b>1 n=1 [7 ] 证明了方程(1.2)具有周期性尖波解,Li[8 ] 讨论了方程(1.2)Cauchy 问题的非均匀依赖性,Freire[9 ] 给出了方程(1.2)在 Sobolev 空间中强解的全局存在性.对于给定 b=2 n=2 [10 ] 给出了方程(1.2)的一些物理解释,Liu 和 Ouyang[11 ] 得到了 c=2 c=1 [12 ] 给出了由三角函数组成的奇异波解,Daros 和 Arruda[13 ] 研究了椭圆行波解的不稳定性.当 b=2 n=3 [14 ] 得到了三次 CH 方程多种行波解的精确表达式.当 b=3 n=2 [11 ] 得到了 c=\frac{5}{2} [15 ] 研究了周期波解及其分支.当 b\not=2 c=\frac{b+2}{2} [16 ] 得到了两种孤立波解及其表达式.当 b\not=0,-2,-3 [17 ] 研究了显式周期波及其极限形式.当 b=0 n=2 [18 ] 研究了方程(1.2)的孤立波解及周期波解, 并给出了解之间的相关联系.当 k=0 b>1 n [19 ] 考虑了方程(1.2)孤立尖波解的存在性及其分支.当 k=0 b=0 n=2 [21 ] 研究了方程(1.2)的精确解及其分支,Li 和 Liu[21 ] 得到了方程五种类型的爆破波解并发现了它们之间的关系. ...
Nonunfiorm dependence for the Cauchy problem of the general b
1
2001
... CH 方程和 DP 方程引起了学者们广泛的兴趣, 在这两个方程的研究基础上,针对不同的参数 b n c b>1 n=1 [7 ] 证明了方程(1.2)具有周期性尖波解,Li[8 ] 讨论了方程(1.2)Cauchy 问题的非均匀依赖性,Freire[9 ] 给出了方程(1.2)在 Sobolev 空间中强解的全局存在性.对于给定 b=2 n=2 [10 ] 给出了方程(1.2)的一些物理解释,Liu 和 Ouyang[11 ] 得到了 c=2 c=1 [12 ] 给出了由三角函数组成的奇异波解,Daros 和 Arruda[13 ] 研究了椭圆行波解的不稳定性.当 b=2 n=3 [14 ] 得到了三次 CH 方程多种行波解的精确表达式.当 b=3 n=2 [11 ] 得到了 c=\frac{5}{2} [15 ] 研究了周期波解及其分支.当 b\not=2 c=\frac{b+2}{2} [16 ] 得到了两种孤立波解及其表达式.当 b\not=0,-2,-3 [17 ] 研究了显式周期波及其极限形式.当 b=0 n=2 [18 ] 研究了方程(1.2)的孤立波解及周期波解, 并给出了解之间的相关联系.当 k=0 b>1 n [19 ] 考虑了方程(1.2)孤立尖波解的存在性及其分支.当 k=0 b=0 n=2 [21 ] 研究了方程(1.2)的精确解及其分支,Li 和 Liu[21 ] 得到了方程五种类型的爆破波解并发现了它们之间的关系. ...
Remarks on strong global solutions of the b-equation
1
2023
... CH 方程和 DP 方程引起了学者们广泛的兴趣, 在这两个方程的研究基础上,针对不同的参数 b n c b>1 n=1 [7 ] 证明了方程(1.2)具有周期性尖波解,Li[8 ] 讨论了方程(1.2)Cauchy 问题的非均匀依赖性,Freire[9 ] 给出了方程(1.2)在 Sobolev 空间中强解的全局存在性.对于给定 b=2 n=2 [10 ] 给出了方程(1.2)的一些物理解释,Liu 和 Ouyang[11 ] 得到了 c=2 c=1 [12 ] 给出了由三角函数组成的奇异波解,Daros 和 Arruda[13 ] 研究了椭圆行波解的不稳定性.当 b=2 n=3 [14 ] 得到了三次 CH 方程多种行波解的精确表达式.当 b=3 n=2 [11 ] 得到了 c=\frac{5}{2} [15 ] 研究了周期波解及其分支.当 b\not=2 c=\frac{b+2}{2} [16 ] 得到了两种孤立波解及其表达式.当 b\not=0,-2,-3 [17 ] 研究了显式周期波及其极限形式.当 b=0 n=2 [18 ] 研究了方程(1.2)的孤立波解及周期波解, 并给出了解之间的相关联系.当 k=0 b>1 n [19 ] 考虑了方程(1.2)孤立尖波解的存在性及其分支.当 k=0 b=0 n=2 [21 ] 研究了方程(1.2)的精确解及其分支,Li 和 Liu[21 ] 得到了方程五种类型的爆破波解并发现了它们之间的关系. ...
New peaked solitary wave solutions of the generalized Camassa-Holm equation
1
2004
... CH 方程和 DP 方程引起了学者们广泛的兴趣, 在这两个方程的研究基础上,针对不同的参数 b n c b>1 n=1 [7 ] 证明了方程(1.2)具有周期性尖波解,Li[8 ] 讨论了方程(1.2)Cauchy 问题的非均匀依赖性,Freire[9 ] 给出了方程(1.2)在 Sobolev 空间中强解的全局存在性.对于给定 b=2 n=2 [10 ] 给出了方程(1.2)的一些物理解释,Liu 和 Ouyang[11 ] 得到了 c=2 c=1 [12 ] 给出了由三角函数组成的奇异波解,Daros 和 Arruda[13 ] 研究了椭圆行波解的不稳定性.当 b=2 n=3 [14 ] 得到了三次 CH 方程多种行波解的精确表达式.当 b=3 n=2 [11 ] 得到了 c=\frac{5}{2} [15 ] 研究了周期波解及其分支.当 b\not=2 c=\frac{b+2}{2} [16 ] 得到了两种孤立波解及其表达式.当 b\not=0,-2,-3 [17 ] 研究了显式周期波及其极限形式.当 b=0 n=2 [18 ] 研究了方程(1.2)的孤立波解及周期波解, 并给出了解之间的相关联系.当 k=0 b>1 n [19 ] 考虑了方程(1.2)孤立尖波解的存在性及其分支.当 k=0 b=0 n=2 [21 ] 研究了方程(1.2)的精确解及其分支,Li 和 Liu[21 ] 得到了方程五种类型的爆破波解并发现了它们之间的关系. ...
A note on solitary waves for modified forms of Camassa-Holm and Degasperis-Procesi equations
2
2007
... CH 方程和 DP 方程引起了学者们广泛的兴趣, 在这两个方程的研究基础上,针对不同的参数 b n c b>1 n=1 [7 ] 证明了方程(1.2)具有周期性尖波解,Li[8 ] 讨论了方程(1.2)Cauchy 问题的非均匀依赖性,Freire[9 ] 给出了方程(1.2)在 Sobolev 空间中强解的全局存在性.对于给定 b=2 n=2 [10 ] 给出了方程(1.2)的一些物理解释,Liu 和 Ouyang[11 ] 得到了 c=2 c=1 [12 ] 给出了由三角函数组成的奇异波解,Daros 和 Arruda[13 ] 研究了椭圆行波解的不稳定性.当 b=2 n=3 [14 ] 得到了三次 CH 方程多种行波解的精确表达式.当 b=3 n=2 [11 ] 得到了 c=\frac{5}{2} [15 ] 研究了周期波解及其分支.当 b\not=2 c=\frac{b+2}{2} [16 ] 得到了两种孤立波解及其表达式.当 b\not=0,-2,-3 [17 ] 研究了显式周期波及其极限形式.当 b=0 n=2 [18 ] 研究了方程(1.2)的孤立波解及周期波解, 并给出了解之间的相关联系.当 k=0 b>1 n [19 ] 考虑了方程(1.2)孤立尖波解的存在性及其分支.当 k=0 b=0 n=2 [21 ] 研究了方程(1.2)的精确解及其分支,Li 和 Liu[21 ] 得到了方程五种类型的爆破波解并发现了它们之间的关系. ...
... [11 ]得到了 c=\frac{5}{2} [15 ] 研究了周期波解及其分支.当 b\not=2 c=\frac{b+2}{2} [16 ] 得到了两种孤立波解及其表达式.当 b\not=0,-2,-3 [17 ] 研究了显式周期波及其极限形式.当 b=0 n=2 [18 ] 研究了方程(1.2)的孤立波解及周期波解, 并给出了解之间的相关联系.当 k=0 b>1 n [19 ] 考虑了方程(1.2)孤立尖波解的存在性及其分支.当 k=0 b=0 n=2 [21 ] 研究了方程(1.2)的精确解及其分支,Li 和 Liu[21 ] 得到了方程五种类型的爆破波解并发现了它们之间的关系. ...
New ansatz for obtaining wave solutions of the generalized Camassa-Holm equation
1
2005
... CH 方程和 DP 方程引起了学者们广泛的兴趣, 在这两个方程的研究基础上,针对不同的参数 b n c b>1 n=1 [7 ] 证明了方程(1.2)具有周期性尖波解,Li[8 ] 讨论了方程(1.2)Cauchy 问题的非均匀依赖性,Freire[9 ] 给出了方程(1.2)在 Sobolev 空间中强解的全局存在性.对于给定 b=2 n=2 [10 ] 给出了方程(1.2)的一些物理解释,Liu 和 Ouyang[11 ] 得到了 c=2 c=1 [12 ] 给出了由三角函数组成的奇异波解,Daros 和 Arruda[13 ] 研究了椭圆行波解的不稳定性.当 b=2 n=3 [14 ] 得到了三次 CH 方程多种行波解的精确表达式.当 b=3 n=2 [11 ] 得到了 c=\frac{5}{2} [15 ] 研究了周期波解及其分支.当 b\not=2 c=\frac{b+2}{2} [16 ] 得到了两种孤立波解及其表达式.当 b\not=0,-2,-3 [17 ] 研究了显式周期波及其极限形式.当 b=0 n=2 [18 ] 研究了方程(1.2)的孤立波解及周期波解, 并给出了解之间的相关联系.当 k=0 b>1 n [19 ] 考虑了方程(1.2)孤立尖波解的存在性及其分支.当 k=0 b=0 n=2 [21 ] 研究了方程(1.2)的精确解及其分支,Li 和 Liu[21 ] 得到了方程五种类型的爆破波解并发现了它们之间的关系. ...
On the instability of elliptic traveling wave solutions of the modified Camassa-Holm equation
1
2019
... CH 方程和 DP 方程引起了学者们广泛的兴趣, 在这两个方程的研究基础上,针对不同的参数 b n c b>1 n=1 [7 ] 证明了方程(1.2)具有周期性尖波解,Li[8 ] 讨论了方程(1.2)Cauchy 问题的非均匀依赖性,Freire[9 ] 给出了方程(1.2)在 Sobolev 空间中强解的全局存在性.对于给定 b=2 n=2 [10 ] 给出了方程(1.2)的一些物理解释,Liu 和 Ouyang[11 ] 得到了 c=2 c=1 [12 ] 给出了由三角函数组成的奇异波解,Daros 和 Arruda[13 ] 研究了椭圆行波解的不稳定性.当 b=2 n=3 [14 ] 得到了三次 CH 方程多种行波解的精确表达式.当 b=3 n=2 [11 ] 得到了 c=\frac{5}{2} [15 ] 研究了周期波解及其分支.当 b\not=2 c=\frac{b+2}{2} [16 ] 得到了两种孤立波解及其表达式.当 b\not=0,-2,-3 [17 ] 研究了显式周期波及其极限形式.当 b=0 n=2 [18 ] 研究了方程(1.2)的孤立波解及周期波解, 并给出了解之间的相关联系.当 k=0 b>1 n [19 ] 考虑了方程(1.2)孤立尖波解的存在性及其分支.当 k=0 b=0 n=2 [21 ] 研究了方程(1.2)的精确解及其分支,Li 和 Liu[21 ] 得到了方程五种类型的爆破波解并发现了它们之间的关系. ...
Bifurcations, exact peakon, periodic peakons and solitary wave solutions of the cubic Camassa-Holm type equation
1
2023
... CH 方程和 DP 方程引起了学者们广泛的兴趣, 在这两个方程的研究基础上,针对不同的参数 b n c b>1 n=1 [7 ] 证明了方程(1.2)具有周期性尖波解,Li[8 ] 讨论了方程(1.2)Cauchy 问题的非均匀依赖性,Freire[9 ] 给出了方程(1.2)在 Sobolev 空间中强解的全局存在性.对于给定 b=2 n=2 [10 ] 给出了方程(1.2)的一些物理解释,Liu 和 Ouyang[11 ] 得到了 c=2 c=1 [12 ] 给出了由三角函数组成的奇异波解,Daros 和 Arruda[13 ] 研究了椭圆行波解的不稳定性.当 b=2 n=3 [14 ] 得到了三次 CH 方程多种行波解的精确表达式.当 b=3 n=2 [11 ] 得到了 c=\frac{5}{2} [15 ] 研究了周期波解及其分支.当 b\not=2 c=\frac{b+2}{2} [16 ] 得到了两种孤立波解及其表达式.当 b\not=0,-2,-3 [17 ] 研究了显式周期波及其极限形式.当 b=0 n=2 [18 ] 研究了方程(1.2)的孤立波解及周期波解, 并给出了解之间的相关联系.当 k=0 b>1 n [19 ] 考虑了方程(1.2)孤立尖波解的存在性及其分支.当 k=0 b=0 n=2 [21 ] 研究了方程(1.2)的精确解及其分支,Li 和 Liu[21 ] 得到了方程五种类型的爆破波解并发现了它们之间的关系. ...
Explicit periodic wave solutions and their bifurcations for generalized Camassa-Holm equation
1
2010
... CH 方程和 DP 方程引起了学者们广泛的兴趣, 在这两个方程的研究基础上,针对不同的参数 b n c b>1 n=1 [7 ] 证明了方程(1.2)具有周期性尖波解,Li[8 ] 讨论了方程(1.2)Cauchy 问题的非均匀依赖性,Freire[9 ] 给出了方程(1.2)在 Sobolev 空间中强解的全局存在性.对于给定 b=2 n=2 [10 ] 给出了方程(1.2)的一些物理解释,Liu 和 Ouyang[11 ] 得到了 c=2 c=1 [12 ] 给出了由三角函数组成的奇异波解,Daros 和 Arruda[13 ] 研究了椭圆行波解的不稳定性.当 b=2 n=3 [14 ] 得到了三次 CH 方程多种行波解的精确表达式.当 b=3 n=2 [11 ] 得到了 c=\frac{5}{2} [15 ] 研究了周期波解及其分支.当 b\not=2 c=\frac{b+2}{2} [16 ] 得到了两种孤立波解及其表达式.当 b\not=0,-2,-3 [17 ] 研究了显式周期波及其极限形式.当 b=0 n=2 [18 ] 研究了方程(1.2)的孤立波解及周期波解, 并给出了解之间的相关联系.当 k=0 b>1 n [19 ] 考虑了方程(1.2)孤立尖波解的存在性及其分支.当 k=0 b=0 n=2 [21 ] 研究了方程(1.2)的精确解及其分支,Li 和 Liu[21 ] 得到了方程五种类型的爆破波解并发现了它们之间的关系. ...
New solitary wave solutions to the modified forms of Degasperis-Procesi and Camassa-Holm equations
1
2007
... CH 方程和 DP 方程引起了学者们广泛的兴趣, 在这两个方程的研究基础上,针对不同的参数 b n c b>1 n=1 [7 ] 证明了方程(1.2)具有周期性尖波解,Li[8 ] 讨论了方程(1.2)Cauchy 问题的非均匀依赖性,Freire[9 ] 给出了方程(1.2)在 Sobolev 空间中强解的全局存在性.对于给定 b=2 n=2 [10 ] 给出了方程(1.2)的一些物理解释,Liu 和 Ouyang[11 ] 得到了 c=2 c=1 [12 ] 给出了由三角函数组成的奇异波解,Daros 和 Arruda[13 ] 研究了椭圆行波解的不稳定性.当 b=2 n=3 [14 ] 得到了三次 CH 方程多种行波解的精确表达式.当 b=3 n=2 [11 ] 得到了 c=\frac{5}{2} [15 ] 研究了周期波解及其分支.当 b\not=2 c=\frac{b+2}{2} [16 ] 得到了两种孤立波解及其表达式.当 b\not=0,-2,-3 [17 ] 研究了显式周期波及其极限形式.当 b=0 n=2 [18 ] 研究了方程(1.2)的孤立波解及周期波解, 并给出了解之间的相关联系.当 k=0 b>1 n [19 ] 考虑了方程(1.2)孤立尖波解的存在性及其分支.当 k=0 b=0 n=2 [21 ] 研究了方程(1.2)的精确解及其分支,Li 和 Liu[21 ] 得到了方程五种类型的爆破波解并发现了它们之间的关系. ...
The explicit periodic wave solutions and their limit forms for a generalized b
1
2016
... CH 方程和 DP 方程引起了学者们广泛的兴趣, 在这两个方程的研究基础上,针对不同的参数 b n c b>1 n=1 [7 ] 证明了方程(1.2)具有周期性尖波解,Li[8 ] 讨论了方程(1.2)Cauchy 问题的非均匀依赖性,Freire[9 ] 给出了方程(1.2)在 Sobolev 空间中强解的全局存在性.对于给定 b=2 n=2 [10 ] 给出了方程(1.2)的一些物理解释,Liu 和 Ouyang[11 ] 得到了 c=2 c=1 [12 ] 给出了由三角函数组成的奇异波解,Daros 和 Arruda[13 ] 研究了椭圆行波解的不稳定性.当 b=2 n=3 [14 ] 得到了三次 CH 方程多种行波解的精确表达式.当 b=3 n=2 [11 ] 得到了 c=\frac{5}{2} [15 ] 研究了周期波解及其分支.当 b\not=2 c=\frac{b+2}{2} [16 ] 得到了两种孤立波解及其表达式.当 b\not=0,-2,-3 [17 ] 研究了显式周期波及其极限形式.当 b=0 n=2 [18 ] 研究了方程(1.2)的孤立波解及周期波解, 并给出了解之间的相关联系.当 k=0 b>1 n [19 ] 考虑了方程(1.2)孤立尖波解的存在性及其分支.当 k=0 b=0 n=2 [21 ] 研究了方程(1.2)的精确解及其分支,Li 和 Liu[21 ] 得到了方程五种类型的爆破波解并发现了它们之间的关系. ...
Bifurcations of solitary waves of a simple equation
1
2020
... CH 方程和 DP 方程引起了学者们广泛的兴趣, 在这两个方程的研究基础上,针对不同的参数 b n c b>1 n=1 [7 ] 证明了方程(1.2)具有周期性尖波解,Li[8 ] 讨论了方程(1.2)Cauchy 问题的非均匀依赖性,Freire[9 ] 给出了方程(1.2)在 Sobolev 空间中强解的全局存在性.对于给定 b=2 n=2 [10 ] 给出了方程(1.2)的一些物理解释,Liu 和 Ouyang[11 ] 得到了 c=2 c=1 [12 ] 给出了由三角函数组成的奇异波解,Daros 和 Arruda[13 ] 研究了椭圆行波解的不稳定性.当 b=2 n=3 [14 ] 得到了三次 CH 方程多种行波解的精确表达式.当 b=3 n=2 [11 ] 得到了 c=\frac{5}{2} [15 ] 研究了周期波解及其分支.当 b\not=2 c=\frac{b+2}{2} [16 ] 得到了两种孤立波解及其表达式.当 b\not=0,-2,-3 [17 ] 研究了显式周期波及其极限形式.当 b=0 n=2 [18 ] 研究了方程(1.2)的孤立波解及周期波解, 并给出了解之间的相关联系.当 k=0 b>1 n [19 ] 考虑了方程(1.2)孤立尖波解的存在性及其分支.当 k=0 b=0 n=2 [21 ] 研究了方程(1.2)的精确解及其分支,Li 和 Liu[21 ] 得到了方程五种类型的爆破波解并发现了它们之间的关系. ...
The existence and bifurcation of peakon and anti-peakon to the n b
1
2018
... CH 方程和 DP 方程引起了学者们广泛的兴趣, 在这两个方程的研究基础上,针对不同的参数 b n c b>1 n=1 [7 ] 证明了方程(1.2)具有周期性尖波解,Li[8 ] 讨论了方程(1.2)Cauchy 问题的非均匀依赖性,Freire[9 ] 给出了方程(1.2)在 Sobolev 空间中强解的全局存在性.对于给定 b=2 n=2 [10 ] 给出了方程(1.2)的一些物理解释,Liu 和 Ouyang[11 ] 得到了 c=2 c=1 [12 ] 给出了由三角函数组成的奇异波解,Daros 和 Arruda[13 ] 研究了椭圆行波解的不稳定性.当 b=2 n=3 [14 ] 得到了三次 CH 方程多种行波解的精确表达式.当 b=3 n=2 [11 ] 得到了 c=\frac{5}{2} [15 ] 研究了周期波解及其分支.当 b\not=2 c=\frac{b+2}{2} [16 ] 得到了两种孤立波解及其表达式.当 b\not=0,-2,-3 [17 ] 研究了显式周期波及其极限形式.当 b=0 n=2 [18 ] 研究了方程(1.2)的孤立波解及周期波解, 并给出了解之间的相关联系.当 k=0 b>1 n [19 ] 考虑了方程(1.2)孤立尖波解的存在性及其分支.当 k=0 b=0 n=2 [21 ] 研究了方程(1.2)的精确解及其分支,Li 和 Liu[21 ] 得到了方程五种类型的爆破波解并发现了它们之间的关系. ...
Bifurcations and exact solutions in a nonlinear wave equation
0
2019
Blow-up solutions for a case of b
2
2020
... CH 方程和 DP 方程引起了学者们广泛的兴趣, 在这两个方程的研究基础上,针对不同的参数 b n c b>1 n=1 [7 ] 证明了方程(1.2)具有周期性尖波解,Li[8 ] 讨论了方程(1.2)Cauchy 问题的非均匀依赖性,Freire[9 ] 给出了方程(1.2)在 Sobolev 空间中强解的全局存在性.对于给定 b=2 n=2 [10 ] 给出了方程(1.2)的一些物理解释,Liu 和 Ouyang[11 ] 得到了 c=2 c=1 [12 ] 给出了由三角函数组成的奇异波解,Daros 和 Arruda[13 ] 研究了椭圆行波解的不稳定性.当 b=2 n=3 [14 ] 得到了三次 CH 方程多种行波解的精确表达式.当 b=3 n=2 [11 ] 得到了 c=\frac{5}{2} [15 ] 研究了周期波解及其分支.当 b\not=2 c=\frac{b+2}{2} [16 ] 得到了两种孤立波解及其表达式.当 b\not=0,-2,-3 [17 ] 研究了显式周期波及其极限形式.当 b=0 n=2 [18 ] 研究了方程(1.2)的孤立波解及周期波解, 并给出了解之间的相关联系.当 k=0 b>1 n [19 ] 考虑了方程(1.2)孤立尖波解的存在性及其分支.当 k=0 b=0 n=2 [21 ] 研究了方程(1.2)的精确解及其分支,Li 和 Liu[21 ] 得到了方程五种类型的爆破波解并发现了它们之间的关系. ...
... [21 ]得到了方程五种类型的爆破波解并发现了它们之间的关系. ...