测不准原理源于物理的量子力学, 对于理解量子力学中粒子运动的不确定性和信号在不同域中的传播的关系有重要作用. 在量子力学中, 测不准原理指的是我们无法同时确定粒子的位置和动量, 如果粒子的位置已经确定, 此时粒子的动量的标准差会变成很大, 则此时粒子的动量波动大; 反之, 如果粒子的动量确定了, 那么此时它的位置标准差也会很大, 也就是粒子的位置和动量两者的标准差无法同时很小, 存在一个下界限制了粒子的位置和动量两者标准差的乘积. 而在信号中, 测不准原理告诉我们信号在时域和频域中不能同时很集中, 用数学语言描述为^[1]

其中 $\sigma_t ^2=\int_{-\infty}^{\infty}(t-\left\langle t\right\rangle)^2 |s(t)|^2{\rm d}t, \sigma_w ^2=\int_{-\infty}^{\infty}(w-\left\langle w\right\rangle)^2 |\hat{s}(w)|^2{\rm d}w.$ 之后, 还可以得到一个更强的下界, 具体请参考文献 [1]. 目前, 测不准原理有很多形式, 例如在文献 [2] 中, Donoho 与 Stark 进一步证明了经典离散 Fourier 变换的测不准原理以及经典 Fourier 变换在测度下的测不准原理, 以上结论均为对于 Fourier 变换得出的结论.

作为经典 Fourier 变换的推广, 分数阶 Fourier 变换可以看作是信号在时频平面上旋转任意角度, 在信号处理等领域有重要的应用. 基于测不准原理在物理和信号分析中的应用, 分数阶 Fourier 变换下的测不准原理已被广泛研究. 在文献 [3] 中, Ozaktas 与 Aytür 得到了针对实信号的连续分数阶 Fourier 变换的测不准关系的一个下界, 而在文献 [4] 中, Shinde 与 Gadre 提出了一个比文献 [3] 更严谨的下界. 在文献 [5] 中, Capus 和 Brown 也讨论了高斯信号及分数阶 Fourier 域中的测不准乘积, 以上这些研究成果均针对连续分数阶 Fourier 变换. 在文献 [6] 中, Shi, Han 与 Zhang 得到了无限离散分数阶 Fourier 变换的测不准关系的一个下界, 这使得测不准关系得到进一步的推广. 据作者所知, 离散分数阶 Fourier 变换以及连续分数阶 Fourier 变换在测度下的测不准原理还未被研究, 因此, 本文将主要针对文献 [2] 中的结论对分数阶 Fourier 变换的测不准原理做进一步研究.

在讨论测不准原理之前, 我们先给出分数阶 Fourier 变换离散和连续的两种定义, 其中离散定义是对文献 [2] 的经典离散 Fourier 变换的推广.

定义2.1 对一长度为 $N$ 的序列 $\{x_t\}\ (t=0,1,\cdots,N-1)$, 称 $\{\hat{x}_w\}\ (w=0,1,\cdots,N-1)$ 为其经典离散 Fourier 变换, 若

下面给出离散分数阶 Fourier 变换的定义

定义2.2 对一长度为 $N$ 的序列 $\{\tilde{x}_n\}\ (n=0,1,\cdots,N-1)$, 称 $\{\hat x_\alpha(u)\}\ (u=0,1,\cdots,$ $N-1)$ 为其离散分数阶Fourier 变换, 若

定义2.3 称 $F_{\alpha}[f](u)$ 为函数 $f$ 的角度为 $\alpha\ (0\le\alpha\le\pi)$ 的连续分数阶 Fourier 变换, 若

$K_\alpha(t,u)$ 如下

且 $a(\alpha)=\frac{1}{2}\cot\alpha, b(\alpha)=\sec\alpha, c(\alpha)=\sqrt{1-j\cot\alpha}.$

当 $\alpha=\pi/2$ 时, $F_{\pi/2}[f](u)=\hat{f}(u)$ 为经典 Fourier 变换. 为方便起见, 下面将 $F_\alpha[f](u)$ 记为 $F_\alpha(u)$. 连续分数阶 Fourier 变换还满足以下性质^[4],[7]

文献 [2] 中给出了以下经典离散 Fourier 变换的测不准原理.

定理3.1 令 $N_t$ 和 $N_w$ 分别表示 $\{x_t\}$, $\{\hat{x}_w\}$ 中非零元素的个数, 若 $N_t\ge1$, 则

下面我们将该定理推广至以下离散分数阶 Fourier 变换的情况.

定理3.2 令 $\tilde{N}_t$ 和 $\tilde{N}_u$ 分别表示 $\{\tilde{x}_n\}$, $\{\hat{x}_\alpha(u)\}$ 中非零元素的个数, 若 $\tilde{N}_t\ge1$, 当 $0<\csc\alpha\le2\pi$ 或 $\csc\alpha>2\pi, \csc\alpha\ne q\pi(q\in\mathbb{Q})$ 时, 有

由定理 3.2 可得

要证明定理 3.2, 先考虑以下引理.

引理3.1 若 $\{\tilde{x}_n\}$ 有 $\tilde{N}_t$ 个非零元素, $\tilde{N}_t\ge1$, 则 $\{\hat{x}_\alpha(u)\}$ 中不能有 $\tilde{N}_t$ 个连续为零的元素 $(0<\csc\alpha\le2\pi$ 或 $\csc\alpha>2\pi, \csc\alpha\ne q\pi, q\in\mathbb{Q})$.

证 令 $\tau_1,\tau_2\cdots\tau_{\tilde{N}_t}$ 表示 $\{\tilde{x}_n\}$ 中非零元素的位置, 令 $\tilde{b}_l\equiv \tilde{x}_{\tau_l}{\rm e}^{\frac{1}{2}j{\tau_l}^2 \cot\alpha}, l=1,2\cdots \tilde{N}_t$ 为 $\{\tilde{x}_n {\rm e}^{\frac{1}{2}jn^2 \cot\alpha}\}$ 这一序列中相应的非零元素, $\tilde{z}_l\equiv {\rm e}^{-\frac{j{\tau_l}\csc\alpha}{N}}, u=m+1,\cdots m+\tilde{N}_t$ ($m\in\mathbb{Z}$), 定义

$\hat{x}_\alpha(m+k)\equiv \tilde{g}_k$, 引理即要证存在 $k\in\{1,\cdots,\tilde{N}_t\}$ 满足 $\tilde{g}_k\ne0$, 现将 (3.1) 式写为矩阵形式, 定义 $\tilde{g}\equiv(\tilde{g}_k), \tilde{b}\equiv(\tilde{b}_l), \tilde{Z}(k,l)\equiv \sqrt{\frac{1-j\cot\alpha}{2\pi}} {\rm e}^{\frac{1}{2}j(m+k)^2\cot\alpha}(\tilde{z}_l)^{m+k}$, 则 $\tilde{g}=\tilde{Z}\tilde{b}.$

现针对 $\tilde{Z}$ 做初等行/列变换 (每一行乘 $\sqrt{\frac{2\pi}{1-j\cot\alpha}}{\rm e}^{-\frac{1}{2}j(m+k)^2\cot\alpha}$, 每一列乘 $1/\tilde{z}_{l}^{m+1}$ ), 可得矩阵 $\tilde{V}$

因为 $\tilde{z}_{l}^{m+1}, \sqrt{\frac{2\pi}{1-j\cot\alpha}}{\rm e}^{-\frac{1}{2}j(m+k)^2\cot\alpha}\ne0$, 所以 $\lvert \tilde{Z}\rvert\ne0$ 等价于 $\lvert \tilde{V}\rvert\ne0$. 而 $\lvert \tilde{V}\rvert=\prod\limits_{1\le p<l\le \tilde{N}_t}(\tilde{z}_l-\tilde{z}_p)$, 若有 $\tilde{z}_l=\tilde{z}_p$, 则 ${\rm e}^{-\frac{j(\tau_l-\tau_p)\csc\alpha}{N}}=1$, 此时需要满足 $\frac{(\tau_l-\tau_p)\csc\alpha}{N}=2K\pi\ (K\in\mathbb{Z})$. 当 $0<\csc\alpha\le2\pi$ 时, $0<\tau_l-\tau_p<N$, 故 $0<(\tau_l-\tau_p)\cdot\frac{\csc\alpha}{N}<2\pi$, 从而 ${\rm e}^{-\frac{j(\tau_l-\tau_p)\csc\alpha}{N}}\ne1$; 或当 $\csc\alpha>2\pi$ 且 $\csc\alpha\ne q\pi\ (q\in\mathbb{Q})$ 时, 同样也有 ${\rm e}^{-\frac{j(\tau_l-\tau_p)\csc\alpha}{N}}\ne1$. 故 $\lvert \tilde{V}\rvert\ne0$, 从而 $\lvert \tilde{Z}\rvert\ne0$.

反设 $\tilde{g}=0$, 而 $\tilde{b}\ne0$, 则 $ \tilde{Z}\tilde{b}=0. $ 此时该齐次线性方程组有非零解, 则 $\lvert \tilde{Z}\rvert=0$, 矛盾. 引理 3.1 得证.

下面给出定理 3.2 的证明.

证 情况 1 当 $\tilde{N}_t|N$, 现将 $\{\tilde{x}_0,\tilde{x}_1,\cdots,\tilde{x}_{N-1}\}$ 等分为 $\frac{N}{\tilde{N}_t}$ 个长度为$\tilde{N}_t$ 的部分, $\{\hat{x}_\alpha(0),\cdots,$ $\hat{x}_\alpha(N-1)\}$ 也同上等分, 则由引理 3.1 知, 在每个部分, $\hat{x}_\alpha(u)$ 不全为零元素, 即至少包含 $\{\hat{x}_\alpha(u)\}$ 一个非零元素, 则

若要等式成立, 则要求 $\tilde{N}_t$ 与 $\tilde{N}_u$ 同时整除 $N$, 且 $\{\hat{x}_\alpha(u)\}$ 的 $\tilde{N}_u$ 个非零元素是等距的. 这是因为由引理 3.1 知, $\{\hat{x}_\alpha(u)\}$ 两两非零元素之间间隔最多 $\tilde{N}_t -1$ 个零元素，若要使得两两非零元素之间的间隔尽可能的大，此时 $\{\hat{x}_\alpha(u)\}$ 为以下等距的形式 (两两非零元素之间恰好均间隔 $\tilde{N}_t -1$ 个零元素)

若非零元素之间不等距且保证非零元素个数仍为 $\frac{N}{\tilde{N}_t}$ 个, 此时定存在某对非零元素之间间隔不小于 $\tilde{N}_t$, 矛盾.

情况 2 当 $\tilde{N}_t\nmid N$, 令 $L=\ulcorner N/\tilde{N}_t\urcorner$ ($\ulcorner x\urcorner$ 表示不小于 $x$ 的最小整数), $L-1<\frac{N}{\tilde{N}_t}<L$, 则 $\tilde{N}_t<\frac{N}{L-1}$, 此时在 $N$ 个位置中分布少于 $L$ 个非零元素却不留下长度大于$\tilde{N}_t$ 的间隔是不可能的, 则 $\tilde{N}_u\ge L$, 此时有

定理 3.2 得证.

下面给出例子说明定理 3.2 中等号是可以成立的.

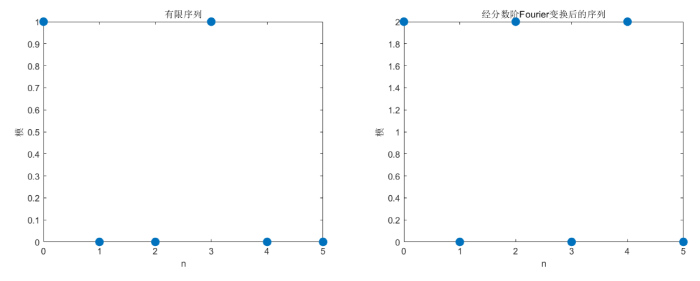
当 $\csc\alpha=2\pi, N=6$ 时, $\{\tilde{x}_n\}$ 满足 $\tilde{x}_0=1, $ $\tilde{x}_1=\tilde{x}_2=0, $ $\tilde{x}_3={\rm e}^{-\frac{9}{2}j\cot\alpha },$ $\tilde{x}_4=\tilde{x}_5=0.$ 此时$\tilde{N}_t=2.$ 经计算, $\hat{x}_\alpha(0)=2\sqrt{\frac{1-\sqrt{4\pi^2-1}j}{2\pi}}, \hat{x}_\alpha(2)=2\sqrt{\frac{1-\sqrt{4\pi^2-1}j}{2\pi}}{\rm e}^{2\sqrt{4\pi^2-1}j}, \hat{x}_\alpha(4)=2\sqrt{\frac{1-\sqrt{4\pi^2-1}j}{2\pi}}{\rm e}^{8\sqrt{4\pi^2-1}j}, \hat{x}_\alpha(1)=\hat{x}_\alpha(3)=\hat{x}_\alpha(5)=0$, 此时满足 $\tilde{N}_u=3$, 则有 $\tilde{N}_t\cdot \tilde{N}_u=N.$ 有限序列 $\{\tilde{x}_n\}$ 与其经分数阶 Fourier 变换后的序列$\{\hat{x}_\alpha(u)\}$ 的元素的模分别如以图 1 所示.

当 $\csc\alpha=3\pi$, 定理 3.2 不成立. 下面给出一反例. $\tilde{x}_0=1, \tilde{x}_1=\tilde{x}_2=\tilde{x}_3=0, \tilde{x}_4=-{\rm e}^{-8j\cot\alpha }, \tilde{x}_5=0.$ 此时$\hat{x}_\alpha(0)=\hat{x}_\alpha(1)=\hat{x}_\alpha(2)=\hat{x}_\alpha(3)=\hat{x}_\alpha(4)=\hat{x}_\alpha(5)=0. \tilde{N}_t=2, \tilde{N}_u=0$, 则 $\tilde{N}_t\cdot \tilde{N}_u<N$, 故定理 3.2 不成立.

设 $f(t)$ 为 $\mathbb{R}$ 上的复值函数, 其连续分数阶 Fourier 变换同 (2.1) 式

现假设 $f(t)$ 的 $L_2$ 范数, $\Vert f\Vert=(\int_{-\infty}^{\infty}\lvert f(t)\rvert^2{\rm d}t)^{1/2}$ 为 1. 由 (2.2) 式知 $\int_{-\infty}^{\infty}\lvert f(t)\rvert^2{\rm d}t=\int_{-\infty}^{\infty}\lvert F_\alpha(u)\rvert^2 {\rm d}u$, 那么 $\Vert F_\alpha\Vert=1$.

定义4.1 称 $f$ 在可测集 $T$ 上 $\epsilon$ 集中, 若存在一定义在 $\mathbb{R}$ 上的函数 $g(t)$ 满足在 $\mathbb{R}/T$ 上 $g(t)=0$ 且 $\Vert f-g\Vert\le\epsilon$.

类似地也可以对 $f(t)$ 的连续分数阶 Fourier 变换 $F_\alpha(u)$ 做以下定义.

定义4.2 称 $F_\alpha(u)$ 在可测集 $W$ 上 $\epsilon$ 集中, 若存在一定义在 $\mathbb{R}$ 上的函数 $H(u)$ 满足在 $\mathbb{R}/W$ 上 $H(u)=0$ 且 $\Vert F_\alpha-H\Vert\le\epsilon$.

根据经典 Fourier 变换及上述的定义, 文献 [2] 给出了经典 Fourier 变换在测度下的测不准原理.

定理4.1 令 $T$ 和 $W$ 均为可测集, $f(t)$ 与其经典 Fourier 变换 $\hat{f}(w)$ 范数均为 1, 且满足 $f$ 在 $T$ 上 $\epsilon_T$ 集中, $\hat{f}(w)$ 在 $W$ 上 $\epsilon_W$ 集中, 那么

现考虑将该定理推广至连续分数阶 Fourier 变换, 在推广前我们先给出以下定义

其中 $T$ 为可测集, $1_T$ 为示性函数.

其中 $W$ 为可测集, $F_\alpha(u)$ 为 $f(t)$ 的连续分数阶 Fourier 变换.

引理4.1 $f(t)$ 在 $T$ 上 $\epsilon$ 集中 $\Leftrightarrow \Vert f-P_T f\Vert\le\epsilon$.

证 先证必要性, 此时存在一定义在 $\mathbb{R}$ 上的函数 $g(t)$ 满足在 $\mathbb{R}/T$ 上 $g(t)=0$ 且 $\Vert f-g\Vert\le\epsilon$, 则

故

再证充分性, 此时 $P_T f$ 满足在 $\mathbb{R}/T$ 上 $P_T f(t)=0$ 且 $\Vert f-P_T f\Vert\le\epsilon$, 则由定义 4.1 知, $f(t)$ 在可测集 $T$ 上 $\epsilon$ 集中. 证毕.

引理4.2 若函数 $g(t)\equiv(L_W f)(t)$, 则其连续分数阶 Fourier 变换 $G_\alpha(u)=F_\alpha(u)1_W$.

证

证毕.

引理4.3 若 $f(t)$ 的连续分数阶 Fourier 变换为 $F_\alpha(u)$, 则 $F_\alpha(u)$ 在 $W$ 上 $\epsilon$ 集中 $\Leftrightarrow\Vert f-L_W f\Vert\le\epsilon.$

证 先证必要性, 此时存在 $H(u)$ 满足在 $\mathbb{R}/W$ 上 $H(u)=0$ 且 $\Vert F_\alpha-H\Vert\le\epsilon$, 则

故

而 $F_\alpha-G_\alpha$ 的角度为 $\alpha$ 的连续分数阶 Fourier 逆变换为 $f-L_W f$, 则由 (2.2) 式知, $\Vert f-L_W f\Vert\le\epsilon$.

再证充分性, 此时 $\Vert F_\alpha-G_\alpha\Vert\le\epsilon$ 且 $G_\alpha$ 满足在 $\mathbb{R}/W$ 上 $G_\alpha(u)=0$. 由定义 4.2 知, $F_\alpha(u)$ 在 $W$ 上 $\epsilon$ 集中. 证毕.

定义4.3 称算子 $Q$ 的范数为 $\Vert Q\Vert$, 若 $\Vert Q\Vert\equiv \sup\limits_{g\in L_2}\frac{\Vert Qg\Vert}{\Vert g\Vert}.$

引理4.4 $\Vert L_W \Vert=1.$

证 现对于任意 $f\in L_2$ 有

故 $\Vert L_W\Vert\le1$. 此时对于函数 $L_W f(t)$, 因为 $G_\alpha(u)=F_\alpha(u)1_W$, 所以

则 $\Vert L_W (L_W f)\Vert=\Vert L_W f\Vert.$

所以, 由定义 4.3 知, $\Vert L_W \Vert=1$. 证毕.

定义4.4 对于算子 $Q$, $(Qf)(t)\equiv\int_{-\infty}^{\infty}q(s,t)f(s){\rm d}s$, 称 $Q$ 的 Hilbert-Schmidt 范数为 $\Vert Q\Vert_{HS}$, 若

下面将定理 4.1 推广到分数阶 Fourier 变换.

定理4.2 令 $T$ 和 $W$ 均为可测集, $f(t)$ 与其连续分数阶 Fourier 变换 $F_\alpha(u)\ (0<\alpha<\pi)$ 范数均为 1, 且满足 $f$ 在 $T$ 上$\epsilon_T$ 集中, $F_\alpha(u)$ 在 $W$ 上 $\epsilon_W$ 集中, 那么

注4.1 当 $\alpha=\pi/2$ 时, 即为定理 4.1.

证

则

下面证 $\Vert L_W P_T\Vert \le\sqrt{\lvert W\rvert\lvert T\rvert}/\sqrt{2\pi \sin\alpha}.$

其中

由定义 4.4 有 $\Vert L_W P_T\Vert_{HS} ^2=\int_{T}\int_{-\infty}^{\infty}\lvert q(s,t)\rvert^2{\rm d}s{\rm d}t.$

现令 $g_t(s)\equiv q(s,t)$, 当 $t\in T$ 时, 其连续分数阶 Fourier 变换 $G_{t\alpha}(u)$ 为

由文献 [8] 知, $\Vert Q\Vert_{HS}\ge\Vert Q\Vert$, 故 $\Vert L_W P_T\Vert \le\sqrt{\lvert W\rvert\lvert T\rvert}/\sqrt{2\pi \sin\alpha}$. 联立 (4.2) 式, 可得结论

证毕.

下面我们给出一个例子来验证定理 4.2.

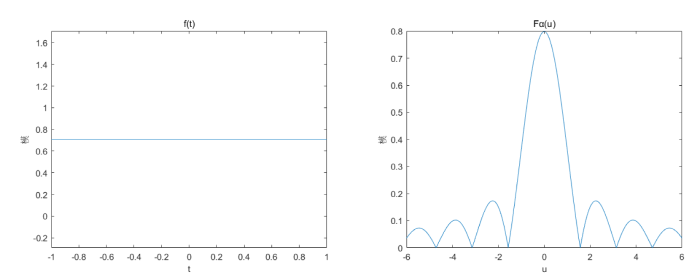
对于函数 $f(t)=\frac{1}{\sqrt{2}}{\rm e}^{-j\cdot \frac{\sqrt{3}}{2}t^2}1_{[-1,1]},$ 满足 $\Vert f\Vert=1,$ 经计算, 当 $\alpha=\frac{\pi}{6}$ 时,

由于 $\lim\limits_{u\rightarrow0}F_\alpha (u)=\sqrt{\frac{1-j\cdot\sqrt{3}}{\pi}}$, 0 为 $F_\alpha (u)$ 的可去间断点, 则以 $F_\alpha(u)$ 在 0 处的极限补充它在该点的定义, 使其为一在 $\mathbb{R}$ 上的函数. 令 $\epsilon_T=0, \epsilon_W=(\frac{1}{\pi}\int_{6}^{\infty}\frac{\sin^2 2u}{u^2}{\rm d}u)^{\frac{1}{2}}<\frac{1}{3}$, 此时 $f$ 在 $T=[-1,1]$ 上 $\epsilon_T$ 集中且 $F_\alpha (u)$ 在 $W=[-6,6]$ 上 $\epsilon_W$ 集中, 这是因为存在定义在 $\mathbb{R}$ 上的 $g(t)=f(t)$ 满足 $\mathbb{R}/T$ 上 $g(t)=0$ 且 $\Vert f-g\Vert=0$, 以及存在定义在 $\mathbb{R}$ 上的函数 $H(u)=F_\alpha (u)1_W$ 满足 $\Vert F_\alpha-H\Vert=\epsilon_W$, 则 $|W|\cdot|T|=24>2\pi\sin\alpha>2\pi \sin\alpha\big(1-(\epsilon_T+\epsilon_W)\big)^2.$ $f(t)$ 及 $F_\alpha(u)$ 的模分别如以图 2 所示.