HIV 感染在宿主体内以 HIV 靶细胞或淋巴组织的形式建立和发展病毒库, 从而进行病毒复制并使 HIV 具有长时间复制的能力. 其中静息感染细胞 (潜伏感染细胞) 中潜在的病毒库是根除游离病毒的最大挑战, 这些静止的记忆细胞不会干扰抗病毒治疗也不会收到免疫反应的影响, 但当它们被相关抗原蛋白激活时, 可以通过裂解释放游离病毒, 从而防止游离病毒被彻底消灭, 在免疫检测和先前的抗逆转录病毒治疗下, 潜伏感染细胞仍允许病毒持续存在. 这些潜伏细胞在被抗原激活后提供了可持续的病毒资源. 因此, 从生物学角度出发建立数学模型来研究潜伏感染细胞及其对 HIV 感染进程的影响是非常有意义的.

近些年来, 已有相关学者建立数学模型以提供对潜伏感染细胞动力学行为的深刻见解. 特别需要提出的是 Rong 等^[1]建立的如下潜伏感染细胞模型

这里$T,T^*,L,V$分别表示易感靶细胞、感染细胞、潜伏感染细胞以及自由病毒的数量. 模型参数$\lambda,d_T$分别表示易感细胞的输入率和自然死亡率,$d_0,\delta,c$分别表示潜伏感染细胞、感染细胞和自由病毒的死亡率. 抗病毒治疗效率用参数$\epsilon$来表示, 双线性感染率用$k$来表示, 参数$\eta$表示潜伏率,$a_1$表示潜伏感染细胞的激活率,$N$表示感染细胞的裂解量. 在文献[1]的基础上, 一系列的工作都已展开, 其中考虑年龄结构的相关模型见文献[2⇓-4],考虑时滞和分布时滞的相关研究见文献[5,6]. 此外考虑 HIV 病毒在宿主体内扩散模型的动力学也有很多学者展开了研究, 其中较为经典的是 Liu 等^[7] 建立了空间异质反应扩散 HIV 细胞模型并考虑了细胞-细胞传播和病毒-细胞感染两种感染途径. 更多关于空间异质反应扩散 HIV 模型动力学研究见文献[8⇓-10]. 考虑到人体一旦感染了 HIV 需要接受终身抗病毒治疗, Wang 等^[11] 建立了周期反应扩散 HIV 细胞模型并研究了周期抗病毒治疗对 HIV 感染动力学的影响. 再此基础上, Wu 等^[12] 建立了具有分布时滞周期反应扩散多菌株 HIV 细胞模型并分析了多菌株之间的演化竞争行为.

虽然上述 HIV 细胞模型包含了常微分方程、泛函微分方程、偏微分方程模型, 相关动力学研究结果也十分丰富, 但是在反应扩散 HIV 细胞模型的基础上考虑非局部感染的研究较少, 尤其是结合周期抗病毒治疗因素的非局部感染空间异质反应扩散 HIV 细胞模型的动力学研究就更加少见. 事实上, 非局部感染在 HIV 感染进程中是十分常见的一个现象, 因为 HIV 不仅会攻击淋巴系统也会随着血液传输进入到其他人体器官组织进行非局部感染和病毒复制. 特别需要提出的是: 这类具有非局部算子的非自治空间异质反应扩散系统的阈值动力学分析是有一定的挑战性. 首先是如何通过更新方程给出模型基本再生数具体泛函表达式而不是抽象的定义, 在此基础上才能利用周期反应扩散模型的耗散性理论和一致持久性理论进行动力学分析; 其次, 非局部算子的存在对模型基本再生数和解动力学行为的数值模拟带来一定的困难. 综上所述, 本文旨在建立具有周期抗病毒治疗和非局部感染的空间异质反应扩散 HIV 细胞模型并对其阈值动力学行为进行分析和数值实现.

受到上述研究的启发，在经典的 HIV 潜伏感染模型^[1] 基础上我们考虑以下三个重要因素

(1) 两种感染途径: 医学研究表明除了病毒对细胞的感染外 (病毒-细胞感染), HIV 感染细胞也可通过与健康的靶细胞直接接触感染 (细胞-细胞传播), 而且其感染能力比病毒的感染能力要强几千倍^[13];

(2) 周期性的抗病毒治疗: 由于现有的 HIV 抗病毒治疗药物不能彻底的消除宿主体内的病毒和感染细胞, 患者需要终身服用 HIV 治疗药物. 目前采用的高效抗病毒治疗 (HAART) 在 HIV 临床治疗过程中主要采用以下几种拮抗剂^[14]: (i) 逆转录酶抑制剂 [RT], 病毒入侵拮抗剂、整合抑制剂 [II], 融合抑制剂 [FI], 蛋白酶抑制剂 [PI]; (ii) 对于细胞间传播, 文献[15]中的研究表明干扰素诱导横跨膜蛋白 (IFITM) [IFI] 可以抑制细胞间的传播; (iii) 对于 HIV 潜伏感染细胞, 文献[16]中的研究证实潜伏在感染细胞中的 HIV 颗粒可以在组蛋白脱乙酶 (HDAC) 抑制剂的刺激下大量释放并进入患者血浆中 (HI). 类似文献[17]中的定义，这些药物的功效可定义为如下函数:$\eta_{RT}(t),\eta_{II}(t),\eta_{PI}(t),\eta_{FI}(t),\eta_{IFI}(t),\eta_{HI}(t):\mathbb{R}\to[0,1],$$\eta_{RT}(t),\eta_{II}(t),\eta_{PI}(t),\eta_{FI}(t),\eta_{IFI}(t),\eta_{HI}(t)\not\equiv 0\ \mbox{或者}\ 1$.由于感染者需要每天定期服用抗病毒药物, 这些药物在摄入的当天其药效会呈现出一个周期性变化即从弱到强再到弱, 因此本文我们假设上述药物功效函数都是$\omega$周期函数, 其中$\omega=12$小时;

(3) 非局部感染: HIV 进入人体后, 首先攻击的是人体的免疫 CD4$^+$T 淋巴细胞, 其主要集中在人体免疫系统中. 但近来医学研究^[18]表明 HIV 病毒可以通过血液攻击人体的消化道系统, 这说明 HIV 不仅仅只是在免疫系统进行局部感染和复制, 也可通过血液传输对人体其他部位的细胞进行非局部感染. Mottoni^[19]提出了以积分算子$(\alpha I):=\int_{\Omega}\alpha(x,y)I(y){\rm d}y$来描述非局部感染,其生物学解释是：在空间$y$位置上的感染个体能有效地以$\alpha(x,y)$的感染率去感染在空间$x$位置上的易感者. 因此, 本文也试图用这种积分算子来描述 HIV 的非局部接触以确保模型的合理性.

考虑以上三个因素, 利用反应扩散模型去研究多感染途径、周期抗病毒治疗、非局部感染以及空间异质性对 HIV 感染进程的综合影响. 为此, 给出如下时间周期非局部接触的 HIV 潜伏感染反应扩散模型

其中$\overline{\Omega}$和$\partial\Omega$分别表示有界区域$\Omega$的闭包和边界. 齐次 Neumann 边界条件意味着个体永远无法穿过区域$\Omega$的边界,$\textbf{n}$表示区域$\Omega$边界的外法向量. 模型中状态变量和参数的生物学意义如下: 状态变量$u_i(x,t)\ (i=1,2,3,4)$表示健康靶细胞、HIV 潜伏感染细胞、具有感染力的感染细胞、自由病毒在空间位置$x$和$t$时刻的分布. 参数$\Lambda(x)$表示健康靶细胞的补充率,$\alpha_1(x,y)$和$\alpha_2(x,y)$分别表示空间位置$y$处的感染细胞和自由病毒与空间位置$x$处的健康靶细胞的有效接触率,$\beta_1(x,t)$和$\beta_2(x,t)$分别表示感染细胞和自由病毒的感染率, 考虑到抗病毒治疗的影响, 我们假设$\beta_1(x,t)=\beta_1(x)(1-\eta_{IFI}(t)),\beta_2(x,t)=\beta_2(x)(1-\eta_{II}(t))(1-\eta_{FI}(t))(1-\eta_{RT}(t))$. 参数$d_i(x)$和$\mu_i(x)\ (x=1,2,3,4)$分别表示健康靶细胞、潜伏感染细胞、感染细胞、自由病毒的扩散率和自然死亡率, 参数$\epsilon(x)\in(0,1)$表示感染细胞进入静息状态的比例,$m(x,t)=m(x)\eta_{HI}(t)$表示潜伏感染细胞的激活率, 参数$\delta(x,t)=\delta(x)(1-\eta_{PI}(t))$表示感染细胞的凋亡率,$N(x)$表示裂解量. 模型中的参数都是依赖于空间$x$, 以此来刻画空间的异质性.

为了后续对系统 (2.1) 进行动力学分析, 首先给出关于模型参数的假设如下

定义 3.1 对于系统 (2.1), 假设

(1)$d_i(x)\ge d_i>0,i=1,2,3,4$, 并且当$x\in\overline{\Omega}$时,$d_i(x)$是严格正的;

(2) 对任意的$(x,t)\in\Omega\times (0,+\infty)$, 有

接下来讨论系统 (2.1) 的适定性问题. 为此, 定义连续的 Banach 空间$X=C(\overline{\Omega},\mathbb{R})$和$Y=X^4$, 其范数定义为

显然$(X,X_+), (Y,Y_+)$都是强有序空间, 其中$X_+,Y_+$分别表示空间$X$和$Y$的正锥. 我们定义空间$X$中的线性算子$\mathcal{A}[\phi](x,t)=\mbox{diag}(\mathcal{A}_i(t))\phi(x)$如下

其定义域$D_i=\{\phi\in X|\nabla(d_i\nabla \phi)\in X, [d_i\nabla\phi]\cdot\textbf{n}=0,x\in\partial\Omega\}$. 由定理 1.2^[20]可知$\mathcal{A}_i\ (i=1,2,3,4)$是紧的且在空间$X$中生成$C_0$半群$\{\mathcal{T}_i\}_{t\ge s}$, 同时存在常数$\gamma_i>0$使得$(\mathcal{T}_i(s,t))\le {\rm e}^{-\gamma_i(t-s)}, t\ge s$. 定义非线性算子$\mathcal{F}[\phi](x,)=(\mathcal{F}_1[\phi](x,t),\cdot\cdot\cdot,\mathcal{F}_4[\phi](x,t))^T$如下

结合 (3.1) 和 (3.2) 式, 将系统 (2.1) 改写为如下抽象柯西问题

接下来, 给出系统(3.3) 的解在空间$Y$中全局存在性定理.

定理 3.1 满足初始条件$\phi=(\phi_1,\phi_2,\phi_3,\phi_4)\in Y_+$的系统 (3.3) 存在唯一的解$(u_1,u_2,u_3,$$u_4)\in [0,\infty)$. 此外, 系统 (3.3) 生成一个连续的解半流$\Phi_t[\phi](\cdot,s)=(u_1(\cdot,t),u_2(\cdot,t),u_3(\cdot,t),$$u_4(\cdot,t); \phi(\cdot,s)), (x,t)\in\Omega\times(s,+\infty), s\in\mathbb{R}_+$, 且$\Phi_t$在$Y_+$中有一个全局吸引子.

证 首先证明系统解的局部存在性. 非线性算子$\mathcal{F}$的局部利普希兹连续性显然是得到保证的, 那么接下来还需要证明

利用文献[21, 定理 3]中的方法很容易得证 (3.4) 式, 从而由文献[22,推论 4.30] 可得系统 (3.3) 在其最大存在区间$\in[0,+T_m)$,$T_m<\infty$上存唯一的广义解$w(x,t;\phi)\in Y_+$. 为了完成定理的证明, 还需要证明系统 (3.3) 的最终有界性. 事实上, 系统 (3.3) 解的局部存在性保证了其唯一解可被表达为

利用比较原理, 从系统(2.1) 第一个方程中得

由文献[23,引理 2.1] 可知 (3.5) 存在唯一全局渐近稳定的正平衡态$u^*_1(x)=(-\mathcal{A}_1)^{-1}(\Lambda(x))$. 不失一般性, 我们假设$s=0,$则有$u_1(\cdot,t)\le\mathcal{T}_1(0,t)\phi_1(\cdot)+\int_0^t\mathcal{T}_1(x,t)\Lambda(\cdot){\rm d}s$, 从而有

继而可得$\sup\limits_{t\in[0,T_m)}||u_1(\cdot,t)||_X\le||\phi_1||_X+\overline{\Lambda}/\gamma_1:=\textbf{B}_1$. 从系统 (2.1) 第三个方程中可得

其中$\underline{\mu}=\min\{\underline{\mu}_1,\underline{\mu}_2,\underline{\mu}_3\}$. 然后可得

进一步可得$\frac{\partial u_2}{\partial t}\le\mathcal{A}_2(x,t)+\overline{\epsilon}\textbf{B}_1(\overline{\beta}_1\overline{\alpha}_1\textbf{B}_3+\overline{\beta}_2\overline{\alpha}_2\textbf{B}_4)$.继而可得

综上, 系统 (2.1) 的解是最终有界的, 也就是说系统 (2.1) 是耗散的, 再结合系统解的局部存在性可知系统 (3.3) 的解是全局存在的.

最后, 定义算子族$\Psi_t[\phi](x,s)=w_t(x,s;\phi)=w(x,s+t;\phi),x\in\overline{\Omega}, t,s\in\mathbb{R}_+$. 由于模型参数的周期性, 显然可知$\Psi_{t+\omega}[x,s+\omega)=\Psi_t(x,s)$. 定义庞加莱映射$\mathcal{P}(\phi)=\Psi_{\omega}(\phi):Y_+\to Y_+$. 由于系统 (2.1) 是耗散的, 可知算子族$\Psi_{\omega}$有全局吸引子$\mathbb{A}$. 定理证毕.

定理 3.1 的结果显示$\Psi_t(\cdot,t)$有一个周期吸引子$\{\mathbb{A}(t)\}_{t\ge 0}$,$\mathbb{A}(t+\omega)=\mathbb{A}(t), t\in\mathbb{R}_+$. 为了后续讨论系统 (2.1) 解的阈值动力学行为, 我们令系统 (2.1) 的初始值都在以下正向不变集中

其中$\hat{B}_j$表达式在定理 3.1 证明过程中已给出.

此节致力于推导系统 (2.1) 的基本再生数. 为此, 定义有序的 Banach 空间:$B_{\omega}(X,\mathbb{R}_+)$, 其包含所有从$\mathbb{R}_+$映射到$X$的$\omega$-周期函数. 空间$B_{\omega}(X,\mathbb{R}_+)$的范数为

类似文献[22,引理 2.1], 有以下关于系统 (2.1) 无感染平衡态$E_0$的存在性结论.

引理4.1 算子$\mathcal{A}_1$如 (2.1) 式中所示, 则系统 (2.1) 有唯一的无感染平衡态$E_0=(u^0_1(\cdot),0,0,0)\in Y_+$, 其中$u^0_1(x)$是系统 (3.5) 的解.

系统 (2.1) 在无感染平衡态$E_0$处的线性化系统 (只包含感染仓室) 如下

对系统 (4.1) 中各个方程关于时间$t$积分可得

其中$\mathcal{T}_j,j=2,3,4$是由线性算子$\mathcal{A}_j$生成的$C_0$-半群. 为了推导下一代再生算子, 从生物学角度出发, 假设一开始只有感染细胞存在, 即$\phi_2=\phi_4=0$. 将式 (4.2) 和 (4.4) 带入到式 (4.3) 中可得

现令$s\to-\infty$, 由于$||\mathcal{T}_j(s,t)||\le {\rm e}^{-\gamma_j(t-s)},t>s$, 从式 (4.5) 中可得$\mathcal{T}_3(s,t)\phi_3(x,s)\to 0$. 因此, 对任意的$\phi\in B_{\omega}, (x,t)\in\overline{\Omega}\times\mathbb{R}_+$, 可定义以下下一代再生算子$\mathcal{R}:B_{\omega}\to B_{\omega}$

注 4.1 为了更好地理解下一代再生算子$\mathcal{R}$的生物学意义, 我们对式 (4.6) 作出如下解释: 假设在 HIV 感染第一次发生时有$\phi$个感染细胞, 那么$\mathcal{T}_3(t-\tau,t)(1-\epsilon(x))u^0_1(x)\beta_1(x,t-\tau)\int_{\Omega}\alpha_1(x,y)\phi(y,t-\tau){\rm d}y$表示在$t-\tau$时刻通过细胞间传播新增的 HIV 具有感染力的感染细胞 (在$t$时刻还具有感染力), 而$\mathcal{T}_3(t-\tau,t)(1-\epsilon(x))u^0_1(x)\beta_2(x,t-\tau)\int_{\Omega}\alpha_2(x,y)\int_0^{+\infty}\mathcal{T}_4(t-\tau-l,t-\tau)\delta(y,t-\tau-l)\phi(y,t-\tau-l){\rm d}l{\rm d}y$表示通过病毒-细胞感染而新增的 HIV 具有感染力的感染细胞. 于此同时, 潜伏感染细胞在通过特异蛋白的作用下重新被激活变成新的具有感染力的感染细胞, 这就是式 (4.6) 中第二个积分项所表达的生物学意义.

根据周期反应扩散传染病模型基本再生数的定义^[23]可得系统 (2.1) 的基本再生数$\mathcal{R}_0=r(\mathcal{R})$, 其中$r(\mathcal{R})$是算子$\mathcal{R}$的谱半径. 此外, 关于算子$\mathcal{R}$, 有如下结论

引理 4.2 下一代再生算子$\mathcal{R}$是强正的和紧的.

证 算子$\mathcal{R}$的强正性是显然的. 接下来, 需要证明它的紧性, 即证明算子$\mathcal{R}$一致有界且等度连续^[10]. 令$\textbf{C}\subset \mathcal{D}$使得$||\phi||_{\textbf{C}}\le B, \phi\in\textbf{C}$. 由式 (4.6) 可得

于是,$\mathcal{R}$的一致有界性得证. 接下来证明算子$\mathcal{R}$的紧性. 定义算子

注意到$\int_{-\infty}^t=\int_0^t+\sum\limits_{n=0}^{\infty}\int_{-(n+1)\omega}^{-n\omega}$, 则有

显然,$\mathcal{R}=\widetilde{\mathcal{R}}_3+\widetilde{\mathcal{R}}_4+\sum\limits_{n=0}^{\infty}[\widetilde{\mathcal{R}}^n_3+\widetilde{\mathcal{R}}^n_4]$. 为了证明$\mathcal{R}$的紧性, 还需证明$\{\mathcal{R}[\phi](t)|\phi\in\textbf{C}\}$是等度连续的. 对任意的$t_k\ (k=1,2)\in\mathbb{R}_+,t_1<t_2$, 有

这说明$\widetilde{\mathcal{R}}_3$是等度连续的. 类似地, 可知$\widetilde{\mathcal{R}}_4$是等度连续的. 同理, 可得

这说明$\widetilde{\mathcal{R}}^n_3$是等度连续的. 类似地, 可知$\widetilde{\mathcal{R}}^n_4$也是等度连续的. 利用 Kolmogorov 定理^[24], 可知$\mathcal{R}$是紧的. 引理证毕.

由于算子$\mathcal{R}$是紧的, 根据 Krein-Rutman 定理^[25]可知$\mathcal{R}_0$是唯一具有正特征向量的正特征值. 定义线性算子$\mathcal{L}:\mathcal{D}_{\omega}\to B_{\omega}$如下

其中$(x,t)\in\overline{\Omega}\times\mathbb{R}_+$, $\phi\in\mathcal{D}_{\omega}:=D^2_{\omega}\oplus D^3_{\omega}\oplus D^4_{\omega}$, $D^j_{\omega}(X,\mathbb{R}_+)=\{\phi_j\in B_{\omega}(X,\mathbb{R}_+):\phi_{t,j}$, $\mathcal{A}_j\phi_{t,j}\in\ B_{\omega}(X,\mathbb{R}_+,[d_j(x)\nabla u_j(x,t)]\times\textbf{n}=0,x\in\partial\Omega, j=2,3,4\}$. 显然算子$\mathcal{L}$是紧的. 定义

分别是算子$\mathcal{L}$的谱和谱界, 其中$\textbf{I}$表示恒等算子. 根据文献[26,引理 3.2], 可得如下引理

引理 4.3 对于(5.2) 式中的算子$\mathcal{L}$, 如果$\lambda$是关于特征问题$\mathcal{L}\tilde{\phi}=\lambda\tilde{\phi}$的主特征值, 其中$\tilde{\phi}$是正的特征函数, 那么, 对任意的$\lambda\in\rho(\mathcal{L})\{\tilde{\lambda}\}$都有$\mbox{Re}\lambda<\tilde{\lambda}$成立, 其中$\tilde{\lambda}$是孤立且代数单的.

对任意的$\lambda\in(c,+\infty),c>0$, 定义拉普拉斯算子$\hat{\mathcal{R}}_{\lambda}:B_{\omega}\to B_{\omega}$

其中$\phi\in C_{\omega}(X,\mathbb{R}_+),t\in\mathbb{R}_+$, 由于$\mathcal{T}_j\ (j=2,3,4)$是紧算子, 可知算子$\hat{\mathcal{R}}_{\lambda}$是正的和紧的. 利用 Krein-Rutman 定理可知$\rho(\mathcal{L})>0$. 根据算子$\mathcal{R}$的定义可得$\mathcal{R}_0=r(\mathcal{R})=r(\hat{\mathcal{R}}_{\lambda})=\rho(0)$. 利用文献[22,引理 3.4] 证明方法可得基本再生数$\mathcal{R}_0$和$\mathcal{L}$的关系如下

引理 4.4 令$s(\mathcal{L})$为线性算子$\mathcal{L}$的谱界, 则$r(\mathcal{R})-1$与$s(\mathcal{L})$同号.

证 此证明方法具体可参见文献[22,引理 3.4] 证明过程. 因此,在这里省略证明的过程. 为了实现文章数值部分对基本再生数$\mathcal{R}_0$值估算, 现给出结论

引理 4.5^{[27,定理 3.8]} 对$\eta\in\mathbb{R}_+$, 下面周期抛物型问题

存在唯一的具有正特征函数$\phi\in\mathcal{D}_{\omega}$的主特征值$\eta_0$且$\eta_0=\mathcal{R}_0$.

此节主要研究系统解依赖于关键阈值-基本再生数$\mathcal{R}_0$的动力学行为. 令$w_t(x,s;\phi)=\Psi_t(x,s;\phi)=(u_1(x,t),u_2(x,t),u_3(x,t),u_4(x,t))$是系统满足初始条件$\phi=(\phi_1,\phi_2,\phi_3,\phi_4)\in Y$的解. 根据反应扩散传染病模型的一致持久性理论^[28], 可知如果存在一常数$\zeta>0$使得对任意的$\phi\in Y$都满足$\phi_j\not\equiv 0$, 那么有$\min\min\limits_{x\in\Omega}\liminf\limits_{t\to+\infty}\Psi(x,s;\phi)\ge\zeta$都成立. 为了对系统进行动力学分析, 首先给出以下引理

引理 5.1 对满足初始条件$\phi\in Y_+$的系统 (2.1) 的解, 有以下结论成立

(1) 如果存在一些$s>0$使得$u_j(\cdot,s;\phi)\not\equiv 0$, 那么当$t>s$时有$u_j(\cdot,s;\phi)>0$;

(2) 对任意的$\phi\in Y_+,t>s$, 有$u_1(\cdot,t;\phi)>0$成立且$\liminf\limits_{t\to+\infty}u_1(\cdot,t;\phi)>\zeta$, 其中$\eta$为正常数.

证 分两步进行证明. 首先证明结论 (1) 成立. 由系统 (2.1) 解的非负性可知

对于系统 (5.1), 如果存在一些常数$s>0$使得$u_j(\cdot,s;\phi)\not\equiv 0$, 那么由极大值原理可知$u_j(\cdot,t;\phi)>0$. 结论 (1) 得证. 接下来证明结论 (2). 由定理 3.1 的结论可知存在两个正数$\tilde{B}_3$和$\tilde{B}_4$使得$\int_{\Omega}u_k(y,t;\phi){\rm d}y\le\tilde{B}_k, k=3,4$. 假设$v(x,t;\phi)$满足如下系统

利用比较原理可得$u_1(x,t;\phi)\ge v(x,t;\phi)>0, (\phi,t)\in X_+\times\mathbb{R}_+$. 继而$\liminf_{t\to+\infty}u_1(x,t;\phi)\ge\inf_{(x,t)\in\overline{\Omega}\times[\omega]}u^0_1(x)$. 结论 (2) 得证. 引理证毕.

下面, 给出系统 (2.1) 无感染平衡态$E_0$的全局稳定性和系统 (2.1) 的一致持久性结论.

定理 5.1 如果系统 (2.1) 的初始条件$\phi\in Y_+$, 那

(1) 当$\mathcal{R}_0<1$时, 无感染平衡态$E_0=(u^0_1(x),0,0,0)$是全局渐近稳定的;

(2) 当$\mathcal{R}_0>1$时, 则系统 (2.1) 是一致持久的,即存在一个正数$\zeta$使得当$\phi_j\not\equiv 0\ (j=2,3,4)$,$\phi\in Y$时, 总有$\min\limits_{x\in\overline{\Omega}}\liminf\limits_{t\to+\infty}u_i(x,t;\phi)\ge\zeta$,$i=1,2,3,4$成立. 此外, 系统 (2.1) 至少存在一个正周期平衡态.

证 从引理 5.1 结论可知存在$n\in\mathbb{N}_+$使得$u_1(x,t)\le u^0_1(x)+\zeta$,$x(x,t)\in\overline{\Omega}\times[n\omega,+\infty)$. 于是可得

定义$\mathcal{L}^{\zeta}:\mathcal{D}_{\omega}(X,\mathbb{R}_+)\to B_{\omega}(X,\mathbb{R}_+)$

其中$\phi\in\mathcal{D}_{\omega}$. 由于模型特征问题的主特征值是连续依赖模型参数的, 因此可知当$\mathcal{R}_0<1$有$\tilde{\lambda}^{\zeta}<0$, 其中$\tilde{\lambda}^{\zeta}$是算子$\mathcal{L}^{\zeta}$的主特征值. 令$\phi_{\zeta}\in\mathcal{D}_{\omega}$是关于特征值$\tilde{\lambda}^{\zeta}$的特征函数. 选择$b_{\zeta}=(b^2_{\zeta},b^3_{\zeta},b^4_{\zeta})$使得$u_j(\cdot,t_{\zeta})\le b^j_{\zeta}\phi^j_{\zeta}(\cdot,t_{\zeta})$. 显然${\rm e}^{\tilde{\lambda}^{\zeta}(t-t_b)}b_{\zeta}\phi_{\zeta}(x,t)$是如下系统的解

利用比较原理[c11]可得$u_j(\cdot,t_{\zeta})\le {\rm e}^{\tilde{\lambda}^{\zeta}(t-t_b)}b_{\zeta}\phi_{j,\zeta}(\cdot,t_{\zeta})$. 由引理 4.4 可知当$\mathcal{R}_0<1$时$\tilde{\lambda}_{\zeta}<0$, 继而有$u_j(\cdot,t)\to 0, t\to+\infty$. 此外, 对固定的$t_{\zeta}\in\mathbb{R}_+$, 定义

从系统 (2.1) 第一个方程中可得

这意味着$||u_1(\cdot,t)-u^0_1(\cdot)||_X\to 0,$$t\to+\infty$. 综上可知当$\mathcal{R}_0<1$时无感染平衡态$E_0$是全局渐近稳定的. 接下来证明结论 (2). 为此, 先给出如下符号定义

其中$\gamma_+(\phi)$是系统解半流的正向轨线. 从引理 5.1 的结论可知$\Psi^a_{\omega}(Y_0)\subset Y_0,\Psi^a_{\omega}(\partial Y_0)\subset \partial Y_0,a\in\mathbb{N}$. 此外, 易知$\omega(\phi)=\{E_0\}, \phi\in M_{\partial}$. 下面证明$E_0$在$Y_+$中是弱排斥的, 即

利用反证法证明 (5.3) 式, 假设式 (5.3) 不成立, 则存在常数$a$使得

因此, 对任意的$t>a_0\omega, x\in\overline{\Omega}$, 有$u_1(x,t;\phi)\ge u^0_1(x)-\zeta_0,u_j(,;\phi)<\zeta_0, j=2,3,4$, 进而从系统 (2.1) 中可得

令$\phi^{\zeta_0}_{\mathcal{P}}$是$\mathcal{P}^{\zeta_0}:Y_+\to Y_+$的特征值$\gamma^{\zeta_0}$对应的特征函数, 其中$\mathcal{P}^{\zeta_0}(\phi)=\Psi^{\zeta_0}_{\omega}(\phi)=w^{\zeta_0}(x,\omega+t;\phi),(x,t)\in\overline{\Omega}\times[0,\omega)$.选取足够小的$b=(b^2_{\zeta_0},b^3_{\zeta_0},b^4_{\zeta_0})$使得

从而得到

其中$(w^{\zeta_0}_2,w^{\zeta_0}_3,w^{\zeta_0}_4)$是以下系统的解

由$\phi^{\zeta_0}_{\mathcal{P}}$的正性可得$u_j(x,t;\phi)\to+\infty, x\in\Omega, a\to+\infty, j=2,3,4$. 这显然与系统 (2.1) 的耗散性矛盾. 因此式 (5.3) 成立, 即$E_0$在$Y_+$中是弱排斥的. 接下来我们继续证明系统 (2.1) 的一致持久性, 即$\liminf_{a\to+\infty}\tilde{\rm d}(\Psi^a_{\omega}(\phi),\partial Y_0)\ge\zeta, \phi\in Y_0$, 其中$\tilde{\rm d}$表示豪斯多夫距离 (Hausdorff distance)^[29]. 通过上述的分析可知$E_0$在$Y_0$中关于$\Psi_{\omega}$是孤立不变集以及$W^s(E_0)\cap Y_0=\emptyset$, 其中$W^s(E_0)$是$E_0$的稳定流行. 根据一致持久性定理的循环定理^[30], 可知$\Psi_{\omega}$关于$(Y_0,\partial Y_0)$是一致持久的. 此外, 由庞加莱映射$\mathcal{P}$的紧性可知$\Psi_{\omega}$存在一个全局吸引子$\mathbb{A}$. 因此,$\Psi_t$存在一个$\omega$-周期吸引子$\mathbb{A}(t)\subset Y_+$. 从而,$\mathbb{A}_0=\Psi_{\omega}\mathbb{A}_0\subset\textbf{C}_0\subset Y_0$, 其中$\textbf{C}_0:=\cup_{t\in(0,\omega]}\Psi_t(\mathbb{A})$, 进而可得$\min\min\limits_{x\in\Omega}\liminf\limits_{t\to+\infty}\{u_1,u_2,u_3,u_4\}\ge\zeta$. 最后, 结合系统 (2.1) 的一致持久性和$\Psi_t$存在$\omega$周期吸引子$\mathbb{A}$, 可保证系统 (2.1) 正周期解的存在性. 定理证毕.

此节对系统 (2.1) 进行数值模拟. 为了简便起见, 假设空间$\Omega=[-20,20]$, 参考文献[12], 模型参数和初值设定如下

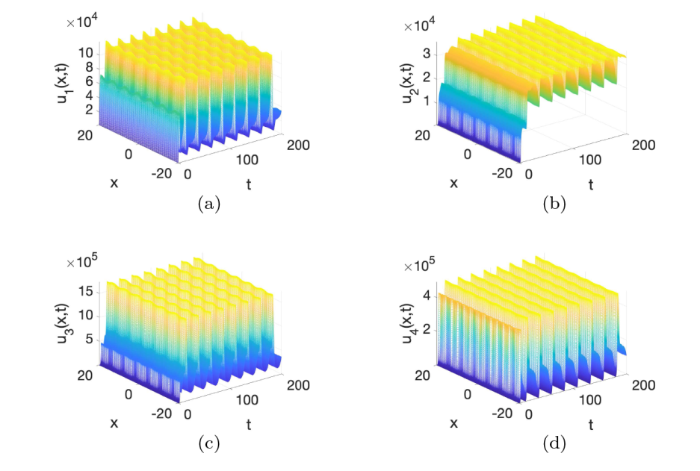
为了对系统解进行数值模拟, 首先要计算模型基本再生数的值. 根据式 (6.1) 中列出的参数值, 利用文献[31]中的计算方法来估算系统 (2.1) 基本再生数的值. 为此, 令空间和时间步长为$\Delta x=\Delta t=40/k, k\in\mathbb{N}$. 记$x_n=-20+n\Delta x, t_n=n\Delta t, n\in\mathbb{N}$. 令$\alpha_{l,nm}=\alpha_{l,nm}=\alpha_{l}(x_n-x_m), n,m\in\mathbb{N}$, $\beta^n_l=\beta_l(x_n), l=1,2$. $d_i(x)=d_i(x_n)$, $\mu_i(x)=\mu_i(x_n)$, $m(x)=m(x_n)$, $\delta(x)=\delta(x_n)$, $\eta_v(t)=\eta_v(t_n)$, $v=PI,HI,RT,II,IFI,FI, i=1,2,3,4$. 然后利用数学软件 MATLAB 可以计算得到系统 (2.1) 基本再生数$\mathcal{R}_0\approx 1.355$(见图1(a)). 当选取$\beta_1(x)=2.05\times 10^{-4}(1+0.15\cos x)$其他参数如式 (6.1) 所示, 计算得到$\mathcal{R}_0\approx 0.6662$(见图1(b)).

从定理 5.1 结论 (1) 中可知当$\mathcal{R}_0<1$时系统 (2.1) 的无感染平衡态是全局渐近稳定的. 事实上, 从图2 中可以看出系统的解$u_2,u_3,u_4$随着时间的推移是趋于 0 平面的, 这验证了定理 5.1 结论 (1) 的正确性, 也就是说当$\mathcal{R}_0<1$时 HIV 感染在宿主体内是被消除的. 从图3 中我们可以看出系统的解随着时间的推移出现周期性振荡的, 这说明 HIV 感染在宿主体内持久存在的, 这验证了当$\mathcal{R}_0>1$时系统 (2.1) 是一致持久的结论的正确性.

在此小节中, 为了研究周期性抗病毒药物治疗对 HIV 在宿主体内感染进程的影响, 令

其他模型参数取值同式 (6.1) 所示. 通过数值模拟发现再增强抗病毒药物药效之后, 潜伏感染细胞、感染细胞、自由病毒粒子在宿主体内的浓度水平明显减少 (见图4(a)-(c) 所示). 通过和图3 比较, 如图4(d)-(f) 所示, 其中橙色曲线是未加强药物疗效时潜伏感染细胞、感染细胞、自由病毒粒子在宿主体内的浓度水平, 蓝色曲线是增强药物疗效后潜伏感染细胞、感染细胞、自由病毒粒子在宿主体内的浓度水平, 对比后我们发现, 虽然持续的高疗效的抗病毒药物治疗并不能彻底的清除宿主体内的 HIV 病毒, 但是可以让宿主体内病毒的浓度长时间维持在低水平, 这有助于延长感染者的存活时间甚至达到让感染者终身处于 HIV 感染状态而不会出现艾滋病病症^[8].

为了研究非局部感染对 HIV 感染动力学的影响, 引用文献[31]介绍的四种非局部内核函数形式如下

对应的基本再生数值以及系统解在$x=0$处的曲线分别如图5和6所示, 模型其他参数取值同式 (6.1). 从图5中可以看出内核函数的形式对基本再生数的值影响非常明显, 同时从图6中可以看出内核函数的形式对 HIV 病毒、感染细胞、潜伏感染细胞在宿主体内的载量也有明显的影响, 这同时也说明了空间异质性对 HIV 的影响也不容忽视. 换句话说, 宿主体内不同器官组织内的 HIV 感染水平是有明显差异的. 因此, 在 HIV 临床治疗过程中需要考虑到人体不同组织器官中 HIV 感染水平的差异性.

为了研究周期性抗病毒治疗、非局部感染以及空间异质性对 HIV 感染进程的影响, 本文建立了一类非自治空间异质反应扩散 HIV 细胞模型去分析 HIV 感染阈值动力学行为. 首先, 通过更新方程推导出下一代再生算子$\mathcal{R}$, 通过证明算子$\mathcal{R}$的一致有界性和等度连续性得到$\mathcal{R}$的紧性, 在利用 Krein-Rutman 定理证明了特征问题具有正特征向量的主特征值的存在性, 从而定义其谱半径为系统的基本再生数,$\mathcal{R}_0$. 随后, 我们分析了模型的动力学行为, 具体地, 当$\mathcal{R}_0<1$时无感染平衡态是全局渐近稳定的; 利用反应扩散传染病模型的耗散性理论和持久生存理论证明了当$\mathcal{R}_0>1$时 HIV 感染在宿主体内是持久存在的并且系统至少存在一个周期正平衡态. 最后, 通过数值模拟分析了关键因素对 HIV 感染的影响. 结果表明: (1) 周期性抗病毒治疗可以将宿主体内的 HIV 病毒载量长期维持在低水平, 这有助于延长患者的存活寿命; (2) 空间异质性对 HIV 感染进行的影响不可忽略; (3) 非局部感染的形式对 HIV 感染进程的影响明显. 因此在临床治疗时更应关注人体不同器官组织的 HIV 感染水平, 这有助于制定更加有效的治疗方案. 本文的不足之处在于并未考虑因药物治疗引起的耐药性所带来的影响, 这是我们未来工作内容的重点之一.