1 引言
(1.1) $\begin{equation}\min f(x), x\in\mathbb{R}^n,\end{equation}$
其中$f(x):\mathbb{R}^n\rightarrow\mathbb{R}$是连续可微函数. 共轭梯度法是解决无约束优化问题(1.1)的有效方法之一, 其一般迭代格式为
(1.2) $\begin{equation}x_{k+1} = x_k + \alpha_k d_k,\end{equation}$
(1.3) $\begin{equation}d_k=\begin{cases} -g_k,\quad &k=1,\\ -g_k+\beta_k d_{k-1}, &k\ge 2,\end{cases}\end{equation}$
其中$g_k:=\nabla f(x),$$\alpha_k$是通过某种线搜索产生的步长,$d_k$为搜索方向,$\beta_k$为共轭参数. 不同的共轭参数对应不同的共轭梯度法, 关于$\beta_k$的著名公式有[1 ⇓ ⇓ ⇓ -5 ]
其中$y_{k-1}=g_k-g_{k-1}.$上面四个公式对应的共轭梯度法分别称为$\rm{FR}$方法,$\rm{DY}$方法,$\rm{PRP}$方法和$\rm{HS}$方法. 特别地, 当目标函数是二次函数且采取精确线搜索, 以上四种算法是等价的.众所周知,$\rm{FR}$方法和$\rm{DY}$方法有良好的收敛性质,$\rm{PRP}$方法和$\rm{HS}$方法有良好的数值表现. 为寻求既保证良好的收敛性又具有优越的数值效果的算法, 许多学者做出了研究, 得到了一些新的算法[6 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -14 ] .
共轭梯度法常见的线搜索有标准 Wolfe 线搜索, 即
(1.4) $\begin{equation}\begin{cases} f(x_k+\alpha_k d_k)\le f(x_k)+\rho \alpha_k g_k^T d_k,\\ g(x_k+\alpha_k d_k)^T d_k\ge \sigma g_k^T d_k,\end{cases}\end{equation}$
(1.5) $\begin{cases} f(x_k+\alpha_k d_k)\le f(x_k)+\rho \alpha_k g_k^T d_k,\\ \vert g(x_k+\alpha_k d_k)^T d_k\vert\le -\sigma g_k^T d_k,\end{cases}$
PRP 方法是目前被认为数值表现最好的共轭梯度法之一, 当产生一个小步长时, PRP 方法产生的搜索方向$d_k$能够自动靠近负梯度方向, 从而具有自动重启的特点. Powell[15 ] 证明了 PRP 方法在精确线搜索下对于一致凸函数的全局收敛性. 对于非凸函数, 为了避免相邻的两个方向趋于反向, Powell 在文献[16 ]中建议将$\beta_k$限制非负. Gilbert 和 Nocedal[17 ] 给出了$\rm{PRP}^{+}$方法, 即
在强 Wolfe 线搜索下和假定充分下降条件成立, 即存在常数$c>0$满足
(1.6) $\begin{equation}g_k^T d_k\le -c\Vert g_k\Vert^2, \forall k\ge 1,\end{equation}$
证明了$\rm{PRP}^{+}$方法对于一般非凸函数的全局收敛性.
文献[18 ]提出了一种修正的 PRP 方法, 我们称为 WYL 共轭梯度法, 其共轭参数为
(1.7) $\begin{equation}\beta_k^{WYL}=\frac{g_k^T (g_k-\frac{\Vert g_k\Vert}{\Vert g_{k-1}\Vert}g_{k-1})}{\Vert g_{k-1}\Vert^2},\end{equation}$
并给出了 WYL 共轭梯度法在强 Wolfe 线搜索下且参数满足$0<\rho<\sigma<\frac{1}{4}$时的全局收敛性.
Birigin 和 Martinez[19 ] 结合谱梯度法和共轭梯度法提出谱共轭梯度法, 将迭代格式(1.3)式推广为如下形式
(1.8) $\begin{equation}d_k=\begin{cases} -g_k,\quad &k=1,\\ -\theta_k g_k+\beta_k d_{k-1}, &k\ge 2,\end{cases}\end{equation}$
虽然上述的谱共轭梯度法在实际计算中有良好的数值表现, 但是不能保证其搜索方向的下降性. 为此, 张和周[20 ] 提出如下形式的谱共轭梯度法
(1.9) $\begin{equation}d_k=\begin{cases}-g_k,\quad &k=1,\\ -(1+\beta_k\frac{g_k^T d_{k-1}}{\Vert g_k\Vert^2}) g_k+\beta_k d_{k-1}, &k\ge 2.\end{cases}\end{equation}$
显然, 上面的搜索方向$d_k$对于任意形式的$\beta_k,$充分下降条件(1.6)式都成立, 且
(1.10) $\begin{equation}g_k^T d_k=-\Vert g_k\Vert^2.\end{equation}$
受文献[18 ]和[20 ]的启发, 为推广 WYL 共轭梯度法在强 Wolfe 线搜索下参数$\sigma$的取值范围, 利用(1.7)和(1.9)式构造搜索方向, 我们提出 WYL 型谱共轭梯度法. 若采用精确线搜索, 则$g_k^T d_{k-1}=0$, 该 WYL 型谱共轭梯度法即是 WYL 共轭梯度法. 特别地, 该 WYL 型谱共轭梯度法能够保证在独立于线搜索的情况下, 其搜索方向满足充分下降性. 在强 Wolfe 线搜索下且参数$0<\rho<\sigma<1$时, 我们证明了其全局收敛性. 最后, 相应的数值实验结果表明, 该 WYL 型谱共轭梯度法的数值效果优于 WYL 和$\rm{PRP}^{+}$共轭梯度法.
2 算法框架和假设
利用强 Wolfe 线搜索(1.5)式, 共轭参数(1.7)式和搜索方向(1.9)式, 我们给出 WYL 型谱共轭梯度算法 (简记为 SWYL 算法) 的算法框架
步骤 1 任取初始点$x_1\in\mathbb{R}^n$, 参数$0<\rho<\sigma<1$. 给定终止精度$\epsilon>0$,$d_1=-g_1$, 令$k:=1.$
步骤 2 若$\Vert g_k\Vert\le\epsilon$, 则终止. 否则, 转步骤3.
步骤 3 采用强Wolfe线搜索准则(1.5)式计算步长$\alpha_k.$
步骤 4 按(1.2)式更新迭代点, 计算$g_{k+1}:=g(x_{k+1}),$利用(1.7)和(1.9)式计算搜索方向$d_{k+1}.$
为了证明 SWYL 算法的全局收敛性, 下面给出所需要的两个常规假设.
(H1) 水平集$\varOmega=\left\{x\in\mathbb{R}^n|f(x)\le f(x_1)\right\}$有界, 即存在常数$B>0$满足
(2.1) $\begin{equation}\Vert x\Vert\le B, \forall x\in\varOmega.\end{equation}$
(H2) 在水平集$\varOmega$的某个邻域$U$上, 梯度函数$g(x)$是Lipschitz连续的, 即存在$L>0$有
(2.2) $\begin{equation}\Vert g(y)-g(x)\Vert\le L\Vert y-x\Vert, \forall x,y\in U.\end{equation}$
在假设(H1)和(H2)成立的情况下, 则存在常数$\overline{\gamma}>0$满足
全文我们总是假设$g_k\neq 0$对所有的$k\ge 1$都成立, 否则我们已经找到稳定点, 算法将会终止.
3 收敛性分析
下面的引理给出著名的 Zoutendijk 条件[21 ] , 其在下降算法的全局收敛性分析中有着重要的作用, 该引理在文献[22 ]中给出了具体的证明.
引理 3.1 若假设(H1)和(H2)成立, 考虑一般迭代格式(1.2)式, 其中$d_k$是下降方向,即$g_k^T d_k<0$,$\alpha_k$满足标准 Wolfe 线搜索(1.4)式, 则有
(3.1) $\begin{equation}\sum_{k\ge1}\frac{(g_k^T d_k)^2}{\Vert d_k\Vert^2}<+\infty.\end{equation}$
特别地, 当$d_k$满足充分下降条件(1.6)式, 则有
(3.2) $\begin{equation}\sum_{k\ge1}\frac{\Vert g_k\Vert^4}{\Vert d_k\Vert^2}<+\infty.\end{equation}$
注3.1 若假设(H1)和(H2)成立, 对于SWYL算法, 由于(1.10)式成立, 故在强Wolfe线搜索下,(3.2)式总是成立的.
下面给出$\beta_k$的一个性质[6 ] . 假设存在正常数$\gamma$和$\overline{\gamma}$使得
(3.3) $\begin{equation}0<\gamma\le\Vert g_k\Vert\le\overline{\gamma}, \forall k\ge 1,\end{equation}$
成立, 存在常数$b>1$和$\lambda>0$对所有的$k\ge 1$都有
(3.4) $\begin{equation}\vert \beta_k\vert\le b,\end{equation}$
(3.5) $\begin{equation}\Vert s_{k-1}\Vert\le\lambda\Rightarrow \vert \beta_k\vert\le\frac{1}{b}.\end{equation}$
(3.6) $\begin{equation}\vert\beta_k^{WYL}\vert\le\frac{2\Vert g_k\Vert^2}{\Vert g_{k-1}\Vert^2}\le\frac{2\overline{\gamma}^2}{\gamma^2}.\end{equation}$
若$\Vert s_{k-1}\Vert\le\lambda,$利用(2.2)和(3.3)式, 有
(3.7) $\begin{equation}\vert\beta_k^{WYL}\vert\le\frac{2\Vert g_k\Vert\Vert g_k-g_{k-1}\Vert}{\Vert g_{k-1}\Vert^2}\le\frac{2L\lambda\overline{\gamma}}{\gamma^2}.\end{equation}$
结合(3.6)和(3.7)式, 取$b=\frac{2\overline{\gamma}^2}{\gamma^2}> 1$和$\lambda=\frac{\gamma^2}{2L\overline{\gamma}b}> 0.$因此,$\beta_k^{WYL}$满足上面的性质(3.4)和(3.5)式.
引理 3.2 若假设(H1)和(H2)成立, 考虑SWYL算法, 且(3.3)式满足. 则$d_k\neq 0,$进一步, 令$u_k=\frac{d_k}{\Vert d_k\Vert},$有
(3.8) $\begin{equation}\sum_{k\ge 2}\Vert u_k-u_{k-1}\Vert^2<+\infty.\end{equation}$
证 由(1.10)式知$d_k\neq 0,$从而$u_k$的定义是有意义的. 根据(3.2)和(3.3)式有
(3.9) $\begin{equation}\sum_{k\ge 1}\frac{1}{\Vert d_k\Vert^2}<+\infty.\end{equation}$
(3.10) $\begin{equation}r_k:=\frac{-\theta_k g_k}{\Vert d_k\Vert}, 和 \delta_k:=\frac{\beta_k^{WYL}\Vert d_{k-1}\Vert}{\Vert d_k\Vert},\end{equation}$
(3.11) $\begin{equation}\theta_k=1+\beta_k^{WYL}\frac{g_k^T d_{k-1}}{\Vert g_k\Vert^2}.\end{equation}$
利用(1.5), (1.7), (1.10)和(3.11)式有
(3.12) $\begin{equation}\vert \theta_k\vert\le 1+ \frac{2\Vert g_k\Vert^2}{\Vert g_{k-1}\Vert^2}\frac{\vert g_k^T d_{k-1}\vert}{\Vert g_k\Vert^2}\le 1+ 2\frac{-\sigma g_{k-1}^T d_{k-1}}{\Vert g_{k-1}\Vert^2}=1+2\sigma.\end{equation}$
当$k\ge 2$时, 利用(1.9),(3.10)和(3.11)式, 则
利用上式及$\Vert u_k\Vert=\Vert u_{k-1}\Vert=1$有
(3.13) $\begin{equation}\Vert r_k\Vert=\Vert u_k-\delta_k u_{k-1}\Vert=\Vert \delta_k u_k-u_{k-1}\Vert.\end{equation}$
因为$\beta_k^{WYL}\ge 0,$则$\delta_k\ge 0.$由(3.13)式和三角不等式有
(3.14) $\begin{matrix}\Vert u_k-u_{k-1}\Vert&\le\Vert (1+\delta_k)u_k-(1+\delta_k)u_{k-1}\Vert\nonumber\\&\le\Vert u_k-\delta_k u_{k-1}\Vert+\Vert \delta_k u_{k}-u_{k-1}\Vert\nonumber\\&=2\Vert r_k\Vert.\end{matrix}$
利用(3.3),(3.9),(3.12)式和$r_k$的定义, 得
(3.15) $\begin{equation}\sum_{k\ge 2}\Vert r_k\Vert^2<+\infty.\end{equation}$
结合(3.14)和(3.15)式, 可知命题成立. 证毕.
注 3.2 结论中的(3.8)式并不意味着序列$\left\{u_k\right\}$收敛, 但是它表明了当$k$充分大时, 向量$u_k$的变化非常缓慢.
现在, 我们记$\mathbb{N}^{+}$为正整数集. 对任意的$\lambda>0$和正整数$\triangle,$定义
记$\vert K_{k,\triangle}^{\lambda}\vert$为集合$K_{k,\triangle}^{\lambda}$中元素的个数. 为了书写简便, 下文的$\beta_k=\beta_k^{WYL},$我们给出如下引理.
引理 3.3 若假设(H1)和(H2)成立, 考虑SWYL算法, 且(3.3)式满足, 则存在常数$\lambda>0,$使得对任意的$\triangle\in\mathbb{N}^{+}$和指标$k_0,$均存在$k\ge k_0$满足
证 用反证法. 假设对任意的$\lambda>0,$存在$\triangle\in\mathbb{N}^{+}$和指标$k_0$有
(3.16) $\begin{equation}\vert K_{k,\triangle}^{\lambda}\vert\le\frac{\triangle}{2}, \forall k\ge k_0.\end{equation}$
根据前面的分析, 对于$\beta_k^{WYL},$存在$b>1$和$\lambda>0$使得(3.4)和(3.5)式成立. 故对$\lambda>0$选择$\triangle$和$k_0$使得(3.16)式成立. 利用(3.4), (3.5)和(3.16)式有
(3.17) $\begin{equation}\prod_{k_0+i\triangle+1}^{k_0+(i+1)\triangle}\vert \beta_k\vert\le b^{\frac{\triangle}{2}}(\frac{1}{b})^{\frac{\triangle}{2}}=1, \forall i\ge 0.\end{equation}$
如果$\beta_k=0,$则(1.9)式中的方向变为$-g_k,$此时算法或者终止或者我们选择$x_k$作为新的起点. 为了不失一般性, 我们总是假定
(3.18) $\begin{equation}\beta_k\neq 0, \forall k\ge 1.\end{equation}$
(3.19) $\begin{equation}\sum_{k\ge 2}\prod_{j=2}^k\beta_j^{-2}=+\infty.\end{equation}$
(3.20) $\begin{matrix}\Vert d_k\Vert^2 &\le(1-\frac{(g_k^T d_k)^2}{\Vert g_k\Vert^2\Vert d_k\Vert^2})^{-1}\beta_k^2\Vert d_{k-1}\Vert^2\nonumber\\&\le\dots\nonumber\\&\le\prod_{j=j_0}^k(1-\frac{(g_j^T d_j)^2}{\Vert g_j\Vert^2\Vert d_j\Vert^2})^{-1}(\prod_{j=j_0}^k\beta_j^2)\Vert d_{j_0-1}\Vert^2.\end{matrix}$
其中$j_0\ge 2.$利用(3.1)和(3.3)式, 则存在常数$c_1>0$使得
(3.21) $\begin{equation}\prod_{j\ge j_0}(1-\frac{(g_j^T d_j)^2}{\Vert g_j\Vert^2\Vert d_j\Vert^2})\ge c_1\end{equation}$
成立. 利用(3.3), (3.19), (3.20)和(3.21)式有
(3.22) $\begin{equation}\sum_{k\ge 1}\frac{\Vert g_k\Vert^4}{\Vert d_k\Vert^2}=+\infty.\end{equation}$
上式与(3.2)式相矛盾, 故假设不成立. 证毕.
利用以上的引理, 下面给出 WYL 型谱共轭梯度法的全局收敛性.
定理 3.1 若假设(H1)和(H2)成立, 则由SWYL算法产生的点列$\left\{x_k\right\}$满足
证 用反证法, 假设结论不成立, 结合假设(H1)和(H2), 从而引理 3.2 和引理 3.3 条件满足. 仍然定义$u_i=\frac{d_i}{\Vert d_i\Vert},$对任意正整数$l,k (l\ge k)$有
对上式两端取模, 并利用(2.1)式和$\Vert u_{k-1}\Vert=1,$有
(3.23) $\begin{matrix}\sum_{i=k}^l\Vert s_{i-1}\Vert &\le \Vert x_l-x_{k-1}\Vert + \sum_{i=k}^l\Vert s_{i-1}\Vert\Vert u_{i-1}-u_{k-1}\Vert\nonumber\\&\le 2B+\sum_{i=k}^l\Vert s_{i-1}\Vert\Vert u_{i-1}-u_{k-1}\Vert.\end{matrix}$
设$\lambda$为引理3.3中给出, 并记$\triangle:=\lceil\frac{8B}{\lambda}\rceil$为不小于$\frac{8B}{\lambda}$的最小整数. 则由引理3.2可知, 存在指标$k_0,$使得
(3.24) $\begin{equation}\sum_{i\ge k_0}\Vert u_{i+1}-u_i\Vert^2\le\frac{1}{4\triangle}.\end{equation}$
而由引理 3.3 可知, 存在$k\ge k_0,$使得
(3.25) $\begin{equation}\vert K_{k,\triangle}^{\lambda}\vert>\frac{\triangle}{2}.\end{equation}$
对任意的$i\in[k,k+\triangle-1],$利用$\rm{Cauchy-Schwarz}$不等式及(3.24)式, 有
从而$\triangle<\frac{8B}{\lambda},$显然与$\triangle$的定义相矛盾, 因此假设不成立, 于是定理得证.
4 数值实验
本节展示算法的数值结果. 在文献[23 ]中选取 33 个无约束优化函数进行数值实验, 分别比较了引言中提到的$\rm{PRP^{+}}$算法[17 ] , WYL 算法[18 ] 和本文提出的 SWYL 算法. 测试函数的维数选取 100, 1000 和 3000, 所有的测试都是在强 Wolfe 线搜索(1.5)式下进行, 相关参数选取为:$\rho=0.4$,$\sigma=0.6$. 测试环境为 Matlab R2019a, Windows10 操作系统,台式电脑 (Inter(R)Core(TM)i7-8700CPU@3.20GHZ)8GB 内存. 本文算法的终止准则为后面两种情形之一:(1)$\Vert g_k\Vert\le 10^{-5}$; (2) 迭代次数$\rm{NI}>1000$.当终止准则 (2) 出现时, 表明该算法对相应测试函数失效, 并记为"F".
在数值实验中, 我们分别对迭代次数 (NI) 和 CPU 计算时间 (CPU time) 进行观察和比较, 数值结果详见表1 ,其中 N 表示序号, Function 表示测试函数的名称, Dim 表示测试函数的维数. 同时, 采用 Dolan 和 Moré[24 ] 性能图对数值结果的迭代次数和 CPU 计算时间进行直观刻画. 以 CPU 计算时间为例, 介绍性能图作图原理. 记$S$为算法$s$的集合, 记$P$为测试问题$p$的集合,$n_p$表示测试问题集中问题的个数, 令$t_{p,s}$为算法$s$求解问题$p$所消耗的 CPU 时间, 定义$r_{p,s}$为算法$s$求解问题$p$的效率,其表达式为
显然$r_{p,s}\ge 1$, 表1 中的"F"的效率$r_{p,s}$定义为$2\max\left\{r_{p,s}:s\in S\right\},$令
我们以$\tau$为图像的横坐标和$\rho_s(\tau)$为图像的纵坐标, 绘制$\rho_s(\tau)$关于$r_{p,s}$的分布函数曲线. 总体来说,$\rho_s(\tau)$的图像越居于上方, 其对应算法的数值性能越好.
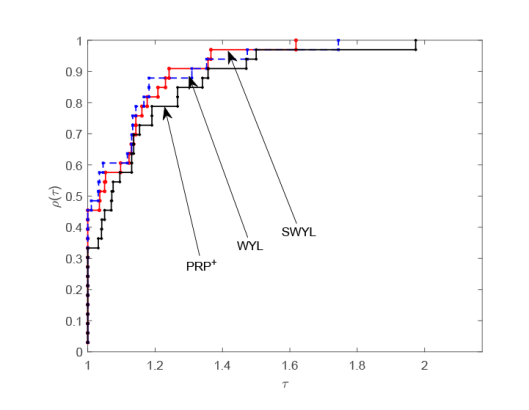
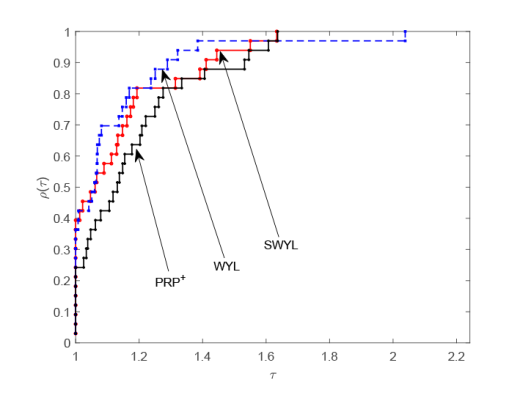
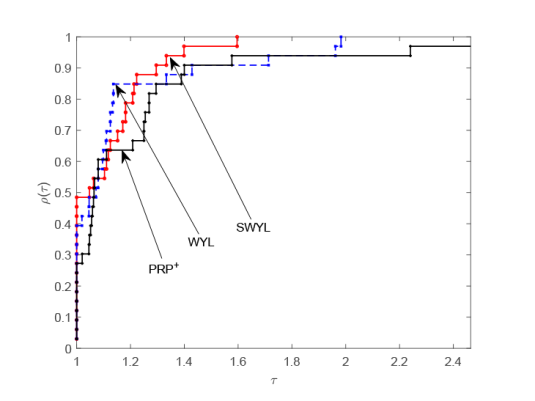
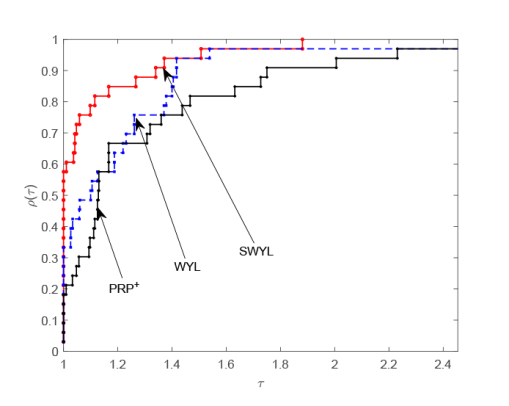
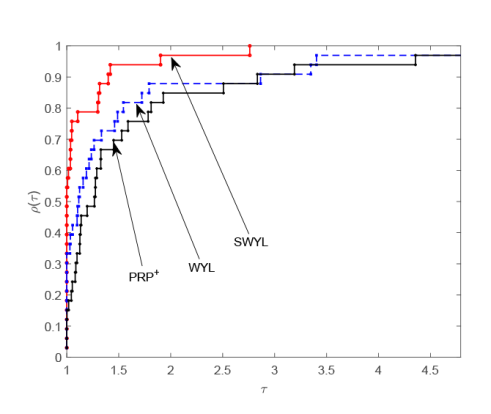
由图1 和图2 可以看出, 当测试函数的维数为 100 时, 无论是对于迭代次数还是 CPU 运行时间,本文的 SWYL 算法与 WYL 算法和$\rm{PRP^{+}}$算法存在着许多交叉和重合, 这表明此时的 SWYL 算法相比 WYL 算法和$\rm{PRP^{+}}$算法在数值表现方面优势并不明显. 当测试函数的维数增加到 1000 时, 由图3 和图4 可以看出, 无论是对于迭代次数还是 CPU 运行时间, SWYL 算法已经基本位于 WYL 算法和$\rm{PRP^{+}}$算法曲线的上方, 这表明此时 SWYL 算法已经基本优于 WYL 算法和$\rm{PRP^{+}}$算法. 随着测试函数的维数进一步增加到 5000 时, 由图5 和图6 可以看出, SWYL 算法明显优于 WYL 算法和$\rm{PRP^{+}}$算法. 由此推测, 随着维数的不断增加,本文的 SWYL 算法在处理大规模无约束优化问题时, 具有一定的竞争力.
图1
图2
图3
图4
图5
图6
5 总结
本文结合谱共轭梯度法和 WYL 共轭梯度法, 提出 WYL 型谱共轭梯度法. 对于任意的线搜索,其搜索方向都满足充分下降性. 如果采用精确线搜索, WYL 型谱共轭梯度法和 WYL 共轭梯度法是等价的. 对于非精确线搜索, 与 WYL 共轭梯度法的全局收敛性相比, WYL 型谱共轭梯度法显著的优点就是扩大了在强 Wolfe 线搜索中参数的取值范围. 最后, 相应的数值实验结果也表明, WYL 型谱共轭梯度法的数值表现优于 WYL 和$\rm{PRP^{+}}$共轭梯度法,是适合求解大规模无约束优化问题的.
参考文献
View Option
[2]
Dai Y H Yuan Y X . A nonlinear conjugate gradient with a strong global convergence property
SIAM Journal Optimization , 1999 , 10 1 ): 177 -182
DOI:10.1137/S1052623497318992
URL
[本文引用: 1]
[3]
Polak E Ribière G . Note surla convergence de directions conjugeèes
Rev Francaise Informat Recherche Operationele , 1969 , 3 16 ): 35 -43
[本文引用: 1]
[4]
Polyak B T . The conjugate gradient method in extreme problems. USSR Computational Mathematic and
Mathematical Physics , 1969 , 9 4 ): 94 -112
[本文引用: 1]
[5]
Hestenes M R Stiefel E . Methods of conjugate gradients for solving linear systems
Journal of Research of National Bureau of Standards , 1952 , 49 6 ): 409 -436
DOI:10.6028/jres.049.044
URL
[本文引用: 1]
[6]
Dai Y H Liao L Z . New conjugacy conditions and related nonlinear conjugate gradient methods
Applied Mathematics and Optimization , 2001 , 43 1 ): 87 -101
DOI:10.1007/s002450010019
URL
[本文引用: 2]
[7]
Hager W W Zhang H C . A new conjugate gradient method with guaranteed descent and efficient line search
SIAM Journal on Optimization , 2005 , 16 1 ): 170 -192
DOI:10.1137/030601880
URL
[本文引用: 1]
[8]
Liu J K Feng Y M Zou L M . Some three-term conjugate gradient methods with the inexact line search condition
Calcolo , 2018 , 55 2 ): 1 -16
DOI:10.1007/s10092-018-0244-9
[本文引用: 1]
[9]
Djordjević S S . New hybrid conjugate gradient method as a convex combination of LS and FR methods
Acta Mathematica Scientia , 2019 , 39B 1 ): 214 -228
[本文引用: 1]
[10]
Yuan G Lu J Wang Z . The PRP conjugate gradient algorithm with a modified WWP line search and its application in the image restoration problems
Applied Numerical Mathematics , 2020 , 152 1 -11
[本文引用: 1]
[11]
马国栋 . 强 Wolfe 线搜索下的修正 PRP 和 HS 共轭梯度法
数学物理学报 , 2021 , 41A 3 ): 837 -847
[本文引用: 1]
Ma G D . Improved PRP and HS conjugate gradient methods with the strong wolfe line search
Acta Math Sci , 2021 , 41A 3 ): 837 -847
[本文引用: 1]
[12]
Jiang X Liao W Yin J , et al . A new family of hybrid three-term conjugate gradient methods with applications in image restoration
Numerical Algorithms , 2022 , 91 1 ): 161 -191
DOI:10.1007/s11075-022-01258-2
[本文引用: 1]
[13]
Liu Y Zhu Z Zhang B . Two sufficient descent three-term conjugate gradient methods for unconstrained optimization problems with applications in compressive sensing
Journal of Applied Mathematics and Computing , 2022 , 68 1 ): 1787 -1816
DOI:10.1007/s12190-021-01589-8
[本文引用: 1]
[14]
Babaie-Kafaki S Mirhoseini N Aminifard Z . A descent extension of a modified Polak-Ribière-Polyak method with application in image restoration problem
Optimization Letters , 2023 , 17 2 ): 351 -367
DOI:10.1007/s11590-022-01878-6
[本文引用: 1]
[15]
Powell M J D . Restart procedure of the conjugate gradient method
Math Program , 1977 , 2 1 ): 241 -254
[本文引用: 1]
[16]
Powell M J D . Convergence properties of algorithms for nonlinear optimization
SIAM Review , 1986 , 28 2 ): 487 -500
DOI:10.1137/1028154
URL
[本文引用: 1]
[17]
Gilbert J C Nocedal J . Global convergence properties of conjugate gradient methods for optimization
SIAM J Optimization , 1992 , 2 1 ): 21 -42
DOI:10.1137/0802003
URL
[本文引用: 2]
[18]
Wei Z X Yao S W Liu L Y . The convergence properties of some new conjugate gradient methods
Applied Mathematics and Computation , 2006 , 183 2 ): 1341 -1350
DOI:10.1016/j.amc.2006.05.150
URL
[本文引用: 3]
[19]
Birgin E G Martinez J M . A spectral conjugate gradient method for unconstrained optimization
Applied Mathematicals and Optimization , 2001 , 43 2 ): 117 -128
[本文引用: 1]
[20]
Zhang L Zhou W J . Two descent hybrid conjugate gradient methods for optimization
Journal of Computation and Applied Mathematics , 2008 , 216 1 ): 251 -264
[本文引用: 2]
[21]
Zoutendijk G Nolinear programming computational methods Abadie J . Integer and Nonlinear Programming
Amsterdam: North-Holland , 1970 (1 ): 37 -86
[本文引用: 1]
[22]
戴彧虹 , 袁亚湘 . 非线性共轭梯度法 . 上海 : 上海科学技术出版社 , 2000
[本文引用: 1]
Dai Y H Yuan Y X . Nonlinear Conjugate Gradient Method . Shanghai : Shanghai Science and Technology Press , 2000
[本文引用: 1]
[23]
Andrei N . An unconstrained optimization test functions collection
Advanced Modeling and Optimization , 2008 , 10 1 ): 147 -161
[本文引用: 1]
[24]
Dolan E D Moré J J . Benchmarking optimization software with performance profiles
Mathematical Programming , 2002 , 91 2 ): 201 -213
DOI:10.1007/s101070100263
URL
[本文引用: 1]
Function minimization by conjugate gradients
1
1964
... 其中$g_k:=\nabla f(x),$$\alpha_k$是通过某种线搜索产生的步长,$d_k$为搜索方向,$\beta_k$为共轭参数. 不同的共轭参数对应不同的共轭梯度法, 关于$\beta_k$的著名公式有[1 ⇓ ⇓ ⇓ -5 ] ...
A nonlinear conjugate gradient with a strong global convergence property
1
1999
... 其中$g_k:=\nabla f(x),$$\alpha_k$是通过某种线搜索产生的步长,$d_k$为搜索方向,$\beta_k$为共轭参数. 不同的共轭参数对应不同的共轭梯度法, 关于$\beta_k$的著名公式有[1 ⇓ ⇓ ⇓ -5 ] ...
Note surla convergence de directions conjugeèes
1
1969
... 其中$g_k:=\nabla f(x),$$\alpha_k$是通过某种线搜索产生的步长,$d_k$为搜索方向,$\beta_k$为共轭参数. 不同的共轭参数对应不同的共轭梯度法, 关于$\beta_k$的著名公式有[1 ⇓ ⇓ ⇓ -5 ] ...
The conjugate gradient method in extreme problems. USSR Computational Mathematic and
1
1969
... 其中$g_k:=\nabla f(x),$$\alpha_k$是通过某种线搜索产生的步长,$d_k$为搜索方向,$\beta_k$为共轭参数. 不同的共轭参数对应不同的共轭梯度法, 关于$\beta_k$的著名公式有[1 ⇓ ⇓ ⇓ -5 ] ...
Methods of conjugate gradients for solving linear systems
1
1952
... 其中$g_k:=\nabla f(x),$$\alpha_k$是通过某种线搜索产生的步长,$d_k$为搜索方向,$\beta_k$为共轭参数. 不同的共轭参数对应不同的共轭梯度法, 关于$\beta_k$的著名公式有[1 ⇓ ⇓ ⇓ -5 ] ...
New conjugacy conditions and related nonlinear conjugate gradient methods
2
2001
... 其中$y_{k-1}=g_k-g_{k-1}.$上面四个公式对应的共轭梯度法分别称为$\rm{FR}$方法,$\rm{DY}$方法,$\rm{PRP}$方法和$\rm{HS}$方法. 特别地, 当目标函数是二次函数且采取精确线搜索, 以上四种算法是等价的.众所周知,$\rm{FR}$方法和$\rm{DY}$方法有良好的收敛性质,$\rm{PRP}$方法和$\rm{HS}$方法有良好的数值表现. 为寻求既保证良好的收敛性又具有优越的数值效果的算法, 许多学者做出了研究, 得到了一些新的算法[6 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -14 ] . ...
... 下面给出$\beta_k$的一个性质[6 ] . 假设存在正常数$\gamma$和$\overline{\gamma}$使得 ...
A new conjugate gradient method with guaranteed descent and efficient line search
1
2005
... 其中$y_{k-1}=g_k-g_{k-1}.$上面四个公式对应的共轭梯度法分别称为$\rm{FR}$方法,$\rm{DY}$方法,$\rm{PRP}$方法和$\rm{HS}$方法. 特别地, 当目标函数是二次函数且采取精确线搜索, 以上四种算法是等价的.众所周知,$\rm{FR}$方法和$\rm{DY}$方法有良好的收敛性质,$\rm{PRP}$方法和$\rm{HS}$方法有良好的数值表现. 为寻求既保证良好的收敛性又具有优越的数值效果的算法, 许多学者做出了研究, 得到了一些新的算法[6 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -14 ] . ...
Some three-term conjugate gradient methods with the inexact line search condition
1
2018
... 其中$y_{k-1}=g_k-g_{k-1}.$上面四个公式对应的共轭梯度法分别称为$\rm{FR}$方法,$\rm{DY}$方法,$\rm{PRP}$方法和$\rm{HS}$方法. 特别地, 当目标函数是二次函数且采取精确线搜索, 以上四种算法是等价的.众所周知,$\rm{FR}$方法和$\rm{DY}$方法有良好的收敛性质,$\rm{PRP}$方法和$\rm{HS}$方法有良好的数值表现. 为寻求既保证良好的收敛性又具有优越的数值效果的算法, 许多学者做出了研究, 得到了一些新的算法[6 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -14 ] . ...
New hybrid conjugate gradient method as a convex combination of LS and FR methods
1
2019
... 其中$y_{k-1}=g_k-g_{k-1}.$上面四个公式对应的共轭梯度法分别称为$\rm{FR}$方法,$\rm{DY}$方法,$\rm{PRP}$方法和$\rm{HS}$方法. 特别地, 当目标函数是二次函数且采取精确线搜索, 以上四种算法是等价的.众所周知,$\rm{FR}$方法和$\rm{DY}$方法有良好的收敛性质,$\rm{PRP}$方法和$\rm{HS}$方法有良好的数值表现. 为寻求既保证良好的收敛性又具有优越的数值效果的算法, 许多学者做出了研究, 得到了一些新的算法[6 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -14 ] . ...
The PRP conjugate gradient algorithm with a modified WWP line search and its application in the image restoration problems
1
2020
... 其中$y_{k-1}=g_k-g_{k-1}.$上面四个公式对应的共轭梯度法分别称为$\rm{FR}$方法,$\rm{DY}$方法,$\rm{PRP}$方法和$\rm{HS}$方法. 特别地, 当目标函数是二次函数且采取精确线搜索, 以上四种算法是等价的.众所周知,$\rm{FR}$方法和$\rm{DY}$方法有良好的收敛性质,$\rm{PRP}$方法和$\rm{HS}$方法有良好的数值表现. 为寻求既保证良好的收敛性又具有优越的数值效果的算法, 许多学者做出了研究, 得到了一些新的算法[6 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -14 ] . ...
强 Wolfe 线搜索下的修正 PRP 和 HS 共轭梯度法
1
2021
... 其中$y_{k-1}=g_k-g_{k-1}.$上面四个公式对应的共轭梯度法分别称为$\rm{FR}$方法,$\rm{DY}$方法,$\rm{PRP}$方法和$\rm{HS}$方法. 特别地, 当目标函数是二次函数且采取精确线搜索, 以上四种算法是等价的.众所周知,$\rm{FR}$方法和$\rm{DY}$方法有良好的收敛性质,$\rm{PRP}$方法和$\rm{HS}$方法有良好的数值表现. 为寻求既保证良好的收敛性又具有优越的数值效果的算法, 许多学者做出了研究, 得到了一些新的算法[6 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -14 ] . ...
强 Wolfe 线搜索下的修正 PRP 和 HS 共轭梯度法
1
2021
... 其中$y_{k-1}=g_k-g_{k-1}.$上面四个公式对应的共轭梯度法分别称为$\rm{FR}$方法,$\rm{DY}$方法,$\rm{PRP}$方法和$\rm{HS}$方法. 特别地, 当目标函数是二次函数且采取精确线搜索, 以上四种算法是等价的.众所周知,$\rm{FR}$方法和$\rm{DY}$方法有良好的收敛性质,$\rm{PRP}$方法和$\rm{HS}$方法有良好的数值表现. 为寻求既保证良好的收敛性又具有优越的数值效果的算法, 许多学者做出了研究, 得到了一些新的算法[6 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -14 ] . ...
A new family of hybrid three-term conjugate gradient methods with applications in image restoration
1
2022
... 其中$y_{k-1}=g_k-g_{k-1}.$上面四个公式对应的共轭梯度法分别称为$\rm{FR}$方法,$\rm{DY}$方法,$\rm{PRP}$方法和$\rm{HS}$方法. 特别地, 当目标函数是二次函数且采取精确线搜索, 以上四种算法是等价的.众所周知,$\rm{FR}$方法和$\rm{DY}$方法有良好的收敛性质,$\rm{PRP}$方法和$\rm{HS}$方法有良好的数值表现. 为寻求既保证良好的收敛性又具有优越的数值效果的算法, 许多学者做出了研究, 得到了一些新的算法[6 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -14 ] . ...
Two sufficient descent three-term conjugate gradient methods for unconstrained optimization problems with applications in compressive sensing
1
2022
... 其中$y_{k-1}=g_k-g_{k-1}.$上面四个公式对应的共轭梯度法分别称为$\rm{FR}$方法,$\rm{DY}$方法,$\rm{PRP}$方法和$\rm{HS}$方法. 特别地, 当目标函数是二次函数且采取精确线搜索, 以上四种算法是等价的.众所周知,$\rm{FR}$方法和$\rm{DY}$方法有良好的收敛性质,$\rm{PRP}$方法和$\rm{HS}$方法有良好的数值表现. 为寻求既保证良好的收敛性又具有优越的数值效果的算法, 许多学者做出了研究, 得到了一些新的算法[6 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -14 ] . ...
A descent extension of a modified Polak-Ribière-Polyak method with application in image restoration problem
1
2023
... 其中$y_{k-1}=g_k-g_{k-1}.$上面四个公式对应的共轭梯度法分别称为$\rm{FR}$方法,$\rm{DY}$方法,$\rm{PRP}$方法和$\rm{HS}$方法. 特别地, 当目标函数是二次函数且采取精确线搜索, 以上四种算法是等价的.众所周知,$\rm{FR}$方法和$\rm{DY}$方法有良好的收敛性质,$\rm{PRP}$方法和$\rm{HS}$方法有良好的数值表现. 为寻求既保证良好的收敛性又具有优越的数值效果的算法, 许多学者做出了研究, 得到了一些新的算法[6 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -14 ] . ...
Restart procedure of the conjugate gradient method
1
1977
... PRP 方法是目前被认为数值表现最好的共轭梯度法之一, 当产生一个小步长时, PRP 方法产生的搜索方向$d_k$能够自动靠近负梯度方向, 从而具有自动重启的特点. Powell[15 ] 证明了 PRP 方法在精确线搜索下对于一致凸函数的全局收敛性. 对于非凸函数, 为了避免相邻的两个方向趋于反向, Powell 在文献[16 ]中建议将$\beta_k$限制非负. Gilbert 和 Nocedal[17 ] 给出了$\rm{PRP}^{+}$方法, 即 ...
Convergence properties of algorithms for nonlinear optimization
1
1986
... PRP 方法是目前被认为数值表现最好的共轭梯度法之一, 当产生一个小步长时, PRP 方法产生的搜索方向$d_k$能够自动靠近负梯度方向, 从而具有自动重启的特点. Powell[15 ] 证明了 PRP 方法在精确线搜索下对于一致凸函数的全局收敛性. 对于非凸函数, 为了避免相邻的两个方向趋于反向, Powell 在文献[16 ]中建议将$\beta_k$限制非负. Gilbert 和 Nocedal[17 ] 给出了$\rm{PRP}^{+}$方法, 即 ...
Global convergence properties of conjugate gradient methods for optimization
2
1992
... PRP 方法是目前被认为数值表现最好的共轭梯度法之一, 当产生一个小步长时, PRP 方法产生的搜索方向$d_k$能够自动靠近负梯度方向, 从而具有自动重启的特点. Powell[15 ] 证明了 PRP 方法在精确线搜索下对于一致凸函数的全局收敛性. 对于非凸函数, 为了避免相邻的两个方向趋于反向, Powell 在文献[16 ]中建议将$\beta_k$限制非负. Gilbert 和 Nocedal[17 ] 给出了$\rm{PRP}^{+}$方法, 即 ...
... 本节展示算法的数值结果. 在文献[23 ]中选取 33 个无约束优化函数进行数值实验, 分别比较了引言中提到的$\rm{PRP^{+}}$算法[17 ] , WYL 算法[18 ] 和本文提出的 SWYL 算法. 测试函数的维数选取 100, 1000 和 3000, 所有的测试都是在强 Wolfe 线搜索(1.5)式下进行, 相关参数选取为:$\rho=0.4$,$\sigma=0.6$. 测试环境为 Matlab R2019a, Windows10 操作系统,台式电脑 (Inter(R)Core(TM)i7-8700CPU@3.20GHZ)8GB 内存. 本文算法的终止准则为后面两种情形之一:(1)$\Vert g_k\Vert\le 10^{-5}$; (2) 迭代次数$\rm{NI}>1000$.当终止准则 (2) 出现时, 表明该算法对相应测试函数失效, 并记为"F". ...
The convergence properties of some new conjugate gradient methods
3
2006
... 文献[18 ]提出了一种修正的 PRP 方法, 我们称为 WYL 共轭梯度法, 其共轭参数为 ...
... 受文献[18 ]和[20 ]的启发, 为推广 WYL 共轭梯度法在强 Wolfe 线搜索下参数$\sigma$的取值范围, 利用(1.7)和(1.9)式构造搜索方向, 我们提出 WYL 型谱共轭梯度法. 若采用精确线搜索, 则$g_k^T d_{k-1}=0$, 该 WYL 型谱共轭梯度法即是 WYL 共轭梯度法. 特别地, 该 WYL 型谱共轭梯度法能够保证在独立于线搜索的情况下, 其搜索方向满足充分下降性. 在强 Wolfe 线搜索下且参数$0<\rho<\sigma<1$时, 我们证明了其全局收敛性. 最后, 相应的数值实验结果表明, 该 WYL 型谱共轭梯度法的数值效果优于 WYL 和$\rm{PRP}^{+}$共轭梯度法. ...
... 本节展示算法的数值结果. 在文献[23 ]中选取 33 个无约束优化函数进行数值实验, 分别比较了引言中提到的$\rm{PRP^{+}}$算法[17 ] , WYL 算法[18 ] 和本文提出的 SWYL 算法. 测试函数的维数选取 100, 1000 和 3000, 所有的测试都是在强 Wolfe 线搜索(1.5)式下进行, 相关参数选取为:$\rho=0.4$,$\sigma=0.6$. 测试环境为 Matlab R2019a, Windows10 操作系统,台式电脑 (Inter(R)Core(TM)i7-8700CPU@3.20GHZ)8GB 内存. 本文算法的终止准则为后面两种情形之一:(1)$\Vert g_k\Vert\le 10^{-5}$; (2) 迭代次数$\rm{NI}>1000$.当终止准则 (2) 出现时, 表明该算法对相应测试函数失效, 并记为"F". ...
A spectral conjugate gradient method for unconstrained optimization
1
2001
... Birigin 和 Martinez[19 ] 结合谱梯度法和共轭梯度法提出谱共轭梯度法, 将迭代格式(1.3)式推广为如下形式 ...
Two descent hybrid conjugate gradient methods for optimization
2
2008
... 虽然上述的谱共轭梯度法在实际计算中有良好的数值表现, 但是不能保证其搜索方向的下降性. 为此, 张和周[20 ] 提出如下形式的谱共轭梯度法 ...
... 受文献[18 ]和[20 ]的启发, 为推广 WYL 共轭梯度法在强 Wolfe 线搜索下参数$\sigma$的取值范围, 利用(1.7)和(1.9)式构造搜索方向, 我们提出 WYL 型谱共轭梯度法. 若采用精确线搜索, 则$g_k^T d_{k-1}=0$, 该 WYL 型谱共轭梯度法即是 WYL 共轭梯度法. 特别地, 该 WYL 型谱共轭梯度法能够保证在独立于线搜索的情况下, 其搜索方向满足充分下降性. 在强 Wolfe 线搜索下且参数$0<\rho<\sigma<1$时, 我们证明了其全局收敛性. 最后, 相应的数值实验结果表明, 该 WYL 型谱共轭梯度法的数值效果优于 WYL 和$\rm{PRP}^{+}$共轭梯度法. ...
Integer and Nonlinear Programming
1
1970
... 下面的引理给出著名的 Zoutendijk 条件[21 ] , 其在下降算法的全局收敛性分析中有着重要的作用, 该引理在文献[22 ]中给出了具体的证明. ...
1
2000
... 下面的引理给出著名的 Zoutendijk 条件[21 ] , 其在下降算法的全局收敛性分析中有着重要的作用, 该引理在文献[22 ]中给出了具体的证明. ...
1
2000
... 下面的引理给出著名的 Zoutendijk 条件[21 ] , 其在下降算法的全局收敛性分析中有着重要的作用, 该引理在文献[22 ]中给出了具体的证明. ...
An unconstrained optimization test functions collection
1
2008
... 本节展示算法的数值结果. 在文献[23 ]中选取 33 个无约束优化函数进行数值实验, 分别比较了引言中提到的$\rm{PRP^{+}}$算法[17 ] , WYL 算法[18 ] 和本文提出的 SWYL 算法. 测试函数的维数选取 100, 1000 和 3000, 所有的测试都是在强 Wolfe 线搜索(1.5)式下进行, 相关参数选取为:$\rho=0.4$,$\sigma=0.6$. 测试环境为 Matlab R2019a, Windows10 操作系统,台式电脑 (Inter(R)Core(TM)i7-8700CPU@3.20GHZ)8GB 内存. 本文算法的终止准则为后面两种情形之一:(1)$\Vert g_k\Vert\le 10^{-5}$; (2) 迭代次数$\rm{NI}>1000$.当终止准则 (2) 出现时, 表明该算法对相应测试函数失效, 并记为"F". ...
Benchmarking optimization software with performance profiles
1
2002
... 在数值实验中, 我们分别对迭代次数 (NI) 和 CPU 计算时间 (CPU time) 进行观察和比较, 数值结果详见表1 ,其中 N 表示序号, Function 表示测试函数的名称, Dim 表示测试函数的维数. 同时, 采用 Dolan 和 Moré[24 ] 性能图对数值结果的迭代次数和 CPU 计算时间进行直观刻画. 以 CPU 计算时间为例, 介绍性能图作图原理. 记$S$为算法$s$的集合, 记$P$为测试问题$p$的集合,$n_p$表示测试问题集中问题的个数, 令$t_{p,s}$为算法$s$求解问题$p$所消耗的 CPU 时间, 定义$r_{p,s}$为算法$s$求解问题$p$的效率,其表达式为 ...