图像分解是图像处理领域一个重要的子课题, 它在目标识别^[1], 图像修复^[2,3] 等领域有着广泛的应用. 所谓图像分解, 本质上是将一幅图像分解成不同的特征成分, 如结构, 纹理及噪声等, 关于此问题的研究, 最早可追溯到 Rudin, Osher, Fatemi^[4] 的工作. 在该工作中, 围绕如何有效提取噪声图像的中的噪声信息, Rudin 等提出了一种全变分去噪声模型 (Total Variation, TV). 该模型在保持图像边缘方面取得了良好的结果. 基于该模型, 一些学者提出了各种模型. 例如, Lv^[5] 提出了一种新的基于 Gabor 函数的非局部 TV-Hilbert 模型来分离图像的结构分量和纹理分量, Starck 等^[6]提出了一种新的图像恢复和图像分解为卡通加纹理的模型, 该模型将 ROF 模型^[4]的总变差最小化与 Meyer^[7] 提出的涉及$H^{-1}$范数的振荡函数范数相结合. 此外, 针对该模型, 众多学者给出了很多理论和数值计算方面的结果^{[8⇓⇓⇓⇓⇓-14]}. 然而 TV 模型结果依赖于参数的选择, 为了有效地解决这个问题, Tadmor 等^[12]提供了一种多尺度图像分解方法, 此方法能达到有界变差空间上的全局最优. 进一步, Tadmor 等给出了初始参数$\lambda_0$的取值范围, 并且在不确定具体范围时, 若参数$\lambda_0$过小, 随着$k$的增加,$2^k\lambda_0$会在某一时刻满足条件, 若参数$\lambda_0$过大, Tadmor 等给出了细化程序以得到缺失的更大尺度的层次表示. 作为 Tadmor 等的改进, Xu 等^[13]通过观察其变分问题的 Euler-Lagrange 方程的结构, 将一系列多尺度优化过程转化成一个和时间参数相关的偏微分方程定解问题, 并给出了此定解问题的一个半隐式格式, 该格式在图像分解方面取得了良好的效果. 然而, Xu 等给出的方法中未给出关于半隐式格式的理论分析的相关结果. 另外, 考虑到半隐式格式存在算法不稳定的缺陷, 本文提出了一种交替方向隐式 (ADI) 格式并分析此方法的稳定性和收敛性条件.

本文具体结构如下: 第 2 节介绍多尺度图像分解模型; 第 3 节给出本文所使用的 ADI 格式, 并证明 ADI 格式在该模型下的收敛性和稳定性; 第 4 节给出数值实验, 将本文图像分解算法与 Xu 等^[13]提出的算法 (在本文中记为 FSI 算法)对比; 第 5 节总结本文的工作.

给定有界定义域$\Omega \subseteq \mathbb{R}^2$上的图像$f: \Omega \rightarrow \mathbb{R}$, 可分解为平滑分量$u$和纹理、噪声分量$v$, 即$f=u+v$. 关于此问题, 最经典的模型是 ROF 模型^[4]

其中$BV(\Omega)=\{u\in L^1(\Omega):\int_{\Omega}|Du|<\infty\}$.

作为 Rudin, Osher, Fatemi^[4]的工作的一个改进, Xu 给出了如下变系数图像分解模型

其中$\alpha (\textbf{x}) \!=\! \frac{1}{{\sqrt {1 + {{\left| {\nabla ({G_\sigma }*f)(\textbf{x})} \right|}^2}/{\beta ^2}} }}$,$G_{\sigma}(\textbf{x},\textbf{x}')\!=\!e^{-\frac{||\textbf{x}-\textbf{x}'||^2}{2\sigma^2}}$,$(f*g)(n)\!=\!\int^{\infty}_{-\infty}f(\eta)g(n-\eta){\rm d}\eta$,$\beta >0$.

通过变分基本引理, 求得(2.2)式所对应的 Euler-Lagrange 方程为

由(2.3)式可以观察到, 在一次分解过程中当$\lambda$很大时,$u_{\lambda}$接近于$f$, 所提取的纹理信息$v=f-u$越少; 当$\lambda$很小时, 更加有利于结构信息$u$的分解, 使得$u$更加平滑. 作为一个平衡, Xu 等人^[13]给出了一种由"粗"到"细"的多尺度图像分解方法. 其具体过程如下: (I) 选择一个较大的$\lambda = {\lambda _0}$, 利用(2.2)式对$f$进行图像分解$f = {u_{{\lambda _0}}} + {v_{{\lambda _0}}}$; (II) 给定$\lambda_1 < {\lambda _0}$, 利用(2.2)式对$u_{{\lambda _0}}$进一步分解 (用${u_{{\lambda _0}}}$代替$f$)${u_{{\lambda _0}}} = {u_{{\lambda _1}}} + {v_{{\lambda _1}}}$; (III) 依此类推, 给定${\lambda _{i + 1}} < {\lambda _i}$$(i = 0,1,2,\cdots,N)$, 利用(2.2)式对${u_{{\lambda _i}}}$进行分解(用${u_{{\lambda _i}}}$代替$f$)${u_{{\lambda _i}}} = {u_{{\lambda _{i+1}}}} + {v_{{\lambda _{i+1}}}}$. 该过程通过不断选取${\lambda _{i + 1}} < {\lambda _i}$进行迭代以得到更粗尺度的平滑图像${u_{{\lambda _{i+1}}}}$^[13]. 由此可得

注意到${v_{\lambda_i} } = -\frac{1}{{2\lambda_i }}\text{div}\big( {\frac{{\alpha \nabla {u_{\lambda_i} }}}{{\left| {\nabla {u_{\lambda_i} }} \right|}}} \big)$, 由(2.3)和(2.4)式可得

引入新变量$t$, 并令$u=u(\textbf{x},t)$, 则(2.5)式实际上是如下方程的离散形式

其中$\lambda(t)$是一个单调递减函数.

对(2.6)式两边关于$t$进行微分, 可得到如下偏微分方程

其中$\varphi (t) = \frac{1}{{2\lambda (t)}}$. 以(2.7)式为基础, 给定初始条件$u(\textbf{x},0) = f(\textbf{x})$和边界条件$\frac{\partial u}{\partial n}|_{\partial\Omega}=0$, 其中$n$为法向量, 则上述多尺度图像分解问题可以转换为以下定解问题

在本文的实验中, 选取$\beta = 0.2$,$\varphi (t) = {1.1^t}$.

在本文中, 设$h$和$\tau$分别表示空间步长和时间步长. 我们使用$u_{i,j}^n$表示$u$在时间$t_n$和空间位置$(x_i,y_j)$处的值, 其中$(x_i,y_j) = (ih,jh)$,$t_n = n\tau$,$i = 0,1,2,\cdots,N + 1,$$j = 0,1,2,\cdots,N + 1,$$n \le W,N,W \in {\mathbb{R}^ + }$. 基于上述记号, 对(2.7)式应用 ADI 格式^[15,16]进行离散, 可得

其中

$D_{-}, D_{0}, D_{+}$分别表示向后, 中心, 向前差分算子.

整理可得

其中${p^n} = \frac{ {\varphi ^{n}} \eta}{{2}}, \eta=\frac{\tau }{h^2}$.

为了简化在证明 ADI 格式的收敛性和稳定性时的叙述, 本文做了以下记号

基于这些记号, 下面考虑 ADI 格式的精度

定理 3.1 ADI格式(3.1)的截断误差是$O({\tau ^2} + {h} )$.

证 先消去其中的$u_{i,j}^{n + \frac{1}{2}}$. 首先将(3.1)式的两个式子相减, 可得

然后, 将(3.1)式的两个式子相加, 可得

将(3.3)式代入(3.4)式, 可得

依次考虑以下式子

根据以上式子, 可得

由此可得 ADI 格式对时间是二阶精度，对空间是一阶精度的, 它的截断误差是$O({\tau ^2} + {h})$. 证毕.

定理 3.2 ADI格式(3.1)无条件稳定.

证 首先将(3.5)式改写成以下形式

再将(3.6)式改写成矩阵形式

其中

$l,p = 1,2,\cdots,N - 1,k = 1,2,\cdots,N$,${\rm diag}(x_1,\cdots,x_n)$表示对角线元素为$x_1,\cdots,x_n$的对角矩阵.

记${\kappa _{{A_1}}}, {\kappa _{{A_2}}}$分别是$A_1$和$A_2$的特征值, 由于$A_1$和$A_2$均为对角占优矩阵, 可知${\kappa _{{A_1}}}\ge 0,$$\kappa _{{A_2}} \ge 0$. 令$E ^n = {(e_{1,1}^n,e_{2,1}^n,\cdots e_{1,N}^n,e_{1,2}^n,\cdots,e_{N,N}^n)^T}$是$U ^n$的计算误差, 因此由(3.7)式可知

其中$Q = {[({I_{{N^2}}} + \frac{{{\varphi ^n}\eta }}{2}{A_1})({I_{{N^2}}} + \frac{{{\varphi ^n}\eta }}{2}{A_2})]^{ - 1}}({I_{{N^2}}} - \frac{{{\varphi ^n}\eta }}{2}{A_1})({I_{{N^2}}} - \frac{{{\varphi ^n}\eta }}{2}{A_2}).$

由于${\kappa _{{A_1}}} \ge 0,{\kappa _{{A_2}}} \ge 0$, 因此有以下式子

这意味着存在$Y>0$使得

进而可得

故可知(3.1)式的 ADI 格式无条件稳定. 证毕.

定理 3.3 设$\overline v _{i,j}^n$是(2.7)式的精确解,$v_{i,j}^n$是(3.1)式的ADI 格式的解, 则对于所有$1 \le n \le N$, 有

其中${\overline v ^n} = {(\overline v _{1,1}^n, \overline v _{2,1}^n,\cdots \overline v _{N,N}^n)^T}, {V^n} = {(v_{1,1}^n,v_{2,1}^n,\cdots,v_{N,N}^n)^T}$.

证 令$e = \overline v - V, e ^n = {(e_{1,1}^n,e_{2,1}^n,\cdots,e_{N,N}^n)^T}$.

由(3.7)式和定理 3.1 可知

其中${\left\| {\varepsilon ^n} \right\|_2} \le c({\tau ^2} + h), n = 0,1,2,\cdots,M, M \in {\mathbb{R}^ + }$.

(3.14)式减去(3.13)式可得

由(3.15)式可得

其中

对于所有的$1\leq k\leq n$迭代, 代入之后,(3.16)式可化成

因此

又因为

基于式(3.9),(3.18)和(3.19)式可得

证毕.

基于(3.2)式, 本文给出以下 ADIS 算法

初始: 原始图像${u^0} = f$, 最大迭代次数$K, n = 0$.

步骤一: 计算$\alpha$.

步骤二: 计算$C_1, C_2, C_3, C_4$.

步骤三: 将${u^n}$作为初始值, 通过(3.2)式的第一个式子, 使用追赶法求解$u_{i,j}^{n + \frac{1}{2}}$($i = 1,2,$$\cdots,N,$$j = 1,2, \cdots,N$).

步骤四: 将${u^{n+\frac{1}{2}}}$作为初始值, 通过(3.2)式的第二个式子, 使用追赶法求解$u_{i,j}^{n +1}$($i = 1,2, \cdots,N,$$j = 1,2, \cdots,N$), 令$n=n+1$.

步骤五: 重复进行步骤二至步骤四直至$n = K$.

为了验证第 3 节中的理论结果, 本文演示了一些数值测试, 并将所提出的算法与 Xu 等^[13]提出的图像分解算法 (FSI) 进行了比较. 本文将使用 SNR (信噪比) 来衡量分解出纹理的多少. 根据信噪比的定义, 信噪比的数值越大, 则提取的纹理部分越多, 反之则越少. 该指标定义如下

注 4.1 由于该多尺度图像分解过程是为了得到更粗尺度的平滑图像$u_{\lambda_{i+1}}$, 因此对于指标SNR而言, SNR的数值越小, 说明从$u_{\lambda_{i}}\ (i=0,1,2,\cdots,N)$中提取的纹理越多, 得到的图像更加平滑.

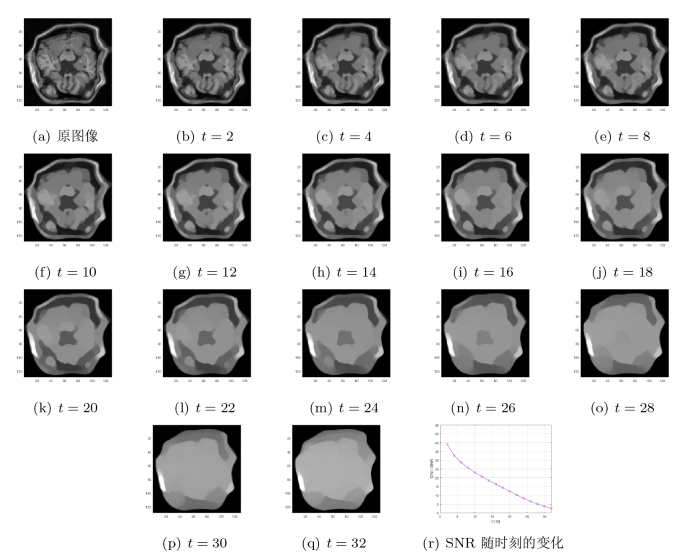
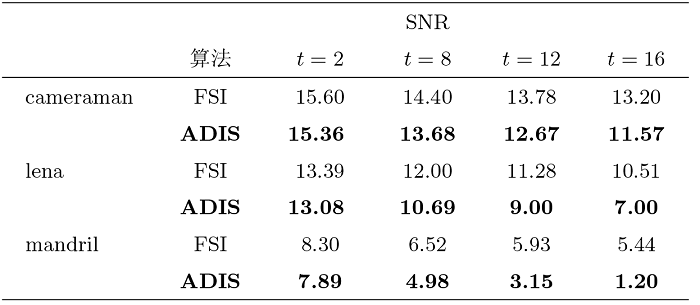
本节分成三个部分: 第一部分给出本文算法在$t=2, 4, 6,\cdots, 32$时的分解结果, 并给出了 SNR 在这些时刻的变化图, 具体可见图1; 第二部分将对四幅医学图像 liver, Brain-M, brain-d, Hand-M 进行图像分解 (具体图像可见图2), 所有医学图像大小均为$129\times 129$, 通过实验将文章提出的 ADIS 算法与 FSI 算法对比, 并分别列出在$t=2, 8, 12, 16$时的结构图像和纹理图像, 所得的结果如图3-图6 所示, 进一步对比不同时刻时的信噪比, 该结果列在表1中; 第三部分主要对三幅自然图像 lena, cameraman, mandril 进行图像分解 (具体图像可见图7), 所有自然图像大小均为$129\times 129$, 将文章提出的 ADIS 算法与 FSI 算法进行对比, 并分别列出在$t=2, 8, 12, 16$时的结构图像和纹理图像, 所得的结果如图8-图10 所示, 进一步, 对比不同时刻时的信噪比, 该结果列在表2中.

由图1可知, 随着时间增加, 结构图像被提取的纹理增加, 在$t=32$时，只剩下一个大致的轮廓, 说明了算法的有效性; 由图1中的图 r SNR 随时刻的变化示意图可得, 本文所提出的算法是收敛的.

由图3-图6的结构图像可以看出, 随着时间的增加, 本文算法所得到的结构图像越来越平滑, 且优于 FSI 算法, 从而说明本文提出的 ADIS 算法所得的结构图像更加平滑, 这也充分验证了第三节中的理论结果, 即本文所提出的算法具有良好的收敛性, 且收敛速度更快. 通过观察图3-图6的纹理图像, 相较于算法 FSI, 本文算法所得到的纹理图像更加清晰, 可以看出本文所提出的算法在相同的时间内提取了更多的纹理, 具有更好的纹理提取效果. 通过表1 可以看出, 在相同时间内 ADIS 算法的信噪比小于 FSI 算法, 且减小的速度更快, 这也进一步说明了 ADIS 算法的收敛速度更快, 且所得的结构图像更加平滑.

由图8-图10的结构图像可以看出, 随着时间的增加, 本文算法所得到的结构图像越来越平滑, 且优于 FSI 算法, 从而说明本文提出的 ADIS 算法所得的结构图像更加平滑, 这也充分验证了第三节中的理论结果, 即本文所提出的算法具有良好的收敛性, 且收敛速度更快. 通过观察图8-图10的纹理图像, 相较于算法 FSI, 本文算法所得到的纹理图像更加清晰, 可以看出本文所提出的算法在相同的时间内提取了更多的纹理, 具有更好的纹理提取效果. 此外, 通过观察图10的图o, 可以看出图像不太稳定. 通过表2可以看出, 在相同时间内 ADIS 算法的信噪比小于 FSI 算法, 且减小的速度更快, 这也进一步说明了 ADIS 算法的收敛速度更快, 且所得的结构图像更加平滑.

本文主要对于加权TV模型^[13]给出了一种 ADI 求解格式, 并且证明了 ADI 格式的收敛性和稳定性.通过对两种不同类型的图像组—医学图像、自然图像进行图像分解, 以信噪比作为指标进行结果分析, 并通过与算法 FSI 进行对比, 进一步说明了本文所提 ADIS 算法的有效性. 经过数值实验可以看出 ADIS 算法的纹理提取效果优于 FSI 算法. 在未来的研究中, 如何更加准确的表现纹理和结构是下一个目标.