数学物理学报, 2023, 43(6): 1943-1960

基于启动时间和可选服务的双阶段休假排队系统的流体模型性能分析

王勋, 徐秀丽,*

燕山大学理学院 河北秦皇岛 066004

Performance Analysis of a Fluid Model Driven by Two-Stage Vacation Queue with Set-up Time and Optional Service

Wang Xun, Xu Xiuli,*

School of Science, Yanshan University, Hebei Qinhuangdao 066004

通讯作者: *徐秀丽，E-mail: xxl-ysu@163.com

收稿日期: 2022-09-15   修回日期: 2023-05-17  

基金资助: 国家自然科学基金(62171143)

Received: 2022-09-15   Revised: 2023-05-17  

Fund supported: NSFC(62171143)

摘要

基于店铺的外卖经营模式, 该文构建并分析了具有启动时间、可选服务和两种混合休假策略的 M/M/1/N 排队系统驱动的流体模型. 首先, 对驱动系统进行模型描述, 并将此二维 Markov 过程的无穷小生成元写成块状雅克比矩阵形式, 运用矩阵几何解方法求出驱动系统的稳态概率分布. 其次, 引入流体模型的净输入率结构, 并利用概率分析方法得到流体库存水平在稳态条件下的微分差分方程组, 进而运用 Laplace 变换 (LT) 和 Laplace-Stieltjes 变换 (LST) 方法得到稳态条件下库存量的均值及空库概率. 最后, 通过数值分析给出各参数变化对系统性能指标和费用的影响.

关键词： 流体模型; 双阶段休假; 启动时间; 有限容量; 库存量

Abstract

Based on the take-out operation model of the store, this paper constructed and analyzed a fluid model driven by the M/M/1/N queueing system with set-up time, optional service and two types of mixed vacations. Firstly, the driving system is described and the infinite small generators of the two-dimensional Markov process are decomposed into a blocky Jacobian matrix form. Then, the stationary probability distribution of the driving system is obtained by using matrix-geometric method. Secondly, based on the net input rate structure of the fluid model, the differential and difference equations satisfied by the fluid level in steady-state conditions are obtained using the probability analysis method. Then, the expected buffer content and the probability of the empty buffer under steady-state conditions are obtained by using Laplace transform(LT) and Laplace-Stieltjes transform(LST) methods. Finally, the influence of parameters changing on the performance indicators and cost function are illustrated in numerical analysis.

Keywords： Fluid model; Two-stage vacation; Set-up time; Finite capacity; Buffer content

PDF (629KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

王勋, 徐秀丽. 基于启动时间和可选服务的双阶段休假排队系统的流体模型性能分析[J]. 数学物理学报, 2023, 43(6): 1943-1960

Wang Xun, Xu Xiuli. Performance Analysis of a Fluid Model Driven by Two-Stage Vacation Queue with Set-up Time and Optional Service[J]. Acta Mathematica Scientia, 2023, 43(6): 1943-1960

1 引言

随着电子信息技术的迭代速度越来越快, 传统的离散排队模型在建模分析中表现出很大的不便性, 流体模型在生产库存系统和互联网产业等领域具有更广泛的应用. Virtamo 和 Norros[1]首先提出了由 M/M/1 排队系统驱动的流体模型, 并运用谱方法和第二类切比雪夫多项式得到库存量的平稳分布. Anda 和 Resing[2]进一步使用嵌入点和修正 Bessel 函数的方法得到库存量平稳分布的表达式, 通过使用合适的积分证明得到的结果与文献 [1] 中的结果一致. 除谱方法外, 逐渐出现了各种排队系统驱动的流体模型及其新的研究方法. Sericola 和 Tuffin[3]运用递归法得到了流体模型平稳库存量的分布函数, 并在文中给出了一种稳定的算法, 进而得到可以预先指定精度的结果. Parthasarathy 等[4]通过连分数法巧妙地给出了稳态条件下流体模型库存量 Laplace-Stieltjes 变换 (LST) 表达式. 考虑系统是有限容量的情形, Parthasarathy 和 Lenin[5]研究了具有可变服务率和无限缓冲器容量的 M/M/1/N 排队系统驱动的流体模型, 使用三角行列式恒等式解析地给出了三对角矩阵的特征值. 毛炳蔚[6]分析了单服务台排队系统驱动的流体模型, 用几种方法分别得到了稳态性能指标的表达式. Ammar 和 Sherif[7]研究了灾难到达的 M/M/1 队列驱动的流体模型, 给出了缓冲器库存量在稳态时分布函数的显性表达式. Wang 和 Mao[8]将启动-关闭期引入到 M/M/1 排队系统, 得到了库存量平稳分布的 LST 及平均库存量.

近些年有学者将休假策略与排队系统驱动的流体模型相结合, 得到了一系列的研究成果. 休假策略主要包括经典休假、工作休假和双阶段休假等策略. Sherif 和 Ammar[9]研究了多重休假 M/M/1 排队系统驱动的流体模型, 运用母函数法和第一类修正 Bessel 函数给出了缓冲器库存量平稳分布的显式表达式. Mao 等[10]将多重休假策略引入到 M/M/1/N 排队系统驱动的流体模型, 并运用矩阵几何解方法得到了稳态下库存量均值的表达式. 徐秀丽等[11]将可选服务策略引入多重休假 M/M/1 排队系统, 得到了流体模型的空库概率及平稳库存量的 LST 和均值的表达式. Vijayashree 和 Anjuka[12]利用连分式和母函数方法得到了微分差分方程组, 并根据第一类修正 Bessel 函数给出了缓冲器库存量稳态联合概率分布的表达式. 考虑系统是有限容量的情形, Vijayashree 和 Anjuka[13]进一步得到多重工作休假 M/M/1/N 排队系统驱动的流体模型的稳态联合概率分布的显性表达式. 李子坤等[14]考虑了多服务台工作休假排队系统驱动的流体模型, 通过矩阵几何解方法得到库存量平稳分布的 LST 表达式, 并给出了稳态下的空库概率和均值. Xu 等[15]将负顾客引入到工作休假排队系统驱动的流体模型中, 既给出了库存量的空库概率和均值, 同时又给出了几类特殊模型. 考虑日常生活中服务台会采用双阶段休假策略的情形, 刘煜飞和叶晴晴[16]基于矩阵几何解和分块矩阵方法研究了双阶段休假 M/M/1 排队系统驱动的流体模型, 并通过数值分析验证了参数变化对性能指标的影响.

随着互联网技术的蓬勃发展和人们收入水平的日益提升, 大众的线上消费倾向日益增长, 促使线上外卖用户的规模不断扩大, 因此越来越多的店铺选择转型线上. 并且由于信息技术的发展导致顾客的到达速率越来越快, 进而导致顾客的到达间隔变得越来越小, 此时可将离散的顾客视为连续的流体. 如果将客流量进入线上平台中一个店铺的过程看作单服务台的排队系统, 营业额看作流体, 线上平台看作缓冲器, 客流量通过缓冲器转化成店铺营业额. 考虑实际情况, 店铺会推出满减优惠促进消费者消费, 即用户下单一个商品后, 为享受优惠, 该消费者会以一定概率在该店铺继续下单. 客流量影响着店铺服务率的高低. 当客流量较多时, 服务率较高, 类似于驱动系统处于正常忙期；当客流量较少时, 服务率就会变低, 类似于驱动系统处于工作休假期；当没有顾客时, 店铺就会停止服务, 类似于驱动系统处于休假期. 为给顾客提供高速度和高质量服务, 店铺会每日限定客流量, 当超过限定值时, 将不再接单. 在此基础上, 本文研究了具有启动时间、可选服务和双阶段休假的 M/M/1/N 排队系统驱动的流体模型, 得到了流体模型平稳库存量的 LST 及均值等性能指标. 最后通过数值分析验证参数变化对各性能指标的影响, 并构建合适的费用函数, 得到系统参数对成本费用的影响. 最终将验证结果应用到店铺的外卖经营过程中, 以优化店铺的成本费用和提升用户黏性, 进而减少库存积累并获得更高的利润.

2 驱动系统描述

考虑一个带有启动时间、可选服务和双阶段休假的 M/M/1/N 排队系统, 其模型描述如下

1) 顾客按照一个 Possion 过程到达容量为 $N$ 的系统, 其到达间隔服从参数为 $\lambda$ 的指数分布. 当系统中顾客数达到 $N$ 时, 顾客不再进入.

2) 当顾客进入系统后首先接受第一次服务, 第一次服务完成后, 顾客以概率 $1 - p$ 离开系统, 或者以概率 $p$ 接受第二次服务. 正规忙期内, 服务台以服务速率 ${\mu _b}$ 和 ${\mu _{b1}}$ 分别为顾客提供第一次服务和第二次服务.

3) 当服务完系统中在场顾客时, 服务台进入一次工作休假. 工作休假期内, 服务台以低服务速率${\mu _w}\left( {{\mu _w} < {\mu _b}} \right)$ 和 ${\mu _{w1}}\left( {{\mu _{w1}} < {\mu _{b1}}} \right)$ 分别为顾客提供第一次服务和第二次服务, 工作休假时间服从参数为 ${\theta _w}$ 的指数分布. 工作休假期结束时, 若系统中顾客数非空, 则服务台直接进入正规忙期, 此时服务台由低服务速率 ${\mu _w}$ 或 ${\mu_{w1}}$ 转换成高服务速率 ${\mu _b}$ 或 ${\mu _{b1}}$ 为顾客提供服务. 否则服务台进入一次经典休假, 休假期内服务台不提供服务, 休假时间服从参数为 ${\theta _v}$ 的指数分布.

4) 当休假期结束, 系统中顾客数非空时, 则服务台结束休假进入正规忙期, 否则, 进入关闭期. 若关闭期内有顾客到达, 系统开始启动, 启动时间服从参数为 ${\alpha}$ 的指数分布. 启动结束后, 服务台进入正规忙期.

5) 假设服务时间、到达间隔时间、休假时间、工作休假时间均两两相互独立. 并且该排队系统服从先到先服务 (FIFO) 的服务规则.

设 ${L\left( t \right)}$ 表示系统在时刻 $t$ 的顾客数, ${J\left( t \right) = 0,1,2,3}$ 表示服务台在时刻 t 分别处于工作休假期、休假期、关闭-启动期和正规忙期, 则 $\left\{ {\left( {L\left( t \right),J\left( t \right)} \right),t \ge 0} \right\}$ 是连续时间的二维马尔可夫过程, 其状态空间为 $\Omega = \left\{ {\left( {0,0} \right),\left( {0,1} \right),\left( {0,2} \right)} \right\} \cup \left\{ {\left( {k,j} \right):1 \le k \le N;j = 0,1,2,3} \right\}$, 把系统状态按照字典序排列能够得到二维马尔可夫过程的无穷小生成元为

$\boldsymbol{Q} = \left( {\begin{array}{*{20}{c}} {{\boldsymbol{A}_{00}}}&{{\boldsymbol{A}_{10}}}&{}&{}&{}&{}\\ {{\boldsymbol{B}_{10}}}&\boldsymbol{B}&\boldsymbol{C}&{}&{}&{}\\ {}&\boldsymbol{A}&\boldsymbol{B}&\boldsymbol{C}&{}&{}\\ {}&{}& \ddots & \ddots & \ddots &{}\\ {}&{}&{}&\boldsymbol{A}&\boldsymbol{B}&\boldsymbol{C}\\ {}&{}&{}&{}&\boldsymbol{A}&{\boldsymbol{B}_{N}} \end{array}} \right),$

记 $H = {\mu _b}\left( {1 - p} \right) + {\mu _b}p{\mu _{b1}}$, $M = {\mu _w}\left( {1 - p} \right) + {\mu _w}p{\mu _{w1}}$, 则 $\boldsymbol{Q}$ 矩阵子块分别如下

${\boldsymbol{A}_{00}} = \left( {\begin{array}{*{20}{c}} { - \left( {\lambda + {\theta _w}} \right)}&{{\theta _w}}&0\\ 0&{ - \left( {\lambda + {\theta _v}} \right)}&{{\theta _v}}\\ 0&0&{ - \lambda } \end{array}} \right), \quad {\boldsymbol{A}_{10}} = \left( {\begin{array}{*{20}{c}} \lambda &0&0&0\\ 0&\lambda &0&0\\ 0&0&\lambda &0 \end{array}} \right),$
${\boldsymbol{B}_{10}} = \left( {\begin{array}{*{20}{c}} M&0&0\\ 0&0&0\\ 0&0&0\\ H&0&0 \end{array}} \right), \quad \boldsymbol{A} = \left( {\begin{array}{*{20}{c}} M&0&0&0\\ 0&0&0&0\\ 0&0&0&0\\ 0&0&0&H \end{array}} \right),$
$\boldsymbol{B} = \left( {\begin{array}{*{20}{c}} { - \left( {\lambda + {\theta _w} + M} \right)}&0&0&{{\theta _w}}\\ 0&{ - \left( {\lambda + {\theta _v}} \right)}&0&{{\theta _v}}\\ 0&0&{ - \left( {\lambda + \alpha } \right)}&\alpha \\ 0&0&0&{ - \left( {\lambda + H} \right)} \end{array}} \right),$
$\boldsymbol{C} = \left( {\begin{array}{*{20}{c}} \lambda &0&0&0\\ 0&\lambda &0&0\\ 0&0&\lambda &0\\ 0&0&0&\lambda \end{array}} \right), \quad {\boldsymbol{B}_N} = \left( {\begin{array}{*{20}{c}} { - \left( {{\theta _w} + M} \right)}&0&0&{{\theta _w}}\\ 0&{ - {\theta _v}}&0&{{\theta _v}}\\ 0&0&{ - \alpha }&\alpha \\ 0&0&0&{ - H} \end{array}} \right).$

由 $\boldsymbol{Q}$ 矩阵为分块三对角矩阵可知, $\left\{ {\left( {L\left( t \right),J\left( t \right)} \right),t \ge 0} \right\}$ 为拟生灭过程. 记驱动系统的服务强度 $\rho = \lambda /H$, 当 $\rho < 1$ 时, 易知二维马尔可夫过程 $\left\{ {\left( {L\left( t \right),J\left( t \right)} \right),t \ge 0} \right\}$ 存在稳态分布, 记为 ${\pi} _{kj} = \mathop {\lim }\limits_{t \to \infty } P\left\{ {L\left( t \right) = k,J\left( t \right) = j} \right\}$, $\left( {k,j} \right) \in \Omega$. 同时引入稳态分布向量 ${\boldsymbol{\pi}} _0 = \left( {{\pi _{00}},{\pi _{01}},{\pi _{02}}} \right)$, $\boldsymbol{\pi} _k = \left( {{\pi _{k0}},{\pi _{k1}},{\pi _{k2}},{\pi _{k3}}} \right)$, $1 \le k \le N$.

引理 2.1 当 $\rho < 1$ 时, 二次矩阵方程 ${\boldsymbol{R}^2}\boldsymbol{A} + \boldsymbol{RB} + \boldsymbol{C} = \boldsymbol{0}$ 存在最小非负解

$\boldsymbol{R} = \left( {\begin{array}{*{20}{c}} r&0&0& {\frac{{{\theta _w}r}}{{H\left( {1 - r} \right)}}}\\ 0&{ \frac{\lambda }{{\lambda + {\theta _v}}}}&0&\rho \\ 0&0& {\frac{\lambda }{{\lambda + \alpha }}}&\rho \\ 0&0&0&\rho \end{array}} \right), $

其中 $r = \frac{{\lambda + {\theta _w} + M - \sqrt {{{\left( {\lambda + {\theta _w} + M} \right)}^2} - 4\lambda M} }}{{2M}}$.

由引理 2.1 可得下述结果.

定理 2.1 当 $\rho < 1$ 时, 二维马尔可夫过程 $\left\{ {L\left( t \right),J\left( t \right),t \ge 0} \right\}$ 的稳态分布为

$\begin{array}{l} \pi_{k 0}=\left\{\begin{array}{l} r^{k} \pi_{00}, \quad 0 \leq k \leq N-1, \\ \frac{\lambda r^{N-1}}{\theta_{w}+M} \pi_{00}, \quad k=N, \end{array}\right. \\ \pi_{k 1}=\left\{\begin{array}{l} \frac{\theta_{w}}{\lambda+\theta_{v}}\left(\frac{\lambda}{\lambda+\theta_{v}}\right)^{k} \pi_{00}, \quad 0 \leq k \leq N-1, \\ \frac{\theta_{w}}{\theta_{v}}\left(\frac{\lambda}{\lambda+\theta_{v}}\right)^{N} \pi_{00}, \quad k=N, \end{array}\right. \\ \pi_{k 2}=\left\{\begin{array}{l} \frac{\theta_{v} \theta_{w}}{\lambda\left(\lambda+\theta_{v}\right)}\left(\frac{\lambda}{\lambda+\alpha}\right)^{k} \pi_{00}, \quad 0 \leq k \leq N-1, \\ \frac{\theta_{v} \theta_{w}}{\alpha\left(\lambda+\theta_{v}\right)}\left(\frac{\lambda}{\lambda+\alpha}\right)^{N-1} \pi_{00}, \quad k=N, \end{array}\right. \\ \pi_{k 3}=\left\{\begin{array}{l} {\left[\frac{r \theta_{w}}{H(1-r)} \sum_{i=1}^{k-1} r^{i} \rho^{k-i-1}+\frac{\lambda \theta_{w}}{\left(\lambda+\theta_{v}\right)^{2}} \sum_{i=1}^{k-1}\left(\frac{\lambda}{\lambda+\theta_{v}}\right)^{k-i-1} \rho^{i}+\frac{\theta_{w}}{H(1-r)} \rho^{k-1}\right.} \\ \left.\quad+\frac{\theta_{v} \theta_{w}}{(\lambda+\alpha)\left(\lambda+\theta_{v}\right)} \sum_{i=1}^{k-1}\left(\frac{\lambda}{\lambda+\alpha}\right)^{k-i-1} \rho^{i}\right] \pi_{00}, 0 \leq k \leq N-1, \\ V_{1} \pi_{00}, \quad k=N, \end{array}\right. \end{array}$

其中

${\pi _{00}} =\ \left\{ {\frac{{1 - {r^N}}}{{1 - r}} + \frac{{\lambda {r^{N - 1}}}}{{{\theta _w} + M}} + \frac{{{\theta _w}}}{{{\theta _v}}} + \frac{{{\theta _v}{\theta _w}\left( {\lambda + \alpha } \right)}}{{\lambda \alpha \left( {\lambda + {\theta _v}} \right)}} + \frac{{{\theta _w}}}{{H\left( {1 - r} \right)}} + {V_1} } \right.\\ + \sum\limits_{k = 2}^{N - 2} \left[ \frac{r\theta _w} {H\left( 1 - r \right)} \sum\limits_{i = 1}^{k - 1} r^i\rho ^{k - i - 1} \right. + \frac{\lambda \theta _w}{\left( \lambda + \theta _v \right)^2} \sum\limits_{i = 1}^{k - 1} \rho ^i\left( \frac{\lambda }{\lambda + \theta _v} \right)^{k - i - 1} \\ \left.\left. + \frac{\theta _w}{H\left( 1 - r \right)}\rho ^{k - 1} + \frac{\theta _v}{\theta _w} \left( \lambda + \alpha \right) \left(\lambda + \theta _v \right) \sum\limits_{i = 1}^{k - 1} \rho ^i\left( \frac{\lambda }{\lambda + \alpha } \right)^{k - i - 1} \right] \right\}^{ - 1},\\ {V_1} =\ \frac{1}{H}\left[ \frac{\lambda r\theta _w}{H\left( 1 - r \right)} \sum\limits_{i = 1}^{N - 2} r^i\rho ^{N - i - 2} + \theta _w\sum\limits_{i = 1}^{N - 2} \left( \frac{\lambda }{\lambda + \theta _v} \right)^{N - i}\rho ^i \right.\\ + \frac{\theta _v}{\theta _w}\left( \lambda + \theta _v \right) \sum\limits_{i = 1}^{N - 2} \rho ^i \left(\frac{\lambda }{\lambda + \alpha } \right)^{N - i - 1} + \frac{\lambda \theta _w}{H\left( {1 - r} \right)} \rho ^{N - 2} + \frac{\lambda \theta _wr^{N - 1}}{\theta _w + M} \\ +\left. \theta _w\left( \frac{\lambda }{\lambda + \theta _v} \right)^N + \frac{\theta _v\theta _w}{\lambda + \theta _v} \left( \frac{\lambda }{\lambda + \alpha } \right)^{N - 1} \right].$

证 拟生灭过程 $\left\{ {L\left( t \right),J\left( t \right),t \ge 0} \right\}$ 的稳态分布存在当且仅当率阵 $\boldsymbol{R}$ 的谱半径 $SP\left( \boldsymbol{R} \right) < 1$, 且 $\left( {{\boldsymbol{\pi} _0},{\boldsymbol{\pi} _1}} \right)\boldsymbol{B}\left[ R \right] = \boldsymbol{0}$ 有正解, 其中

$\boldsymbol{B}\left[ R \right] = \left( {\begin{array}{*{20}{c}} { - \left( {\lambda + {\theta _w}} \right)}& {{\theta _w}}& 0&\lambda &0&0&0\\ 0& { - \left( {\lambda + {\theta _v}} \right)} &{{\theta _v}}&0&\lambda &0&0\\ 0&0&{ - \lambda }&0&0&\lambda &0\\ M&0&0& { - \frac{\lambda }{r}} &0&0&{\frac{{{\theta _w}}}{{1 - r}}}\\ 0&0&0&0&{ - \left( {\lambda + {\theta _v}} \right)}&0&{\lambda + {\theta _v}}\\ 0&0&0&0&0& { - \left( {\lambda + \alpha } \right)} &{\lambda + \alpha }\\ H&0&0&0&0&0&{ - H} \end{array}} \right).$

由 $\left( {{\boldsymbol{\pi} _0},{\boldsymbol{\pi} _1}} \right)\boldsymbol{B}\left[ R \right] = \boldsymbol{0}$, 得到以下方程组

$\left\{ \begin{array}{lll} - \left( {\lambda + {\theta _w}} \right){\pi _{00}} + M{\pi _{10}} + H{\pi _{13}} = 0,\\ {\theta _w}{\pi _{00}} - \left( {\lambda + {\theta _v}} \right){\pi _{01}} = 0,\\ {\theta _v}{\pi _{01}} - \lambda {\pi _{02}} = 0,\\ \lambda {\pi _{00}} - \frac{\lambda }{r}{\pi _{10}} = 0,\\ \lambda {\pi _{01}} - \left( {\lambda + {\theta _v}} \right){\pi _{11}} = 0,\\ \lambda {\pi _{02}} - \left( {\lambda + \alpha } \right){\pi _{12}} = 0,\\ \frac{{{\theta _w}}}{{1 - r}}{\pi _{10}} + \left( {\lambda + {\theta _v}} \right){\pi _{11}} + \left( {\lambda + \alpha } \right){\pi _{12}} - H{\pi _{13}} = 0.\end{array} \right.$

求解得到

${\pi _{01}} = \frac{{{\theta _w}}}{{\lambda + {\theta _v}}}{\pi _{00}},\ {\pi _{02}} = \frac{{{\theta _v}{\theta _w}}}{{\lambda \left( {\lambda + {\theta _v}} \right)}}{\pi _{00}},\ {\pi _{10}} = r{\pi _{00}},$
${\pi _{11}} = \frac{{\lambda {\theta _w}}}{{{{\left( {\lambda + {\theta _v}} \right)}^2}}}{\pi _{00}},\ {\pi _{12}} = \frac{{{\theta _v}{\theta _w}}}{{\left( {\lambda + \alpha } \right)\left( {\lambda + {\theta _v}} \right)}}{\pi _{00}},\ {\pi _{13}} = \frac{{{\theta _w}}}{{H\left( {1 - r} \right)}}{\pi _{00}}.$

利用拟生灭过程和矩阵几何解方法得到

$\left\{ \begin{array}{lll}{\boldsymbol{\pi} _k} = {\boldsymbol{\pi} _1}{\boldsymbol{R}^{k - 1}},1 \le k \le N - 1,\\ \lambda {\pi _{N - 1,0}} - \left( {{\theta _w} + M} \right){\pi _{N,0}} = 0,\\ \lambda {\pi _{N - 1,1}} - {\theta _v}{\pi _{N,1}} = 0,\\ \lambda {\pi _{N - 1,2}} - \alpha {\pi _{N,2}} = 0,\\ \lambda {\pi _{N - 1,3}} + {\theta _w}{\pi _{N,0}} + {\theta _v}{\pi _{N,1}} + \alpha {\pi _{N,2}} -H{\pi _{N,3}} = 0, \end{array} \right.$

其中

${\boldsymbol{R}^{k - 1}} = \left( {\begin{array}{*{20}{c}} {{r^{k - 1}}}&0&0& {\frac{{{\theta _w}}}{{H\left( {1 - r} \right)}}\sum\limits_{i = 1}^{k - 1} {{r^i}{\rho ^{k - i - 1}}} }\\ 0& {{{\left( {\frac{\lambda }{{\lambda + {\theta _v}}}} \right)}^{k - 1}}}&0& {\sum\limits_{i = 1}^{k - 1} {{{\left( {\frac{\lambda }{{\lambda + {\theta _v}}}} \right)}^{k - i - 1}}{\rho ^i}} }\\ 0&0&\quad {{{\left( {\frac{\lambda }{{\lambda + \alpha }}} \right)}^{k - 1}}}\quad& {\sum\limits_{i = 1}^{k - 1} {{{\left( {\frac{\lambda }{{\lambda + \alpha }}} \right)}^{k - i - 1}}{\rho ^i}} }\\ 0&0&0&{{\rho ^{k - 1}}} \end{array}} \right).$

求解 (2.4) 式得出

$\begin{aligned} &{\pi _{k0}} = \left\{ \begin{array}{ll} {r^{k - 1}}{\pi _{10}}, \, \, &1 \le k \le N - 1,\\ \frac{\lambda }{{{\theta _w} + M}}{\pi _{N - 1,0}}, \, \, &k = N, \end{array} \right.\\ &{\pi _{k1}} = \left\{ \begin{array}{ll} {\left( {\frac{\lambda }{{\lambda + {\theta _v}}}} \right)^{k - 1}}{\pi _{11}}, \, \, &1 \le k \le N - 1,\\ \frac{\lambda }{{{\theta _v}}}{\pi _{N - 1,1}}, \, &k = N, \end{array} \right.\\ &{\pi _{k2}} = \left\{ \begin{array}{ll} {\left( {\frac{\lambda }{{\lambda + \alpha }}} \right)^{k - 1}}{\pi _{12}}, \, \, &1 \le k \le N - 1,\\ \frac{\lambda }{\alpha }{\pi _{N - 1,2}}, \, \, &k = N, \end{array} \right.\\ &{\pi _{k3}} = \left\{ \begin{array}{ll} \frac{{{\theta _w}}}{{H\left( {1 - r} \right)}}\sum\limits_{i = 1}^{k - 1} {{r^i}{\rho ^{k - i - 1}}} {\pi _{10}} + \sum\limits_{i = 1}^{k - 1} {{{\left( {\frac{\lambda }{{\lambda + {\theta _v}}}} \right)}^{k - i - 1}}{\rho ^i}} {\pi _{11}}\\ \quad + \sum\limits_{i = 1}^{k - 1} {{{\left( {\frac{\lambda }{{\lambda + \alpha }}} \right)}^{k - i - 1}}{\rho ^i}} {\pi _{12}} + {\rho ^{k - 1}}{\pi _{13}}, \, \qquad\qquad 1 \le k \le N - 1,\\ \frac{\lambda }{H}\left( {{\pi _{N - 1,3}} + \frac{{{\theta _w}}}{{{\theta _w} + M}}{\pi _{N - 1,0}} + {\pi _{N - 1,1}} + {\pi _{N - 1,2}}} \right), \, \, k = N. \end{array} \right. \end{aligned}$

联立 (2.2), (2.3) 和 (2.5) 式, 并利用归一化条件

$\sum\limits_{k = 0}^N {\left( {{\pi _{k0}} + {\pi _{k1}} + {\pi _{k2}}} \right)} + \sum\limits_{k = 1}^N {{\pi _{k3}}} = 1$

求解得到 ${\pi _{00}}$, 进而整理可得到 (2.1) 式. 定理 2.1 得证.

3 流体模型稳态分析

定义 ${C\left( t \right)}$ 为缓冲器在时刻$t$时的库存量. 库存量是指流体在缓冲器内的总量, 显然它是一个非负随机变量, 则 $\left\{ {\left( {L\left( t \right),J\left( t \right),C\left( t \right)} \right),t \ge 0} \right\}$ 构成一个随机过程. 设缓冲器的净流入率 (流入率-流出率) 为过程 $\left\{ {\left( {L\left( t \right),J\left( t \right),C\left( t \right)} \right),t \ge 0} \right\}$ 的函数

$\frac{{{\rm d}C\left( t \right)}}{{{\rm d}t}} = \left\{ \begin{array}{lll} {\sigma _0},\left( {L\left( t \right),J\left( t \right)} \right) = \left( {k,0} \right),k \ge 1,\\ {\sigma _1},\left( {L\left( t \right),J\left( t \right)} \right) = \left( {k,1} \right),k \ge 1,\\ {\sigma _2},\left( {L\left( t \right),J\left( t \right)} \right) = \left( {k,2} \right),k \ge 1,\\ {\sigma _3},\left( {L\left( t \right),J\left( t \right)} \right) = \left( {k,3} \right),k \ge 1,\\ \sigma,\left( {L\left( t \right),J\left( t \right)} \right) = \left( {0,0} \right) \cup \left( {0,1} \right) \cup \left( {0,2} \right),C\left( t \right) > 0,\\ 0,\left( {L\left( t \right),J\left( t \right)} \right) = \left( {0,0} \right),C\left( t \right) = 0, \end{array} \right.$

其中 $\sigma < 0$, $0 < {\sigma _0} < {\sigma _1} < {\sigma _2} < {\sigma _3}$. 以上函数表达式代表着当服务台处于工作休假、休假或关闭状态, 且驱动系统中没有顾客时, 库存量以速率 $-\sigma$ 减少, 直至库存量为空. 当服务台处于正规忙期状态, 且驱动系统中顾客数非空时, 库存量以速率 $\sigma _3$ 增加. 当服务台处于启动状态, 且驱动系统中顾客数非空时, 库存量以速率 ${\sigma _2}$ 增加. 当服务台处于休假状态, 且驱动系统中顾客数非空时, 库存量以速率 $\sigma _1$ 增加. 当服务台处于工作休假状态, 且驱动系统中顾客数非空时, 库存量以速率 $\sigma _0$ 增加.

根据以上描述, 带启动时间、可选服务和双阶段休假的 M/M/1/N 排队系统驱动的流体模型可看作具有净输入率结构的三维马尔可夫过程 $\left\{ {\left( {L\left( t \right),J\left( t \right),C\left( t \right)} \right),t \ge 0} \right\}$, 其状态空间 $\Omega ' = \left[ 0 \right.,\left. { + \infty } \right)\times \Omega $ 为混合型.

记 $d = {\pi _{00}} + {\pi _{01}} + {\pi _{02}} + {\sigma _0}\sum\limits_{k = 1}^N {{\pi _{k0}}} + {\sigma _1}\sum\limits_{k = 1}^N {{\pi _{k1}}} + {\sigma _2}\sum\limits_{k = 1}^N {{\pi _{k2}}} + {\sigma _3}\sum\limits_{k = 1}^N {{\pi _{k3}}}$, 其中 ${\pi _{kj}}\left( {\left( {k,j} \right) \in \Omega } \right)$ 可由定理 2.1 得到, $d$ 称为流体模型的平均漂移. 且由文献 [16] 可知, 当 $d < 0$, $\rho < 1$ 时, 流体模型是稳定的. 当流体模型的稳态条件均满足时, 记其稳态向量为 $\left( {L,J,C} \right)$, 定义流体模型稳态联合分布为

${F_{kj}}\left( u \right) = \mathop {\lim }\limits_{t \to \infty } P\left\{ {C\left( t \right) \le u,L\left( t \right) = k,J\left( t \right) = j} \right\} = P\left\{ {C \le u,L = k,J = j} \right\},\left( {k,j} \right) \in \Omega.$

运用全概率公式, 得到库存量的平稳分布函数为

$F\left( u \right) = P\left\{ {C \le u} \right\} = {F_{00}}\left( u \right) + {F_{01}}\left( u \right) + {F_{02}}\left( u \right) + \sum\limits_{k = 1}^N {\sum\limits_{j = 0}^3 {{F_{kj}}\left( u \right)} }.$

记 ${\boldsymbol{F}_0}\left( u \right) = \left( {{F_{00}}\left( u \right),{F_{01}}\left( u \right),{F_{02}}\left( u \right)} \right)$, ${\boldsymbol{F}_k}\left( u \right) = \left( {{F_{k0}}\left( u \right),{F_{k1}}\left( u \right),{F_{k2}}\left( u \right),{F_{k3}}\left( u \right)} \right),$ $1 \le k \le N$. 运用概率分析方法, 得到 ${{F}_k}\left( u \right)$ 满足以下矩阵微分方程形式

$\frac{{\rm d}}{{{\rm d}u}}\left( {{\boldsymbol{F}_0}\left( u \right),{\boldsymbol{F}_1}\left( u \right), \cdots,{\boldsymbol{F}_N}\left( u \right)} \right)\boldsymbol{G} = \left( {{\boldsymbol{F}_0}\left( u \right),{\boldsymbol{F}_1}\left( u \right), \cdots,{\boldsymbol{F}_N}\left( u \right)} \right)\boldsymbol{Q},$

其中

$\boldsymbol{G} = \rm{diag}\left( {\sigma,\sigma,\sigma,{\sigma _0},{\sigma _1},{\sigma _2},{\sigma _3},{\sigma _0},{\sigma _1},{\sigma _2},{\sigma _3}, \cdots,{\sigma _0},{\sigma _1},{\sigma _2},{\sigma _3}} \right).$

同时, (3.1) 式满足边界条件

$\begin{array}{lll} {F_{00}}\left( 0 \right) = a,\ {F_{kj}}\left( 0 \right) = 0,\ \left( {k,j} \right) \in \Omega /\left( {0,0} \right),\ {F_{kj}}\left( \infty \right) = {\pi _{kj}}, \end{array}$

这里 $a = {F_{00}}\left( 0 \right)$ 称为稳态条件下库存量的空库概率.

为方便计算, 定义 ${F_{kj}}\left( u \right)$ 的 Lapalace 变换为

${{\hat F}_{kj}}\left( s \right) = \int_0^\infty {{{\rm e}^{ - su}}} {F_{kj}}\left( u \right){\rm d}u,s \ge 0,\left( {k,j} \right) \in \Omega,\nonumber$

则 $F\left( u \right)$ 的 Lapalace 变换为

${\hat F}\left( s \right) = \sum\limits_{k = 0}^N {\left( {{{\hat F}_{k0}}\left( s \right) + {{\hat F}_{k1}}\left( s \right) + {{\hat F}_{k2}}\left( s \right)} \right)} + \sum\limits_{k = 1}^N {{{\hat F}_{k3}}\left( s \right)}.\nonumber$

对 (3.1) 式的两边进行 Laplace 变换, 结合 ${\hat F_{kj}}\left( s \right)$, ${\hat F}\left( s \right)$ 的表达式和边界条件, 整理得到

$\left( {{{\hat F}_{00}}\left( s \right),{{\hat F}_{01}}\left( s \right),{{\hat F}_{02}}\left( s \right),{{{\hat{F}}}_1} \left( s \right), \cdots, {{{\hat{F}}}_N} \left( s \right)} \right)\left( {\boldsymbol{Q} - \boldsymbol{sG}} \right) = \left( { - a\sigma,0,0, \cdots,0} \right).$

结合文献 [15], 可得到以下引理.

引理 3.1 当任意 $s \ge 0$, $\rho < 1$ 时, 方程 $M{z^2} - \left( {\lambda + {\theta _w} + M + s{\sigma _0}} \right)z + \lambda = 0$ 拥有两个相异实根, 分别为

$r\left( s \right) = \frac{{\lambda + {\theta _w} + M + s{\sigma _0} - \sqrt {{{\left( {\lambda + {\theta _w} + M + s{\sigma _0}} \right)}^2} - 4\lambda M} }}{{2M}},$
${r_1}\left( s \right) = \frac{{\lambda + {\theta _w} + M + s{\sigma _0} + \sqrt {{{\left( {\lambda + {\theta _w} + M + s{\sigma _0}} \right)}^2} - 4\lambda M} }}{{2M}},$

且满足 $0 < r\left( s \right) < 1$, ${r_1}\left( s \right) \ge 1$, $r\left( 0 \right) = r.$

引理 3.2 当任意 $s \ge 0$, $\rho < 1$时, 方程 $H{z^2} - \left( {\lambda + H + s{\sigma _3}} \right)H + \lambda = 0$ 拥有两个相异实根, 分别为

$h\left( s \right) = \frac{{\lambda + H + s{\sigma _3} - \sqrt {{{\left( {\lambda + H + s{\sigma _3}} \right)}^2} - 4\lambda H} }}{{2H}},$
${h_1}\left( s \right) = \frac{{\lambda + H + s{\sigma _3} + \sqrt {{{\left( {\lambda + H + s{\sigma _3}} \right)}^2} - 4\lambda H} }}{{2H}},$

且满足 $0 < h\left( s \right) < 1$, ${h_1}\left( s \right) \ge 1$, $h\left( 0 \right) = \rho$, ${h_1}\left( 0 \right) = 1.$

为方便表示, 引入矩阵

$\boldsymbol{B}\left( s \right) = \left( {\begin{array}{*{20}{c}} { - \left( {\lambda + {\theta _w} + M + s{\sigma _0}} \right)}&0&0&{{\theta _w}}\\ 0&{ - \left( {\lambda + {\theta _v} + s{\sigma _1}} \right)}&0&{{\theta _v}}\\ 0&0&{ - \left( {\lambda + \alpha + s{\sigma _2}} \right)}&\alpha \\ 0&0&0&{ - \left( {\lambda + H + s{\sigma _3}} \right)} \end{array}} \right),$

可得到下述引理.

引理 3.3 对任意 $s \ge 0$, 二次矩阵方程 ${\left( {\boldsymbol{R}\left( s \right)} \right)^2}\boldsymbol{A} + \boldsymbol{R}\left( s \right)\boldsymbol{B}\left( s \right) + \boldsymbol{C} = \boldsymbol{0}$ 的最小非负解存在, 记为

$\boldsymbol{R}\left( s \right) = \left( {\begin{array}{*{20}{c}} {r\left( s \right)}&0&0&{\varphi \left( s \right)}\\ 0&{{m_1}\left( s \right)}&0&{{\eta _1}\left( s \right)}\\ 0&0&{{m_2}\left( s \right)}&{{\eta _2}\left( s \right)}\\ 0&0&0&{h\left( s \right)} \end{array}} \right),$

其中

$\varphi \left( s \right) = \frac{{{\theta _w}r\left( s \right)}}{{\lambda + s{\sigma _3} + {H}\left( {1 - r\left( s \right) - h\left( s \right)} \right)}}, {\eta _1}\left( s \right) = \frac{{{\theta _v}{m_1}\left( s \right)}}{{\lambda + s{\sigma _3} + {H}\left( {1 - {m_1}\left( s \right) - h\left( s \right)} \right)}},$
${\eta _2}\left( s \right) = \frac{{\alpha {m_2}\left( s \right)}}{{\lambda + s{\sigma _3} + {H}\left( {1 - {m_2}\left( s \right) - h\left( s \right)} \right)}}, {m_1}\left( s \right) = \frac{\lambda }{{\lambda + {\theta _v} + s{\sigma _1}}}, {m_2}\left( s \right) = \frac{\lambda }{{\lambda + \alpha + s{\sigma _2}}}.$

根据引理 3.1-3.3, 可得到下述结论.

定理 3.1 当 $d < 0,\rho < 1$ 时, ${{\hat F}_{kj}}\left( s \right)\left( {\left( {k,j} \right) \in \Omega } \right)$ 的表达式为

$\begin{aligned} &{{\hat F}_{k0}}\left( s \right) = \left\{ \begin{array}{lll} {\left( {r\left( s \right)} \right)^k}{{\hat F}_{00}}\left( s \right),&0 \le k \le N - 1,\\ \frac{{\lambda {{\left( {r\left( s \right)} \right)}^{N - 1}}}}{{{\theta _w} + M + s{\sigma _0}}}{{\hat F}_{00}}\left( s \right),\ &k = N, \end{array} \right.\\ &{{\hat F}_{k1}}\left( s \right) = \left\{ \begin{array}{lll} \frac{{{\theta _w}{{\left[ {{m_1}\left( s \right)} \right]}^k}}}{{\lambda + {\theta _v} + s\sigma }}{{\hat F}_{00}}\left( s \right),&0 \le k \le N - 1,\\ \frac{{\lambda {\theta _w}{{\left[ {{m_1}\left( s \right)} \right]}^{N - 1}}}}{{\left( {{\theta _v} + s{\sigma _1}} \right)\left( {\lambda + {\theta _v} + s\sigma } \right)}}{{\hat F}_{00}}\left( s \right),\ &k = N, \end{array} \right.\\ &{{\hat F}_{k2}}\left( s \right) = \left\{ \begin{array}{lll} \frac{{{\theta _v}{\theta _w}{{\left[ {{m_2}\left( s \right)} \right]}^k}}}{{\left( {\lambda + s\sigma } \right)\left( {\lambda + {\theta _v} + s\sigma } \right)}}{{\hat F}_{00}}\left( s \right),&0 \le k \le N - 1,\\ \frac{{\lambda {\theta _v}{\theta _w}{{\left[ {{m_2}\left( s \right)} \right]}^{N - 1}}}}{{\left( {\alpha + s{\sigma _2}} \right)\left( {\lambda + s\sigma } \right)\left( {\lambda + {\theta _v} + s\sigma } \right)}}{{\hat F}_{00}}\left( s \right),\ &k = N, \end{array} \right.\\ & {{\hat F}_{k3}}\left( s \right) = \left\{ \begin{array}{lll} \left[ {\varphi \left( s \right)\sum\limits_{i = 1}^{k - 1} {{{\left( {r\left( s \right)} \right)}^{k - i}}{{\left( {h\left( s \right)} \right)}^{i - 1}}} + \frac{{{\eta _1}\left( s \right){\theta _w}}}{{\left( {\lambda + {\theta _v} + s\sigma } \right)}}\sum\limits_{i = 1}^{k - 1} {{{\left( {{m_1}\left( s \right)} \right)}^{k - i}}{{\left( {h\left( s \right)} \right)}^{i - 1}}} } \right.\\ \left. { + \frac{{{{\left( {h\left( s \right)} \right)}^k}L\left( s \right)}}{\lambda } + \frac{{{\eta _2}\left( s \right){\theta _v}{\theta _w}}}{{\left( {\lambda + s\sigma } \right)\left( {\lambda + {\theta _v} + s\sigma } \right)}}\sum\limits_{i = 1}^{k - 1} {{{\left( {{m_2}\left( s \right)} \right)}^{k - i}}{{\left( {h\left( s \right)} \right)}^{i - 1}}} } \right]{{\hat F}_{00}}\left( s \right),\\ \hskip 6cm 1 \le k \le N - 1,\\ \frac{\lambda }{H + s\sigma _3} \bigg[ \varphi \left( s \right)\sum\limits_{i = 1}^{N - 2} \left( r\left( s \right) \right)^{N - i - 1} \left( h\left( s \right) \right)^{i - 1} + \frac{\left( h\left( s \right) \right)^{N - 1}L\left( s \right)}{\lambda } \\ + \frac{\theta _w\left(r\left( s \right) \right)^{N - 1}} {\theta _w + M + s\sigma _0} + \frac{{{\eta _1}\left( s \right){\theta _w}}}{{\left( {\lambda + {\theta _v} + s\sigma } \right)}}\sum\limits_{i = 1}^{N - 2} {{{\left( {{m_1}\left( s \right)} \right)}^{N - i - 1}}{{\left( {h\left( s \right)} \right)}^{i - 1}}} \\ + \frac{{{\eta _2}\left( s \right){\theta _v}{\theta _w}}}{{\left( {\lambda + s\sigma } \right)\left( {\lambda + {\theta _v} + s\sigma } \right)}}\sum\limits_{i = 1}^{N - 2} {{{\left( {{m_2}\left( s \right)} \right)}^{N - i - 1}}{{\left( {h\left( s \right)} \right)}^{i - 1}}} \\ + { \frac{{{\theta _v}{\theta _w}{{\left( {{m_1}\left( s \right)} \right)}^{N - 1}}}}{{\left( {{\theta _v} + s{\sigma _1}} \right)\left( {\lambda + {\theta _v} + s\sigma } \right)}} + \frac{{\alpha {\theta _v}{\theta _w}{{\left( {{m_2}\left( s \right)} \right)}^{N - 1}}}}{{\left( {\alpha + s{\sigma _2}} \right)\left( {\lambda + s\sigma } \right)\left( {\lambda + {\theta _v} + s\sigma } \right)}}} \bigg]{{\hat F}_{00}}\left( s \right),k = N. \end{array} \right. \end{aligned}$

其中

${\hat F_{00}}\left( s \right) = a\sigma {\left[ {\lambda + {\theta _w} + s\sigma - \left( {Mr\left( s \right) + H{\lambda ^{ - 1}}h\left( s \right)L\left( s \right)} \right)} \right]^{ - 1}},$
$L\left( s \right) = \left( {b\varphi \left( s \right) + {\theta _w}} \right)r\left( s \right) + \frac{{\left( {H{\eta _1}\left( s \right) + {\theta _v}} \right){m_1}\left( s \right){\theta _w}}}{{\left( {\lambda + {\theta _v} + s\sigma } \right)}} + \frac{{\left( {H{\eta _2}\left( s \right) + \alpha } \right){\theta _v}{\theta _w}{m_2}\left( s \right)}}{{\left( {\lambda + s\sigma } \right)\left( {\lambda + {\theta _v} + s\sigma } \right)}}.$

证 引入矩阵函数

${\boldsymbol{A}_{00}}\left( s \right) = \left( {\begin{array}{*{20}{c}} { - \left( {\lambda + {\theta _w} + s{\sigma _0}} \right)}&{{\theta _w}}&0\\ 0&{ - \left( {\lambda + {\theta _v} + s{\sigma _1}} \right)}&{{\theta _v}}\\ 0&0&{ - \left( {\lambda + s{\sigma _2}} \right)} \end{array}} \right)$.

展开 (3.2) 式可写成如下形式

$\left\{ \begin{array}{lll} \left( {{{\hat F}_{00}}\left( s \right),{{\hat F}_{01}}\left( s \right),{{\hat F}_{02}}\left( s \right)} \right){\boldsymbol{A}_{00}}\left( s \right) + {{\hat {\boldsymbol F}}_1}\left( s \right){\boldsymbol{B}_{10}} = \left( { - a\sigma,0,0} \right),\\ \left( {{{\hat F}_{00}}\left( s \right),{{\hat F}_{01}}\left( s \right),{{\hat F}_{02}}\left( s \right)} \right){\boldsymbol{A}_{10}} + {{\hat {\boldsymbol F}}_1}\left( s \right)\boldsymbol{B}\left( s \right) + {{\hat {\boldsymbol F}}_2}\left( s \right)\boldsymbol{A} = \boldsymbol{0},\\ {{\hat {\boldsymbol F}}_k}\left( s \right)\boldsymbol{C} + {{\hat {\boldsymbol F}}_{k + 1}}\left( s \right)\boldsymbol{B}\left( s \right) + {{\hat {\boldsymbol F}}_{k + 2}}\left( s \right)\boldsymbol{A} = \boldsymbol{0},\ 1 \le k \le N - 2,\\ \lambda {{\hat F}_{N - 1,0}}\left( s \right) - \left( {{\theta _w} + M + s{\sigma _0}} \right){{\hat F}_{N0}}\left( s \right) = 0,\\ \lambda {{\hat F}_{N - 1,1}}\left( s \right) - \left( {{\theta _v} + s{\sigma _1}} \right){{\hat F}_{N1}}\left( s \right) = 0,\\ \lambda {{\hat F}_{N - 1,2}}\left( s \right) - \left( {\alpha + s{\sigma _2}} \right){{\hat F}_{N2}}\left( s \right) = 0,\\ \lambda {{\hat F}_{N - 1,3}}\left( s \right) + {\theta _w}{{\hat F}_{N0}}\left( s \right) + {\theta _v}{{\hat F}_{N1}}\left( s \right) + \alpha {{\hat F}_{N2}}\left( s \right) - \left( {H + s{\sigma _3}} \right){{\hat F}_{N3}}\left( s \right) = 0. \end{array} \right.$

由于矩阵 $\boldsymbol{Q} - \boldsymbol{sG}$ 为分块三对角矩阵, 参考矩阵几何解方法整理可得

$\left( {{{\hat F}_{00}}\left( s \right),{{\hat F}_{01}}\left( s \right),{{\hat F}_{02}}\left( s \right), {{\hat {\boldsymbol F}}_1}\left( s \right)} \right)\boldsymbol{B}\left[ {R\left( s \right)} \right] = \left( { - a\sigma,0,0,0,0,0,0} \right),$
${{\hat{\boldsymbol F}}_k}\left( s \right) = {{\hat{\boldsymbol F}}_1}\left( s \right){\left[ {\boldsymbol{R}\left( s \right)} \right]^{k - 1}},\ 1 \le k \le N - 1,{{\hat{\boldsymbol F}}_{N - 1}}\left( s \right)\boldsymbol{C} + {{\hat{\boldsymbol F}}_N}\left( s \right){\boldsymbol{B}_N}\left( s \right) = \boldsymbol{0},$

其中

$\begin{array}{lll} \boldsymbol{B}\left[ {R\left( s \right)} \right] = \left( {\begin{array}{*{20}{c}} { - \left( {\lambda + {\theta _w} + s\sigma } \right)}&{{\theta _w}}&0\\ 0&{ - \left( {\lambda + {\theta _v} + s\sigma } \right)}&{{\theta _v}}\\ 0&0&{ - \left( {\lambda + s\sigma } \right)}\\ M&0&0\\ 0&0&0\\ 0&0&0\\ H&0&0 \end{array}} \right.\\ \begin{array}{*{20}{c}} {}&{}&{}&{} \end{array}\left. {\begin{array}{*{20}{c}} \lambda &0&0&0\\ 0&\lambda &0&0\\ 0&0&\lambda &0\\ { - \frac{\lambda }{{r\left( s \right)}}}&0&0&{H\varphi \left( s \right) + {\theta _w}}\\ 0&{ - \left( {\lambda + {\theta _v} + s{\sigma _1}} \right)}&0&{H{\eta _1}\left( s \right) + {\theta _v}}\\ 0&0&{ - \left( {\lambda + \alpha + s{\sigma _2}} \right)}&{H{\eta _2}\left( s \right) + \alpha }\\ 0&0&0&{ - \frac{\lambda }{{h\left( s \right)}}} \end{array}} \right). \end{array}$

对 (3.5) 式求解得到

$\left\{ \begin{array}{lll} {{\hat F}_{00}}\left( s \right) = \frac{{a\sigma }}{{K\left( s \right)}},{{\hat F}_{01}}\left( s \right) = \frac{{{\theta _w}}}{{\lambda + {\theta _v} + s\sigma }}{{\hat F}_{00}}\left( s \right),{{\hat F}_{02}}\left( s \right) = \frac{{{\theta _v}{\theta _w}}}{{\left( {\lambda + s\sigma } \right)\left( {\lambda + {\theta _v} + s\sigma } \right)}}{{\hat F}_{00}}\left( s \right),\\ {\hat F_{10}}\left( s \right) = r\left( s \right){\hat F_{00}}\left( s \right), {{\hat F}_{11}}\left( s \right) = \frac{{{\theta _w}{m_1}\left( s \right)}}{{\lambda + {\theta _v} + s\sigma }}{{\hat F}_{00}}\left( s \right),\\ {{\hat F}_{12}}\left( s \right) = \frac{{{\theta _v}{\theta _w}{m_2}\left( s \right)}}{{\left( {\lambda + s\sigma } \right)\left( {\lambda + {\theta _v} + s\sigma } \right)}}{{\hat F}_{00}}\left( s \right),{{\hat F}_{13}}\left( s \right) = \frac{{h\left( s \right)}}{\lambda }L\left( s \right){{\hat F}_{00}}\left( s \right), \end{array} \right.$

联立 (3.4) 和 (3.6) 式, 整理得到 (3.3) 式. 定理 3.1 得证.

结合定理 3.1 整理得到

$\hat F\left( s \right) = {{\hat{\boldsymbol F}}_0}\left( s \right){e} + {{\hat{\boldsymbol F}}_1}\left( s \right)\left[ {\boldsymbol{I} - {{\left( {\boldsymbol{R}\left( s \right)} \right)}^{N - 1}}} \right]{\left( {\boldsymbol{I} - \boldsymbol{R}\left( s \right)} \right)^{ - 1}}\boldsymbol{e} + {{\hat{\boldsymbol F}}_N}\left( s \right)\boldsymbol{e},$

其中

${{\hat{\boldsymbol F}}_0}\left( s \right) = \left( {{{\hat F}_{00}}\left( s \right),{{\hat F}_{01}}\left( s \right),{{\hat F}_{02}}\left( s \right)} \right),$
${{\hat{\boldsymbol F}}_k}\left( s \right) = \left( {{{\hat F}_{k0}}\left( s \right),{{\hat F}_{k1}}\left( s \right),{{\hat F}_{k2}}\left( s \right),{{\hat F}_{k3}}\left( s \right)} \right),\quad 1 \le k \le N,$

这里 $\boldsymbol{I}$ 是相应阶数的单位矩阵, $\boldsymbol{e}$ 是相应维数的全1列向量.

计算矩阵 $\boldsymbol{I} - \boldsymbol{R}\left( s \right)$ 的谱半径, 可得

$SP\left( {\boldsymbol{R}\left( s \right)} \right) = \max \left( {\left| {1 - r\left( s \right)} \right|,\left| {1 - {m_1}\left( s \right)} \right|,\left| {1 - {m_2}\left( s \right)} \right|,\left| {1 - h\left( s \right)} \right|} \right) < 1.$

由 (3.8) 式可知矩阵 $\boldsymbol{I} - \boldsymbol{R}\left( s \right)$ 是非奇异的, 进而得到

${\left( {{I} - {R}\left( s \right)} \right)^{ - 1}} = \left( {\begin{array}{*{20}{c}} {\frac{1}{{1 - r\left( s \right)}}}&0&0& {\frac{{\varphi \left( s \right)}}{{\left( {1 - h\left( s \right)} \right)\left( {1 - r\left( s \right)} \right)}}}\\ 0& {\frac{1}{{1 - {m_1}\left( s \right)}}}&0& {\frac{{{\eta _1}\left( s \right)}}{{\left( {1 - h\left( s \right)} \right)\left( {1 - {m_1}\left( s \right)} \right)}}}\\ 0&0& {\frac{1}{{1 - {m_2}\left( s \right)}}}& {\frac{{{\eta _2}\left( s \right)}}{{\left( {1 - h\left( s \right)} \right)\left( {1 - {m_2}\left( s \right)} \right)}}}\\ 0&0&0& {\frac{1}{{1 - h\left( s \right)}}} \end{array}} \right).$

根据 (3.6) 和 (3.7) 式, 得到

$\hat F\left( s \right) = \ {\hat F}_{00} \left( s \right)\left\{ \frac{1 - \left(r\left( s \right) \right)^N} {1 - r\left( s \right)} + \frac{\lambda \left( r\left( s \right) \right)^{N - 1}} {\theta _w + M + s\sigma _0} \right. \\ + \frac{\theta _w}{\lambda + \theta _v + s\sigma } \left[ \frac{1 - \left( m_1\left( s \right) \right)^N} {1 - m_1\left( s \right)} + \frac{\lambda \left( m_1\left( s \right) \right)^{N - 1}} {\theta _v + s\sigma _1} \right] \\ + \frac{\theta _v\theta _w} {\left( \lambda + s\sigma \right)\left( \lambda +\theta _v+ s\sigma \right)} \left[ \frac{1 - \left( m_2\left( s \right) \right)^N} {1 - m_2\left( s \right)} \right. + \left. \frac{\lambda \left( m_2\left( s \right) \right)^{N - 1}} {\alpha + s\sigma _2} \right] \\ + \frac{\left[\sum\limits_{k = 1}^{N - 2} \left( 1 - \left( r\left( s \right) \right)^k \right)\left( h\left( s \right) \right)^{N - 2 - k } \right]\varphi \left( s \right)r\left( s \right)}{1 - r\left( s \right)}\\ + \frac{{{\theta _w}{\eta _1}\left( s \right)}}{{\lambda + {\theta _v} + s\sigma }}\sum\limits_{k = 1}^{N - 2} {\left( {1 - {{\left( {{m_1}\left( s \right)} \right)}^k}} \right){{\left( {h\left( s \right)} \right)}^{N - 2 - k}}} \!+\! \frac{{h\left( s \right)L\left( s \right)}}{{\lambda \left( {1 - h\left( s \right)} \right)}}\left( {1 - {{\left( {h\left( s \right)} \right)}^{N - 1}}} \right)\\ + \frac{\theta _v\theta _w\eta _2\left( s \right)} {\left( \lambda + s\sigma \right)\left(\lambda + \theta _v+ s\sigma \right)} \sum\limits_{k = 1}^{N - 2} \left( 1 - \left( m_2\left( s \right) \right)^k \right) \left( h\left( s \right) \right)^{N - 2 - k}\\ + \frac{\lambda }{H + s\sigma _3} \left[ \frac{\theta _v\theta _w\left( m_1\left( s \right) \right)^{N - 1}} {\left( \theta _v + s\sigma _1 \right)\left( \lambda + \theta _v + s\sigma \right)} \right.\\ + \frac{{{\eta _1}\left( s \right){\theta _w}}}{{\left( {\lambda + {\theta _v} + s\sigma } \right)}}\sum\limits_{i = 1}^{N - 2} {{{\left( {{m_1}\left( s \right)} \right)}^{N - i - 1}}{{\left( {h\left( s \right)} \right)}^{i - 1}}} + \varphi \left( s \right)\sum\limits_{i = 1}^{N - 2} {{{\left( {r\left( s \right)} \right)}^{N - i - 1}}{{\left( {h\left( s \right)} \right)}^{i - 1}}} \\ + \frac{{{\theta _w}{{\left( {r\left( s \right)} \right)}^{N - 1}}}}{{{\theta _w} + M + s{\sigma _0}}} + \frac{{{\eta _2}\left( s \right){\theta _v}{\theta _w}}}{{\left( {\lambda + s\sigma } \right)\left( {\lambda + {\theta _v} + s\sigma } \right)}}\sum\limits_{i = 1}^{N - 2} {{{\left( {{m_2}\left( s \right)} \right)}^{N - i - 1}}{{\left( {h\left( s \right)} \right)}^{i - 1}}} \\ + \frac{{{{\left( {h\left( s \right)} \right)}^{N - 1}}L\left( s \right)}}{\lambda }\left. {\left. { + \frac{{\alpha {\theta _v}{\theta _w}{{\left( {{m_2}\left( s \right)} \right)}^{N - 1}}}}{{\left( {\alpha + s{\sigma _2}} \right)\left( {\lambda + s\sigma } \right)\left( {\lambda + {\theta _v} + s\sigma } \right)}}} \right]} \right\}.$

为方便计算稳态条件下库存量的空库概率及均值, 定义库存量的 Laplace-Stieltjes 变换 ${f^*}\left( s \right)$ 为

${f^*}\left( s \right) = \int_0^\infty {{{\rm e}^{ - su}}} {\rm d}F\left( u \right) = s\hat F\left( s \right).$

由正规化条件 $\mathop {\lim }\limits_{s \to 0} {f^*}\left( s \right) = 1$, 进而得到空库概率的表达式为

$a = \ \left[ {1 - \frac{1}{\sigma }\left( {Mr'\left( 0 \right) + \frac{{F{\theta _w}}}{{\lambda \left( {1 - r} \right)}}h'\left( 0 \right) + L'\left( 0 \right)} \right)} \right]\left\{ {\frac{{1 - {r^N}}}{{1 - r}} + \frac{{\lambda {r^{N - 1}}}}{{{\theta _w} + M}} + \frac{{{\theta _w}}}{{{\theta _v}}}} \right.\\ + \frac{\theta _v\theta _w\left( \lambda + \alpha \right)} {\lambda \alpha \left( \lambda + \theta _v \right)} + \frac{\theta _w}{H} \left( \frac{r}{1 - r} \right)^2 \sum\limits_{k = 1}^{N - 2} \left[ \left( 1 -r^k \right) \rho ^{N - 2 - k} \right] \\ + \frac{\theta _w}{\lambda + \theta _v} \sum\limits_{k = 1}^{N - 2} \left( 1 - \left( \frac{\lambda }{\lambda +\theta _v} \right)^k \right)\rho ^{N - 1 - k} + \frac{\theta _v\theta _w} {\lambda \left( \lambda + \theta _v \right)} \sum\limits_{k = 1}^{N - 2} \left( 1 - \left( \frac{\lambda }{\lambda + \alpha } \right)^k \right) \rho ^{N - 1 - k}\\ + \frac{\theta _w\left( 1 - \rho ^{N - 1} \right)} {\left( 1 - r \right)\left( H - \lambda \right)} + \rho \left[ \frac{r\theta _w}{H\left( 1 - r \right)} \sum\limits_{i = 1}^{N - 2} r^{N - i - 1}\rho ^{i - 1} \right. + \frac{\theta _w}{\left( \lambda + \theta _v \right)} \sum\limits_{i = 1}^{N - 2} \left( \frac{\lambda }{\lambda + \theta _v} \right)^{N - i - 1}\rho ^i \\ + \frac{\rho ^{N - 1}\theta _w} {\lambda \left( 1 - r \right)} + \frac{\theta _v\theta _w} {\left( \lambda + s\sigma \right)\left( \lambda + \theta _v+ s\sigma \right)} \left. \sum\limits_{i = 1}^{N - 2} \ \left( \frac{\lambda }{\lambda + \alpha } \right)^{N - i - 1}\rho ^i \right]\\ + \frac{1}{H}\left[ {\frac{{\lambda {\theta _w}{r^{N - 1}}}}{{{\theta _w} + M}}} \right. + {\theta _w}{\left( {\frac{\lambda }{{\lambda + {\theta _v}}}} \right)^N}{\left. {\left. { + \frac{{\alpha {\theta _v}{\theta _w}{\lambda ^{N - 1}}}}{{\left( {\lambda + {\theta _v}} \right){{\left( {\lambda + \alpha } \right)}^{N - 1}}}}} \right]} \right\}^{ - 1}},$

其中

$r'\left( 0 \right) = \frac{{{\sigma _0}\left( {1 - \left( {\lambda + {\theta _w} + M} \right){{\left[ {{{\left( {\lambda + {\theta _w} + M} \right)}^2} - 4\lambda M} \right]}^{ - \frac{1}{2}}}} \right)}}{{2M}},\ h'\left( 0 \right) = \frac{{\rho {\sigma _3}}}{{\lambda - H}},\\ m_1^\prime\left( 0 \right) = \frac{{ - \lambda {\sigma _1}}}{{{{\left( {\lambda + {\theta _v}} \right)}^2}}},\ m_2^\prime\left( 0 \right) = \frac{{ - \lambda {\sigma _2}}}{{{{\left( {\lambda + \alpha } \right)}^2}}},\ \varphi '\left( 0 \right) = \frac{{{\theta _w}\left( {br'\left( 0 \right) - r{\sigma _3} + rbh'\left( 0 \right)} \right)}}{{{H^2}{{\left( {1 - r} \right)}^2}}},\\ \eta_1^\prime\left( 0 \right) = \frac{{\left( {\lambda + {\theta _v}} \right)}}{{{\theta _v}{b^2}}}\left[ {\left( {\lambda + {\theta _v}} \right)m_1^\prime\left( 0 \right)b - \lambda {\sigma _3} + \lambda Hh'\left( 0 \right)} \right],\\ \eta_2^\prime\left( 0 \right) = \frac{{\lambda + \alpha }}{{\alpha {H^2}}}\left[ {\left( {\lambda + \alpha } \right)m_2^\prime\left( 0 \right)H - \lambda {\sigma _3} + \lambda Hh'\left( 0 \right)} \right],\\ L'\left( 0 \right) = rH\varphi '\left( 0 \right) + \frac{{{\theta _w}r'\left( 0 \right)}}{{1 - r}} + \frac{{{\theta _w}}}{{\lambda + {\theta _v}}}\left[ {\frac{{H\lambda \eta_1^\prime\left( 0 \right)}}{{\lambda + {\theta _v}}} + \left( {\lambda + {\theta _v}} \right)m_1^\prime\left( 0 \right) - \frac{{\lambda \sigma }}{{\lambda + {\theta _v}}}} \right]\\ \qquad\qquad + \frac{{{\theta _v}{\theta _w}}}{{\lambda \left( {\lambda + {\theta _v}} \right)}}\left[ {\frac{{H\lambda \eta_2^\prime\left( 0 \right)}}{{\lambda + \alpha }} + \left( {\lambda + \alpha } \right)m_2^\prime\left( 0 \right) - \frac{{\sigma \left( {2\lambda + {\theta _v}} \right)}}{{\lambda + {\theta _v}}}} \right].$

进一步得到平均库存量的表达式

$E\left( C \right) = - \mathop {\lim }\limits_{s \to 0} \frac{\rm d}{{{\rm d}s}}{f^*}\left( s \right) = - \mathop {\lim }\limits_{s \to 0} \hat F'\left( s \right)s{{\hat F}_{00}}\left( s \right) - \mathop {\lim }\limits_{s \to 0} \hat F\left( s \right){\left( {s{{\hat F}_{00}}\left( s \right)} \right)^\prime },$

运用洛必达法则对 (3.9) 式进行计算, 整理得到

$E\left( C \right) =\ \frac{{a\sigma {K_2}}}{{2{{\left( {K_1} \right)}^2}}}\left\{ {\frac{{1 - {r^N}}}{{1 - r}} + \frac{{\lambda {r^{N - 1}}}}{{{\theta _w} + M}} + \frac{{{\theta _w}}}{{{\theta _v}}} + \frac{{{\theta _v}{\theta _w}\left( {\lambda + \alpha } \right)}}{{\lambda \alpha \left( {\lambda + {\theta _v}} \right)}} } \right.\\ + \frac{{{\theta _w}}}{H}{{\left( {\frac{r}{{1 - r}}} \right)}^2}\sum\limits_{k = 1}^{N - 2} {\left( {1 - {r^k}} \right){\rho ^{N - 2 - k}}} + \frac{{{\theta _w}}}{{\lambda + {\theta _v}}}\sum\limits_{k = 1}^{N - 2} {\left( {1 - {{\left( {\frac{\lambda }{{\lambda + {\theta _v}}}} \right)}^k}} \right){\rho ^{N - 1 - k}}}\\ + \frac{{{\theta _v}{\theta _w}}}{{\lambda \left( {\lambda + {\theta _v}} \right)}}\sum\limits_{k = 1}^{N - 2} {\left[ {1 - {{\left( {\frac{\lambda }{{\lambda + \alpha }}} \right)}^k}} \right]{\rho ^{N - 1 - k}}} + \frac{{{\theta _w}\left( {1 - {\rho ^{N - 1}}} \right)}}{{\left( {1 - r} \right)\left( {H - \lambda } \right)}} \\ + \rho \left[ {\frac{{r{\theta _w}}}{{H\left( {1 - r} \right)}}\sum\limits_{i = 1}^{N - 2} {{r^{N - i - 1}}{\rho ^{i - 1}}} } \right. + \frac{{{\theta _w}}}{{\left( {\lambda + {\theta _v}} \right)}}\sum\limits_{i = 1}^{N - 2} {{\rho ^i}{{\left( {\frac{\lambda }{{\lambda + {\theta _v}}}} \right)}^{N - i - 1}}} \\ + \frac{{{\rho ^{N - 1}}{\theta _w}}}{{\lambda \left( {1 - r} \right)}} + \frac{{{\theta _v}{\theta _w}}}{{\left( {\lambda + s\sigma } \right)\left( {\lambda + {\theta _v} + s\sigma } \right)}}\left. {\sum\limits_{i = 1}^{N - 2} {{{\left( {\frac{\lambda }{{\lambda + \alpha }}} \right)}^{N - i - 1}}{\rho ^i}} } \right]\\ + \frac{1}{H}\left[ {\frac{{\lambda {\theta _w}{r^{N - 1}}}}{{{\theta _w} + M}}} \right. + \left. { {\theta _w}{{\left( {\frac{\lambda }{{\lambda + {\theta _v}}}} \right)}^N} + \left. {\frac{{\alpha {\theta _v}{\theta _w}{\lambda ^{N - 1}}}}{{\left( {\lambda + {\theta _v}} \right){{\left( {\lambda + \alpha } \right)}^{N - 1}}}}} \right]} \right\}\\ + \frac{{a\sigma \sum\limits_{k = 0}^8 {{H_k}} }}{{\sigma - \left( {Mr'\left( 0 \right) + \frac{{H{\theta _w}}}{{\lambda \left( {1 - r} \right)}}h'\left( 0 \right) + L'\left( 0 \right)} \right)}},$

其中

${K_1} =\ \sigma - \left[ {Mr'\left( 0 \right) + \frac{H}{\lambda }\left( {\frac{{{\theta _w}h'\left( 0 \right)}}{{1 - r}} + \rho L'\left( 0 \right)} \right)} \right],$
${K_2} =\ - \left[ {Mr'\left( 0 \right) + \frac{H}{\lambda }\left( {\frac{{{\theta _w}h''\left( 0 \right)}}{{1 - r}} + 2h'\left( 0 \right)L'\left( 0 \right) + \rho L''\left( 0 \right)} \right)} \right],$
${H_0} =\ \frac{{r'\left( 0 \right)}}{{{{\left( {1 - r} \right)}^2}}}\left( {1 - {r^N} - N{r^{N - 1}} - N{r^N}} \right) + \frac{{\lambda {r^{N - 2}}}}{{{{\left( {M + {\theta _w}} \right)}^2}}}\left[ {\left( {N - 1} \right)\left( {M + {\theta _w}} \right)r'\left( 0 \right) - r{\sigma _0}} \right],$
${H_1} =\ \frac{{ - {\theta _w}\sigma }}{{{{\left( {\lambda + {\theta _v}} \right)}^2}}}\left[ {\frac{{1 - {{\left( {{m_1}\left( 0 \right)} \right)}^N}}}{{1 - {m_1}\left( 0 \right)}} + \frac{\lambda }{{{\theta _v}}}{{\left( {{m_1}\left( 0 \right)} \right)}^{N - 1}}} \right] \\ + \frac{{{\theta _w}}}{{\lambda + {\theta _v}}}\left[ {\frac{{m_1^\prime\left( 0 \right)}}{{{{\left( {1 - {m_1}\left( 0 \right)} \right)}^2}}}} \right.\left( {1 - {{\left( {{m_1}\left( 0 \right)} \right)}^N}} \right. - N{\left( {{m_1}\left( 0 \right)} \right)^{N - 1}} + \left. {N{{\left( {{m_1}\left( 0 \right)} \right)}^N}} \right) \\ + \left. {\frac{{\lambda {{\left( {{m_1}\left( 0 \right)} \right)}^{N - 2}}}}{{{{\left( {{\theta _v}} \right)}^2}}}\left( {\left( {N - 1} \right)m_1^\prime\left( 0 \right){\theta _v} - {\sigma _1}{m_1}\left( 0 \right)} \right)} \right],$
${H_2} =\ \frac{{ - {\theta _v}{\theta _w}\sigma \left( {2\lambda + {\theta _v}} \right)}}{{{\lambda ^2}{{\left( {\lambda + {\theta _v}} \right)}^2}}}\left[ {\frac{{1 - {{\left( {{m_2}\left( 0 \right)} \right)}^N}}}{{1 - {m_2}\left( 0 \right)}} + \frac{\lambda }{\alpha }{{\left( {{m_2}\left( 0 \right)} \right)}^{N - 1}}} \right]\\ + \frac{{{\theta _v}{\theta _w}}}{{\lambda \left( {\lambda + {\theta _v}} \right)}}\left[ {\frac{{m_2^\prime\left( 0 \right)}}{{{{\left( {1 - {m_1}\left( 0 \right)} \right)}^2}}}} \right.\left( {1 - {{\left( {{m_2}\left( 0 \right)} \right)}^N}} \right. - N{\left( {{m_2}\left( 0 \right)} \right)^{N - 1}} + \left. {N{{\left( {{m_2}\left( 0 \right)} \right)}^N}} \right) \\+ \left. {\frac{{\lambda {{\left( {{m_2}\left( 0 \right)} \right)}^{N - 2}}}}{{{\alpha ^2}}}\left( {\left( {N - 1} \right)m_2^\prime\left( 0 \right)\alpha - {\sigma _2}{m_2}\left( 0 \right)} \right)} \right],$
${H_3} =\ \frac{{\left( {1 - r} \right)\left( {\varphi '\left( 0 \right)r + \varphi \left( 0 \right)r'\left( 0 \right)} \right) + r\varphi \left( 0 \right)r'\left( 0 \right)}}{{{{\left( {1 - r} \right)}^2}}}\sum\limits_{k = 1}^{N - 2} {\left( {1 - {r^k}} \right){\rho ^{N - 2 - k}}} \\ + \frac{{r\varphi \left( 0 \right)}}{{1 - r}}\sum\limits_{k = 1}^{N - 2} {\left[ { - k{r^{k - 1}}r'\left( 0 \right){\rho ^{N - 2 - k}} + \left( {1 - {r^k}} \right)\left( {N - 2 - k} \right){\rho ^{N - 3 - k}}h'\left( 0 \right)} \right]},$
${H_4} =\ \frac{{{\theta _w}}}{{{{\left( {\lambda + {\theta _v}} \right)}^2}}}\left( {\eta_1^\prime\left( 0 \right)\left( {\lambda + {\theta _v}} \right) - {\eta _1}\left( 0 \right)\sigma } \right)\sum\limits_{k = 1}^{N - 2} {\left( {1 - {{\left( {{m_1}\left( 0 \right)} \right)}^k}} \right){\rho ^{N - 2 - k}}} \\ + \frac{{{\theta _w}{\eta _1}\left( 0 \right)}}{{\lambda + {\theta _v}}}\sum\limits_{k = 1}^{N - 2} {\left[ { - k{{\left( {{m_1}\left( 0 \right)} \right)}^{k - 1}}} \right.} m_1^\prime\left( 0 \right){\rho ^{N - 2 - k}}\\ + \left. {\left( {1 - {{\left( {{m_1}\left( 0 \right)} \right)}^k}} \right)\left( {N - 2 - k} \right){\rho ^{N - 3 - k}}h'\left( 0 \right)} \right],$
${H_5} =\ \frac{{ - \lambda {\sigma _3}}}{{{H^2}}}\left[ {\frac{{{\theta _w}{r^{N - 1}}}}{{{\theta _w} + M}} + \frac{{{\theta _w}{{\left( {{m_1}\left( 0 \right)} \right)}^{N - 1}}}}{{\lambda + {\theta _v}}} + \frac{{{\theta _v}{\theta _w}{{\left( {{m_2}\left( 0 \right)} \right)}^{N - 1}}}}{{\lambda \left( {\lambda + {\theta _v}} \right)}}} \right]\\ + \frac{\lambda }{H}\left\{ {\frac{{{\theta _w}}}{{{{\left( {{\theta _w} + M} \right)}^2}}}\left[ {\left( {N - 1} \right){r^{N - 2}}r'\left( 0 \right)\left( {{\theta _w} + M} \right) - {r^{N - 1}}{\sigma _0}} \right]} \right.\\ + \frac{{{\theta _w}}}{{{\theta _v}{{\left( {\lambda + {\theta _v}} \right)}^2}}}\left[ { - {\theta _w}{\sigma _1}{{\left( {{m_1}\left( 0 \right)} \right)}^{N - 1}}\left( {\left( {\lambda + {\theta _v}} \right){\sigma _1} + {\theta _v}\sigma } \right)} \right.\\ + \left. {\left( {N - 1} \right){{\left( {{m_1}\left( 0 \right)} \right)}^{N - 2}}m_1^\prime\left( 0 \right){\theta _v}\left( {\lambda + {\theta _v}} \right)} \right]\\ + \left[ -{\left( {N - 1} \right){{\left( {{m_2}\left( 0 \right)} \right)}^{N - 2}}m_2^\prime\left( 0 \right)\lambda \alpha \left( {\lambda + {\theta _v}} \right)} \right.\\ + \left. {{{\left( {{m_2}\left( 0 \right)} \right)}^{N - 1}}\left( {\left( {\lambda + {\theta _v}} \right)\lambda {\sigma _2} + \alpha \sigma \left( {\lambda + 2{\theta _v}} \right)} \right)} \right]\left. {\frac{{ - {\theta _v}{\theta _w}}}{{{\lambda ^2}{{\left( {\lambda + {\theta _v}} \right)}^2}}}} \right\},$
${H_6} =\ \frac{{{\theta _v}{\theta _w}}}{{{\lambda ^2}{{\left( {\lambda + {\theta _v}} \right)}^2}}}\left( {\eta_2^\prime\left( 0 \right)\lambda \left( {\lambda + {\theta _v}} \right) - {\eta _2}\left( 0 \right)\sigma \left( {2\lambda + {\theta _v}} \right)} \right)\sum\limits_{k = 1}^{N - 2} {\left( {1 - {{\left( {{m_1}\left( 0 \right)} \right)}^k}} \right){\rho ^{N - 2 - k}}} \\ + \frac{{{\theta _w}{\eta _1}\left( 0 \right)}}{{\lambda + {\theta _v}}}\sum\limits_{k = 1}^{N - 2} {\left[ { - k{{\left( {{m_2}\left( 0 \right)} \right)}^{k - 1}}m_2^\prime\left( 0 \right){\rho ^{N - 2 - k}}} \right.} \\ + \left. {\left( {1 - {{\left( {{m_2}\left( 0 \right)} \right)}^k}} \right)\left( {N - 2 - k} \right){\rho ^{N - 3 - k}}h'\left( 0 \right)} \right],$
${H_7} =\ \frac{1}{{\lambda {{\left( {1 - \rho } \right)}^2}}}\left[ {\left( {h'\left( 0 \right)L\left( 0 \right) + \rho L'\left( 0 \right)} \right)\left( {1 - \rho } \right) + \rho L\left( 0 \right)h'\left( 0 \right)} \right] \\- \frac{{\rho L\left( 0 \right)}}{{\lambda \left( {1 - \rho } \right)}}\left( {N - 1} \right){\rho ^{N - 2}}h'\left( 0 \right),$
${H_8} =\ \frac{{ - \lambda {\sigma _3}}}{{{H^2}}}\left\{ {\varphi \left( 0 \right)\sum\limits_{k = 1}^{N - 2} {{r^{N - 1 - k}}{\rho ^{k - 1}}} + \frac{{{\eta _1}\left( 0 \right){\theta _w}}}{{\lambda + {\theta _v}}}\left[ {\sum\limits_{k = 1}^{N - 2} {{{\left( {{m_1}\left( 0 \right)} \right)}^{N - 1 - k}}{\rho ^{k - 1}}} } \right.} \right.\\+ \left. {\left. { \frac{{{\eta _2}\left( 0 \right){\theta _v}{\theta _w}}}{{\lambda \left( {\lambda + {\theta _v}} \right)}}\sum\limits_{k = 1}^{N - 2} {{{\left( {{m_2}\left( 0 \right)} \right)}^{N - 1 - k}}{\rho ^{k - 1}}} \frac{{{\rho ^{N - 1}}}}{\lambda }L\left( 0 \right)} \right]} \right\} + \frac{\lambda }{H}\bigg\{ {\varphi '\left( 0 \right)}\sum\limits_{k = 1}^{N - 2} {{r^{N - 1 - k}}{\rho ^{k - 1}}} \\ + \varphi \left( 0 \right)\sum\limits_{k = 1}^{N - 2} {\left[ {\left( {N - 1 - k} \right){r^{N - 2 - k}}r'\left( 0 \right){\rho ^{k - 1}}\left( {k - 1} \right){r^{N - 1 - k}}{\rho ^{k - 2}}h'\left( 0 \right)} \right]} \\ + \frac{{{\theta _w}}}{{{{\left( {\lambda + {\theta _v}} \right)}^2}}}\left( {\eta_1^\prime\left( 0 \right)\left( {\lambda + {\theta _v}} \right) - {\eta _1}\left( 0 \right)\sigma } \right)\sum\limits_{k = 1}^{N - 2} {{{\left( {{m_1}\left( 0 \right)} \right)}^{N - 1 - k}}{\rho ^{k - 1}}} \\ + \frac{{{\theta _w}{\eta _1}\left( 0 \right){{\left( {{m_1}\left( 0 \right)} \right)}^{N - 2 - k}}}}{{\lambda + {\theta _v}}}\sum\limits_{k = 1}^{N - 2} {\left[ {\left( {N - 1 - k} \right)m_1^\prime\left( 0 \right){\rho ^{k - 1}} + \left( {k - 1} \right){m_1}\left( 0 \right){\rho ^{k - 2}}h'\left( 0 \right)} \right]} \\ + \frac{{{\theta _v}{\theta _w}}}{{{\lambda ^2}{{\left( {\lambda + {\theta _v}} \right)}^2}}}\left( {\eta_2^\prime\left( 0 \right)\lambda \left( {\lambda + {\theta _v}} \right) - {\eta _2}\left( 0 \right)\sigma \left( {2\lambda + {\theta _v}} \right)} \right)\sum\limits_{k = 1}^{N - 2} {{{\left( {{m_2}\left( 0 \right)} \right)}^{N - 1 - k}}{\rho ^{k - 1}}} \\ + \frac{{{\eta _2}\left( 0 \right){\theta _v}{\theta _w}}}{{\lambda \left( {\lambda + {\theta _v}} \right)}}\sum\limits_{k = 1}^{N - 2} {\left[ {\left( {N - 1 - k} \right){{\left( {{m_2}\left( 0 \right)} \right)}^{N - 2 - k}}m_2^\prime\left( 0 \right){\rho ^{k - 1}}} \right.} \\+ \left. {h'\left( 0 \right){{\left( {{m_2}\left( 0 \right)} \right)}^{N - 1 - k}}\left( {k - 1} \right){\rho ^{k - 2}}} \right] + \frac{{{\rho ^{N - 2}}}}{\lambda } {\left[ {\left( {N - 1} \right)h'\left( 0 \right)L\left( 0 \right) + \rho L'\left( 0 \right)} \right]} \bigg\}.$

4 数值分析

在店铺的外卖运营过程中, 用户通过线上平台在一个店铺下单的过程可当作一个服务台的排队系统, 店铺的营业额可看作流体, 线上平台可看作缓冲器. 下面给出系统参数变化对性能指标和费用函数的影响.

4.1 参数敏感性分析

本节考虑接受第二次服务的概率 $p$, 服务台的启动率, 净流入率 $\sigma$ 对系统性能指标的影响. 结合店铺线上外卖的运营过程, 空库概率 $a$ 可看作店铺未能接收到下单金额, 即店铺无营业额的概率, 平均库存量 $E\left( C \right)$ 可看作店铺的平均营业额. 假设缓冲区容量 $N=7$, 系统参数 $\lambda = 4$, ${\mu _b} = 5$, ${\mu _{b1}} =3$, ${\mu _w} = 4$, ${\mu _{w1}} = 2$, ${\theta _w} = 4$, ${\theta _v} = 5$, ${\alpha} = 4$, $\sigma = -5$, ${\sigma _0} = 1$, ${\sigma _1} =2$, ${\sigma _2} = 3$, ${\sigma _3} = 4$, $p=0.4$.

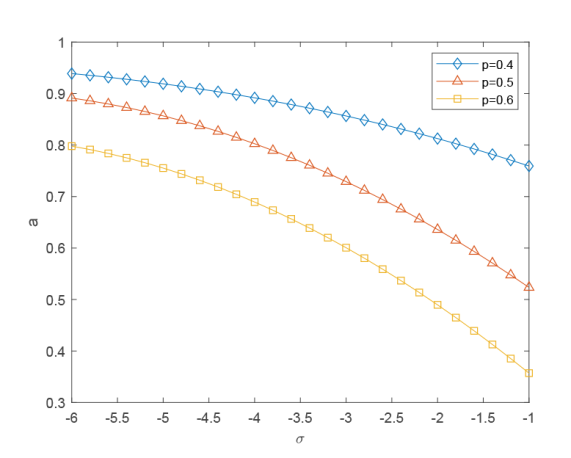
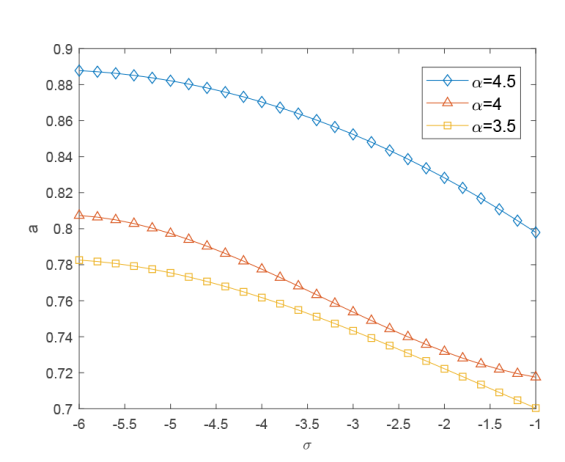
通过图1 可以看出, 当 $\sigma$ 一定时, 随着 $p$ 变大, $a$ 随之变小; 当 $p$ 一定时, 随着 $\sigma$ 变大, $a$ 随之变小. 这是因为当 $\sigma$ 一定时, $p$ 增大代表顾客选择继续下单的概率变大, 店铺收到营业额的概率也会变大, 即 $a$ 会随之变小. 通过图2 可以看出, 当$\alpha$ 一定时, 随着 $\sigma$ 变大, $a$ 随之变小; 当$\sigma$ 一定时, 随着 $\alpha$ 变大, $a$ 随之变大. 这是因为当$\sigma$ 一定时, $\alpha$ 增大代表服务台启动时间的增加, 即店铺完成订单的时间变长, 导致顾客下单量的流失, 即 $a$ 会随之变大. 而当 $p$ 和 $\alpha$ 一定时, 净流入率的增大代表会有更多的顾客进入该店铺并有概率选择在该店铺下单, 导致店铺收到更多的营业额, 即 $a$ 会随之变小.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   $a$ 随 $p$ 和 $\sigma$ 的变化曲线


图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   $a$ 随 $\sigma$ 和 $\alpha$ 的变化曲线


通过图3 可以看出, 当 $\alpha$ 一定时, 随着净流入率 $\sigma$ 变大, $E\left(C\right)$ 随之变大; 当净流入率 $\sigma$ 一定时, 随着$\alpha$ 变大, $E\left(C\right)$ 随之变小. 这是因为当 $\sigma$ 一定时, $\alpha$ 变大代表服务台启动时间变长, 店铺完成订单的效率变低, 进而导致店铺完成订单的数量减少, 最终影响到平均营业额的增加, 即 $E\left(C\right)$ 会随之变小. 通过图4 可以看出, 当 $p$ 一定时, 随着净流入率 $\sigma$ 变大, $E\left(C\right)$ 随之变大; 当净流入率 $\sigma$ 一定时, 随着 $p$ 变大, $E\left(C\right)$ 随之变大. 这是因为当 $\sigma$ 一定时, $p$ 变大代表顾客在该店铺选择继续下单的概率变大, 使店铺能够收到更多的营业额, 导致平均营业额的增加, 即 $E\left( C \right)$ 随之变大. 而当 $p$ 和 $\alpha$ 一定时, 净流入率的增大代表线上平台里的用户进入该店铺的数量增加, 使用户选择下单的概率变大, 导致店铺能够获得更多的订单数量和营业额, 即 $E\left(C\right)$ 随之变大.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   $E\left( C \right)$ 随 $\sigma$ 和 $\alpha$ 的变化曲线


图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   $E\left( C \right)$ 随 $\sigma$ 和 $p$ 的变化曲线


4.2 费用分析

根据给出的性能指标, 记 $C_1$ 表示单位顾客单位时间内的等待费用, $C_2$ 表示休假时服务台单位时间内造成的成本费用, $C_3$ 表示空库时单位时间的损失费用, $C_4$ 表示单位时间内由于库存积压造成的损失费用, 则构造系统的费用函数为

$F = {C_1}{L_q} + {C_2}{\pi _{00}} + {C_3}a + {C_4}E\left( C \right),$

其中驱动系统平均等待队长 ${L_q} = \sum\limits_{i = 1}^N {\sum\limits_{j = 0}^3 {i{\pi _{ij}}} }$.

为直观地给出不同的系统参数对费用函数的影响, 下面假设 $C_1=1.5$, $C_2=2$, $C_3=4$, $C_4=7$, $N=7$, $\lambda = 4$, ${\mu _b} = 5$, ${\mu _{b1}} =3$, ${\mu _w} = 4$, ${\mu _{w1}} = 2$, ${\theta _w} = 4$, ${\theta _v} = 5$, ${\alpha} = 0.5$, $\sigma = -5$, ${\sigma _0} = 1$, ${\sigma _1} =2$, ${\sigma _2} = 3$, ${\sigma _3} = 4$, $p=0.4$.

通过图5 可以看出, 当 $\alpha$ 一定时, 随着 $p$ 的增大, 所需费用随之增加, 并慢慢趋于平稳. 这是因为 $p$ 的增大导致顾客下单的数量增多, 使店铺需要准备更多的商品, 导致店铺的成本费用会越来越大. 但是当 $p$ 增长到一定数值时, 店铺的承载量也会达到极限, 这就导致所需费用会趋于平缓. 当 $p$ 一定时, 随着 $\alpha$ 的增大, 所需费用也随之增加. 这是因为 $\alpha$ 的增大, 代表着服务台启动时间的增加, 会使等待时间加长, 进而导致等待费用的增加.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   $F$ 随 $p$ 和 $\alpha$ 的变化曲线


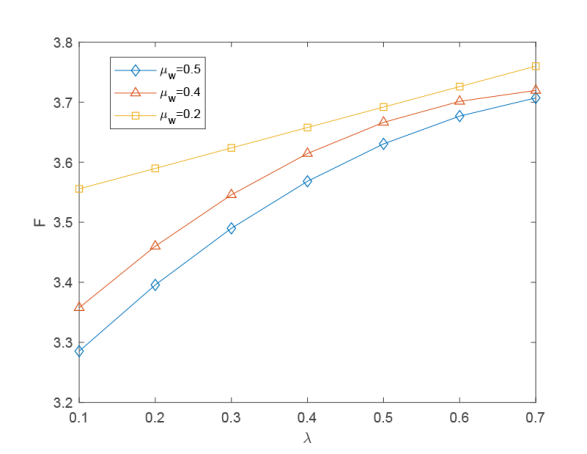
通过图6 可以看出, 当 $\lambda$ 一定时, 随着 $\mu_w$ 的增大, 所需费用随之减小. 这是因为 $\mu_w$ 的增大使店铺完成订单的速率变大, 进而导致等待费用的减少. 当 $\mu_w$ 一定时, 随着 $\lambda$ 的增大, 所需费用也随之增加. 这是因为 $\lambda$ 的增大, 代表着会有更多的顾客在店铺下单, 店铺则需要准备大量的商品, 同时 $\lambda$ 的增大会使顾客的等待时间变长, 最终导致等待费用和库存费用的增加.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   $F$ 随 $\lambda$ 和 $\mu_w$ 的变化曲线


从图5-6 可看到随着系统参数达到一定数值后, 费用函数的上升趋势均慢慢趋于平缓. 因此, 店铺可通过限流, 升级最新设备用来减少启动时间并提升服务效率或提高商品优惠促使用户继续下单, 使得费用最小.

5 总结

本文研究了具有启动时间、可选服务和双阶段休假 M/M/1/N 排队系统驱动的流体模型, 运用矩阵几何解方法、LT 和 LST 变换方法给出流体模型在稳态条件下的空库概率及均值等性能指标的表达式. 并结合店铺的外卖经营模式, 通过数值分析得到了系统参数变化对性能指标和费用函数的影响, 以帮助店铺合理控制所需费用, 提升用户黏性, 提高市场占有率, 进而获得更多的利润.

参考文献

Virtamo J, Norros I.

Fluid queue driven by an M/M/1 queue

Queueing Systems, 1994, 16(3/4): 373-386

DOI:10.1007/BF01158963      URL     [本文引用: 2]

Adan I, Resing J.

Simple analysis of a fluid queue driven by an M/M/1 queue

Queueing Systems, 1996, 22(1/2): 171-174

DOI:10.1007/BF01159399      URL     [本文引用: 1]

Sericola B, Tuffin B.

A fluid queue driven by a Markovian queue

Queueing Systems Theory and Applications, 1999, 31(3/4): 253-264

DOI:10.1023/A:1019114415595      URL     [本文引用: 1]

Parthasarathy P, Vijayashree K, Lenin R.

An M/M/1 driven fluid queue-continued fraction approach

Queueing Systems, 2002, 42(2): 189-199

DOI:10.1023/A:1020157021703      URL     [本文引用: 1]

Lenin R, Parthasarathy P.

Fluid queues driven by an M/M/1/N queue

Mathematical Problems in Engineering, 2015, 6(5): 439-460

DOI:10.1155/S1024123X00001423      URL     [本文引用: 1]

In this paper, we consider fluid queue models with infinite buffer capacity which receives and releases fluid at variable rates in such a way that the net input rate of fluid into the buffer (which is negative when fluid is flowing out of the buffer) is uniquely determined by the number of customers in anM/M/1/Nqueue model (that is, the fluid queue is driven by this Markovian queue) with constant arrival and service rates. We use some interesting identities of tridiagonal determinants to find analytically the eigenvalues of the underlying tridiagonal matrix and hence the distribution function of the buffer occupancy. For specific cases, we verify the results available in the literature.

毛炳蔚. M/M/1 休假排队系统驱动的流排队模型. 秦皇岛: 燕山大学, 2011

[本文引用: 1]

Mao B W. Fluid Models Driven by an M/M/1 Vacation Queue[D]. Qinhuangdao: Yanshan University, 2011

[本文引用: 1]

Ammar S.

Fluid queue driven by an M/M/1 disasters queue

International Journal of Computer Mathematics, 2014, 91(7): 1497-1506

DOI:10.1080/00207160.2013.844799      URL     [本文引用: 1]

Wang F W, Mao B W.

Fluid model driven by an M/M/1 queue with set-up and close-down period

Applied Mechanics and Materials, 2014, 513-517: 3377-3380

[本文引用: 1]

Ammar S.

Analysis of an M/M/1 driven fluid queue with multiple exponential vacations

Applied Mathematics and Computation, 2014, 227: 329-334

DOI:10.1016/j.amc.2013.10.084      URL     [本文引用: 1]

Mao B W, Wang F W, Tian N S.

Fluid model driven by an M/M/1/N queue with exponential vacations

Journal of Computational Information Systems, 2010, 6(6): 1809-1816

[本文引用: 1]

徐秀丽, 王现英, 徐彪.

可选服务的M/M/1多重休假排队系统驱动的流模型

数学的实践与认识, 2018, 48(6): 155-161

[本文引用: 1]

Xu X, Wang X, Xu B.

A fluid model driven by an M/M/1 vacations queue with optional service

Mathematics in Practice and Theory, 2018, 48(6): 155-161 (in Chinese)

[本文引用: 1]

Vijayashree K, Anjuka A.

Stationary analysis of a fluid queue driven by an M/M/1 queue with working vacation

Quality Technology and Quantitative Management, 2016, 15(2): 1-22

DOI:10.1080/16843703.2017.1304044      URL     [本文引用: 1]

Vijayashree K, Anjuka A.

Fluid queue modulated by an M/M/1/N queue subject to multiple exponential working vacation

International Journal of Pure and Applied Mathematics, 2017, 113(13): 153-162

[本文引用: 1]

李子坤, 徐秀丽, 岳德权.

单重工作休假 M/M/c 排队驱动的流体模型分析

数学物理学报, 2021, 41A(1): 254-268

[本文引用: 1]

Li Z, Xu X, Yue D.

Analysis of the fluid model driven by M/M/c queue with single working vacation

Acta Mathematica Scientia, 2021, 41A(1): 254-268

[本文引用: 1]

Xu X, Wang X, Song X, et al.

Fluid model modulated by an M/M/ 1 working vacation queue with negative customer

Acta Mathematicae Applicatae Sinica, 2018, 34(2): 404-415

DOI:10.1007/s10255-018-0751-0      [本文引用: 2]

刘煜飞, 叶晴晴.

基于矩阵分析方法的具有双阶段休假的排队系统驱动的流模型性能分析

数学的实践与认识, 2021, 51(4): 189-199

[本文引用: 2]

Liu Y F, Ye Q Q.

Performance analysis of the fluid model driven by M/M/1 queuing system with two-stage vacation based on matrix analysis method

Mathematics in Practice and Theory, 2021, 51(4): 189-199 (in Chinese)

[本文引用: 2]

/

〈 〉

版权所有 © 《数学物理学报》杂志社
地址： 武汉市71010号信箱(430071)　电话: 027-87199206(中文版)　027-87199087(英文版)
E-mail: actams@apm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发