1 引言
传统的节点重要性评估方法如度中心性[8]、介数中心性[9]、特征向量中心性[8]、 半局部中心性[2]、H-指数中心性[11]等, 其基本思想都是挖掘节点的邻居、最短路径等信息, 并对这些信息进行统计, 以此定量刻画节点的重要性. 这些方法对某一类信息进行挖掘, 简单直观, 但是信息类型过于单一, 只在特定场景中应用效果明显, 不具备普适性. K-shell 分解法[1]认为节点的重要性由节点在网络中所处的位置决定, 节点越接近网络的核心位置其重要程度就越高. 然而 K-shell 分解法对节点重要性的区分过于粗粒化, 许多基于 K-shell 分解法的改进方法如混合度分解法[12]、K 核迭代因子法[13]等, 考虑了节点更加详细的位置信息, 相较于 K-shell 分解法, 评估效果显著提高. 由于应用场景不同, 上述方法在评估节点重要性时的角度各有侧重, 但本质上都是基于图论的数据挖掘, 并且数据的信息类型较为单一. 研究表明, 将从不同角度对节点重要性进行评估的指标融合能得到更好的评估结果[14,15].
引力模型揭示了两个物体之间相互作用的规律, 即两个物体之间的相互作用即引力的大小与它的质量成正比, 与它们之间的距离平方成反比, 复杂网络节点之间的相互影响同样符合这一规律. 此外, 引力模型在预测物体间相互作用力时, 需要定义物体质量、物体间的距离以及引力系数三种影响相互作用力的变量. 因此, 应用引力模型进行节点重要性评估时, 根据节点的多种属性信息定义引力模型中的三种变量, 可以有效融合不同角度的评估指标, 使评估结果更为合理. Ma 等[16]提出一种引力模型方法 Gravity 来评估节点的重要程度, 该方法将节点的 K-shell 值视为节点质量, 节点间的最短距离视为节点间距离, 模拟万有引力公式计算节点与邻域节点的相互作用力之和作为节点的重要性值. Li 等[17]则认为度大的节点往往更重要, 并且更容易影响其近邻节点, 因此将节点的度作为物体的质量, 提出了局部引力模型 LGM. Gravity 和 LGM 将所有节点之间的引力系数视为相同的, 引力系数值均为 1. 实际上, 不同的节点拓扑结构存在差异, 节点与其邻域节点之间的引力系数也不尽相同, 因此可以根据节点拓扑结构分析节点与其邻域节点之间的引力系数, 用以调整节点间相互作用力. Liu 等[18]在 LGM 的基础上提出一种广义的引力模型 GMM, 将节点的特征向量中心性作为节点与其邻域节点间的引力系数. Yang 等[19]指出在网络中心位置的节点比在边缘位置的节点更具吸引力, 而 K-shell 指标[1]反映了节点位置的核心程度, 因此提出了一种基于 K-shell 的引力模型方法 KSGC, 根据节点与邻域节点的相对位置确定节点与其邻域节点间的引力系数. 总之, 合理定义引力模型中的节点质量、节点间距离和引力系数这三个变量是引力模型方法是能有效评估节点重要性的关键.
现有的大多数基于引力模型的节点重要性评估方法仅将节点的度或节点的 K-shell 值作为物体的质量, 考虑的节点信息不够全面, 并且缺乏对节点拓扑结构的深度挖掘. 本文提出一种基于邻居层级分布的引力模型 (Hierarchical distribution based gravity model, 简称 HDGM) 来评估节点的重要性, 首先, 将节点的邻居信息和位置信息融合作为节点的质量; 然后分析节点的邻居数量、邻居所处的网络位置等节点的拓扑结构信息, 利用邻间拓扑结构的相似度来确定节点与邻域节点间的引力系数; 并将节点与邻域节点的距离设置为小于等于网络半径, 使得距离范围随实际网络大小动态变化; 最后, 模拟万有引力公式, 利用节点与邻域节点之间的相互作用力之和来定义节点的重要性.
2 理论基础
2.1 K-shell分解迭代次数
K-shell 分解法[1]就是由边缘到核心逐渐划分网络的过程, 其核心思想是递归地删除度小于等于 K 的节点, 并将被删除的节点标记 为 K-shell. K-shell 值反映了节点网络位置的核心程度, K-shell 值越大说明节点在网络中所处的位置越核心. K-shell 分解法递归删除的方式使得网络快速消解, 算法因此具有较低的时间复杂度, 但是大量结构与功能存在明显差异的节点被赋予相同的 K-shell 值, 导致算法对节点重要性的区分粗粒度. Wang 等[13]指出可以根据 K-shell 分解过程中节点删除的顺序定义新的反映节点网络位置核心程度的指标, 该指标能有效区分具有相同 K-shell 值的节点, 并且反映的节点位置信息也更加精确.
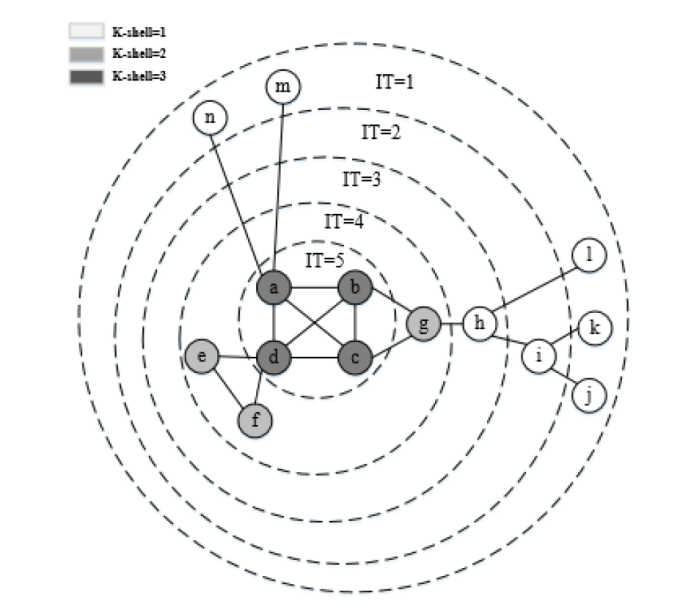
定义 2.1 给定无权无向网络 G=(V,E), 在 K-shell 分解过程中, 节点 vi 在第 IT 次被删除, 则称 IT 为节点 vi 的 K-shell 迭代次数.
图1
2.2 引力模型
引力模型 (Gravity Model) 由牛顿万有引力定律发展而来, 万有引力定律指出: 任何两个物体之间的相互作用即引力的大小与它的质量成正比, 与它们之间的距离平方成反比. 万有引力公式表示为
其中, G 为引力系数, M 和 m 分别表示两物体的质量, r 为两物体的距离. 引力模型是一种分析和预测的空间相互作用模型, 应用十分广泛, 保持万有引力公式的基本形式不变, 只要适当改变参数和分量的定义, 就可将引力模型应用于不同的问题.
Ma 等[16]首次将引力模型应用于节点重要性评估, 他认为节点的近邻节点的 K-shell 值越大, 节点的影响力越大, 而两个节点之间的相互作用会随着距离的增加而减小, 这说明节点间相互作用符合物体间相互作用的规律, 即万有引力定律. 受万有引力公式的启发, 将节点的 K-shell 值视为其质量, 将两个节点之间的最短路径距离作为节点间的距离, 提出一种基于引力模型的节点重要性评估方法 Gravity, 表示为
其中, φ(i) 表示与节点 vi 的距离小于等于给定值 r 的近邻节点集, 为了减小算法的复杂度, r 设为 3, ksi 和 ksi 分别表示节点 vi和节点 vj 的 K-shell 值, dij 表示节点 vi 到节点 vj 的距离.
3 基于邻居层级分布的引力模型方法
由于节点的度和IT值是两个不同的量纲, 不能直接相加, 为了综合节点局部邻居和全局位置这两方面的特征, 引入一个均衡因子 γ, γ 为网络平均度与网络平均 IT 值之比, 表示为
其中, ⟨k⟩ 表示网络平均度, 表示网络平均 ⟨IT⟩ 值. 因此, 将节点的局部邻居信息和全局位置信息进行融合, 节点 vi 的质量 m(i) 可以表示为
利用引力模型计算节点间相互作用力时, 不仅需要合理定义节点的质量, 节点间的引力系数对节点间相互作用力的影响也不容忽视. 引力公式将节点与邻域节点的相互作用力之和作为节点的重要性值, 高聚类系数的节点与其邻域节点连接紧密、相关性强, 重要性值高. 实际上, 聚类系数高反而不利于节点影响力的传播, 如果传播从高聚类系数节点发起, 容易局限于节点邻域的小范围内, 很难延伸至更广泛的网络范围, 所以引力公式度量节点重要性容易出现高聚类系数的节点的重要性虚高的现象[20]. 因此需要根据邻间拓扑结构设置引力系数, 矫正引力公式计算的节点重要性值与节点实际影响力之间的偏差.
定义 3.1 层级分布向量 (Hierarchy Distribution Vector)
其中, Nki 表示节点在第 k 层级的邻居数目, SNIi=∑j∈Γ(i)ITj 为节点的所有邻居的 IT 值总和, h=ITmax 为图中最大的层级.
如图2 所示, 图中节点的 IT 值最大为 5, 所以 h=5. 节点 g 有 e, f, p, m 4 个邻居, 其中节点 e 和节点 f 的层级为 4, 节点 h 的层级为 2, 节点 m 的层级为 1, 邻居 IT 值总和为 11. 因此, 节点 g 的邻居层级分布向量可以表示为: HDV_{\rm g} = \left\{ {\frac{1}{{11}},\frac{2}{{11}},0,\frac{8}{{11}},0} \right\}. 同理, 节点d和节点f的邻居层级分布向量分别表示为: HDV_{\rm d} = \left\{ {0,0,0,\frac{8}{{23}},\frac{{15}}{{23}}} \right\}, HDV_{\rm f} = \left\{ {0,0,\frac{3}{{12}},\frac{4}{{12}},\frac{{5}}{{12}}} \right\}.
图2
定义 3.2 层级分布相似性 (Hierarchy Distribution Similarity), 表示节点与邻居拓扑结构的相似程度, 以此来量化邻间相关程度. 用海林格距离 (Hellinger Distance) 计算节点 v_i 与邻居节点 v_j 的相似性可以表示为
邻居层级分布相似性越大, 表示节点与邻居的拓扑结构相似度越高, 邻间的相关性越强, 对节点影响力的负面作用越强, 因此引入引力系数来校正节点的重要性值, 避免出现高聚类程度的节点根据邻间相互作用力得出的重要性高于实际值的情况, 引力系数定义为
经典的引力模型方法 Gravity 将节点间距离设置为小于等于 3, 即计算节点与 3 步长内的邻居之间的相互作用力. 在小型数据集中, 很多节点 3 步长内的邻居几乎涵盖了网络中大部分节点, 从而无法区分这些节点的重要性. 在大型数据集中, 节点影响力辐射的范围超过了 3 阶, 节点与 3 步长内的邻居的相互作用力不能全面地反映节点的影响力. 因此, 将节点与邻居的距离设置为小于等于网络半径, 使得距离范围根据方法所评估的网络大小动态变化.
最后, 模拟万有引力公式计算节点间的相互作用力, 基于邻居层级分布和引力模型的方法 HDGM 表示为
其中, R 表示网络半径, 是网络最短路径平均值的一半.
4 实验结果及分析
4.1 实验数据集与对比方法
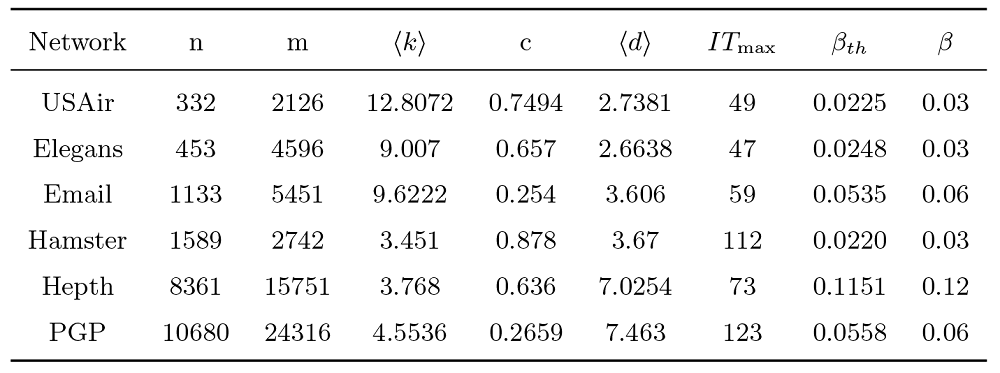
实验选取了 6 个不同领域的真实数据集, 分别是: 美国航空网络 USAir, 线虫网络 Elegans, 电子邮件网络 Email, 社交关系网络 Hamster, 科学家合作网络 Hepth, 隐私保护算法的用户网络 PGP. 网络的统计特征如表1 所示, 其中 n 为节点数, m 为边数, \langle k\rangle 为网络平均度, c 为聚类系数, \langle d\rangle 平均最短路径, \beta_{th}=\langle k\rangle /\langle k^{2}\rangle 为 SIR 模型传播阈值, \beta 为实际传播率取值.
4.2 单调性分析
为了对比各节点重要性排序方法的单调性, 引入单调函数 M(R)[25] 来评价节点重要性排序结果的单调程度, 单调函数值越大, 代表方法对节点重要性的区分能力越强. 单调函数表达式如下
其中, R 为节点重要性值排序序列, N 为网络的节点数, {N_r} 为重要性值相同的节点数. M\left( R \right) \in \left[ {0,1} \right], 当 M\left( R \right) = 1 时, 排序向量 R 完全单调, 表示网络中所有节点的重要性都不同. 当 M\left( R \right) = 0 时, 则表示网络中所有节点的重要性都相同.
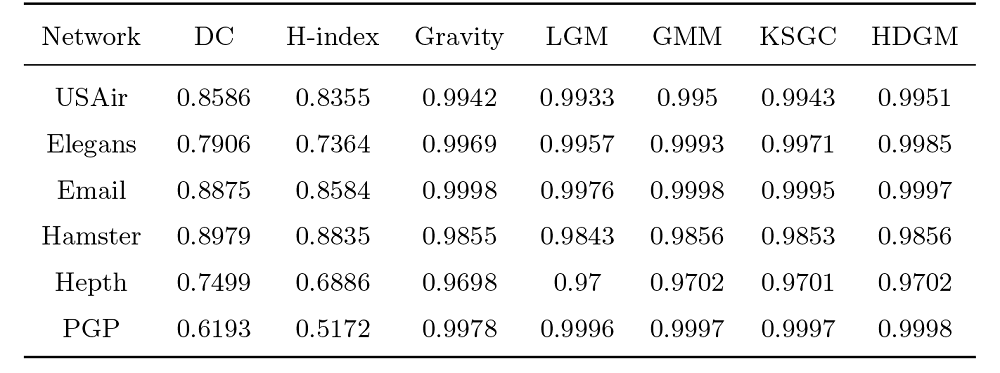
不同评估方法在 6 个真实网络数据集中得出的节点重要性排序的单调性指标如表2 所示. HDGM 算法在 6 个数据集中均有优异的表现, 在 USAir、Hamster、Hepth 和 PGP 数据集中的排序结果的单调性指标均为最高值, 并且数值接近为 1, 在 Elegans、Email 数据集中的排序结果的单调性指标仅次于最高值. 因此, 综合来看 HDGM 算法相较于其他6种方法能够更好地区分节点的重要性.
4.3 基于传播动力学模型的有效性分析
其中, {n_c} 是相关观察组的数量, {n_c} 是不相关观察组的数量, {n} 为观察组的总数.
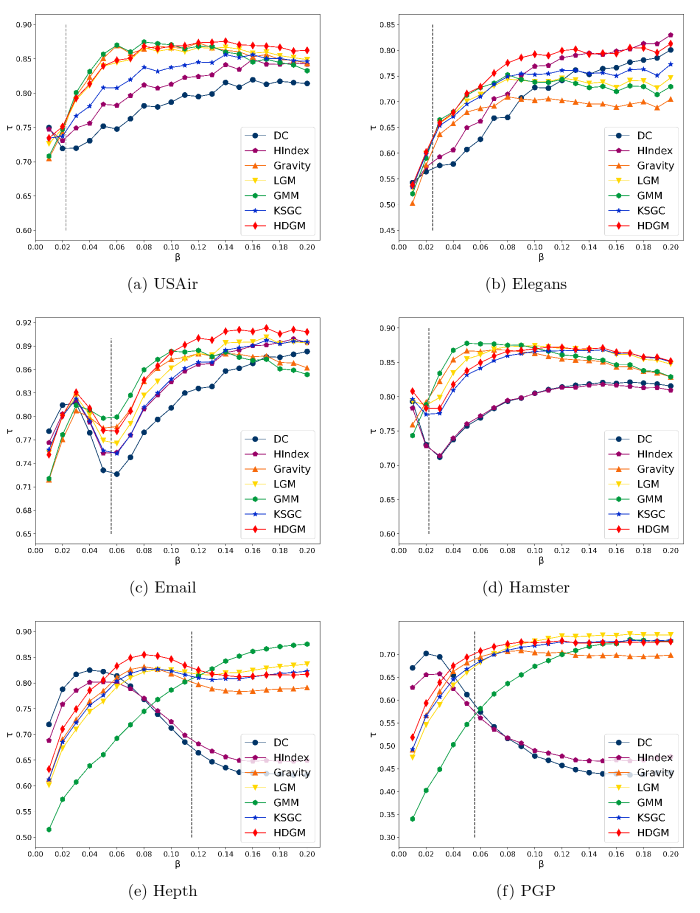
为了验证本文所提方法相较于其他评估方法对于重要性排序结果的准确性, 对比各评估方法的排序结果与不同传播概率下 SIR 模型得到节点影响力排序结果之间的肯德尔相关系数, 实验结果如图3 所示, 图中垂直虚线的横坐标取值为传播阈值 {\beta _{th}}. 当传播率较大时, HDGM 方法的肯德尔系数明显高于其他方法, 而当传播率较小时, DC、H-index、Gravity 和 LGM 方法的表现要优于 HDGM 方法, 这是因为传播率偏小时, 信息的传播容易局限在局部, 此时节点的影响力主要由度值决定, 而当传播率提高后, HDGM 方法的肯德尔系数值高于其他方法.
图3
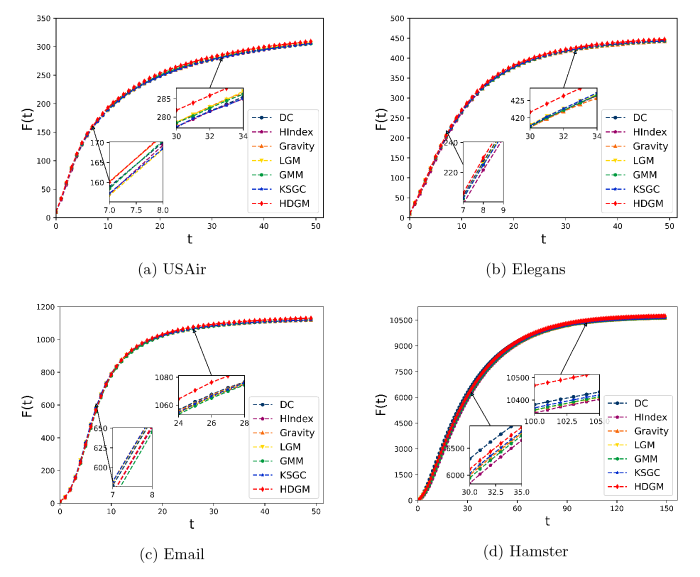
为了进一步验证节点重要性评估方法的准确性, 判断方法能否准确识别出复杂网络中的关键节点. 采用 SI 模型[10]模拟节点影响力扩散的过程, 根据网络中受影响的节点数目变化的快慢评价各节点重要性评估方法的优劣. 实验选取各评估方法得分 Top-10 的节点作为初始感染节点, 在 USAir、Elegans、Email 和 PGP 四个全连通数据集网络上运行 SI 模型, 记录网络中感染态节点数目 F(t) 随时间步长 t 的变化情况. 如图4 所示, 在 USAir 和 Elegans 网络中, 以 HDGM 算法评估的重要性排名前十的节点作为初始感染节点时, 网络中感染节点数目上升的速度是最快的, 说明 HDGM 算法识别出的重要节点能在网络中更快速地传播信息, 影响力最大. 而在 Email 和 PGP 网络中, 传播初期, HDGM 算法的效果略差于 KSGC 算法, 是因为网络较为稀疏, 传播不容易扩散; 但在当传播进行一段时间后, 感染节点数目加速上升, HDGM 算法得分前十的初始感染节点率先感染了网络中的所有节点. 整体来看, HDGM 算法更能准确的识别网络中最具影响力的节点.
图4
4.4 基于网络鲁棒性的有效性分析
基于传播动力学模型的评价方法考察的是节点对其他节点的影响程度, 而基于网络鲁棒性的评价方法着重考察移除节点后网络结构和功能的变化幅度, 变化幅度越大, 说明移除的节点越重要. 为了从网络鲁棒性角度评价各节点重要性评估方法的有效性, 实验选用最大连通子图的相对规模作为鲁棒性指标. 最大连通子图的相对规模定义为
其中, \sigma(i/n) 表示移除比例 i/n 的节点后, 网络中最大连通子图的节点数占网络节点总数的比例. i/n 表示当前最大连通子图的节点数, N 表示初始网络的节点数.
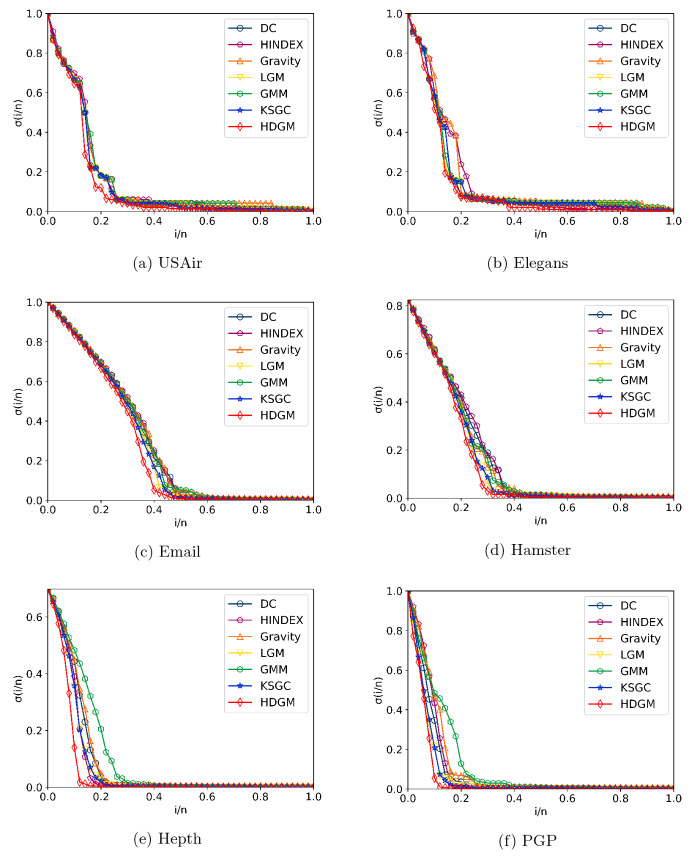
首先, 根据各评估方法计算网络中节点的重要性, 然后按照重要性从高到低的顺序依次移除节点, 并且记录每次移除节点后的鲁棒性指标, 直到网络中的所有节点都被移除. 如图5 所示, 6 个真实网络的最大连通子图的相对规模随着移除节点比例 i/n 的变化情况. 不难看出, 在 Email、Hamster、Hepth 和 PGP 数据集中, 移除 HDGM 算法选出的关键节点网络的最大连通子图相对规模下降明显快于其他方法. 而在 USAir 和 Elegans 数据集中, 图像中 7 种方法的变化曲线出现重合的情况, 这是因为 USAir 和 Elegans 网络的连边数远大于节点数, 网络过于稠密, 移除不同的节点对网络的连通性影响较小, 所以各评估方法的效果差异不明显. 综合来看, HDGM 方法识别出的重要节点对网络结构和功能的影响要大于其他方法.
图5
5 结论
准确评估复杂网络中节点的重要程度是网络科学研究的热点问题, 并且具有广泛的应用价值. 本文提出了基于邻居层级分布引力模型的节点重要性评估算法, 能有效评估复杂网络中节点的重要性. 所提方法综合了节点的局部邻居信息和全局位置信息, 弥补了现存方法考虑因素单一的不足, 并且根据节点邻间拓扑结构相似性构建了引力模型中的引力系数, 依此来调整节点与邻居的相互作用力, 避免出现高聚类系数节点的重要性虚高的现象, 因此, 对节点重要程度的评估更加准确. 在 6 个真实数据集上进行仿真实验的结果表明, 与其他引力模型相关方法相比, 所提方法能更有效地区分节点重要性的差异, 对节点重要性的评估也更加准确.
本文所提方法参照经典的引力模型, 将节点间的最短路径作为物体间距离, 实际上, 节点间的真实距离还与除最短路径以外的其他可达路径相关, 接下来的研究工作将从这一角度出发, 探究更加有效的复杂网络节点重要性评估方法.
参考文献
Identification of influential spreaders in complex networks
DOI:10.1038/nphys1746 [本文引用: 4]
融合多元信息的多关系社交网络节点重要性研究
Research on node importance fused multi-information for multi-relational social networks
基于复杂网络模型的地铁系统脆弱性分析
Vulnerability analysis of metro system based on complex network model
复杂网络上疫情与舆情的传播及其基于免疫的控制策略
Controlling epidemic outbreaks and publics sentiment spreading by vaccination in complex network
基于多属性决策的电力网络关键节点识别
Critical node identification of a power grid based on multi-attribute decision
基于功能贡献度的网络化防空节点重要性评价方法
DOI:10.11896/j.issn.1002-137X.2018.02.031
[本文引用: 1]

In order to evaluate the importance of node in air defense networks which is a kind of functional social network,on the basis of analyzing the shortcomings of current evaluation method for network node importance,a evaluation method for node importance based on functional contribution was put forward.The method comprehensively considers the functional properties and structural properties of the node.In order to verify the validity and superiority of the method,two types of efficiency index for networked systems,such as network connectivity efficiency and combat loop,were built,and the evaluation method was used to evaluate the node importance in ARPA and air defense networks.Experimental results show that the evaluation method has some advantages in accuracy and applicability of the network node importance evaluation.
Evaluation method for node importance in air defense networks based on functional contribution degree
DOI:10.11896/j.issn.1002-137X.2018.02.031
[本文引用: 1]

In order to evaluate the importance of node in air defense networks which is a kind of functional social network,on the basis of analyzing the shortcomings of current evaluation method for network node importance,a evaluation method for node importance based on functional contribution was put forward.The method comprehensively considers the functional properties and structural properties of the node.In order to verify the validity and superiority of the method,two types of efficiency index for networked systems,such as network connectivity efficiency and combat loop,were built,and the evaluation method was used to evaluate the node importance in ARPA and air defense networks.Experimental results show that the evaluation method has some advantages in accuracy and applicability of the network node importance evaluation.
Factoring and weighting approaches to status scores and clique identification
DOI:10.1080/0022250X.1972.9989806 URL [本文引用: 3]
A set of measures of centrality based on betweenness
DOI:10.2307/3033543 URL [本文引用: 1]
The H-index of a network node and its relation to degree and coreness
DOI:10.1038/ncomms10168
PMID:26754161
[本文引用: 2]

Identifying influential nodes in dynamical processes is crucial in understanding network structure and function. Degree, H-index and coreness are widely used metrics, but previously treated as unrelated. Here we show their relation by constructing an operator H, in terms of which degree, H-index and coreness are the initial, intermediate and steady states of the sequences, respectively. We obtain a family of H-indices that can be used to measure a node's importance. We also prove that the convergence to coreness can be guaranteed even under an asynchronous updating process, allowing a decentralized local method of calculating a node's coreness in large-scale evolving networks. Numerical analyses of the susceptible-infected-removed spreading dynamics on disparate real networks suggest that the H-index is a good tradeoff that in many cases can better quantify node influence than either degree or coreness.
Ranking spreaders by decomposing complex networks
DOI:10.1016/j.physleta.2013.02.039 URL [本文引用: 1]
Influence maximization in social networks based on TOPSIS
DOI:10.1016/j.eswa.2018.05.001 URL [本文引用: 1]
An extended best-worst multi-criteria decision-making method by belief functions and its application in hospital service evaluation
DOI:10.1016/j.cie.2020.106355 URL [本文引用: 1]
Identifying influential spreaders by gravity model
DOI:10.1038/s41598-019-44930-9
PMID:31182773
[本文引用: 3]

Identifying influential spreaders in complex networks is crucial in understanding, controlling and accelerating spreading processes for diseases, information, innovations, behaviors, and so on. Inspired by the gravity law, we propose a gravity model that utilizes both neighborhood information and path information to measure a node's importance in spreading dynamics. In order to reduce the accumulated errors caused by interactions at distance and to lower the computational complexity, a local version of the gravity model is further proposed by introducing a truncation radius. Empirical analyses of the Susceptible-Infected-Recovered (SIR) spreading dynamics on fourteen real networks show that the gravity model and the local gravity model perform very competitively in comparison with well-known state-of-the-art methods. For the local gravity model, the empirical results suggest an approximately linear relation between the optimal truncation radius and the average distance of the network.
GMM: A generalized mechanics model for identifying the important of nodes in complex networks
DOI:10.1016/j.knosys.2019.105464 URL [本文引用: 3]
An improved gravity model to identify influential nodes in complex networks based on k-shell method
DOI:10.1016/j.knosys.2021.107198 URL [本文引用: 3]
基于引力方法的复杂网络节点重要度评估方法
Node importance ranking method in complex network based on gravity model
Identifying influential nodes in large-scale directed networks: The role of clustering
DOI:10.1371/journal.pone.0077455 URL [本文引用: 2]
Role of clustering and gridlike ordering in epidemic spreading
DOI:10.1103/PhysRevE.69.066116 URL [本文引用: 1]
Maximal planar networks with large clustering coefficient and power-law degree distribution
DOI:10.1103/PhysRevE.71.046141 URL [本文引用: 1]
Collective dynamics of `small-world' networks
Locating multiple sources of contagion in complex networks under the SIR model
DOI:10.3390/app9204472
URL
[本文引用: 1]

Simultaneous outbreaks of contagion are a great threat against human life, resulting in great panic in society. It is urgent for us to find an efficient multiple sources localization method with the aim of studying its pathogenic mechanism and minimizing its harm. However, our ability to locate multiple sources is strictly limited by incomplete information about nodes and the inescapable randomness of the propagation process. In this paper, we present a valid approach, namely the Potential Concentration Label method, which helps locate multiple sources of contagion faster and more accurately in complex networks under the SIR(Susceptible-Infected-Recovered) model. Through label assignment in each node, our aim is to find the nodes with maximal value after several iterations. The experiments demonstrate that the accuracy of our multiple sources localization method is high enough. With the number of sources increasing, the accuracy of our method declines gradually. However, the accuracy remains at a slight fluctuation when average degree and network scale make a change. Moreover, our method still keeps a high multiple sources localization accuracy with noise of various intensities, which shows its strong anti-noise ability. I believe that our method provides a new perspective for accurate and fast multi-sources localization in complex networks.
On the size of the class of bivariate extreme-value copulas with a fixed value of Spearman's rho or Kendall's tau
DOI:10.1016/j.jmaa.2018.11.057
[本文引用: 1]

A bivariate extreme-value copula is characterized by a function of one variable, called a Pickands dependence function, which is convex and comprised between two bounds. The authors identify the smallest possible compact set containing the graph of all Pickands dependence functions whose corresponding bivariate extreme-value copula has a fixed value of Spearman's rho or Kendall's tau. The consequences of this result for statistical modeling are outlined. (C) 2018 The Author(s). Published by Elsevier Inc.