1 引言
期权定价和保险定价本质上都是对更广泛意义上的未定权益的权利价值进行定价, 这就为期权定价方法和保险定价方法的交叉融合提供了可能. 保险证券化产品的急剧发展, 特别是保险期权等产品的相继面市, 对这两种定价方法的融合提出了迫切的要求. 因此, 研究期权定价方法和保险定价方法的融合, 具有重要的理论意义和现实意义. 本文主要研究将保险定价中的概率扭曲变换应用到期权定价中, 并讨论由此得到的期权价格是否无套利的问题.
在保险精算理论中, 概率变换是一种常用的风险定价方法. 设随机变量
其中
基于标准正态分布, Wang[1]提出了著名的王变换
为了刻画收益率的非正态性质, 国内外学者提出了很多模型模拟收益率. VG(Variance Gamma)过程就是其中之一. VG过程是具有有限变差的纯跳Lévy过程, 其增量分布具有尖峰厚尾性质, 这些性质非常适合刻画资产价格的收益率. 本文利用概率变换思想, 基于VG分布定义了一类新的概率扭曲算子—VG扭曲算子, 证明了在VG模型中, 按VG扭曲算子得到的期权价格和在均值修正鞅测度(mean correcting martingale measure)下的期权价格一致, 从而说明了按VG扭曲算子得到的期权价格无套利. 数值计算结果表明, 按VG扭曲算子得到的期权价格比较准确.
2 VG分布和VG过程
定义2.1 如果随机变量
其中
由于VG分布无穷可分, 因而可以如下定义VG过程.
定义2.2 概率空间
(1)
(2)
(3)
其中
其中
显然,
其中
记
Madan等[12]给出了VG过程的特征三元组为
3 VG扭曲算子
本节基于VG分布提出VG扭曲算子, 并研究VG扭曲算子对VG随机变量的影响.
定义3.1 设
为VG扭曲算子.
与王变换只有一个参数不一样, VG扭曲算子有5个参数. 本质上, VG扭曲算子就是把
其中参数
定理3.1 设
证 对
将VG扭曲算子
两边积分, 即可得到(3.2)式.
从定理3.1的证明可看到, 我们只要求随机变量
定理3.2 设随机变量
4 期权定价
本节研究VG扭曲算子在期权定价中的应用.
假设市场中有两种资产, 一种为无风险资产, 其价格过程为
另一种资产称为股票, 其价格过程为
其中, 无风险利率
引理4.1 在模型(4.1)中, 设
其中,
在模型(4.1)中, 设
其中,
则有
换句话说, 在VG扭曲算子
后面的证明和数值计算需要用到如下定理.
定理4.1 设
证 只需证明
最后等式表明
下面的定理说明在指数VG模型中, 由VG扭曲算子得到的期权价格等于均值修正鞅测度下的期权价格.
定理4.2 在模型(4.1)中, 如果
其中
证 令
记
由引理4.1, 在均值修正鞅测度
因此, 定理的结论成立.
5 数值分析
S1. 输入
S2. 计算
S3. 利用王变换(1.1)式, 求出参数
S4. 计算欧式看涨期权
S5. 计算期权价格
S6. 计算各模型下期权的理论价格和
由于NIG、VG扭曲算子计算相对误差的算法, 除了需要参数估计外, 其他完全类似, 这里不再列出.
理论上, 在将要讨论的四个模型中, 股票价格的下确界为0, 上确界为
情况1 若
注意到三种扭曲算子可以统一写成
这就意味着一旦执行价格
情况2 当
于是有
另外, 模型的理论价格在执行价格
注5.1 以上结论与扭曲算子和模型无关. 因此, 对于深度虚值期权和深度实值期权而言, 比较三种扭曲算子的准确性就没有什么实际意义. 基于这个原因, 下面只讨论在执行价格偏离股票初始价格
5.1 B-S模型
在模型(4.1)中, 令
图1
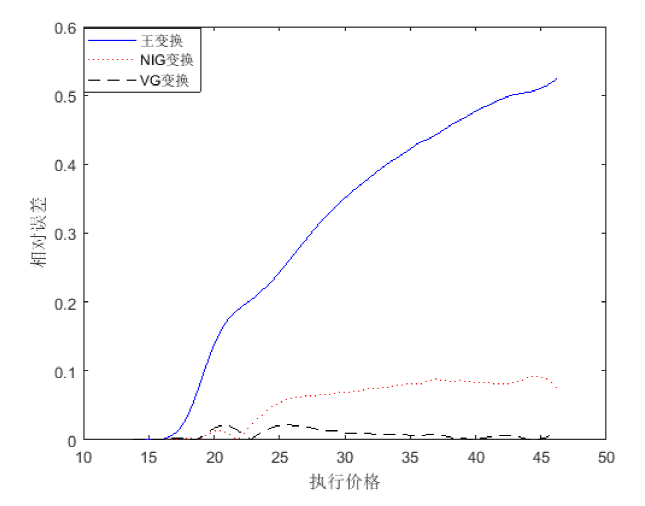
5.2 Merton跳扩散模型
Merton[14]考虑了跳扩散模型
其中
其中,
与B-S模型的做法类似, 给定参数
由三种扭曲算子得到的期权价格的相对误差见图2. 我们可以看到NIG价格和VG价格比较准确, 王变换价格比较差.
图2
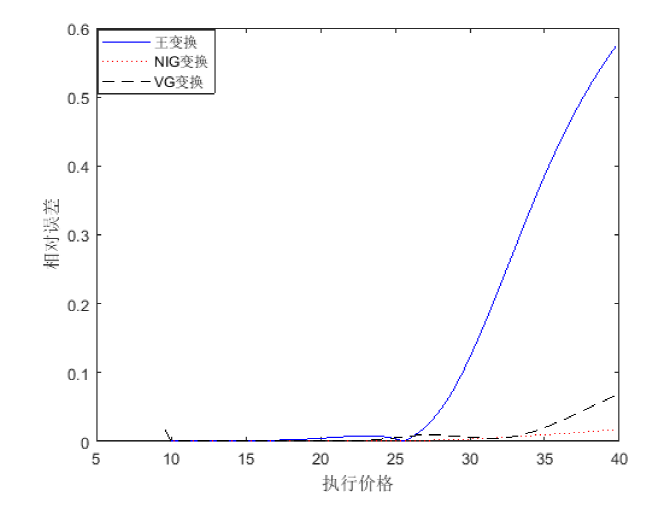
5.3 NIG模型
在模型(4.1)中, 设
图3给出了由三种扭曲算子得到的期权价格的相对误差(相对于均值修正鞅测度下欧式看涨期权的理论价格). 在NIG模型中, 还是可以看到, NIG价格和VG价格比较准确, 王变换价格比较差.
图3
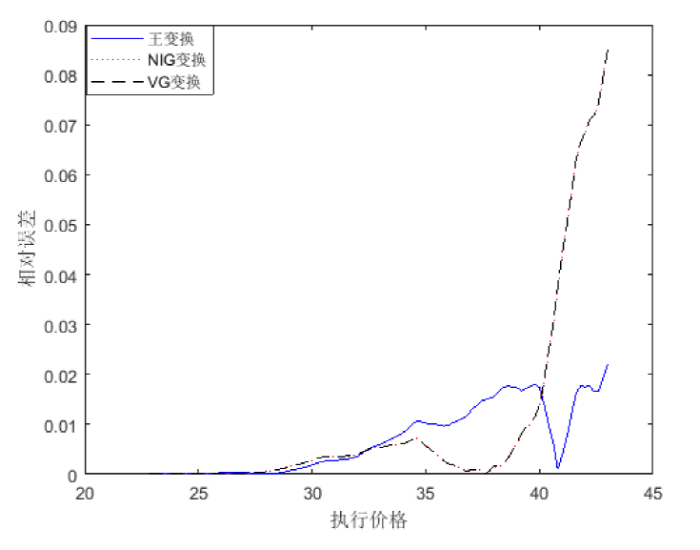
5.4 VG模型
设模型(4.1)中的
图4给出了由三种扭曲算子得到的期权价格的相对误差(相对于均值修正鞅测度下欧式看涨期权的理论价格). 在VG模型中, 仍然可以看到, NIG价格和VG价格比较准确, 王变换价格比较差.
图4
综合上面的数值结果, 可以发现两点. 第一, 在收益率为正态分布时, 王变换价格是非常准确的; 在收益率为非正态分布时, 王变换价格较差. 这和Hamada等[4]的结果一致. 第二, 无论收益率是否为正态分布, VG价格和NIG价格都非常准确. 因此, VG扭曲算子为我们提供了一种新的期权定价思路.
参考文献
A class of distortion operators for pricing financial and insurance risks
DOI:10.2307/253675 URL [本文引用: 2]
Pricing exotic options using the Wang transform
DOI:10.1016/j.najef.2012.06.008 URL [本文引用: 1]
A note on the Wang transform for stochastic volatility pricing models
DOI:10.1016/j.frl.2016.07.011 URL [本文引用: 1]
Contingent claim pricing using probability distortion operators: Methods from insurance risk pricing and their relationship to financial theory
DOI:10.1080/1350486032000069580 URL [本文引用: 4]
CAT bond pricing using probability transforms
An extension of the Wang transform derived from Bühlmann's economic premium principle for insurance risk
DOI:10.1016/j.insmatheco.2007.10.010 URL [本文引用: 1]
Contingent claim pricing using a normal inverse gaussian probability distortion operator
DOI:10.1111/jori.2012.79.issue-3 URL [本文引用: 4]
A general class of distortion operators for pricing contingent claims with applications to CAT bonds
DOI:10.1080/03461238.2019.1581837 URL [本文引用: 1]
The distortion principle for insurance pricing: Properties, identification and robustness
DOI:10.1007/s10479-018-3119-1 [本文引用: 1]
The Variance-Gamma model for share market returns
Option pricing with V.G. martingale components
DOI:10.1111/mafi.1991.1.issue-4 URL [本文引用: 1]
The variance gamma process and option pricing
DOI:10.1023/A:1009703431535 URL [本文引用: 2]
Option pricing when underlying stock returns are discontinuous
DOI:10.1016/0304-405X(76)90022-2 URL [本文引用: 2]