互联网信息技术的迅速发展引领人们进入了大数据时代, 大数据所展现出的规模与复杂性使得传统的统计方法遭受巨大的冲击, 由于传统的统计分析理论仅适用于协变量维数远小于样本量的情形, 因此不再普遍适用于高维模型. 随着高维数据在生物信息、金融管理等领域^[1]的广泛普及, 人们对高维模型中的变量选择问题提出了更高的要求, 即寻求更简约和科学的预测变量以分析与响应变量的关系, 提高模型的解释能力.

在高维模型的变量选择问题中, 高维变量间通常具有很强的相关性, 如同一行业的股票往往表现出显著的相关收益; 基因表达经常受到细胞因子的刺激或受到生物过程的调控等. 若忽视变量间的强相关性, 则会使得高维统计推断方法产生较大的系统性偏差而降低效率. 一般的线性回归模型已不足以解决这类问题, 但是引入随机效应可以有效克服该模型的缺陷, 提高模型的预测精度和建模的灵活性. 因此, 研究高维随机效应线性回归模型^[2]至关重要.

当前人们普遍利用正则化方法产生稀疏解以实现变量选择的目的. 而是否具有渐近性质是用来判断正则化方法优劣的重要指标, 该性质刻画了当主体数量趋于无穷大时, 其解所具有的一致性和Oracle性质. 在实践中, 人们发现这些具有强相关性的高维预测变量间具有自发的分组结构, 很多学者^[3]利用这一特性合并这些有用的信息, 简化模型以改进统计建模和推断. 如Diaz-Uriarte等(2003)利用主成分分析构建寻找一组高度相关的基因. Hastie等(2003)使用有监督的学习方法选择由层次化学聚类发现的预测基因组. 故分组效应^[4]对于高维随机效应线性回归模型中的变量选择问题是必要的.

下面是几种典型且应用广泛的正则化方法.$\!\!$1970年,$\!\!$Hoerl和Kennard^[5]提出L$_2$正则化方法, 尽管L$_2$惩罚能保证函数的凸性使其具备分组效应, 但它无法产生稀疏解, 不具备渐近性质.$\!\!$1996年, Tibshirani^[6]提出Lasso惩罚方法, 其基本思想是用L$_1$正则项代替L$_2$正则项, 该方法能产生稀疏解, 但不具备渐近性质. 此外, 当协变量间具有强相关性时, Lasso方法无法表现出分组效应. 为克服上述惩罚方法的缺点, Fan和Li^[7]提出了一种典型的非凸正则化模型SCAD惩罚法, 该方法能产生稀疏解, 具有渐近性质但不具备分组效应.$\!\!$2005年, Zou和Hastie^[8]充分结合了L$_1$与L$_2$正则化方法的优势, 提出了弹性网惩罚. 其中L$_1$正则项会导致该惩罚在系数估计时存在有偏性, 不具备渐近性质; L$_2$正则项则保证了弹性网具有分组效应.$\!\!$2010年, Zeng等^[9]受到弹性网的启发, 通过将SCAD函数与L$_2$惩罚结合起来, 提出了SCAD_L$_2$惩罚方法, 并证明了该方法不仅具有SCAD函数的优良性质, 还具备分组效应. 综上, 易得SCAD_L$_2$是唯一兼具分组效应和渐近性质的惩罚函数, 表现出优良的变量选择能力和系数估计效果. 此外, 当不要求分组效应时, SCAD惩罚由于具有较好的变量选择能力和系数估计效果, 能在一定程度上节约运行成本, 故成为最佳变量选择方法.

针对高维随机效应线性回归模型, 如何同时选择固定效应和随机效应是解决上述问题的关键. 很多学者提出了一些变量选择的方法, 如2011年, Joseph等^[10]提出了基于SCAD和自适应Lasso的混合惩罚方法以同时选择高维随机效应线性回归模型中的固定效应和随机效应, 并证明了该方法具有渐近性质. 虽然他们通过数值实验发现该方法减小了过拟合问题, 但其在处理相关性较大的数据集上有所欠缺, 不具有分组效应.$\!\!$2012年, Zeng等^[9]提出将SCAD_L$_2$惩罚用于一般的线性回归模型并利用该模型进行数值实验. 即考虑了高维随机效应线性回归模型中$a_i=0$的情形, 他们发现该惩罚下的模型选择结果虽然表现出了很好的分组效应, 但无法解决实际应用中带有随机性的数据选取问题.$\!\!$2021年, 有学者^[11]提出了双SCAD分位回归方法, 但该方法也不具有分组效应. 本文改进了现有的基于双惩罚思想的变量选择方法, 综合考虑上述不同惩罚函数的性质, 提出了基于SCAD_L$_2$和SCAD的混合惩罚方法, 即对高维随机效应线性回归模型中的固定效应和随机效应分别施加SCAD_L$_2$惩罚和SCAD惩罚以使固定效应具有实际问题中同时需要的渐近性质和分组效应, 并使随机效应满足渐近性质, 且在一定程度上提高了计算机的运行效率.

本文其余部分结构如下: 第2节介绍了高维随机效应线性回归模型, 且提出了混合惩罚方法并在理论上证明其优良的统计性质; 第3节给出基于混合惩罚的高维随机效应线性回归模型的两步迭代算法; 第4-5节在不同信噪比和随机效应下对模型进行蒙特卡洛模拟和实例验证, 给出该惩罚方法与其他惩罚方法的对比结果; 第6节为总结与展望.

本文将研究如下形式的高维随机效应线性回归模型^[12]

其中 $n$ 代表主体的数量, $n_i$ 代表对第 $i$ 个主体进行的观察次数, $i=1,2,\cdots,n$, $Y_{ij}$ 代表响应变量, 表示对第 $i$ 个主体的第 $j$ 次观测样本, $j=1,2,\cdots,n_i$, $x_{ij}^{\rm T}$ 表示 $n\times k$ 维已知设计矩阵的行向量, $\beta=(\beta_1,\beta_2,\cdots,\beta_k)^{\rm T}$ 代表 $k$ 维固定效应的系数向量, $z_{ij}$ 表示与随机效应相对应的 $p$ 维协变量, $\alpha_i=(\alpha_{i1},\alpha_{i2},\cdots,\alpha_{ip})^{\rm T}$ 表示对应于第 $i$ 个主体的 $p$ 维随机效应的系数向量.

针对模型(2.1), 本文提出了一种结合罚函数SCAD_L$_2$与SCAD的混合惩罚函数模型, 其形式如下所示

其中 $\lambda_i>0\ (i=1,2,3)$ 是调节参数, 惩罚函数

其中 $a>2$ 为调节参数,并且 $\sum\limits_{j=1}^{k}P_{\lambda_1}(|\beta_j|)+\lambda_2 \Vert \beta \Vert^2$ 代表对固定效应系数施加 SCAD_L$_2$ 惩罚, 而 $\sum\limits_{i=1}^{n}\sum\limits_{t=1}^{p}P_{\lambda_3}(|\alpha_{it}|)$ 代表对随机效应系数施加 SCAD 惩罚.

为方便探讨模型(2.2)的性质, 这里参考文献[15]将其重新表述为如下形式

当$n$很大时,模型(2.3)可以使得惩罚函数项和残差和项具有相当的权重. 通过这种调整后的惩罚形式, 调节参数也发生了相应的尺度变化, 例如: 模型 (2.2)中的调节参数$\lambda_2$等价于模型(2.3)中的调节参数$n\lambda_2$. 相仿地本文用$\lambda_1(n)$和$\lambda_3(n)$分别来强调$\lambda_1$和$\lambda_3$随$n$变化而变化的情形. 对于一组独立分布的数据$\left\{ {\left( {{x_{ij}},{Y_{ij}}} \right),i = 1,\cdots,n;j = 1,\cdots,{n_i}} \right\}$, 下面分析混合惩罚方法的渐近性质.

定理 2.1 (一致性) 对于模型(2.2), 若当$n$趋于$\infty$时, $\lambda_1(n)$, $\lambda_3(n)$和$\sqrt n\lambda_2(n)$均收敛于$0$, 则存在${L^*}(\alpha,\beta )$的局部极小值点$\hat \beta \left( n \right)$和$\hat \alpha \left( n \right)$满足

其中${\beta ^ * } = \left( {\beta _1^{*},\cdots,\beta_k^{*}} \right)^T$为固定效应变量的真实系数, ${\alpha ^ * } = \left( {\alpha _1^{*},\cdots,\alpha_p^{*}} \right)^T$为随机效应变量的真实系数.

注 2.1 这里对$\hat\beta(n)$系数估计的一致性证明可参见文献$[9]$, 同理可证$\hat\alpha(n)$系数估计的一致性.

定理 2.2 (Oracle性质) 对于模型(2.2), 若当$n$趋于$+\infty$时, $\lambda_1(n)$, $\lambda_3(n)$和$\sqrt n\lambda_2(n)$均收敛于$0$, 而 $\sqrt n\lambda_1(n)$和$\sqrt n\lambda_3(n)$ 趋于$+\infty$, 则模型(2.3)的一致局部极小值点

以概率1满足

(1)稀疏性: ${\hat \beta_Z}\left(n\right) = 0$, ${\hat \alpha _{{Z_1}}}\left( n \right) = 0$.

(2)渐近正态性

其中${\Sigma _M}$、${\Sigma _{M_1}}$ 均为正定阵, 这里假设前$d$个向量均为非零向量, 且令$\beta_{M}^* = {({\beta_{1}^*},\cdots,{\beta_{d}^*})^T}$代表固定效应中非零的系数向量, $\beta _Z^* = {({\beta _{d + 1}},\cdots,{\beta _k})^T}$代表固定效应中为零的系数向量. 同样令$\alpha _{M1}^* = {\left( {{\alpha _1^*},\cdots,{\alpha _r^*}} \right)^T}$代表随机效应中非零系数向量, $\alpha _{Z1}^* = {\left( {\alpha_{ r + 1}^*,\cdots,\alpha_p^*} \right)^T}$代表随机效应中为0的系数向量.

注 2.2 对固定效应中$\hat\beta(n)$稀疏性和渐近正态性的证明具体可参考文献$[9]$, 同理可证明$\hat\alpha(n)$的稀疏性和渐近正态性.

为验证混合惩罚方法对固定效应的系数估计具有分组效果, 下面证明模型 (2.2)的分组效应.

定理 2.3^[9] 记 $P_{{\lambda _1},{\lambda _2},{\lambda _3}}\left( {\theta,{\alpha _j}} \right) = P_{\lambda _1}\left( \theta \right) + {\lambda _2}{\theta ^2} + P_{\lambda _3}\left( {{\alpha _j}} \right).$ 如果存在 ${\theta _1}$ 和 ${\theta _2}$ 满足 ${\theta _1} \cdot {\theta _2} > 0,$ 且 ${\lambda _2} > 1/2\left( {a - 1} \right)$, 则有

其中 $P_{\lambda _1}\left( \theta \right)$ 和 $P_{\lambda _3}\left( \theta \right)$ 由模型 (2.2)定义, $P{'_{{\lambda _1},{\lambda _2},{\lambda _3}}}(\theta,{\alpha _j})$ 为 ${P_{{\lambda _1},{\lambda _2},{\lambda _3}}}(\theta,{\alpha _j})$ 关于 $\theta$的导数, $C = 2{\lambda _2} - 1/(a - 1)$.

下面利用定理2.3给出模型(2.2)的分组定理.

定理 2.4 (分组定理) 对于给定的数据 $\left({x_{ij}^T,{Y_{ij}}} \right)$ 和系数 ${\lambda _1}$ 与 ${\lambda _2}$, 以响应变量 ${Y_{ij}}$ 为中心, 将解释变量 $x_{ij}^T$ 进行标准化处理. 若对于固定的 $j$, 相应的解释变量 $x_{{i_1},j}^{\rm T}$ 和 $x_{{i_2},j}^{\rm T}$ 的系数 ${\beta _{{i_1}}}$ 和 ${\beta _{{i_2}}}$ 之间的距离 $D_{{\lambda _1},{\lambda _2}}\left({{i_1},{i_2}} \right)$ 满足

其中 $\rho = {x_{{i_1},j}^{\rm T}}x_{{i_2},j}$ 为样本相关性, 系数 $D_{{\lambda _1},{\lambda _2}}\left( {{i_1},{i_2}} \right) = 1/{\left| y \right|_1} \cdot \left| {{{\hat \beta }_{{i_1}}}\left( {\lambda_1,\lambda_2} \right) - {{\hat \beta }_{{i_2}}}\left( {\lambda_1,\lambda_2} \right)} \right|$, $\hat \beta \left( {\lambda_1,\lambda_2} \right)$ 代表估计系数, 则模型(2.2)的解具有分组效应.

证 为方便起见, 将模型(2.2)改写如下形式

其中 ${\beta _{{i_1}}}$ 代表混合惩罚函数中对 $\beta$ 估计系数的第 ${i_1}$ 项.

对 ${\beta _{{i_1}}}$ 求偏导可得

令式(2.6)为 0, 且将任意两项相减可得

根据定理2.3可得

由于

所以

又因为

故

证毕.

注 2.3 定理2.4给出了两个估计系数间距离的上界. 如果两个估计系数之间相关系数的绝对值接近于$\mathrm{1}$, 则定理2.4可以保证两个估计系数非常接近. 因此, 定理2.4表现了模型(2.2)的解具有分组效应.

综上, 该混合惩罚方法在理论上是一种优良的变量选择和系数估计方法.

本节利用模型(2.2)的结构特性, 采用两步迭代法求解模型(2.2). 下面给出模型 (2.2)中惩罚参数的选取准则和算法描述.

根据模型(2.2)可以看到惩罚函数有三个调优参数 $\lambda_1$, $\lambda_2$ 和 $\lambda_3$. 综合考虑不同参数选取原则的优劣性, 本文采用广义交叉验证法^[15](Generalized Cross Validation, GCV) 确定它们的取值. 具体流程为: 为待选参数设置一个三维网格, 其中令 $\lambda_1$ 和 $\lambda_3$ 的取值范围均为 $(0.01,10];$ 从$\{0.001, 0.01, 0.1, 1, 10\}$中选取 $\lambda_2$; 通过最小化 GCV 误差

其中

$e(\lambda_{\rm{1}},\lambda_{\rm{2}},\lambda_{\rm{3}})$ 代表参数计算误差, 从而得到最优参数集. 根据选择出的最佳参数, 进一步采用两步迭代法计算模型 (2.2), 下面给出两步迭代法的描述.

两步迭代法的描述如下.

步 1 初次迭代求解时令 ${\hat \alpha _i}^{(s)} = 0{\rm{ }}\ (i = 1,2,\cdots,n)$, 则原式等价于只含系数 $\beta$ 的 SCAD_${L_2}$ 惩罚线性回归模型. 然后利用 LQA 方法对该模型进行求解, 可得 ${\hat \beta ^{\left( s \right)}}{\rm{ = }}\arg \min L(\beta,0),$ 这里 $s=0$.

步 2 将求解出的 $\hat\beta^{(s)}$ 代入模型(2.2)中, 则可以看作调整残差为 ${r_{ij}}^{\left( s \right)} = {y_{ij}} - x_{ij}^T{\hat \beta ^{\left( s \right)}}$, 此时模型中只有系数 $\alpha_i$. 求解模型 $\hat \alpha _i^{\left( {s + 1} \right)}{\rm{ = }}\arg {\min _\alpha }L({\hat \beta ^{\left( s \right)}},{\alpha _i})$, 将求解出的 ${\hat \alpha_i ^{\left( s+1 \right)}}$ 代入模型(2.2)中, 则可以看作调整响应变量为 $y_{ij}^ * = {y_{ij}} - z_{ij}^T\hat \alpha _i^{\left( {s + 1} \right)}$, 此时模型中只有系数 $\beta$, 再利用 LQA 方法求解得到 ${\hat \beta ^{\left( {s + 1} \right)}} = \arg {\min _\beta }L(\beta,\hat \alpha _i^{\left( {s + 1} \right)}){\rm{ }}$$s = 0,1,\cdots.$

步 3 反复迭代步 2, 当 ${\max _l}\big| {\hat \beta _l^{\left( {s + 1} \right)} - \hat \beta _l^{\left( s \right)}} \big| < \varepsilon {\rm{ }}\ (l = 1,2,\cdots,p)$ 时停止迭代, 这里取 $\varepsilon = {10^{ - 4}}$.

本节将该混合惩罚方法与双 Lasso 惩罚方法, 双 SCAD 惩罚方法以及不考虑随机效应的 SCAD_${L_2}$ 惩罚方法的模型选择能力和系数估计效果进行比较.

下面利用下述模型^[14]生成数据

其中 ${\beta _0} = 0$, ${\rm{ }}\beta = {(3, - 1.5,0,0,2,0,0,0)^T}$, $x_{ij}^T = ({x_{i{j_1}}},{x_{i{j_2}}},\cdots,{x_{i{j_8}}})$$(i = 1,2\cdots,n; j = 1,$$\cdots,{n_i})$, $\sigma$ 表示相应于随机误差 $\epsilon_{ij}$ 的信噪比. 这里取 $n = 30$, ${n_i} = 100$$(i = 1,2,\cdots,30)$. 对于固定的 $i$ 和 $j$, 将解释变量 $x_{ij}^{\rm T}$ 中的每个分量均看作随机变量, 并且假设它们均服从标准正态分布. 令 $x_{ij}^{\rm T}$ 中任意两个分量 $x_{ij_l}$ 和 $x_{ij_k}$ 之间的相关系数为 ${\hat \rho ^{\left| {l - k} \right|}}$, 其中 $\hat \rho$ 为常数 $(0<\hat \rho <1)$, 且在模拟实验中取 $\hat \rho = 0.8$. 并令截距和第一个自变量具有随机效应, 即 $z_{ij}^T = (1,{x_{i{j_1}}})$, 同时对于 $i=1,2,\cdots,n$, 令相应的随机变量 ${\alpha _i} = (\alpha _{i0},\alpha _{i1})^{\rm T} \mathop \sim\limits^{i.i.d.} N_2(0,1),$随机误差 $\varepsilon _{ij} \mathop \sim\limits^{i.i.d.} N(0,1)$. 在下文所有的模拟实验中规定: 若系数估计值的绝对值小于 $10^{-4}$ 则将该项视为 0.

下面引入三个衡量指标以比较在不同信噪比和随机效应下混合惩罚方法变量选择能力的差异.

本文采用均方误差 (Mean Square Error, MSE) 作为评价混合惩罚方法的系数估计效果的衡量指标之一. 通过综合考虑运行时间成本, 本文对模型(4.1)进行了 100 次模拟实验. 根据该模型生成的数据, MSE 的定义如下所示

其中 ${\rm{ }}{\hat \beta ^m}$ 代表第 $m$ 次模拟时 $\beta$ 的估计值. 由式 (4.2)可知: MSE 值越大代表混合惩罚方法的系数估计效果越差, 反之, 系数估计效果越好.

另外, 本文采用两个常用指标$F1$和$F2$来衡量混合惩罚方法的变量选择效果, 其定义^[16]分别如下

注4.1 由$F1$与$F2$的定义可知: 它们的值均介于[0,1]. $F1$越接近于$1$代表其选择重要自变量的能力越强, 反之越弱; $F2$越接近于$1$代表其排除非重要自变量的能力越强, 反之越弱.

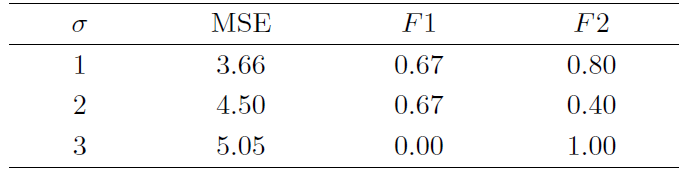
下面根据上述三个衡量指标比较不同“信噪比”下混合惩罚方法的系数估计效果和变量选择能力. 利用模型(4.1)生成模拟数据, 为进一步体现随机效应的影响, 本文设置 $z_{ij}^{\rm T} = (1,{x_{i{j_1}}},\cdots,{x_{i{j_6}}})$, 并使相应的随机效应系数 ${\alpha _i} = ({\alpha _{i0}}, {\alpha _{i1}},\cdots,{\alpha _{i6}})^{\rm T}\mathop \sim\limits^{i.i.d.} {N_7}(0,D),$ 其中 $D = diag(1,1,1,1,0,0,0)$. 本文分别给出信噪比 $\sigma$ 取值为 1, 2 和 3 时, 该混合惩罚方法的系数估计效果和变量选择能力, 所得结果均为经过100次测试后得到的平均值, 如表1所示.

下面将根据表1给出如下模拟结果分析: 当信噪比逐渐增大时, 混合惩罚方法筛选正确变量的能力和系数估计效果均在下降; 而其排除无关变量的能力均有不同程度的变化, 当$\sigma$ 取值为1和3时, $F2$均能达到较高的水平. 故当$\sigma$ 取值为1时, 混合惩罚方法的系数估计效果和变量选择能力基本达到最佳水平.

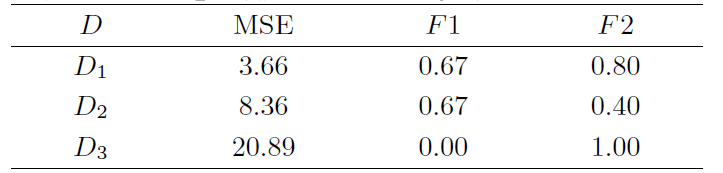
下面根据上述三个衡量指标比较不同随机效应影响下混合惩罚方法的系数估计效果和变量选择能力. 同样利用模型(4.1)产生模拟数据, 基于前述信噪比对混合惩罚方法的影响分析, 这里取 $\sigma = 1$, 并将随机效应的协方差 $D$ 分别取为

这里协方差矩阵 $D_i$ 的值参考了随机效应模型研究中通常选取的数值^[11], 即依次增加了随机效应对模型(4.1)的干扰程度, 所得实验结果均为经过 100 次测试后得到的平均值, 如下所示.

下面将根据表2给出如下模拟结果分析: 当随机效应增强时, 混合惩罚方法系数估计效果下降且误差受随机效应因素影响较大; 当随机效应的干扰程度较小或较大时, 混合惩罚方法的变量选择能力几乎不受影响且保持在较高水平, 故当随机效应的协方差为$D_1$时, 混合惩罚方法的系数估计效果和变量选择能力基本达到最佳水平.

本节将在上述实验中确定的最佳信噪比和随机效应下, 从衡量指标效果和分组效应效果两方面比较该混合惩罚方法、双Lasso惩罚方法、双SCAD惩罚方法和不考虑随机效应的SCAD_L${_2}$惩罚方法的性能. 下面先从衡量指标效果的角度进行分析.

下面利用模型(4.1)产生数据, 然后分别讨论固定系数在系数模型和稠密模型两种情况下的系数估计效果和变量选择能力.

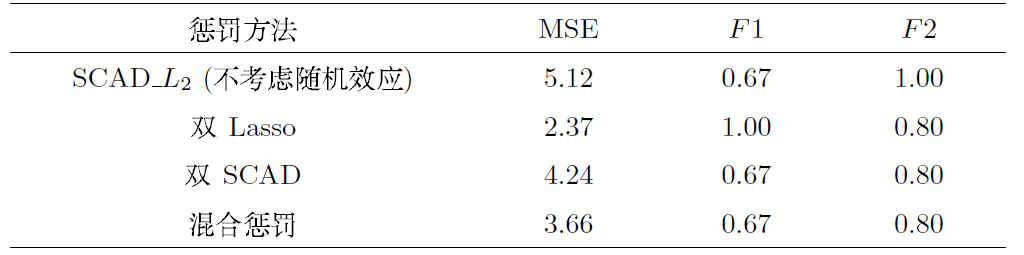
情况 1 稀疏模型取

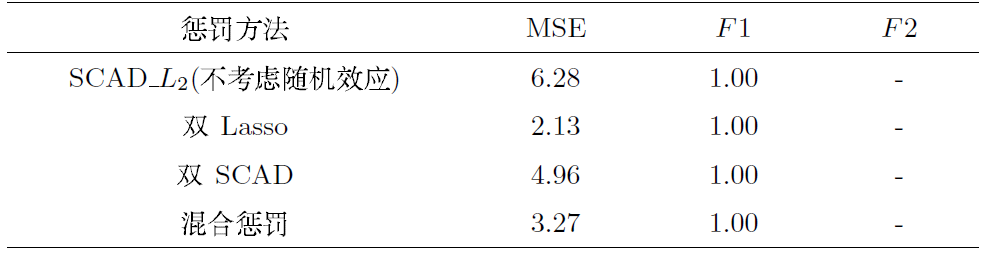
情况 2 稠密模型取

这里均选取相同的 $\sigma$ 和 $D$, 即 $\sigma = 1$, $D = diag(1,1,1,1,0,0,0)$, 并令误差 ${\varepsilon _{ij}}\sim N(0,1)$. 由数值结果得到稀疏模型情况下不同惩罚方法的效果比较表, 所得实验结果均为经过 100 次测试后得到的平均值, 见表3.

下面将根据表3给出如下模拟结果分析: 从衡量指标MSE的计算结果发现: 双Lasso惩罚方法$>$混合惩罚方法$>$双SCAD惩罚方法$>$SCAD_L$_2$惩罚方法(不考虑随机效应); 从衡量指标$F1$和$F2$的计算结果发现: 四种方法均具有较好的变量选择能力且差距不大. 故对于高维稀疏模型, 混合惩罚方法具有较好的系数估计效果和变量选择能力.

下面将根据表4给出如下模拟结果分析: 从衡量指标MSE的计算结果发现: 双Lasso惩罚方法$>$双SCAD惩罚方法$>$混合惩罚方法$>$SCAD_L$_2$惩罚方法(不考虑随机效应); 从衡量指标$F1$的计算结果发现: 上述四种方法均能准确地筛选出重要变量. 故对于高维稠密模型, 混合惩罚方法具有较好的系数估计效果和变量选择能力.

结合表3-4, 我们可以发现无论是对于高维稀疏模型还是高维稠密模型, 双 Lasso 方法均具有较好的系数估计效果和变量选择能力. 但是从理论上分析, 该方法不具有渐近性质, 故不适用于大样本数据;双SCAD方法对于高维稠密模型更加有效; 此外对于模型(4.1)而言, 仅针对固定效应系数施加惩罚是不够的, 具有一定程度的误差; 而该混合惩罚方法则更加适用于当前热门研究课题中的高维稀疏化模型.

下面从分组效应角度来分析上述不同惩罚方法的效果差异.

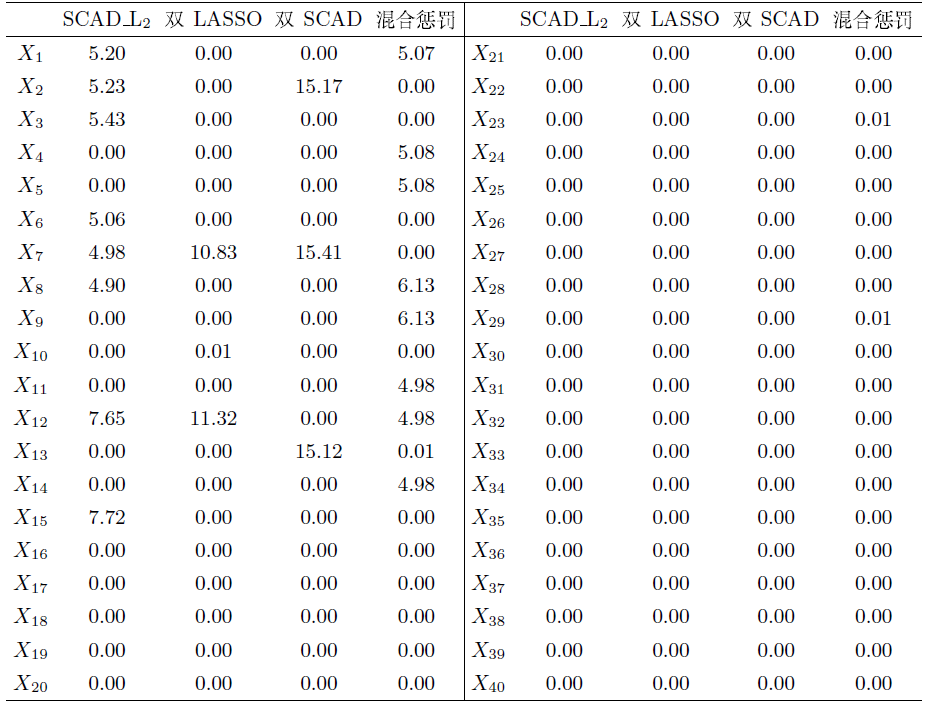
下面将考虑在更高维数的稀疏模型下比较四种不同惩罚方法的分组效果, 这里根据模型 (4.1)生成数据. 为使分组效应^[17]在实验中有更明显的结果, 这里需要重新确定各变量的取值, 取 $\beta = (\underbrace {3,\cdots,3}_{15},\underbrace {0,\cdots,0}_{25})$, $k=40$, $j=1$, 其中设计矩阵 $X = {\left( {{x_{ij}}} \right)_{{\rm{40}} \times 1}}$ 分成四组以确保每一组设计矩阵中变量间的相关系数趋近于 1, 并且每组均按如下准则随机产生

其中 ${\alpha _{ij}}\sim N(0,0.01), {\rm{ }}i = 1,2,\cdots,15, {\rm{ }}j{\rm{ = 1}}$. 在仿真实验中,令随机误差 ${\varepsilon _{ij}}\sim N(0,1)$, 并且将 $\sigma$ 恒定设置为 1; 在有适当随机变量干扰程度的影响下, 综合考虑计算机的运行速度, 这里令随机效应的协方差为 $D = diag(1,1,1,1,0)$; 然后由广义GCV参数选取准则得到的调优参数$(\lambda_1,\lambda_2,\lambda_3)$对模型进行训练拟合, 最后将所得结果用于测试集中以检验系数估计效果; 取混合惩罚函数中的常数$a$为3.7(见参考文献[7]). 由四种不同惩罚方法得到的分组效应结果见表5, 其中 ${X_i} = {x_{ij}}$, 且各列数据代表由不同惩罚方法得到的系数估计$\beta$. 下面将根据表5给出如下模拟结果分析

(1) 在高维稀疏模型中, 利用混合惩罚方法所得系数估计结果更加准确, 并且在以每五个相关性很高的变量为一组的情况下, 相应筛选出来的变量系数近似相等且与真实系数最为接近, 即混合惩罚方法表现了很好的分组效果.

(2) 不考虑随机效应的SCAD_L$_2$惩罚方法虽然对固定效应体现了分组效应, 但是其对第三组变量的系数估计值与真实系数值存在较大偏差, 故仅考虑固定效应是不够的.

(3) 在高维稀疏模型下, 无论是对模型(2.1)施加双SCAD惩罚方法还是双Lasso惩罚方法, 所得结果均不具备分组效应.

(4) 结合上述三条分析得出: 对于更高维数的稀疏模型, 混合惩罚方法具有很好的分组效应.综上, 该混合惩罚方法具有很好的分组效应, 表现出更优良的系数估计效果和变量选择能力.

本节将通过实例验证该混合惩罚方法的统计效果. 本文将混合惩罚方法应用于在线新闻流行度数据集^[18]研究中, 该数据集总结了一组关于在两个阶段发布的全球之声文章的异构特性, 其研究目的在于使得所发布的文章在社交网络中获得更多的人气.

本文从HTML代码中提取了一个广泛的特性集, 其描述了文章不同方面的特征, 这些特征被认为可能是影响文章流行度的相关因素, 如表6所示. 其中一些特性依赖于Mashable服务的特殊性: 如文章经常引用在同一服务中发布的其他文章等. 本文还提取了一些自然言语处理的特征, 如LDA算法应用于所有Mashable文本, 并据此确定5个最重要的相关主题, 衡量当前文章与这些主题的密切程度. 这里用$X_i\ (i=1,2,\cdots,60)$表示相应的自变量.

本文借鉴了Fernandes^[18]所提出的方法以判断文章是否受欢迎, 这里采用Scikit学习库对预测模型进行拟合, 首先假设一个二元分类任务, 如果其中一篇文章的分享数高于一个固定的决策阈值(这里选用1000), 则认为其是“受欢迎的”, 否则认为是“不受欢迎的”. 对于预测实验, Fernandes在文献[18]中采用了滚动窗口方案, 即取训练窗口大小为10000进行29次迭代, 每次迭代进行1000个样本的预测, 并据此测试了五种分类模型. 结果表明, 随机森林(RF)模型在AUC度量方面的表现最佳, 得到的最佳结果(AUC=0.73)比随机分类器高23%, 达到了较好的辨别水平, 是一个良好的分类器. 本文据此对上述四种不同的分类方法做了相似的实验, 结果表明, 该混合惩罚方法在AUC度量方面的表现最佳, 达到72.8%, 与RF模型的分类水平相近, 表明了混合惩罚在该阈值下同样有较好的分类效果.

为了更加直观地验证混合方法的分组效应, 本文根据原始数据分别求得各变量间的相关系数, 结果得到仅$X_{36}$和$X_{38}$及$X_{44}$和$X_{50}$这两组解释变量间具有很高的相关性, 其相关系数分别为0.662和0.632; 利用上述四种不同的惩罚方法对影响新闻流行度的所有自变量进行变量选择和 系数估计并计算均方误差(Root Mean Squared Error, RMSE), 相应的系数估计结果如表7所示, 其中表7中非零 系数对应的变量为筛选出的与人气值最为相关的重要变量, 其余均为非重要变量.

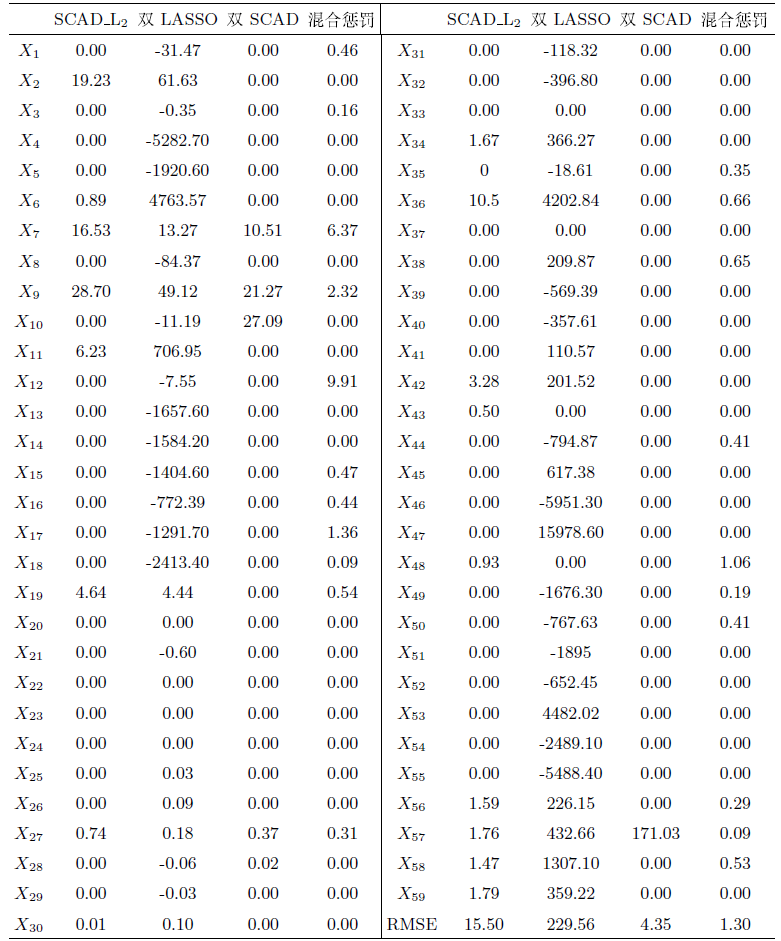
根据表7发现针对$X_{36}$和$X_{38}$及$X_{44}$和$X_{50}$这两组具有强相关性的解释变量, 只有利用混合惩罚方法所得的$X_{36}$和$X_{38}$的估计系数近似相等; 同样$X_{44}$和$X_{50}$对应的估计系数也十分接近. 这体现了混合惩罚方法具有很好的分组效应, 并且所得RMSE最低仅为1.30, 说明混合惩罚方法具有更优良的系数估计效果和变量选择能力.

综上,该混合惩罚方法具有的优良统计性质有利于筛选出影响在线新闻流行度的相关变量以使发布的文章获得最佳人气.

本文对模型(2.1)提出了一种基于SCAD_L$_2$惩罚和SCAD惩罚的混合惩罚方法, 论证了在混合惩罚下固定效应不仅具有良好的变量选择能力和系数估计能力, 还具有很好的分组效应, 并且随机效应也具有良好的变量选择能力, 这是由两种不同惩罚方法的性质所决定的. 进一步通过蒙特卡洛模拟对该混合惩罚方法的统计性质进行了验证, 结果表明: 与其他惩罚方法相比, 在不同信噪比和随机效应下该混合惩罚方法具有较好的系数估计和分组效应效果. 同时通过在线新闻流行度的实例验证了混合惩罚方法具有更优良的统计性质, 适用于高维稀疏模型.

仍有大量工作值得今后继续研究, 如: 将混合惩罚方法进一步应用到随机效应分位回归模型等其他模型中; 对两步迭代算法加以改进以节约模拟实验中计算机的运行时间; 在基因表达和前列腺癌症等实例中验证混合惩罚方法的系数估计和分组效应效果等.