该文考虑如下目标函数和约束函数带不可分结构的大规模非凸优化问题

其中 $f:\mathbb{R} ^{n_{1}+n_2}\rightarrow \mathbb{R} $, $h(x, y)=(h_1(x,y),\cdots,h_m(x,y))^\top: \mathbb{R} ^{n_{1}+n_2}\rightarrow \mathbb{R} ^m$, 均光滑但不一定凸, $l=(l_1,\cdots,l_{m_1})^\top$, $ v=( v_1,\cdots, v_{m_1})^\top$, $-\infty\leqslant l_i< v_i\leqslant+\infty$, $s=(s_1,\cdots,s_{m_2})^\top$, $r=(r_1,\cdots,r_{m_2})^\top$, $-\infty\leqslant s_i<r_i\leqslant+\infty$, 矩阵 $C\in \mathbb{R} ^{m_1\times n_1},\ D\in \mathbb{R} ^{m_2\times n_2}$.

定义问题(1.1)的 (部分) 增广拉格朗日函数

其中, $(x,y)$ 和 $\lambda$ 分别称为原始变量和对偶变量 (乘子), $\beta>0$ 为罚参数.

分裂算法是求解带可分结构问题十分有效的算法之一, 主要的分裂算法有 Douglas-Rachford (DR) 分裂算法^[1] 和 Peaceman-Rachford (PR) 分裂算法^[2]. 经典的乘子交替方向法 (ADMM) 本质上是将 DR 分裂算法直接应用于求解凸两分块优化的对偶问题, 其算法和一些拓展变体的ADMM 可以将大规模的问题分解成若干个较小规模的问题进行交互求解, 进而降低求解难度和减少计算成本.

对于带等式约束的可分优化问题

其中函数 $f:\mathbb{R} ^{n_{1}}\rightarrow \mathbb{R} $, $\theta:\mathbb{R} ^{n_{2}}\rightarrow \mathbb{R},\ h(x)=(h_1(x),\cdots,h_m(x))^\top: \mathbb{R} ^{n_{1}}\rightarrow \mathbb{R} ^m$, $g(y)=(g_1(y),\cdots,g_m(y))^\top: \mathbb{R} ^{n_{2}}\rightarrow \mathbb{R} ^m$, 闭凸集${\cal X}\in \mathbb{R} ^{n_1}$ 和${\cal Y}\in \mathbb{R} ^{n_2}$. 求解问题 (1.3) 的经典 ADMM 迭代模式为

其中, $L_{\beta}(\cdot)$为问题(1.3)的(部分)增广拉格朗日函数, $\lambda$为拉格朗日乘子, $\beta>0$为罚参数.

近年来, 许多学者对非凸优化进行广泛研究, 并取得一系列成果, 如文献[3⇓⇓⇓⇓⇓⇓-10]. 对于目标函数可分的非凸优化问题, 文献[3-4]对ADMM 两个子问题均加上 Bregman 距离, 提出了 Bregman 正则化 ADMM, 在效益函数满足Kurdyka-Lojasiewicz (KL) 性质的条件下, 分析了相应算法的收敛性. 文献[5]在一般条件下论证经典 ADMM 求解问题(1.3)在具有仿射线性约束时的收敛性和收敛率. 文献[6]在迭代第二个子问题时加入惯性技术, 获得惯性邻近版本的ADMM.

而对于非凸不可分优化问题, 其收敛性仍是一个公开问题. 文献[11]指出, 当目标函数存在不可分结构$h(x,y)$ 时, 即使在凸情形下收敛性证明仍具挑战. 文献[12]研究了一类特殊问题, 即问题(1.3)中目标函数带不可分结构 $h(x,y)$, 约束为仿射线性约束 $h(x)+g(y)=Ax+By-b$, 得到经典 ADMM 的收敛性. 文献[13]运用线性化技术对目标函数中可微项进行线性化处理, 给出线性化版本的 ADMM. 文献[14]基于 PR 分裂算法, 结合线性近似技术和 Bregman 距离, 提出一种不可分优化线性近似 Bregman 型 PR 分裂算法, 在常规假设条件下获得算法全局收敛性, 在效益函数满足 KL性质时证得强收敛性. 当 KL 性质关联函数具有特殊结构时, 分析收敛率结果.

另一方面, 序列二次规划 (SQP) 算法是求解带线性或非线性约束优化问题最有效算法之一, 由 Wilson^[15]首先提出, 因其具有良好的理论性质和高效的计算效果, 尤其对于中小规模问题来说, 这一优势更加显著. 因此, SQP 算法深受研究者欢迎, 理论成果丰富, 如文献[16⇓⇓⇓-20]. 充分吸收 ADMM 和 SQP 算法高效求解的优势, 文献[21] 首次提出了 ADMM-SQP 算法, 该算法基于 ADMM 的分解降维思想, 将 SQP 思想所需求解的 QP 子问题分解为两个互相独立的小规模 QP 子问题, 再利用 Armijo 线搜索技术产生新的迭代点, 在合理的假设下论证了算法良好的理论性质.

文献[22] 中, 考虑问题(1.3)的二次约束二次规划 (QCQP) 近似子问题, 对 QCQP 子问题的增广拉格朗日问题应用分裂算法思想, 获得两个小规模子问题; 再以原问题的增广拉格朗日函数为效益函数, 执行 Armijo 型线搜索, 获得新的原始迭代点, 提出一个基于 QCQP 的分裂 SQP 算法.

基于以上分析, 为进一步探究和发展分裂 SQP 算法的研究, 针对目标函数和约束函数均带不可分结构的大规模非凸优化问题, 该文提出了一个新型的分裂序列二次规划算法. 所提出的算法具有以下特征: (1) 充分利用目标函数和约束函数的可微性, 构造二次逼近子问题, 从而降低子问题的求解难度; (2) 对两个小规模 QP 子问题“并行”求解, 获得其最优解, 进而构造算法的搜索方向, 并利用增广拉格朗日函数进行Armijo 线搜索; (3) 在适当的条件下, 论证了其全局收敛性.

记号:对于列向量 $x, y, \lambda, \cdots $,指标集$I\subset\{1, \cdots, n\}$, 矩阵 $H$, 记

$(x, y, \lambda, \cdots ):=\left(x^{\top}, y^{\top}, \lambda^{\top}, \cdots \right)^{\top},\ \|x\|_{H}^{2}:=x^{\top} H x,\ x \perp y \Leftrightarrow x^{\top} y=0,\ x_{I}:=\left(x_{i}, i \in I\right),$$\left \| x \right \|$ 和 $\left \| Q \right \|$ 分别表示向量和矩阵的 $\ell _{2} $ 范数, 矩阵$A\succ B$ 意味着矩阵$A-B$是正定的.

为了便于分析，我们记 $\left \{ -\infty,+\infty \right \}$ 和实数集 ${\cal R}$ 之间的操作如下

首先, 给出问题 (1.1) 的拉格朗日函数

对于当前迭代点 $u_k:=(x_k,y_k)\in {\cal X} \times {\cal Y}$, 将 SQP 算法思想应用于求解问题 (1.1), 考虑二次逼近子问题

其中 $H_{k}^{f}$ 为拉格朗日函数 $L(x,y,\lambda_k)$ 在 $u_k$ 处的近似 Hessian 阵, 即

接下来, 考虑 QP 子问题 (2.2) 的增广拉格朗日函数和增广拉格朗日问题

和

其中 $\lambda_k\in \mathbb{R} ^m$ 为等式约束的拉格朗日乘子. 受分裂降维思想的启示, 可将问题 (2.5) 分裂为两个 QP 子问题

和

显然, 以上两个 QP 子问题分别等价于

和

其中, 二次系数矩阵 $B^x_{k}$ 和 $B^y_{k}$ 分别为

和

注意到子问题(2.8)和(2.9)有可行解 $x_k$ 和 $y_k$, 当二次系数矩阵 $B^x_k$ 和 $B^y_k$ 正定时, QP 子问题(2.8)和(2.9)均有唯一最优解, 记为 $\tilde{x}_{k+1}$ 和 $\tilde{y}_{k+1}$, 且与 KKT 点等同. 因此, 存在乘子向量 $(\alpha^x_k, \gamma^x_k)\in \mathbb{R} ^{m_1}\times \mathbb{R} ^{m_1}$ 和 $(\alpha^y_k, \gamma^y_k)\in \mathbb{R} ^{m_2}\times \mathbb{R} ^{m_2}$ 满足

其中 $d^x_k:=\tilde{x}_{k+1}-x_{k}$, $d^y_k:=\tilde{y}_{k+1}-y_{k}$.

此外, 由(1.2)式有

进而, 结合(2.14)和(1.15)式, 两个QP子问题(2.8)和(2.9)可简化为

和

因此, KKT 条件(2.12)和(2.13)亦可进一步简化为

和

由此可得

此表明 $L_\beta(w_k)$ 在 $u_k$ 处沿方向 $(d_k^x,d_k^y)$ 有良好的下降性.

关于 QP 子问题(2.16)和(2.17)解的基本性质, 由^{[19,推论 3.6]}有如下引理.

引理 2.1 设由(2.10)和(2.11)式产生的矩阵 $B^{x}_{k}$ 和 $B^{y}_{k}$ 在~$\mathbb{R} ^{n_1}$ 和 $\mathbb{R} ^{n_2}$ 正定, 则 QP 子问题(2.16)和(2.17)均有唯一最优解, 且最优解与其 KKT 点等同.

基于以上分析, 现给出算法的具体步骤.

算法 2.1

步骤0 (初始化) 选取参数 $\rho,\ \sigma\in(0,1),\ \beta,\ \xi>0$. 初始迭代点 $w_{0}=(x_{0},y_{0},\lambda_{0})\in {\mathcal X} \times {\mathcal Y} \times\mathbb{R} ^{m}$, 初始对称正定矩阵 $B_{0}^{x}$ 和 $B_{0}^{y}$. 置 $k:=0.$

步骤 1 (求解 QP 子问题) 求解两个 QP 子问题 (2.16) 和 (2.17), 产生 (唯一) 最优解 $\tilde{x}_{k+1}$ 和 $\tilde{y}_{k+1}.$

步骤 2 (产生搜索方向) 按

产生搜索方向 $d^{u}_k$. 若 $d^{u}_k=0, $$h(x_k,y_k)=0$, 则 $(x_{k},y_{k})$ 为问题(1.1)的 KKT 点, 停止. 否则进入步骤 3.

步骤 3 (采用 Armijo 线搜索) 计算 $\{t = \sigma^{i}:i=0,1,2,\cdots \}$ 满足

的最大值 $t_{k}.$

步骤 4 (更新) 产生新的迭代点, 即

步骤 5 (计算新矩阵 $B_{k+1}^{x}$ 和 $B_{k+1}^{y}$) 通过(2.10)和(2.11)式产生新的对称阵 $B_{k+1}^{x}$ 和 $ B_{k+1}^{y},$ 使得 $B_{k+1}^{x}\succ 0, B_{k+1}^{y}\succ 0.$令 $k:=k+1,$ 返回步骤 1.

下面引理给出算法2.1的适定性和单调性.

引理 2.2 算法2.1的迭代是适定的, 步长 $t_k>0$, 且序列 $\{L_{\beta}(w_k)\}$ 具有单调性

证 首先, 由 $B^{x}_{k}$ 和 $B^{y}_{k}$ 的正定性及引理2.1知, 算法所求解的两个 QP 子问题有唯一最优解. 其次, 当 $d_u^k=0$ 时, 显然, 单位步长 1 满足线搜索不等式. 否则, 由 Taylor 展式及 (2.20) 和 (2.21)式的下降性可知

其中矩阵 $B_k={\rm diag}(B_k^x,B_k^y)$. 故当 $t$ 为充分小的正数时, 线搜索不等式(2.23)成立. 因此, 算法2.1是适定的.

为证不等式(2.25). 首先, 由 $L_\beta(x,y,\lambda)$ 的定义(1.2)有

则由(2.23),(2.24b)及(2.27), 有

故不等式(2.25)获证.

引理 2.3 若由(2.22)式定义的方向 $d^{x}_{k}=0$ 和 $d^{y}_{k}=0$, 以及 $h(x_k,y_k)=0$, 则当前迭代点 $(x_{k},y_{k})$ 为问题 (1.1) 的 KKT 点, 对应的乘子向量为 $(\lambda_{k},{\alpha}_{k}^{x},{\gamma}_{k}^{x},{\alpha}_{k}^{y},{\gamma}_{k}^{y}).$

证 由 $d^{x}_k=0$, $d^{y}_k=0$, $h(x_k,y_k)=0$, 以及公式 (2.14), (2.15) 和 (2.22) 知

再结合 KKT 条件(2.18),(2.19)及(2.29)得

故 $(x_{k},y_{k})$ 为问题 (1.1) 的 KKT 点, 对应的乘子为 $(\lambda_{k},{\alpha}_{k}^{x},{\gamma}_{k}^{x},{\alpha}_{k}^{y},{\gamma}_{k}^{y}).$

如果算法2.1有限步终止于 $(x_k,y_k)$, 故由引理2.3及算法步骤 2 知迭代点 $(x_k,y_k)$ 是问题 (1.1) 的一个 KKT 点. 下面将假设算法 2.1 产生一个无限迭代序列 $\{(x_k,y_k)\}$, 证明该序列的任意一个聚点 $(x_*,y_*)$ 是问题 (1.1) 的一个 KKT 点, 即证明算法2.1的全局收敛性. 为此, 记 QP 子问题(2.16)和(2.17)在其最优解 $\tilde{x}_{k+1}$ 和 $\tilde{y}_{k+1}$ 处关于不等式约束的积极集分别为

其中 $I=\{1,\cdots, m_1\},\ J= \{1,\cdots, m_2\}$, $C_i$ 和 $D_j$ 分别为矩阵 C 和 D 的第 $i$ 个和第 $j$ 个行向量.进而定义相应的子矩阵

为获得算法 2.1 的全局收敛性, 需如下的常规假设.

假设 1 (i) 函数 $f(x,y),\ h(x,y)$ 均是一阶连续可微的, 即光滑的;

(ii) 对于算法 2.1 产生的序列 $\{w_k\}$ 的每个有界子序列 $\{w_k\}_{\cal K}:= \{w_k: k\in {\cal K}\}$, 矩阵子列 $\{B^x_k\}_{\cal K}$ 和 $\{B^y_k\}_{\cal K}$ 有界, 且一致正定, 即存在正数 $\eta$, 使得

假设 2 对于算法 2.1 产生的序列 $\{w_k\}$ 的每个有界子序列 $\{w_k\}_{\cal K}$, $k\in {\cal K}$ 充分大时, 矩阵 $C_{\tilde{I}_{k}}$ 和 $D_{\tilde{J}_{k}}$ 均是行满秩的, 此等价于矩阵 $G_k$ 行满秩.

假设 2 的作用是保证乘子序列 $\{(\alpha^x_k, \gamma^x_k, \alpha^y_k, \gamma^y_k)\}$ 的有界性. 其一个易于检验的充分条件是: 对于问题(1.1)的每个部分可行点 $(x,y)\in {\cal X}\times {\cal Y}$, 不等式约束中积极约束的梯度向量线性无关. 特别地, 当 $C$ 及 $D$ 均为单位阵, 假设 2 成立.

引理 3.1 设算法 2.1 产生的点列 $\{w_k\}$ 的子序列 $\{w_k\}_{\cal K}$ 有界且假设 1 和 2 成立, 则相应的子序列 $\{d^{u}_{k}\}_{{\cal K}}, $$\{u_{k+1}\}_{{\cal K}}$ 及 $\{({\alpha}_{k}^{x},{\alpha}_{k}^{y}, {\gamma}_{k}^{x},{\gamma}_{k}^{y})\}_{{\cal K}}$ 均有界.

证 首先, 注意到 $x_k$ 和 $\tilde{x}_{k+1}$ 分别为(2.16)式的可行解和最优解, 并结合(3.3)式, 有$q_{k}^{f}\left(x_{k}\right)=0 \geqslant q_{k}^{f}\left(\tilde{x}_{k+1}\right)=\nabla_{x} L_{\beta}\left(w_{k}\right)^{\top} d_{k}^{x}+\frac{1}{2}\left\|d_{k}^{x}\right\|_{B_{k}^{x}}^{2} \geqslant-\left\|\nabla_{x} L_{\beta}\left(w_{k}\right)\right\|\left\|d_{k}^{x}\right\|+\frac{1}{2} \eta\left\|d_{k}^{x}\right\|^{2}$又由 $\{w_{k}\}_{\cal K}$ 的有界性及 $f$ 和 $h$ 的一阶连续可微性知, 存在常数 $M > 0$, 使得 $\|\nabla_x L_{\beta}(w_k)\| \leqslant M,$$ \forall\ k \in {\cal K}.$此结合上式得 $\|d^x_k\| \leqslant 2M/\eta$, 此不等式蕴含 $\{d^x_k\}_{\cal K}$ 有界.同理可证 $\{d_{k}^{y}\}_{{\cal K}}$ 有界. 因此 $\{d_{k}^{u}\}_{{\cal K}}$ 有界, 并且 $\left\{u_{k+1}:=u_{k}+t_{k} d_{k}^{u}\right\}_{{\cal K}}$ 有界.

其次, 由 KKT 条件(2.18a),(2.19a),(3.1)和(3.2),可得

进而, 由假设 2 可得

再根据假设 1 知 $\{({\alpha}_{k}^{x}-{\gamma}_{k}^{x})\}_{{\cal K}}, \{{(\alpha}_{k}^{y}-{\gamma}_{k}^{y})\}_{{\cal K}}$ 有界, 且 ${\alpha}_{k}^{x}\perp{\gamma}_{k}^{x},{\alpha}_{k}^{y}\perp{\gamma}_{k}^{y}$.故

因此序列 $\{{\alpha}_{k}^{x}\}_{{\cal K}}$ 和 $\{{\alpha}_{k}^{y}\}_{{\cal K}}$ 有界. 进而序列 $\{{\gamma}_{k}^{x}\}_{{\cal K}}$ 和 $\{{\gamma}_{k}^{y}\}_{{\cal K}}$ 有界. 引理获证.

现假设 $w_*$ 是序列 $\{w_k\}$ 的一个聚点, 则存在一个无限子序列 ${\cal K}$ 使得 $w_*=(x_*, y_*, \lambda_*)\in \Omega \neq \emptyset$. 由引理 3.1 知, 有

引理 3.2 设假设1成立, 算法2.1产生的点列$\{w_k\}$ 有聚点, 其聚点集 (记为 $\Omega$) 非空, 则

(i) 数列 $\{L_{\beta}(w_k)\}$ 整列收敛, 且

因此, 目标函数 $f(x,y)$ 在迭代序列 $\{w_k\}$ 的聚点集$\Omega$ 上取常数值;

(ii) $\lim\limits_{k\rightarrow \infty}h{(u_k)}=0$, $\lim\limits_{k\rightarrow \infty}t_k\|d^x_k\|^2=0$, $\lim\limits_{k\rightarrow \infty}t_k\|d^y_k\|^2=0$;

(iii) 对于每个收敛子列 $\{w_k\}_{\cal K}$, 有 $\lim\limits_{k\in {\cal K}}(d^x_k, d^y_k)=(0,0).$

证 先证结论 (i) 和 (ii). 首先, 由(2.25)和(3.4)式以及 $L_\beta(\cdot)$ 的连续性知, 数列 $\{L_\beta(w_k)\}$ 整列单调下降, 且有收敛子列 $\{L_\beta(w_k)\}_{{\cal K}}$. 进而由 ^{[17,定理 1.1.5]} 知, $\{L_\beta(w_k)\}$整列收敛. 其次, 由其单调下降性和连续性知, $\lim\limits_{k\rightarrow \infty} L_{\beta}(w_k)= \inf\limits_k L_{\beta}(w_k)= L_{\beta}(w_*).$ 令 $k \rightarrow \infty$, 对不等式 (2.25) 取极限, 并结合 (3.3)式, $\{L_\beta(w_k)\}$ 收敛及 $\xi > 0$, 可知结论(ii)成立. 最后, 由 $\lim\limits_{k\rightarrow \infty}h{(u_k)}=0$ 有 $L_{\beta}(w_*)=f(x_*, y_*)$. 因此, 结论 (i) 成立.

下面证明结论 (iii). 先证 $d^u_*=0$. 若不然, 则存在 $k_0 \in {\cal K},$ 使得 $\|d^u_k\|> 0,\ \forall\ k \in {\cal K}_0:=\{k\in {\cal K}: k\geqslant k_0\}$. 往证 $t_*:=\inf\{t_k,\ k\in {\cal K}_0\}>0$. 由 Taylor 展式, $\{(x_{k}, y_k, d^u_k, \lambda_{k})\}_{{\cal K}}$ 的有界性及(2.20), (2.21) 和 (3.3) 式可知, 对于所有的 $k \in {\cal K}_0$ 及充分小的正数 $t$, 有

此结合线搜索不等式 (2.23) 可知 $t_* > 0$ 成立. 于是, $t_k\|d^u_k\|^2 \geqslant t_*\|d^u_*\|^2/4> 0,\ \forall\ k \in {\cal K}_0$. 这与 $\lim\limits_{k \rightarrow \infty} t_k\|d^u_k\|^2=0 $ 矛盾, $d^u_*=0$ 获证. 引理证毕.

基于引理 3.1 和 3.2, 下面论证算法 2.1 的全局收敛性.

定理 3.1 设假设 1 和 2 成立, 则算法 2.1 或有限次迭代终止于问题 (1.1) 的 KKT 点 $(x_{k},y_{k})$, 或产生一个无穷迭代点列 $\{w_{k}\}$, 使得其任意聚点 $w_{*}=(x_{*},y_{*},\lambda_{*})$ 中的 $(x_{*},y_{*})$ 是问题 (1.1) 的 KKT 点, 且存在指标集 ${\cal K}$, 使得 $\{(w_{k},{\alpha}_{k}^{x},{\gamma}_{x}^{k},{\alpha}_{k}^{y},{\gamma}_{k}^{y})\}_{{\cal K}}$ 收敛到 KKT 点对 $(w_{*},{\alpha}_{*}^{x},{\gamma}_{*}^{x},{\alpha}_{*}^{*},{\gamma}_{*}^{y}),$ 即算法是全局收敛的.

证 对于给定聚点 $w_{*}$, 由引理 3.1 知, 存在无穷迭代指标集 ${\cal K}$, 使得

由引理3.2知 $d^u_{*}=0,$ 进而

在KKT条件(2.18),(2.19)中对 $k\stackrel{{\cal K}}\longrightarrow\infty$ 取极限, 得

此说明 $(x_{*},y_{*})$ 为问题 (1.1) 的 KKT 点, 相应的乘子为 $(\lambda_{*},{\alpha}^{x}_{*},{\gamma}^{x}_{*},{\alpha}^{y}_{*},{\gamma}^{y}_{*}).$ 定理证毕.

为验证本文所设计算法 2.1 的有效性, 将用于求解一类具有可分和不可分结构的非凸数学模型. 鉴于文献[22] 的算法是求解非凸可分优化问题, 首先将算法 2.1 与其进行数值比对. 所有测试程序代码均在MATLAB 2016b 上编写执行, 电脑配置为 Intel(R) Core(TM) i5-10210U, CPU 1.60 GHz, RAM 8.00 GB, Windows 10.0 (64 位).

$\bullet$ 算例的构造: 由文献[22] 两分块优化例子 (6.1) 式拓展为以下形如 (1.1) 的非凸不可分光滑优化算例 (其中 $\tau\geqslant 5$, sign($\cdot$) 为符号函数)

其中

$M$ 为 $2\tau$ 阶待定矩阵, $c\in \mathbb{R} ^{2\tau}$ 和 $a_i\in \mathbb{R} $ 为选定参数.

显然, 当$M=0_{2\tau},\ c=0,\ a_i=0\ (i=6,\cdots,\tau)$ 时, 算例(4.1) 退化为文献[22]中算例(6.1). 特别地, 当 $\tau=5$ 时, 上述算例进一步退化为文献[23]中的算例 HS118, 此例子是一个凸二次规划, 其最优解和最优值是已知的, 即

将不可分模型(4.1)按 $\tilde{x}$ 和 $\tilde{y}$ 的变量分为两块, 该模型可重组为问题(1.1), 并用算法2.1对其进行数值测试.

算法 2.1 所选取的参数、初始迭代点以及罚参数 $\beta$ 的修正策略均与文献[22] 中算法 QCQP-SSQP 一致, 即

$\bullet$ 参数选取: $\rho=0.1,\ \sigma=0.5,\ \xi=0.001$.

$\bullet$ 初始迭代点:

$\bullet$ 罚参数 $\beta$ 的修正策略:

算法 QCQP-SSQP 用 $\min\{1000,\ 1.5\beta\}$ 来更新罚参数 $\beta$, 算法 2.1 用 $\min\{1000,\ 4.5\beta\}$ 来更新 $\beta$.

$\bullet$ 终止准则及精度: 算法 2.1 及算法 QCQP-SSQP 采用终止准则

其中精度 $\epsilon=10^{-8}$.

本文采取类似于文献[22] 中的方式产生 $B^x_{k}$ 和$B^y_{k}$, 即

其中正定化映射 ${\rm PD}_{\varsigma}(B): {\cal S}^{n_1} \rightarrow {\cal S}^{n_1}_{+}$ 或 ${\cal S}^{n_2} \rightarrow {\cal S}^{n_2}_{+}$,

其中, ${\cal S}^n$ 表示 $n$ 阶对称阵, $\lambda_{\rm min}(B)$ 为矩阵 $B$ 的最小特征值, $E_n$ 是 $n$ 阶单位阵, $\varsigma$ 是一个充分小的正数, 试验中取 $\varsigma=0.0001$.

下面测试算法 2.1 当算例 (4.1) 中 $M=0_{2\tau},\ c=0$ 及$a_i=0\ (i=6,\cdots,\tau)$ 的数值效果, 即测试算法 2.1 非凸可分优化情形, 为检验算法的数值有效性和精准性, 与算法 QCQP-SSQP 进行比较.

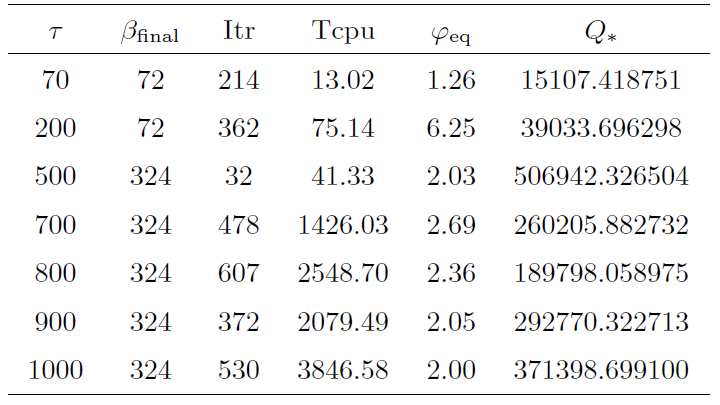
$\bullet$ 数值结果及分析: 数值结果于表1, 其中 Itr 表示迭代次数, Tcpu 表示算法运行时间(单位为秒), $Q_{*}$ 为所求得的目标最优值. 程序终止时的(近似)最优解 $(x^*,y^*)$ 关于等式约束的可行性度量为$\label{phieq} \varphi_{\rm eq}:=\| h(x^*,y^*)\|_{\infty},$$\beta_{\rm final}$ 表示程序终止时的罚参数.从表1的实验结果, 可得到如下结论:

(i) 当 $\tau=5$ 时, 算法 2.1 能够在较少迭代次数和较短时间内求得十分接近已知最优值 $Q((\tilde{x},\tilde{y})^*_{\tau=5})=664.820455$ 的近似最优解.

(ii) 对于 $\tau>5$ 的算例, 算法 2.1 和算法 QCQP-SSQP 所求近似最优值 $Q_*$ 基本相近, 但算法 2.1 在算法终止时的等式约束可行性度量$\varphi_{\rm eq}$ 总体表现更佳.

(iii) 当问题规模较大 ($\tau\geqslant 600$) 时, 不论是算法迭代次数 Itr, 还是运行时长 Tcpu, 本文算法 2.1 都优于算法 QCQP-SSQP.

由于本文所设计的算法是求解具有不可分结构的非凸优化问题(1.1), 故进一步测试算法2.1求解具有不可分情形的算例(4.1), 取 $M=E_{2\tau}$ (单位阵), $c=(1,\cdots,1)$, $a_i= 1$.

$\bullet$ 数值结果及分析: 相关数值实验结果于表2所示. 在此部分的数值试验中, 算法 2.1 测试了算例对应于不同 $\tau$ 值的例子, 从运算时间成本和关于等式约束的精度看, 算法 2.1 的数值效果尚佳. 因此, 本文所设计的算法 2.1 是有效的.

本文针对目标函数和约束函数带不可分结构的大规模非凸优化问题, 提出一种新型且高效的分裂序列二次规划算法. 在常规假设下, 获得了该算法的全局收敛性. 通过对构造的数学算例进行测试, 包括非凸可分和不可分优化问题, 数值结果表明本文设计的新算法是有效的.