数学物理学报, 2023, 43(4): 1170-1178

二维范德瓦尔斯气体磁流体绕凸拐角的超声流动

王可凤,, 由守科,*

新疆大学数学与系统科学学院 乌鲁木齐 830017

Supersonic Flow of Two-dimensional Van Der Waals Gas Magnetic Fluid Around Convex Corner

Wang Kefeng,, You Shouke,*

College of Mathematics and System Science, Xinjiang University, Urumqi 830017

通讯作者: *由守科, E-mail: youshouke2008@163.com

收稿日期: 2022-06-27   修回日期: 2023-02-13  

基金资助: 国家自然科学基金(11961063)
新疆维吾尔自治区自然科学基金(2021D01C003)

Received: 2022-06-27   Revised: 2023-02-13  

Fund supported: NSFC(11961063)
Natural Science Foundation of Xinjiang Uygur Autonomous Region(2021D01C003)

作者简介 About authors

王可凤,E-mail:wangkefeng0215@163.com

摘要

该文研究了二维等熵范德瓦尔斯气体磁流体绕凸拐角的超声流动问题. 根据超声速来流比容的取值, 对凸拐角处的流动进行分类讨论, 证明了超声速来流通过中心稀疏波、声速激波或它们构成的复合波绕过凸拐角, 并得到了出现真空现象的临界角度.

关键词： 凸拐角; 范德瓦尔斯气体; 复合波; 真空

Abstract

In this paper, we study the supersonic flow of two-dimensional isentropic van der Waals magnetic fluid around convex corners. According to the value of the specific volume of the incoming flow, the flow at the convex corner is discussed by classification. It is shown that the supersonic incoming flow can turn the convex corner by a centered rarefaction wave, a sonic shock or a composite wave of them, and the critical angle of the corner corresponding to the appearance of the vacuum phenomenon is obtained.

Keywords： Convex corner; Van der Waals gas; Composite wave; Vacuum.

PDF (445KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

王可凤, 由守科. 二维范德瓦尔斯气体磁流体绕凸拐角的超声流动[J]. 数学物理学报, 2023, 43(4): 1170-1178

Wang Kefeng, You Shouke. Supersonic Flow of Two-dimensional Van Der Waals Gas Magnetic Fluid Around Convex Corner[J]. Acta Mathematica Scientia, 2023, 43(4): 1170-1178

1 引言

气体绕凸拐角的流动问题是气体动力学研究领域的一个重要问题, 受到国内外众多学者的青睐. 早在上世纪40年代中期, Courant和Friedrichs[1]证明了多方气体等熵无旋定常超声速水平来流可以通过中心稀疏波绕过凸拐角流动. 在Courant和Friedrichs研究的推动下, 近年来气体绕凸拐角流动问题的研究进展迅速, 内容主要涉及凸拐角处简单波的构造、真空扩散问题等. 在中心简单波的构造方面, Sheng和You[2]、Sheng和Yao[3]分别构造了多方气体和等温气体超声速流在凸拐角处的中心稀疏波和中心压缩波, 证明了常状态超声速来流可通过中心稀疏波或压缩波绕过凸拐角. 气体绕凸拐角流动问题的研究进一步推动了管口射流问题的研究, 相关研究参见文献[4⇓-6]等. 在气体向真空扩散研究方面, Sheng和You[7]利用特征分解和先验估计方法证明了凸拐角处多方气体等熵无旋拟定常超音速常状态来流向真空扩散问题整体解的存在性. 此后, Lai和Sheng[8]进一步完成了常状态来流是声速或亚声速情形整体解的存在性证明.更多关于气体绕凸拐角向真空扩散问题的研究可参考文献[9-10]等.

本文主要研究二维等熵无旋定常范德瓦尔斯气体磁流体绕凸拐角的超声流动问题, 流体满足方程组[11]

$ \begin{equation}\left\{\begin{array}{l} (\rho u)_x+(\rho v)_y=0,\\ \rho(uu_x+vu_y)+(p_{\rho}+\mu HH_{\rho})\rho_x=0,\\\rho(uv_x+vv_y)+(p_{\rho}+\mu HH_{\rho})\rho_y=0, \end{array}\right. \end{equation}$

其中$\vec{q}=(u,v)$表示速度, $\mu$是磁导率常数, $\rho$为密度, 沿着流线有$H=k_0 \rho,k_0$为常数, $p$是气体压力. 等熵范德瓦尔斯气体状态方程为

$\begin{equation} \displaystyle p=p(\tau)=\frac{A}{(\tau-b)^{\delta+1}}-\frac{a}{\tau^2}, \end{equation} $

其中$\tau=\frac{1}{\rho}$ 表示比容, $A, a, b$为正常数, $a$表示粒子间的吸引力, $b$代表气体中分子的压缩极限, $\delta$ 为大于0小于1的常数.

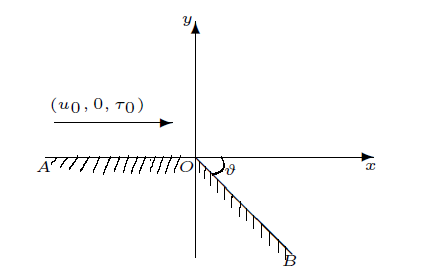
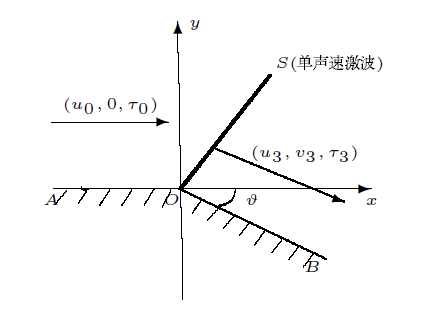
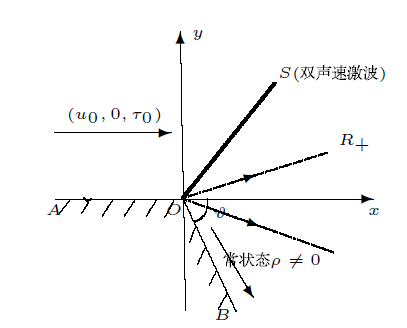
如图1所示, 水平固壁$AO$和倾斜固壁$OB$构成凸拐角$AOB$, 拐角角度为$\vartheta(\vartheta<0)$. 范德瓦尔斯气体磁流体水平超声速常状态来流$(u_0,0,\tau_0)$沿固壁$AO$流动, 其中$u_0>0$. 研究的问题是来流$(u_0,0,\tau_0)$如何绕过凸拐角$AOB$沿固壁$OB$流动.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   绕凸拐角的超声速流动问题


为方便研究, 类似文献[12], 做以下基本假设.

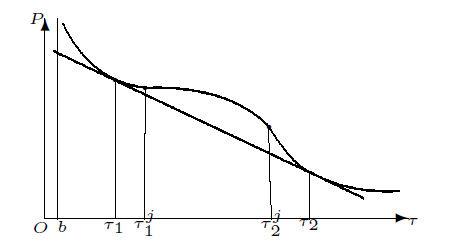
(H$_1$) 函数$P(\tau)=p(\tau)+\frac{\mu}{2}H^2$在$(\tau,P)$ -平面上的图像只有两个拐点$\tau_1^j,\tau_2^j$ (见图2), 满足

$\begin{equation} p''(\tau_1^j)+3\mu k_0^2(\tau_1^j)^{-4}=p''(\tau_2^j)+3\mu k_0^2(\tau_2^j)^{-4}=0,uad b<\tau_1^j<\tau_2^j,\\[5pt]\end{equation}$

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   在$\tau-P$平面的$P(\tau)$曲线


(H$_2$)~ $p'(\tau)<0$, 且当$\tau>\tau_2^j$时,

$\begin{equation} -2\tau p'(\tau)-\tau^2p''(\tau)-\mu k_0^2\tau^{-2}<0.\end{equation}$

在假设(H$_1)$和(H$_2)$成立下, 本文得到以下主要定理.

定理 1.1 当$\tau_0\geq\tau_1$时, 范德瓦尔斯气体磁流体超声速来流$(u_0,0,\tau_0)$通过中心稀疏波$R_+$、 声速激波$S$或者复合波$SR_+$绕过凸拐角以常状态流动, 并且当凸拐角角度$\vartheta <\nu$ 时, 固壁$OB$ 附近出现真空, 其中$\nu=\min\{\hat{\theta},\check{\theta},\bar{\theta}\}$. 这里$\hat{\theta}, \check{\theta}, \bar{\theta}$ 是由来流确定的三个常数.

本文主要内容安排如下: 第二节构造和分析二维等熵无旋定常范德瓦尔斯气体磁流体动力学方程的中心简单波解和声速激波解; 第三部分根据来流比容取值, 分情况构造超声速来流绕过凸拐角的流动结构, 并给出了真空现象发生的拐角条件.

2 中心简单波解与声速激波解

为讨论范德瓦尔斯气体磁流体绕凸拐角的流动问题, 本节构造方程组(1.1)的中心简单波解与声速激波解.

首先, 为构造中心简单波解, 对方程组(1.1)做自相似变换$\xi=\frac{y}{x}$得到

$\begin{equation} \left(\begin{array}{cccc}-\xi & 1 &-\tau^{-1}(v-\xi u)\\v-\xi u& 0 &\tau^{-1}(c^2+\mu k_0^2\tau^{-1})\xi\\0& v-\xi u& -\tau^{-1}(c^2+\mu k_0^2\tau^{-1})\\\end{array}\right)\left(\begin{array}{cccc}{\rm d}u\\{\rm d}v\\{\rm d}\tau\\\end{array}\right)=\left(\begin{array}{cccc}0\\0\\0\\\end{array}\right),\end{equation}$

其中$c=\sqrt{-\tau^2 p'(\tau)}$为声速, $\sqrt{c^2+\mu k_0^2\tau^{-1}}$ 为磁声速. 当$q=\sqrt{u^2+v^2}>\sqrt{c^2+\mu k_0^2\tau^{-1}}$ 时, 磁流体为超声速流体; 当$q=\sqrt{c^2+\mu k_0^2\tau^{-1}}$ 时, 磁流体为声速流体; 当$q<\sqrt{c^2+\mu k_0^2\tau^{-1}}$ 时, 磁流体为亚声速流体.考虑方程组(2.1)的非常数解, 令

$\begin{equation}\left|\begin{array}{cccc}-\xi & 1 &-\tau^{-1}(v-\xi u)\\v-\xi u& 0 &\tau^{-1}(c^2+\mu k_0^2\tau^{-1})\xi\\0& v-\xi u &-\tau^{-1}(c^2+\mu k_0^2\tau^{-1})\\\end{array}\right|=0,\end{equation}$

则

$\begin{equation} \displaystyle (v-\xi u)[(v-\xi u)^2-(c^2+\mu k_0^2\tau^{-1})(\xi^2+1)]=0.\end{equation}$

当磁流体为超声速流体时, 方程(2.3)有三个不等实根

$\xi=\frac{v}{u}=:\lambda_0 $

和

$\begin{equation} \xi=\frac{uv\pm\sqrt{c^2+\mu k_0^2\tau^{-1}}\sqrt{u^2+v^2-c^2-\mu k_0^2\tau^{-1}}}{u^2-c^2-\mu k_0^2\tau^{-1}}=:\lambda_\pm.\end{equation}$

将(2.4)式代入(2.1)式可得

$\begin{equation}\left\{ \begin{array}{lll} {\rm d}u=-\lambda_\pm {\rm d}v,\\(\lambda_\pm u-v){\rm d}v=\tau(p'(\tau)-\mu k_0^2\tau^{-3}){\rm d}\tau, \end{array}\right.\end{equation}$

称微分方程组(2.5)在$(u,v,\tau)$空间中的积分曲线为中心简单波曲线, 记为$R_\pm$. 若$R_\pm$过点$(\bar{u},\bar{v},\bar{\tau})$, 则记为$R_\pm(\bar{u},\bar{v},\bar{\tau})$.

引理 2.1 若$\tau>\tau_2^j$, 则沿着$R_+$有$\frac{{\rm d}\lambda_+}{{\rm d}\tau}<0$ 成立, 而沿着$R_-$ 有$\frac{{\rm d}\lambda_-}{{\rm d}\tau}>0$成立.

证 首先考虑满足$\tau>\tau_2^j$的中心稀疏波$R_+$. 因为$\lambda_+$ 满足

$(v-\lambda_+u)^2-(c^2+\mu k_0^2\tau^{-1})(1+\lambda_+^2)=0.$

所以两边对$\tau$求导可得

$\begin{equation} \frac{{\rm d}\lambda_+}{{\rm d}\tau}=\frac{(v-\lambda_+ u)(\frac{{\rm d}v}{{\rm d}\tau}-\lambda_+\frac{{\rm d}u}{{\rm d}\tau})-(\sqrt{c^2+\mu k_0^2\tau^{-1}})(\lambda_+ ^2+1)\frac{d(\sqrt{c^2+\mu k_0^2\tau^{-1}})}{{\rm d}\tau}}{u(v-\lambda_+ u)+(c^2+\mu k_0^2\tau^{-1})\lambda_+}.\\\end{equation}$

简单计算可知(2.6)式中的分母满足

$\begin{equation} u(v-\lambda_+ u)+(c^2+\mu k_0^2\tau^{-1})\lambda_+=-\sqrt{c^2+\mu k_0^2\tau^{-1}}\sqrt{u^2+v^2-c^2-\mu k_0^2\tau^{-1}}<0,\end{equation}$

另外, 由(2.5)式可得(2.6)式中的分子满足

$\begin{matrix} & &(v-\lambda_+ u)(\frac{{\rm d}v}{{\rm d}\tau}-\lambda_+\frac{{\rm d}u}{{\rm d}\tau})-(\sqrt{c^2+\mu k_0^2\tau^{-1}})(\lambda_+ ^2+1)\frac{d(\sqrt{c^2+\mu k_0^2\tau^{-1}})}{{\rm d}\tau}\\ &=&(\lambda_+^2+1)(\frac{1}{2}\tau ^{2}p''(\tau)+\frac{3}{2}\mu k_0^2\tau^{-2})>0.\end{matrix}$

联立(2.6)、(2.7)和(2.8)式可得

$\begin{equation} \displaystyle \frac{{\rm d}\lambda_+}{{\rm d}\tau}<0.\end{equation}$

同理,可证明当$\tau>\tau_2^j$时, 沿$R_-$有$\frac{{\rm d}\lambda_-}{{\rm d}\tau}>0$成立. 证毕.

引理 2.2 若$\tau_1<\tau_0<\tau_2^j$, 则方程组(1.1)存在波前为$(u_0,0,\tau_0)$、波后为$(u_3,v_3,\tau_3)$ 的单声速激波解$S$, 其中

$\arctan{\frac{v_3}{u_3}}<0,$
$u_3=\frac{u_0^2\tau_3^2+\tau_0(\tau_3-\tau_0)(-\tau_3^2p'(\tau_3)+\mu k_0^2\tau_3^{-1})}{u_0\tau_3^2},$
$v_3=\frac{(\tau_0-\tau_3)\sqrt{(-\tau_3^2p'(\tau_3)+\mu k_0^2\tau_3^{-1})(u_0^2+\tau_0^2(p'(\tau_3)-\mu k_0^2\tau_3^{-3}))}}{u_0\tau_3},$

$\tau_{3}$ 为介于$\tau_2^j$ 和$\tau_2$ 之间的一个常数, 且满足$p'(\tau_3)-\mu k_0^2\tau_3^{-3}=\frac{p(\tau_3)+\frac{\mu}{2}k_0^2\tau_3^{-2}-p(\tau_0)-\frac{\mu}{2}k_0^2\tau_0^{-2}}{\tau_3-\tau_0}.$

证 由假设(H$_1$)可知存在$\tau_{3}\in(\tau_2^j,\tau_2)$ 满足

$\begin{equation} p'(\tau_3)-\mu k_0^2\tau_3^{-3}=\frac{p(\tau_3)+\frac{\mu}{2}k_0^2\tau_3^{-2}-p(\tau_0)-\frac{\mu}{2}k_0^2\tau_0^{-2}}{\tau_3-\tau_0}. \end{equation} $

构造连接常状态$(u_0,0,\tau_0)$和$(u_3,v_3,\tau_3)$且斜率为$k$的单声速激波(single sonic shock)[15]$S$, 其中$u_3, v_3, k$待定且$k>0$. 设$N_0$和$L_0$分别为速度$(u_0,0)$在垂直和平行于$S$ 方向上的分量, $N_3$和$L_3$分别为速度$(u_3,v_3)$在垂直和平行于$S$方向上的分量. 根据文献[5]和[15], $S$ 满足Rankine-Hugonit条件

$\begin{equation} \left\{\begin{array}{ll} \tau_0^{-1}N_0=\tau_3^{-1}N_3,\\[2mm] \tau_0^{-1}N_0^2+p(\tau_0)+\frac{\mu}{2}k_0^2\tau_0^{-2}=\tau_3^{-1}N_3^2+p(\tau_3)+\frac{\mu}{2}k_0^2\tau_3^{-2},\\ L_0=L_3, \end{array}\right.\end{equation}$

其中

$\begin{equation} N_0=\frac{u_0k}{\sqrt{1+k^2}},uad L_0=\frac{u_0}{\sqrt{1+k^2}},uad N_3=\frac{u_3k-v_3}{\sqrt{1+k^2}},uad L_3=\frac{u_3+v_3k}{\sqrt{1+k^2}}.\end{equation}$

由方程组(2.11)前两式可得

$\begin{equation} \frac{p(\tau_3)+\frac{\mu}{2}k_0^2\tau_3^{-2}-p(\tau_0)-\frac{\mu}{2}k_0^2\tau_0^{-2}}{\tau_3-\tau_0}=-\tau_3^{-2}N_3^2.\end{equation}$

联立(2.10)和(2.13)式可得

$\begin{equation} N_3=\sqrt{-\tau_3^2p'(\tau_3)+\mu k_0^2\tau_3^{-1}},\end{equation}$

故$S$为单声速激波[15].根据方程组(2.11)的第一式和(2.14)式可得

$\begin{equation} N_0=\frac{\tau_0\sqrt{-\tau_3^2p'(\tau_3)+\mu k_0^2\tau^{-1}_3}}{\tau_3},uad L_0=\frac{\sqrt{\tau_3^2u_0^2+\tau_0^2\tau_3^2p'(\tau_3)-\tau_0^2\mu k_0^2\tau_3^{-1}}}{\tau_3},\end{equation}$

从而

$\begin{equation} k=\frac{\tau_0\sqrt{-\tau_3^2p'(\tau_3)+\mu k_0^2\tau_3^{-1}}}{\sqrt{\tau_3^2u_0^2+\tau_0^2\tau_3^2p'(\tau_3)-\tau_0^2\mu k_0^2\tau_3^{-1}}}.\end{equation}$

联立(2.12)、(2.14)、(2.15)、(2.16)四式可得

$u_3=\frac{u_0^2\tau_3^2+\tau_0(\tau_3-\tau_0)(-\tau_3^2p'(\tau_3)+\mu k_0^2\tau_3^{-1})}{u_0\tau_3^2},$
$v_3=\frac{(\tau_0-\tau_3)\sqrt{(-\tau_3^2p'(\tau_3)+\mu k_0^2\tau_3^{-1})(u_0^2+\tau_0^2(p'(\tau_3)-\mu k_0^2\tau_3^{-3}))}}{u_0\tau_3}.$

因为$\tau_0<\tau_3$, 所以$\arctan{\frac{v_3}{u_3}}<0$. 证毕.

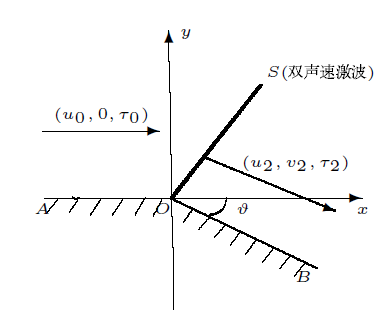
引理 2.3 若$\tau_0=\tau_1$, 则方程组(1.1)存在波前为$(u_0,0,\tau_0)$、$波后为$(u_2,v_2,\tau_2)$的双声速激波解$S$, 其中

$\arctan{\frac{v_2}{u_2}}<0,$
$u_2=\frac{u_0^2+\tau_0^2p'(\tau_0)-\mu k_0^2\tau_0^{-1}+\sqrt{(-\tau_0^2p'(\tau_0)+\mu k_0^2\tau_0^{-1})(-\tau_2^2p'(\tau_2)+\mu k_0^2\tau_2^{-1})}}{u_0},$
$v_2=\frac{\sqrt{u_0^2+\tau_0^2p'(\tau_0)-\mu k_0^2\tau_0^{-1}}(\sqrt{-\tau_0^2p'(\tau_0)+\mu k_0^2\tau_0^{-1}}-\sqrt{-\tau_2^2p'(\tau_2)+\mu k_0^2\tau_2^{-1}})}{u_0},$

$\tau_{2}$是大于$\tau_2^j$的一个常数, 且满足

$\begin{equation}p'(\tau_0)-\mu k_0^2\tau^{-3}_0=p'(\tau_2)-\mu k_0^2\tau^{-3}_2=\frac{p(\tau_0)+\frac{\mu}{2}k_0^2\tau_0^{-2}-p(\tau_2)-\frac{\mu}{2}k_0^2\tau_2^{-2}}{\tau_0-\tau_2}.\end{equation}$

证 当$\tau_0=\tau_1$时, 由假设(H$_1$)可知, 存在$\tau_2>\tau_2^j$, 满足(2.17)式. 下面构造连接$(u_0,0,\tau_0)$和$(u_2,v_2,\tau_2)$的双声速激波(double sonic shock)[15]$S$, 其中速度$(u_2,v_2)$待定, $S$ 的斜率为

$\begin{equation} k=\sqrt{\frac{c_0^2+\mu k_0^2 \tau_0^{-1}}{u_0^2-(c_0^2+\mu k_0^2 \tau_0^{-1})}}.\end{equation}$

根据文献[5]和[15], 类似引理2.2的讨论, 该双声速激波满足Rankine-Hugonit 条件

$\begin{equation}\left\{\begin{array}{ll} \tau_0^{-1}N_0=\tau_2^{-1}N_2,\\[2mm]\tau_0^{-1}N_0^2+p(\tau_0)+\frac{\mu}{2}k_0^2\tau_0^{-2}=\tau_2^{-1}N_2^2+p(\tau_2)+\frac{\mu}{2}k_0^2\tau_2^{-2},\\ L_0=L_2.\end{array}\right.\end{equation}$

其中$N_2$和$L_2$分别是速度$(u_2,v_2)$在垂直和平行于双声速激波$S$上的分量. 于是

$\begin{equation} L_0=L_2=\sqrt{u_0^2-N_0^2},uad u_2=\frac{L_0+N_2k}{\sqrt{1+k^2}},uad v_2=\frac{kL_2-N_2}{\sqrt{1+k^2}}.\end{equation}$

根据(2.17)与(2.19)式可得

$\begin{equation} N_0=\sqrt{-\tau_0^2p'(\tau_0)+\mu k_0^2\tau_0^{-1}},uad N_2=\sqrt{-\tau_2^2p'(\tau_2)+\mu k_0^2\tau_2^{-1}}.\end{equation}$

联立(2.18)、(2.20)和(2.21)式可得

$u_2=\frac{u_0^2+\tau_0^2p'(\tau_0)-\mu k_0^2\tau_0^{-1}+\sqrt{(-\tau_0^2p'(\tau_0)+\mu k_0^2\tau_0^{-1})(-\tau_2^2p'(\tau_2)+\mu k_0^2\tau_2^{-1})}}{u_0},$
$v_2=\frac{\sqrt{u_0^2+\tau_0^2p'(\tau_0)-\mu k_0^2\tau_0^{-1}}(\sqrt{-\tau_0^2p'(\tau_0)+\mu k_0^2\tau_0^{-1}}-\sqrt{-\tau_2^2p'(\tau_2)+\mu k_0^2\tau_2^{-1}})}{u_0}.$

根据来流$(u_0,0,\tau_0)$是超声速流可知$u_2>0$, 并且由$\tau_0<\tau_2$和(2.17)式可得$v_2<0$, 故$\arctan\frac{v_2}{u_2}$$<0$. 证毕.

3 绕凸拐角的流动

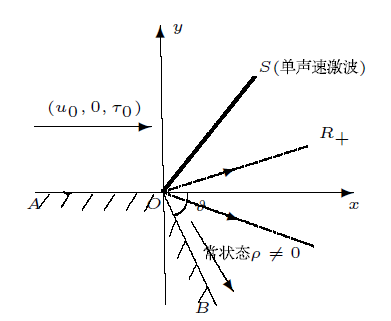
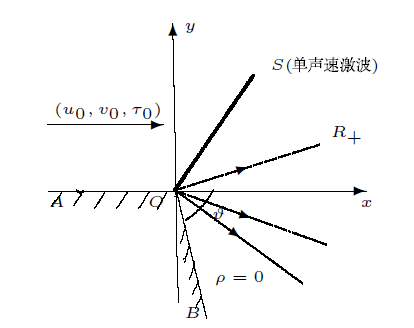
定理 3.1 当$\tau_0\geq\tau_2^j, \vartheta>\hat{\theta}$ 时, 水平超声速来流$(u_0,0,\tau_0)$通过不完全中心稀疏波$R_+$绕过凸拐角以常状态沿固壁$OB$流动, 如图3所示; 当$ \tau_0\geq\tau_2^j, \vartheta\leq \hat{\theta}$ 时, 超声速来流$(u_0,0,\tau_0)$通过完全中心稀疏波$R_+$ 绕过凸拐角并 在固壁$OB$附近出现真空, 如图4所示, 这里

$\hat{\theta}=-\int_{u_0}^{\hat{q}}\frac{\sqrt{\eta^2-c^2(\eta)-\mu k_0^2\tau^{-1}(\eta)}} {\eta\sqrt{c^2(\eta)+\mu k_0^2\tau^{-1}(\eta)}}{\rm d}\eta,uad\hat{q}=\sqrt{u_0^2+2\mu k_0^2 \tau_0^{-1}-2\int_{\tau_0}^{+\infty}\tau p'(\tau){\rm d}\tau}.$

证 第一步 构造波前为$(u_0,0,\tau_0)$的中心稀疏简单波.

根据与常状态相邻的非常状态流动是简单波流动[13], 可在拐角处构造由方程组(2.5)和来流$(u_0,0,\tau_0)$ 确定的中心简单波$R_+(u_0,0,\tau_0)$, $\tau>\tau_0$. 由引理2.1可知沿该中心简单波$\frac{{\rm d}\lambda_+}{{\rm d}\tau}<0$, 即该中心简单波是稀疏波. 为说明磁流体能够通过该中心稀疏波绕过凸拐角沿固壁流动, 需证明流角$\theta$满足 $\frac{{\rm d}\theta}{{\rm d}\tau}<0.$

事实上, 由于该中心稀疏波与常状态来流相邻, 故中心简单波$R_+(u_0,0,\tau_0)$区域为无旋流动区域[14], 可引入黎曼不变量

$\begin{equation} r_+=\theta+\int_{u_0}^q h(\eta){\rm d}\eta, uad r_-=\theta-\int_{u_0}^q h(\eta){\rm d}\eta,\end{equation}$

其中$h(\eta)=\frac{\sqrt{\eta^2-c^2(\eta)-\mu k_0^2\tau^{-1}(\eta)}}{\eta\sqrt{c^2(\eta)+\mu k_0^2\tau^{-1}(\eta)}}.$

由来流$(u_0,0,\tau_0)$和$\bar{\partial}_-r_+=0$, 可得

$\begin{equation} \theta=-\int_{u_0}^{q}h(\eta){\rm d}\eta.\end{equation}$

对(3.2)式两边求导可得

$\begin{equation} \frac{{\rm d}\theta}{{\rm d}q}=-\frac{\sqrt{q^2-(c^2+\mu k_0^2\tau^{-1})}}{q\sqrt{(c^2+\mu k_0^2\tau^{-1})}}<0.\end{equation}$

因为流动是无旋的, 由方程组(1.1)可知伯努利定律为

$\begin{equation}const.=\frac{1}{2}q^2+\int_{\tau_0}^{\tau}\tau p'(\tau){\rm d}\tau+\mu k_0^2\tau^{-1}.\end{equation}$

根据假设(H$_2)$, 由(3.4)式可得

$\begin{equation} \frac{{\rm d}q}{{\rm d}\tau}=\frac{-\tau^2p'(\tau)+\mu k_0^2\tau^{-1}}{\tau q}>0.\end{equation}$

根据(3.3)和(3.5)式可知沿着该中心稀疏波$\frac{{\rm d}\theta}{{\rm d}\tau}<0$.

第二步 确定中心稀疏波$R_+$扩散到真空的流角临界值.

根据来流$(u_0,0,\tau_0)$和伯努利定律(3.4)式可知

$\begin{equation} \lim_{\tau\rightarrow+\infty}\frac{1}{2}q^2(\tau)+\lim_{\tau\rightarrow+\infty}\int_{\tau_0}^\tau\tau p'(\tau){\rm d}\tau+\lim_{\tau\rightarrow+\infty}\mu k_0^2\tau^{-1}=\frac{1}{2}u_0^2+\mu k_0^2\tau_0^{-1},\end{equation}$

解得

$\begin{equation}\lim_{\tau\rightarrow+\infty}q(\tau)=\sqrt{u_0^2+2\mu k_0^2\tau_0^{-1}-2\int_{\tau_0}^{+\infty}\tau p'(\tau){\rm d}\tau}=:\hat{q}.\end{equation}$

由(3.2)式可得对应真空的流角临界角度

$\begin{equation} \hat{\theta}=-\lim_{\tau\rightarrow+\infty}\int_{u_0}^{q(\tau)}h(\eta){\rm d}\eta=-\int_{u_0}^{\hat{q}}h(\eta){\rm d}\eta.\end{equation}$

于是根据(3.3)和(3.5)式可知, 当$\tau>\tau_0$时完全中心稀疏波$R_+(u_0,0,\tau_0)$可抽象的表示为以流角$\theta$为参数的方程

$\begin{equation} u=u(\theta), uad v=v(\theta), uad \tau=\tau(\theta),uad \hat{\theta}\leq\theta\leq 0.\end{equation}$

综上所述, 当$\vartheta> \hat{\theta}$时, 来流通过波前$(u_0,0,\tau_0)$、波后为$(u(\vartheta),v(\vartheta),\tau(\vartheta))$ 的不完全中心稀疏波$R_+$ 绕过凸拐角流动, 如图3所示;当$\vartheta\leq \hat{\theta}$时, 来流$(u_0,0,\tau_0)$通过完全中心稀疏波$R_+$绕过凸拐角并在固壁$OB$附近形成真空, 如图4所示. 证毕.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   不完全中心稀疏波$R_+$,}$\vartheta>\hat{\theta}$


图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   完全中心稀疏波$R_+,$}$\vartheta\leq\hat{\theta}$


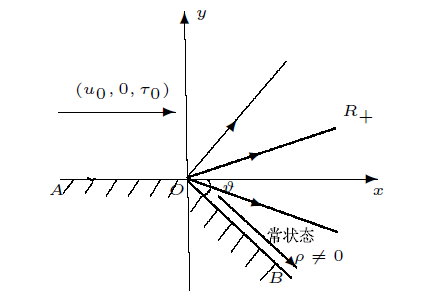
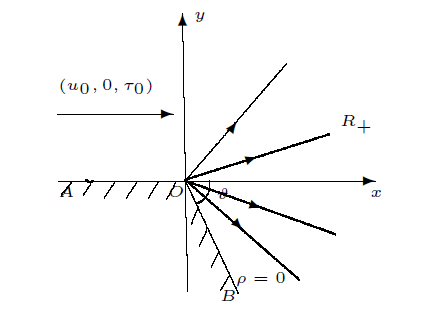
定理 3.2 假若来流比容$\tau_0$满足$\tau_1<\tau_0<\tau_2^j$, 则超声速来流$(u_0,0,\tau_0)$分以下三种情况绕过凸拐角: 当$\vartheta=\arctan\frac{v_3}{u_3}$时, 超声速来流通过波前为$(u_0,0,\tau_0)$、波后为$(u_3,v_3,\tau_3)$的单声速激波$S$绕过凸拐角流动, 如图5所示; 当$\check{\theta}<\vartheta<\arctan{\frac{v_3}{u_3}}$时, 超声速来流通过由单声速激波和不完全中心稀疏波构成的复合波$SR_+$绕过凸拐角, 如图6所示; 当$\vartheta\leq\check{\theta}$时, 超声速来流通过由单声速激波和完全中心稀疏波构成的复合波$SR_+$ 绕过凸拐角, 并在固壁$OB$附近出现真空, 如图7所示. 这里

$\begin{equation} \check{\theta}=\arctan{\frac{v_3}{u_3}}-\int_{q_3}^{\check{q}}h(\eta){\rm d}\eta,\end{equation}$

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   单声速激波$S$


图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   不完全稀疏复合波 $\vartheta>\check{\theta}$


图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   完全稀疏复合波$\vartheta\leq\check{\theta}$


其中

$\begin{equation} \check{q}=\sqrt{q_3^2+2\mu k_0^2\tau_3^{-1}-2\int_{\tau_3}^{+\infty}\tau p'(\tau){\rm d}\tau}.\end{equation}$

证 若$\vartheta=\arctan\frac{v_3}{u_3}$, 则根据引理2.2可知来流通过连接常状态$(u_0,0,\tau_0)$和常状态$(u_3,v_3,\tau_3)$ 的单声速激波绕过凸拐角, 并以常状态$(u_3,v_3,\tau_3)$ 沿固壁流动, 如图5所示.若$\vartheta<\arctan\frac{v_3}{u_3}$, 则可在构造波前为$(u_0,0,\tau_0)$、波后为$(u_3,v_3,\tau_3)$的单声速激波的基础上, 进一步构造波前为$(u_3,v_3,\tau_3)$的中心稀疏波$R_+, \tau>\tau_3$. 类似于定理3.1中的推导, 可求得稀疏波$R_+(u_3,v_3,\tau_3)$稀疏至真空时流角的临界角$\check{\theta}$ 和速度的临界值$\check{q}$, 并且它们分别满足(3.12)和(3.13).所以, 当$\vartheta>\check{\theta}$时, 来流$(u_0,0,\tau_0)$通过不完全稀疏复合波绕过凸拐角, 沿固壁$OB$流动, 如图6所示; 当$\vartheta\leq\check{\theta}$时, 来流可通过由单声速激波和中心稀疏波构成的完全稀疏复合波$SR_+$ 绕过凸拐角, 如图7所示. 证毕.

定理 3.3 假若来流比容$\tau_0=\tau_1$, 则超声速来流$(u_0,0,\tau_0)$分以下三种情况绕过凸拐角: 当$\vartheta=\arctan\frac{v_2}{u_2}$时, 超声速来流通过波前为$(u_0,0,\tau_0)$、波后为$(u_2,v_2,\tau_2)$的双声速激波$S$绕过凸拐角流动, 如图8所示; 当$\bar{\theta}<\vartheta<\arctan{\frac{v_2}{u_2}}$时, 超声速来流通过由双声速激波和不完全中心稀疏波构成的复合波$SR_+$绕过凸拐角, 如图9所示; 当$\vartheta\leq\bar{\theta}$时, 超声速来流通过由双声速激波和完全中心稀疏波构成的复合波$SR_+$绕过凸拐角, 并在固壁$OB$ 附近出现真空, 如图10所示. 这里

$\begin{equation} \bar{\theta}=\arctan{\frac{v_2}{u_2}}-\int_{q_2}^{\bar{q}}h(\eta){\rm d}\eta,\end{equation}$

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   双声速激波$S$


图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   不完全稀疏复合波 $\vartheta>\bar{\theta}$


图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   完全稀疏复合波$\vartheta\leq\bar{\theta}$


其中

$\begin{equation} \bar{q}=\sqrt{q_2^2+2\mu k_0^2\tau_2^{-1}-2\int_{\tau_2}^{+\infty}\tau p'(\tau){\rm d}\tau}.\end{equation}$

证 若$\vartheta=\arctan\frac{v_2}{u_2}$, 则根据引理2.3可知来流通过双声速激波绕过凸拐角, 并以常状态$(u_2,v_2,\tau_2)$沿固壁$OB$流动, 如图8所示.

若$\vartheta<\arctan\frac{v_2}{u_2}$, 则可在构造波前为$(u_0,0,\tau_0)$、波后为$(u_2,v_2,\tau_2)$的双声速激波的基础上, 进一步构造波前为$(u_2,v_2,\tau_2)$的中心稀疏波$R_+(u_2,v_2,\tau_2),\tau>\tau_2$, 利用伯努利定律和黎曼不变量, 类似于定理3.1的证明, 可求得稀疏波$R_+(u_2,v_2,\tau_2)$稀疏至真空时流角的临界角$\bar{\theta}$和速度的临界值$\bar{q}$, 且它们分别满足$(\ref{3.381})$和$(\ref{3.371})$式. 所以, 当$\vartheta>\bar{\theta}$ 时, 来流通过不完全稀疏复合波绕过凸拐角, 以常状态沿固壁$OB$流动, 如图9所示;当$\vartheta\leq\bar{\theta}$时, 来流可通过由双声速激波和中心稀疏波构成的完全稀疏复合波$SR_+$ 绕过凸拐角, 如图10所示. 证毕.

综合定理3.1、定理3.2和定理3.3可知定理1.1成立.

参考文献

Courant R, Friedrichs K. Supersonic Flow and Shock Waves. New York: Interscience, 1948

[本文引用: 1]

Sheng W C, You S K.

The two-dimensional unsteady supersonic flow around a convex corner

Journal of Hyperbolic Differential Equtions, 2018, 15: 443-461

[本文引用: 1]

Sheng W C, Yao A D.

Centered simple waves for the two-dimensional pseudo-steady isothermal flow around a convex corner

Applied Mathematics and Mechanics, 2019, 40(5): 117-130

[本文引用: 1]

Chen S X, Qu A F.

Interaction of rarefaction waves in jet stream

Journal Differential Equations, 2010, 248(12): 2931-2954

DOI:10.1016/j.jde.2010.03.004      URL     [本文引用: 1]

Lai G.

Interaction of fan-jump-fan composite waves in a two-dimensional steady jet for van der Waals gases

Journal of Hyperbolic Differential Equations, 2017, 14(1): 74-134

[本文引用: 3]

Lai G.

Interaction of jump-fan composite waves in a two-dimensional jet for van der Waals gases

Journal of Mathematical Physics, 2015, 56(6): 061504

DOI:10.1063/1.4922443      URL     [本文引用: 1]

Sheng W C, You S K.

Interaction of a centered simple wave and a planar rarefaction wave of the two-dimensional Euler equations for pseudo-steady compressible flow

Journal de Mathématiques Pures et Appliquées, 2018, 114: 29-50

DOI:10.1016/j.matpur.2017.07.019      URL     [本文引用: 1]

Lai G, Sheng W C.

Two-dimensional pseudosteady flows around a sharp corner

Arch Ration Mech Anal, 2021, 241(2): 805-884

DOI:10.1007/s00205-021-01665-0      [本文引用: 1]

Yao A D, Sheng W C.

Two-dimensional pseudo-steady supersonic flow around a sharp corner

Journal of Applied Mathematics and Mechanics, 2022, 102(2): e201800270

[本文引用: 1]

Chen J J, Yin G, You S K.

Expansion of gas by a sharp corner into vacuum for 2-D pesudo-steady compressible magnetohydrodynamics system

Nonlinear Analysis Real World Applications, 2019, 52: 102955

DOI:10.1016/j.nonrwa.2019.06.005      URL     [本文引用: 1]

Chen J J, Sheng W C.

Simple waves of the two dimensional compressible Euler equations in magnetohydrodynamics

Applied Mathematics Letters, 2018, 75: 24-29

DOI:10.1016/j.aml.2017.05.023      URL     [本文引用: 1]

Lai G.

On the expansion of a wedge of van der Waals gas II

Journal Differential Equations, 2016, 260: 3538-3575

DOI:10.1016/j.jde.2015.10.048      URL     [本文引用: 1]

Chen J J, Sheng W C.

Simple waves of the two dimensional compressible Euler equations in magnetohydrodynamics

Applied Mathematics Letters, 2017, 75: 24-49

DOI:10.1016/j.aml.2017.05.023      URL     [本文引用: 1]

Li J Q, Zhang T, Zheng Y X.

Simple waves and a characteristic decomposition of the two dimensional compressible Euler equations

Communications in Mathematical Physics, 2006, 267(1): 1-12

DOI:10.1007/s00220-006-0033-1      URL     [本文引用: 1]

Cramer M S, Sen R.

Exact solutions for sonic shocks in van der Waals gases

Physics of Fluids, 1987, 30(2): 377-385

[本文引用: 5]

/

〈 〉

版权所有 © 《数学物理学报》杂志社
地址： 武汉市71010号信箱(430071)　电话: 027-87199206(中文版)　027-87199087(英文版)
E-mail: actams@apm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发