由人类免疫缺陷病毒(HIV) 引起的艾滋病已成为严重威胁人类健康并在全球范围内迅速蔓延的传染病. 为探索HIV病毒在人体内的感染机制, 寻找防治艾滋病的方法, 数学模型逐渐被用来研究HIV病毒的动力学问题^[1-5]. 文献[1–2] 研究了最基本的HIV感染模型, 之后许多学者对其进行了修改和完善^[3-6]. 文献[3]在考虑饱和发生率和胞内时滞的情况下, 提出了以下HIV感染动力学模型

(1.1) $ \begin{equation} \begin{array}{ll} { } \dot{x}(t) =\lambda-dx(t)-\frac{\beta x(t) v(t)}{1+\alpha v(t)}, \\ { } \dot{y}(t) =\frac{\beta e^{-m\tau} x(t-\tau)v(t-\tau)}{1+\alpha v(t-\tau)}-ay(t), \\ \dot{v}(t) =ky(t)-uv(t), \end{array} \end{equation} $

这里, $ x(t) $、$ y(t) $、$ v(t) $分别表示在$ t $时刻易感靶细胞、被感染靶细胞和游离HIV病毒的浓度, 参数$ \lambda $、$ d $、$ \beta $、$ \alpha $、$ \tau $、$ m $、$ a $、$ k $、$ u $均为正常数. $ \lambda $、$ d $分别表示易感靶细胞的产生率和死亡率, $ \beta $表示易感靶细胞和病毒粒子之间的有效接触率, $ \alpha $表示由游离病毒粒子的拥挤效应产生的抑制效应的恒定速率, $ \tau $表示从病毒进入易感靶细胞到产生新病毒粒子所需的时间, $ e^{-m\tau} $表示被感染靶细胞从$ t-\tau $时刻到$ t $时刻的存活概率, $ a $表示被感染靶细胞的死亡率, $ k $表示每个被感染靶细胞产生游离病毒粒子的平均速率, $ u $表示病毒的清除率.

我们注意到, 模型(1.1) 忽略了宿主体内的CTL免疫反应. 然而, 在病毒感染期间免疫反应是普遍存在的, 是消除或控制病毒增殖的重要途径. 抗体、细胞因子、自然杀伤细胞和T细胞等是免疫反应的重要组成部分. 在大多数病毒感染中, 细胞毒性T淋巴细胞(CTLs) 通过杀死或裂解被病毒感染的靶细胞在细胞免疫中发挥着关键作用^[7]. 因此, 在过去的几十年中, 由CTL介导的细胞免疫受到了广泛关注^{[5, 7-8]}. 基于文献[7], 可以将模型(1.1) 修改为

(1.2) $ \begin{equation} \begin{array}{ll} { } \dot{x}(t) =\lambda-dx(t)-\frac{\beta x(t) v(t)}{1+\alpha v(t)}, \\ { } \dot{y}(t) =\frac{\beta e^{-m\tau} x(t-\tau)v(t-\tau)}{1+\alpha v(t-\tau)}-ay(t)-py(t)z(t)\\ \dot{v}(t) =ky(t)-uv(t), \\ \dot{z}(t) =cy(t)-bz(t), \end{array} \end{equation} $

这里, $ z(t) $表示在$ t $时刻T细胞的浓度, $ p $、$ c $、$ b $都是正常数, $ p $表示T细胞对被感染靶细胞的清除率, $ c $、$ b $分别表示T细胞的产生率和死亡率, 其他变量和参数的意义与模型(1.1) 中相同.

在模型(1.2) 中, 文献[7] 假设细胞免疫过程遵循质量作用原理, 即每个T细胞对被感染靶细胞的清除率是恒定的. 然而, 文献[9] 中的报道表明微寄生虫感染率是随寄生虫剂量增加的增长函数(即, 形状呈S型), 文献[9–11] 中的研究也说明比起简单的双线性函数, 一些非线性函数可以在细胞免疫过程中更好地再现饱和效应. 基于此, 文献[4] 修改了具有CTL免疫反应的病毒感染模型, 用非线性函数$ \frac{p y(t)z(t)}{1+\omega z(t)} $代替双线性函数$ py(t)z(t) $. 此外, 我们注意到, 模型(1.2) 只考虑了抗原可以刺激免疫而忽略了它引起的免疫损害. 事实上, 宿主的免疫可以被某些病原体抑制甚至破坏, 特别是在病原体负荷过大的情况下, 因此, 抗原会损害免疫^{[5, 12]}. 根据这一事实, 文献[4, 12–13]等提出用$ ny(t)z(t) $表示免疫损害并将其纳入了HIV动力学问题研究中.

基于上述讨论及受文献[4–6, 13] 的启发, 本文考虑如下HIV感染动力学模型

(1.3) $ \begin{equation} \begin{array}{ll} { } \dot{x}(t) =\lambda-dx(t)-\frac{\beta x(t) v(t)}{1+\alpha v(t)}, \\ { } \dot{y}(t) =\frac{\beta e^{-m\tau} x(t-\tau)v(t-\tau)}{1+\alpha v(t-\tau)}-ay(t)-\frac{p y(t) z(t)}{1+\omega z(t)}, \\ \dot{v}(t) =ky(t)-uv(t), \\ \dot{z}(t) =cy(t)-bz(t)-ny(t)z(t), \end{array} \end{equation} $

其中, $ \omega $、$ n $都是正常数, $ \omega $表示CTL免疫反应的抑制率, $ n $表示免疫损害率, 其他变量和参数的意义与模型(1.1)、(1.2) 中相同.

系统(1.3) 的初始条件如下

(1.4) $ \begin{equation} \begin{array}{ll} x(\theta) =\phi_{1}(\theta), y(\theta)=\phi_{2}(\theta), v(\theta)=\phi_{3}(\theta), z(\theta)=\phi_{4}(\theta), \\ \phi_{i}(\theta) \ge 0, \theta \in [-\tau, 0], \phi_{i}(0)> 0, i=1, 2, 3, 4. \end{array} \end{equation} $

其中$ (\phi_{1}(\theta), \phi_{2}(\theta), \phi_{3}(\theta), \phi_{4}(\theta))\in C([-\tau, 0], {{\Bbb R}} ^{4}_{+}) $, $ {{\Bbb R}} ^{4}_{+}=\{(x_{1}, x_{2}, x_{3}, x_{4})|x_{i}\geq0, i=1, 2, 3, 4\} $.

本节我们将讨论系统(1.3) 解的适定性问题. 根据泛函微分方程基本理论^[14]可知系统(1.3) 存在满足初始条件(1.4) 的唯一解. 下面将证明系统(1.3) 解的正性和最终有界性.

定理2.1  对于$ t \ge 0 $, 系统(1.3) 满足初始条件(1.4) 的解$ \bigl(x(t), y(t), z(t), v(t)\bigl) $非负且最终有界.

证  先证明解的非负性. 假设$ x(t) $不恒为正, 则存在最小的$ t_{1}\ge 0 $使得$ x(t_{1})=0 $, 又由系统(1.3) 的第一个方程和初始条件(1.4) 有$ \dot{x}(t_{1}) =\lambda>0 $, 因此, 由函数的连续性可知: 存在足够小的$ \varepsilon>0 $, 使得对于任意$ t\in(t_{1}-\varepsilon, t_{1}) $, 都有$ x(t)<0 $, 与假设矛盾, 故对于所有$ t\ge0 $都有$ x(t)>0 $. 从系统(1.3) 的后三个方程和初始条件(1.4), 可得

$ y(t) =e^{-\int^{t}_{0}a+\frac{pz(r)}{1+\omega z(r)}{\rm d}r}\biggl(y(0)+\int^{t}_{0}\frac{\beta e^{-m\tau} x(r-\tau)v(r-\tau)}{1+\alpha v(r-\tau)}e^{\int^{r}_{0}a+\frac{pz(i)}{1+\omega z(i)}{\rm d}i}{\rm d}r\biggr), {\nonumber} $

$ { } v(t) =e^{-ut}\biggl(v(0)+k\int^{t}_{0}y(r)e^{ur}{\rm d}r \biggr), $

$ { } z(t) =e^{-\int^{t}_{0}(b+ny(r)){\rm d}r}\biggl(z(0)+\int^{t}_{0}cy(r)e^{\int^{r}_{0}(b+ny(i)){\rm d}i}{\rm d}r\biggr), $

故对于任意$ t\in[0, \tau] $, 都有$ y(t)\geq0, v(t)\geq0, z(t)\geq 0 $.同理, 上述结论在$ [\tau, 2\tau] $, $ [2\tau, 3\tau] $, $ \dots $上仍然成立, 于是, 由归纳法可得: 对于所有$ t\ge0 $都有$ y(t)\ge0, v(t)\ge0, z(t)\ge0 $.

下面证明解的最终有界性. 定义

$ G(t)=x(t)+e^{m\tau}y(t+\tau). $

沿系统(1.3) 计算$ G(t) $的导数可得

$ \dot{G}(t)= \lambda-\big(dx(t)+ae^{m\tau}y(t+\tau)\big)-\frac{pe^{m\tau}y(t+\tau) z(t+\tau)}{1+\omega z(t+\tau)} \leq \lambda-hG(t), {\nonumber} $

其中, $ h=\min\{a, d\} >0 $, $ G(0)=x(0)+e^{m\tau}y(\tau) $. 故

$ \limsup\limits_{t\rightarrow \infty}G(t)\leq \frac{\lambda}{h}. $

从而, 对任意$ \varepsilon_{1}>0 $, 存在$ T>0 $, 使得当$ t>T $时有

$ G(t)=x(t)+e^{m\tau}y(t+\tau)<\frac{\lambda}{h}+\varepsilon_{1}, $

令

$ M=e^{-m\tau}\frac{\lambda}{h}+e^{-m\tau}\varepsilon_{1}, $

则有$ y(t)<M, t\in[T+\tau, +\infty) $. 又由系统(1.3) 的第三、四个方程可得

$ \limsup\limits_{t\rightarrow \infty}v(t)\leq \frac{k}{u}M, \;\limsup\limits_{t\rightarrow \infty}z(t)\le\frac{c}{b}M. $

综上所述, 系统(1.3) 满足初始条件(1.4) 的解非负且最终有界.证毕.

通过上述分析我们知道, 集合

$ {\it\Omega}:=\biggl\{(x(t), y(t), v(t), z(t))\in {{\Bbb R}} _{+}^{4}:x(t)+e^{m\tau}y(t+\tau)\le\frac{\lambda}{h}, \; v(t)\le\frac{k}{u}M, z(t)\le\frac{c}{b}M\biggl\} $

是系统(1.3) 的正不变集.

本节我们计算系统(1.3) 的病毒感染基本再生率并研究各可行平衡点的存在性.

显然, 系统(1.3) 总存在病毒未感染平衡点$ E_{0}\bigl(\frac{\lambda}{d}, 0, 0, 0\bigl) $. 利用下一代矩阵方法^[15-16]计算系统(1.3) 的病毒感染基本再生率, 根据系统(1.3) 的第二、三个方程可给出

$ {\cal F}={\left[\begin{array}{c} { } \frac{\beta e^{-m\tau} x(t-\tau)v(t-\tau)}{1+\alpha v(t-\tau)}\\ 0 \end{array} \right]}, {\cal V}={\left[\begin{array}{c} { } ay(t)+\frac{p y(t)z(t)}{1+\omega z(t)}\\ -ky(t)+uv(t) \end{array} \right]}.{\nonumber} $

计算$ {\cal F} $和$ {\cal V} $在病毒未感染平衡点$ E_{0} $处的Jacobian矩阵得

$ F={\left[\begin{array}{cc} 0{\quad} & { } \frac{\lambda\beta e^{-m\tau}}{d}\\ 0{\quad} & 0 \end{array} \right]}, \ V={\left[\begin{array}{cc} a {\quad}& 0\\ -k {\quad}& u \end{array} \right]}.{\nonumber} $

易得

$ FV^{-1}={\left[\begin{array}{cc} { } \frac{\lambda\beta ke^{-m\tau}}{aud} {\quad}&{ } \frac{\lambda\beta e^{-m\tau}}{ud}\\ 0{\quad} & 0 \end{array} \right]}.{\nonumber} $

故由$ \Re_{0}=\rho(FV^{-1}) $可得

$ \Re_{0}=\frac{\lambda\beta ke^{-m\tau}}{aud}, $

这里, $ \Re_{0} $称为系统(1.3) 的病毒感染基本再生率, 表示一个被感染靶细胞在其生命周期中新感染的易感靶细胞的数量^[16]. 当$ \Re_{0}>1 $时, 系统(1.3) 存在病毒感染平衡点$ E_{1}(x_{1}, y_{1}, v_{1}, z_{1}) $, 其中

(3.1) $ \begin{equation} x_{1}=\frac{\lambda(1+\alpha v_{1})}{d+\beta v_{1}+\alpha dv_{1}}, v_{1}=\frac{k}{u}y_{1}, z_{1}=\frac{cy_{1}}{b+ny_{1}}, \end{equation} $

这里, $ y_{1} $是方程$ Ay^2+By+C=0 $的唯一正根, 其中

$ A=(\beta+\alpha d)\bigl(pck+ak(n+\omega c)\bigl)>0, $

$ B=ab\beta k+pcdu+a\alpha bdk+aud(n+\omega)(1-\Re_{0}), $

$ C=abdu(1-\Re_{0})<0.{\nonumber} $

在本小节, 我们将通过分析对应特征方程根的分布来研究系统(1.3) 各可行平衡点的局部渐近稳定性.

定理4.1  当$ \Re_{0}<1 $时, 系统(1.3) 的病毒未感染平衡点$ E_{0} \bigl(\frac{\lambda}{d}, 0, 0, 0 \bigl) $局部渐近稳定.

证  系统(1.3) 在$ E_{0} $处的特征方程为

(4.1) $ \begin{equation} (s+b)(s+d)\biggl[s^{2}+(a+u)s+au-\frac{\beta\lambda ke^{-m\tau}}{d}e^{-s\tau}\biggl]=0. \end{equation} $

显然, $ s=-b $, $ s=-d $是(4.1) 的两个根, (4.1) 的其它根由以下方程确定

(4.2) $ \begin{equation} s^{2}+(a+u)s+au-\frac{\beta\lambda ke^{-m\tau}}{d}e^{-s\tau}=0. \end{equation} $

当$ \tau=0 $时, 方程(4.2) 可化为

$ s^{2}+(a+u)s+au(1-\Re_{0})=0. $

故当$ \tau=0 $且$ \Re_{0}<1 $时, 方程(4.2) 的根都具有负实部.

当$ \tau>0 $时, 设$ {\rm i}w\, (w>0) $是方程(4.1) 的根, 则$ {\rm i}w $满足

$ ({\rm i}w)^{2}+(a+u){\rm i}w+au=\frac{\beta\lambda ke^{-m\tau}}{d}e^{-{\rm i}w\tau}. $

分离上述方程的实部和虚部并整理得

(4.3) $ \begin{equation} \begin{array}{ll} { } (a+u)w =-\frac{\beta\lambda ke^{-m\tau}}{d}\sin w\tau, \\ { } au-w^{2} =\frac{\beta\lambda ke^{-m\tau}}{d}\cos w\tau. \end{array} \end{equation} $

将(4.3) 的两个方程两边同时平方再相加得

(4.4) $ \begin{equation} w^{4}+\bigl(a^{2}+u^{2}\bigl)w^{2}+a^{2}u^{2}\bigl(1-\Re_{0}^{2}\bigl)=0. \end{equation} $

令$ g=w^{2} $, 方程(4.4) 化为

$ g^{2}+\bigl(a^{2}+u^{2}\bigl)g+a^{2}u^{2}\bigl(1-\Re_{0}^{2}\bigl)=0. $

故当$ \Re_{0}<1 $时, 方程(4.1) 的根都具有负实部, 即平衡点$ E_{0} $局部渐近稳定. 证毕.

定理4.2  当$ \Re_{0}>1 $时, 系统(1.3) 的病毒感染平衡点$ E_{1}(x_{1}, y_{1}, v_{1}, z_{1}) $局部渐近稳定.

证  系统(1.3) 在平衡点$ E_{1} $处的特征方程为

(4.5) $ \begin{eqnarray} &&(s+u)\biggl(s+d+\frac{\beta v_{1}}{1+\alpha v_{1}}\biggl)\biggl[\frac{py_{1}(c-nz_{1})}{(1+\omega z_{1})^{2}}+(s+b+ny_{1})\biggl(s+a+\frac{pz_{1}}{1+\omega z_{1}}\biggl)\biggl]{}\\ & =&(s+d)(s+b+ny_{1})\frac{\beta kx_{1}e^{-m\tau}}{(1+\alpha v_{1})^{2}}e^{-s\tau}. \end{eqnarray} $

设$ s={\rm Re}s+{\rm iIm}s $ ($ {\rm Re}s\geq0 $) 是方程(4.5) 的根, 易得

(4.6) $ \begin{equation} \biggl|s+d+\frac{\beta v_{1}}{1+\alpha v_{1}}\biggr|\geq\bigl|(s+d)e^{-s\tau}\bigl|. \end{equation} $

由$ z_{1}=\frac{cy_{1}}{b+ny_{1}}>0 $, 可知

(4.7) $ \begin{equation} c-nz_{1}=\frac{bz_{1}}{y_{1}}>0, \end{equation} $

将(4.6) 和(4.7) 式代入(4.5)式并计算可得

(4.8) $ \begin{eqnarray} &&\biggl|(s+u)\biggl[\frac{py_{1}(c-nz_{1})}{(1+\omega z_{1})^{2}}+(s+b+ny_{1})\biggl(s+a+\frac{pz_{1}}{1+\omega z_{1}}\biggl)\biggl]\biggl|{}\\ &\geq& u\biggl|\frac{bpz_{1}}{(1+\omega z_{1})^{2}}+(s+b+ny_{1})\biggl(s+a+\frac{pz_{1}}{1+\omega z_{1}}\biggl)\biggl|{}\\ &> &u\bigl|(s+b+ny_{1})\bigl|\biggl(a+\frac{pz_{1}}{1+\omega z_{1}}\biggl). \end{eqnarray} $

又由(3.1)式有

$ u\biggl(a+\frac{pz_{1}}{1+\omega z_{1}}\biggl)=\frac{\beta kx_{1}e^{-m\tau }}{1+\alpha v_{1}}. $

将上述等式代入(4.8) 式并整理得

(4.9) $ \begin{eqnarray} && \biggl|(s+u)\biggl[\frac{py_{1}(c-nz_{1})}{(1+\omega z_{1})^{2}}+(s+b+ny_{1})\biggl(s+a+\frac{pz_{1}}{1+\omega z_{1}}\biggl)\biggl]\biggl|{}\\ &>&\biggl|(s+b+ny_{1})\frac{\beta kx_{1}e^{-m\tau }}{(1+\alpha v_{1})}\biggl|. \end{eqnarray} $

比较方程(4.5) 和不等式(4.9) 可知: $ s={\rm Re}s+{\rm iIm}s $ ($ \rm{Re}s\geq0 $) 不是方程(4.5) 的根, 与假设矛盾, 故方程(4.5) 的根都具有负实部. 因此, 当$ \Re_{0}>1 $时, 平衡点$ E_{1}(x_{1}, y_{1}, v_{1}, z_{1}) $局部渐近稳定.证毕.

在本小节, 我们将通过构造适当的Lyapunov泛函和应用LaSalle不变性原理研究系统(1.3) 各可行平衡点的全局渐近稳定性.

定理4.3  当$ \Re_{0}<1 $时, 系统(1.3) 的病毒未感染平衡点$ E_{0} \bigl(\frac{\lambda}{d}, 0, 0, 0 \bigl) $全局渐近稳定.

证  构造如下Lyapunov泛函

$ \begin{eqnarray*} V_{0}(t)&=& x_{0}\Biggl(\frac{x(t)}{x_{0}}-1-\ln\frac{x(t)}{x_{0}}\Biggl)+e^{m\tau}y(t)+\frac{\beta\lambda}{du}v(t)\\ &&+\frac{1}{c}ae^{m\tau}(1-\Re_{0})z(t)+\int^{t}_{t-\tau}\frac{\beta x(s) v(s)}{1+\alpha v(s)}{\rm d}s, \end{eqnarray*} $

其中$ x_{0}=\frac{\lambda}{d} $. 沿系统(1.3) 的解对$ V_{0}(t) $求导, 并整理可得

$ \begin{eqnarray*} \label{key} \dot{V}_{0}(t) &=& dx_{0}\biggl(2-\frac{x_{0}}{x(t)}-\frac{x(t)}{x_{0}}\biggl)-\frac{\alpha\beta x_{0}\big(v(t)\big)^{2}}{1+\alpha v(t)}-\frac{pe^{m\tau}y(t) z(t)}{1+\omega z(t)}{\nonumber}\\ &&-\frac{1}{c}ae^{m\tau}(1-\Re_{0})\bigl (bz(t)+ny(t)z(t)\bigl).{\nonumber} \end{eqnarray*} $

由此可得, $ \dot{V}_{0}(t) \le0 $, 当且仅当$ x(t)=x_{0}, y(t)=0, v(t)=0, z(t)=0 $时等式成立. 此外, 容易验证$ M_{0}=\{E_{0}\}\subset{\it\Omega} $是$ \{(x(t), y(t), v(t), z(t)):\dot{V}_{0}(t)=0\} $的最大不变子集. 故由定理4.1和LaSalle不变性原理可知: 当$ \Re_{0}<1 $时, 平衡点$ E_{0} $全局渐近稳定.证毕.

定理4.4  当$ \Re_{0}>1 $时, 系统(1.3) 的病毒感染平衡点$ E_{1}(x_{1}, y_{1}, v_{1}, z_{1}) $全局渐近稳定.

证  构造如下Lyapunov泛函

$ \begin{eqnarray*} V_{1}(t)& =& x_{1}\biggl(\frac{x(t)}{x_{1}}-1-\ln\frac{x(t)}{x_{1}}\biggl)+e^{m\tau}y_{1}\biggl(\frac{y(t)}{y_{1}}-1-\ln\frac{y(t)}{y_{1}}\biggl){\nonumber}\\ & &+\frac{\beta x_{1}v_{1}}{u(1+\alpha v_{1})}\biggl(\frac{v(t)}{v_{1}}-1-\ln\frac{v(t)}{v_{1}}\biggl)+\frac{e^{m\tau}py_{1}z_{1}}{b(1+\omega z_{1})^{2}}\biggl(\frac{z(t)}{z_{1}}-1-\ln\frac{z(t)}{z_{1}}\biggl){\nonumber}\\ & &+\frac{\beta x_{1}v_{1}}{1+\alpha v_{1}}\int^{t}_{t-\tau}\biggl[\frac{x(s) v(s)(1+\alpha v_{1})}{x_{1}v_{1}\big(1+\alpha v(s)\big)}-1-\ln\frac{x(s) v(s)(1+\alpha v_{1})}{x_{1}v_{1}\big(1+\alpha v(s)\big)}\biggl]{\rm d}s {\nonumber} . \end{eqnarray*} $

沿系统(1.3) 的解计算$ V_{1}(t) $的导数, 并整理可得

$ \begin{eqnarray*} \dot{V}_{1}(t) &=& dx_{1}\biggl(2-\frac{x_{1}}{x(t)}-\frac{x(t)}{x_{1}}\biggl) +\frac{e^{m\tau}pny_{1}z_{1}y(t)}{b(1+\omega z_{1})^{2}}\biggl(2-\frac{z(t)}{z_{1}}-\frac{z_{1}}{z(t)}\biggr)\\ &&-\frac{\beta x_{1}v_{1}}{1+\alpha v_{1}}\biggl(\frac{ x(t-\tau)v(t-\tau)(1+\alpha v_{1})y_{1}}{x_{1}v_{1}\big(1+\alpha v(t-\tau)\big)y(t)}-1-\ln\frac{ x(t-\tau)v(t-\tau)(1+\alpha v_{1})y_{1}}{x_{1}v_{1}\big(1+\alpha v(t-\tau)\big)y(t)}\biggr)\\ & &-\frac{\beta x_{1}v_{1}}{1+\alpha v_{1}}\biggl(\frac{1+\alpha v(t)}{1+\alpha v_{1}}-1-\ln\frac{1+\alpha v(t)}{1+\alpha v_{1}}\biggr)-\frac{\beta x_{1}v_{1}}{1+\alpha v_{1}}\biggl(\frac{v_{1}y(t)}{v(t)y_{1}}-1-\ln\frac{v_{1}y(t)}{v(t)y_{1}}\biggr)\\ &&-\frac{\beta x_{1}v_{1}}{1+\alpha v_{1}}\biggl(\frac{x_{1}}{x(t)}-1-\ln\frac{x_{1}}{x(t)}\biggl) -\frac{e^{m\tau}p\big(y(t)+\omega y_{1}z(t)\big)\big(z(t)-z_{1}\big)^{2}}{z(t)\big(1+\omega z(t)\big)(1+\omega z_{1})^{2}}\\ &&-\frac{\alpha\beta x_{1}\big(v(t)-v_{1}\big)^{2}}{\big(1+\alpha v(t)\big)(1+\alpha v_{1})^{2}}.{\nonumber} \end{eqnarray*} $

由此可得, $ \dot{V}_{1}(t) \le 0 $, 当且仅当$ x(t)=x_{1}, y(t)=y_{1}, v(t)=v_{1}, z(t)=z_{1} $时等式成立. 此外, 容易验证$ M_{1}=\{E_{1}\} \subset {\it\Omega} $是$ \{(x(t), y(t), v(t), z(t)) :\dot{V}_{1}(t)=0\} $的最大不变子集. 故由定理4.2和LaSalle不变性原理知: 当$ \Re_{0}>1 $时, 平衡点$ E_{1} $全局渐近稳定. 证毕.

本节将对系统(1.3) 的病毒感染基本再生率$ \Re_{0} $进行参数敏感性分析, 以确定影响病毒感染基本再生率的关键参数.

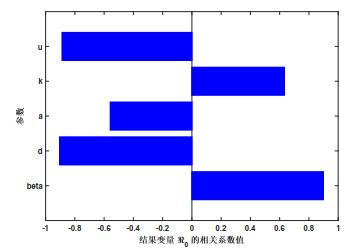
根据文献[17], 我们将采用LHS (Latin hypercube sampling) 和PRCCs (Partial rank correlation coefficients) 对病毒感染基本再生率$ \Re_{0} $进行参数敏感性分析. LHS是一种有效的抽样方法, 目前已被引入疾病建模^[17]. PRCCs是一种灵敏度分析方法, 提供了参数与病毒感染基本再生率$ \Re_{0} $线性相关强度的一种度量, 从而有助于识别对病毒感染基本再生率$ \Re_{0} $最重要的参数^[17]. 参考文献[6] 中参数的取值, 令$ \lambda=50({\rm cells\cdot ml/day}), $$ \beta=4.8\times10^{-7}({\rm ml\cdot virion/day}), m=1.39, a=0.015({\rm /day}), k=1.1349({\rm cells\cdot virion/day}), $$ u=0.5({\rm /day}), \tau=0.5({\rm day}), d=4.6\times10^{-3}({\rm /day}) $对病毒感染基本再生率$ \Re_{0} $进行参数敏感性分析, 分析结果见图 1.

从图 1中可以看出: $ \beta $、$ k $是病毒感染基本再生率$ \Re_{0} $的正相关变量, $ a $、$ u $、$ d $是病毒感染基本再生率$ \Re_{0} $的负相关变量. 同时, 根据$ \beta $、$ k $、$ a $、$ u $、$ d $与$ \Re_{0} $的线性相关性强度可知: $ d $、$ \beta $、$ u $是对$ \Re_{0} $的值的变化影响最大的三个参数.

本文研究了一类具有饱和发生率、CTL免疫反应、免疫损害和胞内时滞的HIV感染动力学模型. 首先, 证明了系统解的非负性和最终有界性; 之后, 通过下一代矩阵法得到了系统的病毒感染基本再生率; 通过分析相应特征方程根的分布讨论了系统各可行平衡点的局部渐近稳定性; 通过构造适当的Lyapunov泛函和应用LaSalle不变性原理证明了系统(1.3) 的全局动力学性态由病毒感染基本再生率完全确定: 当病毒感染基本再生率小于1时, 病毒未感染平衡点全局渐近稳定; 当病毒感染基本再生率大于1时, 病毒感染平衡点全局渐近稳定.