近年来, 生物种群模型由于其重要性而得到了广泛的研究^[1], 其中最有代表性的是捕食-食饵模型, 它在研究外来物种的生物入侵、疾病传播、生化反应等问题中起着重要的作用. 大量的研究表明捕食-食饵模型呈现出丰富的动力学行为, 比如分支、极限环、混沌、行波解、稳态模式^[2-9]. 但是也有例外, 一个典型的例子是众所周知的Leslie-Gower捕食-食饵扩散模型^[10]

(1.1) $ \begin{equation} \left\{ \begin{array}{ll} { } \frac{\partial u}{\partial t}-d_{1}\Delta u=ru\left( 1-\frac{u}{K}\right) -\alpha uv, & x\in \Omega , t>0, \\ { } \frac{\partial v}{\partial t}-d_{2}\Delta v=sv\left( 1-\frac{v}{\beta u} \right) , & x\in \Omega , t>0, \\ \partial _{\eta }u=\partial _{\eta }v=0, & x\in \partial \Omega , t>0, \\ u(x, 0)=u_{0}(x)>0, \ v(x, 0)=v_{0}(x)\geq , \ \neq 0, & x\in \overline{\Omega }, \end{array} \right. \end{equation} $

其中$ u $和$ v $分别表示食饵和捕食者在$ t $时刻空间位置为$ x\in \Omega $处的密度. $ {r} $和$ s $分别是食饵和捕食者的内禀增长率. $ K $是食饵的环境容纳量. $ \alpha $为捕食者平均消费率, 也叫功能反应函数^[11]. $ \beta $表示食饵提供给捕食者出生的食物质量. $ \Delta $为$ {{\Bbb R}} ^{n} $空间上的拉普拉斯算子. $ d_{1} $和$ d_{2} $分别为食饵和捕食者的扩散系数. $ \Omega \subset {{\Bbb R}} ^{n} $是具有光滑边界$ \partial \Omega $的有界区域. $ \eta $是$ \partial \Omega $上的标准单位外法向. 零流边界条件表示穿过边界的种群数量为零. $ r, $$ K, $$ \alpha , $$ s $和$ \beta $都是正常数.

文献[12] 研究了模型(1.1) 对应的常微分方程模型, 研究发现唯一的正常数平衡解$ \left( u^{\ast }, v^{\ast }\right) $是全局渐近稳定的. 当条件$ \frac{r}{K\alpha }\geq \frac{\beta }{4} $成立时, 模型(1.1) 有类似的结果^[10], 并且Du和Hsu^[10]猜测: 条件$ \frac{r}{K\alpha } $可以忽略, 即模型(1.1) 的$ \left( u^{\ast }, v^{\ast }\right) $也是全局渐近稳定的, 这意味着模型(1.1) 没有任何时空动力学模式.

从人类需求出发, 生物源开发和种群收获是人类在渔业、林业和野生生物管理中的共同目的^{[13, 14]}, 因此有必要在捕食-食饵模型中考虑种群收获. 有很多学者研究了具有收获的Leslie-Gower捕食-食饵模型. May等^[15]建立了如下的具有各种收获项的Leslie-Gower捕食-食饵模型

(1.2) $ \begin{equation} \left\{ \begin{array}{ll} { } \frac{{\rm d}x}{{\rm d}t}=rx\left( 1-\frac{x}{K}\right) -\alpha xy-H_{1}, & \\ { } \frac{{\rm d}y}{{\rm d}t}=sy\left( 1-\frac{y}{\beta x}\right) -H_{2}, & \end{array} \right. \end{equation} $

其中$ H_{1} $和$ H_{2} $分别描述食饵和捕食者的收获影响. 作者提出了两类收获项: (1) 常数收获, 表示不依赖种群数量. (2) 比例收获, 表示与种群数量成正比关系. 在文献[16] 中, 作者研究了模型(1.2) 中捕食者有常数收获的情况($ H_{1}=0, $$ H_{2}=h_{2} $), 并给出了前人已有的研究结果, 包括: (a) 无收获项($ H_{1}=H_{2}=0 $)^[12], (b) 食饵和捕食者都具有比例收获项($ H_{1}=r_{1}h_{1}x, $$ H_{2}=r_{2}h_{2}y $)^[17], (c) 食饵有常数收获捕食者有比例收获($ H_{1}=h_{1} $, $ H_{2}=r_{2}h_{2}y $)^[18], (d) 食饵和捕食者都有常数收获($ H_{1}=h_{1} $, $ H_{2}=h_{2} $)^[18], (e) 仅食饵有常数收获($ H_{1}=h_{1} $, $ H_{2}=0 $)^{[19, 20]}. 然而, 从生物和经济的观点来说, 非线性收获更符合实际^[21], 并且要好于常数收获和比例收获^[22]. Clark^[23]首次提出了非线性收获项$ H(E, x)=\frac{qEx}{m_{1}E+m_{2}x} $, 并将其称为Michaelis-Menten型渔获率, 其中$ q $为获取能力系数, $ E $是收获的外在努力, $ m_{1} $和$ m_{2} $为常数. Cupta等^[21]在模型(1.2) 中考虑了Michaelis-Menten型收获(即, $ H_{1}=\frac{qEx}{m_{1}E+m_{2}x} $, $ H_{2}=0 $). 他们发现在大的初值范围内, 种群趋于灭绝. 他们也研究了极限环存在性和稳定性, 生态平衡点存在的条件以及奇异最优控制问题.

事实上, 种群是空间非齐次的, 为了增加生存的可能性, 个体会倾向于迁移到种群密度较低的地方^[24]. 因此种群是空间分布的并且在生存的空间区域内相互作用. 出于以上原因, 本文将文献[21] 的研究模型推广到空间扩散情况, 即模型(1.1) 中考虑食饵有Michaelis-Menten收获, 得到如下模型

(1.3) $ \begin{equation} \left\{ \begin{array}{ll} { } \frac{\partial u}{\partial t}-d_{1}\Delta u=ru\left( 1-\frac{u}{K}\right) -\alpha uv-\frac{qEu}{m_{1}E+m_{2}u}, & x\in \Omega , t>0, \\ { } \frac{\partial v}{\partial t}-d_{2}\Delta v=sv\left( 1-\frac{v}{\beta u} \right) , & x\in \Omega , t>0, \\ \partial _{\eta }u=\partial _{\eta }v=0, & x\in \partial \Omega , t>0, \\ u(x, 0)=u_{0}(x)>0, \ v(x, 0)=v_{0}(x)\geq , \ \neq 0, & x\in \overline{\Omega }. \end{array} \right. \end{equation} $

令

$ \begin{eqnarray*} \widehat{u}=\frac{u}{K}, \widehat{v}=\frac{v}{\beta K}, \widehat{t}=rt, \widehat{d}_{1}=\frac{d_{1}}{r} \widehat{d} _{2}=\frac{d_{2}}{r}, b=\frac{\alpha \beta K}{r}, c=\frac{ m_{1}E}{m_{2}K}, h=\frac{qE}{rm_{2}K}, \rho =\frac{s}{r}. \end{eqnarray*} $

为了记号的简单省略掉字母上面的尖号, 模型(1.3) 变为

(1.4) $ \begin{equation} \left\{ \begin{array}{ll} { } \frac{\partial u}{\partial t}-d_{1}\Delta u=u\left( 1-u\right) -buv-\frac{hu }{c+u}, & x\in \Omega , t>0, \\ { } \frac{\partial v}{\partial t}-d_{2}\Delta v=\rho v\left( 1-\frac{v}{u} \right) , & x\in \Omega , t>0, \\ \partial _{\eta }u=\partial _{\eta }v=0, & x\in \partial \Omega , t>0, \\ u(x, 0)=u_{0}(x)>0, \ v(x, 0)=v_{0}(x)\geq , \ \neq 0, & x\in \overline{\Omega }. \end{array} \right. \end{equation} $

近年来, 生化系统中种群间相互作用的时空模式已成为研究的主流课题. 其兴趣之一是多种群相互作用的模型种群之间是否可以共存. 当种群是齐次分布时，共存意味着模型达到一个常数平衡点. 然而当种群非齐次分布时，共存意味着有非常数稳态解, 也就是所谓的稳态模式. 自从奠基性论文[25]之后, 扩散和交错扩散是产生稳态模式的主要因素.

目前不清楚Michaelis-Menten型收获是否会影响模型(1.1) 的动力学特性. 本文的主要目的是研究Michaelis-Menten型收获对模型(1.1) (即(1.4))的动力学特性和稳态模式的影响. 本文结构安排如下: 第二节研究模型(1.4) 的一致持久性. 第三节研究非负常数平衡解的局部稳定性, 并且利用Lyapunov函数和上下解方法研究正常数平衡解的全局渐近稳定性. 第四节研究模型(1.4) 对应稳态系统的非常数正解的存在和不存在性. 第五节是本文结论.

本节研究模型(1.4) 的持久性, 其含义是无论扩散系数如何, 食饵和捕食者在生存区域内的任何时间任何地方可以永久共存下去.

命题2.1  模型(1.4) 的所有解非负, 并且其非负解$ (u, v) $满足如下条件

(2.1) $ \begin{equation} \lim\limits_{t\rightarrow \infty }\sup \max\limits_{\overline{\Omega }}u(\cdot , t)\leq 1, \lim\limits_{t\rightarrow \infty }\sup \max\limits_{\overline{\Omega }}v(\cdot , t)\leq 1. \end{equation} $

证  由于初值非负, 因此模型(1.4) 解的非负性是显然的. 下面只需讨论有界性. 因为

$ u\left( 1-u\right) -buv-\frac{hu}{c+u}\leq u\left( 1-u\right) , (x, t)\in \Omega \times \lbrack 0, \infty ). $

所以由抛物方程的比较原理可得(2.1) 式中的第一个不等式. 这时存在$ T\in (0, \infty ) $使得对任意$ \epsilon >0 $, $ u(x, t)\leq 1+\epsilon $在$ \overline{\Omega }\times \lbrack T, \infty ) $时成立. 又因为

$ \rho v\left( 1-\frac{v}{u}\right) \leq \rho v\left( 1-\frac{v}{1+\epsilon } \right) =\rho v\frac{1+\epsilon -v}{1+\epsilon }, (x, t)\in \overline{ \Omega }\times \lbrack T, \infty ), $

由比较原理可得

$ \lim\limits_{t\rightarrow \infty }\sup \max\limits_{\overline{\Omega }} v(\cdot , t)\leq 1+\epsilon , $

由$ \epsilon $的任意性可得(2.1) 式中的第二个不等式. 证毕.

定义2.1  对任意非负初值$ (u_{0}(x), v_{0}(x)) $, 存在一个正常数$ \epsilon _{0}=\epsilon _{0}\left( u_{0}, v_{0}\right) $使得模型(1.4) 的解$ (u(x, t), v(x, t)) $满足

$ \lim\limits_{t\rightarrow \infty }\inf \min\limits_{\overline{\Omega }}u(\cdot , t)\geq \epsilon _{0}, \lim\limits_{t\rightarrow \infty }\inf \min\limits_{\overline{\Omega }}v(\cdot , t)\geq \epsilon _{0}, $

则称模型(1.4) 是一致持久的.

命题2.2  如果$ h<c(1-b), $则模型(1.4) 是一致持久的.

证  注意到

$ u\left( 1-u\right) -buv-\frac{hu}{c+u}\geq u\left( 1-u-b-\frac{h}{c}\right) $

并且$ 1-\frac{h}{c}-b>0, $则可得

(2.2) $ \begin{equation} \lim\limits_{t\rightarrow \infty }\inf \min\limits_{\overline{\Omega }} u(\cdot , t)\geq 1-\frac{h}{c}-b\triangleq A>0. \end{equation} $

于是, 对任意$ \epsilon $$ \left( 0<\epsilon <A\right) , $存在$ T\in \left( 0, \infty \right) $使得$ u(x, t)\geq A-\epsilon $在$ \overline{\Omega }\times \lbrack T, \infty ) $时成立. 因此$ v $满足

$ \rho v\left( 1-\frac{v}{u}\right) \geq \rho v\left( 1-\frac{v}{A-\epsilon } \right) =\rho v\frac{A-\epsilon -v}{A-\epsilon }, (x, t)\in \overline{ \Omega }\times \lbrack T, \infty ). $

由比较原理以及$ \epsilon \rightarrow 0 $时的连续性可得

$ \lim\limits_{t\rightarrow \infty }\inf \min\limits_{\overline{\Omega }} v(\cdot , t)\geq A. $

证毕.

假设

(H1) $ c<h<\frac{\left( 1+c(1+b)\right) ^{2}}{4(1+b)} $且$ c<\frac{1}{1+b}. $

(H2) $ c>h $或者$ c=h<\frac{1}{1+b}. $

(H3) $ h=\frac{\left( 1+c(1+b)\right) ^{2}}{4(1+b)} $且$ c< \frac{1}{1+b}. $

(H4) $ c<h<\frac{\left( 1+c\right) ^{2}}{4} $且$ c<1. $

(H5) $ c>h $或者$ c=h<1. $

(H6) $ h=\frac{\left( 1+c\right) ^{2}}{4} $且$ c<1. $

则有如下结果.

命题3.1  模型(1.4) 的非负常数平衡解的存在性如下

(i) 若(H1) 成立, 则模型(1.4) 有两个正常数平衡解: $ \widetilde{{\bf u}}_{1}=( \widetilde{u}_{1}, \widetilde{u}_{1}), $$ \widetilde{{\bf u}}_{2}=( \widetilde{u}_{2}, \widetilde{u}_{2}) $, 其中

$ \begin{eqnarray*} \widetilde{u}_{1} &=&\frac{1}{2(1+b)}\left( 1-c(1+b)-\sqrt{B}\right) , \\ \widetilde{u}_{2} &=&\frac{1}{2(1+b)}\left( 1-c(1+b)+\sqrt{B}\right) . \end{eqnarray*} $

且$ B=\left( 1+c(1+b)\right) ^{2}-4(1+b)h. $

(ii) 若(H2) 成立, 则模型(1.4) 有唯一的正常数平衡解$ \widetilde{{\bf u}}_{2}=( \widetilde{u}_{2}, \widetilde{u}_{2}). $

(iii) 若(H3) 成立, 则$ \widetilde{{\bf u}} _{1} $和$ \widetilde{{\bf u}}_{2} $相等, 记为$ \widetilde{ {\bf u}}_{3}=(\widetilde{u}_{3}, \widetilde{u}_{3}), $其中$ \widetilde{u} _{3}=\frac{1-c(1+b)}{2(1+b)}. $

(iv) 若(H4) 成立, 则模型(1.4) 有两个半平凡常数平衡解: $ \widetilde{{\bf u}}_{4}=( \widetilde{u}_{4}, 0), $$ \widetilde{{\bf u}}_{5}=(\widetilde{u}_{5}, 0) $, 其中

$ \begin{eqnarray*} \widetilde{u}_{4} &=&\frac{1}{2}\left( 1-c-\sqrt{\left( 1+c\right) ^{2}-4h} \right) , \\ \widetilde{u}_{1} &=&\frac{1}{2}\left( 1-c+\sqrt{\left( 1+c\right) ^{2}-4h} \right) . \end{eqnarray*} $

(v) 若(H5) 成立, 则模型(1.4) 有唯一的半平凡常数平衡解$ \widetilde{{\bf u}}_{5}=( \widetilde{u}_{5}, 0). $

(vi) 若(H6) 成立, 则$ \widetilde{{\bf u}} _{4} $和$ \widetilde{{\bf u}}_{5} $相等, 记为$ \widetilde{ {\bf u}}_{6}=(\widetilde{u}_{6}, 0) $, 其中$ \widetilde{u}_{6}=\frac{1-c}{2} . $

记$ -\Delta $算子在$ \Omega $上关于齐次Neumann边界条件的特征值为$ \lambda _{n} $$ (n\in {\Bbb N} _{0}=\{0, 1, \cdots \}) $, 其中$ 0=\lambda _{0}<\lambda _{1}<\cdots <\lambda _{n}<\cdots . $下面给出常数平衡解的局部稳定性结果.

定理3.1  (i) 假设$ h<\left( c+\widetilde{u}_{2}\right) ^{2} $或$ \rho >\overline{\rho } $成立, 则常数平衡解$ (\widetilde{u}_{2}, \widetilde{u}_{2}) $是局部渐近稳定的, 其中

$ \begin{eqnarray*} \overline{\rho }=\max \left\{ \widetilde{u}_{2}\left( \frac{h}{\left( c+ \widetilde{u}_{2}\right) ^{2}}-1\right) , \frac{d_{2}\lambda _{n} \left[ \widetilde{u}_{2}\left( \frac{h}{\left( c+\widetilde{u}_{2}\right) ^{2}}-1\right) -d_{1}\lambda _{n}\right] }{\frac{\widetilde{u}_{2}}{c+ \widetilde{u}_{2}}\sqrt{\Delta _{0}}+d_{1}\lambda _{n}}\right\} \end{eqnarray*} $

(ii) 若$ \rho <\widetilde{u}_{3}\left( \frac{h}{\left( c+ \widetilde{u}_{3}\right) ^{2}}-1\right), $则常数平衡解$ (\widetilde{u}_{3}, \widetilde{u} _{3}) $是不稳定的.

(iii) $ \widetilde{{\bf u}}_{1}, $$ \widetilde{{\bf u}}_{4}, $$ \widetilde{{\bf u}}_{5} $和$ \widetilde{{\bf u}}_{6} $总是不稳定的.

下面分别利用Lyapunov函数和上下解两种方法证明常数平衡解$ (\widetilde{u}_{2}, \widetilde{u}_{2}) $的全局渐近稳定性.

定理3.2  假设$ h<c(1-b), $$ h\leq (c+A)^{2} $和$ (2+b)A> \frac{1}{4}+\frac{h}{c}+b^{2} $ ($ A $为(2.2) 式) 成立, 则$ ( \widetilde{u}_{2}, \widetilde{u}_{2}) $是全局渐近稳定的.

证  令$ (u(x, t), v(x, t)) $为模型(1.4) 的正解. 构造如下的Lyapunov函数

$ L(t)=\int_{\Omega }W(u(x, t), v(x, t)){\rm d}x, $

其中$ W(u, v)=\int \frac{u^{2}-\widetilde{u}_{2}^{2}}{u^{2}}{\rm d}u+\frac{1}{\rho }\int \frac{v-\widetilde{u}_{2}}{v}{\rm d}v. $

由复合函数求导法则可得

$ \begin{eqnarray*} \frac{{\rm d}L}{{\rm d}t} &=&\int_{\Omega }\left\{ W_{u}(u(x, t), v(x, t))u_{t}+W_{v}(u(x, t), v(x, t))v_{t}\right\} {\rm d}x \\ &=&\int_{\Omega }\left\{ d_{1}\frac{u^{2}-\widetilde{u}_{2}^{2}}{u^{2}} \Delta u+\frac{d_{2}}{\rho }\frac{v-\widetilde{u}_{2}}{v}\Delta v\right\} {\rm d}x \\ &&+\int_{\Omega }\left\{ \frac{u^{2}-\widetilde{u}_{2}^{2}}{u}\left( 1-u-bv- \frac{h}{c+u}\right) +\left( v-\widetilde{u}_{2}\right) \left( 1-\frac{v}{u} \right) \right\} {\rm d}x \\ &=&L_{1}(t)+L_{2}(t), \end{eqnarray*} $

其中

$ \begin{eqnarray*} L_{1}(t) &=&\int_{\Omega }\left\{ d_{1}\frac{u^{2}-\widetilde{u}_{2}^{2}}{ u^{2}}\Delta u+\frac{d_{2}}{\rho }\frac{v-\widetilde{u}_{2}}{v}\Delta v\right\} {\rm d}x \\ &=&-\int_{\Omega }\left\{ d_{1}\frac{2\widetilde{u}_{2}^{2}}{u^{3}} \left\vert \nabla u\right\vert ^{2}+\frac{d_{2}\widetilde{u}_{2}}{\rho v^{2}} \left\vert \nabla v\right\vert ^{2}\right\} {\rm d}x\leq 0 \\ L_{2}(t) &=&\int_{\Omega }\left\{ \frac{u^{2}-\widetilde{u}_{2}^{2}}{u} \left( 1-u-bv-\frac{h}{c+u}\right) +\left( v-\widetilde{u}_{2}\right) \left( 1-\frac{v}{u}\right) \right\} {\rm d}x \\ &=&\int_{\Omega }\left\{ \frac{u^{2}-\widetilde{u}_{2}^{2}}{u}\left[ -\left( u-\widetilde{u}_{2}\right) -b(v-\widetilde{u}_{2})+\frac{h\left( u- \widetilde{u}_{2}\right) }{(c+\widetilde{u}_{2})(c+u)}\right] \right. \\ &&\left. +\frac{\left( u-\widetilde{u}_{2}\right) (v-\widetilde{u}_{2})}{u}- \frac{\left( v-\widetilde{u}_{2}\right) ^{2}}{u}\right\} {\rm d}x \\ &=&-\int_{\Omega }\frac{1}{u}\bigg\{ \left( u-\widetilde{u}_{2}\right) ^{2}(u+\widetilde{u}_{2})\left[ 1-\frac{h}{(c+\widetilde{u}_{2})(c+u)}\right] \\ && +\left[ b(u+\widetilde{u}_{2})-1\right] \left( u-\widetilde{u} _{2}\right) (v-\widetilde{u}_{2})+\left( v-\widetilde{u}_{2}\right) ^{2}\bigg\} {\rm d}x \\ &=&-\int_{\Omega }\frac{1}{u}\left\{ (u+\widetilde{u}_{2})\left[ 1-\frac{h}{ (c+\widetilde{u}_{2})(c+u)}\right] \xi ^{2} +\left[ b(u+\widetilde{u}_{2})-1\right] \xi \eta +\eta ^{2}\right\} {\rm d}x \\ &=&-\int_{\Omega }\frac{1}{u}\left( \xi , \eta \right) \left( \begin{array}{cc} p(u, v)& q(u, v) \\ q(u, v)& 1 \end{array} \right) \left( \begin{array}{c} \xi \\ \eta \end{array} \right) {\rm d}x, \end{eqnarray*} $

并且$ \xi =u-\widetilde{u}_{2}, $$ \eta =v-\widetilde{u}_{2}, $

$ \begin{eqnarray*} p(u, v) &=&(u+\widetilde{u}_{2})\left[ 1-\frac{h}{(c+\widetilde{u}_{2})(c+u)} \right] , \\ q(u, v) &=&\frac{1}{2}\left[ b(u+\widetilde{u}_{2})-1\right] . \end{eqnarray*} $

$ {\rm d}L(t)/{\rm d}t=L_{1}(t)+L_{2}(t)<0 $当且仅当矩阵$ \left( \begin{array}{cc} p(u, v)& q(u, v) \\ q(u, v)& 1 \end{array} \right) $是正定的, 即等价于$ p(u, v)+1>0 $和$ \varphi (u, v)=p(u, v)-q^{2}(u, v)>0, $其中

$ \begin{eqnarray*} \varphi (u, v)=u+\widetilde{u}_{2}-\frac{h\left( u-\widetilde{u}_{2}\right) }{ (c+\widetilde{u}_{2})(c+u)}-\frac{1}{4}-\frac{b^{2}\left( u+\widetilde{u} _{2}\right) ^{2}}{4}+\frac{b\left( u+\widetilde{u}_{2}\right) }{2}. \end{eqnarray*} $

由假设条件$ h\leq (c+A)^{2} $可知$ p(u, v)>0. $并且当

$ \begin{eqnarray*} (2+b)A>\frac{1}{4}+\frac{h}{c}+b^{2} \end{eqnarray*} $

时$ \varphi (u, v)>0 $成立. 于是在$ \left[ L^{\infty }\left( \Omega \right) \right]^{2} $下可得$ (u(x, t), v(x, t))\rightarrow (\widetilde{u}_{2}, \widetilde{u}_{2}) $, 因此对$ x\in \overline{\Omega } $恒有

$ \lim\limits_{t\rightarrow \infty }u(x, t)=\widetilde{u}_{2}, \lim\limits_{t\rightarrow \infty }v(x, t)=\widetilde{u}_{2}. $

证毕.

利用上下解方法可以优化定理3.2的结果.

定理3.3  若$ h<c(1-b) $成立, 则$ (\widetilde{u}_{2}, \widetilde{ u}_{2}) $是全局渐近稳定的.

证   因为$ h<c(1-b) $成立, 可以选择$ \varepsilon $满足

(3.1) $ \begin{equation} 0<\varepsilon <\frac{c(1-b)-h}{2c(1+b)}. \end{equation} $

从$ u(x, t) $的方程可得

$ \frac{\partial u}{\partial t}-d_{1}\Delta u=u\left( 1-u\right) -buv-\frac{hu }{c+u}\leq u\left( 1-u\right) , $

由抛物方程比较原理, 存在$ t_{1} $, 使得对任意$ t>t_{1}, $有$ u(x, t)\leq \overline{c}_{1} $成立, 其中$ \overline{c}_{1}=1+\varepsilon . $由模型(1.4) 的第二个方程可得

$ \frac{\partial v}{\partial t}-d_{2}\Delta v=\rho v\left( 1-\frac{v}{u} \right) \leq \rho v\left( 1-\frac{v}{1+\varepsilon }\right) $

对$ t>t_{1} $成立. 于是存在$ t_{2} $, 使得对任意$ t>t_{2}, $有$ v(x, t)\leq \overline{c}_{2} $成立, 其中$ \overline{c}_{2}=1+\varepsilon +\varepsilon . $这意味着

$ \frac{\partial u}{\partial t}-d_{1}\Delta u=u\left( 1-u\right) -buv-\frac{hu }{c+u}\geq \left( 1-b(1+2\varepsilon )-\frac{h}{c}\right) u-u^{2} $

对$ t>t_{2} $成立. 因为$ h<c(1-b) $, 则对(3.1) 式中选取的$ \varepsilon $, 有

$ 1-b(1+2\varepsilon )-\frac{h}{c}>0\ \mbox{ 和 }\ 1-b(1+2\varepsilon )-\frac{h}{c }-\varepsilon >0. $

于是存在$ t_{3}>t_{2} $, 使得对任意$ t>t_{3}, $有$ u(x, t)\geq \underline{c}_{1} $成立, 其中$ \underline{c}_{1}=1-b(1+2\varepsilon )-\frac{h}{c} -\varepsilon . $最后由$ u $的下界, 对$ t>t_{3}, $方程$ v $满足

$ \frac{\partial v}{\partial t}-d_{2}\Delta v=\rho v\left( 1-\frac{v}{u} \right) \geq \rho v\left( 1-\frac{v}{\underline{c}_{1}}\right). $

由(3.1) 式中选取的$ \varepsilon $可得

$ 1-b(1+2\varepsilon )-\frac{h}{c}-2\varepsilon >0, $

于是存在$ t_{4}>t_{3} $, 使得对任意$ t>t_{4}, $有$ v(x, t)\geq \underline{c}_{2}>0 $成立, 其中$ \underline{c}_{2}=1-b(1+2\varepsilon )-\frac{h}{ c}-2\varepsilon . $因此当$ t>t_{4} $时可得

$ \underline{c}_{1}\leq u(x, t)\leq \overline{c}_{1}, \underline{c} _{2}\leq v(x, t)\leq \overline{c}_{2}, $

并且$ \underline{c}_{1}, $$ \overline{c}_{1}, $$ \underline{c}_{2}, $$ \overline{ c}_{2} $满足

(3.2) $ \begin{equation} \left\{ \begin{array}{ll} { } 0\geq 1-\overline{c}_{1}-b\underline{c}_{2}-\frac{h}{c+\overline{c}_{1}}, 0\geq \rho \left( 1-\frac{\overline{c}_{2}}{\overline{c}_{1}}\right) , \\ { } 0\geq 1-\underline{c}_{1}-b\overline{c}_{2}-\frac{h}{c+\underline{c}_{1}}, 0\geq \rho \left( 1-\frac{\underline{c}_{2}}{\underline{c}_{1}}\right) . \end{array} \right. \end{equation} $

由文献[26] 中上下解定义可知, (3.2) 式表明$ \left( \overline{c}_{1}, \overline{c}_{2}\right) $和$ \left( \underline{c}_{1}, \underline{c} _{2}\right) $是模型(1.4) 的一对上下解. 这时存在$ K>0 $, 使得对任意$ \left( \underline{c}_{1}, \underline{c}_{2}\right) \leq $$ \left( u_{1}, v_{1}\right) , $$ \left( u_{2}, v_{2}\right) \leq \left( \overline{c}_{1}, \overline{c}_{2}\right), $不等式

$ \left\vert u_{1}\left( 1-u_{1}\right) -bu_{1}v_{1}-\frac{hu_{1}}{c+u_{1}} -u_{2}\left( 1-u_{2}\right) +bu_{2}v_{2}+\frac{hu_{2}}{c+u_{2}}\right\vert \leq {K}\left( \left\vert u_{1}-u_{2}\right\vert +\left\vert v_{1}-v_{2}\right\vert \right) , $

$ \left\vert \rho v_{1}\left( 1-\frac{v_{1}}{u_{1}}\right) -\rho v_{2}\left( 1- \frac{v_{2}}{u_{2}}\right) \right\vert \leq {K}\left( \left\vert u_{1}-u_{2}\right\vert +\left\vert v_{1}-v_{2}\right\vert \right) $

成立. 定义两个迭代序列$ \left( \overline{c}_{1}^{(m)}, \overline{c}_{2}^{(m)}\right) $和$ \left( \underline{c}_{1}^{(m)}, \underline{c}_{2}^{(m)}\right) $, 对$ m\geq 1 $满足

$ \begin{eqnarray*} \overline{c}_{1}^{(m)} &=&\overline{c}_{1}^{(m-1)}+\frac{1}{{K}}\left( \overline{c}_{1}^{(m-1)}-\left( \overline{c}_{1}^{(m-1)}\right) ^{2}-b \underline{c}_{2}^{(m-1)}\overline{c}_{1}^{(m-1)}-\frac{h\overline{c} _{1}^{(m-1)}}{c+\overline{c}_{1}^{(m-1)}}\right) , \\ \overline{c}_{2}^{(m)} &=&\overline{c}_{2}^{(m-1)}+\frac{1}{{K}}\left( \rho \overline{c}_{2}^{(m-1)}-\frac{\rho \left( \overline{c} _{2}^{(m-1)}\right) ^{2}}{\overline{c}_{1}^{(m-1)}}\right) , \\ \underline{c}_{1}^{(m)} &=&\underline{c}_{1}^{(m-1)}+\frac{1}{{K}} \left( \underline{c}_{1}^{(m-1)}-\left( \underline{c}_{1}^{(m-1)}\right) ^{2}-b\overline{c}_{2}^{(m-1)}\underline{c}_{1}^{(m-1)}-\frac{h\underline{c} _{1}^{(m-1)}}{c+\underline{c}_{1}^{(m-1)}}\right) , \\ \underline{c}_{2}^{(m)} &=&\underline{c}_{2}^{(m-1)}+\frac{1}{{K}} \left( \rho \underline{c}_{2}^{(m-1)}-\frac{\rho \left( \underline{c} _{2}^{(m-1)}\right) ^{2}}{\underline{c}_{1}^{(m-1)}}\right) , \end{eqnarray*} $

其中$ \left( \overline{c}_{1}^{(0)}, \overline{c}_{2}^{(0)}\right) =\left( \overline{c}_{1}, \overline{c}_{2}\right) $和$ \left( \underline{c}_{1}^{(0)}, \underline{c}_{2}^{(0)}\right) =\left( \underline{c}_{1}, \underline{c}_{2}\right) $. 则对$ m\geq 1, $$ \left( \underline{c}_{1}, \underline{c}_{2}\right) \leq \left( \underline{c}_{1}^{(m)}, \underline{c}_{2}^{(m)}\right) \leq \left( \underline{c}_{1}^{(m+1)}, \underline{c}_{2}^{(m+1)}\right) \leq \left( \overline{c}_{1}^{(m+1)}, \overline{c}_{2}^{(m+1)}\right) \leq \left( \overline{c}_{1}^{(m)}, \overline{c}_{2}^{(m)}\right) \leq \left( \overline{c}_{1}, \overline{c}_{2}\right) $, 且存在$ \left( \widetilde{c}_{1}, \widetilde{c}_{2}\right) $和$ \left( \widehat{c}_{1}, \widehat{c}_{2}\right) $使得$ \left( \underline{c}_{1}, \underline{c}_{2}\right) \leq \left( \widehat{c} _{1}, \widehat{c}_{2}\right) \leq \left( \widetilde{c}_{1}, \widetilde{c}_{2}\right) \leq \left( \overline{c}_{1}, \overline{c} _{2}\right) $, 因此有$ \lim\limits_{m\rightarrow \infty }\overline{c}_{1}^{(m)}= \widetilde{c}_{1}, $$ \lim\limits_{m\rightarrow \infty }\overline{c}_{2}^{(m)}= \widetilde{c}_{2}, $$ \lim\limits_{m\rightarrow \infty }\underline{c}_{1}^{(m)}= \widehat{c}_{1}, $$ \lim\limits_{m\rightarrow \infty }\underline{c}_{2}^{(m)}= \widehat{c}_{2} $并且

(3.3) $ \begin{equation} \left\{ \begin{array}{ll} { } 0=1-\widetilde{c}_{1}-b\widehat{c}_{2}-\frac{h}{c+\widetilde{c}_{1}}, 0=\rho \left( 1-\frac{\widetilde{c}_{2}}{\widetilde{c}_{1}}\right) , \\ { } 0=1-\widehat{c}_{1}-b\widetilde{c}_{2}-\frac{h}{c+\widehat{c}_{1}}, 0=\rho \left( 1-\frac{\widehat{c}_{2}}{\widehat{c}_{1}}\right) . \end{array} \right. \end{equation} $

(3.3) 式简化为

(3.4) $ \begin{equation} \left\{ \begin{array}{ll} { } 1-\widetilde{c}_{1}-\frac{h}{c+\widetilde{c}_{1}}=b\widehat{c}_{1}, \\ { } 1-\widehat{c}_{1}-\frac{h}{c+\widehat{c}_{1}}=b\widetilde{c}_{1}. \end{array} \right. \end{equation} $

(3.4) 式中第二式减去第一式可得

(3.5) $ \begin{equation} \left( b-1+\frac{h}{(c+\widetilde{c}_{1})(c+\widehat{c}_{1})}\right) ( \widetilde{c}_{1}-\widehat{c}_{1})=0. \end{equation} $

假设$ \widetilde{c}_{1}\neq \widehat{c}_{1} $, 则

(3.6) $ \begin{equation} 1-b=\frac{h}{(c+\widetilde{c}_{1})(c+\widehat{c}_{1})}. \end{equation} $

(3.6) 式代入(3.4)式可得

$ \begin{eqnarray*} (1-b)(1-\widetilde{c}_{1})(c+\widetilde{c}_{1}) &=&h-bc(1-b)(c+\widetilde{c} _{1}), \\ (1-b)(1-\widehat{c}_{1})(c+\widehat{c}_{1}) &=&h-bc(1-b)(c+\widehat{c}_{1}). \end{eqnarray*} $

于是方程

(3.7) $ \begin{equation} (1-b)(1-x)(c+x)=h-bc(1-b)(c+x) \end{equation} $

有两个正根$ \widetilde{c}_{1} $和$ \widehat{c}_{1}. $方程(3.7) 变为

$ \begin{eqnarray*} (1-b)x^{2}-(1-b)(1-c+bc)x+[h-c(1-b)]-bc^{2}(1-b)=0. \end{eqnarray*} $

因为$ h<c(1-b) $, 所以方程(3.7) 不存在两个正根. 于是$ \widetilde{c}_{1}=\widehat{c}_{1}, $进而有$ \widetilde{c}_{2}= \widehat{c}_{2}. $由文献[26] 可知, 模型(1.4) 的解$ \left( u(x, t), v(x, t)\right) $在$ x\in \overline{\Omega } $内恒满足

$ \lim\limits_{t\rightarrow \infty }u(x, t)=\widetilde{u}_{2}, \lim\limits_{t\rightarrow \infty }v(x, t)=\widetilde{u}_{2}. $

证毕.

注3.1  从定理3.2和3.3可以看出, 在研究正常数平衡解$ (\widetilde{u}_{2}, \widetilde{u}_{2}) $的全局渐近稳定性时, 上下解方法要好于Lyapunov函数的方法.

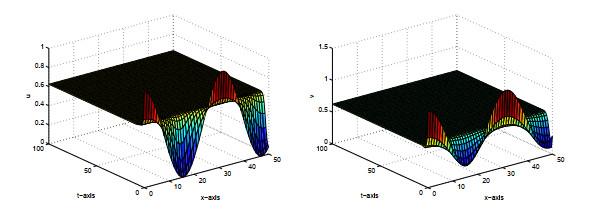
下面给出一个数值模拟的例子.

例3.1  在模型(1.4) 中令$ \Omega =(0, 50) $, $ (d_{1}, d_{2}, b, c, h, \rho)=(1, 20, 0.5, 1, 0.1, 1). $则(H2) 和$ h<c(1-b) $都成立, 因此模型(1.4) 有唯一正常数平衡解$ (\widetilde{u}_{2}, \widetilde{u} _{2})=(0.6257, 0.6257) $, 并且该解是全局渐近稳定的. 图 1为全局渐近稳定的解$ (0.6257, 0.6257) $的数值模拟.

本节利用Leray-Schauder度理论研究如下稳态系统

(4.1) $ \begin{equation} \left\{ \begin{array}{ll} { } -d_{1}\Delta u=u\left( 1-u\right) -buv-\frac{hu}{c+u}, & x\in \Omega , \\ -d_{2}\Delta v=\rho v\left( 1-\frac{v}{u}\right) , & x\in \Omega , \\ \partial _{\eta }u=\partial _{\eta }v=0, & x\in \partial \Omega \end{array} \right. \end{equation} $

的非常数正解的存在性和不存在性.

本小节给出正解的上下界的先验估计. 首先列出如下的已知结果.

命题4.1(最大值原理^[27])  令$ g(x, w)\in C(\Omega \times {{\Bbb R}} ^{1}) $和$ b_{j}(x)\in C(\overline{ \Omega }) $, $ j=1, \cdots , N. $

$ ( $1$ ) $如果$ w\in C^{2}(\Omega )\cap C^{1}(\overline{\Omega }) $满足

$ \begin{eqnarray*} \left\{ \begin{array}{l} { } -\Delta w(x)\leq \sum\limits_{j=1}^{N}b_{j}(x)w_{x_{j}}+g(x, w(x)), \; \; x\in\Omega , \\ { } \frac{\partial w}{\partial \nu }\leq 0, \; \; x\in \partial \Omega . \end{array} \right. \end{eqnarray*} $

记$ w(x_{0})=\max\limits_{\overline{\Omega }}w $, 则$ g(x_{0}, w(x_{0}))\geq 0. $

$ ( $2$ ) $如果$ w\in C^{2}(\Omega )\cap C^{1}(\overline{\Omega }) $满足

$ \begin{eqnarray*} \left\{ \begin{array}{l} { } -\Delta w(x)\geq \sum\limits_{j=1}^{N}b_{j}(x)w_{x_{j}}+g(x, w(x)), \; \; x\in\Omega , \\ { }\frac{\partial w}{\partial \nu }\geq 0, \; \; x\in \partial \Omega . \end{array} \right. \end{eqnarray*} $

记$ w(x_{0})=\min\limits_{\overline{\Omega }}w $, 则$ g(x_{0}, w(x_{0}))\leq 0. $

命题4.2(Harnack不等式^[28])  令$ w\in C^{2}(\Omega )\cap C^{1}(\overline{\Omega }) $为齐次Neumann边界下方程$ -\Delta w(x)=c(x)w(x) $的一个正解, 且$ c(x)\in C(\overline{\Omega }) $, 则存在一个依赖于$ \left\Vert c\right\Vert _{\infty } $的正常数$ C_{\ast } $使得$ \max\limits_{\overline{\Omega }}w\leq C_{\ast }\min\limits_{\overline{\Omega }}w $成立.

利用命题4.1和4.2可得如下结果.

定理4.1(上界)  系统(4.1) 的任意正解$ (u, v) $满足

(4.2) $ \begin{equation} \max\limits_{\overline{\Omega }}u(x)\leq 1, \max\limits_{\overline{\Omega } }v(x)\leq 1. \end{equation} $

证   系统(4.1) 的第一个方程使用命题4.1可得(4.2) 式中的第一个不等式. 因为$ 0<v<\left\Vert u\right\Vert _{\infty }\leq 1, $则在$ \overline{\Omega } $内有$ v(x)\leq 1 $.

定理4.2(下界)  记$ d^{\ast } $为一个固定常数. 假设$ h<c $, 则存在一个正常数$ \underline{C}=\underline{C}(c, b, h, \rho , d^{\ast }) $使得当$ d_{1}, d_{2}\geq d^{\ast } $时, 系统(4.1) 的任意正解$ (u, v) $满足

(4.3) $ \begin{equation} \min\limits_{\overline{\Omega }}u(x)\geq \underline{C}, \min\limits_{\overline{ \Omega }}v(x)\geq \underline{C}. \end{equation} $

证   令

$ u(x_{0})=\min\limits_{\overline{\Omega }}u(x), u(x_{1})=\max\limits_{\overline{ \Omega }}u(x), v(y_{0})=\min\limits_{\overline{\Omega }}v(x), v(y_{1})=\max\limits_{\overline{\Omega }}v(x). $

由命题4.1可得

$ 1-u(x_{0})-bv(x_{0})-\frac{h}{c+u(x_{0})}\leq 0, 1-\frac{v(y_{0})}{ u(y_{0})}\leq 0, 1-\frac{v(y_{1})}{u(y_{1})}\geq 0, $

故而

(4.4) $ \begin{equation} u(x_{0})\leq u(y_{0})\leq v(y_{0}), \end{equation} $

(4.5) $ \begin{equation} v(y_{1})\leq u(y_{1})\leq u(x_{1}). \end{equation} $

由(4.5) 式可知

$ 1-\frac{h}{c}-u(x_{0})\leq 1-u(x_{0})-\frac{h}{c+u(x_{0})}\leq bv(x_{0})\leq bv(y_{1})\leq bu(x_{1}). $

这一估计意味着

$ 1-\frac{h}{c}\leq u(x_{0})+bu(x_{1}). $

定义

$ \widehat{c}(x)=d_{1}^{-1}\left( 1-u-bv-\frac{h}{c+u}\right) , $

则$ u $满足

$ \left\{ \begin{array}{ll} \Delta u+\widehat{c}(x)u=0, & x\in \Omega , \\ \partial _{\eta }u=0, & x\in \partial \Omega . \end{array} \right. $

命题4.2表明

$ \max\limits_{\overline{\Omega }}u(x)\leq C_{\ast }\min\limits_{\overline{\Omega }}u(x), $

其中$ C_{\ast } $是依赖于$ \left\Vert \widehat{c} \right\Vert _{\infty } $的正常数. 因此可得

$ 1-\frac{h}{c}\leq u(x_{0})+bC_{\ast }u(x_{0}), $

这时有

$ u(x_{0})=\min\limits_{\overline{\Omega }}u(x)\geq \frac{1-\frac{h}{c}}{1+bC_{\ast }} :=\underline{C}. $

由(4.4)式可得$ v(y_{0})=\min\limits_{\overline{\Omega }}v(x)\geq \underline{C}. $证毕.

定理4.3  存在一个常数$ d $, 使得当$ d_{1}, $$ d_{2}\geq d $时, 系统(4.1) 不存在非常数正解.

证   令$ (u, v) $为系统(4.1) 的正解, 记

$ \begin{eqnarray*} \overline{u}=\frac{1}{\left\vert \Omega \right\vert }\int_{\Omega }u(x){\rm d}x, \overline{v}=\frac{1}{\left\vert \Omega \right\vert }\int_{\Omega }v(x){\rm d}x. \end{eqnarray*} $

系统(4.1) 中的方程$ u $两边同乘以$ u-\overline{u} $, 然后在$ \Omega $上积分可得

$ d_{1}\int_{\Omega }\left\vert \nabla (u-\overline{u})\right\vert ^{2}{\rm d}x=\int_{\Omega }(u-\overline{u})u\left( 1-u-\frac{h}{c+u}\right) {\rm d}x-\int_{\Omega }b(u-\overline{u})uv{\rm d}x\equiv {\cal I}_{1}+{\cal I}_{2}, $

$ {\cal I}_{1} =\int_{\Omega }(u-\overline{u})^{2}\left\{ 1-(u+\overline{u })-\frac{hc}{(c+u)(c+\overline{u})}\right\} {\rm d}x \leq \int_{\Omega }(u-\overline{u})^{2}{\rm d}x. $

取$ d^{\ast }=1, $由定理4.2可得

$ \begin{eqnarray*} {\cal I}_{2} &=&-b\int_{\Omega }\left\{ (u-\overline{u})^{2}v+\overline{u} (u-\overline{u})v\right\} {\rm d}x \\ &\leq &-b\int_{\Omega }\left\{ \underline{C}(u-\overline{u})^{2}+\overline{u} (u-\overline{u})v\right\} {\rm d}x \\ &=&-b\int_{\Omega }\left\{ \underline{C}(u-\overline{u})^{2}+\overline{u}(u- \overline{u})(v-\overline{v})\right\} {\rm d}x \\ &\leq &\frac{b(1-2\underline{C})}{2}\int_{\Omega }(u-\overline{u})^{2}{\rm d}x+ \frac{b}{2}\int_{\Omega }(v-\overline{v})^{2}{\rm d}x. \end{eqnarray*} $

因此有

$ \begin{eqnarray*} d_{1}\int_{\Omega }\left\vert \nabla (u-\overline{u})\right\vert ^{2}{\rm d}x\leq \left( \frac{b(1-2\underline{C})}{2}+1\right) \int_{\Omega }(u-\overline{u} )^{2}{\rm d}x+\frac{b}{2}\int_{\Omega }(v-\overline{v})^{2}{\rm d}x. \end{eqnarray*} $

由定理4.2可知

$ u(x)\leq C_{\ast }v(x), u(x)\leq C_{\ast }\overline{v}, \frac{ \overline{v}^{2}}{\overline{u}u(x)}\leq C_{\ast }^{2}, \forall x\in \overline{\Omega }. $

类似于上面的分析可得

$ \begin{eqnarray*} d_{2}\int_{\Omega }\left\vert \nabla (v-\overline{v})\right\vert ^{2}{\rm d}x &=&\int_{\Omega }\rho v(v-\overline{v})\left( 1-\frac{v}{u}\right) {\rm d}x \\ &=&\rho \int_{\Omega }\left\{ (v-\overline{v})^{2}\left( 1-\frac{v}{u} \right) +\overline{v}(v-\overline{v})\left( 1-\frac{v}{u}\right) \right\} {\rm d}x \\ &=&\rho \int_{\Omega }\left\{ (v-\overline{v})^{2}\left( 1-\frac{v}{u} \right) -(v-\overline{v})^{2}\frac{\overline{v}}{u}-(v-\overline{v})\frac{ \overline{v}^{2}}{u}\right\} {\rm d}x \\ &=&\rho \int_{\Omega }\left\{ (v-\overline{v})^{2}\left( 1-\frac{v+\overline{ v}}{u}\right) +(v-\overline{v})\frac{\overline{v}^{2}}{\overline{u}}-(v- \overline{v})\frac{\overline{v}^{2}}{u}\right\} {\rm d}x \\ &=&\rho \int_{\Omega }\left\{ (v-\overline{v})^{2}\left( 1-\frac{2}{C_{\ast } }\right) +(v-\overline{v})\frac{\overline{v}^{2}}{\overline{u}}-(v-\overline{ v})\frac{\overline{v}^{2}}{u}\right\} {\rm d}x \\ &=&\rho \int_{\Omega }\left\{ (v-\overline{v})^{2}\left( 1-\frac{2}{C_{\ast } }\right) +(v-\overline{v})(u-\overline{u})\frac{\overline{v}^{2}}{\overline{u }u}\right\} {\rm d}x \\ &\leq &\rho \left( 1-\frac{2}{C_{\ast }}+\frac{C_{\ast }^{2}}{2}\right) \int_{\Omega }(v-\overline{v})^{2}{\rm d}x+\frac{\rho C_{\ast }^{2}}{2} \int_{\Omega }(u-\overline{u})^{2}{\rm d}x. \end{eqnarray*} $

由上面的估计可知, 对某正常数$ M>0 $有

$ \begin{eqnarray*} d_{1}\int_{\Omega }\left\vert \nabla (u-\overline{u})\right\vert ^{2}{\rm d}x+d_{2}\int_{\Omega }\left\vert \nabla (v-\overline{v})\right\vert ^{2}{\rm d}x\leq M\int_{\Omega }\left[ (u-\overline{u})^{2}+(v-\overline{v})^{2} \right] {\rm d}x, \end{eqnarray*} $

利用Poincaré 不等式, 存在一个常数$ {\cal C} $使得

$ \begin{eqnarray*} d_{1}\int_{\Omega }\left\vert \nabla (u-\overline{u})\right\vert ^{2}{\rm d}x+d_{2}\int_{\Omega }\left\vert \nabla (v-\overline{v})\right\vert ^{2}{\rm d}x\leq {\cal C}\int_{\Omega }\left( \left\vert \nabla (u-\overline{u} )\right\vert ^{2}+\left\vert \nabla (v-\overline{v})\right\vert ^{2}\right) {\rm d}x. \end{eqnarray*} $

故而, 当$ d_{1}, $$ d_{2}\gg 1 $时, $ \nabla (u-\overline{u})=\nabla (v-\overline{v})=0, $即$ u\equiv \overline{u}, $$ v\equiv \overline{v}. $证毕.

令$ {\bf u}=(u, v)^{T}, $$ \widetilde{{\bf u}}_{k}=(\widetilde{u}_{k}, \widetilde{u}_{k}) $$ (k=1, 2, 3), $$ \Phi ({\bf u})=\left( d_{1}u, d_{2}v\right) ^{T}, $则系统(4.1) 简写为

$ \begin{eqnarray*} \left\{ \begin{array}{ll} -\Delta \Phi ({\bf u})=F\left( {\bf u}\right) , & x\in \Omega , \\ \partial _{\eta }{\bf u}=0, & x\in \partial \Omega . \end{array} \right. \end{eqnarray*} $

其中

$ \begin{eqnarray*} F\left( {\bf u}\right) =\left( \begin{array}{c} { } u\left( 1-u\right) -buv-\frac{hu}{c+u} \\ { } \rho v\left( 1-\frac{v}{u}\right) \end{array} \right) . \end{eqnarray*} $

$ {\bf u} $是系统(4.1) 的正解当且仅当

$ \begin{eqnarray*} \Psi ({\bf u})\triangleq {\bf u-(I-}\Delta {\bf )}^{-1}\{{\bf \Phi }_{{\bf u}}^{-1}{\bf (u)[F(u)+\nabla u{\bf \Phi }_{{\bf uu}} {\bf (u)}\nabla u]+u}\}={\bf 0}\mbox{.} \end{eqnarray*} $

并且

$ \begin{eqnarray*} D_{{\bf u}}\Psi (\widetilde{{\bf u}}_{k})={\bf I-(I-}\Delta {\bf )}^{-1}\{{\bf \Phi }_{{\bf u}}^{-1}{\bf (\widetilde{{\bf u}} _{k})F}_{{\bf u}}{\bf (\widetilde{{\bf u}}_{k})+I}\}. \end{eqnarray*} $

利用不动点指数计算公式^[29]

$ \begin{eqnarray*} index\left( I-\Psi (\cdot ), \widetilde{{\bf u}}_{k}\right) =(-1)^{\sum\limits_{n\geq 0, H(\lambda _{n})<0}m(\lambda _{n})}, \end{eqnarray*} $

其中$ m(\lambda _{n}) $是$ \lambda _{n} $的重数, 可知为了计算指数$ index\left( I-\Psi (\cdot ), \widetilde{{\bf u }}_{k}\right) $, 需要确定$ H_{k}(\lambda ) $的符号, 其中$ H_{k}(\lambda ) $定义为

$ \begin{eqnarray*} H_{k}(\lambda )=\det \left\{ {\bf \Phi }_{{\bf u}}^{-1}{\bf ( \widetilde{{\bf u}}_{k})}\right\} \det \{\lambda {\bf \Phi }_{{\bf u }}{\bf (\widetilde{{\bf u}}_{k})-F}_{{\bf u}}{\bf (\widetilde{ {\bf u}}_{k})}\}. \end{eqnarray*} $

直接计算可得$ \det \left\{ {\bf \Phi }_{{\bf u}}^{-1} {\bf (\widetilde{{\bf u}}_{k})}\right\} $为正, 并且

$ \begin{eqnarray*} \det \{\lambda {\bf \Phi }_{{\bf u}}{\bf (\widetilde{{\bf u}} _{k})-F}_{{\bf u}}{\bf (\widetilde{{\bf u}}_{k})} \}=d_{1}d_{2}\lambda ^{2}+\left( d_{1}\rho -d_{2}p_{k}\right) \lambda -\rho \left( p_{k}-b\widetilde{u}_{k}\right) , \end{eqnarray*} $

其中

$ \begin{eqnarray*} p_{k}=\widetilde{u}_{k}\left( \frac{h}{(c+\widetilde{u}_{k})^{2}}-1\right) . \end{eqnarray*} $

如果$ \Delta _{k}=\left( d_{1}\rho -d_{2}p_{k}\right) ^{2}+4d_{1}d_{2}\rho \left( p_{k}-b\widetilde{u}_{k}\right) >0 $成立, 则$ H_{k}(\lambda )=0 $有两个正根$ \lambda _{\pm }^{k}, $其中

$ \begin{eqnarray*} \lambda _{-}^{k} &=&\frac{d_{2}p_{k}-d_{1}\rho -\sqrt{\left( d_{1}\rho -d_{2}p_{k}\right) ^{2}+4d_{1}d_{2}\rho \left( p_{k}-b\widetilde{u} _{k}\right) }}{2d_{1}d_{2}}, \\ \lambda _{+}^{k} &=&\frac{d_{2}p_{k}-d_{1}\rho +\sqrt{\left( d_{1}\rho -d_{2}p_{k}\right) ^{2}+4d_{1}d_{2}\rho \left( p_{k}-b\widetilde{u} _{k}\right) }}{2d_{1}d_{2}}. \end{eqnarray*} $

情况I  假设(H1) 成立.

在这种情况下, 系统(4.1) 有两个正常数解$ \widetilde{ {\bf u}}_{k}=(\widetilde{u}_{k}, \widetilde{u}_{k}) $, $ k=1, 2. $

定理4.4  假设$ p_{2}>0, $对某$ \tau \geq 1 $, $ \frac{p_{1}}{d_{1}}\in \left( \lambda _{\tau }, \lambda _{\tau +1}\right) $, 并且对某$ \sigma \geq 1 $, $ \frac{p_{2}}{d_{2}}\in \left( \lambda _{\sigma }, \lambda _{\sigma +1}\right) $. 如果$ \sum\limits_{n=1}^{\tau }m(\lambda _{n})+\sum\limits_{n=0}^{\sigma }m(\lambda _{n}) $是偶数, 则存在$ d_{2}^{\ast } $使得当$ d_{2}\geq d_{2}^{\ast } $时系统(4.1) 至少有一个非常数正解.

证  易得$ p_{1}>0, $$ p_{1}-b\widetilde{u}_{1}=\frac{ \widetilde{u}_{1}}{c+\widetilde{u}_{1}}\sqrt{B}>0, $$ p_{2}-b\widetilde{u} _{2}=-\frac{\widetilde{u}_{2}}{c+\widetilde{u}_{2}}\sqrt{B}<0. $可以找到一个$ \widehat{d}_{2}\gg 1 $使得$ \Delta _{k}>0 $对所有$ d_{2}\geq \widehat{d}_{2} $成立, 并且$ H_{k}(\lambda )=0 $的两个根满足

$ \begin{eqnarray*} \lambda _{-}^{1}<0<\lambda _{+}^{1}, 0<\lambda _{-}^{2}<\lambda _{+}^{2}, \end{eqnarray*} $

(4.6) $ \begin{equation} \lim\limits_{d_{2}\rightarrow \infty }\lambda _{-}^{2}=0, \lim\limits_{d_{2}\rightarrow \infty }\lambda _{+}^{k}=\frac{p_{k}}{d_{1} }, k=1, 2. \end{equation} $

$ \frac{p_{1}}{d_{1}}\in \left( \lambda _{\tau }, \lambda _{\tau +1}\right) $和$ \frac{p_{2}}{d_{2}}\in \left( \lambda _{\sigma }, \lambda _{\sigma +1}\right) $意味着存在一个$ d_{0}>\widehat{d}_{2} $使得

$ \begin{eqnarray*} 0<\lambda _{-}^{2}<\lambda _{1}, \lambda _{+}^{1}\in \left( \lambda _{\tau }, \lambda _{\tau +1}\right) , \lambda _{+}^{2}\in \left( \lambda _{\sigma }, \lambda _{\sigma +1}\right) , \forall d_{2}\geq d_{0}. \end{eqnarray*} $

定理4.3可知存在$ d_{1}^{\ast }>d_{0} $使得对所有$ d_{1}, $$ d_{2}\geq d_{1}^{\ast } $系统(4.1) 没有非常数正解, 选取$ d_{1}^{\ast } $充分大使得$ \frac{p_{k}}{d_{1}^{\ast }}<\lambda _{1}, k=1, 2. $再次利用(4.6)式, 存在一个常数$ d_{2}^{\ast }>d_{1}^{\ast } $使得

(4.7) $ \begin{equation} 0<\lambda _{+}^{1}<\lambda _{1}, 0<\lambda _{-}^{2}<\lambda _{+}^{2}<\lambda _{1}. \end{equation} $

下面将证明对任意$ d_{2}\geq d_{2}^{\ast }, $系统(4.1) 至少有一个非常数正解. 一方面, 假设对某$ d_{2}\geq d_{2}^{\ast }, $系统(4.1) 没有正解.

对这些固定的$ d_{1}^{\ast }, $$ d_{2}^{\ast }, $$ d_{1} $和$ d_{2} $, 定义

$ \begin{eqnarray*} \Phi (t;{\bf u})=\left( (td_{1}+(1-t)d_{1}^{\ast })u, (td_{2}+(1-t)d_{2}^{\ast })v\right) ^{T}, 0\leq t\leq 1, \end{eqnarray*} $

并且考虑如下问题

(4.8) $ \begin{equation} \left\{ \begin{array}{ll} -\Delta \Phi ({\bf t;u})=F\left( {\bf u}\right) , & x\in \Omega , \\ \partial _{\eta }{\bf u}=0, & x\in \partial \Omega . \end{array} \right. \end{equation} $

显然, 对$ 0\leq t\leq 1, $$ (\widetilde{u}_{1}, \widetilde{u}_{1}) $和$ ( \widetilde{u}_{2}, \widetilde{u}_{2}) $是系统(4.1) 仅有的两个正常数解, 并且$ {\bf u} $是系统(4.1) 的一个正解当且仅当$ {\bf u} $是系统(4.8) 在$ t=1 $的一个正解. $ {\bf u} $是系统(4.8) 的一个正解当且仅当

$ \begin{eqnarray*} \Psi (t;{\bf u})\triangleq {\bf u-(I-}\Delta {\bf )}^{-1}\{{\bf \Phi }_{{\bf u}}^{-1}{\bf (t;u)[F(u)+\nabla u{\bf \Phi }_{{\bf uu }}{\bf (t;u)}\nabla u]+u}\}={\bf 0}. \end{eqnarray*} $

由前面分析可知问题的关键是确定$ H_{k}(t;d_{1}, d_{2};\lambda ) $的符号. 由(4.7) 式可知

$ \begin{eqnarray*} H_{1}(0;d_{1}^{\ast }, d_{2}^{\ast };0) &<&0, \\ H_{1}(0;d_{1}^{\ast }, d_{2}^{\ast };\lambda _{n}) &>&0, \forall \lambda _{n}>0, \\ H_{2}(0;d_{1}^{\ast }, d_{2}^{\ast };\lambda _{n}) &>&0, \forall \lambda _{n}\geq 0. \end{eqnarray*} $

计算可得

$ \begin{eqnarray*} H_{1}(1;d_{1}, d_{2};\lambda _{n}) &<&0, 0\leq n\leq \tau , \\ H_{1}(1;d_{1}, d_{2};\lambda _{n}) &>&0, n\geq \tau +1, \\ H_{2}(1;d_{1}, d_{2};\lambda _{0}) &>&0, \\ H_{2}(1;d_{1}, d_{2};\lambda _{n}) &<&0, 1\leq n\leq \sigma , \\ H_{2}(1;d_{1}, d_{2};\lambda _{n}) &>&0, n\geq \sigma +1. \end{eqnarray*} $

利用不动点指数计算公式有

$ \begin{eqnarray*} index\left( I-\Psi (0;{\bf \cdot }), (\widetilde{u}_{1}, \widetilde{ u}_{1})\right) &=&(-1)^{m(\lambda _{0})}=-1, \\ index\left( I-\Psi (0;{\bf \cdot }), (\widetilde{u}_{2}, \widetilde{ u}_{2})\right) &=&(-1)^{0}=1, \\ index\left( I-\Psi (1;{\bf \cdot }), (\widetilde{u}_{1}, \widetilde{ u}_{1})\right) &=&(-1)^{\sum\limits_{n=1}^{\tau }m(\lambda _{n})+1}, \\ index\left( I-\Psi (1;{\bf \cdot }), (\widetilde{u}_{2}, \widetilde{ u}_{2})\right) &=&(-1)^{\sum\limits_{n=0}^{\tau }m(\lambda _{n})-1}. \end{eqnarray*} $

由定理4.1和4.2可知, 系统(4.1) 的任何正解必属于$ {\cal B} $, 其中$ {\cal B} =\{(u, v)\in C(\Omega )\times C(\Omega ):\underline{C}<u, v<2\} $, 并且在边界$ \partial {\cal B} $上有$ \Psi (t; {\bf u})\neq 0 $. 因此$ deg(\Psi (t;{\bf u}), {\cal B}, 0) $是有意义的. 由度的同伦不变性可知

(4.9) $ \begin{equation} deg(\Psi (1;{\bf \cdot }), {\cal B}, 0)=deg(\Psi (0;{\bf \cdot }), {\cal B}, 0). \end{equation} $

由假设, $ \Psi (1;{\bf u})=0 $和$ \Psi (0;{\bf u})=0 $在$ {\cal B} $内仅有两个正解$ (\widetilde{u}_{1}, \widetilde{u}_{1}) $和$ (\widetilde{u}_{2}, \widetilde{u}_{2}) $, 这时有

$ \begin{eqnarray*} deg(\Psi (0;{\bf \cdot }), {\cal B}, 0) &=&index\left( I-\Psi (0;{\bf \cdot }), (\widetilde{u}_{1}, \widetilde{u}_{1})\right) +index\left( I-\Psi (0;{\bf \cdot }), (\widetilde{u}_{2}, \widetilde{u} _{2})\right) =0, \\ deg(\Psi (1;{\bf \cdot }), {\cal B}, 0) &=&index\left( I-\Psi (1;{\bf \cdot }), (\widetilde{u}_{1}, \widetilde{u}_{1})\right) +index\left( I-\Psi (1;{\bf \cdot }), (\widetilde{u}_{2}, \widetilde{u} _{2})\right) \\ &=&(-1)^{\sum\limits_{n=1}^{\tau }m(\lambda _{n})+1}+(-1)^{\sum\limits_{n=0}^{\tau }m(\lambda _{n})-1}. \end{eqnarray*} $

如果$ \sum\limits_{n=1}^{\tau }m(\lambda _{n})+\sum\limits_{n=0}^{\sigma }m(\lambda _{n}) $是偶数, 可以推出

$ \begin{eqnarray*} 0=deg(\Psi (0;{\bf \cdot }), {\cal B}, 0)\neq deg(\Psi (1;{\bf \cdot } ), {\cal B}, 0)=\pm 2, \end{eqnarray*} $

这与(4.9) 式矛盾.证毕.

情况II  假设(H2) 成立.

在这种情况下, 系统(4.1) 有唯一正常数解$ \widetilde{{\bf u}}_{2}=(\widetilde{u}_{2}, \widetilde{u}_{2}) $.

定理4.5  假设$ p_{2}>0, $对某$ s\geq 1 $, $ \frac{p_{2}}{d_{1}}\in \left( \lambda _{s}, \lambda _{s+1}\right) $成立. 如果$ \sum\limits_{n=1}^{s}m(\lambda _{n}) $是奇数, 则存在$ d_{2}^{\ast \ast } $使得当$ d_{2}\geq d_{2}^{\ast } $时系统(4.1) 至少有一个非常数正解.

情况III  假设(H3) 成立.

在这种情况下, 系统(4.1) 有唯一正常数解$ \widetilde{{\bf u}}_{3}=(\widetilde{u}_{3}, \widetilde{u}_{3}) $.

定理4.6  假设对某$ r\geq 1 $, $ \frac{p_{3}}{d_{1}}\in \left( \lambda _{r}, \lambda _{r+1}\right) $成立. 如果$ \sum\limits_{n=1}^{r}m(\lambda _{n}) $是奇数, 则存在$ \widetilde{d}_{2} $使得当$ d_{2}\geq \widetilde{d}_{2} $时系统(4.1) 至少有一个非常数正解.

上面两个定理的证明和定理4.4类似, 这里不再证明.

下面利用Fourier谱方法^[30]进行数值模拟.

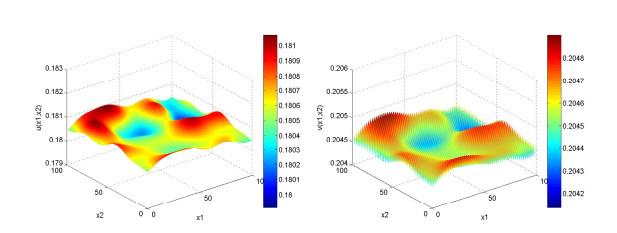
例4.1  在模型(1.4)中, 令$ \Omega =(0, 100)\times (0, 100)\subset {{\Bbb R}} ^{2} $并且$ (d_{1}, d_{2}, b, c, h, \rho )=(3, 30, \\1, 0.45, 0.45, 1). $则(H2) 成立, 并且模型(1.4) 有唯一的正常数平衡解$ (\widetilde{u}_{2}, \widetilde{u}_{2})=(0.2, 0.2) $. 计算可得$ p_{2}=0.013>0, $并且在定理4.5中令$ s=2 $, 则$ \lambda _{1}=\frac{\pi ^{2}}{10000}, $$ \lambda _{2}=\frac{\pi ^{2}}{5000}, $$ \lambda _{3}=\frac{\pi ^{2}}{2500} $且$ \frac{p_{2}}{d_{1}}=0.0033\in \left( \lambda _{s}, \lambda _{s+1}\right) =\left( \lambda _{2}, \lambda _{3}\right) , $$ \sum\limits_{n=1}^{s}m(\lambda _{n})=m(\lambda _{1})+m(\lambda _{2})=3. $因此定理4.5的条件成立, 故而模型(1.4) 在$ d_{2}\geq d_{2}^{\ast } $时至少存在一个非常数正稳态解. 图 2为$ d_{2}=30 $时非常数正稳态解的数值模拟. 图 3为模型(1.4) 的稳态模式(图灵模式)的数值模拟.

本文研究了食饵具有Michaelis-Menten型收获的Leslie-Gower捕食-食饵模型的动力学性质和稳态模式. 通过适当尺度变换, 原来的Michaelis-Menten收获项变为一个仅有两个参数($ h $和$ c $) 的非线性收获项. 非线性收获项中的两个参数$ h $和$ c $影响非负常数平衡解的个数和稳定性. 研究得到了模型一致持久的充分条件; 分别利用Lyapunov函数和上下解两种方法建立了正常数平衡$ (\widetilde{u}_{2}, \widetilde{u}_{2}) $解全局渐近稳定的充分条件; 并且利用能量估计和度理论研究了正稳态解的存在性和不存在性.

研究结果表明: 如果收获系数较低(即$ h<c(1-b) $), 则无论任何时候任何位置食饵和捕食者可以共存(命题2.2) 而且最终趋于正常数平衡解$ (\widetilde{u}_{2}, \widetilde{u}_{2}) $ (定理3.3). 从生物意义的角度来说, 本文给出了收获策略以保证食饵和捕食者免于灭绝, 并且决策者可以给出最优收获策略以确保生态的可持续发展.

一方面, 在没有扩散的情况下模型(1.4) 退化为常微分模型(1.2), 其中$ H_{1}=\frac{qEx}{m_{1}E+m_{2}x} $, Cupta等^[21]证明了在大范围初值时无扩散模型(1.4) 走向灭绝, 并且通过Hopf分支观察到不同情况下极限环的存在性. 与文献[21] 的结果相比, 模型(1.4) 产生了新的时空模式. 另一方面, 食饵没有Michaelis-Menten型扩散的情况下(即$ h=0 $), 模型(1.4) 变为经典的Leslie-Gower捕食-食饵模型(1.1), 这时存在唯一全局渐近稳定的正常数平衡解^[10]. 也就是说, 本文的模型在没有收获项时不会产生任何时空模型. 然而在食饵具有Michaelis-Menten型收获时, 模型(1.4) 产生非常数正稳态解(即稳态模式). 因此, 研究结果反映了Michaelis-Menten型收获在时空模式的形成中扮演了重要的作用, 这与没有收获的情况形成了鲜明的对比. 一个有趣的问题是模型(1.4) 是否存在其它时空动力学行为, 比如Hopf分支, 稳态分支以及Turing-Hopf分支, 这将是后续要研究的问题.