1 引言
现实世界中的许多复杂优化问题多为动态的, 会随时间发生变化. 例如, 在调度问题中, 新任务不断到达, 产品原材料质量不断变化, 机器随时间增加不断磨损等[1]. 演化算法是求解复杂优化问题效果显著的一种智能算法, 在求解优化问题时无需考虑函数本身的可微性、可导性、连续性等信息, 具有较强的自适应性和自组织性[2], 已在求解静态优化问题上取得了很好的效果, 因此许多研究者致力于在演化算法中寻求解决动态优化问题的方法改进和创新. 动态优化问题的最优解是不断变化的, 求解动态优化问题的算法要能够在动态环境中及时跟踪到最优解[3, 4]. 因此, 对动态环境进行检测与响应已成为动态优化问题的研究热点.
为了跟踪随环境变化而变化的最优解, 首先要及时准确地检测环境的变化. 其次在环境变化后, 优化算法要及时采取响应策略紧密地跟踪解的变化以获得最优解. 许多研究者对这两方面进行了研究, 主要工作有: Hu和Eberhart [5]通过监测全局最优解和次最优解的适应值变化来估计环境的变化, Carisle [6]提出随机选择"Sentry"粒子作为检测环境变化的感应粒子, 单世民和邓贵仕[7]根据个体极值的适应值变化情况来判断环境是否变化. 在响应策略上, 他们选择重新初始化种群或部分个体. 姜立强等[8]将种群分为跟踪和搜索两个种群, 也是通过监测跟踪种群的当前最优解和次优解来判断环境是否发生变化. 当发现环境发生变化时, 重新初始化搜索种群, 并对两个种群采取不同的变异策略, 提高搜索新最优解的效率. 胡静等[9-10]通过监测相近粒子前后两代适应值与距离比值的变化率来检测环境变化, 并构造种群多样性函数, 通过粒子的扩散运动响应环境变化. 唐剑等[11]通过激活种群中的停滞粒子适应环境变化. 赵传信等[12]通过监测全局最优个体和距离其最远的个体的适应值变化来检测环境变化, 环境变化后进行以种群为中心的扩散运动. 成照乾等[13]根据均匀分布的静态粒子的适应值变化来判断环境是否变化. 当静态粒子检测到某个区域环境变化后, 每个粒子都朝该区域运动以响应环境变化. 朱庆保等[14]设置多组粒子进行搜索, 通过监测每组最优解的适应值变化来检测环境变化. 环境变化后, 令多样性较差的一组粒子向最优粒子周围扩散. 陈健等[15]和袁亦川等[16]都专门设置一个种群来检测环境变化, 种群中至少有一个个体的适应值变化时, 认为环境发生了变化. 环境变化后, 初始化种群以适应新的环境.
动态优化问题环境检测的实质是检测最优解是否变化及如何变化, 目前环境检测方法主要是通过监测某些点的适应值变化情况来检测环境的变化. 在已有检测方法中, 如果所选的监测点与最优解差异较大, 则会降低环境检测的准确性. 如: 最优解发生了较明显的变化, 但这些点的适应值变化却相对不明显; 或最优解没有发生明显变化, 而这些点的适应值的变化却相对较明显. 因此, 在环境检测方法设计中, 如何设置监测点十分重要. 在响应策略方面, 研究者们采用重新初始化种群或部分个体、扩散种群、激活粒子等方法. 这些响应方法在一定程度上提高了算法的空间搜索能力. 但是, 重新初始化方法没有很好地利用之前的信息, 而且不断地初始化也会降低算法性能. 此外, 没有检测到环境变化后的最优解所在区域就扩散种群或者激活粒子的做法具有一定的盲目性和随机性, 并不能快速准确地跟踪到变化后的最优解.
正交试验设计是一种多因素多水平的优化试验设计方法, 它从全面试验的样本点中挑选出部分有代表性的样本点进行试验, 只用较少的试验次数就能找出因素水平间的最优搭配[17]. 一些研究者将正交试验设计思想引入到优化算法的交叉步骤中以获得更好的子代, 例如, 李志勇等[18]将正交试验设计方法用到多目标优化算法中, 设计了正交交叉算子. 具体做法为: 对父代的两个个体进行量化和分解操作, 使其适应于四因素三水平的正交表, 通过正交试验产生子代. 此外, 正交试验设计也是确定输入变量(因素)关键区域的有效方法, 张晓丽等[19]利用正交表区间收缩法求函数极值, 其方法大致为: 将自变量作为因子, 将自变量的取值区间二等分作为两个水平, 取区间中点为试验点, 截除实验结果“差”的试验点所在区间的一部分, 逐步缩小自变量的取值区间, 最终得到函数极值. 但是选取区间中点为试验点可能会导致极值点所在的区间被舍去, 进而导致结果不准确(见本文3.3节例子).
基于以上分析, 本文首先对文献[19]中提出的正交表区间收缩方法进行改进. 具体的, 将自变量每一维的取值区间等分为多个子区间, 在每个子区间中随机选取试验点, 分析结果; 重复多次, 挑选出现率高的子区间作为函数极值区间. 实验表明: 改进的方法能有效提高正交试验结果的准确性.
在环境检测方法的改进上, 本文在适应值备选函数的最优解区域内、外, 按一定比例选取勘探粒子, 并根据勘探粒子的适应值变化情况来检测环境变化. 而在环境响应方面, 针对群智能算法, 如粒子群算法、差分进化算法等, 引入记忆机制存储环境信息, 环境变化后根据环境信息和最优解变化情况, 在环境变化后的最优解区域内、外, 按一定比例选取个体以适应新的环境. 算法测试结果证明: 本文提出的环境检测与响应方法能够有效监测最优解的变化情况, 在环境变化后能够及时准确地跟踪变化后的最优解. 改进后的方法充分利用了过去的环境信息, 提高了算法快速收敛到最优解的能力.
在实际中, 动态优化问题的环境可能受到某些随机因素的影响, 从而导致动态优化问题对应的目标函数
本文其余部分结构如下: 第2章介绍随机动态优化问题和正交试验设计; 第3章给出改进后的函数最优解区间收缩方法一般步骤, 进行模拟实验证明该方法的可行性, 并与其它方法比较; 第4章基于函数最优解区间收缩方法, 提出动态优化问题的环境检测与响应方法, 通过粒子群算法进行测试并与其它算法比较, 验证了方法的优良性; 第5章针对受随机扰动的动态优化问题, 给出扰动前后环境检测无变化对应的随机扰动标准差上限, 并检验本文环境检测与响应方法处理这类随机动态优化问题的有效性; 第6章为总结与展望.
2 预备知识
本节介绍随机动态优化问题和正交试验设计.
2.1 随机动态优化问题
其中
给定备选函数空间
其中
随机动态优化问题没有统一定义, 依据随机性来源而定. 下面先给出文献[20]具有马氏性随机动态优化问题的数学定义.
假设已知动态优化问题的环境变化时刻为
其中,
对于最优解受随机扰动发生随机偏移的随机动态优化问题, 其目标函数需要加上随机扰动. 设
则本文受随机扰动的动态优化问题可描述为
其中
2.2 正交试验设计
在试验设计中, 假设需要考虑
3 函数最优解区间收缩方法
目前动态优化问题的环境检测方法主要是通过监测某些点的适应值变化情况来检测环境的变化. 设置监测点的方法主要分为两种, 一是监测个体最优解、全局最优解等特殊点, 二是在整个搜索空间中随机设置一些监测点. 这两种方法都有一定的盲目性, 如果监测点与最优解的差异较大, 那么环境检测的准确性将大大降低. 因此要在最优解周围设置监测点, 需要先找出最优解所在的较小区域.
3.1 函数最优解区间收缩方法
问题描述:
文献[19]正交表区间收缩方法过程如下.
将自变量作为因子, 将自变量的取值区间二等分作为两个水平, 取区间中点为试验点, 选择正交表安排试验, 并计算试验指标值. 若某个因子取第一个水平时, 对应的试验指标最大, 则该因子从左端去掉
本文改进后的函数最优解区间收缩方法步骤如下
(1) 问题转化, 把求
(2) 根据因子和水平个数选择合适的正交表, 在每个等长子区间内随机选取一点作为试验点, 根据正交表安排试验, 计算正交表上每个试验对应的指标值.
(3) 采用极差分析法分析结果, 找出函数
3.2 模拟实验
本节选用最优解已知的单峰函数和多峰函数进行模拟实验, 检验利用函数最优解区间收缩方法确定函数最优解所在区域的可行性.
实验1 选取单峰三元函数
(1) 将各因子
(2) 采用极差分析法对结果进行分析, 找出三元函数
(3) 把
图 1
维数设置为3, 将
对于单峰多元函数来说, 它在定义域内只有一个极小值点, 利用函数最优解区间收缩方法不断缩小各因子的取值区间, 最后能得到函数全局最小值点所在的较小区域. 对于多峰函数来说, 它在定义域内存在多个极小值点, 从逻辑上来说, 利用函数最优解区间收缩方法可能得到的是函数某个极小值点所在的区域. 但是该方法在每个区间选取试验点时是随机选取的, 而且重复100次实验, 如果函数足够光滑, 那么就能保证全局最小值点所在的区间不会被舍去, 因此最后得到的是函数全局最小值点所在的较小区域, 实验2的结果证明了该方法的准确性. 因此, 对于光滑的多维单峰和多峰函数在给定区域的最值问题, 可以利用函数最优解区间收缩方法寻找函数最优解所在的较小区域.
3.3 与文献[19]方法比较
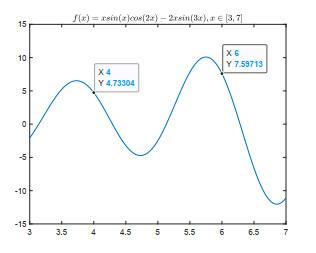
本节将分别利用文献[19]及本文改进后的函数最优解区间收缩方法, 求
图 2
根据函数最优解区间收缩方法步骤, 选用
比较两种方法可知, 文献[19]中正交表区间收缩法将自变量原来的取值区间两等分, 并分别选取区间中点为试验点, 最小值点位于区间
4 环境检测与响应
本节基于函数最优解区间收缩方法, 改进现有动态优化问题的环境检测与响应策略, 利用粒子群算法进行测试并与其它算法比较.
4.1 对环境变化的检测
为了提高算法对动态环境的适应能力, 对环境变化进行检测是求解动态优化问题要完成的首要工作. 环境检测主要包括两个部分: 勘探粒子的选取以及衡量环境变化的标准设置. 现有勘探粒子的选取是随机的, 衡量环境变化的标准则依据勘探粒子适应值变化情况而定. 常用衡量变化的标准有如下三个
(1) 满足
(2)
(3)
在实际问题中, 依据最优解的精度要求选择合适的标准并设置阈值
环境检测的实质是检测最优解是否变化及如何变化. 本节将改进现有勘探粒子的选取方式, 在一定程度上避免现有方法的随机性和盲目性, 提高环境检测的准确性. 首先利用函数最优解区间收缩方法, 找出所有适应值备选函数的最优解所在区域(称这些区域为重点区域), 在重点区域设置一定数目的勘探粒子, 而在其他非重点区域设置少量勘探粒子, 然后根据勘探粒子的适应值变化情况来判断环境是否变化. 具体的, 由函数最优解区间收缩方法得出适应值备选函数
4.2 对环境变化的响应
就粒子群算法和差分进化算法等群智能算法而言, 对环境变化的响应实质上是选取新的种群来适应变化后的环境, 使其能更好追踪变化后的最优解. 因此环境变化后, 新的种群要在最优解周围选取个体. 此外, 动态优化问题的环境虽然是变化的, 但某些环境也会在不同时刻再次出现. 因此, 算法设计中要充分利用前面的环境信息, 在响应环境变化的策略中引入记忆机制. 每次检测到环境发生变化后, 将上一环境信息以
检测到环境发生变化后的响应步骤如下
(1) 检测上一环境信息是否已存储, 将未存储的上一环境信息存储到记忆中,
(2) 判断变化后的环境是否为新环境, 若是新出现的环境, 则在环境变化后的最优解区域内随机选取
(3) 计算种群中所有个体的适应值, 并重新计算个体最优解的适应值.
(4) 将当前个体适应值与个体最优解的适应值比较, 选择较优个体的位置作为新的个体最优解, 从新的个体最优解中选择最优个体的位置作为新的全局最优解.
4.3 与其它算法比较
其中,
比较本文算法与IPSO算法[10]、LDPSO算法[14]的收敛性. 初始时
表 1 环境变化前后算法收敛到最优解的平均迭代次数比较
| offset | IPSO | LDPSO | 本文算法 | |||
| before | after | before | after | before | after | |
| 0.00001 | 169.75* | 0* | 128.311+ | 0+ | 0 | 0 |
| 0.0001 | 175.0* | 0* | 无 | 无 | 0 | 0 |
| 0.001 | 174.4* | 0.25* | 132.17+ | 0+ | 0 | 0 |
| 0.01 | 177.9* | 12.4* | 无 | 无 | 106.39 | 8.23 |
| 0.1 | 167.4* | 54.7* | 126.79+ | 51.2+ | 100.12 | 24.86 |
| 1 | 162.3* | 104.95* | 112.44+ | 89.16+ | 122.46 | 34.83 |
| 10 | 167.1* | 159.75* | 无 | 无 | 97.63 | 23.64 |
IPSO算法和LDPSO算法在环境检测时考虑了种群多样性, 多样性较差时才响应环境变化. 而本文算法在所有适应值备选函数的最优解区域设置了勘探粒子, 环境变化当代就准确检测到环境变化, 立即采取响应策略. 响应环境变化时, IPSO算法和LDPSO算法都是对种群进行某种扩散运动, 并没有准确找出变化后的最优解所在的区域, 因此粒子有“迷茫期”, 环境变化后不能及时跟踪新的最优解. 而本文算法在变化后的最优解周围选取个体以适应新的环境, 更具有针对性, 因此本文算法收敛速度更快, 对动态环境适应性更强.
5 随机扰动标准差上限及环境检测与响应方法的有效性
本节针对受随机扰动的动态优化问题, 给出扰动前后环境检测无变化对应的随机扰动标准差的上限, 并检验本文环境检测与响应方法处理此类问题的有效性.
5.1 随机扰动标准差上限
为了使随机扰动不影响动态优化问题的环境检测与响应, 需在一定的概率下保证扰动后的最优解仍位于原最优解区域. 本节将给出扰动前后环境检测无变化对应的随机扰动标准差上限.
设定最优解位置度量
给定置信水平
由(5.2) 式可知, 要以
由于动态优化问题最优解的具体位置未知, 则
命题5.1 设原目标函数的最优解
(i) 固定
(ii) 固定
证
(i) 对任意的
因为
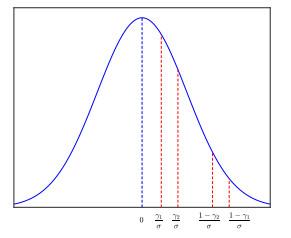
由图 3容易得
图 3
所以
(ii) 对任意的
由(5.3) 式可得
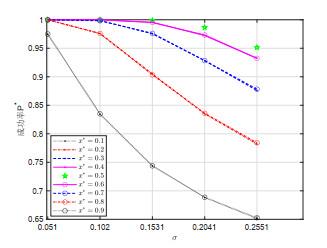
为验证上述结论, 设原最优解
图 4
从实验结果可以看出
(1) 关于区间中点对称的两个最优解的成功率曲线几乎完全重合, 因此扰动后的最优解仍位于原最优解区域所对应随机扰动标准差
(2) 对于同一
(3) 观察图 4容易发现
当
当
当
当
当
图像上其它点的成功率虽然没有达到0.95, 但是都大于0.65, 说明由
下面从算法性能角度确定扰动前后环境检测无变化所对应的随机扰动标准差
(1) 利用函数最优解区间收缩方法找出
(2)
(3) 设置算法运行60代, 前50代适应值函数为
表 2 两种算法的平均误差比较
| γ | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
| 算法一 | 0.0302 | 0.0820 | 0.1580 | 0.2739 | 0.4247 |
| 算法二 | 0.1169 | 0.1337 | 0.1595 | 0.1992 | 0.2589 |
由表 2可知, 当
加上服从均值为0, 标准差满足(5.4) 式的正态分布的随机扰动之后, 最优解发生了一定的偏移, 但以一定的概率保证了扰动后的最优解仍位于原最优解附近, 因此认为环境无变化, 仍可利用扰动前的环境信息追踪新的最优解.
5.2 改进方法处理受随机扰动动态优化问题的有效性
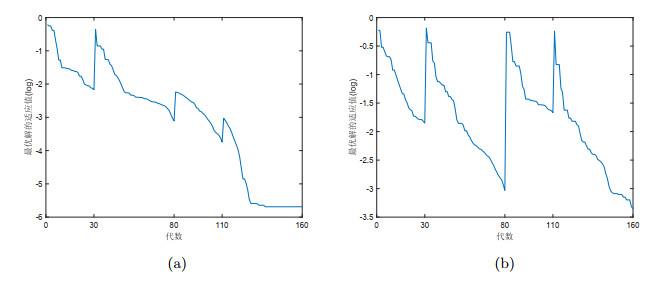
图 5
分别计算两种算法每代全局最优解适应值的误差并求平均, 可得原算法的平均误差为0.0313, 不含记忆机制的算法的平均误差为0.0696, 原算法的平均误差更小. 由此可知, 本文算法的响应策略中含有记忆机制, 在重复出现的环境中跟踪最优解的性能更为优良.
测试函数2 (移动峰函数): 动态优化问题目标函数如下
其中,
表 4 环境变化时算法的误差
| 环境变化 | 0 | 1 | 2 | 3 | 4 | 5 |
| 绝对误差 | 0.0033 | 0.0088 | 0.1263 | 0.3037 | 0.0397 | 0.0637 |
| 相对误差 | 0.0003 | 0.0003 | 0.0025 | 0.0304 | 0.0013 | 0.0013 |
分析表 4可知, 环境变化时算法的绝对误差和相对误差均在合理的范围内, 算法在每次环境变化后都可以逼近真实最优解, 环境检测的准确率高达
针对受随机扰动的动态优化问题, 本文提出的环境检测与响应方法不仅能够准确检测到环境变化, 对于最优解发生随机偏移的情况, 响应策略可直接调取记忆机制中存储的过去相同环境中的最后一代个体参与迭代, 充分利用了过去有用的环境信息, 同时也加快了算法收敛速度.
6 总结与展望
动态优化问题广泛存在于生产调度、人工智能、工程设计等诸多领域, 环境检测与响应是解决这类问题的前提. 然而在已有的环境检测与响应方法中, 还存在着环境检测不准确和过去的信息利用不充分等不足. 本文将正交试验设计思想用于环境检测, 给出了函数最优解区间收缩方法, 进而改进了动态优化问题的环境检测与响应方法. 之后, 确定了扰动前后环境检测无变化所对应的随机扰动的标准差上限, 并验证了本文环境检测与响应方法对于受随机扰动的动态优化问题的有效性.
本文提出的环境检测与响应方法通过正交试验设计对适应值备选函数预集成处理, 即利用函数最优解区间收缩方法找出所有适应值备选函数的最优解所在区域, 在此基础上设置勘探粒子检测环境变化, 提高了环境检测的准确性. 环境变化后, 根据最优解变化情况采取有针对性的响应策略, 并引入记忆机制存储环境信息, 当环境重复出现时, 直接利用之前环境中的最后一代个体进行迭代, 充分利用了过去有用的环境信息. 实验结果表明该方法能够准确检测并跟踪最优解的变化, 提高了算法对动态环境的适应能力. 因正交试验设计受因素个数的限制, 故本文提出的环境检测与响应方法难以处理高维自变量动态优化问题, 将在后续的工作中尝试利用灵敏度分析方法进行降维处理.
参考文献
一种求解动态优化问题的免疫文化基因算法
DOI:10.19734/j.issn.1001-3695.2018.03.0165 [本文引用: 1]
An immune cultural genetic algorithm for solving dynamic optimization problems
DOI:10.19734/j.issn.1001-3695.2018.03.0165 [本文引用: 1]
Evolutionary optimization in uncertain environments-a survey
DOI:10.1109/TEVC.2005.846356 [本文引用: 1]
Evolutionary optimization in non-stationary environments
Adaptive Particle Swarm Optimization: Detection and Response to Dynamic Systems//Proceedings of the 2002 Congress on Evolutionary Computation
Tracking changing extrema with adaptive particle swarm optimizer
动态环境下一种改进的自适应微粒群算法
DOI:10.3321/j.issn:1000-6788.2006.03.006 [本文引用: 1]
An improved adaptive particle swarm optimization algorithm in dynamic environment
DOI:10.3321/j.issn:1000-6788.2006.03.006 [本文引用: 1]
求解动态优化问题的改进差分进化算法
DOI:10.3969/j.issn.1000-1220.2013.12.036 [本文引用: 1]
An improved differential evolution algorithm for solving dynamic optimization problems
DOI:10.3969/j.issn.1000-1220.2013.12.036 [本文引用: 1]
动态环境下基于种群多样性的微粒群算法
DOI:10.3969/j.issn.1004-731X.2007.21.021 [本文引用: 2]
Particle swarm optimization algorithm based on population diversity in dynamic environment
DOI:10.3969/j.issn.1004-731X.2007.21.021 [本文引用: 2]
动态环境下一种改进的微粒群算法
DOI:10.3321/j.issn:1000-6788.2008.04.013 [本文引用: 4]
An improved particle swarm algorithm in dynamic environment
DOI:10.3321/j.issn:1000-6788.2008.04.013 [本文引用: 4]
动态环境下分布式自适应粒子群优化算法
Distributed adaptive particle swarm optimization algorithm in dynamic environment
动态环境下的种群扩散粒子群优化算法
DOI:10.3969/j.issn.1000-3428.2010.19.008 [本文引用: 1]
Population diffusion particle swarm optimization algorithm in dynamic environment
DOI:10.3969/j.issn.1000-3428.2010.19.008 [本文引用: 1]
基于对称粒子群算法的动态环境问题求解
Dynamic environmental problem solving based on symmetric particle swarm algorithm
一种新的求解动态连续优化的分层粒子群算法
A new hierarchical particle swarm optimization algorithm for dynamic continuous optimization
求解动态优化问题的多种群骨干粒子群算法
Multi-group backbone particle swarm optimization algorithm for solving dynamic optimization problems
求解动态优化问题的多种群竞争差分进化算法
Multi-group competition differential evolution algorithm for solving dynamic optimization problems
基于正交设计的动态多目标优化算法
Dynamic multi-objective optimization algorithm based on orthogonal design
动态环境下基于马氏链预测和记忆机制的遗传算法
Genetic algorithm based on markov chain prediction and memory mechanism in dynamic environment
Optimization in dynamic environments: a survey on problems, methods and measures