1 引言
随机数是许多应用中的关键因素, 在数值模拟计算、机器学习、密码学等方面起到非常重要的作用. 任何确定性算法都无法产生真正的随机数, 因此伪随机数发生器(pseudo random number generator, PRNG) 产生的随机数序列, 严格意义上来说不是真正的随机数序列, 但在实际应用中希望这些序列在某种意义上类似于真正的随机数序列, 也就是具有真正的随机数序列的一些统计性质, 比如独立性、均匀性和不可预测性等. 有两类测试方法用于评估PRNG的性能——理论测试和统计测试. 理论测试检查给定发生器的内在结构, 不一定需要生成随机数序列, 例如晶格测试[1]和光谱测试[2], 这类测试对每一类发生器都是不同的. 而统计测试是在PRNG产生的序列上进行的, 不需要知道它是如何产生的. 这类测试的主要目的是检查由PRNG产生的伪随机数序列是否具有类似于真正随机数序列的统计性质, 比如独立性、均匀性等.
统计测试试图找到反对零假设(
PRNG的随机性通常以能否通过检验均匀性、独立性或者不可预测性的统计测试来衡量, 但所有PRNG相比较, 仍然无法确定哪种发生器最好, 因为它们没有定量分析, 现有的随机性测试仍缺乏PRNG之间的比较手段[7]. 因此, 分析每个PRNG的随机性性能, 或者比较PRNG的随机性仍是一项重要任务. 单个统计测试的结果通常以
近年来, 一些新的测试方法被引入用来对PRNG进行严格的测试. 这类方法的核心思想是: 选择一些适用于真正随机数序列的概率定律, 并将相应统计量的理论分布与给定PRNG生成的伪随机数序列的经验分布进行比较, 比如可以根据在零假设下经过适当计算所得统计量的
1998年, Rudnick和Sarnak提出了
论文结构组织如下: 第二节介绍了典型的伪随机数发生器、泊松对相关的概念以及相关定理; 第三节引入基于泊松对相关的PRNG的测试方法; 第四节介绍分析PPC测试对多个PRNG的测试结果; 最后总结全文.
2 伪随机数发生器和泊松对相关
2.1 伪随机数发生器
伪随机数发生器是一种能够产生具有某些随机性的数字序列的确定性算法, 利用数学公式迭代产生随机数. 下面按照Asmussen和Glynn的描述给出一个严格的定义[13].
定义2.1 一个伪随机数发生器定义在一个5元组
对于
本文提出的PPC测试方法被用于测试不同的伪随机数发生器, 包括线性同余发生器、RANDU、MT19937-32[14]、Matlab.rand函数、BBS发生器、Python.random库中random函数、Excel.RAND函数、SPSS.RV.UNIFORM函数、多重递归发生器以及基于无理数
线性同余发生器(Linear Congruential Generator, LCG)是利用求余运算来产生随机数, 其递推公式为
其中
多重递归发生器(Multiple Recursive Generator, MRG) 是线性同余发生器的一个自然推广, 其递推公式为
其初始值
Blum Blum Shub(BBS)生成器是由Lenore Blum, Manuel Blum和Michael Shub于1986年共同提出的一种非线性同余发生器, 其递推公式为
其中
基于无理数
2.2 泊松对相关(PPC)
1998年Rudnick和Sarnak提出了在
则称该序列满足泊松对相关, 其中
泊松对相关是对
定理2.1[16] 若实数序列
即当
证 令
记
因此
于是
令随机变量
那么
所以随机变量
则有
即对任意
等价于
即当
泊松对相关与均匀分布之间的关系同样也备受关注, Larcher和Grepstad以及Aistleitner等人都证明了满足泊松对相关的
序列服从均匀分布可以看作是一种伪随机性, 而
3 基于泊松对相关性的测试方法
本节利用
则PRNG的每一组生成序列都可以产生一个PPC序列
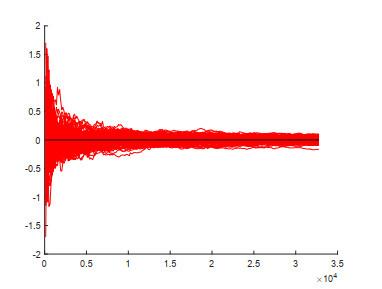
图 1
此时判别伪随机数序列是否满足泊松对相关可转化成判断当
由图 1可以看出, PPC折线图的波动随着
PPC测试方法的重点在于参数
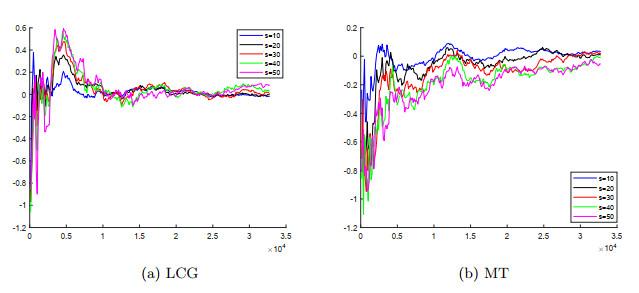
图 2
为了更直观地感受
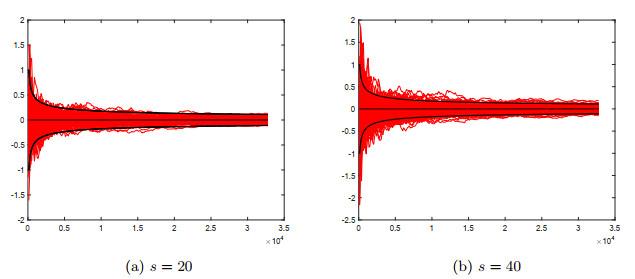
图 3
在任意取定
(1) 由PRNG产生PPC折线图.
由PRNG生成若干个相同长度的伪随机数序列, 则可以产生若干个
其中
(2) 处理
图 1显示由生成的伪随机数序列产生的折线图振动幅度初始时较大后来逐渐变小, 且PPC折线图在
(3) 利用幂函数进行拟合.
接下来取修改后每组数据
即不同的
(4) 综合所有发生器的拟合结果, 选取合适的参数
对于收敛速度
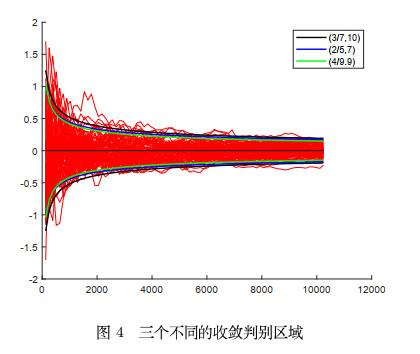
图 4
图 4中两条黑色线表示收敛区域
关于阈值
(1) 固定
(2) 固定
(3) 固定
4 测试结果
本文认为可以通过PPC统计量
本节展示一些广泛使用的PRNG的测试结果, 这些PRNG是用Matlab编程语言实现的. 我们将PPC测试应用于不同的PRNG, 以及由
具体的PPC测试PRNG的实验步骤如下.
(1) 由给定的PRNG生成100组长为
(2) 确定参数
(3) 选择合适的收敛判别标准, 计算PPC折线图落在判别区域内的点的占比
表 1给出了每个发生器生成的100个伪随机数序列产生的PPC序列落在区域
表 1 生成序列的子序列产生的PPC序列落在收敛域中的结果
| PRNG | 标准差 | 变异系数 | |
| LCG | 0.9810 | 0.0314 | 0.0320 |
| MT | 0.9761 | 0.0438 | 0.0448 |
| SPSS | 0.9759 | 0.0435 | 0.0446 |
| RANDU | 0.9725 | 0.0478 | 0.0492 |
| MRG | 0.9717 | 0.0517 | 0.0532 |
| Matlab | 0.9713 | 0.0610 | 0.0628 |
| Python | 0.9704 | 0.0621 | 0.0640 |
| Excel | 0.9672 | 0.0808 | 0.0835 |
| BBS | 0.9647 | 0.0962 | 0.0998 |
| 0.9453 | 0.1013 | 0.1072 | |
| 0.1478 | 0.0287 | 0.1945 |
从表 1中可以看出, 前9种发生器生成的100组伪随机数序列的PPC测试结果的标准差和变异系数都小于0.1. 变异系数较小说明同一个发生器生成的伪随机数序列的PPC测试结果
基于无理数
图 5
本文选用基本的一级测试方法卡方检验和序列检验来测试生成序列的均匀性, 游程检验和自相关检验来测试伪随机数序列的独立性, 表 2显示了每个发生器生成的的100个实数序列通过基本测试的比例以及在三个不同判别标准下的PPC测试结果.
表 2 生成序列通过基本测试的比例和PPC测试的结果
| PRNG | 卡方检验 | 序列检验 | 游程检验 | 自相关检验 | |||
| LCG | 0.9810 | 0.9676 | 0.9230 | 99% | 99% | 98% | 97% |
| MT | 0.9761 | 0.9602 | 0.9167 | 100% | 100% | 99% | 100% |
| SPSS | 0.9759 | 0.9584 | 0.9173 | 98% | 98% | 99% | 99% |
| RANDU | 0.9725 | 0.9568 | 0.9162 | 100% | 99% | 94% | 99% |
| MRG | 0.9717 | 0.9557 | 0.9157 | 99% | 98% | 100% | 100% |
| Matlab | 0.9713 | 0.9504 | 0.9046 | 99% | 98% | 100% | 100% |
| Python | 0.9704 | 0.9541 | 0.9134 | 97% | 98% | 100% | 100% |
| Excel | 0.9672 | 0.9506 | 0.9116 | 100% | 99% | 99% | 97% |
| BBS | 0.9647 | 0.9479 | 0.9084 | 100% | 100% | 99% | 100% |
| 0.9453 | 0.9209 | 0.8593 | 98% | 0% | 0% | 100% | |
| 0.1478 | 0.1389 | 0.1229 | 100% | 0% | 0% | 0% |
由表 2可知前面几种发生器的PPC测试结果相差不大, 为了判断这些发生器的PPC测试结果是否有明显的差异, 对前9种发生器的PPC测试结果进行单因素方差分析. 结果显示在0.01的显著性水平下, 所研究的PRNG性能之间不存在显著差异. 但是这9个发生器的性能明显优于基于无理数
总之, 当生成的伪随机数序列的长度较短时(本文只检验了长度为
通过对比三个不同的收敛判别区域下各发生器的PPC测试结果, 可以看出阈值
5 结论
PRNG在数值模拟计算[26]、密码学[27]等许多方面都起到非常重要的作用. 本文提出了一种基于泊松对相关的PRNG的测试方法, 该方法灵活稳健, 可操作性强, 并且具有强有效的理论支撑, 作为一个测试
此外不同的PRNG收敛速度都会有一定的差异, 文献[12] 认为实数序列产生PPC折线图的收敛速度可以用来衡量序列的均匀性和独立性, 所以在后续的工作中将继续研究参数s, 收敛速度以及收敛判别区域之间的关系, 对判别标准做出调整, 使得该测试方法更加严格, 更容易揭示生成序列以及发生器的一些缺陷, 有助于设计更稳健可靠的测试套件, 进而评估由PRNG生成的伪随机数序列的质量.
参考文献
TestU01: A C library for empirical testing of random number generators
DOI:10.1145/1268776.1268777 [本文引用: 1]
A visual analysis method of randomness for classifying and ranking pseudo-random number generators
On testing pseudorandom generators via statistical tests based on the arcsine law
On statistical distance based testing of pseudo random sequences and experiments with PHP and Debian OpenSSL
The pair correlation function of fractional parts of polynomials
DOI:10.1007/s002200050348 [本文引用: 2]
On pair correlation and discrepancy
DOI:10.1007/s00013-017-1060-1 [本文引用: 3]
Mersenne twister: a 623-dimensionally equidistributed uniform pseudo-random number generator
DOI:10.1145/272991.272995 [本文引用: 1]
A search for good multiple recursive random number generators
DOI:10.1145/169702.169698 [本文引用: 1]
Localized quantitative criteria for equidistribution
DOI:10.4064/aa170410-22-5 [本文引用: 1]
Pair correlations and equidistribution
A pair correlation problem, and counting lattice points with the zeta function
DOI:10.1007/s00039-021-00564-6 [本文引用: 1]
Pair correlation and equidistribution on manifolds
DOI:10.1007/s00605-019-01308-3 [本文引用: 1]
Equidistribution of Kronecker sequences along closed horocycles
DOI:10.1007/s00039-003-0445-4 [本文引用: 1]
On the pair correlations of powers of real numbers
数据流的非平稳性度量
Nonstationarity measure of data stream
基于非平稳性度量的彩票数据实证分析
Empirical analysis of lottery data based on non-stationarity measure
线性回归模型参数估计方法的分辨率
Parameter resolution of estimation methods for linear regression models