1 引言
近年来, 保险公司的最优投资与再保险问题是精算界关注的热点问题之一. 在金融市场中的投资是保险公司获取利润的重要经营活动, 而再保险是保险公司规避或转移过度风险的主要手段. 适当的投资与再保险策略不仅可以对索赔的风险进行对冲, 而且能够增加收益. 因此如何合理地分配投资与购买再保险成为保险公司需要面对的重要问题.
在以往的研究中, 大多数学者基于三种优化准则来研究最优投资与再保险问题, 第一种是终端财富期望效用最大化准则, 其中常用的效用函数有指数效用函数[1−2], 和幂效用函数[3−4]; 第二种是最小化破产概率准则[5−6]; 第三种是均值-方差准则[7−8]. 基于这些优化准则来研究最优策略忽略了决策者可能具有损失厌恶特征, 事实上, 许多决策者不可能在任何时刻都保持理性, Kahneman和Tversky[9]从认知心理学的角度研究了决策者的决策行为, 并提出了损失厌恶的概念. 现实中的许多决策者关注的不是财富本身的绝对水平, 而是与一个预设参考点相关的得失情况, 通常决策者对损失比对收益更敏感, 基于这些考虑, Kahneman和Tversky[9]提出用
通常保险公司将资金进行集中管理, 保险公司的社会目标要求其拥有偿付能力, 但实际上任何一个公司在运营过程中都存在破产风险. 如果保险公司破产, 无疑是将风险再次转移到保险购买者身上, 因此需要保证保险公司不会破产, 这意味着保险公司的财富在终端时刻必须不低于一个合适的正水平, 以保证公司的正常运行. 以上提到的
在上述文献研究的基础上, 该文同时考虑了决策者的损失厌恶特征, 以及保险公司在实际运营过程中面临的通胀风险和破产风险, 对保险公司的最优投资与再保险问题进行了进一步的研究. 在假设保险公司决策者是损失厌恶的非理性人的前提下, 该文充分结合实际, 用
该文其余部分安排如下: 在第二节, 我们给出了指数债券, 股票, 无风险资产以及盈余过程模型, 介绍了
2 模型建立
设
假设金融市场由三种可交易的资产组成: 通胀指数债券, 无风险资产和股票. 为了描述通货膨胀风险, 定义服从几何布朗运动的随机价格水平
其中
指数债券
其中
无风险债券
其中
股票
其中
在不考虑再保险情形时, 假设保险盈余过程
其中
其中
其中
则
这是经典的保险盈余扩散过程模型[22]. 因此(2.5) 式是推广的保险盈余扩散过程模型, 其中参数均假设为时间
保险公司可通过购买再保险或获取新业务来分散保险风险,
除了购买再保险或获取新业务, 保险公司还将资金投资于金融市场来获取收益. 设
其中
实证结果表明, 决策者习惯根据某些参考水平做出决定, 而且损失比收益更容易引起不适, 即损失引起的负面情绪通常大于同等收益引起的正面情绪. 此外, 大多数决策者对收益是风险厌恶的, 但当他们必须对潜在的损失做出决策时, 多数经济个体会转变为风险偏好者. 基于此, Kahneman和Tversky[9]提出了
其中,
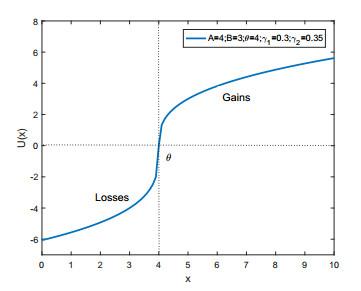
图 1
假设保险公司为保证公司的正常运营设定了最低绩效保障, 为了方便分析不同的最低绩效保障对最优策略的影响, 设最低绩效保障为常数
定义2.1 投资与再保险策略
(1)
(2) 对于所有的
(3) 随机微分方程(2.7) 存在唯一强解;
(4)
所有可容许策略构成的集合记为
保险公司在可容许策略集
3 最优策略
首先给出最低绩效保障
以及随机折现因子
下面引理在使用鞅方法时会用到.
引理3.1 令
证 由(3.1) 和(3.2) 式及Itô公式得
所以
定理3.1 在
保险公司的最优终端财富值为
其中
证明过程见附录A.
注3.1 定理3.1表明, 损失厌恶型保险公司的最优终端财富的分布是不连续的, 并将达到
在获得最优终端财富值以后, 我们可以计算得到
定理3.2
其中
最优投资与再保险策略为
其中
若
则最优投资与再保险策略可写为
证明过程见附录B.
注3.2 注意到
若进一步假设模型不存在最低绩效保障, 并且再保险为廉价情形, 即
4 数值模拟
本节对投资与再保险策略进行了数值模拟, 并基于这些模拟结果, 给出了一些经济学解释. 本节主要讨论最优投资与再保险策略关于
以下的分析均为
参考点是损失厌恶型决策者的关键变量, 首先讨论参考点对投资与再保险策略的影响. 如图 2所示, 随着参考点的增大, 保险业务的自留比例以及投资于股票和指数债券的比例呈“
图 2
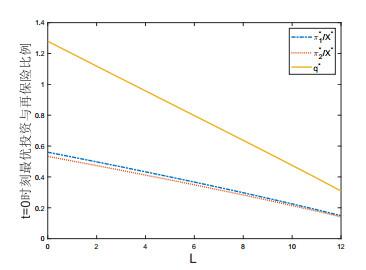
图 3表示最低绩效保障
图 3
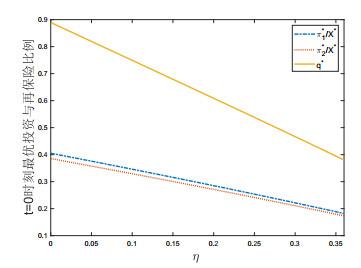
图 4描述保险公司的安全负荷因子
图 4
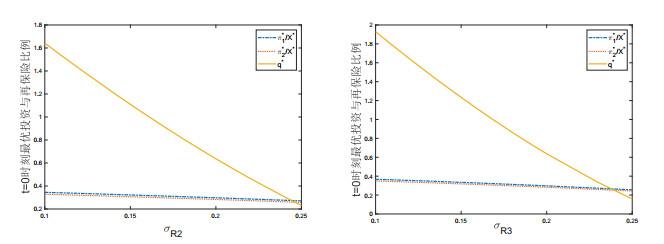
图 5描述了盈余过程的波动率
图 5
5 小结
该文研究了损失厌恶型保险公司的最优投资与再保险策略问题. 假设保险公司可将资金投资于无风险资产, 股票以及指数债券, 并可购买比例再保险. 该文与实际紧密联系, 考虑了保险公司决策者损失厌恶的特征, 并且考虑了保险公司在实际运营过程中的破产风险和通胀风险, 以期望
该文的研究中假设股票及通胀指数债券价格过程信息是完全可观测的, 并未考虑在实际中它们仅是部分观测的情形. 此外, 我们还可以考虑投资带抑制的情形, 比如卖空抑制. 对于这些有意义的问题, 我们将继续深入研究.
附录A
在此附录中, 为了方便, 用
其中
我们可以将优化问题(A.2) 分为两部分来求解. 先假设
再求解有关
(1) 首先求解问题(A.3), 省略
效用函数(2.12) 是先凸后凹的, 将其重写为以下分段形式
我们分别求出(A.5) 式在
求得局部最优解为
若
a) 当
全局最优解为
b) 当
当
综合以上讨论可知问题(A.5) 的最优解
(2) 接下来求解问题(A.4) 以确定最优的
若
由
(3) 最后验证由(3.5) 式给出的
则
其中第一个不等式成立是由于
附录B
由引理3.1知
(1) 计算式(B.1)的第一部分
即
设
则
由于
根据(B.4) 式和(B.5)式可得
由此可得
令
(2) 计算式(B.1) 的第二部分
则
其中
(3) 计算式(B.1) 中的
综上所述
再根据
根据(2.7)式以及
记
由(B.14)式即得
最后验证
从而
参考文献
指数保费准则下的最优投资和比例再保险
Optimal investment and proportional reinsurance under exponential premium calculation
Optimal investment for an insurer: the martingle approach
DOI:10.1016/j.insmatheco.2006.05.003 [本文引用: 1]
Optimal reinsurance and investment strategies for insurer under interest rate and inflation risks
DOI:10.1016/j.insmatheco.2014.01.007 [本文引用: 2]
Asset liability management for an ordinary insurance system with proportional reinsurance in a CIR stochastic interest rate and Heston stochastic volatility framework
索赔次数为复合Poisson-Geometric过程下的破产概率和最优投资和再保险策略
Ruin probability and optimal investment and reinsurance strategy for an insurer with a compound poisson-geometric risk process
On reinsurance and investment for large insurance portfolios
DOI:10.1016/j.insmatheco.2007.04.002 [本文引用: 1]
Optimality of excess-loss reinsurance under a mean-variance criterion
DOI:10.1016/j.insmatheco.2017.05.001 [本文引用: 1]
Optimal investment-reinsurance strategies with state dependent risk aversion and VaR constraints in correlated markets
DOI:10.1016/j.insmatheco.2018.11.007 [本文引用: 1]
Prospect theory: An analysis of decision under risk
Prospect theory and asset prices
DOI:10.1162/003355301556310 [本文引用: 1]
Optimal portfolio choice under loss aversion
DOI:10.1162/0034653043125167 [本文引用: 1]
Optimun consumption and portfolio policies when asset prices follow a diffusion process
DOI:10.1016/0022-0531(89)90067-7 [本文引用: 3]
Explicit solution of a general consumption/investment problem
DOI:10.1287/moor.11.2.261 [本文引用: 2]
基于损失规避行为的最优保险投资与再保险策略选择
Optimal Investment and Reinsurance Strategy Selection Based on Behavior of Loss Aversion
S型效用下比例再保险的最优投资策略
Optimal proportional reinsurance and investment problem for insurers with loss aversion
Beating a moving target: Optimal portfolio strategies for outperforming a stochastic benchmark
DOI:10.1007/s007800050063 [本文引用: 1]
Optimal investment with minimum performance constrains
DOI:10.1016/S0165-1889(99)00066-4 [本文引用: 2]
随机利率及随机收益保证下的投资策略
DOI:10.3969/j.issn.1007-6093.2010.04.010 [本文引用: 1]
Investment strategies in the presence of a minimum performance guarantee under stochastics interest rate
DOI:10.3969/j.issn.1007-6093.2010.04.010 [本文引用: 1]
通货膨胀影响下基于随机微分博弈的最优再保险和投资
DOI:10.3969/j.issn.1001-4268.2016.02.004 [本文引用: 1]
Optimal reinsurance and investment for stochastic differential games with inflation influence
DOI:10.3969/j.issn.1001-4268.2016.02.004 [本文引用: 1]
Optimal reinsurance-investment strategy under risks of interest rate, exchange rate and inflation
DOI:10.1007/s11009-018-9630-7 [本文引用: 1]
Asset allocation under loss aversion and minimum performance constraint in a DC plan with inflation risk
DOI:10.1016/j.insmatheco.2017.05.009 [本文引用: 1]
Lifetime portfolio selection under uncertainty: the countinous time model
Optimum consumption and portfolio rules in a continuous-time model
DOI:10.1016/0022-0531(71)90038-X [本文引用: 1]