1 引言
这一节, 首先介绍一下研究背景, 并给出一些基本概念和引理, 这些将在本文后续定理的证明中被用到.
1.1 背景介绍
本文将研究具有以下形式的高维非齐次标量守恒律方程
本文的结构分为以下几个部分: 第二节, 先列出本文的主要定理, 其证明过程放在后面几节; 第三节, 计算从初值间断发出的稀疏波的轮廓:
1.2 预备知识
定义1.1[7] 假设方程
成立, 那么就称
定义1.2(Rankine-Hugoniot条件)[12] 假设
则
其中
定义1.3(
成立, 则称Riemann问题
定义1.4
成立, 则称
给定下面
其中
根据文献[5], Riemann问题(1.6)–(1.7) 的解由下面命题给出.
命题1.1[5] 假设
其中
而且, 激波曲面由下面方程给出
激波曲面
其中
确定的稀疏波区域上的全局隐函数
2 主要定理
本文主要研究下面二维非齐次Burgers方程Riemann问题的解及其结构
其中
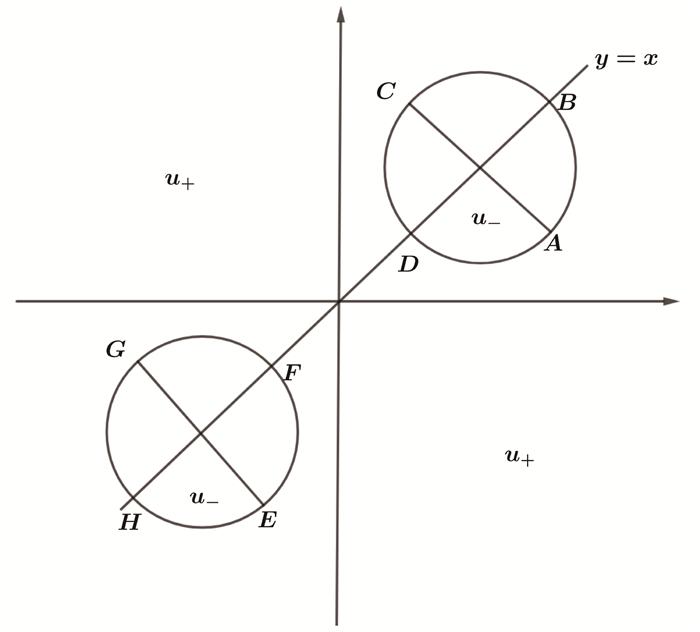
图 1
这一节先给出主要的定理: 定理2.1–2.3, 这三个定理的证明过程放在第3–5节中.
定理2.1 若
其中
解
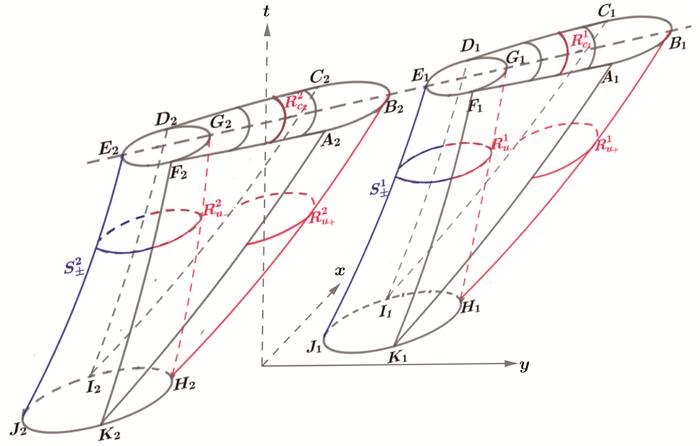
图 2
图 2
当
注2.1
定理2.2 若
其中
解
图 3
图 3
当
注2.2
注2.3
定理2.3 若
其中
解
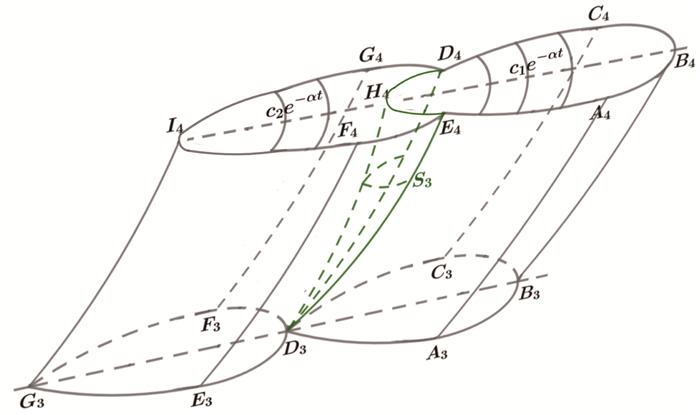
图 4
当
注2.4
注2.5
事实上,
注2.6 由引理3.8, 当
这里
注2.7 根据引理4.2, 当
这里
本文接来下的章节将通过引理3.1–3.8, 4.1–4.2证明定理2.1–2.3.
3 定理2.1的证明
先求解(2.1)–(2.2) 的特征方程
得到
记
将
分别由图 1中弧
将
分别由图 1中弧
下面再讨论由初值间断
3.1 从 M_1=0
由(3.1)–(3.2)式,
第一步 求解
由命题1.1,
其中
唯一确定的稀疏波区域上的全局隐函数
对于固定的
求解(3.5) 式中的隐函数
在
以及
设
则
由命题1.1,
激波曲面为
第二步 处理
由命题1.1, 激波曲面
将
而后对任意固定的
记
若
因为
从而关于
引理3.1 若
在引理3.1这种情形下,
引理3.2 若
在引理3.2这种情形下, 新的激波会在
求解
设
则在
考虑
其特征方程为
其中
求解常微分方程(3.14).
首先计算(3.14) 式中的
由(3.14) 式得到
又根据(3.11) 式得到
从而
由(3.15)–(3.16) 式可得
根据(3.7)和(3.17) 式就有
其次, 简化方程(3.14) 并求其解.
由(3.14)和(3.18)式, 有
又由(3.14), (3.16)式, 进一步得到
令
则(3.14) 式可转化为
容易验证方程(3.22) 的积分因子为
从(3.17) 式导出
将(3.21) 和(3.24) 式代入(3.23) 式得到
事实上, 容易验证
验证
从而
通过(3.25) 式又得到
于是
由(3.26)–(3.27) 式即可得到
也就是
验证
也就是说
讨论激波曲面
接下来讨论
对
若
此外, 由
也即
由(3.9) 式即得
当
另外
于是, 根据(3.28)和(3.30) 式可得: 当
至此, 在不考虑
接下来, 讨论由初值间断
3.2 从 M_2=0
由(3.3)–(3.4)式,
事实上, 初值间断
从初值间断
其中
确定的稀疏波区域上的唯一全局隐函数
由(3.32) 式得出隐函数
其中
设
则
从初始间断
激波曲面为
关于
引理3.3 若
在引理3.3这种情形下,
引理3.4 若
在引理3.4这种情形下, 新的激波会在
设
则在
而且
此外, 当
当
至此, 在不考虑
考虑
令
若
由
若
而后就有
由二次方程(3.43) (
类似地, 关于
引理3.5 若
引理3.6 若
当
接下来类似处理
将
则
那么由
由
将
因为当
注意到
于是, 关于
引理3.7 若
引理3.8
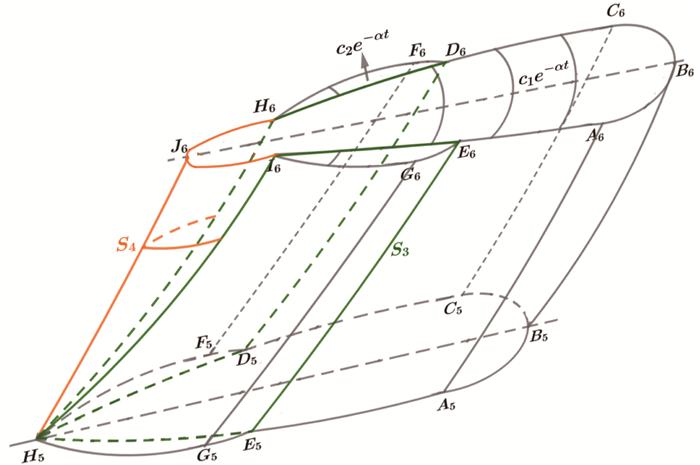
图 5
引理3.7结合引理3.2, 引理3.4以及引理3.5, 就能得到定理2.1.
4 定理2.2的证明
根据引理3.8, 已经得到了定理2.2的结论(i). 此外, 若
求解激波
考虑
其特征方程组为
其中
首先计算(4.3) 式中的
由(4.3) 式容易得到
令
则
从(4.1), (4.4)和(4.5) 式可得
由
进而由(4.4) 式得到
由(4.6)–(4.7)式, 有
于是由(3.7) 式以及(3.33) 式有
其次, 化简并求解方程(4.3).
由(4.3)和(4.10)式, 有
从(4.8) 式进一步得到
令
从而(4.3) 式能转化为如下常微分方程
求解方程(4.14) 得
由(4.9) 式, 有
将(4.13)和(4.16) 式代入(4.15) 式得到
其中
因为
至此, 我们已经弄清楚了激波
根据
当
显然,
令
因此, 对
若
即
则当
若
即
则
也就是说
当
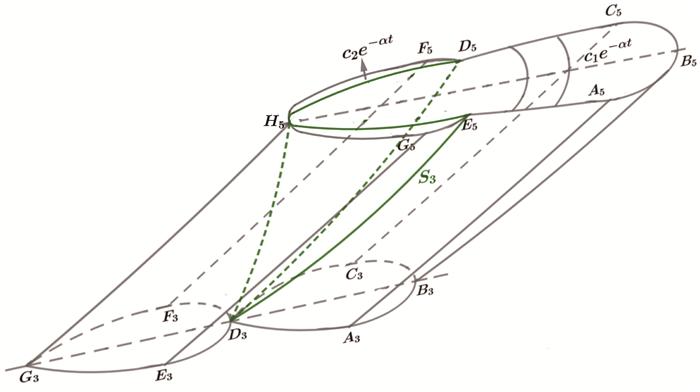
图 6
进而, 关于激波
引理4.1 若
引理4.2 若
引理4.1结合引理3.8, 定理2.2得证.
5 定理2.3的证明
由引理4.2, 若
求解激波
激波
考虑到
其特征方程为
其中
首先计算方程(5.3) 中的
由(5.3) 式可得
令
则
由(5.1)式, 有
从而
求解方程(5.7), 得到
因此
进而由(5.4) 式可得
于是由(3.7)和(5.9) 式, 有
其次, 简化并求解方程(5.3).
由(5.3)和(5.10) 式, 有
由(5.1) 以及(5.8)式, 进一步得到
令
则特征方程(5.3) 就此转化为如下常微分方程
容易验证方程(5.14) 的积分因子为
由(5.9) 式, 有
将(5.13)和(5.16) 式代入(5.15) 式得到
其中
因为
至此, 已经得到了
参考文献
Uniqueness and stability theorem for the generalized solution of the initial-value problem for a class of quasi-linear equations in several sapce variables
DOI:10.1007/BF00276782 [本文引用: 1]
Global solutions of the Cauchy problem for Quasi-linear first-order equations in several spaces variables
The Riemann problem and interaction of waves in Gas Dynamics
Structure of Riemann solutions for 2-dimensional scalar conservation laws
DOI:10.1006/jdeq.1996.0065 [本文引用: 1]
Global structure of admissible solutions of multi-dimensional non-homogeneous scalar conservation law with Riemann-type data
DOI:10.1016/j.jde.2017.03.007 [本文引用: 6]
Shocks and rarefactions in two space dimensions
DOI:10.1007/BF00251604 [本文引用: 1]
First order quasilinear equations in several independent variables
DOI:10.1070/SM1970v010n02ABEH002156 [本文引用: 2]
Nonlinear resonance for quasilinear hyperbolic equation
DOI:10.1063/1.527751 [本文引用: 1]
On the Gunn effect and other physical examples of perturbed conservation equations
DOI:10.1017/S0022112070001854 [本文引用: 1]
Two-dimensional Riemann problem for scalar conservation laws
DOI:10.1006/jdeq.2001.4124 [本文引用: 1]
The space BV and quasilinear equations
DOI:10.1070/SM1967v002n02ABEH002340 [本文引用: 1]
The Riemann problem in two space dimensions for a single conservation law
Multi-dimensional Riemann problem of scalar conservation law
DOI:10.1016/S0252-9602(17)30629-X [本文引用: 4]
The singular structure of non-selfsimilar global solutions of n dimensional Burgers equation
Global smooth solution of multi-dimensional non-homogeneous conservation laws
Generalized characteristic analysis and Guckenheimer structure
Two-dimensional Riemann problem for a single conservation law