1 引言
本文将运用边界层函数法研究一类带有积分初边值条件的弱非线性临界情况下的奇异摄动问题, 不但构造了一致有效的形式渐近解, 而且证明了解的存在性、唯一性, 并给出一个例子来验证了我们的结果.
2 奇异摄动问题
考虑以下弱非线性临界情况带有积分初边值问题
其中
由于积分初边值条件的引入, 使得原本就很复杂的临界问题(2.1)–(2.2)变得更加复杂. 因此, 为了降低复杂程度, 将方程组(2.1)–(2.2)转化为如下等价奇异初边值问题
对以上复杂临界问题(2.1)–(2.2)作如下假设.
[H
令
得到退化方程的解
复杂临界问题(2.1)–(2.2)方程右端等于零, 求平衡点
得到方程的解
使方程(2.1), (2.2)右端在点
其中
[H
因此, 方程(2.1)–(2.2)具有临界稳定情形.
2.1 构造形式渐近解
使用边界层函数法构造渐近解, 系统(2.4)–(2.5)渐近级数
正则级数
边界层级数
利用边界层函数法可得正则部分的零次方程为
通过(2.13)式可求得
其中
求解边界层部分的零次主项的方程为
相对应的零次初边值条件为
由(2.15), (2.16)式求得:
求解正则部分一次主项的方程为
其中符号"
联立(2.13), (2.16), (2.17)式可得
其中
考虑(2.16), (2.17)式联立得到的如下边值问题
[H
联立(2.18), (2.19), (2.21)式可求得
以上
通过(2.15)式求得
其中
其中
零次主项
求解边界层级数一次主项方程为
其中
相对应的一次初边值条件为
通过(2.25), (2.26)式可求得
因此,
求解正则部分的二次项的方程为
其中
通过(2.28)式变换可得
其中
其中
由(2.17), (2.26), (2.28)式可得
联立(2.31), (2.32)式求得
以上
为了求得
由于方程(2.34)是非自共轭的, 不能直接套用公式. 但是, 可把(2.34)式化成自共轭方程后就能用公式
这里
一次主项
至此, 已确定了形式渐近解的全部零次及一次主项, 接下来, 给出确定渐近解
用归纳法可以证明渐近级数(2.10)中的以后各项
求解
对应的
求解
其中
由(2.37), (2.38)式可求得
因此,
求解
其中
此时, 由于归纳法假设, 我们前
通过(2.40)式变换可得
其中
其中
由(2.36), (2.37), (2.40)式可得
联立(2.43), (2.44)式得
以上
为了求得
由于方程(2.46)是非自共轭的, 不能直接套用公式. 但是, 可把(2.45)式化成自共轭方程后就能用公式
这里
由
因此,
3 解的存在唯一性证明
定理3.1 当满足条件[H
证 令
因此, 我们得到下面方程组
而
(1)
(2)
为了更加方便地分析, 对
其中
由(3.3)式可得
把它代入(3.3)式, 有
把(3.5)式写成等价的积分方程
不难看出算子
由于(3.3)式中的后两个关于
最后对(3.6)式采用逐次逼近法, 可证明方程(3.3)解的存在和估计
4 例子
讨论奇异摄动初边值问题
为了简化计算, 可把(4.1)式改写为
求解正则零次项、一次项的方程为
求解边界层零次项的方程为
以及零次初边值条件为
通过以上方法可解出零次主项为
从而求得问题(4.1)形式渐近解为
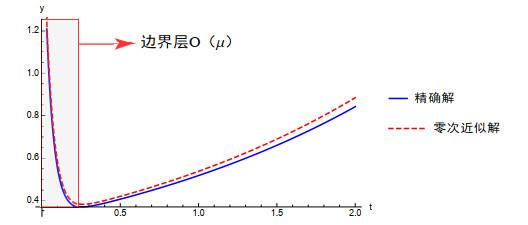
图 1
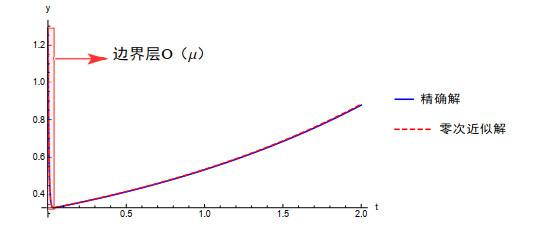
图 2
下面分别给出了在
5 总结
而在研究的过程中, 发现方程(2.1)中
(1) 当方程(2.1)右端
由(5.1)式可得
观察发现(5.2)式具有很强的非线性, 所以, 无法得到边界层
(2) 当方程(2.1)右端由于
(I) 当
由于带有无穷大初值, 故对于渐近解的边界层级数
将(5.4)式代入方程(5.3)可得
通过观察计算发现,
(II) 当
参考文献
On a system of singularly perturbed second-order quasilinear ordinary differential equations in the critical cases
On systems of two singularly perturbed quasilinear second-order equations
DOI:10.1007/s10958-008-0145-6 [本文引用: 1]
A class of singularly perturbed delayed boundary value problem in the critical case
DOI:10.1186/s13662-014-0331-4 [本文引用: 1]
Numerical solution of the singularly perturbed problem with nonlocal boundary condition
DOI:10.1007/BF02456971 [本文引用: 2]
A finite difference method for the singularly perturbed problem with nonlocal boundary condition
DOI:10.1016/j.amc.2003.11.035 [本文引用: 1]
具有积分边界条件的非线性二阶奇摄动问题
Nonlinear second-order singularly perturbed problems with integral boundary conditions
带有积分边界条件的奇异摄动边值问题的渐近解
DOI:10.3969/j.issn.1003-3998.2020.05.008 [本文引用: 2]
Asymptotic solutions of singularly perturbed boundary value problems with integral boundary conditions
DOI:10.3969/j.issn.1003-3998.2020.05.008 [本文引用: 2]