本文考虑如下广义绝对值方程组(GAVE)

(1.1) $ \begin{equation} Ax-|Bx-c|=d, \end{equation} $

其中$ A, B\in{{\Bbb R}} ^{n\times n} $, $ c $, $ d\in{{\Bbb R}} ^n $, $ |x| $表示对向量$ x\in{{\Bbb R}} ^n $按分量取绝对值.当$ B=I $ ($ I $为单位矩阵)且$ c=0 $时, GAVE (1.1)归结为绝对值方程组(AVE)

(1.2) $ \begin{equation} Ax-|x|=d. \end{equation} $

AVE (1.2)也是另外两类GAVE

(1.3) $ \begin{equation} Ax + B|x| = d \end{equation} $

和

(1.4) $ \begin{equation} Ax - |Bx| = d \end{equation} $

的特例.当$ c=0 $时, GAVE (1.1)变为GAVE (1.4).然而, GAVE (1.1)本质上和GAVE (1.3)不同.这是称GAVE (1.1)为一类新GAVE的原因.

近年来, 对GAVE/AVE的研究是一个热点问题.其原因主要包括两个方面:首先, 区间线性方程组的求解与AVE (1.2)息息相关^[13]; 其次, GAVE/AVE (1.1)–(1.4)与许多数学规划问题可以相互转化, 例如线性互补问题(LCP)、二次规划、双矩阵对策及均衡问题等^{[8, 10, 11]}.

对于AVE (1.2)和GAVE (1.3), 目前已有许多理论和算法方面的研究工作, 例如文献[8, 10, 12]等探究了方程(1.2)和(1.3)解的存在性及唯一性的充分或必要条件; 文献[3, 4, 9]及其中的参考文献建立了求解方程(1.2)和(1.3)的各类数值方法.但是, 对于GAVE (1.1)和(1.4)的研究还比较匮乏.据笔者所知, Wu^[14]首次研究了GAVE (1.4)解的存在唯一性条件, 而且文献[14]的结果可以被推广用来确定GAVE (1.1)的解的性质.然而, 目前还没有求解GAVE (1.1)的动力学模型.为此, 本文提出了求解GAVE (1.1)的动力学模型, 分析了所提出的模型的稳定性, 并用数值实验验证了模型的可行性和有效性.

本文余下部分组织如下:第2节陈述一些预备知识; 第3节提出了一个动力学模型来求解GAVE (1.1);第4节对动力学模型解的存在性和平衡点的稳定性进行分析; 第5节给出一个数值算例; 第6节对本文的研究内容做了简要总结.

本节给出本文所需的一些预备知识.

定义2.1^[2]  矩阵$ M\in{{\Bbb R}} ^{n\times n} $叫做$ P $ -矩阵, 如果对$ \forall\, 0\neq x\in{{\Bbb R}} ^n $, 存在分量$ x_k\neq0 $, 使得$ x_k(Mx)_k >0 $.

注2.1  显然, 正定矩阵是$ P $ -矩阵.

定义2.2^[6]  给定向量值函数$ F $: $ {{\Bbb R}} ^n\rightarrow {{\Bbb R}} ^n $, 称$ F $是$ \rm Lipschitz $连续的, 如果存在一个常数$ L>0 $, 使得对$ {\forall}x, y\in{{\Bbb R}} ^n $, 有

$ \begin{eqnarray*} ||F(x)-F(y)||\leq L||x-y||. \end{eqnarray*} $

引理2.1^[15]  设$ a, b\in{{\Bbb R}} $, 则$ a\ge 0, b\ge 0, ab=0 $当且仅当$ a+b=|a-b| $.

当$ a, b\in{{\Bbb R}} ^n $时, $ a\ge 0, b\ge 0, ab=0 $$ \Leftrightarrow $$ a_i\ge 0, b_i\ge 0, a_ib_i=0 (i=1, 2, \cdots, n) $, 故引理2.1的结果可以推广到$ {{\Bbb R}} ^n $上.

推广文献[14]中的定理3.2, 可得如下引理.

引理2.2  假设$ A+B $非奇异, 则GAVE (1.1)对$ \forall c, d\in{{\Bbb R}} ^n $有唯一解当且仅当$ (A-B){(A+B)}^{-1} $是$ P $ -矩阵.

在后续的稳定性分析中需要使用以下投影映射的性质.

引理2.3^[7]  设$ \Omega $是$ {{\Bbb R}} ^n $的一个非空闭凸子集, 则对$ {\forall}v\in{{\Bbb R}} ^n $, $ {\forall}u\in \Omega $, 有

$ {(v-P_{\Omega}(v))}^\top(u-P_\Omega(v))\leq0, $

其中$ P_{\Omega}[v] = \arg\min \{\|v-y\|:y\in \Omega \} $.

以下定理陈述了GAVE (1.1)和广义线性互补问题(GLCP)之间的关系, 这为后续动力学模型的建立奠定了基础.它的证明受文献[14]的启发.

定理2.1  GAVE (1.1)等价于以下GLCP:

(2.1) $ \begin{equation} \begin{array}{ll} Q(x) =(A+B)x-c-d\geq 0, \\ F(x) =(A-B)x+c-d\geq 0, \\ \langle Q(x), F(x)\rangle=0. \end{array} \end{equation} $

证  方程(1.1)可以表示成$ Ax-d=|Bx-c| $.令

$ \begin{eqnarray*} && u+v=Ax-d, \\ && u-v=Bx-c, \end{eqnarray*} $

则

$ \begin{eqnarray*} && u=\frac{(A+B)x - c - d}{2}, \\ && v=\frac{(A-B)x + c -d}{2}. \end{eqnarray*} $

从而由引理2.1, 定理得证.

本节最后根据文献[6]介绍自治动力系统的一些基本概念和理论.自治动力系统可表示为

(2.2) $ \begin{equation} \frac{{\rm d}x}{{\rm d}t}=f(x), \end{equation} $

其中, $ f $是从$ {{\Bbb R}} ^n $到$ {{\Bbb R}} ^n $的函数.关于自治动力系统的下述定义和定理, 可以参考文献[6, Chapters 2-3].

定义2.3  若$ f(x^*)=0 $, 则称$ x^* $为动力系统(2.2)的平衡点.

定义2.4  设$ x^* $是动力系统(2.2)的平衡点, 若对任意$ \epsilon>0 $, 存在$ \delta=\delta(\epsilon)>0 $, 使得当$ ||x(t_0)-x^*||<\delta $时

$ ||x(t;x(t_0))-x^*||<\epsilon, \quad {\forall}t\geq t_0, $

则称系统(2.2)的平衡点$ x^* $是稳定的.这里及后文中, $ x(t;x(t_0)) $表示在初始时刻$ t_0 $处取值为$ x(t_0) $时动力系统(2.2)对应的解.

定义2.5  若动力系统(2.2)的平衡点$ x^* $是稳定的, 且存在$ \delta>0 $, 使得当$ ||x(t_0)-x^*||<\delta $时

$ \lim\limits_{t\rightarrow +\infty}x(t;x(t_0))=x^*, $

则称系统(2.2)的平衡点$ x^* $是渐近稳定的.

对于动力系统(2.2), 有如下解的存在性定理.

定理2.2  假设$ f $: $ {{\Bbb R}} ^n\rightarrow {{\Bbb R}} ^n $是一个连续函数, 则对$ {\forall}t_0\geq0 $且$ x(t_0)=x_0\in {{\Bbb R}} ^n $, 系统(2.2)存在一个局部解$ x(t;x(t_0)) $, $ t\in[t_0, \tau] $, $ \tau>t_0 $.此外, 如果$ f $在$ x_0 $处是局部$ \rm Lipschitz $连续的, 那么动力系统(2.2)的解$ x(t;x(t_0)) $是唯一的.如果$ f $在$ {{\Bbb R}} ^n $上是$ \rm Lipschitz $连续的, 那么$ \tau $可以拓展到$ +\infty $.

在结束本节前, 给出判定动力系统(2.2)的平衡点的稳定性判定定理.

定理2.3  设$ x^* $是系统(2.2)的平衡点, $ x(t) $是(2.2)的轨迹, 且$ X\subset {{\Bbb R}} ^n $是包含$ x^* $的邻域.如果存在一个连续可微的函数$ V $: $ X\rightarrow {{\Bbb R}} $, 使得

$ \begin{eqnarray*} && V(x^*)=0 \quad\mbox{且}\quad V(x)>0, \quad {\forall}x\in X\setminus\{x^*\}, \\ && \frac{{\rm d}V(x(t))}{{\rm d}t}={\nabla V(x(t))}^\top f(x(t))\leq0, \quad {\forall}x(t)\in X, \end{eqnarray*} $

则$ x^* $是稳定的.如果

$ \frac{{\rm d}V(x(t))}{{\rm d}t}<0, \quad{\forall}x(t)\in X\setminus\{x^*\}, $

则$ x^* $是渐近稳定的.

定理2.4  设$ x^* $是系统(2.2)的平衡点, $ x(t) $是(2.2)的轨迹.设$ V $: $ {{\Bbb R}} ^n\rightarrow {{\Bbb R}} $是一个可微连续函数, 使得

$ \begin{eqnarray*} && V(x^*)=0 \quad \mbox{且}\quad V(x)>0, \quad {\forall}x\neq x^*, \\ && \frac{{\rm d}V(x(t))}{{\rm d}t}<0, \quad {\forall}x(t)\neq x^*, \\ && ||x-x^*||\rightarrow \infty \Rightarrow V(x) \rightarrow \infty, \end{eqnarray*} $

则$ x^* $是全局渐近稳定的.

本节, 在Chen等人工作^[3]的基础上, 提出求解GAVE (1.1)的一个动力学模型.

类似文献[3], 可以证明$ x^* $是GAVE (1.1)的解当且仅当$ x^* $满足投影方程

(3.1) $ \begin{equation} Q(x)=P_\Omega[Q(x)-F(x)], \end{equation} $

其中$ \Omega=\{x\in{{\Bbb R}} ^n|x\geq0\} $.事实上, 类似文献[3]可以证明如下定理.

定理3.1   $ x^* $是$ \rm GAVE $ (1.1)的解当且仅当$ r(x^*)=0 $, 其中

(3.2) $ \begin{equation} r(x)=Q(x)-P_\Omega[Q(x)-F(x)]=Ax-|Bx-c|-d. \end{equation} $

基于定理3.1, 提出以下求解GAVE (1.1)的动力学模型

(3.3) $ \begin{equation} \frac{\mathrm{d}x(t)}{\mathrm{d}t}=\frac{1}{2}\gamma A^\top\{P_\Omega[Q(x(t))-F(x(t))]-Q(x(t))\}, \end{equation} $

其中$ \gamma>0 $是收敛率参数.将(3.2)式代入(3.3)式可得

(3.4) $ \begin{equation} \frac{\mathrm{d}x(t)}{\mathrm{d}t}=\frac{1}{2}\gamma A^\top[|Bx(t)-c|+d-Ax(t)]=h(x(t)). \end{equation} $

显然, 当$ A $非奇异时, 动力学模型(3.4)的平衡点等价于GAVE (1.1)的解, 即有如下定理.

定理3.2  假设$ A $是非奇异的, 则$ x^* $是GAVE (1.1)的解当且仅当$ x^* $是动力学模型(3.4)的平衡点.

本节分析动力学模型(3.4)解的存在性及其平衡点的稳定性.

为了证明解的存在性, 给出如下引理.

引理4.1  由(3.4)式所定义的函数$ h $在$ {{\Bbb R}} ^n $上是$ \rm Lipschitz $连续的.

证  对$ {\forall}x, y\in{{\Bbb R}} ^n $, 有

$ \begin{eqnarray*} ||h(x)-h(y)||&=&\left\| \frac{1}{2}\gamma A^\top(|Bx-c|+d-Ax)-\frac{1}{2}\gamma A^\top(|By-c|+d-Ay)\right\|\\ &=&\frac{1}{2}\gamma\left\|A^\top[A(y-x)+(|Bx-c|-|By-c|) ] \right\|\\ &\leq&\frac{1}{2}\gamma||A^\top||(||A||+||B||)||x-y||, \end{eqnarray*} $

即得函数$ h $在$ {{\Bbb R}} ^n $上是$ \rm Lipschitz $连续的, 且其$ \rm Lipschitz $常数为$ \frac{1}{2}\gamma||A^\top||(||A||+||B||) $.

由定理2.1和引理4.1可得如下解的存在性定理.

定理4.1  给定初始值$ x(t_0)=x_0 $, 则动力学模型(3.4)存在唯一解$ x(t;x(t_0)) $, $ t\in[0, \infty) $.

分析动力学模型(3.4)的稳定性, 需要如下定理, 它的证明受到文献[5, 定理2]的启发.

定理4.2  设$ x^* $是GAVE (1.1)的解, 且$ A^\top A\succeq B^\top B $, 则对$ {\forall}x\in{{\Bbb R}} ^n $有

(4.1) $ \begin{equation} {(x-x^{*})}^\top A^\top r(x)\geq\frac{1}{2}||r(x)||^{2}. \end{equation} $

证  由于$ \Omega=\{x\in{{\Bbb R}} ^n|x\geq0\}\subseteq{{\Bbb R}} ^n $是闭凸子集且$ Q(x^*)\in\Omega $, 则由引理2.3可得

$ {(v-P_\Omega(v))}^\top(P_ \Omega(v)-Q(x^*))\geq0, \quad {\forall}v\in{{\Bbb R}} ^n. $

令$ v:=Q(x)-F(x) $, 可以得到

$ {[r(x)-F(x)]}^\top\{P_\Omega[Q(x)-F(x)]-Q(x^*)\}\geq0. $

由$ P_\Omega[\cdot]\in\Omega $, $ F(x^*)\geq0 $和$ {Q(x^*)}^\top F(x^*)=0 $, 可得

$ {F(x^*)}^\top\{P_\Omega[Q(x)-F(x)]-Q(x^*)\}\geq0. $

利用前面得到的两个不等式和

$ P_\Omega[Q(x)-F(x)]-Q(x^*)=[Q(x)-Q(x^*)]-r(x)\nonumber $

可以得到

$ \{r(x)-(F(x)-F(x^*))\}^\top\{(Q(x)-Q(x^*))-r(x)\}\geq0, \nonumber $

从而

$ \{[Q(x)-Q(x^*)]+[F(x)-F(x^*)]\}^\top r(x)\geq||r(x)||^2+[Q(x)-Q(x^*)]^\top[F(x)-F(x^*)]. \nonumber $

将(2.1)式的$ Q, F $的表达式代入上式可得

$ 2r(x)^\top A(x-x^*)\geq||r(x)||^2+(x-x^*)^\top (A^\top A-B^\top B)(x-x^*), \quad {\forall}x\in{{\Bbb R}} ^n. $

因为$ A^\top A\succeq B^\top B $, 故

$ (x-x^*)^\top A^\top r(x)\geq\frac{1}{2}||r(x)||^2, \quad{\forall}x\in{{\Bbb R}} ^n. $

定理证毕.

注4.1  若$ A^\top A\succ B^\top B $, 即$ x^\top(A^\top A-B^\top B)x>0 $, $ \forall 0\neq x\in{{\Bbb R}} ^n $, 这等价于$ x^\top (A+B)^\top(A-B)x>0 $, $ \forall 0\neq x\in{{\Bbb R}} ^n $.令$ x=(A+B)^{-1}y $, 则可以得到$ y^\top (A-B)(A+B)^{-1}y>0 $, 即$ (A-B)(A+B)^{-1} $是正定矩阵.从而, 由注记2.1和引理2.2知此时GAVE (1.1)对$ \forall c, d\in{{\Bbb R}} ^n $有唯一解.又由定理3.2知此时动力学模型(3.4)有唯一的平衡点(假设$ A $非奇异).

现在, 可以分析动力学模型(3.4)的稳定性.具体地, 有如下定理.

定理4.3  假设$ A $非奇异, 且$ A^\top A\succeq B^\top B $, 则动力学模型(3.4)的平衡点$ x^* $是渐近稳定的.进一步, 如果$ A^\top A\succ B^\top B $, 则动力学模型(3.4)的平衡点$ x^* $唯一且全局渐近稳定.

证  由定理4.1可知, 对于任意$ x(t_0) = x_0\in {{\Bbb R}} ^n $动力学模型(3.4)在$ [t_0, \infty) $有唯一解.设$ x(t)=x(t;x(t_0)) $是模型(3.4)的解.构造Lyapunov函数

$ E(x)=e^{\|x-x^*\|^2}-1, \quad x\in{{\Bbb R}} ^n. $

易知$ E(x^*)=0 $, 且$ E(x)>0 $, $ {\forall}x\neq x^* $.由(4.1)可得

$ \begin{eqnarray*} \frac{{\rm d}}{{\rm d}t}E(x(t))&=&\frac{{\rm d}E}{{\rm d}x}\frac{{\rm d}x}{{\rm d}t} =-\gamma e^{||x(t)-x^*||^2}(x(t)-x^*)^\top A^\top r(x(t)) \\ &\leq&-\frac{1}{2}\gamma e^{||x(t)-x^*||^2}||r(x(t))||^2<0, \quad {\forall}x(t)\neq x^*. \end{eqnarray*} $

则由定理2.3可知$ x^* $是渐近稳定的.

当$ A^\top A\succ B^\top B $时, 由注记4.1知动力学模型(3.4)有唯一的平衡点.因为当$ ||x-x^*||\rightarrow \infty $时$ E(x)\rightarrow \infty $, 由定理2.4可知此时$ x^* $是全局渐近稳定的.

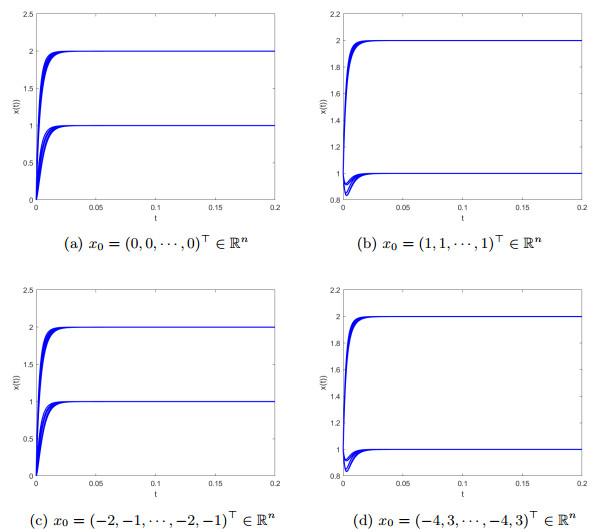
本节给出一个数值例子说明所提出的算法的有效性.算法通过MATLAB R2014b编程实现.在数值模拟的过程中, 使用MATLAB内置函数"ode45"对常微分方程(3.4)进行求解.

例5.1  对文献[1]中的例5.1进行转化, 可以得到GAVE (1.1)的系数矩阵和向量如下

$ A = M + I, \quad B = M -I, \quad c = d = -q, $

其中$ M = \hat{A} + \mu I $, $ q = -Mx^* $, $ x^*=(1, 2, 1, 2\cdots1, 2)^\top\in{{\Bbb R}} ^n $, 且

$ \hat{A} =\left( \begin{array}{cccccc} S &{\quad} -I{\quad} & 0 & {\quad}\cdots {\quad}& 0 &{\quad} 0 \\ -I & S & -I & \cdots & 0 & {\quad}0 \\ 0 & -I & S & \cdots & 0 & {\quad}0 \\ \vdots & \vdots & & \ddots & \vdots &{\quad}\vdots\\ 0 & 0 & \cdots & \cdots & S & {\quad}-I\\ 0 & 0 & \cdots & \cdots & -I & {\quad} S \end{array} \right)\in{{\Bbb R}} ^{n\times n}, $

$ S = \left( \begin{array}{cccccc} 4 & {\quad}-1{\quad} & 0 & {\quad}\cdots {\quad}& 0 &{\quad} 0 \\ -1 & 4 & -1 & \cdots & 0 & {\quad}0 \\ 0 & -1 & 4 & \cdots & 0 & {\quad}0 \\ \vdots & \vdots & & \ddots & \vdots &{\quad}\vdots\\ 0 & 0 & \cdots & \cdots & 4 &{\quad} -1\\ 0 & 0 & \cdots & \cdots & -1 &{\quad} 4 \end{array} \right)\in{{\Bbb R}} ^{m\times m}. $

据此, $ n = m^2 $且$ x^* $是GAVE (1.1)的唯一解.

在数值模拟的过程中, 取$ \mu=6 $, $ m=16 $, $ \gamma=5 $, 且当$ \frac{\|x(t)-x^*\|}{\|x^*\|}\le 10^{-10} $时终止算法.由前面的理论分析知道, 此时动力学模型(3.4)的平衡点是全局渐近稳定的.为了体现这一理论结果, 选取不同的初始点进行测试.模拟的结果见图 1.从图 1可以看出, 动力学模型(3.4)的轨迹均收敛于其平衡点$ x^* $, 数值结果与理论分析相吻合.

本文建立了求解一类新的广义绝对值方程组的动力学模型, 在适当的条件下证明了该动力学模型解的存在性并且构造了Lyapunov函数给出了所提出的动力学模型(3.4)全局稳定的充分条件.数值实验验证了所提出的动力学模型是可行且有效的.本文所研究的新的广义绝对值方程组与线性互补问题等价^[14], 因此对此类新的广义绝对值方程组的数值算法的继续研究具有重要意义.