带两条平行切换直线多项式微分系统的极限环分支

带两条平行切换直线多项式微分系统的极限环分支

姜雪丽, 邓璇, 文邱浩, 熊艳琴^,

南京信息工程大学数学与统计学院南京 210044

Limit Circle Bifurcations of Polynomial Differential System with Two Parallel Switch Straight Lines

Jiang Xueli, Deng Xuan, Wen Qiuhao, Xiong Yanqin^,

School of Mathematics and Statistics, Nanjing University of Information Science & Technology, Nanjing 210044

通讯作者: 熊艳琴, E-mail: yqxiong@nuist.edu.cn

收稿日期: 2021-08-12

基金资助:

国家自然科学基金. 11701289

Received: 2021-08-12

Fund supported:

the NSFC. 11701289

Abstract

In this paper, the limit cycle bifurcation problem is investigated for a class of polynomial differential system with two parallel switch straight lines. We use the generalized first order Melnikov function and related qualitative theory of knowledge to export the algebraic and corresponding coefficients of expression, then, use coefficient of change to research generalized double homoclinic bifurcation, and get a lower bound of its ring number.

Keywords： Discontinuous planar system ; Limit cycle ; Melnikov function ; Homoclinic bifurcations

PDF (378KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

姜雪丽, 邓璇, 文邱浩, 熊艳琴. 带两条平行切换直线多项式微分系统的极限环分支. 数学物理学报[J], 2022, 42(2): 353-364 doi:

Jiang Xueli, Deng Xuan, Wen Qiuhao, Xiong Yanqin. Limit Circle Bifurcations of Polynomial Differential System with Two Parallel Switch Straight Lines. Acta Mathematica Scientia[J], 2022, 42(2): 353-364 doi:

1 引言和主要结果

近年来, 控制理论、电路原理、医学和生物学等许多学科中的问题都得用不连续的微分方程来模拟, 使得此类微分方程受到广泛关注^[1-3]. 而分支问题是微分方程定性理论所要考虑的重要问题之一, 这也与著名的Hilbert第16问题的第二部分密切相关^[4]. 因此, 建立研究不连续微分系统分支理论的方法是非常有实际意义的.

最简单的不连续微分系统就是带一条切换直线的分片光滑微分系统

$\begin{equation} \dot{x}=F(x, y), \dot{y}=G(x, y), \end{equation}$

(1.1)

其中

$F(x, y) =\left\{\begin{array}{ll} F^{+}(x, y), & x\geq 0, \\ F^{-}(x, y), & x<0, \end{array}\right. \quad G(x, y) =\left\{\begin{array}{ll} G^{+}(x, y), & x\geq 0, \\ G^{-}(x, y), & x<0, \end{array}\right.$

$F^{\pm}(x, y), G^{\pm}(x, y)$ 都是 $C^{\infty}$ 上的函数. 系统(1.1) 在 $y$ 轴上的非光滑性产生了许多在光滑情况下不可能发生的复杂的行为, 如滑动同宿分支、滑膜振荡等^{[3, 5-7]}. 文献[8] 给出了研究微分系统(1.1) 极限环分支问题的广义的首阶Melnikov函数的公式, 之后相关学者利用此种方法对特定的微分系统(1.1) 进行研究, 研究其Hopf分支、同宿分支、异宿分支及Poincaré 分支等^{[9, 10]}. 最近, 文献[11] 把微分系统(1.1) 的切换线推广到从原点出发的任意条射线, 并获得首阶Melnikov的表达式, 此公式对任意条平行直线也成立^[12].

基于以上讨论, 本文研究如下带两条平行切换直线的多项式微分系统

$\begin{equation} \dot{x}=y+\varepsilon p(y), \dot{y}=-g(x)+\varepsilon y q(x), \end{equation}$

(1.2)

其中 $0<\varepsilon\ll1$ ,

$(g(x), p(y), q(x))=\left\{\begin{array}{ll} { } (x-1, \sum\limits_{i=0}^m a^+_{i}y^i, \sum\limits_{i=0}^{m-1}{b_{i}^{+}x^i}), &x\geq1, \\ { } (-x, \sum\limits_{i=0}^m a_i y^i, \sum\limits_{i=0}^{m-1}{b_i x^i}), &-1\leq x<1, \\ { } (-1, \sum\limits_{i=0}^m a_i^- y^i, \sum\limits_{i=0}^{m-1}{b_i^- x^i}), &x<-1. \end{array}\right.$

那么, 微分系统(1.2) 有以下三个子系统

$\dot{x}=y+\varepsilon \sum\limits_{i=0}^m a_i^+ y^i, \quad \dot{x}=-(x-1)+\varepsilon \sum\limits_{i=0}^{m-1} b_i^+ x^i y,$

(1.2a)

$\dot{x}=y+\varepsilon \sum\limits_{i=0}^{m} a_i y^i, \quad \dot{y}=x+\varepsilon \sum\limits_{i=0}^{m-1} b_i x^i y,$

(1.2b)

$\dot{x}=y+\varepsilon \sum\limits_{i=0}^m a_i^- y^i, \quad \dot{y}=1+\varepsilon \sum\limits_{i=0}^{m-1} b_i^- x^i y,$

(1.2c)

当 $\varepsilon=0$ 时, (1.2a), (1.2b), (1.2c) 分别是Hamiltonian微分系统, 且Hamiltonian函数分别为

$H^+ (x, y)=\frac{1}{2}y^2+\frac{1}{2}(x-1)^2,$

$H(x, y)=\frac{1}{2}y^2-\frac{1}{2}x^2,$

$H^+ (x, y)=\frac{1}{2}y^2-(x+1).$

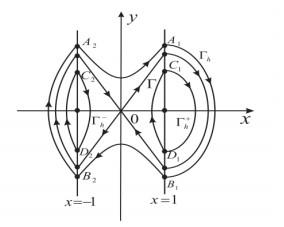
另外, 易得未扰动系统(1.2) $|_{\varepsilon=0}$ 有如下三簇周期轨道

$\begin{eqnarray*} \Gamma_h^+&=&\big\{(x, y)\; |\; H^+(x, y)=h+\frac{1}{2}, \; 1< x<2\big\}\cup\big\{(x, y)\; |\; H(x, y)=h, \; 0<x<1\big\}, \\ &&{\quad} h\in(-\frac{1}{2}, 0);\\ \Gamma_h^-&=&\big\{(x, y)\; |\; H^-(x, y)=h+\frac{1}{2}, \; 1<-x<\frac{3}{2}\big\}\cup\big\{(x, y)\; |\; H(x, y)=h, \; 0<-x<1\big\}, \\ &&{\quad} h\in(-\frac{1}{2}, 0);\\ \Gamma_h&=&\big\{(x, y)\; |\; H^+(x, y)=h+\frac{1}{2}, \; x>1\big\}\cup\big\{(x, y)\; |\; H(x, y)=h, \; -1<x<1\big\}\\ &&{\quad} \cup\big\{(x, y)\; |\; H^-(x, y)=h+\frac{1}{2}, \; x<-1\big\}, \ \ h\in(0, +\infty). \end{eqnarray*}$

不难发现当 $h\to-\frac{1}{2}$ 时, $\Gamma_h^+$ 和 $\Gamma_h^-$ 分别趋近于广义初等中心 $(1, 0)$ 和 $(-1, 0)$ ; 当 $h\to0$ 时, $\Gamma_h$ 趋近于广义的双同宿环. 闭曲线 $\Gamma_h^+$ (或 $\Gamma_h^-$ ) 顺时针穿过直线 $x=1$ (或 $x=-1)$ 分别交于两点 $C_1(h)=(1, \sqrt{2h+1})$ 和 $D_1(h)=(1, -\sqrt{2h+1})$ (或 $C_2(h)=(-1, \sqrt{2h+1})$ ) 和 $D_2(h)=(-1, -\sqrt{2h+1})$ ), 这里 $h\in{(-\frac{1}{2}, 0)}.$ 周期轨道 $\Gamma_h$ 和直线 $x=\pm1$ 依次相交于四点 $A_1(h)=(1, \sqrt{2h+1}), \; B_1(h)=(1, -\sqrt{2h+1}), \; B_2(h)=(-1, -\sqrt{2h+1})$ 和 $A_2(h)=(-1, \sqrt{2h+1})$ , 其中 $h\in(0, +\infty)$ . 图 1展示了微分系统 $(1.2)|_{\varepsilon=0}$ 在平面上的相图.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1 微分系统 $(1.2)|_{\varepsilon=0}$ 的相图

根据文献[11, 12], 相对应于上面三簇周期轨道, 分别有如下首阶Melnikov函数

$\begin{equation} \begin{array}{ll} M^{\pm}(h)=M^{\pm}_1(h)+M^{\pm}_2(h), \quad h\in(-\frac{1}{2}, 0), \\ M(h)=M_1(h)+M_2(h)+M_3(h)+M_4(h), {\quad} h\in(0, +\infty), \end{array} \end{equation}$

(1.3)

其中

$\begin{equation} M^+_1(h)=\int_{\widehat{C_1D_1}} \sum\limits_{i=0}^{m-1} b_i^+x^iy{\rm d}x-\sum\limits_{i=0}^m a_i^+y^i{\rm d}y, \quad M^+_2(h)=\int_{\widehat{D_1C_1}} \sum\limits_{i=0}^{m-1} b_ix^iy{\rm d}x-\sum\limits_{i=0}^m a_iy^i{\rm d}y, \end{equation}$

(1.4)

$\begin{equation} M^-_1(h)=\int_{\widehat{C_2D_2}} \sum\limits_{i=0}^{m-1} b_ix^iy{\rm d}x-\sum\limits_{i=0}^m a_i^+y^i{\rm d}y, \quad M^-_2(h)=\int_{\widehat{D_2C_2}} \sum\limits_{i=0}^{m-1} b_i^-x^iy{\rm d}x-\sum\limits_{i=0}^m a_i^-y^i{\rm d}y, \\ \end{equation}$

(1.5)

$\begin{equation} M_1(h)=\int_{\widehat{A_1B_1}} \sum\limits_{i=0}^{m-1} b_i^+x^iy{\rm d}x-\sum\limits_{i=0}^m a_i^+y^i{\rm d}y, \quad M_2(h)=\int_{\widehat{B_1B_2}} \sum\limits_{i=0}^{m-1} b_ix^iy{\rm d}x-\sum\limits_{i=0}^m a_iy^i{\rm d}y, \\ \end{equation}$

(1.6)

$\begin{equation} M_3(h)=\int_{\widetilde{B_2A_2}} \sum\limits_{i=0}^{m-1} b_i^-x^iy{\rm d}x-\sum\limits_{i=0}^m a_i^+y^i{\rm d}y, \quad M_4(h)=\int_{\widehat{A_2A_1}} \sum\limits_{i=0}^{m-1} b_ix^iy{\rm d}x-\sum\limits_{i=0}^m a_iy^i{\rm d}y. \end{equation}$

(1.7)

则, 利用上述函数, 我们可证明如下结论:

定理1.1 当 $0<\varepsilon\ll1$ , 微分系统(1.2) 在广义双同宿环 $\Gamma$ 附近可分支出 $3m+[\frac{m+1}{2}]+1$ 个极限环.

定理1.1的证明将在本文的第二部分给出.

2 广义双同宿环分支

首先, 我们来推导 $M^{\pm}_i(h), i=1, 2$ 和 $M_i(h), i=1, 2, 3, 4$ 在(1.4)–(1.7) 式中的具体表达式.

引理2.1 由公式(1.4) 给出的函数 $M^+_1(h)$ 可表示成

$\begin{equation} M^+_1(h)=\sum\limits_{i=0}^m A^+_i(2h+1)^{\frac{i}{2}+\frac{1}{2}}, \quad h\in(-\frac{1}{2}, 0), \end{equation}$

(2.1)

其中

$\begin{eqnarray} &&A^+_0=2a^+_0, {}\\ &&A^+_{2i+1}=\sum\limits_{k=2i}^{m-1}b^+_k\alpha_{k, 2i}, \; i=0, \; 1, \cdots, \; [\frac{m-1}{2}], \\ &&A^+_{2i}=\frac{a^+_{2i}}{2i+1}+\sum\limits_{k=2i-1}^{m-1}b^+_k\alpha_{k, 2i-1}, \; i=1, \; 2, \cdots, \; [\frac{m}{2}], {} \end{eqnarray}$

(2.2)

这里 $\alpha_{ki}>0$ 且为常数.

证沿着曲线 $\widehat{C_1D_1}$ , 有 $\frac{1}{2}y^2+\frac{1}{2}(x-1)^2=h+\frac{1}{2}$ . 再根据(1.4) 式, 可得

$\begin{equation} M^+_1(h)=\sum\limits_{i=0}^{m-1}2b^+_i\int_1^{1+\sqrt{2h+1}}x^i[2h+1-(x-1)^2]{\rm d}x-\sum\limits_{i=0}^ma_i^+\int_{\sqrt{2h+1}}^{-\sqrt{2h+1}}y^i{\rm d}y. \end{equation}$

(2.3)

对上式中的第一个定积分做变量变换 $x=\sqrt{2h+1}\sin\theta+1$ , 那么(2.3) 式可变为

$\begin{eqnarray} M^+_1(h)&=&\sum\limits_{i=0}^{m-1}2b^+_i(2h+1)\int_0^{\frac{\pi}{2}}(\sqrt{2h+1}\sin\theta+1)^i\cos^2\theta {\rm d}\theta+\sum\limits_{2i=0}^m \frac{2a^+_{2i}}{2i+1}(2h+1)^{i+\frac{1}{2}}{}\\ &=&\sum\limits_{i=0}^{m-1}2b^+_i(2h+1)\int_0^{\frac{\pi}{2}}\sum\limits_{r=0}^iC_i^r\cos^2\theta {\rm d}\theta+\sum\limits_{2i=0}^m \frac{2a^+_{2i}}{2i+1}(2h+1)^{i+\frac{1}{2}}{}\\ &=&\sum\limits_{i=0}^{m-1}b^+_i\sum\limits_{r=0}^i\alpha_{ir}(2h+1)^{\frac{r}{2}+1}+\sum\limits_{i=0}^{[\frac{m}{2}]} \frac{2a^+_{2i}}{2i+1}(2h+1)^{i+\frac{1}{2}}{}\\ &=&\sum\limits_{i=0}^{m}(\sum\limits_{k=i-1}^{m-1}b_k^+\alpha_{k, i-1}) (2h+1)^{\frac{i }{2}+\frac{1}{2}}+\sum\limits_{i=0}^{[\frac{m}{2}]}\frac{2a^+_{2i}}{2i+1}(2h+1)^{i+\frac{1}{2}}, \end{eqnarray}$

(2.4)

其中

$\alpha_{ir}=2C_i^r\int_0^{\frac{\pi}{2}}\sin^r\theta\cos^2\theta {\rm d}\theta=C_i^r{\bf B}(\frac{r+1}{2}, \frac{3}{2})>0.$

这里 ${\bf B}$ 是Beta函数. 那么, 依据(2.4) 式, 不难得到(2.1) 式. 证毕.

注2.1 由(1.6) 式所定义的函数 $M_1(h)$ 同样有(2.3) 式中的表达形式, 不过这里 $h>0$ .

引理2.2 对于(1.4) 式中所定义的函数 $M^+_2(h)$ , 当 $h\in(-\frac{1}{2}, 0)$ 时, 有

$\begin{eqnarray} M^+_2(h)&=&-\sum\limits_{i=0}^{[\frac{m}{2}]}\frac{2a_{2i}}{2i+1}(2h+1)^{i+\frac{1}{2}}+\sum\limits_{i=1}^{m-1}2b_i\frac{(2h+1)^\frac{3}{2}}{i+2}(1+\sum\limits_{j=1}^{[\frac{i+1}{2}]-1}\beta_{ij}h^j){}\\ &&+\sum\limits_{i=0}^{[\frac{m-1}{2}]}2b_{2i}\gamma_ih^i\int^{1}_{\sqrt{-2h}}(2h+x^2)^{\frac{1}{2}}{\rm d}x, \end{eqnarray}$

(2.5)

其中 $\beta_{ij}$ 和 $\gamma_{ij}$ 是常数.

证在曲线 $\widehat{D_1C_1}$ 上, 我们有 $\frac{1}{2}y^2-\frac{1}{2}x^2=h$ , 其中 $0<x<1$ . 则, 由(1.4) 式可得

$\begin{eqnarray} M^+_2(h)&=&\sum\limits_{i=0}^{m-1}2b_i\int_{\sqrt{-2h}}^1x^i\sqrt{2h+x^2}-\sum\limits_{i=0}^ma_i\int_{-\sqrt{2h+1}}^{\sqrt{2h+1}}y^i{\rm d}y{}\\ &=&\sum\limits_{i=0}^{m-1}2b_iI_i(h)-\sum\limits_{i=0}^{[\frac{m}{2}]}\frac{2a_{2i}}{2i+1}(2h+1)^{i+\frac{1}{2}}, \end{eqnarray}$

(2.6)

其中

$\begin{equation} I_i(h)=\int_{\sqrt{-2h}}^1x^i(2h+x^2)^{\frac{1}{2}}{\rm d}x. \end{equation}$

(2.7)

又因为

$\begin{equation} \int x^i(2h+x^2)^{\frac{1}{2}}{\rm d}x=\frac{x^{i-1}(2h+x^2)^{\frac{3}{2}}}{i+2}\int x^{i-2}(2h+x^2)^{\frac{1}{2}}, \quad i\ge1, \end{equation}$

(2.8)

则, 可得到下列递推关系

$I_i(h)=\frac{(2h+1)^{\frac{3}{2}}}{i+2}+\frac{(1-i)2h}{i+2}I_{i-2}(h), \quad i\ge1.$

因此, 有

$\begin{equation} I_i(h)=\frac{(2h+1)^{\frac{3}{2}}}{i+2}(1+\sum\limits_{i=1}^{[\frac{i+1}{2}]-1}\beta_{ij}h^j)+\gamma_{i, [\frac{i+1}{2}]}h^{[\frac{i}{2}]}I_0(h), \quad i\ge1, \end{equation}$

(2.9)

其中

$\begin{equation} \beta_{ij}=\prod\limits_{r=1}^{j-1}\frac{2(2r+1-i)}{i-2r}, \quad \gamma_{i, [\frac{i+1}{2}]}=\prod\limits_{r=0}^{[\frac{i+1}{1}]-1}\frac{2(2r+1-i)}{i+2-2r}, \quad i, \; j\ge1. \end{equation}$

(2.10)

注意到, 当 $i$ 为奇数时, $\gamma_{i, [\frac{i+1}{2}]}=0$ . 因此, 将 $\gamma_{2i, i}$ 简写为 $\gamma_i$ , 即 $\gamma_i=\prod\limits_{r=0}^{i-1}\frac{2r+1-2i}{i+1-r}, i\ge1$ , 同时令 $\gamma_0=1$ . 把(2.9) 式代入(2.6) 式, 同时根据(2.10) 式, 不难推导出(2.5) 式成立. 证毕.

引理2.3 由(1.5) 式所定义的函数 $M^-_1(h)$ 可写成

$\begin{eqnarray} M_1^-(h)&=&\sum\limits_{i=0}^{[\frac{m}{2}]}\frac{2a_{2i}}{2i+1}(2h+1)^{i+\frac{1}{2}}+\sum\limits_{i=1}^{m-1}2(-1)^ib_i\frac{(2h+1)^{\frac{3}{2}}}{i+2}(1+\sum\limits_{j=1}^{[\frac{i+1}{2}]-1}\beta_{ij}h^j){}\\ &&+\sum\limits_{i=1}^{[\frac{m-1}{2}]}2b_{2i}\gamma_ih^i\int_{\sqrt{-2h}}^1(2h+x^2)^{\frac{1}{2}}{\rm d}x, \quad h\in(-\frac{1}{2}, 0), \end{eqnarray}$

(2.11)

其中 $\beta_{ij}$ 和 $\gamma_i$ 的定义与(2.5) 式中相同.

证因为在曲线 $\widehat{C_2D_2}$ 上, 有 $\frac{1}{2}y^2-\frac{1}{2}x^2=h, -1<x<0$ , 所以

$\begin{eqnarray*} M^-_1(h)&=&2\int_{-1}^{-\sqrt{-2h}}\sum\limits_{i=0}^{m-1} b_i x^i\sqrt{2h+x^2}{\rm d}x-\sum\limits_{i=0}^m a_i\int_{\sqrt{2h+1}}^{-\sqrt{2h+1}}y^i{\rm d}y{\nonumber}\\ &=&\sum\limits_{i=0}^{m-1}2(-1)^ib_i\int_{\sqrt{-2h}}^1x^i\sqrt{2h+x^2}{\rm d}x+\sum\limits_{i=0}^{[\frac{m}{2}]}\frac{2a_{2i}}{2i+1}(2h+1)^{i+\frac{1}{2}}{\nonumber}\\ &=&\sum\limits_{i=0}^{m-1}2(-1)^ib_i I_i(h)+\sum\limits_{i=0}^{[\frac{m}{2}]}\frac{2a_{2i}}{2i+1}(2h+1)^{i+\frac{1}{2}}, \end{eqnarray*}$

这里函数 $I_i(h)$ 由(2.7) 式给出. 根据引理2.2的证明过程, 易得到(2.11) 式. 证毕.

引理2.4 对于(1.5) 式中的函数 $M^-_2(h)$ , 成立

$\begin{equation} M^-_2(h)=\mathop \sum \limits_{i = 0}^m A^-_i(2h+1)^{i +\frac{1}{2}}, h\in(-\frac{1}{2}, 0), \end{equation}$

(2.12)

其中

$\begin{equation} \begin{array}{ll} { } A^-_0=-2a^-_0, \\ { } A^-_1=-\frac{2}{3}a^-_2 +\frac{2}{3}b^-_0 +O(| b^-_1 , \cdots, b^-_{m-1}|), \\ { } A^-_1=-\frac{2a^-_{2i}}{2i+1}+\frac{2}{3}(-1)^{i-1}b^-_{i-1} \mathop \prod \limits_{r = 0}^{i - 2} \frac{i-r}{5+2r} +O(| b^-_i, b^-_i+1, \cdots, b^-_{m-1}|), \ \ i=2, 3, \cdots, [\frac{m}{2}], \\ { } A^-_1=\frac{2}{3} (-1)^{i-1} b^-_{i-1} \mathop \prod \limits_{r = 0}^{i - 2} \frac{i-r}{5+2r} +O(| b^-_i , b^-_{i+1} , \cdots, b^-_{m-1} |), \; i=[\frac{m}{2}]+1, [\frac{m}{2}]+2, \cdots, m. \end{array} \end{equation}$

(2.13)

证沿着曲线 $\widehat{D_2C_2}$ , 有 $y^2=2h+1+2(x+1)$ . 与上述处理方法相同, 类似可得

$\begin{eqnarray} M^-_2(h)&=&2\int^{-1}_{-\frac{2h+3}{2}} \mathop \sum \limits_{i = 0}^{m - 1} b^-_i x^i [2h+1+2(x+1)]^{\frac{1}{2} }{\rm d}x-\mathop \sum \limits_{i = 0}^m a^-_i \int^{\sqrt(2h+1)}_{-\sqrt(2h+1)} y^i {\rm d}y{}\\ &=&2\mathop \sum \limits_{i = 0}^{m - 1} b^-_i J_{i1}(h) -\mathop \sum \limits_{i = 0}^{[\frac{m}{2}]} \frac{2a^-_{2i}}{2i+1} (2h+1)^{i+\frac{1}{2}}, \end{eqnarray}$

(2.14)

这里

$J_{ik} (h)=\int^{-1}_{-\frac{2h+3}{2}}x^i[2h+1+2(x+1)]^{\frac{k}{2}}{\rm d}x, \; i, \; k\in \mathbb{N}.$

对于任意给定的一对正整数 $(i, k)$ , 有如下等式

$J_{ik} (h)=\frac{(-1)^i}{k+2}(2h+1)^{\frac{k+2}{2}}-\frac{i}{k+2}J_{i-1, k+2}(h), \; i, \; k\in \mathbb{N}.$

通过数学归纳法得到

$\begin{eqnarray} J_{i1}(h)&=&\frac{(-1)^i}{3} (2h+1)^{\frac{3}{2}}[1+\sum\limits_{j=1}^{i-1}\prod\limits_{r=0}^{j-1}\frac{i-r}{5+2r}(2h+1)^j]+(-1)^j\prod\limits_{r=0}^{i-1}\frac{i-r}{3+2r}J_{0, 2i+1}(h){}\\ &=&\frac{(-1)^i}{3}(2h+1)^{\frac{3}{2}}\big[1+\sum\limits_{j=1}^{i-1}\prod\limits_{r=0}^{j-1}\frac{i-r}{5+2r}(2h+1)^j\big]. \end{eqnarray}$

(2.15)

将(2.15) 式代入(2.14) 式可得(2.12) 式. 证毕.

注2.2 由(1.7) 式中所定义的函数 $M_3(h)$ 也有(2.12) 式中的形式表达式, 这里 $h>0$ .

引理2.5 由(1.6) 式给出的函数 $M_2(h)$ , 可以被表示为

$\begin{equation} M_2(h)=\sum\limits_{i=1}^{[\frac{m-1}{2}]}b_{2i}\frac{(2h+1)^\frac{3}{2}}{i+1}(1+\sum\limits_{j=1}^{i-1}\beta_{2i, j}h^j)+\sum\limits_{i=0}^{[\frac{m-1}{2}]}b_{2i}\gamma_i h^i\int_{-1}^1(2h+x^2)^{\frac{1}{2}}{\rm d}x, \end{equation}$

(2.16)

这里的 $\beta_{2i, j}$ 和 $\gamma_i$ 与(2.5) 式中给出的定义相同. 此外, 对于 $h>0$ , 有

$\begin{equation} M_2(h)=M_4(h), \end{equation}$

(2.17)

其中 $M_4(h)$ 由(1.7) 式给出.

证沿着曲线 $\widehat{B_1B_2}, \; y^2-x^2=2h, -1<x<1.$ 由(1.6) 式所定义的函数 $M_2(h)$ 可被改写为如下的表达式

$\begin{eqnarray} M_2(h)&=&\int_1^{-1}\sum\limits_{i=0}^{m-1}b_ix^i(-\sqrt{2h+x^2}){\rm d}x-\int_1^{-1}\sum\limits_{i=0}^{m}a_i(-1)^{i+1}\sqrt{2h+x^2} {\rm d}\sqrt{2h+x^2}{}\\ &=&\sum\limits_{i=0}^{[\frac{m-1}{2}]}b_i\overline{I}_i(h), \end{eqnarray}$

(2.18)

其中 $\overline{I}_i(h)=\int_{-1}^{1}x^{2i}\sqrt{2h+x^2}{\rm d}x$ .

利用(2.8) 式中, 不难发现成立

$\overline{I}_i(h)=\frac{(2h+1)^{\frac{3}{2}}}{i+1}+\frac{1-2i}{i+1}\overline{I}_{i-1}(h).$

因此, 易推出

$\begin{equation} \overline{I}_i(h)=\frac{(2h+1)^\frac{3}{2}}{i+1}\big(1+\sum\limits_{j=1}^{i-1}\prod\limits_{r=1}^{i-1}\frac{2r+1-2i}{i-r}h^j\big)+\prod\limits_{r=1}^{i-1}\frac{2r+1-2i}{i-r}h^i\overline{I}_0(h). \end{equation}$

(2.19)

将(2.19) 式代入(2.18) 式, 同时结合(2.10) 式, 易得(2.16) 式中的表达式.

同样, 我们可以推导出(1.7) 式中函数 $M_4(h)$ 的显示表达式, 易知其表达式与 $M_2(h)$ 所对应的相同. 证毕.

对于(2.5) 式和(2.16) 式中的定积分部分, 我们有

引理2.6 当 $h>-\frac{1}{2}$ 时, 成立

$\begin{equation} \begin{array}{ll} { } \int_{\sqrt{-2h}}^1\sqrt{2h+x^2}{\rm d}x&=\frac{1}{2}(-h\ln|h|+\phi(h)), \ \ -\frac{1}{2}<h<0, \\ { } \int_{-1}^1\sqrt{2h+x^2}{\rm d}x&=-h\ln|h|+\phi(h), h>0, \end{array} \end{equation}$

(2.20)

其中 $\phi(h)=\sqrt{2h+1}+2h\ln(1+\sqrt{2h+1})-h\ln2$ .

证注意到

$\int\sqrt{x^2\pm a^2}{\rm d}x=\frac{1}{2}[x\sqrt{x^2\pm a^2}\pm a^2\ln(x+\sqrt{x^2\pm a^2})],$

其中 $a$ 是一个常数. 因此, 我们有

$\int_{\sqrt{-2h}}^1\sqrt{2h+x^2}{\rm d}x=\frac{1}{2}\sqrt{2h+1}+h\ln(1+\sqrt{2h+1})-\frac{1}{2}h\ln2-\frac{1}{2}h\ln|h|, \ \ h\in(-\frac{1}{2}, 0),$

$\int_{\sqrt{-1}}^1\sqrt{2h+x^2}{\rm d}x=\sqrt{2h+1}+2h\ln(1+\sqrt{2h+1})-h\ln2-h\ln|h|, \ \ h>0.$

由此可得到(2.20) 式. 证毕.

现在, 我们研究微分系统(1.2) 的广义双同宿环 $\Gamma$ 附近的极限环分支问题. 为此, 引入

$d_\tau=\frac{(-1)^{\tau-1}}{\prod\limits_{i=0}^{\tau-1}(k_2+ki)}, \ \ d_j=(-1)^{j-1}\frac{\prod\limits_{i=0}^{j-\tau-1}(k_1+ki)}{(k_2+ki)}, j\geq\tau+1,$

其中 $k_1, k_2$ 和 $k$ 都是正常数且 $k_1\neq k_2$ . 然后, 对于任意给定的一对正整数 $(s, t), \; s\geq t \geq\tau, \; s, \; t\in N.$ 再利用 $d_j$ 构建一个 $(s-t+1)\times(s-t+1)$ 矩阵

$\begin{equation} {\cal D}_{s, t}(k_1, k_2, k, s)= \left(\begin{array}{cccccc} d_s&d_{s-1}&d_{s-2}&\cdots&d_t\\ d_{s+1}&d_s&d_{s-1}&\cdots&d_{t+1}\\ d_{s+2}&d_{s+1}&d_s&\cdots&d_{t+1}\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ d_{2s-t}&d_{2s-t-1}&d_{2s-t-2}&\cdots&d_s \end{array}\right). \end{equation}$

(2.21)

那么, 我们有

引理2.7 对于(2.21) 式中的矩阵 ${\cal D}_{s, t}(k_1, k_2, k, \tau)$ , 成立

${\cal D}_{s, t}(k_1, k_2, k, \tau)\neq0.$

证对于(2.21) 式中的矩阵 ${\cal D}_{s, t}(k_1, k_2, k, \tau)$ , 我们做如下初等变换:

(1) 第 $i$ 列乘以 $(-1)^{i-1}, i=2, 3, \cdots, s-t+1$ ;

(2) 第 $i$ 行除以 $(-1)^{i-1}, i=1, 2, \cdots, s-t+1$ .

那么 ${\cal D}_{s, t}(k_1, k_2, k, \tau)$ 经过上面一系列的操作变成另一个矩阵, 我们用 ${\cal D}_0$ 表示. 这里

$\begin{equation} {\cal D}_{s, t}(k_1, k_2, k, \tau)\sim {\cal D}_0, \end{equation}$

(2.22)

其中

${\cal D}_0= \left(\begin{array}{cccccc} { }\frac{e_{s-\tau}}{f_s}&{ }\frac{e_{s-1-\tau}}{f_{s-1}}&{ }\frac{e_{s-2-\tau}}{f_{s-2}}&\cdots&{ }\frac{e_{t-\tau}}{f_t}\\ { }\frac{e_{s+1-\tau}}{f_{s+1}}&{ }\frac{e_{s-\tau}}{f_s}&{ }\frac{e_{s-1-\tau}}{f_{s-1}}&\cdots&{ }\frac{e_{t+1-\tau}}{f_{t+1}}\\ { }\frac{e_{s+2-\tau}}{f_{s+2}}&{ }\frac{e_{s+1-\tau}}{f_{s+1}}&{ }\frac{e_{s-\tau}}{f_s}&\cdots&{ }\frac{e_{t+2-\tau}}{f_{t+2}}\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ { }\frac{e_{2s-t-\tau}}{f_{2s-t}}& { }\frac{e_{2s-t-1-\tau}}{f_{2s-t-1}}&{ }\frac{e_{2s-t-2-\tau}}{f_{2s-t-2}}&\cdots&{ }\frac{e_{s-\tau}}{f_s} \end{array}\right),$

这里

$e_0=f_0=1, \ \ e_j=\prod\limits_{i=0}^{j-1}(k_1+ki), \ \ f_j=\prod\limits_{i=0}^{j-1}(k_2+ki), j\geq1.$

从文献[9, 引理3.1]可发现, $\det({\cal D}_0)\neq0$ . 因此, 可以从(2.22) 式可得结论成立. 证毕.

定理1.1的证明 我们分为如下四种情况进行讨论:

$m=2l+1, \; l=2k, \ \ \ m=2l+1, \; l=2k+1, \ \ \ m=2l, \; l=2k, \ \ \ m=2l, \; l=2k+1.$

首先, 我们证明 $m=2l+1, l=2k$ 的情况, 通过(1.3) 式, (2.1) 式和(2.5) 式可推导出

$\begin{eqnarray} \frac{M^+(h)}{\sqrt{2h+1}} &=&\sum\limits_{i=0}^{2l+1}A_i^+(2h+1)^{\frac{i}{2}}-\sum\limits_{i=0}^l\frac{2a_{2i}}{2i+1}(2h+1)^i+\sum\limits_{i=0}^{2l}2b_i\frac{2h+1}{i+2}(1+\sum\limits_{j=1}^{[\frac{i+1}{2}]-1}\beta_{ij}h^j){}\\ &&+\sum\limits_{i=0}^l2b_{2i}\gamma_ih^i\frac{\int_{\sqrt{2h}}^1(2h+x^2)^{\frac{1}{2}}{\rm d}x}{\sqrt{2h+1}}{}\\ &=&\sum\limits_{i=0}^l(A_{2i}^+-\frac{2a_{2i}}{2i+1})(2h+1)^i +\sum\limits_{i=1}^{2l}2b_i\frac{2h+1}{i+2}(1+\sum\limits_{j=1}^{[\frac{i+1}{2}]-1}\beta_{ij}h^j){}\\ &&+\sum\limits_{i=0}^{l}A_{2i+1}^+(2h+1){i+\frac{1}{2}}+\sum\limits_{i=0}^l2b_{2i}\gamma_ih^i\frac{\int_{\sqrt{2h}}^1(2h+x^2)^{\frac{1}{2}}{\rm d}x}{\sqrt{2h+1}}. \end{eqnarray}$

(2.23)

另一方面, 对于 $|h|>0$ 且足够小

$\begin{equation} \begin{array}{ll} { } (2h+1)^\frac{1}{2}=1+\sum\limits_{i\geq1}A_ih^i, \; A_1=1, \; A_i=(-1)^{i-1}\frac{\prod\limits_{r=0}^{i-2}(2r+1)}{\prod\limits_{r=0}^{i-1}(r+1)}, \; i\geq2, \\ { } (2h+1)^{-\frac{1}{2}}=1+\sum\limits_{i\geq1}\bar{A}_ih^i, \; \bar{A}_1=1, \; \bar{A}_i=(-1)^{i}\prod\limits_{r=0}^{i-1}\frac{2r+1}{r+1}, \; i\geq2. \end{array} \end{equation}$

(2.24)

那么, 根据引理2.6, 对于 $0<-h\ll1$ , (2.23) 式能够写成

$\begin{eqnarray} \frac{M^{+}(h)}{\sqrt{2h+1}}&=&\sum\limits_{i=1}^l(A_{2i}^+ - \frac{2a_{2i}}{2i+1})\sum\limits_{r=0}^i C_i^r 2^r h^r + \sum\limits_{i=1}^{2l} 2b_i \frac{2h+1}{i+2} \big(1 + \sum\limits_{j=1}^{[\frac{i+1}{2}]-1} \beta_{ij}h^j\big){}\\ &&+\sum\limits_{i=0}^l A_{2i+1}^+ \sum\limits_{r=0}^i C_i^r 2^r h^r (1+\sum\limits_{i\geq1} A_i h^i) + \sum\limits_{i=0}^l b_{2i} \gamma_i h^i \big(-h\ln|h|+1+O(h)\big){}\\ &=&\sum\limits_{i=0}^l(B_i^+ + D_i h \ln|h|)h^i+\sum\limits_{i \geq 0}B_{l+1+i}^+h^{l+1+i}, \end{eqnarray}$

(2.25)

其中

$\begin{equation} \begin{array}{ll} D_i = -2b_{2i}\gamma_i, \quad i=0, 1, \cdots, l, \\ B_i^+ ={ } 2^i(A_{2i}^+ - \frac{2a_{2i}}{2i+1})+O(| A_{2(i+1)}^+, A_{2(i+2)}^+, \cdots, A_{2l}^+, a_{2(i+1)}, a_{2(i+2)}, \\ {\quad}{\qquad} \cdots, a_{2l}, A_1^+, A_3^+, \cdots, A_{2l+1}^+, b_0, b_1, \cdots, b_{2l} | ), \quad i=0, 1, \cdots, l, \\ B_{l+1+i}^+ ={ } \sum\limits_{i=1}^l A_{2i+1}^+ \sum\limits_{r=0}^i C_i^r 2^r A_{l+1+i-r}, \quad i\geq0. \end{array} \end{equation}$

(2.26)

此外, 利用(1.3) 式, (2.11)–(2.12) 式可得到

$\begin{eqnarray*} \frac{M^{-}(h)}{\sqrt{2h+1}}&=&\sum\limits_{i=1}^{2l+1}A_i^- (2h+1)^i+\sum\limits_{i=1}^l \frac{2a_{2i}}{2i+1}(2h+1)^i+\sum\limits_{i=1}^l 2(-1)^ib_i\frac{(2h+1)}{i+2}(1+\sum\limits_{j=1}^{[\frac{i+1}{2}]-1} \beta_{ij}h^j){\nonumber}\\ &&+\sum\limits_{i=0}^l 2b_{2i} \gamma_i h^i \frac{\int_{\sqrt{-2h}}^1 (2h+x^2)^{\frac{1}{2}}{\rm d}x}{\sqrt{2h+1}}. \end{eqnarray*}$

再利用(2.24) 式, 进一步得到

$\begin{eqnarray} \frac{M^{-}(h)}{\sqrt{2h+1}}&=&\sum\limits_{i=1}^{2l+1}A_{i}^-\sum\limits_{r=0}^i C_i^r 2^r h^r + \sum\limits_{i=1}^l \frac{2a_{2i}}{2i+1} \sum\limits_{r=0}^i C_i^r 2^r h^r{}\\ &&+ \sum\limits_{i=1}^{2l}2(-1)^ib_i\frac{2h+1}{i+2}(1+\sum\limits_{j=1}^{[\frac{i+1}{2}]-1} \beta_{ij}h^j) +\sum\limits_{i=0}^l b_{2i} \gamma_i h^i\big(-h \ln|h|+ 1 + O(h)\big){}\\ &=&\sum\limits_{i=0}^l(B_i^- + D_i h \ln|h|)h^i + \sum\limits_{i \geq 0}B_{l+1+i}^- h^{l+1+i}, \end{eqnarray}$

(2.27)

其中 $D_i$ 与(2.24) 式中给出相同, 且

$\begin{equation} B_i^- = 2^i A_i^- + O(| A_{i+1}^-, A_{i+2}^-, \cdots, A_{2l+1}^-, a_0, a_2, \cdots, a_{2l}, b_0, b_1, \cdots, b_{2l}| ). \end{equation}$

(2.28)

现在, 我们导出 $\frac{M(h)}{\sqrt{2h+1}}$ 的表达式, 利用引理2.1–2.5和注2.1和注2.2, 不难得到, 对于 $h>0$ , 有

$\frac{M(h)}{\sqrt{2h+1}}=\frac{M^{+}(h)}{\sqrt{2h+1}}+\frac{M^{-}(h)}{\sqrt{2h+1}}.$

那么, 鉴于(2.25) 式和(2.27) 式, 当 $0<h\ll 1$ 时, 有

$\begin{equation} \frac{M(h)}{\sqrt{2h+1}}=\sum\limits_{i=0}^l\big[(B_i^+ + B_i^-)+2D_i h \ln{| h | }\big]h^i + \sum\limits_{i \geq 0}(B_{l+1+i}^+ + B_{l+1+i}^-)h^{l+1+i}. \end{equation}$

(2.29)

为了证明 $B_0^+, B_1^+, \cdots , B_{2l+1}^+, B_0^-, B_1^-, \cdots , B_{2l+1}^-, D_0, D_1, \cdots , D_l$ 是相互独立的参数, 依据(2.26) 式和(2.28) 式, 以及(2.2) 式和(2.13) 式, 我们只需要证明下式成立:

$\begin{equation} \det\frac{\partial(B_{l+1}^+, B_{l+2}^+, \cdots , B_{2l+1}^+)}{\partial(A_1^+, A_3^+, \cdots , A_{2l+1}^+)}=\det({\cal D})\neq0, \end{equation}$

(2.30)

其中

${\cal D}= \left(\begin{array}{cccccc} A_{l+1} &{ }\sum\limits_{r=0}^1 C_l^r 2^r A_{l+1-r} & { }\sum\limits_{r=0}^2 C_l^r 2^r A_{l+1-r} &\cdots &{ }\sum\limits_{r=0}^l C_l^r 2^r A_{l+1-r} \\ A_{l+2} &{ }\sum\limits_{r=0}^1 C_l^r 2^r A_{l+2-r} & { }\sum\limits_{r=0}^2 C_l^r 2^r A_{l+2-r} &\cdots &{ }\sum\limits_{r=0}^l C_l^r 2^r A_{l+2-r} \\ A_{l+3} &{ }\sum\limits_{r=0}^1 C_l^r 2^r A_{l+3-r} &{ } \sum\limits_{r=0}^2 C_l^r 2^r A_{l+3-r} &\cdots &{ }\sum\limits_{r=0}^l C_l^r 2^r A_{l+3-r} \\ \vdots &\vdots &\vdots &\ddots &\vdots \\ A_{2l+1} &{ }\sum\limits_{r=0}^1 C_l^r 2^r A_{2l+1-r} & { }\sum\limits_{r=0}^2 C_l^r 2^r A_{2l+1-r} &\cdots &{ }\sum\limits_{r=0}^l C_l^r 2^r A_{2l+1-r} \end{array}\right).$

我们对矩阵 $D$ 做以下初等变换:

(1) 用 $-C_{j-1}^{i-1}$ 乘第 $i$ 列加到第 $j$ 列, $j=i+1, \; i+2, \cdots, \; l+1, \; i=1, \; 2, \cdots, \; l;$

(2) 第 $i$ 列除以 $\frac{1}{2^{i-1}}, \ \ i=1, \; 2, \cdots, \; l+1;$

(3) 第 $i$ 列乘以 $\frac{1}{2^{l+2-i}}, \ \ i=1, \; 2, \cdots, \; l+1;$

(4) 第 $i$ 行乘以 $\frac{1}{2^{i-1}}, \ \ i=1, \; 2, \cdots, \; l+1$ .

那么, 矩阵 $D$ 可化为矩阵 $\tilde{D}$ :

$\tilde{D}= \left(\begin{array}{cccccc} { }\frac{A_{l+1}}{2^{l+1}} &{ }\frac{A_l}{2^l} &{ }\frac{A_{l+1}}{2^{l-1}} &\cdots &{ }\frac{A_1}{2}\\ { }\frac{A_{l+2}}{2^{l+2}} &{ }\frac{A_{l+1}}{2^{l+1}} &{ }\frac{A_{l}}{2^{l}} &\cdots &{ }\frac{A_2}{2^2}\\ { }\frac{A_{l+3}}{2^{l+3}} &{ }\frac{A_{l+2}}{2^{l+2}} &{ }\frac{A_{l+3}}{2^{l+1}} &\cdots &{ }\frac{A_3}{2^3}\\ \vdots &\vdots &\vdots &\ddots &\vdots\\ { }\frac{A_{2l+1}}{2^{2l+1}} &{ }\frac{A_{2l}}{2^{2l}} &{ }\frac{A_{2l-1}}{2^{2l-1}} &\cdots &{ }\frac{A_{l+1}}{2^{l+1}} \end{array}\right)=\left(\begin{array}{cccccc} \tilde{A}_{l+1} &\tilde{A}_{l} &\tilde{A}_{l-1} &\cdots &\tilde{A}_{1}\\ \tilde{A}_{l+2} &\tilde{A}_{l+1} &\tilde{A}_{l} &\cdots &\tilde{A}_{2}\\ \tilde{A}_{l+3} &\tilde{A}_{l+2} &\tilde{A}_{l+1} &\cdots &\tilde{A}_{3}\\ \vdots &\vdots &\vdots &\ddots &\vdots\\ \tilde{A}_{2l+1} &\tilde{A}_{2l} &\tilde{A}_{2l-1} &\cdots &\tilde{A}_{l+1} \end{array}\right),$

其中

$\tilde{A}_i=\frac{1}{2}, \; \tilde{A}_i=(-1)^{i-1}\frac{\prod \limits_{r=0}^{i-2}(2r+1)}{\prod \limits_{r=0}^{i-1}(2r+2)}, \ \ i\geq 2.$

在引理2.7中, 令 $s=l+1, t=1, k_1=1.k_2=2, k=2$ 和 $\tau=1$ , 那么, 我们有

$\det(\tilde{{\cal D}})=\det({\cal D}_{l+1, l}(1, 2, 2, 1))\neq0.$

因此(2.30) 式恒成立. 从而(2.25) 式, (2.27) 式, (2.29) 式中的系数

$B_0^+, B_1^+, \cdots, B_{2l+1}^+, B_0^-, B_1^-, \cdots, B_{2l+1}^-, D_0, D_1, \cdots, D_l$

能够当作自由参数. 注意到 $l=2k$ , 对以上参数可选择满足如下

$\begin{eqnarray*} 0&<&B_0^-\ll B_0^+ \ll D_0 \ll B_1^- \ll B_1^+ \ll D_1 \ll \cdots \ll B_{2k-1}^- \ll B_{2k-1}^+ \ll D_{2k-1} \\ &\ll &B_{2k}^- \ll B_{2k}^+ \ll D_{2k} \ll -B_{2k+1}^- \ll B_{2k+1}^+ \ll B_{2k+2}^+ \ll -B_{2k+2}^- \ll -B_{2k+3}^- \\ &\ll&\cdots \ll -B_{4k-2}^- \ll -B_{4k-1}^- \ll B_{4k-1}^+ \ll B_{4k}^+ \ll -B_{4k}^- \ll -B_{4k+1}^- \ll B_{4k+1}^+ \ll 1. \end{eqnarray*}$

这意味着(2.25) 式, (2.27) 式, (2.29) 式中的函数 $\frac{M^+(h)}{\sqrt{2h+1}}$ , $\frac{M^-(h)}{\sqrt{2h+1}}$ , $\frac{M(h)}{\sqrt{2h+1}}$ , 其符号分别改变了如下次数：

$4k+1+1, \ \ 4k+1, \ \ 4k+1+2k+1,$

则其总体改变了次数如下

$3(4k+1)+2k+1+1=3m+[\frac{m+1}{2}]+1.$

所以, 再根据隐函数定理, 微分系统(1.2) 在广义双同宿环附近可分支出 $3m+[\frac{m+1}{2}]+1$ 个极限环. 对其他情况, 可类似证明. 定理1.1证毕.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

di Bernardo M, Budd C J, Champneys A R, Kowalczyk P. Piecewise Smooth Dynamical Systems, Theory and Applications. London: Springer-Verlag, 2008

[本文引用: 1]

[2]

Budd C J. Non-smooth dynamical systems and the grazing bifurcation//Aston P J. Nonlinear Mathematics and Its Applications. Cambridge: Cambridge University Press, 1996: 219-235

[3]

Filipov A F. Differential equations with discontionuous righthand sides. Netherlands: Kluwer Academic, 1988

[本文引用: 2]

[4]

Hilbert

Mathematical Problems

Bull Amer Math, 1902, 8: 437- 479

DOI:10.1090/S0002-9904-1902-00923-3 [本文引用: 1]

[5]

, Zhang

The sliding bifurcations in planar piecewise sooth differential systems

J Dyn Diff Equa, 2013, 25: 1001- 1026

DOI:10.1007/s10884-013-9327-0 [本文引用: 1]

[6]

Dankowicz

, Nordmark

A B

On the origin and bifurcations of stick-slip oscillations

Physica D, 2000, 136: 280- 302

DOI:10.1016/S0167-2789(99)00161-X

[7]

Feigin

M I

Doubling of the oscillation period with C-bifurcations in piecewise-continuous systems

J Appl Math Mech, 1970, 34: 822- 830

DOI:10.1016/0021-8928(70)90064-X [本文引用: 1]

[8]

Liu

, Han

Bifurcation of limit cycles by perturbing piecewise Hamiltonian systems

Internat J Bifur Chaos, 2010, 5: 1- 12

[本文引用: 1]

[9]

Xiong

, Han

Limit cycle bifurcations in a class of perturbed piecewise smooth systems

Applied Mathematics and Computation, 2014, 242: 47- 64

DOI:10.1016/j.amc.2014.05.035 [本文引用: 2]

[10]

Liang

, Han

, Romanovskic

V G

Bifurcation of limit cycles by perturbing a piecewise linear Hamiltonian system with a homoclinic loop

Nonlinear Analysis, 2012, 75: 4355- 4374

DOI:10.1016/j.na.2012.03.022 [本文引用: 1]

[11]

, Du

Bifurcation of periodic orbits emanated from a vertex in discontinuous planar systems

Commun Nonlinear Sci Numer Simulat, 2013, 18: 3436- 3448

DOI:10.1016/j.cnsns.2013.05.012 [本文引用: 2]

[12]

Xiong

, Han

Limit cycle bifurcations in discontinuous planar systems with multiple lines

Journal of Applied Analysis and Computation, 2020, 10: 361- 377

DOI:10.11948/20190274 [本文引用: 2]

... 近年来, 控制理论、电路原理、医学和生物学等许多学科中的问题都得用不连续的微分方程来模拟, 使得此类微分方程受到广泛关注^[1-3]. 而分支问题是微分方程定性理论所要考虑的重要问题之一, 这也与著名的Hilbert第16问题的第二部分密切相关^[4]. 因此, 建立研究不连续微分系统分支理论的方法是非常有实际意义的. ...

...

$F^{\pm}(x, y), G^{\pm}(x, y)$

都是

$C^{\infty}$

上的函数. 系统(1.1) 在

$y$

轴上的非光滑性产生了许多在光滑情况下不可能发生的复杂的行为, 如滑动同宿分支、滑膜振荡等^{[3, 5-7]}. 文献[8] 给出了研究微分系统(1.1) 极限环分支问题的广义的首阶Melnikov函数的公式, 之后相关学者利用此种方法对特定的微分系统(1.1) 进行研究, 研究其Hopf分支、同宿分支、异宿分支及Poincaré 分支等^{[9, 10]}. 最近, 文献[11] 把微分系统(1.1) 的切换线推广到从原点出发的任意条射线, 并获得首阶Melnikov的表达式, 此公式对任意条平行直线也成立^[12]. ...

Mathematical Problems

1902

The sliding bifurcations in planar piecewise sooth differential systems

2013

...

$F^{\pm}(x, y), G^{\pm}(x, y)$

都是

$C^{\infty}$

上的函数. 系统(1.1) 在

$y$

On the origin and bifurcations of stick-slip oscillations

2000

Doubling of the oscillation period with C-bifurcations in piecewise-continuous systems

1970

...

$F^{\pm}(x, y), G^{\pm}(x, y)$

都是

$C^{\infty}$

上的函数. 系统(1.1) 在

$y$

Bifurcation of limit cycles by perturbing piecewise Hamiltonian systems

2010

...

$F^{\pm}(x, y), G^{\pm}(x, y)$

都是

$C^{\infty}$

上的函数. 系统(1.1) 在

$y$

Limit cycle bifurcations in a class of perturbed piecewise smooth systems

2014

...

$F^{\pm}(x, y), G^{\pm}(x, y)$

都是

$C^{\infty}$

上的函数. 系统(1.1) 在

$y$

... 从文献[9, 引理3.1]可发现,

$\det({\cal D}_0)\neq0$

. 因此, 可以从(2.22) 式可得结论成立. 证毕. ...

Bifurcation of limit cycles by perturbing a piecewise linear Hamiltonian system with a homoclinic loop

2012

...

$F^{\pm}(x, y), G^{\pm}(x, y)$

都是

$C^{\infty}$

上的函数. 系统(1.1) 在

$y$

Bifurcation of periodic orbits emanated from a vertex in discontinuous planar systems

2013

...

$F^{\pm}(x, y), G^{\pm}(x, y)$

都是

$C^{\infty}$

上的函数. 系统(1.1) 在

$y$

... 根据文献[11, 12], 相对应于上面三簇周期轨道, 分别有如下首阶Melnikov函数 ...

Limit cycle bifurcations in discontinuous planar systems with multiple lines

2020

...

$F^{\pm}(x, y), G^{\pm}(x, y)$

都是

$C^{\infty}$

上的函数. 系统(1.1) 在

$y$

... 根据文献[11, 12], 相对应于上面三簇周期轨道, 分别有如下首阶Melnikov函数 ...

〈

〉