1 引言
研究优化问题的另一种方法是基于等价鞅测度和鞅表示定理的鞅方法. Ye[7]考虑了具有随机寿命的最优人寿保险, 消费和投资组合选择问题, 并用鞅方法进行了求解. Michelbrink和Le[8]使用鞅方法研究了跳-扩散模型下使消费和终端财富的预期效用最大化的最优投资-消费策略, 并获得了幂和对数效用函数情形下最优策略的显式解. Kwak等[9]探讨了一个家庭的最优投资, 消费和人寿保险购买问题, 利用鞅方法找到了价值函数和最优策略的显式解. Liang和Guo[10]研究了不完备市场中工资型企业的最优保险消费投资问题, 利用鞅方法得到了最优策略. Guambe和Kufakunesu[11]研究了当投资者受限于资本担保时的最优投资, 消费和人寿保险问题, 并得到了幂效用函数下的最优策略的显式解.
2 模型
令
该文假定
在保险市场中, 令
其中
假设一职员在退休时间
且
在死亡时刻
定义准则函数
其中
令
其中
值函数定义为
由
其中
3 最优解的一般形式
令
对
其是下面方程的解
且
(3.4)式被称为鞅条件, 关于鞅条件的详细讨论可参见文献[17]. 由Girsanov定理, 有
是测度
是
其中
定义3.1[12, 定义1] 若(3.7)式的解存在且与(2.10) 式的解吻合, 则称
下面讨论优化问题(2.10)的对偶问题
利用Lagrange乘子
等号成立当且仅当
对任意
并假定
定理3.1 若(3.10)式有解, 则(3.8)和(3.7)式有解. 用
证 考虑函数
当
由于
下面证明对
当
4 效用函数为 U(x)=\ln(x), x>0
假设职员的效用函数为
其中
将(4.1)式代入(4.2)式可得
解该方程得到
其中
由
将(4.6)式代入(4.5)式可得
将(4.1)式代入(2.7)式可得
比较(4.7)和(4.8)式中
可验证当
将(4.1)式代入(3.8)式可得
其中
因此, 只需计算
其中
由(4.10)式可得
将(4.15)和(4.16)式代入(4.11)式可得
令
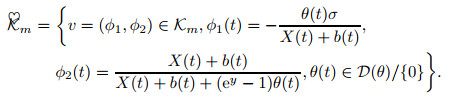
问题(4.14)可表示为
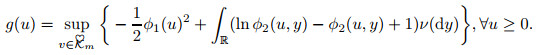
定理4.1 对
其中
最优保险、消费和投资策略为
其中
5 效用函数为 U(x)=-\frac{1}{\alpha}\exp\{-\alphax\}, \alpha>0
本节讨论效用函数为指数效用函数时(2.10)的解, 即
对(3.9)式, 由一阶条件
其中
将(5.1)式代入(5.3)式可得
由Bayes'公式, (3.5)式和(3.6)式可得
其中
将(5.4)式代入(5.3)式可得
其中
另一方面
将(5.1)式代入上面的方程可得
比较(5.6)式和(5.8)式中
可验证
其是
将(5.13)式代入(5.11)式可得
定理5.1 对
最优保险、消费和投资策略为
其中
其中
6 效用函数为 U(x)=\beta\frac{x^{\gamma}}{\gamma}, \beta>0, \gamma\neq0, \gamma<1
假设职员的效用函数为幂效用函数, 即
其中
其中
对
其中
另一方面
比较(6.3)和(6.4)式中
可验证鞅条件(3.4)满足. 将(6.1)式代入(3.8)式可得
等价于
对
其中
令
定理6.1 对
最优保险、消费和投资的最优策略为
其中
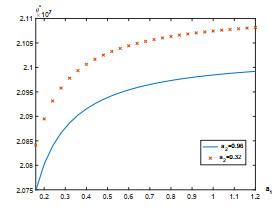
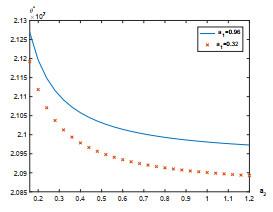
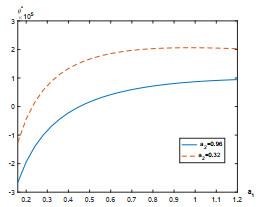
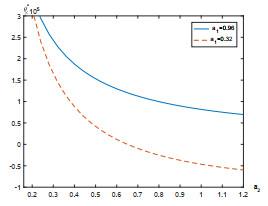
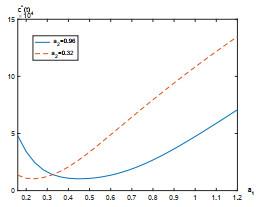
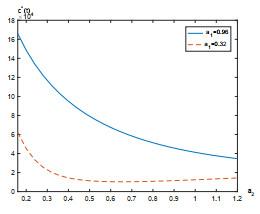
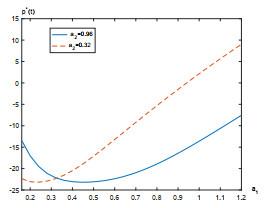
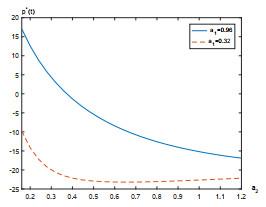
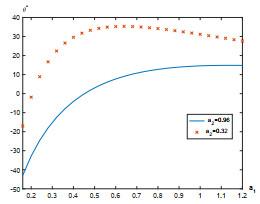
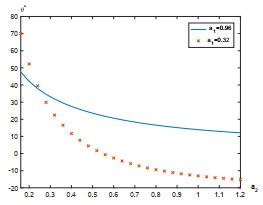
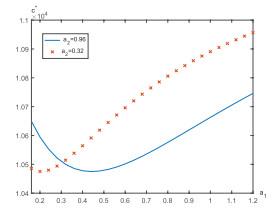
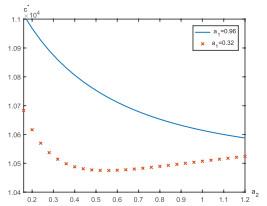
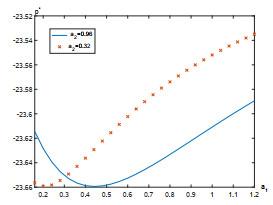
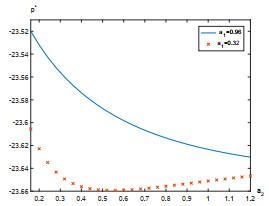
7 数值实例
本节给出一个数值例子来研究股票价格的跳如何影响最优策略. 假设Lévy测度
假设职员年龄为25, 她/他将在
图 1
图 2
图 3
图 4
图 5
图 6
图 7
图 8
图 9
图 10
图 11
图 12
图 13
图 14
参考文献
Optimal consumption, portfolio and life insurance rules for an uncertain lived individual in a continuous time model
DOI:10.1016/0304-405X(75)90004-5 [本文引用: 1]
Lifetime portfolio selection under uncertainty: the continuous time case
Optimal consumption and portfolio rules in a continuous-time model
DOI:10.1016/0022-0531(71)90038-X [本文引用: 1]
Optimal life insurance purchase and consumption/investmet under uncertain lifetime
DOI:10.1016/j.jbankfin.2006.10.015 [本文引用: 1]
Portfolio choice and life insurance: the CRRA case
Optimal life-insurance selection and purchase within a market of several life-insurance providers
DOI:10.1016/j.insmatheco.2016.01.002 [本文引用: 1]
A martingale approach to optimal portfolios with jump-diffusions
DOI:10.1137/100784412 [本文引用: 1]
Optimal investment and consumption decision of a family with life insurance
DOI:10.1016/j.insmatheco.2010.10.012 [本文引用: 1]
Optimal investment, consumption, and life insurance in an incomplete market
DOI:10.1080/03610926.2014.911907 [本文引用: 1]
Optimal investment-consumption and life insurance with capital constraints
DOI:10.1080/03610926.2018.1549246 [本文引用: 1]
Consumption and portfolio policies with incomplete markets and short-sale constraints: the infinite dimensional case
DOI:10.1016/0022-0531(91)90123-L [本文引用: 2]
Martingale and duality methods for utility maximization in an incomplete market
Minimax and minimal distance martingale measures and their relationship to portfolio optimization
DOI:10.1007/s007800100052 [本文引用: 1]
A predictable decomposition in an infinite assets model with jumps. Application to hedging and optimal investment
DOI:10.1080/104511203100001621237 [本文引用: 1]