1 引言
数学模型在研究传染病的传播规律和预防控制方面起着重要的作用. 在疾病的传播过程中, 病原体不仅可以通过飞沫、血液、接触、虫媒等方式在生物体之间进行传播, 也可以在环境中长期存在(如霍乱弧菌, 新型冠状病毒等), 一旦有生物体接触也会被感染. 因此, 在传染病的数学建模中, 考虑病原体在环境与生物体之间传播是十分有必要的[1, 2]. 此外, 随着世界经济, 文化的交流日益增多, 人们的流动越来越频繁, 这为传染病的跨区域传播提供了"肥沃的土壤". 从数学建模的角度, 众多国内外学者建立并讨论了各类具有反应扩散的传染病模型[3−5]. 特别地, Dwyer[6]提出了如下生物体具有反应扩散而环境病原体不具有反应扩散的传染病模型
基于上述讨论, 本文提出一类具有水平传播和环境传播的反应扩散传染病模型, 讨论模型解的适定性, 疾病的持久性与灭绝性等阈值动力学行为.
2 模型建立与解的适定性
令
满足Neumann边界条件
记
根据文献[9, 推论7.2.3] 可知,
其中
这里
引理2.1 对于任意初值函数
证 由文献[10, 推论4], 只需证明, 对于任意
事实上, 对于任意
故当
为讨论模型(2.1) 全局正解的存在性, 我们考虑下面的反应扩散模型
关于模型(2.3) 的动力学行为, 直接应用文献[11, 定理3.15和3.16], 有下面的结论.
引理2.2 对于任意
直接应用文献[12, 引理1], 关于反应扩散模型
稳态解的存在性与稳定性, 我们有下面的引理
引理2.3 假设
定理2.1 对于任意初值函数
证 令
和初值条件
因此对于充分大的
根据(2.6) 式, 存在
3 基本再生数
模型(2.1) 的稳态解满足如下椭圆方程
且满足Neumann边界条件
且满足Neumann边界条件
假设模型(3.3) 有形如
且满足Neumann边界条件
引理3.1 特征值问题(3.4) 有一主特征值
记
由文献[13, 定理3.12] 容易知道
引理3.2 设
为得到基本再生数
引理3.3 设
的主特征值, 则
证 令
其中
所以
即
因此,
从引理3.3可知,
注3.1 当模型(2.1) 的所有参数都是常数时, 易得
4 阈值动力学
定理4.1 若
证 对于
有一主特征值
由引理3.2可知当
对于任意
满足Neumann边界条件
因为
证毕.
由于模型(2.1) 没有考虑感染宿主具有生殖能力, 当宿主感染疾病后, 宿主只能通过死亡或恢复离开感染仓室, 宿主种群规模在减少, 基于生物背景, 提出如下假设
为了证明模型(2.1) 的一致持续性, 我们先证明下面的引理.
引理4.1 设模型(2.1) 满足初值条件
证 首先证明(ⅰ). 令
下证(ⅱ). 由(2.1) 的第二个方程可知
矛盾. 因此, 结论(ⅱ) 成立. 证毕.
定理4.2 若
证 令
令
如果
另一方面, 由引理3.2可知, 当
的主特征值且有一强正特征值
下证
(ⅰ) 若
且满足Neumann边界条件
记
满足Neumann边界条件
因为
(ⅱ) 若
定义
由
定义一个连续函数
显然,
由文献[19, 定理4.7] 知
5 数值模拟
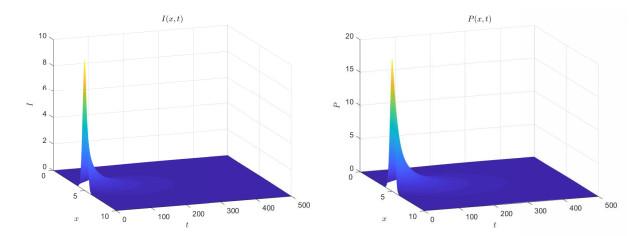
固定参数
图 1
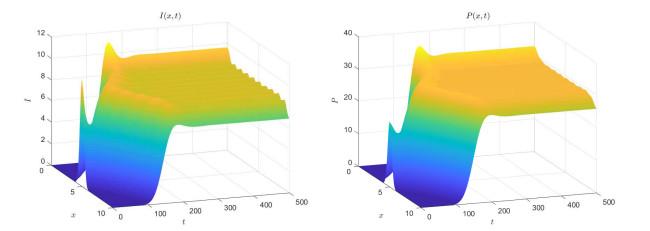
进一步, 选取参数
图 2
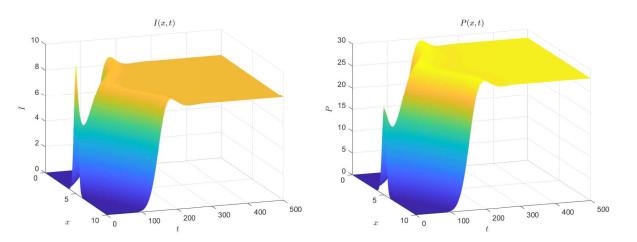
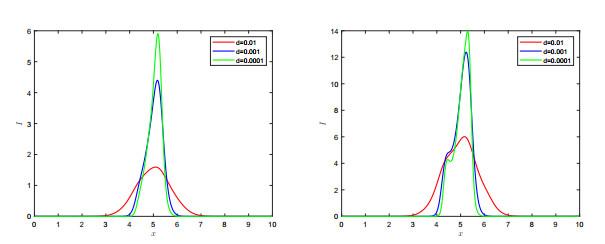
此外, 如果选取
图 3
图 4
6 结论与展望
本文建立并分析了一类具有空间异质性的反应扩散传染病模型, 这里假设宿主具有Logistic增长, 病毒不仅可以在宿主和环境之间传播, 也可以宿主之间传播(水平传播). 首先将模型转化为对应的积分方程得到了全局正解的存在性与唯一性(引理2.1和定理2.1). 进一步, 利用下一代算子方法得到基本再生数
由于考虑到空间异质性, 本文并没有给出地方病稳态解的精确表达式. 同时, 在模型(2.1) 中也假设宿主和病原体具有相同的扩散速率, 这在证明解的最终有界性起到重要的作用. 但在现实生活中, 易感宿主, 感染宿主和病原体可能以不同的速率扩散, 因此考虑不同的扩散速率更能反映实际情况. 这些都是值得进一步研究的课题.
参考文献
考虑部分免疫和环境传播的麻疹传染病模型的全局稳定性
DOI:10.3969/j.issn.1003-3998.2019.04.018 [本文引用: 1]
Global stability of a measles epidemic model with partial immunity and environmental transmission
DOI:10.3969/j.issn.1003-3998.2019.04.018 [本文引用: 1]
Dynamics of indirectly transmitted infectious diseases with immunological threshold
DOI:10.1007/s11538-008-9384-4 [本文引用: 1]
On a vector-host epidemic model with spatial structure
DOI:10.1088/1361-6544/aae1e0 [本文引用: 1]
Analysis of a reaction-diffusion cholera model with distinct dispersal rates in the human population
DOI:10.1007/s10884-019-09820-8
一类非局部时滞的SVIR反应扩散模型的全局吸引性
DOI:10.3969/j.issn.1003-3998.2021.06.023 [本文引用: 1]
Global attractivity of a nonlocal delayed and diffusive SVIR model
DOI:10.3969/j.issn.1003-3998.2021.06.023 [本文引用: 1]
Density dependence and spatial structure in the dynamics of insect pathogens
Dynamics and profiles of a diffusive host-pathogen system with distinct dispersal rates
DOI:10.1016/j.jde.2017.12.027 [本文引用: 1]
Analysis of a reaction-diffusion host-pathogen model with horizontal transmission
DOI:10.1016/j.jmaa.2019.123481 [本文引用: 1]
Monotone Dynamical Systems: An Introduction to the Theory of Competitive and Cooperative Systems
Abstract functional differential equations and reaction-diffusion systems
A reaction-diffusion malaria model with incubation period in the vector population
DOI:10.1007/s00285-010-0346-8 [本文引用: 1]
Spectral bound and reproduction number for infinite-dimensional population structure and time heterogeneity
DOI:10.1137/080732870 [本文引用: 2]
Basic reproduction number for reaction-diffusion epidemic models
DOI:10.1137/120872942 [本文引用: 4]
Convergence results and a Poincare-Bendixson trichotomy for asymptotically autonomous differential equations
On a system of reaction-diffusion equations arising from competition with internal storage in an unstirred chemostat
DOI:10.1016/j.jde.2009.12.014 [本文引用: 1]
Robust persistence for semidynamical systems
DOI:10.1016/S0362-546X(01)00678-2 [本文引用: 3]
Global attractors and steady states for uniformly persistent dynamical systems
DOI:10.1137/S0036141003439173 [本文引用: 1]