1 引言
设
矩阵
2010年, Baksalary和Trenkler[12]提出Core逆的概念: 设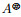
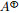
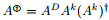
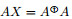
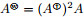
在弱群逆, 弱Core逆研究的基础上, 本文引入新的广义逆, 研究它的性质刻画和应用. 本文结构如下, 在第二节, 我们基于Moore-Penrose逆和弱Core逆提出Moore-Penrose弱Core逆(MPWC逆)的概念, 分别从代数和几何角度给出其刻画, 并研究MPWC逆与非奇异加边矩阵之间的关系. 在第三节中, 我们应用Hartwig-Spindelböck分解和Core-EP分解给出MPWC逆的分解形式. 并给出
2 MPWC逆
在本节, 基于Moore-Penrose逆和弱Core逆, 从代数角度引出MPWC逆的概念.
定理2.1 设
有唯一解
证 令
下面证明解的唯一性. 设
定义2.1 设
注2.1 由
注2.2 因为
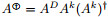
下面, 我们用一个具体的例子来说明MPWC逆和其他广义逆的区别.
例2.1 设
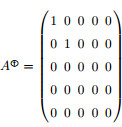
定理2.2 设
证 由
于是
所以
所以
从而
所以
下面, 我们给出矩阵的MPWC逆的若干等价刻画.
定理2.3 设
证
注2.3 观察上面定理可以发现
下面, 我们研究
称之为
定理2.4 设
证 因为
和
令
从而
故
在下面的定理中,我们从另一个角度刻画MPWC逆.
定理2.5 设
有唯一解
证 令
若
于是
接下来我们给出
定理2.6 设
证
众所周知, 广义逆可以表示为具有给定值域和零空间的一种特殊的外逆. 接下来, 我们将给出MPWC逆的类似刻画.
定理2.7 设
证 由于
故
于是得
下面, 我们给出MPWC逆与非奇异加边矩阵之间的关系.
定理2.8 设
是非奇异的, 且
证 由
设
可得
类似地可以验证
下面我们利用
定理2.9 设
有唯一解
证 如果
定理2.10 设
给出, 其中
证 由于
由定理2.8, 可以得到
因此有
3 MPWC逆的两种标准型及其应用
在本节中, 我们通过矩阵分解给出了MPWC逆的两种标准形式, 并将其用于研究
其中
和
通过
定理3.1 设
其中
证 设
由
由于
(3.5)式左乘
故
(3.5)式左乘
由
可以写成
因此, 可得
于是
下面我们利用Core-EP分解[33], 给出
和
故
其中
众所周知, 如果
为了得到MPWC逆的一个类似表示形式, 我们对奇异矩阵
引理3.3[34] 设
定理3.2 设
存在唯一的矩阵
和唯一的矩阵
此时, 有
证 假设
满足(3.10)式中所有等式. 下面证明解的唯一性. 设
从而可以得到
所以
类似地, 我们可以验证
满足(3.11)式中所有等式. 其中
下面证明
其中
由
又因为
其中
于是由
因为
于是
从而由引理3.3可以得到
下面我们给出MPWC逆的扰动分析.
定理3.3 设

进一步有,
证 设
于是
可得
其中

又由
参考文献
Generalized inverse of a matrix and its applications
Linearized bregman iterations for compressed sensing
DOI:10.1090/S0025-5718-08-02189-3 [本文引用: 1]
On the reciprocal of the general algebraic matrix
A generalized inverse for matrices
DOI:10.1017/S0305004100030401 [本文引用: 1]
Matrices for which A* and A† commmute
DOI:10.1080/03081088308817561 [本文引用: 3]
A Family of higher-order convergent iterative methods for computing the Moore-Penrose inverse
Representations of the Moore-Penrose inverse of 2 × 2 block operator valued matrices
Natural structures on semigroups with involution
DOI:10.1090/S0002-9904-1978-14442-5 [本文引用: 1]
Pseudo-inverses in associative rings and semigroups
DOI:10.1080/00029890.1958.11991949 [本文引用: 1]
Core inverse of matrices
DOI:10.1080/03081080902778222 [本文引用: 2]
Characterizations of the core inverse and the core partial ordering
DOI:10.1080/03081087.2014.975702 [本文引用: 1]
Characterizations and representations of the core inverse and its applications
DOI:10.1080/03081087.2019.1588847 [本文引用: 1]
On a new generalized inverse for matrices of an arbitrary index
Core-EP inverse
DOI:10.1080/03081087.2013.791690 [本文引用: 1]
On a new generalized inverse of matrices
DOI:10.1080/03081087.2017.1336200 [本文引用: 1]
The DMP inverse for rectangular matrices
DOI:10.2298/FIL1719015M [本文引用: 1]
Revisiting the core EP inverse and its extension to rectangular matrices
DOI:10.2989/16073606.2017.1377779
Representations and properties of the W-weighted core-EP inverse
DOI:10.1080/03081087.2018.1535573
Further results on weighted core-EP inverse of matrices
DOI:10.1007/s00025-020-01296-z
The CMP inverse for rectangular matrices
Characterizations and representations for the CMP inverse and its application
DOI:10.1080/03081087.2021.1907275
New characterizations of the CMP inverse of matrices
DOI:10.1080/03081087.2018.1518401 [本文引用: 1]
Weak group inverse
DOI:10.1515/math-2018-0100 [本文引用: 1]
Representations for the weak group inverse
DOI:10.1016/j.amc.2021.125957 [本文引用: 1]
Further characterizations of the weak group inverse of matrices and the weak group matrix
DOI:10.3934/math.2021542 [本文引用: 1]
A weak group inverse for rectangular matrices
Weighted weak group inverse for Hilbert space operators
DOI:10.1007/s11464-020-0847-8 [本文引用: 1]
The weak core inverse
DOI:10.1007/s00010-020-00752-z [本文引用: 6]
Expressions and properties of weak core inverse
DOI:10.1016/j.amc.2021.126704 [本文引用: 1]
Weighted weak core inverse of operators
DOI:10.1080/03081087.2021.1902462 [本文引用: 1]
Core-EP decomposition and its applications
DOI:10.1016/j.laa.2016.08.008 [本文引用: 2]
On one-sided (B, C)-inverses of arbitrary matrices
DOI:10.13001/1081-3810.3487 [本文引用: 1]
A note on Rao and Mitra's constrained inverse and Drazin's (b, c) inverse
DOI:10.1016/j.laa.2017.02.025 [本文引用: 1]
Maximal classes of matrices determining generalized inverses


