1 引言
麻疹、肺结核、艾滋病等许多传染病的感染者在疾病发展的某个阶段会呈现与年龄相关联的特征, 这是影响疾病传播的重要因素之一. 麻疹是由麻疹病毒引起的呼吸道传染病, 病毒存在于患者口、鼻、咽、眼结合膜分泌物内, 通过喷嚏、咳嗽和说话等由飞沫传播, 传染性极强, 易感者接触后其发病率可高达95% 以上, 通常发病年龄为1–5周岁, 约占总发病数的80% 左右. 目前避免发病传染最有效的办法是接种疫苗, 接种疫苗后7–12天就可产生抗体, 比直接感染后产生抗体的时间短, 因此对易感者进行应急接种可控制疫情蔓延或终止流行. 国内规定初种年龄为8个月左右, 但仍有10%–30% 的人群接种后其免疫力随时间的推移而逐年下降最后成为易感者[1, 2]. 麻疹潜伏期多为7–14天, 最长可达21天.麻疹痊愈与患者年龄有关, 患者痊愈后, 由于防护不力会感染麻疹病毒而再次发病. 麻疹主要是在儿童间发生的传染病, 故年龄特征在麻疹传染病的传播动力学中扮演着非常重要的角色. 近年来研究麻疹疾病的文章已有许多, 如姜翠翠等[3]对具有部分免疫和潜伏期的麻疹传染病模型的稳定性进行了分析; 佘文兵[4]建立了一类具有接种的麻疹模型; 靖晓洁等[5]考虑了部分免疫和环境传播的麻疹传染病模型的全局稳定性; Huang等[6]考虑了一个有周期性传播率的麻疹模型, 并分析其动力学行为, 提高了人们对麻疹的认识; Zhou等[7]验证了具有年龄结构的离散型SIR流行病模型的稳定性, 并将这些理论结果应用在麻疹疫苗的接种策略中. 然而考虑年龄结构的麻疹传染病模型的研究工作相对较少, 故建立疾病接种、复发的年龄结构麻疹模型, 并对其动力学性质进行研究有一定的理论意义和实际应用价值.
本文内容安排如下: 在第2节, 建立了一类年龄结构的麻疹传染病动力学模型; 在第3节, 讨论模型解的适定性; 在第4节, 证明疾病的一致持续性; 在第5节, 建立平衡态的局部和全局稳定性的判别准则; 在第6节, 给出数值例子和模拟; 最后, 第7节是一个简短的总结.
2 模型的建立
结合上述麻疹的主要传播特征和机理, 我们建立一类具有接种、复发的年龄结构SVEIR麻疹传染病模型. 将人群分为互不重合的五类, 设
其中
(A) 函数
3 解的适定性
模型(2.1) 的相空间定义为
此范数表示各仓室人口总和. 模型(2.1) 解的初始值为
由文献[8]可知模型(2.1) 在时刻
进一步, 给出如下记号:
由假设(A) 可以推出
另外, 对任意复数
当
可知
将模型(2.1) 的第1、3、4方程和式(3.2)、(3.3) 放在一起,则模型(2.1) 被表示为所谓的Volterra型积分方程.
定义集合
有如下结果.
定理3.1
证 对任意初值
那么从模型(2.1) 可得
由此进一步得到
当
进一步由式(3.4) 得知, 对任意
由定理3.1, 根据半流定义, 模型(2.1) 的解
引理3.1 设常数
证 若
定义3.1[10] 对任意非空有界闭集
引理3.2[10] 对于解半流
则解半流
下面我们将使用引理3.2来证明模型(2.1) 的解半流
于是对任意
命题3.1 设
证 显然对任何
注意到对任意
命题3.1得证.
为了验证引理3.2的条件
引理3.3[11] 常数
则
命题3.2 对任意
证 对任意常数
注意到式(3.1) 以及引理3.1的结论(ⅰ) 可以得到:
下面证明条件(ⅰ) 成立, 对充分小的
其中
于是最终得到
由此进一步得到:
由命题3.1、命题3.2和引理3.2, 最终得到如下结论:
定理3.2 由模型(2.1) 生成的解半流
作为定理3.2的结论, 我们得到关于模型(2.1) 全局吸引子存在性的结论.
推论3.1 模型(2.1) 生成的解半流
证 由定理3.2, 模型的解半流
4 疾病的一致持续性
定义集合
我们有
参考文献[13], 模型(2.1) 的基本再生数
可将上式写为
其中
显然, 模型(2.1) 总有无病平衡点
引理4.1 若
证 首先由
若结论不成立, 则存在模型(2.1) 的解
其中
由此, 对任意
参考文献[14]中年龄依赖偏微分方程的比较原理, 对于所有
其中
且满足初始条件
由系统(4.3) 的第3个方程我们得
将系统(4.3) 的第一个方程和(4.4) 代入(4.3) 的第二个方程可得
由此得到系统(4.3) 的特征方程为
显然
其中
对任何
定理4.1 如果
证 由引理3.1, 存在常数
考虑下述比较系统
它具有全局渐近稳定的平衡点
对于任意初值
设
接下来证明
显然, 由系统(4.8) 得到
由
由模型(2.1) 解半流
5 平衡点的稳定性
定理5.1 如果
证 令
设
求解(5.3), (5.6) 式后同(5.4) 式一起代入(5.2) 和(5.5)式中联立可得
由于
由于
并且
于是如果
假设
并且
则有
定理5.2 如果
证 选择Lyapunov函数如下
这里
由于
因此
其中
由于
定理5.3 如果
证 令
设
求解(5.9) 和(5.12) 式后, 将其代入其他方程联立可得
由于
假设方程(5.13) 有一个根
则产生矛盾. 则(5.13) 式的所有特征根具有严格负实部, 即
定理5.4 如果
证 选择Lyapunov函数如下
其中
由于
和
由此可得
其中
因此有
其中等号成立当且仅当
6 数值模拟
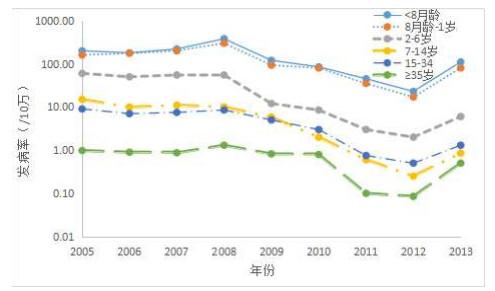
图 1
(1) 假设中国人的平均寿命为840月(70年), 故死亡率
(2) 使用最小二乘法拟合数据得到参数
(3) 选择模型参数
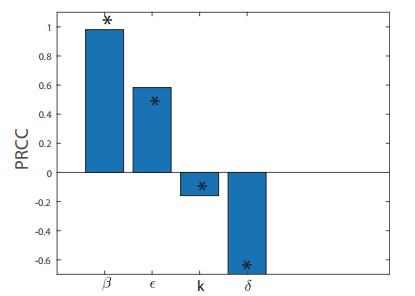
基本再生数是决定疾病是否流行的重要指标. 本文所建立模型的基本再生数
偏置相关系数(PRCC) 已被广泛用于分析参数的敏感性, 由
图 2
取
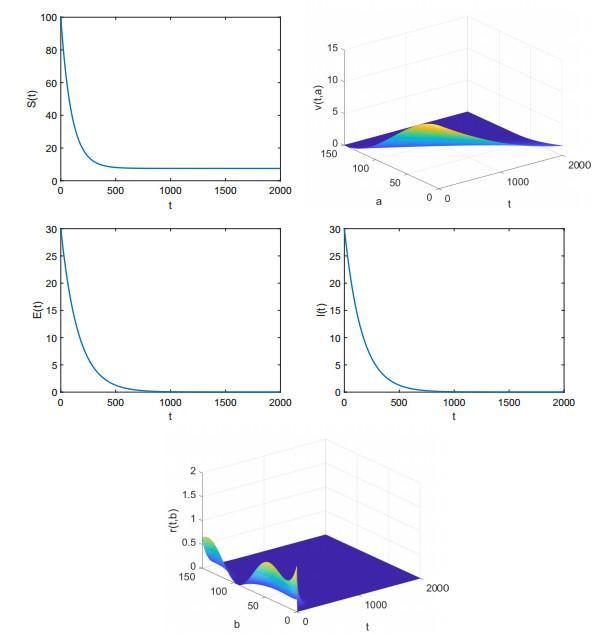
图 3
图 3
取
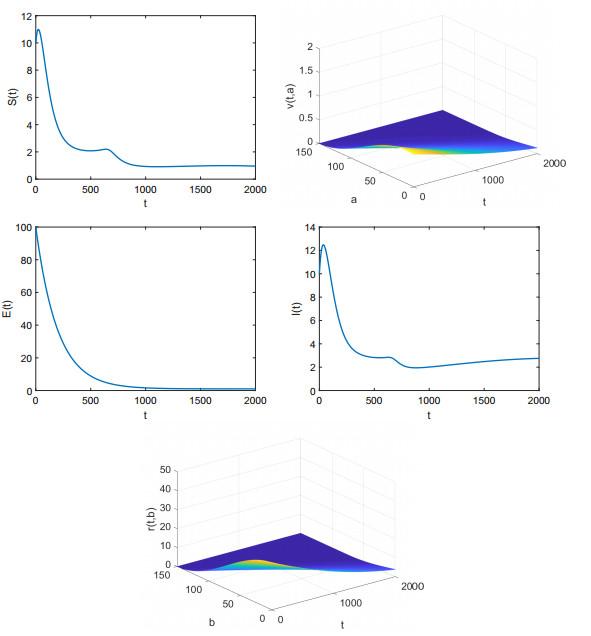
图 4
图 4
取
7 结论
本文建立了一类具有接种和复发的年龄结构SVEIR麻疹传染病模型. 计算得到模型的基本再生数为
参考文献
麻疹流行病学研究现状
DOI:10.3969/j.issn.1006-1533.2011.08.010 [本文引用: 1]
Status of epidemiology of measles
DOI:10.3969/j.issn.1006-1533.2011.08.010 [本文引用: 1]
考虑部分免疫和潜伏期的麻疹传染病模型的稳定性分析
Stability analysis of a measles epidemic model with partial immunity and latency
一类具有接种的麻疹模型的动力学分析
On dynamical analysis of a measles model with vaccination
考虑部分免疫和环境传播的麻疹传染病模型的全局稳定性
DOI:10.3969/j.issn.1003-3998.2019.04.018 [本文引用: 1]
Global stability of a measles epidemic model with partial immunity and environmental transmission
DOI:10.3969/j.issn.1003-3998.2019.04.018 [本文引用: 1]
Seasonal transmission dynamics of measles in China
DOI:10.1007/s12064-018-0271-8 [本文引用: 1]
Global dynamics of a discrete age-structured SIR epidemic model with applications to measles vaccination strategies
Persistence in infinite-dimensinal systems
On the definition and the couputation of the basic reproduction ratioin models for infectious diseases in heterogeneous populations
Comparison principles and Lipschitz regularity for some nonlinear degenerate elliptic equations
Global stability for an SEI model of infectious disease with immigration
中国2010年麻疹流行病学特征与消除麻疹进展
Measles epidemiological characteristics and progress of measles elimination in China, 2010
Global stability of an epidemic model with ages of vaccination and latency
DOI:10.1016/j.camwa.2014.06.002 [本文引用: 1]
Global stability of an epidemic model with age-dependent vaccination, latent and relapse
DOI:10.1016/j.chaos.2017.10.027
一类具有年龄结构的传染病模型的持续性质
DOI:10.3969/j.issn.1000-4424.2007.03.001 [本文引用: 1]
Disease persistence for a kind of age-structured epidemic models
DOI:10.3969/j.issn.1000-4424.2007.03.001 [本文引用: 1]