1 引言
设
其中映射
其中映射
对于算法(1.2)–(1.4), 其步长
其中
这里映射
最近, Gibali等[13]给出了一种黏度投影算法, 在其算法中步长
Gibali等在映射
2 相关定义与引理
记
对于任意的
定义2.1[8] 设
则称
定义2.2 设
则称
引理2.1[2] 设
引理2.2[2] 设
引理2.3[14] 设
引理2.4[15] 设
其中
本文假设
3 算法与收敛性证明
设
算法3.1 选取初始点
步骤1 令
如果
步骤2 计算
其中
并计算
步骤3 计算
令
引理3.1 假设条件
证 该引理的证明与文献[12]中引理
引理3.2 设
证
类似可得
因此
故
注3.1 由引理
引理3.3 假设条件
证 由
上式等价于
即
因为
注意到
由于
结合
下证
由于
上式等价于
下证
又因为
所以
又由
即
定理3.1 假设条件
证 该定理的证明分为以下六步进行.
第一步 首先证明
事实上
由
由此可得
第二步 证明序列
注意到
因为
由
另一方面
将
因此,
第三步 证明
其中
记
则
由
又由
其中
上式等价于
其中
第四步 证明
事实上
结合
上式等价于
又由引理
故
由
再由
第五步 证明
其中
另一方面
由
第六步 证明序列
情形1 若存在
这就意味着
又因为
另一方面,
由
又由于
同理, 因为
故由引理
因此
最后由引理
情形2 若存在序列
在这种情况下, 由引理
则由
因此
类似于情形
以及
联立
由此可得
故由
再由
注3.2 定理
注3.3 定理
4 数值实验
例1 设
范数
令
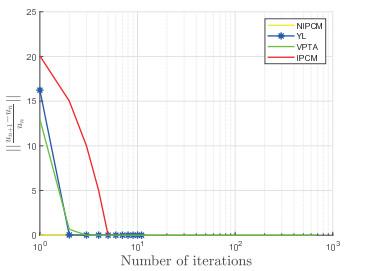
表 1 改变初始值取值
| Iter | Time | Iter | Time | Iter | Time | |||
| NIPCM | 6 | 0.0429 | 8 | 0.0535 | 7 | 0.0427 | ||
| VPTA | 33 | 0.0238 | 125 | 0.1098 | 78 | 0.0573 | ||
| Y.L | 340 | 0.0437 | 340 | 0.0319 | 340 | 0.0525 | ||
| IPCM | 533 | 0.0567 | 533 | 0.0612 | 533 | 0.0633 | ||
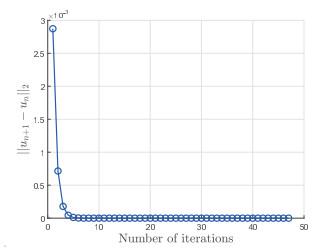
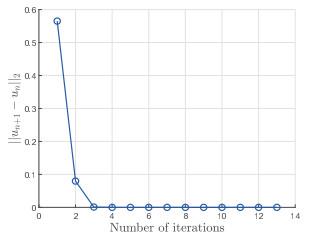
图 1
图 2
图 3
图 4
图 5
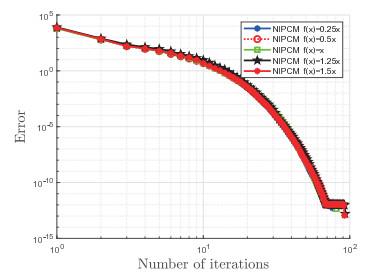
例2 设算子
其中
其中
表 2 改变终止条件精度
| Iter | Time | Iter | Time | Iter | Time | Iter | Time | ||||
| NIPCM | 32 | 0.7108 | 61 | 1.1787 | 79 | 1.4880 | 88 | 2.1495 | |||
| VTPA | 40 | 9.0375 | 40 | 10.3125 | 40 | 10.8281 | 40 | 9.8906 | |||
| Y.L | 64 | 3.2096 | 66 | 2.4719 | 69 | 3.3800 | 68 | 2.9023 | |||
| IPCM | - | - | - | - | |||||||
图 6
注4.1 从数值实验的结果来看, 我们有如下结论:
参考文献
A class of projection and contraction methods for monotone variational inequalities
DOI:10.1007/s002459900037 [本文引用: 1]
On the O(1/t) convergence rate of the projection and contraction methods for variational inequalities with Lipschitz continuous monotone operators
The subgradient extragradient method for solving variational inequalities in Hilbert space
A modified forward-backward splitting method for maximal monotone mappings
Complementarity problems over cones with monotone and pseudo-monotone maps
DOI:10.1007/BF00932654 [本文引用: 2]
The extragradient method for finding saddle points and other problems
Inertial projection and contraction algorithms for variational inequalities
DOI:10.1007/s10898-017-0506-0 [本文引用: 2]
New strong convergence theorem of the inertial projection and contraction method for variational inequality problems
DOI:10.1007/s11075-019-00755-1 [本文引用: 8]
Strong convergence result for solving monotone variational inequalities in Hilbert space
DOI:10.1007/s11075-018-0504-4 [本文引用: 4]
Two simple projection-type methods for solving variational inequalities
DOI:10.1007/s13324-019-00330-w [本文引用: 6]
A hybrid extragradient-viscosity method for monotone operators and fixed point problems
DOI:10.1137/060675319 [本文引用: 1]
Iterative algorithms for nonlinear operators
DOI:10.1112/S0024610702003332 [本文引用: 1]