1 引言
孤立子波在光波散射、流体力学、激波、场论、神经网络、量子力学中都有很广泛的应用[1-8].近来,相关学者已经研究了许多求解孤立子波的方法.例如:齐次平衡法、辅助方程法、双曲函数法、椭圆函数法、(G'/G)展开法、Riccati函数法、符号计算法等[9-13].当前, 求解非线性问题的方法已不断深化.很多科学研究者, 例如Abid等[14], Hovhannisyan等[15], Recke等[16]和Graef等[17]讨论了有关非线性问题.研究者也对一类非线性问题的激波、孤波、激光脉冲和大气物理等方面的模型作了讨论[18-29].本文是涉及近代物理中的一个被广泛重视的非线性NNV (Nizhnik-Novikov-Veselov)动力系统微分模型, 利用了有效而简捷的泛函分析广义变分迭代方法得到了系统模型的孤立子波渐近行波解.这种方法具有广泛的应用前景.
上式中
先对模型(1.1)–(1.2)作如下行波变换
上式中
2 典型非线性动力系统模型
现先考虑系统(1.4)–(1.5)中的扰动项
由(2.1)–(2.2)式得到
上式中
再用双曲函数待定系数法来求得方程(2.3)的孤立子波解.设
上式中
将(2.5)–(2.7)式代入(2.3)式, 合并同类项并令对应项系数为零得
因此得到
由此便得到行波变换(1.3)为
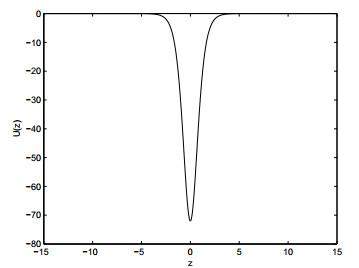
于是由(2.5)式, 得到系统(2.3)–(2.4)的一组孤立子波解
图 1
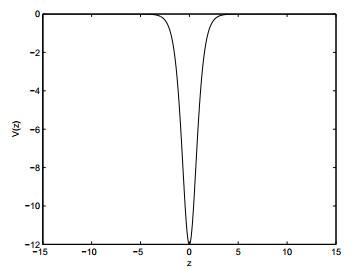
图 2
3 广义扰动动力系统(1.4)–(1.5)渐近解
在上一节中, 我们是对典型非线性NNV系统模型求出了其行波解.现在用泛函分析广义变分法来构造非线性扰动动力系统(1.4)–(1.5)的渐近解.
计算泛函(3.1)–(3.2)的广义变分
显然由(3.3)–(3.4)式有
其中
由(3.1)–(3.5)式, 构造系统(1.4)–(1.5)孤立子波渐近解的迭代关系式(
上式中
现取孤立子波渐近解的初始迭代为系统(1.4)–(1.5)的一组孤立子波解(2.9)–(2.10).即
由迭代式(3.8), (3.9), 取
4 例子
考虑如下的一个特殊的动力系统模型
由(3.10)–(3.11)式, 动力系统(4.1)–(4.2)的一个孤立子波渐近解的初始近似
用泛函分析广义变分迭代法,由(3.8)–(3.9)式可得动力系统模型(4.1)–(4.2)孤立子波渐近解的一次渐近解
上式中
再由迭代式(3.8)–(3.9)和(4.5)–(4.6), 可得到系统模型(4.1)–(4.2)的一组孤立子波的二阶渐近解
上式中
由(2.8)式利用行波变换式
上式中
5 结论
广义泛函分析变分迭代法求扰动动力系统模型的孤立子波的渐近解是一个简捷有效的方法.由它得到的渐近解不同于简单的离散数值解.因为它还可以进行解析运算,它还可继续对模型解作定性, 定量的分析.例如通过广义扰动动力系统模型的孤立子波的渐近解, 进行某些微分,积分等解析运算,可以得到其它相关的物理量,从而扩大了对相应物理量的研究范围.另外,本文选取初始近似是用非扰动情形下的典型系统的孤立子波解.它决定了广义扰动动力系统模型比较快地得对应的孤立子波在所要求的精度范围内的渐近解析解.
参考文献
Slowdown of the meridional overturning circulation in the upper Pacific ocean
Interdecadal climate fluctuations that depend on exchanges between the tropics and extratropics
(2+1)维Boiti-Leon-Pempinelli系统的混沌行为及孤立子波间的相互作用
The interaction between solitons and chaotic behaviours of (2+1)-dimensional Boiti-Leon-Pempinelli system
The variable coefficient Hele-Shaw problem, integrability and quadrature identities
Low-frequency nonlinear stationary waves and fast shocks: hydrodynamical description
DOI:10.1063/1.872681
Some periodic and solitary travelling-wave solutions of the short-pulse equation
DOI:10.1016/j.chaos.2006.10.055
Landau-Ginzburg-Higgs方程的微扰理论
The theory of the perturbation for Landau-Ginzburg-Higgs equation
一般变换下双Jacobi椭圆函数展开法及应用
DOI:10.3321/j.issn:1000-3290.2006.08.012 [本文引用: 1]
Double Jacobian elliptic function expansion method under a general function transform and its applications
DOI:10.3321/j.issn:1000-3290.2006.08.012 [本文引用: 1]
(3+1)维Burgers系统的新精确解及其特殊孤立子波结构
New exact solutions and special soliton structures for the (3+1)-dimensional Burgers system
(G'/G)展开法和(2+1)维非对称Nizhnik-Novikov-Veselov系统的新精确解
DOI:10.3321/j.issn:1000-3290.2009.07.001 [本文引用: 1]
(G'/G)-expansion method and new exact solutions for (2+1)-dimensional asymmetrical Nizhnik-Novikov-Veselov system
DOI:10.3321/j.issn:1000-3290.2009.07.001 [本文引用: 1]
(2+1)维孤立子波系统的多孤立子波解和分形结构
DOI:10.7498/aps.59.7540 [本文引用: 1]
Multi-soliton solutions and fractal structures in a (2+1)-dimensional soliton system
DOI:10.7498/aps.59.7540 [本文引用: 1]
一类广义Boussinesq方程和Boussinesq-Burgers方程新的显式精确解
DOI:10.3321/j.issn:1000-3290.2007.04.005
New explicit exact solutions of one type of generalized Boussinesq equations and the Boussinesq-Burgers equation
DOI:10.3321/j.issn:1000-3290.2007.04.005
Gerdjikov-Ivanov方程的精确解
DOI:10.3321/j.issn:1000-3290.2008.04.008 [本文引用: 1]
Exact solutions of Gerdjikov-Ivanov equation
DOI:10.3321/j.issn:1000-3290.2008.04.008 [本文引用: 1]
Weak solutions of quasilinear biharmonic problems with positive, increasing and convex nonlinearities
DOI:10.1142/S0219530508001134 [本文引用: 1]
Stability inequalities for one-dimensional singular perturbation problems
Boundary layer solutions to problems with infinite-dimensional singular perturbations
Solutions of second order multi-point boundary value problems
DOI:10.1017/S0305004108001424 [本文引用: 1]
Singular perturbation for a class of nonlinear reaction diffusion systems
Asymptotic solution for a class of sea-air oscillator model for El-Nino-southern oscillation
Asymptotic solution of activator inhibitor systems for nonlinear reaction diffusion equations
Perturbed solving method for interdecadal sea-air oscillator model
Variational iteration solvi ng method for a class of generalized Boussinesq equation
DOI:10.1088/0256-307X/26/6/060202
Homotopiv mapping solving method for gain fluency of a laser pulse amplifier
Variational iteration solution of a sea-air oscillator model for the ENSO
DOI:10.1080/10020070612331343252
一类尘埃等离子体孤子解
Solitary wave solution for a class of dusty plasma
广义扰动Nizhnik-Novikov-Veselov系统的孤波解的孤波解
The solutions to solitary wave for generalized disturbed Nizhnik-Novikov-Veselov system
一类广义鸭轨迹系统轨线的构造
Constructing path curve for a class of generalized phase tracks of canard system
一类厄尔尼诺海-气时滞振子的渐近解
A class of asymptotic solution of sea-air time delay oscillator for the El Nino-southern oscillation mechanism
Solving a class of burning disturbed problem with shock layer
DOI:10.1088/1674-1056/21/5/050203 [本文引用: 1]
Variational iteration method–a kind of nonlinear analytical technique: Some examples
DOI:10.1016/S0020-7462(98)00048-1 [本文引用: 3]